2025年中考数学复习--板块五 规律探究(含答案)
文档属性
| 名称 | 2025年中考数学复习--板块五 规律探究(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 419.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
板块五 规律探究
专题突破 1 等差、等比规律
典例精讲
类型一 等差数列
【例1】 (2024 德阳)将一组数. n,…,按如图方式进行排列,则第八行左起第1个数是( )
A.7
类型二 等比数列
【例2】 (2024广安)如图,直线 与x 轴相交于点 A ,以OA 为边作等边△OA B ,点 B 在第一象限内,过点 B 作x轴的平行线与直线l交于点A ,与y轴交于点C ,以C A 为边作等边△C A B (点B 在点 B 的上方),以同样的方式依次作等边△C A B ,等边△C A B ,…,则点A 的横坐标为 .
典题精练
1.(2023重庆)用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,…,按此规律排列下去,则第⑧个图案用的木棍根数是( )
A.39 B.44 C.49 D.54
2.(2024江岸区)如图,在平面直角坐标系中,点 A ,A ,A ,…是x轴正半轴上的点,且 分别过点 A ,A ,A ,…,作 y轴平行线交双曲线 于点 B ,B ,B ,…,则△A B B 的面积是( )
A. /n B. /n
专题突破2 一般规律
典例精讲
类型一 平方规律
【例】 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3 开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5);(7,10);(13,17);(21,26);(31,37);….如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律,则第n个数对为 .
典题精练
类型二 斐波那契数列
1.斐波那契数列指的是这样一列数:1,1,2,3,5,8,…(从第3个数起,每个数是前面两数的和),如图,用以这些数为边长的正方形拼成长方形,再以这些数为边长的正方形中作出圆心角为90°的圆弧,则接下来一段圆弧对应的扇形面积是( )
B.16π
类型三 裂项规律
2.如图,将形状、大小完全相同的“·”和线段按照一定规律摆成以下图形.第1幅图形中“·”的个数为a ,第2幅图形中“·”的个数为a ,第3幅图形中“·”的个数为a ,…,以此类推,那么 的值为( )
A. B .
类型四 周期规律
3.(2024江汉区)在平面直角坐标系中有三个点A(1,-1),B(--1,-1),C(0,1),点 P(0,2)关于A的对称点为 P ,P 关于B 的对称点 P ,P 关于C的对称点为 P ,按此规律继续以A,B,C为对称中心重复前面的操作,依次得到P ,P ,P ,…,则点 P 的坐标是 .
专题突破3 实践操作
典例精讲
类型一 图形分析
【例】 (2024武汉中考)如图,小好同学用计算机软件绘制函数 的图象,发现它关于点(1,0)中心对称.若点 A (0.1,y ),A (0.2,y ),A (0.3,y ),…,A (1.9,y ),A (2,y ):都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则 的值是( )
A. -1 B. -0.729 C.0 D.1
典题精练
类型二 逻辑推理
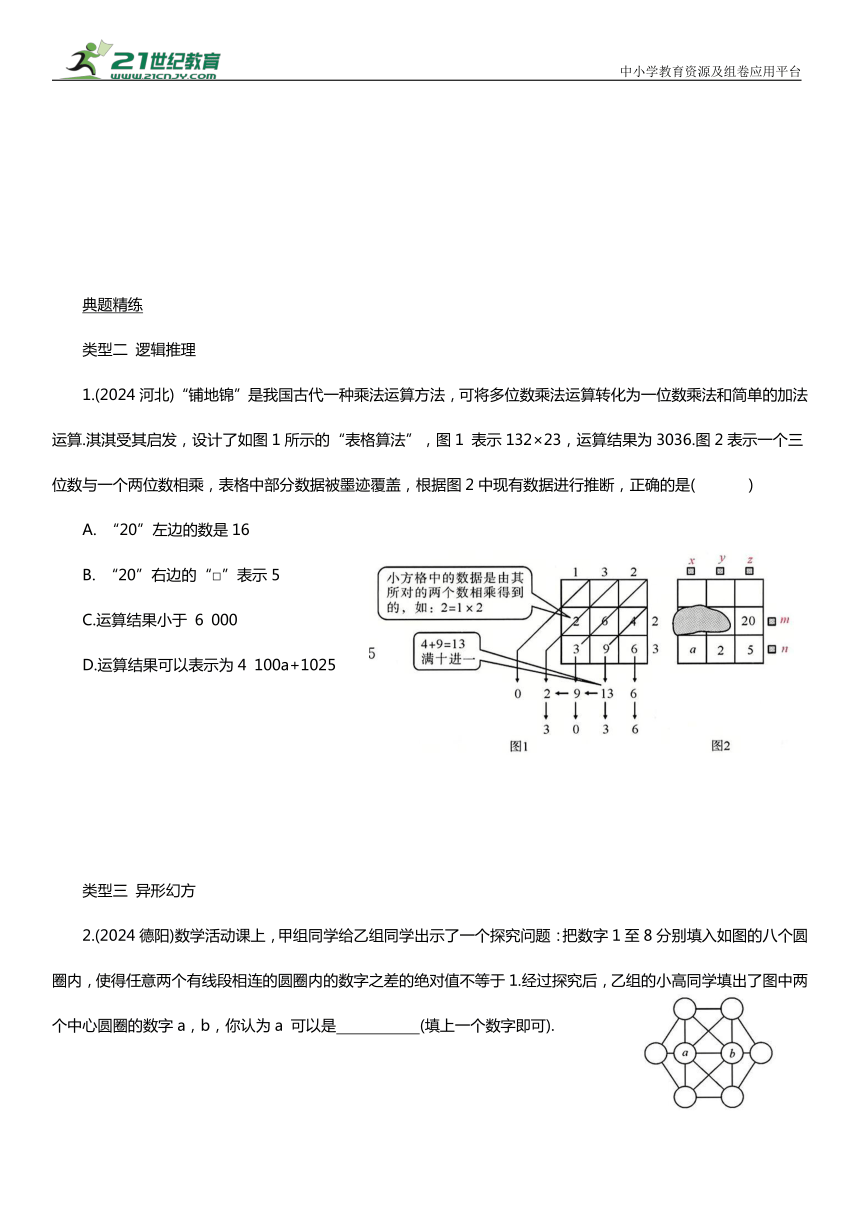
1.(2024河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1 表示132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( )
A. “20”左边的数是16
B. “20”右边的“□”表示5
C.运算结果小于 6 000
D.运算结果可以表示为4 100a+1025
类型三 异形幻方
2.(2024德阳)数学活动课上,甲组同学给乙组同学出示了一个探究问题:把数字1至8分别填入如图的八个圆圈内,使得任意两个有线段相连的圆圈内的数字之差的绝对值不等于1.经过探究后,乙组的小高同学填出了图中两个中心圆圈的数字a,b,你认为a 可以是 (填上一个数字即可).
板块五 规律探究
专题突破1 等差、等比规律
典例精讲
类型一 等差数列
【例1】 (2024 德阳)将一组数 n,…,按如图方式进行排列,则第八行左起第1个数是( C )
A.7
类型二 等比数列
【例2】 (2024广安)如图,直线 与x 轴相交于点A ,以 OA 为边作等边△OA B ,点 B 在第一象限内,过点 B 作x轴的平行线与直线l交于点A ,与y轴交于点C ,以C A 为边作等边△C A B (点B 在点 B 的上方),以同样的方式依次作等边△C A B ,等边△C A B ,…,则点A 的横坐标为
解:”
同理,A 的横坐标为
∴点 A 024 的横坐标为
1.(2023重庆)用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,…,按此规律排列下去,则第⑧个图案用的木棍根数是( B )
A.39 B.44 C.49 D.54
2.(2024江岸区)如图,在平面直角坐标系中,点A ,A ,A ,…是x轴正半轴上的点,且 分别过点 A ,A ,A ,…,作 y轴平行线交双曲线 于点 B ,B ,B ,…,则△A B B 的面积是( A )
A. /n B. /n
专题突破2 一般规律
典例精讲
类型一 平方规律
【例】 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5);(7,10);(13,17);(21,26);(31,37);….如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现… 37其中的规律,则第 n个数对为
解:由题知,第n个数对的第一个数为 第n 个数对的第二个数为( ∴第n个数对为( 故答案为
典题精练
类型二 斐波那契数列
1.斐波那契数列指的是这样一列数:1,1,2,3,5,8,…(从第3个数起,每个数是前面两数的和),如图,用以这些数为边长的正方形拼成长方形,再以这些数为边长的正方形中作出圆心角为90°的圆弧,则接下来一段圆弧对应的扇形面积是( C )
B.16π
类型三 裂项规律
2.如图,将形状、大小完全相同的“·”和线段按照一定规律摆成以下图形.第1幅图形中“·”的个数为a ,第2幅图形中“·”的个数为a ,第3幅图形中“·”的个数为a ,…,以此类推,那么 的值为( C )
A.
类型四 周期规律
3.(2024江汉区)在平面直角坐标系中有三个点A(1,--1),B(--1,-1),C(0,1),点 P(0,2)关于A的对称点为 P ,P 关于B 的对称点 P ,P 关于C的对称点为 P ,按此规律继续以A,B,C为对称中心重复前面的操作,依次得到 P ,P ,P ,…,则点 P 的坐标是 (0,2) .
解:P (2,-4),P (-4,2),P (4,0),P (-2,-2),P (0,0),P (0,2),P (2,-4),…,
∴每6个操作循环一次.∵2016÷6=336,∴点 P 的坐标与P。的坐标相同,即(0,2).
专题突破3 实践操作
典例精讲
类型一 图形分析
【例】 (2024武汉中考)如图,小好同学用计算机软件绘制函数 的图象,发现它关于点(1,0)中心对称.若点 A (0.1,y ),A (0.2,y ),A (0.3,y ),…,A (1.9,y ),A (2,y )都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则 的值是( D )
A. -1 B.-0.729 C.0 D.1
解:∵这20个点的横坐标从0.1开始依次增加0.1,. ),即y =0, 当x=2时,y =1, 故选 D.
典题精练
类型二 逻辑推理
1.(2024河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1 表示 132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( D )
A. “20”左边的数是 16
B. “20”右边的“□”表示5
C.运算结果小于 6 000
D.运算结果可以表示为4 100a+1025
解:设一个三位数与一个两位数分别为100x+10y+z 和10m+n,则由题意,得 mz=20,nz=5, ny=2, nx=a,∴∥x=4,即m=4n,
∴n=1,y=2,m=4,z=5,x=a,
∴“20”左边的数是2×4=8, “20”右边的“□”表示4,a 上面的数应为4a,
∴运算结果可以表示为1000(4a+1)+100a+25=4100a+1025,∴仅D选项符合题意.故选 D.
类型三 异形幻方
2.(2024德阳)数学活动课上,甲组同学给乙组同学出示了一个探究问题:把数字1至8分别填入如图的八个圆圈内,使得任意两个有线段相连的圆圈内的数字之差的绝对值不等于1.经过探究后,乙组的小高同学填出了图中两个中心圆圈的数字a,b,你认为a 可以是 1(或8) (填上一个数字即可).
解:∵a,b分别有6根连线,若填入2,3,4,5,6,7,其中任何一个数字,只剩下5个数字可选,不满足6个空的圆圈需要.∴a,b 只可能是1或者8.故答案为1(或8).
板块五 规律探究
专题突破 1 等差、等比规律
典例精讲
类型一 等差数列
【例1】 (2024 德阳)将一组数. n,…,按如图方式进行排列,则第八行左起第1个数是( )
A.7
类型二 等比数列
【例2】 (2024广安)如图,直线 与x 轴相交于点 A ,以OA 为边作等边△OA B ,点 B 在第一象限内,过点 B 作x轴的平行线与直线l交于点A ,与y轴交于点C ,以C A 为边作等边△C A B (点B 在点 B 的上方),以同样的方式依次作等边△C A B ,等边△C A B ,…,则点A 的横坐标为 .
典题精练
1.(2023重庆)用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,…,按此规律排列下去,则第⑧个图案用的木棍根数是( )
A.39 B.44 C.49 D.54
2.(2024江岸区)如图,在平面直角坐标系中,点 A ,A ,A ,…是x轴正半轴上的点,且 分别过点 A ,A ,A ,…,作 y轴平行线交双曲线 于点 B ,B ,B ,…,则△A B B 的面积是( )
A. /n B. /n
专题突破2 一般规律
典例精讲
类型一 平方规律
【例】 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3 开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5);(7,10);(13,17);(21,26);(31,37);….如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律,则第n个数对为 .
典题精练
类型二 斐波那契数列
1.斐波那契数列指的是这样一列数:1,1,2,3,5,8,…(从第3个数起,每个数是前面两数的和),如图,用以这些数为边长的正方形拼成长方形,再以这些数为边长的正方形中作出圆心角为90°的圆弧,则接下来一段圆弧对应的扇形面积是( )
B.16π
类型三 裂项规律
2.如图,将形状、大小完全相同的“·”和线段按照一定规律摆成以下图形.第1幅图形中“·”的个数为a ,第2幅图形中“·”的个数为a ,第3幅图形中“·”的个数为a ,…,以此类推,那么 的值为( )
A. B .
类型四 周期规律
3.(2024江汉区)在平面直角坐标系中有三个点A(1,-1),B(--1,-1),C(0,1),点 P(0,2)关于A的对称点为 P ,P 关于B 的对称点 P ,P 关于C的对称点为 P ,按此规律继续以A,B,C为对称中心重复前面的操作,依次得到P ,P ,P ,…,则点 P 的坐标是 .
专题突破3 实践操作
典例精讲
类型一 图形分析
【例】 (2024武汉中考)如图,小好同学用计算机软件绘制函数 的图象,发现它关于点(1,0)中心对称.若点 A (0.1,y ),A (0.2,y ),A (0.3,y ),…,A (1.9,y ),A (2,y ):都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则 的值是( )
A. -1 B. -0.729 C.0 D.1
典题精练
类型二 逻辑推理
1.(2024河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1 表示132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( )
A. “20”左边的数是16
B. “20”右边的“□”表示5
C.运算结果小于 6 000
D.运算结果可以表示为4 100a+1025
类型三 异形幻方
2.(2024德阳)数学活动课上,甲组同学给乙组同学出示了一个探究问题:把数字1至8分别填入如图的八个圆圈内,使得任意两个有线段相连的圆圈内的数字之差的绝对值不等于1.经过探究后,乙组的小高同学填出了图中两个中心圆圈的数字a,b,你认为a 可以是 (填上一个数字即可).
板块五 规律探究
专题突破1 等差、等比规律
典例精讲
类型一 等差数列
【例1】 (2024 德阳)将一组数 n,…,按如图方式进行排列,则第八行左起第1个数是( C )
A.7
类型二 等比数列
【例2】 (2024广安)如图,直线 与x 轴相交于点A ,以 OA 为边作等边△OA B ,点 B 在第一象限内,过点 B 作x轴的平行线与直线l交于点A ,与y轴交于点C ,以C A 为边作等边△C A B (点B 在点 B 的上方),以同样的方式依次作等边△C A B ,等边△C A B ,…,则点A 的横坐标为
解:”
同理,A 的横坐标为
∴点 A 024 的横坐标为
1.(2023重庆)用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,…,按此规律排列下去,则第⑧个图案用的木棍根数是( B )
A.39 B.44 C.49 D.54
2.(2024江岸区)如图,在平面直角坐标系中,点A ,A ,A ,…是x轴正半轴上的点,且 分别过点 A ,A ,A ,…,作 y轴平行线交双曲线 于点 B ,B ,B ,…,则△A B B 的面积是( A )
A. /n B. /n
专题突破2 一般规律
典例精讲
类型一 平方规律
【例】 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5);(7,10);(13,17);(21,26);(31,37);….如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现… 37其中的规律,则第 n个数对为
解:由题知,第n个数对的第一个数为 第n 个数对的第二个数为( ∴第n个数对为( 故答案为
典题精练
类型二 斐波那契数列
1.斐波那契数列指的是这样一列数:1,1,2,3,5,8,…(从第3个数起,每个数是前面两数的和),如图,用以这些数为边长的正方形拼成长方形,再以这些数为边长的正方形中作出圆心角为90°的圆弧,则接下来一段圆弧对应的扇形面积是( C )
B.16π
类型三 裂项规律
2.如图,将形状、大小完全相同的“·”和线段按照一定规律摆成以下图形.第1幅图形中“·”的个数为a ,第2幅图形中“·”的个数为a ,第3幅图形中“·”的个数为a ,…,以此类推,那么 的值为( C )
A.
类型四 周期规律
3.(2024江汉区)在平面直角坐标系中有三个点A(1,--1),B(--1,-1),C(0,1),点 P(0,2)关于A的对称点为 P ,P 关于B 的对称点 P ,P 关于C的对称点为 P ,按此规律继续以A,B,C为对称中心重复前面的操作,依次得到 P ,P ,P ,…,则点 P 的坐标是 (0,2) .
解:P (2,-4),P (-4,2),P (4,0),P (-2,-2),P (0,0),P (0,2),P (2,-4),…,
∴每6个操作循环一次.∵2016÷6=336,∴点 P 的坐标与P。的坐标相同,即(0,2).
专题突破3 实践操作
典例精讲
类型一 图形分析
【例】 (2024武汉中考)如图,小好同学用计算机软件绘制函数 的图象,发现它关于点(1,0)中心对称.若点 A (0.1,y ),A (0.2,y ),A (0.3,y ),…,A (1.9,y ),A (2,y )都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则 的值是( D )
A. -1 B.-0.729 C.0 D.1
解:∵这20个点的横坐标从0.1开始依次增加0.1,. ),即y =0, 当x=2时,y =1, 故选 D.
典题精练
类型二 逻辑推理
1.(2024河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1 表示 132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( D )
A. “20”左边的数是 16
B. “20”右边的“□”表示5
C.运算结果小于 6 000
D.运算结果可以表示为4 100a+1025
解:设一个三位数与一个两位数分别为100x+10y+z 和10m+n,则由题意,得 mz=20,nz=5, ny=2, nx=a,∴∥x=4,即m=4n,
∴n=1,y=2,m=4,z=5,x=a,
∴“20”左边的数是2×4=8, “20”右边的“□”表示4,a 上面的数应为4a,
∴运算结果可以表示为1000(4a+1)+100a+25=4100a+1025,∴仅D选项符合题意.故选 D.
类型三 异形幻方
2.(2024德阳)数学活动课上,甲组同学给乙组同学出示了一个探究问题:把数字1至8分别填入如图的八个圆圈内,使得任意两个有线段相连的圆圈内的数字之差的绝对值不等于1.经过探究后,乙组的小高同学填出了图中两个中心圆圈的数字a,b,你认为a 可以是 1(或8) (填上一个数字即可).
解:∵a,b分别有6根连线,若填入2,3,4,5,6,7,其中任何一个数字,只剩下5个数字可选,不满足6个空的圆圈需要.∴a,b 只可能是1或者8.故答案为1(或8).
同课章节目录
