新课标--立体几何理论知识总结
图片预览
文档简介
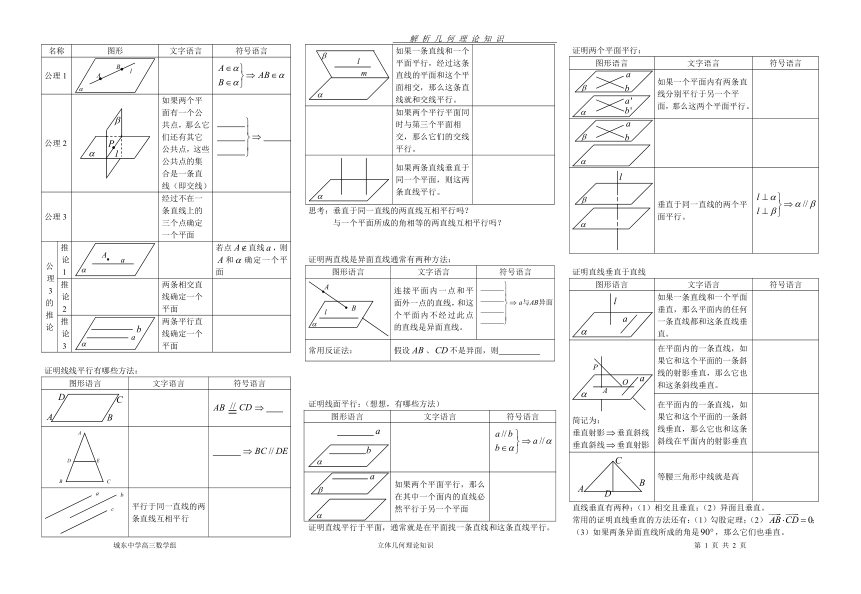
名称 图形 文字语言 符号语言
公理1
公理2 如果两个平面有一个公共点,那么它们还有其它公共点,这些公共点的集合是一条直线(即交线)
公理3 经过不在一条直线上的三个点确定一个平面
公理3的推论 推论1 若点直线,则和确定一个平面
推论2 两条相交直线确定一个平面
推论3 两条平行直线确定一个平面
证明线线平行有哪些方法:
图形语言 文字语言 符号语言
平行于同一直线的两条直线互相平行
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
如果两条直线垂直于同一个平面,则这两条直线平行。
思考:垂直于同一直线的两直线互相平行吗?
与一个平面所成的角相等的两直线互相平行吗?
证明两直线是异面直线通常有两种方法:
图形语言 文字语言 符号语言
连接平面内一点和平面外一点的直线,和这个平面内不经过此点的直线是异面直线。
常用反证法: 假设、不是异面,则
证明线面平行:(想想,有哪些方法)
图形语言 文字语言 符号语言
如果两个平面平行,那么在其中一个面内的直线必然平行于另一个平面
证明直线平行于平面,通常就是在平面找一条直线和这条直线平行。
证明两个平面平行:
图形语言 文字语言 符号语言
如果一个平面内有两条直线分别平行于另一个平面,那么这两个平面平行。
垂直于同一直线的两个平面平行。
证明直线垂直于直线
图形语言 文字语言 符号语言
如果一条直线和一个平面垂直,那么平面内的任何一条直线都和这条直线垂直。
简记为:垂直射影垂直斜线垂直斜线垂直射影 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直
等腰三角形中线就是高
直线垂直有两种:(1)相交且垂直;(2)异面且垂直。
常用的证明直线垂直的方法还有:(1)勾股定理;(2) ;
(3)如果两条异面直线所成的角是,那么它们也垂直。
证明平面垂直于平面:
图形语言 文字语言 符号语言
如果一个平面经过另一个平面的 ,那么这两个平面互相 。简记为“线面垂直面面垂直”
常用就只一种,记住它。
证明直线垂直于平面:
图形语言 文字语言 符号语言
如果两个平面互相垂直,那么在一个平面内 的直线垂直于另一个平面。
两条异面直线的距离公式:
图形语言 要结合图形帮助记忆本公式
根据、同侧异侧选择+、-
公式中永远是“+”符号。
以上三条公式选一条记忆。
空间两条直线的位置关系:
位置关系 公共点的个数
共面直线 相交直线 有且仅有一个公共点
平行直线 在 内,没有公共点
异面直线 不同在 平面内,没有公共点
空间直线与平面的关系:
位置关系 公共点个数
直线在平面内 直线上有 个点在平面内,则这条直线在平面内。
直线在平面外 直线和平面相交 直线与平面有且仅有 个公共点。
直线和平面平行 直线与平面 公共点,则称为平行。
其它一些公式:
图形语言 文字语言 符号语言
简单多面体的顶点数、棱数及面数间有关系
半径为的球的体积是 体积是3次方,面积是2次方,可以帮助记忆
半径为的球的面积是
棱柱的体积公式是
棱锥的体积公式是
正棱柱不仅要求底面是正多边形,还要求是直棱柱。
正棱柱的底面是正多边形,顶点在底面的射影是底面的中心,各侧棱均相等,但侧棱不需要等于底面边长。
知识的总结升华:
看图,你能理清下列关系吗?它们各是用什么定理推导的?
解 析 几 何 理 论 知 识
城东中学高三数学组 立体几何理论知识 第 1 页 共 2 页
公理1
公理2 如果两个平面有一个公共点,那么它们还有其它公共点,这些公共点的集合是一条直线(即交线)
公理3 经过不在一条直线上的三个点确定一个平面
公理3的推论 推论1 若点直线,则和确定一个平面
推论2 两条相交直线确定一个平面
推论3 两条平行直线确定一个平面
证明线线平行有哪些方法:
图形语言 文字语言 符号语言
平行于同一直线的两条直线互相平行
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
如果两条直线垂直于同一个平面,则这两条直线平行。
思考:垂直于同一直线的两直线互相平行吗?
与一个平面所成的角相等的两直线互相平行吗?
证明两直线是异面直线通常有两种方法:
图形语言 文字语言 符号语言
连接平面内一点和平面外一点的直线,和这个平面内不经过此点的直线是异面直线。
常用反证法: 假设、不是异面,则
证明线面平行:(想想,有哪些方法)
图形语言 文字语言 符号语言
如果两个平面平行,那么在其中一个面内的直线必然平行于另一个平面
证明直线平行于平面,通常就是在平面找一条直线和这条直线平行。
证明两个平面平行:
图形语言 文字语言 符号语言
如果一个平面内有两条直线分别平行于另一个平面,那么这两个平面平行。
垂直于同一直线的两个平面平行。
证明直线垂直于直线
图形语言 文字语言 符号语言
如果一条直线和一个平面垂直,那么平面内的任何一条直线都和这条直线垂直。
简记为:垂直射影垂直斜线垂直斜线垂直射影 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直
等腰三角形中线就是高
直线垂直有两种:(1)相交且垂直;(2)异面且垂直。
常用的证明直线垂直的方法还有:(1)勾股定理;(2) ;
(3)如果两条异面直线所成的角是,那么它们也垂直。
证明平面垂直于平面:
图形语言 文字语言 符号语言
如果一个平面经过另一个平面的 ,那么这两个平面互相 。简记为“线面垂直面面垂直”
常用就只一种,记住它。
证明直线垂直于平面:
图形语言 文字语言 符号语言
如果两个平面互相垂直,那么在一个平面内 的直线垂直于另一个平面。
两条异面直线的距离公式:
图形语言 要结合图形帮助记忆本公式
根据、同侧异侧选择+、-
公式中永远是“+”符号。
以上三条公式选一条记忆。
空间两条直线的位置关系:
位置关系 公共点的个数
共面直线 相交直线 有且仅有一个公共点
平行直线 在 内,没有公共点
异面直线 不同在 平面内,没有公共点
空间直线与平面的关系:
位置关系 公共点个数
直线在平面内 直线上有 个点在平面内,则这条直线在平面内。
直线在平面外 直线和平面相交 直线与平面有且仅有 个公共点。
直线和平面平行 直线与平面 公共点,则称为平行。
其它一些公式:
图形语言 文字语言 符号语言
简单多面体的顶点数、棱数及面数间有关系
半径为的球的体积是 体积是3次方,面积是2次方,可以帮助记忆
半径为的球的面积是
棱柱的体积公式是
棱锥的体积公式是
正棱柱不仅要求底面是正多边形,还要求是直棱柱。
正棱柱的底面是正多边形,顶点在底面的射影是底面的中心,各侧棱均相等,但侧棱不需要等于底面边长。
知识的总结升华:
看图,你能理清下列关系吗?它们各是用什么定理推导的?
解 析 几 何 理 论 知 识
城东中学高三数学组 立体几何理论知识 第 1 页 共 2 页
