第20章 数据的分析 单元练习题(含详解) 人教版八年级数学下册
文档属性
| 名称 | 第20章 数据的分析 单元练习题(含详解) 人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 148.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 08:38:34 | ||
图片预览



文档简介
人教版八年级数学下册《第20章数据的分析》单元同步练习题
一、选择题
1.测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时,出现了一处错误:将最高成绩写得更高了,计算结果不受影响的是( )
A.方差 B.标准差 C.中位数 D.平均数
2.在中考体育加试中,某班30名男生的跳远成绩如下表:
成绩/m 1.95 2.00 2.05 2.10 2.15 2.25
人数 2 3 9 8 5 3
这些男生跳远成绩的众数、中位数分别是( )
A.2.10,2.05 B.2.10,2.10 C.2.05,2.10 D.2.05,2.05
3.下列数据:75,80,85,85,85,则这组数据的众数和极差是( )
A.85,10 B.85,5 C.80,85 D.80,10
4.2016年6月4日﹣5日贵州省第九届“贵青杯”﹣“乐韵华彩”全省中小学生器乐交流比赛在省青少年活动中心举行,有45支队参赛,他们参赛的成绩各不相同,要取前23名获奖,某代表队已经知道了自己的成绩,他们想知道自己是否获奖,只需再知道这45支队成绩的( )
A.中位数 B.平均数 C.最高分 D.方差
5.张老师买了一辆启辰R50X汽车,为了掌握车的油耗情况,在连续两次加油时做了如下工作:(1)把油箱加满油;
(2)记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:
加油时间 加油量(升) 加油时的累计里程(千米)
2022年4月28日 18 6200
2022年5月16日 30 6600
则在这段时间内,该车每100千米平均耗油量为( )
A.3升 B.5升 C.7.5升 D.9升
6.某校九年级模拟考试中,1班的六名学生的数学成绩如下:96,108,102,110,108,82.下列关于这组数据的描述不正确的是( )
A.众数是108 B.中位数是105 C.平均数是101 D.方差是93
7.某校开设了艺术、体育、劳动、书法四门拓展性课程,要求每一位学生都要选且只能选一门课.小黄同学统计了本班50名同学的选课情况,并将结果绘制成条形统计图(如图,不完全),则选书法课的人数有( )
A.12名 B.13名 C.15名 D.50名
8.为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,得分情况如表所示:
得分 6 7 8 9 10
人数 4 10 15 11 10
则抽取的居民得分的平均数为( )
A.8 B.8.26 C.9.2 D.10
9.一组数据﹣3,3,﹣2,3,1的中位数是( )
A.﹣3 B.﹣2 C.1 D.3
10.小明把自己一周的支出情况用如图所示的统计图来表示,下面说法正确的是( )
A.从图中可以直接看出具体消费数额
B.从图中可以直接看出总消费数额
C.从图中可以直接看出各项消费数额占总消费数额的百分比
D.从图中可以直接看出各项消费数在一周中的具体变化情况
二、填空题
11.一组数据4,3,x,1,5的众数是5,则x= .
12.某班学生经常采用“小组合作学习”的方式进行学习,王老师每周对各小组合作学习的情况进行综合评分.下表是各小组其中一周的得分情况:
组别 一 二 三 四 五 六 七 八
得分 90 95 90 88 90 92 85 90
这组数据的众数是 .
13.某计算机程序第一次算得m个数据的平均数为x,第二次算得另外n个数据的平均数为y,则这(m+n)个数据的平均数等于 .
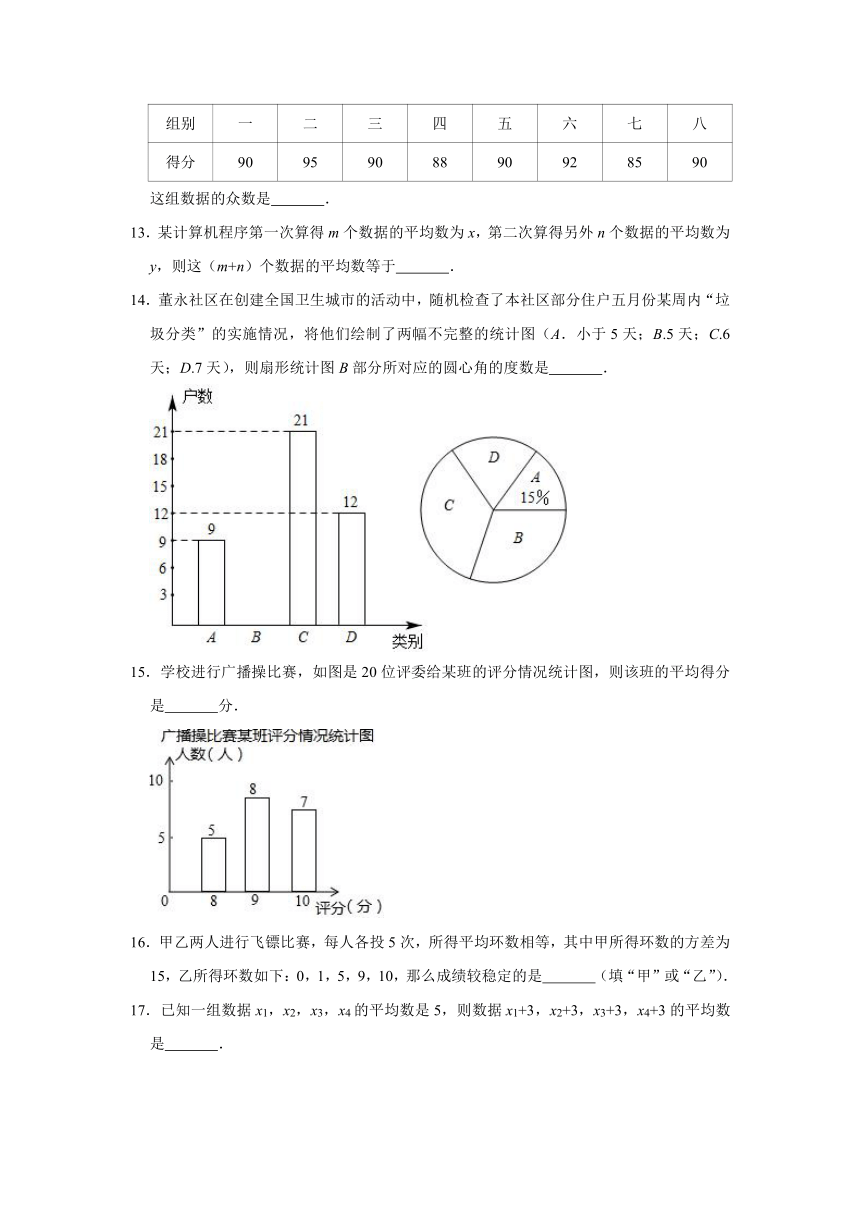
14.董永社区在创建全国卫生城市的活动中,随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况,将他们绘制了两幅不完整的统计图(A.小于5天;B.5天;C.6天;D.7天),则扇形统计图B部分所对应的圆心角的度数是 .
15.学校进行广播操比赛,如图是20位评委给某班的评分情况统计图,则该班的平均得分是 分.
16.甲乙两人进行飞镖比赛,每人各投5次,所得平均环数相等,其中甲所得环数的方差为15,乙所得环数如下:0,1,5,9,10,那么成绩较稳定的是 (填“甲”或“乙”).
17.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是 .
18.小明为了解所在小区居民各类生活垃圾的投放情况,他随机调查了该小区50户家庭某一天各类生活垃圾的投放量,统计得出这50户家庭各类生活垃圾的投放总量是100千克,并画出各类生活垃圾投放量分布情况的扇形图(如图所示),根据以上信息,估计该小区300户居民这一天投放的可回收垃圾共约 千克.
19.某班五个兴趣小组的人数分别为4,4,5,x,6.已知这组数据的平均数是5,则这组数据的中位数是 .
三、解答题
20.某企业为了解员工安全生产知识掌握情况,随机抽取了部分员工进行安全生产知识测试,测试试卷满分100分.测试成绩按A、B、C、D四个等级进行统计,并将统计结果绘制了如下两幅不完整的统计图.(说明:测试成绩取整数,A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
请解答下列问题:
(1)该企业员工中参加本次安全生产知识测试共有 人;
(2)补全条形统计图;
(3)若该企业共有员工800人,试估计该企业员工中对安全生产知识的掌握能达到A级的人数.
21.为了解某校八年级学生一门课程的学习情况,小佳和小丽分别对八年级1班和2班本门课程的期末成绩进行了调查分析.
小佳对八年级1班全班学生(25名)的成绩进行分析,过程如下:
收集、整理数据:
表一
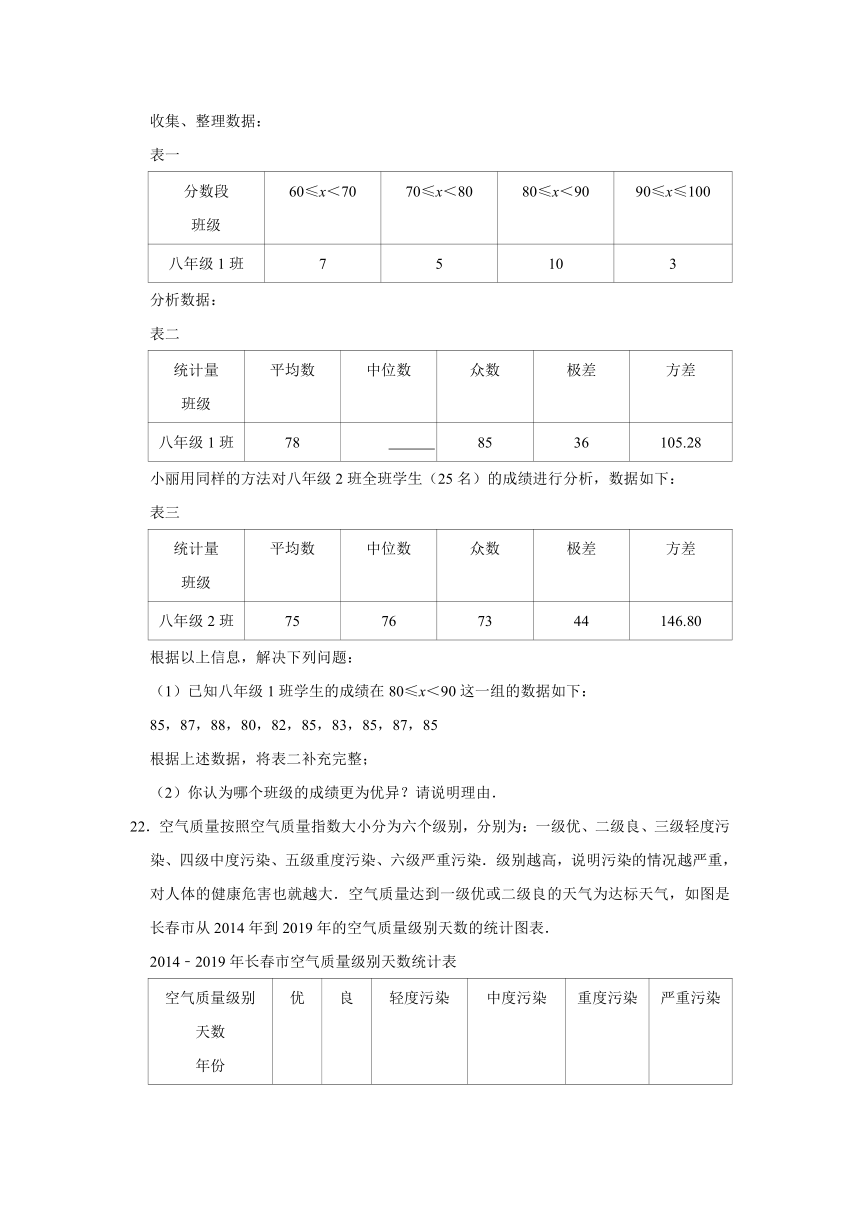
分数段 班级 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
八年级1班 7 5 10 3
分析数据:
表二
统计量 班级 平均数 中位数 众数 极差 方差
八年级1班 78 85 36 105.28
小丽用同样的方法对八年级2班全班学生(25名)的成绩进行分析,数据如下:
表三
统计量 班级 平均数 中位数 众数 极差 方差
八年级2班 75 76 73 44 146.80
根据以上信息,解决下列问题:
(1)已知八年级1班学生的成绩在80≤x<90这一组的数据如下:
85,87,88,80,82,85,83,85,87,85
根据上述数据,将表二补充完整;
(2)你认为哪个班级的成绩更为优异?请说明理由.
22.空气质量按照空气质量指数大小分为六个级别,分别为:一级优、二级良、三级轻度污染、四级中度污染、五级重度污染、六级严重污染.级别越高,说明污染的情况越严重,对人体的健康危害也就越大.空气质量达到一级优或二级良的天气为达标天气,如图是长春市从2014年到2019年的空气质量级别天数的统计图表.
2014﹣2019年长春市空气质量级别天数统计表
空气质量级别 天数 年份 优 良 轻度污染 中度污染 重度污染 严重污染
2014 30 215 73 28 13 6
2015 43 193 87 19 15 8
2016 51 237 58 15 5 0
2017 65 211 62 16 9 2
2018 123 202 39 0 1 0
2019 126 180 38 16 5 0
根据上面的统计图表回答下列问题:
(1)长春市从2014年到2019年空气质量为“达标”的天数最多的是 年.
(2)长春市从2014年到2019年空气质量为“重度污染”的天数的中位数为 天,平均数为 天.
(3)长春市从2015年到2019年,和前一年相比,空气质量为“优”的天数增加最多的是 年,这一年空气质量为“优”的天数的年增长率约为 (精确到1%).
(空气质量为“优”的天数的增长率=
×100%)
(4)你认为长春市从2014年到2019年哪一年的空气质量好?请说明理由.
23.小明为了了解本校学生的假期活动方式,随机对本校的部分学生进行了调查.收集整理数据后,小明将假期活动方式分为五类:A.读书看报;B.健身活动;C.做家务;D.外出游玩;E.其他方式,并绘制了不完整的统计图如图.统计后发现“做家务”的学生人数占调查总人数的20%.
请根据图中的信息解答下列问题:
(1)本次调查的总人数是 人;
(2)补全条形统计图;
(3)根据调查结果,估计本校2360名学生中“假期活动方式”是“读书看报”的有多少人?
24.某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人 笔试成绩/分 面试成绩/分
甲 90 88
乙 84 92
丙 x 90
丁 88 86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
25.某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 学生人数
1 15
2 a
3 b
4 5
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?
26.某公司员工的月工资如下:
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7000 4400 2400 2000 1900 1800 1800 1800 1200
经理、职员C、职员D从不同的角度描述了该公司员工的收入情况.
设该公司员工的月工资数据(见上述表格)的平均数、中位数、众数分别为k、m、n,请根据上述信息完成下列问题:
(1)k= ,m= ,n= ;
(2)上月一个员工辞职了,从本月开始,停发该员工工资,若本月该公司剩下的8名员工的月工资不变,但这8名员工的月工资数据(单位:元)的平均数比原9名员工的月工资数据(见上述表格)的平均数减小了.你认为辞职的那名员工可能是 .
27.4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min)
30 60 81 50 40 110 130 146 90 100
60 81 120 140 70 81 10 20 100 81
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间x(min) 0≤x<40 40≤x<80 80≤x<120 120≤x<160
等级 D C B A
人数 3 8
分析数据:补全下列表格中的统计量:
平均数 中位数 众数
80
得出结论:
(1)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ;
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
参考答案
一、选择题
1.解:因为中位数是将数据按照大小顺序重新排列,代表了这组数据值大小的“中点”,不受极端值影响,
所以将最高成绩写得更高了,计算结果不受影响的是中位数,
故选:C.
2.解:由表可知,2.05出现次数最多,所以众数为2.05;
由于一共调查了30人,
所以中位数为排序后的第15人和第16人的平均数,即:2.10.
故选:C.
3.解:众数为85,
极差:85﹣75=10,
故选:A.
4.解:共有45名学生参加预赛,全省中小学生器乐交流比赛,要取前23名获奖,所以某代表队已经知道了自己的成绩是否进入前23名.我们把所有同学的成绩按大小顺序排列,第23名的成绩是这组数据的中位数,此代表队知道这组数据的中位数,才能知道自己是否获奖.
故选:A.
5.解:由题意可得:两次加油间耗油30升,行驶的路程为6600﹣6200=400(千米)
所以该车每100千米平均耗油量为:30÷(400÷100)=7.5(升).
故选:C.
6.解:把六名学生的数学成绩从小到大排列为:82,96,102,108,108,110,
∴众数是108,中位数为=105,平均数为=101,
方差为[(82﹣101)2+(96﹣101)2+(102﹣101)2+(108﹣101)2+(108﹣101)2+(110﹣101)2]≈94.3≠93;
故选:D.
7.解:选书法课的人数有50﹣13﹣15﹣10=12,
故选:A.
8.解:根据题意得:
=8.26(分),
答:抽取的居民得分的平均数为8.26分.
故选:B.
9.解:把这些数从小到大排列为:﹣3,﹣2,1,3,3,最中间的数是1,
则中位数是1;
故选:C.
10.解:观察图可知:这是一幅扇形统计图,从图中可以直接看出各项消费数额占总消费额的百分比,
如:午餐支出占总支出的40%,车费支出占总支出的25%,文具支出占总支出的15%,其它支出占总支出的20%,
故选:C.
二、填空题
11.解:∵数据4,3,x,1,5的众数是5,
∴x=5,
故答案为:5.
12.解:90出现了4次,出现的次数最多,则众数是90;
故答案为:90
13.解:∵某计算机程序第一次算得m个数据的平均数为x,第二次算得另外n个数据的平均数为y,
则这m+n个数据的平均数等于:.
故答案为:.
14.解:∵被调查的总户数为9÷15%=60(户),
∴B类别户数为60﹣(9+21+12)=18(户),
则扇形统计图B部分所对应的圆心角的度数是360°×=108°,
故答案为:108°.
15.解:该班的平均得分是:×(5×8+8×9+7×10)
=9.1(分).
故答案为:9.1.
16.解:乙组数据的平均数=(0+1+5+9+10)÷5=5,
乙组数据的方差S2=[(0﹣5)2+(1﹣5)2+(9﹣5)2+(10﹣5)2]=16.4,
∵S2甲<S2乙,
∴成绩较为稳定的是甲.
故答案为:甲.
17.解:∵x1,x2,x3,x4的平均数为5
∴x1+x2+x3+x4=4×5=20,
∴x1+3,x2+3,x3+3,x4+3的平均数为:
=(x1+3+x2+3+x3+3+x4+3)÷4
=(20+12)÷4
=8,
故答案为:8.
18.解:估计该小区300户居民这一天投放的可回收垃圾共约×100×15%=90(千克),
故答案为:90.
19.解:∵某班五个兴趣小组的人数分别为4,4,5,x,6,已知这组数据的平均数是5,
∴x=5×5﹣4﹣4﹣5﹣6=6,
∴这一组数从小到大排列为:4,4,5,6,6,
∴这组数据的中位数是5.
故答案为:5.
三、解答题
20.解:(1)20÷50%=40,
所以该企业员工中参加本次安全生产知识测试共有40人;
故答案为40;
(2)C等级的人数为40﹣8﹣20﹣4=8(人),
补全条形统计图为:
(3)800×=160,
所以估计该企业员工中对安全生产知识的掌握能达到A级的人数为160人.
21.解:(1)共有25个数据,第13个数落在80≤x<90这一组中,此组最小的数为第13个数,
所以八年级1班学生的成绩的中位数为80;
故答案为80;
(2)八年级1班学生的成绩更为优异.
理由如下:八年级1班学生的成绩的平均数比2班高,1班的中位数比2班的中位数大,并且1班的众数为85,比2班的众数大,1班的方差比2班小,比较稳定.
22.解:(1)从折线统计图中“达标”天数的折线的最高点,相应的年份为2018年,
故答案为:2018;
(2)将这6年的“重度污染”的天数从小到大排列,处在中间位置的两个数的平均数为=7,因此中位数是7天,
这6年的“重度污染”的天数的平均数为=8天,
故答案为:7,8;
(3)前一年相比,空气质量为“优”的天数增加量为:
2015年,43﹣30=13天;
2016年,51﹣43=8天;
2017年,65﹣51=14天;
2018年,123﹣65=58天;
2019年,126﹣123=3天,
因此空气质量为“优”的天数增加最多的是2018年,增长率为≈89%,
故答案为:2018,89%;
(4)从统计表中数据可知,2018年空气质量好,2018年“达标天数”最多,重度污染、中度污染、严重污染的天数最少.
23.解:(1)本次调查的总人数是8÷20%=40(人),
故答案为:40;
(2)D活动方式的人数为40﹣(6+12+8+4)=10(人),
补全图形如下:
(3)估计本校2360名学生中“假期活动方式”是“读书看报”的有2360×=354(人).
24.解:(1)这四名候选人面试成绩的中位数为:=89(分);
(2)由题意得,x×60%+90×40%=87.6
解得,x=86,
答:表中x的值为86;
(3)甲候选人的综合成绩为:90×60%+88×40%=89.2(分),
乙候选人的综合成绩为:84×60%+92×40%=87.2(分),
丁候选人的综合成绩为:88×60%+86×40%=87.2(分),
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
25.解:(1)由题意可得,
m=15÷30%=50,b=50×40%=20,a=50﹣15﹣20﹣5=10,
即m的值是50,a的值是10,b的值是20;
(2)(1×15+2×10+3×20+4×5)×=1150(本),
答:该年级全体学生在这次活动中课外阅读书籍的总量大约是1150本.
26.解:(1)平均数k=(7000+4400+2400+2000+1900+1800×3+1200)÷9=2700,
9个数据从大到小排列后,第5个数据是1900,所以中位数m=1900,
1800出现了三次,次数最多,所以众数n=1800.
故答案为:2700,1900,1800;
(2)由题意可知,辞职的那名员工工资高于2700元,所以辞职的那名员工可能是经理或副经理.
故答案为:经理或副经理.
27.解:(1)根据上表统计显示:样本中位数和众数都是81,平均数是80,都是B等级,
故估计该校学生每周的用于课外阅读时间的情况等级为B.
(2)∵=160
∴该校现有学生400人,估计等级为“B”的学生有160名.
(3)以平均数来估计:
×52=26
∴假设平均阅读一本课外书的时间为160分钟,以样本的平均数来估计该校学生每人一年(按52周计算)平均阅读26本课外书.
故答案为:5,4,81,81,B;
一、选择题
1.测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时,出现了一处错误:将最高成绩写得更高了,计算结果不受影响的是( )
A.方差 B.标准差 C.中位数 D.平均数
2.在中考体育加试中,某班30名男生的跳远成绩如下表:
成绩/m 1.95 2.00 2.05 2.10 2.15 2.25
人数 2 3 9 8 5 3
这些男生跳远成绩的众数、中位数分别是( )
A.2.10,2.05 B.2.10,2.10 C.2.05,2.10 D.2.05,2.05
3.下列数据:75,80,85,85,85,则这组数据的众数和极差是( )
A.85,10 B.85,5 C.80,85 D.80,10
4.2016年6月4日﹣5日贵州省第九届“贵青杯”﹣“乐韵华彩”全省中小学生器乐交流比赛在省青少年活动中心举行,有45支队参赛,他们参赛的成绩各不相同,要取前23名获奖,某代表队已经知道了自己的成绩,他们想知道自己是否获奖,只需再知道这45支队成绩的( )
A.中位数 B.平均数 C.最高分 D.方差
5.张老师买了一辆启辰R50X汽车,为了掌握车的油耗情况,在连续两次加油时做了如下工作:(1)把油箱加满油;
(2)记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:
加油时间 加油量(升) 加油时的累计里程(千米)
2022年4月28日 18 6200
2022年5月16日 30 6600
则在这段时间内,该车每100千米平均耗油量为( )
A.3升 B.5升 C.7.5升 D.9升
6.某校九年级模拟考试中,1班的六名学生的数学成绩如下:96,108,102,110,108,82.下列关于这组数据的描述不正确的是( )
A.众数是108 B.中位数是105 C.平均数是101 D.方差是93
7.某校开设了艺术、体育、劳动、书法四门拓展性课程,要求每一位学生都要选且只能选一门课.小黄同学统计了本班50名同学的选课情况,并将结果绘制成条形统计图(如图,不完全),则选书法课的人数有( )
A.12名 B.13名 C.15名 D.50名
8.为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,得分情况如表所示:
得分 6 7 8 9 10
人数 4 10 15 11 10
则抽取的居民得分的平均数为( )
A.8 B.8.26 C.9.2 D.10
9.一组数据﹣3,3,﹣2,3,1的中位数是( )
A.﹣3 B.﹣2 C.1 D.3
10.小明把自己一周的支出情况用如图所示的统计图来表示,下面说法正确的是( )
A.从图中可以直接看出具体消费数额
B.从图中可以直接看出总消费数额
C.从图中可以直接看出各项消费数额占总消费数额的百分比
D.从图中可以直接看出各项消费数在一周中的具体变化情况
二、填空题
11.一组数据4,3,x,1,5的众数是5,则x= .
12.某班学生经常采用“小组合作学习”的方式进行学习,王老师每周对各小组合作学习的情况进行综合评分.下表是各小组其中一周的得分情况:
组别 一 二 三 四 五 六 七 八
得分 90 95 90 88 90 92 85 90
这组数据的众数是 .
13.某计算机程序第一次算得m个数据的平均数为x,第二次算得另外n个数据的平均数为y,则这(m+n)个数据的平均数等于 .
14.董永社区在创建全国卫生城市的活动中,随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况,将他们绘制了两幅不完整的统计图(A.小于5天;B.5天;C.6天;D.7天),则扇形统计图B部分所对应的圆心角的度数是 .
15.学校进行广播操比赛,如图是20位评委给某班的评分情况统计图,则该班的平均得分是 分.
16.甲乙两人进行飞镖比赛,每人各投5次,所得平均环数相等,其中甲所得环数的方差为15,乙所得环数如下:0,1,5,9,10,那么成绩较稳定的是 (填“甲”或“乙”).
17.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是 .
18.小明为了解所在小区居民各类生活垃圾的投放情况,他随机调查了该小区50户家庭某一天各类生活垃圾的投放量,统计得出这50户家庭各类生活垃圾的投放总量是100千克,并画出各类生活垃圾投放量分布情况的扇形图(如图所示),根据以上信息,估计该小区300户居民这一天投放的可回收垃圾共约 千克.
19.某班五个兴趣小组的人数分别为4,4,5,x,6.已知这组数据的平均数是5,则这组数据的中位数是 .
三、解答题
20.某企业为了解员工安全生产知识掌握情况,随机抽取了部分员工进行安全生产知识测试,测试试卷满分100分.测试成绩按A、B、C、D四个等级进行统计,并将统计结果绘制了如下两幅不完整的统计图.(说明:测试成绩取整数,A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
请解答下列问题:
(1)该企业员工中参加本次安全生产知识测试共有 人;
(2)补全条形统计图;
(3)若该企业共有员工800人,试估计该企业员工中对安全生产知识的掌握能达到A级的人数.
21.为了解某校八年级学生一门课程的学习情况,小佳和小丽分别对八年级1班和2班本门课程的期末成绩进行了调查分析.
小佳对八年级1班全班学生(25名)的成绩进行分析,过程如下:
收集、整理数据:
表一
分数段 班级 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
八年级1班 7 5 10 3
分析数据:
表二
统计量 班级 平均数 中位数 众数 极差 方差
八年级1班 78 85 36 105.28
小丽用同样的方法对八年级2班全班学生(25名)的成绩进行分析,数据如下:
表三
统计量 班级 平均数 中位数 众数 极差 方差
八年级2班 75 76 73 44 146.80
根据以上信息,解决下列问题:
(1)已知八年级1班学生的成绩在80≤x<90这一组的数据如下:
85,87,88,80,82,85,83,85,87,85
根据上述数据,将表二补充完整;
(2)你认为哪个班级的成绩更为优异?请说明理由.
22.空气质量按照空气质量指数大小分为六个级别,分别为:一级优、二级良、三级轻度污染、四级中度污染、五级重度污染、六级严重污染.级别越高,说明污染的情况越严重,对人体的健康危害也就越大.空气质量达到一级优或二级良的天气为达标天气,如图是长春市从2014年到2019年的空气质量级别天数的统计图表.
2014﹣2019年长春市空气质量级别天数统计表
空气质量级别 天数 年份 优 良 轻度污染 中度污染 重度污染 严重污染
2014 30 215 73 28 13 6
2015 43 193 87 19 15 8
2016 51 237 58 15 5 0
2017 65 211 62 16 9 2
2018 123 202 39 0 1 0
2019 126 180 38 16 5 0
根据上面的统计图表回答下列问题:
(1)长春市从2014年到2019年空气质量为“达标”的天数最多的是 年.
(2)长春市从2014年到2019年空气质量为“重度污染”的天数的中位数为 天,平均数为 天.
(3)长春市从2015年到2019年,和前一年相比,空气质量为“优”的天数增加最多的是 年,这一年空气质量为“优”的天数的年增长率约为 (精确到1%).
(空气质量为“优”的天数的增长率=
×100%)
(4)你认为长春市从2014年到2019年哪一年的空气质量好?请说明理由.
23.小明为了了解本校学生的假期活动方式,随机对本校的部分学生进行了调查.收集整理数据后,小明将假期活动方式分为五类:A.读书看报;B.健身活动;C.做家务;D.外出游玩;E.其他方式,并绘制了不完整的统计图如图.统计后发现“做家务”的学生人数占调查总人数的20%.
请根据图中的信息解答下列问题:
(1)本次调查的总人数是 人;
(2)补全条形统计图;
(3)根据调查结果,估计本校2360名学生中“假期活动方式”是“读书看报”的有多少人?
24.某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人 笔试成绩/分 面试成绩/分
甲 90 88
乙 84 92
丙 x 90
丁 88 86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
25.某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 学生人数
1 15
2 a
3 b
4 5
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?
26.某公司员工的月工资如下:
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7000 4400 2400 2000 1900 1800 1800 1800 1200
经理、职员C、职员D从不同的角度描述了该公司员工的收入情况.
设该公司员工的月工资数据(见上述表格)的平均数、中位数、众数分别为k、m、n,请根据上述信息完成下列问题:
(1)k= ,m= ,n= ;
(2)上月一个员工辞职了,从本月开始,停发该员工工资,若本月该公司剩下的8名员工的月工资不变,但这8名员工的月工资数据(单位:元)的平均数比原9名员工的月工资数据(见上述表格)的平均数减小了.你认为辞职的那名员工可能是 .
27.4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min)
30 60 81 50 40 110 130 146 90 100
60 81 120 140 70 81 10 20 100 81
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间x(min) 0≤x<40 40≤x<80 80≤x<120 120≤x<160
等级 D C B A
人数 3 8
分析数据:补全下列表格中的统计量:
平均数 中位数 众数
80
得出结论:
(1)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ;
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
参考答案
一、选择题
1.解:因为中位数是将数据按照大小顺序重新排列,代表了这组数据值大小的“中点”,不受极端值影响,
所以将最高成绩写得更高了,计算结果不受影响的是中位数,
故选:C.
2.解:由表可知,2.05出现次数最多,所以众数为2.05;
由于一共调查了30人,
所以中位数为排序后的第15人和第16人的平均数,即:2.10.
故选:C.
3.解:众数为85,
极差:85﹣75=10,
故选:A.
4.解:共有45名学生参加预赛,全省中小学生器乐交流比赛,要取前23名获奖,所以某代表队已经知道了自己的成绩是否进入前23名.我们把所有同学的成绩按大小顺序排列,第23名的成绩是这组数据的中位数,此代表队知道这组数据的中位数,才能知道自己是否获奖.
故选:A.
5.解:由题意可得:两次加油间耗油30升,行驶的路程为6600﹣6200=400(千米)
所以该车每100千米平均耗油量为:30÷(400÷100)=7.5(升).
故选:C.
6.解:把六名学生的数学成绩从小到大排列为:82,96,102,108,108,110,
∴众数是108,中位数为=105,平均数为=101,
方差为[(82﹣101)2+(96﹣101)2+(102﹣101)2+(108﹣101)2+(108﹣101)2+(110﹣101)2]≈94.3≠93;
故选:D.
7.解:选书法课的人数有50﹣13﹣15﹣10=12,
故选:A.
8.解:根据题意得:
=8.26(分),
答:抽取的居民得分的平均数为8.26分.
故选:B.
9.解:把这些数从小到大排列为:﹣3,﹣2,1,3,3,最中间的数是1,
则中位数是1;
故选:C.
10.解:观察图可知:这是一幅扇形统计图,从图中可以直接看出各项消费数额占总消费额的百分比,
如:午餐支出占总支出的40%,车费支出占总支出的25%,文具支出占总支出的15%,其它支出占总支出的20%,
故选:C.
二、填空题
11.解:∵数据4,3,x,1,5的众数是5,
∴x=5,
故答案为:5.
12.解:90出现了4次,出现的次数最多,则众数是90;
故答案为:90
13.解:∵某计算机程序第一次算得m个数据的平均数为x,第二次算得另外n个数据的平均数为y,
则这m+n个数据的平均数等于:.
故答案为:.
14.解:∵被调查的总户数为9÷15%=60(户),
∴B类别户数为60﹣(9+21+12)=18(户),
则扇形统计图B部分所对应的圆心角的度数是360°×=108°,
故答案为:108°.
15.解:该班的平均得分是:×(5×8+8×9+7×10)
=9.1(分).
故答案为:9.1.
16.解:乙组数据的平均数=(0+1+5+9+10)÷5=5,
乙组数据的方差S2=[(0﹣5)2+(1﹣5)2+(9﹣5)2+(10﹣5)2]=16.4,
∵S2甲<S2乙,
∴成绩较为稳定的是甲.
故答案为:甲.
17.解:∵x1,x2,x3,x4的平均数为5
∴x1+x2+x3+x4=4×5=20,
∴x1+3,x2+3,x3+3,x4+3的平均数为:
=(x1+3+x2+3+x3+3+x4+3)÷4
=(20+12)÷4
=8,
故答案为:8.
18.解:估计该小区300户居民这一天投放的可回收垃圾共约×100×15%=90(千克),
故答案为:90.
19.解:∵某班五个兴趣小组的人数分别为4,4,5,x,6,已知这组数据的平均数是5,
∴x=5×5﹣4﹣4﹣5﹣6=6,
∴这一组数从小到大排列为:4,4,5,6,6,
∴这组数据的中位数是5.
故答案为:5.
三、解答题
20.解:(1)20÷50%=40,
所以该企业员工中参加本次安全生产知识测试共有40人;
故答案为40;
(2)C等级的人数为40﹣8﹣20﹣4=8(人),
补全条形统计图为:
(3)800×=160,
所以估计该企业员工中对安全生产知识的掌握能达到A级的人数为160人.
21.解:(1)共有25个数据,第13个数落在80≤x<90这一组中,此组最小的数为第13个数,
所以八年级1班学生的成绩的中位数为80;
故答案为80;
(2)八年级1班学生的成绩更为优异.
理由如下:八年级1班学生的成绩的平均数比2班高,1班的中位数比2班的中位数大,并且1班的众数为85,比2班的众数大,1班的方差比2班小,比较稳定.
22.解:(1)从折线统计图中“达标”天数的折线的最高点,相应的年份为2018年,
故答案为:2018;
(2)将这6年的“重度污染”的天数从小到大排列,处在中间位置的两个数的平均数为=7,因此中位数是7天,
这6年的“重度污染”的天数的平均数为=8天,
故答案为:7,8;
(3)前一年相比,空气质量为“优”的天数增加量为:
2015年,43﹣30=13天;
2016年,51﹣43=8天;
2017年,65﹣51=14天;
2018年,123﹣65=58天;
2019年,126﹣123=3天,
因此空气质量为“优”的天数增加最多的是2018年,增长率为≈89%,
故答案为:2018,89%;
(4)从统计表中数据可知,2018年空气质量好,2018年“达标天数”最多,重度污染、中度污染、严重污染的天数最少.
23.解:(1)本次调查的总人数是8÷20%=40(人),
故答案为:40;
(2)D活动方式的人数为40﹣(6+12+8+4)=10(人),
补全图形如下:
(3)估计本校2360名学生中“假期活动方式”是“读书看报”的有2360×=354(人).
24.解:(1)这四名候选人面试成绩的中位数为:=89(分);
(2)由题意得,x×60%+90×40%=87.6
解得,x=86,
答:表中x的值为86;
(3)甲候选人的综合成绩为:90×60%+88×40%=89.2(分),
乙候选人的综合成绩为:84×60%+92×40%=87.2(分),
丁候选人的综合成绩为:88×60%+86×40%=87.2(分),
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
25.解:(1)由题意可得,
m=15÷30%=50,b=50×40%=20,a=50﹣15﹣20﹣5=10,
即m的值是50,a的值是10,b的值是20;
(2)(1×15+2×10+3×20+4×5)×=1150(本),
答:该年级全体学生在这次活动中课外阅读书籍的总量大约是1150本.
26.解:(1)平均数k=(7000+4400+2400+2000+1900+1800×3+1200)÷9=2700,
9个数据从大到小排列后,第5个数据是1900,所以中位数m=1900,
1800出现了三次,次数最多,所以众数n=1800.
故答案为:2700,1900,1800;
(2)由题意可知,辞职的那名员工工资高于2700元,所以辞职的那名员工可能是经理或副经理.
故答案为:经理或副经理.
27.解:(1)根据上表统计显示:样本中位数和众数都是81,平均数是80,都是B等级,
故估计该校学生每周的用于课外阅读时间的情况等级为B.
(2)∵=160
∴该校现有学生400人,估计等级为“B”的学生有160名.
(3)以平均数来估计:
×52=26
∴假设平均阅读一本课外书的时间为160分钟,以样本的平均数来估计该校学生每人一年(按52周计算)平均阅读26本课外书.
故答案为:5,4,81,81,B;
