【期中押题卷】湖北省武汉市2024-2025学年六年级下学期期中综合测试数学试卷人教版(含解析)
文档属性
| 名称 | 【期中押题卷】湖北省武汉市2024-2025学年六年级下学期期中综合测试数学试卷人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 275.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 07:40:37 | ||
图片预览




文档简介
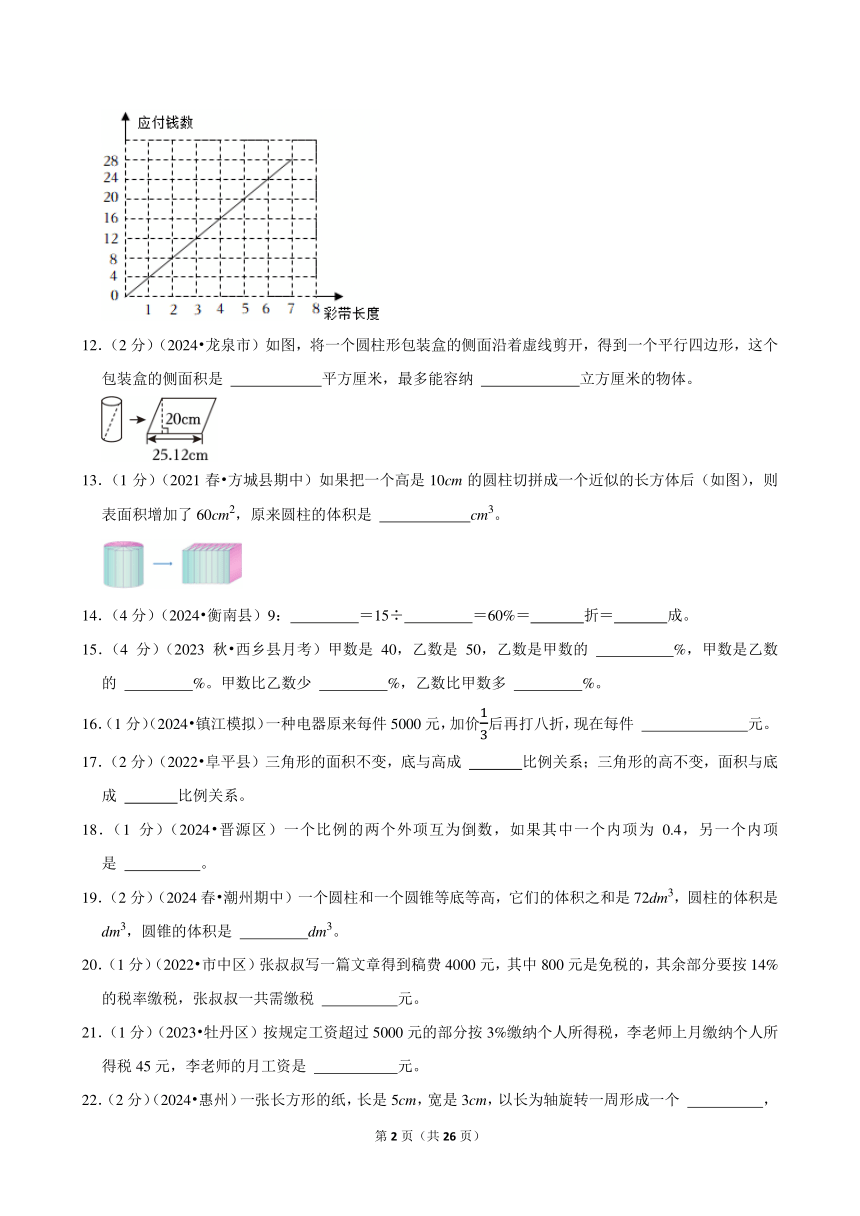
湖北省武汉市2024-2025学年六年级下学期期中综合测试数学试卷
一.选择题(共5小题,满分5分,每小题1分)
1.(1分)(2022秋 海州区期末)连云港某天的最高气温是7℃,最低气温是﹣2℃,这天气温最高和最低相差( )
A.9℃ B.5℃ C.6℃ D.7℃
2.(1分)(2022春 沂源县期末)某商厦出售两台不同品牌的空调,其中一台赚了20%,另一台赔了20%,这两台空调的售价都是3600元,那么在这次销售中商厦( )
A.赚了 B.赔了
C.不赚不赔 D.不确定赔赚
3.(1分)(2022春 杭州期中)底面积相等的圆柱和圆锥,它们体积也相等,圆锥的高是9cm,圆柱的高是( )cm。
A.3 B.1.5 C.18 D.24
4.(1分)(2022 德宏州)等底等高的圆柱和圆锥体积之和是20m3,圆锥体积是( )
A.5m3 B.20m3 C.15m3 D.5m2
5.(1分)(2023 平果市)给一个正方体的六个面图上红、黄、蓝、绿四种颜色(每个面只涂一种颜色),不论怎么涂,至少有( )个面涂的颜色相同。
A.5 B.4 C.3 D.2
二.判断题(共4小题,满分4分,每小题1分)
6.(1分)(2023 兴庆区)数轴上,右边的数总比左边的数大,﹣1.5和1.5在数轴上与0的距离是相等的。
7.(1分)(2021春 华容区期中)满100减40,实际上就是打六折。
8.(1分)(2023春 金昌期中)在72:0.9=16:2中,0.9和16是比例的内项,72和2是比例的外项。
9.(1分)(2022 张家川县模拟)若xy,那么x和y成反比例。
三.填空题(共14小题,满分25分)
10.(1分)(2024 遵义)新蒲新区是一个适宜人居的城市,冬季白天的最高气温是14℃,到了晚上12时,气温下降了16℃,该地当晚12时的气温是 ℃。
11.(2分)(2022 双桥区)如图是买彩带米数和应付钱数之间关系图。买彩带米数和应付钱数成 比例关系;照这样计算,付40元,是买了 米彩带。
12.(2分)(2024 龙泉市)如图,将一个圆柱形包装盒的侧面沿着虚线剪开,得到一个平行四边形,这个包装盒的侧面积是 平方厘米,最多能容纳 立方厘米的物体。
13.(1分)(2021春 方城县期中)如果把一个高是10cm的圆柱切拼成一个近似的长方体后(如图),则表面积增加了60cm2,原来圆柱的体积是 cm3。
14.(4分)(2024 衡南县)9: =15÷ =60%= 折= 成。
15.(4分)(2023秋 西乡县月考)甲数是40,乙数是50,乙数是甲数的 %,甲数是乙数的 %。甲数比乙数少 %,乙数比甲数多 %。
16.(1分)(2024 镇江模拟)一种电器原来每件5000元,加价后再打八折,现在每件 元。
17.(2分)(2022 阜平县)三角形的面积不变,底与高成 比例关系;三角形的高不变,面积与底成 比例关系。
18.(1分)(2024 晋源区)一个比例的两个外项互为倒数,如果其中一个内项为0.4,另一个内项是 。
19.(2分)(2024春 潮州期中)一个圆柱和一个圆锥等底等高,它们的体积之和是72dm3,圆柱的体积是 dm3,圆锥的体积是 dm3。
20.(1分)(2022 市中区)张叔叔写一篇文章得到稿费4000元,其中800元是免税的,其余部分要按14%的税率缴税,张叔叔一共需缴税 元。
21.(1分)(2023 牡丹区)按规定工资超过5000元的部分按3%缴纳个人所得税,李老师上月缴纳个人所得税45元,李老师的月工资是 元。
22.(2分)(2024 惠州)一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个 ,这个立体图形的体积是 cm3。
23.(1分)一副扑克牌有54张,最少要抽取 张牌,才能保证其中至少有3张牌有相同的点数。
四.计算题(共3小题,满分31分)
24.(10分)(2024 濉溪县)直接写得数。
1÷0.25= 5.6= 1+10%= 401×49≈
1.6×0.3= 0.33=
25.(9分)(2024春 夏邑县校级期中)解方程。
(1)x:5.4=8:0.6
(2)
(3)
26.(12分)(2024 渝北区)计算题。
(1)3.1 (2)[()]
(3) (4)[15﹣()×24]
五.操作题(共2小题,满分11分)
27.(5分)(2024秋 南昌县期末)图书馆在小兰家南偏东50°方向上,距离是450m。
(1)根据上面的描述,在平面图上标出图书馆的位置。
(2)小红家在图书馆的正东方向上,小红家不可能在小兰家 方向上。
A.东偏南
B.南偏东
C.南偏西
28.(6分)(2024春 惠民县期中)计算圆柱的表面积和圆锥的体积。(单位:厘米)
(1)
(2)
六.应用题(共6小题,满分23分)
29.(4分)(2024 武汉模拟)从A城到B城,在比例尺是1:50000000的图上量得两地间的距离是6.3cm。一架飞机早上8时从A城飞往B城,如果每小时飞行700千米,中途休息1小时30分,请问到达B城是什么时间?
30.(4分)(2023 七里河区模拟)某商场进了50件防晒衣,每件的进价为100元,售价为160元,在卖出60%后,由于天气转冷而滞销,店主将余下的打五折出售,并且全部售完。请问:该商店是亏了还是赚了?亏还是赚了多少钱?
31.(4分)(2022 北辰区)一辆货车箱是一个长方体,它的长是4米,宽是1.5米,高是4米,装满一车沙,卸后堆成一个高是8分米的圆锥体,沙堆底面面积是多少平方米?
32.(4分)六年级全体同学参加升旗仪式,按各列人数相等的规定排列站队,如果每列站25人,要排24列。 ?
根据以上信息,请你先补充一个条件,并提出一个能用反比例关系解答的问题,最后再解答。(条件和问题直接补充在横线上)
33.(4分)(2022秋 海门区期末)王老师准备在网上购买一套书(共5册)。A网店和B网店的价格信息如图。王老师在哪家网店购买比较合算?
A网店:每册19元,免运费
B网店:每套80元,运费8元
34.(3分)一文具店购进了一批钢笔,以每支19.5元的价格出售,当卖出56%时,老板发现还差54元就能收回全部成本,于是决定降价20%销售,很快就全部售出,最终共获得利润289.2元。问:文具店购进这批钢笔的价格是每支多少元?
湖北省武汉市2024-2025学年六年级下学期期中综合测试数学试卷
参考答案与试题解析
一.选择题(共5小题,满分5分,每小题1分)
1.(1分)(2022秋 海州区期末)连云港某天的最高气温是7℃,最低气温是﹣2℃,这天气温最高和最低相差( )
A.9℃ B.5℃ C.6℃ D.7℃
【考点】正、负数的运算.
【专题】整数的认识;数据分析观念.
【答案】A
【分析】结合数轴理解可知,最高气温是7℃到0℃的距离是7,最低气温是﹣2℃到0℃的距离是2,那么7℃到﹣2℃的距离是7+2=9,也就是这天气温最高和最大相差9℃。据此解答。
【解答】解:7+2=9(℃)
连云港某天的最高气温是7℃,最低气温是﹣2℃,这天气温最高和最低相差9℃。
故选:A。
【点评】本题考查负数的认识,关键结果数轴观察两数之间的距离是多少来解答。
2.(1分)(2022春 沂源县期末)某商厦出售两台不同品牌的空调,其中一台赚了20%,另一台赔了20%,这两台空调的售价都是3600元,那么在这次销售中商厦( )
A.赚了 B.赔了
C.不赚不赔 D.不确定赔赚
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】B
【分析】先把赚钱空调的进价看成单位“1”,则售价是进价的(1+20%),由此用除法求出进价,再求出它赚了多少钱;
再把赔钱空调的进价看成单位“1”,则售价是进价的(1﹣20%),由此用除法求出进价,再求出它赔了多少钱;
再把赚的钱数和亏的钱数比较即可。
【解答】解:3600÷(1+20%)
=3600÷120%
=3000(元)
赚了:3600﹣3000=600(元)
3600÷(1﹣20%)
=3600÷80%
=4500(元)
亏了:4500﹣3600=900(元)
因为900>600,所以卖这两台空调是赔了。
故选:B。
【点评】解答此题的关键是分清两个不同的单位“1”,分别求出进价,进而求解。
3.(1分)(2022春 杭州期中)底面积相等的圆柱和圆锥,它们体积也相等,圆锥的高是9cm,圆柱的高是( )cm。
A.3 B.1.5 C.18 D.24
【考点】圆锥的体积;圆柱的体积.
【专题】空间观念;推理能力;应用意识.
【答案】A
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此解答即可。
【解答】解:93(厘米)
答:圆柱的高是3厘米。
故选:A。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
4.(1分)(2022 德宏州)等底等高的圆柱和圆锥体积之和是20m3,圆锥体积是( )
A.5m3 B.20m3 C.15m3 D.5m2
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】应用意识.
【答案】A
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积和相当于圆锥体积的(3+1)倍。根据已知一个数的几倍是多少,求这个数,用除法解答。
【解答】解:20÷(3+1)
=20÷4
=5(立方厘米)
答:圆锥的体积是5立方厘米。
故选:A。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
5.(1分)(2023 平果市)给一个正方体的六个面图上红、黄、蓝、绿四种颜色(每个面只涂一种颜色),不论怎么涂,至少有( )个面涂的颜色相同。
A.5 B.4 C.3 D.2
【考点】抽屉原理.
【专题】压轴题;模型思想;应用意识.
【答案】D
【分析】把红、黄、蓝、绿四种颜色看做4个抽屉,6个面看做6个元素,利用抽屉原理最差情况:要使涂的颜色相同的面数最少,只要使每个抽屉的元素数尽量平均,即可解答。
【解答】解:6÷4=1(个)......2(个)
1+1=2(个)
答:至少有2个面涂的颜色相同。
故选:D。
【点评】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑。
二.判断题(共4小题,满分4分,每小题1分)
6.(1分)(2023 兴庆区)数轴上,右边的数总比左边的数大,﹣1.5和1.5在数轴上与0的距离是相等的。 √
【考点】数轴的认识.
【专题】整数的认识;数据分析观念.
【答案】√
【分析】
像这样表示出正数、0和负数的直线,叫作数轴。
直线上0表示起点,0右边的数表示正数,左边的数表示负数;因此,数轴上,右边的数总是比左边的大;
用有正数和负数的直线可以表示距离和相反的方向;﹣1.5位于0的左边,距离0有1.5个单位的距离、1.5在数轴的右边,距离0有1.5个单位的距离。
【解答】解:由分析得:数轴上,右边的数总比左边的数大,﹣1.5和1.5在数轴上与0的距离是相等的;原题说法正确。
故答案为:√。
【点评】考查了对于数轴上正数、负数的位置,及正负数与0的距离的关系的理解,需要充分了解数轴的概念、特征。
7.(1分)(2021春 华容区期中)满100减40,实际上就是打六折。 √
【考点】百分数的实际应用.
【专题】应用意识.
【答案】√
【分析】把原价看作单位“1”,打几折就是现价是原价的百分之几十,把数代入计算即可。
【解答】解:(100﹣40)÷100
=60÷100
=60%
=六折
所以每满100元减40元,刚好满100元时才是打六折,原题说法正确。
故答案为:√。
【点评】本题主要考查百分数的应用,关键找到单位“1”,利用数量关系做题。
8.(1分)(2023春 金昌期中)在72:0.9=16:2中,0.9和16是比例的内项,72和2是比例的外项。 ×
【考点】比例的意义和基本性质.
【专题】比和比例;数据分析观念.
【答案】×
【分析】表示两个比相等的式子,叫做比例,据此解答。
【解答】解:因为72:0.9=80,16:2=8,比值相等,所以72:0.9与16:2不能组成比例,原题说法错误。
故答案为:×。
【点评】本题主要考查比例的意义,注意判断能否组成比例可以用求比值的方法,求出比值,比值相等两个比就能组成比例。
9.(1分)(2022 张家川县模拟)若xy,那么x和y成反比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:因为xy,所以xy
是x、y的乘积一定,
所以x、y成反比例。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
三.填空题(共14小题,满分25分)
10.(1分)(2024 遵义)新蒲新区是一个适宜人居的城市,冬季白天的最高气温是14℃,到了晚上12时,气温下降了16℃,该地当晚12时的气温是 ﹣2 ℃。
【考点】正、负数的运算.
【专题】运算顺序及法则;数据分析观念.
【答案】﹣2。
【分析】利用白天的温度减去下降的温度即可。
【解答】解:14℃﹣16℃=﹣2℃
答:该地当晚12时的气温是﹣2℃。
故答案为:﹣2。
【点评】本题考查了正负数的运算及应用。
11.(2分)(2022 双桥区)如图是买彩带米数和应付钱数之间关系图。买彩带米数和应付钱数成 正 比例关系;照这样计算,付40元,是买了 10 米彩带。
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】正,10。
【分析】买彩带米数和应付钱数之间关系图像是一条射线,所以买彩带米数和应付钱数之间关系成正比例关系。据此解答。
【解答】解:因为买彩带米数和应付钱数之间关系图像是一条射线,所以买彩带米数和应付钱数之间关系成正比例关系。
设付40元,是买了x米彩带,得:
1:4=x:40
4x=1×40
4x=40
4x÷4=40÷4
x=10
答:付40元,是买了10米彩带。
故答案为:正,10。
【点评】此题考查了正比例关系的图像积用比例解决问题,需灵活掌握。
12.(2分)(2024 龙泉市)如图,将一个圆柱形包装盒的侧面沿着虚线剪开,得到一个平行四边形,这个包装盒的侧面积是 502.4 平方厘米,最多能容纳 1004.8 立方厘米的物体。
【考点】圆柱的侧面积、表面积和体积.
【专题】应用题;应用意识.
【答案】(1)502.4;(2)1004.8。
【分析】(1)通过观察图形可知,这个圆柱的侧面展开后是一个底是25.12厘米,高是20厘米的平行四边形,根据平行四边形的面积公式:S=ah,把数据代入公式解答。
(2)根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式解答。
【解答】解:(1)25.12×20=502.4(平方厘米)
答:它的侧面积是502.4平方厘米。
(2)3.14×(25.12÷3.14÷2)2×20
=3.14×16×20
=50.24×20
=1004.8(立方厘米)
答:这个包装盒最多能容纳1004.8立方厘米的物体。
故答案为:(1)502.4;(2)1004.8。
【点评】此题主要考查圆柱的侧面积公式、圆柱的体积(容积)公式的灵活运用,关键是熟记公式。
13.(1分)(2021春 方城县期中)如果把一个高是10cm的圆柱切拼成一个近似的长方体后(如图),则表面积增加了60cm2,原来圆柱的体积是 282.6 cm3。
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;几何直观.
【答案】282.6。
【分析】根据圆柱体积公式的推导过程可知,把圆柱切拼成一个近似长方体体积不变,但是拼成的长方体的表面积比圆柱的表面积增加了两个长方形的面积,每个长方形的长等于圆柱的高,宽等于圆柱的底面半径,已知拼成后长方体的表面积比原来圆柱的表面积增加了60cm2,据此可以求出圆柱的底面半径,然后根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:60÷2÷10
=30÷10
=3(cm)
3.14×32×10
=3.14×9×10
=282.6(cm3)
答:原来圆柱的体积是282.6cm3。
故答案为:282.6。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导过程,以及圆柱的表面积、体积公式的灵活运用,关键是熟记公式。
14.(4分)(2024 衡南县)9: 15 =15÷ 25 =60%= 六 折= 六 成。
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化;折扣;成数.
【专题】数感.
【答案】15,25,六,六。
【分析】把60%化成分母是100的分数并化简是,根据比与分数的关系3:5,再根据比的性质比的前、后项都乘3就是9:15;根据分数与除法的关系3÷5,再根据商不变的性质被除数、除数都乘5就是15÷25;根据折扣的意义60%就是六折;根据成数的意义60%就是六成。
【解答】解:9:15=15÷25=60%=六折=六成
故答案为:15,25,六,六。
【点评】此题主要是考查除法、比、百分数、折扣、成数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
15.(4分)(2023秋 西乡县月考)甲数是40,乙数是50,乙数是甲数的 125 %,甲数是乙数的 80 %。甲数比乙数少 20 %,乙数比甲数多 25 %。
【考点】百分数的加减乘除运算.
【专题】运算能力.
【答案】125,80,20,25。
【分析】(1)把甲数看作单位“1”,用乙数除以甲数即可解答;
(2)把乙数看作单位“1”,用甲数除以乙数即可解答;
(3)把乙数看作单位“1”,先求出乙数比甲数多的数,再除以乙数即可解答;
(4)把甲数看作单位“1”,先求出乙数比甲数多的数,再除以甲数即可解答。
【解答】解:(1)50÷40=125%
答:乙数是甲数125%。
(2)40÷50=80%
答:甲数是乙数80%。
(3)(50﹣40)÷50
=10÷50
=20%
答:甲数比乙数少20%。
(4)(50﹣40)÷40
=10÷40
=25%
答:乙数比甲数多25%。
故答案为:125,80,20,25。
【点评】本题主要考查了百分数除法的意义,解答本题的关键是明确以谁为标准量。
16.(1分)(2024 镇江模拟)一种电器原来每件5000元,加价后再打八折,现在每件 5333.33 元。
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】5333.33。
【分析】加价,是以原价5000元为单位“1”,加价后占原价的1,在加价后再打八折,现价是加价后的80%,据此列式计算。
【解答】解:5000×(1)×80%
=50000.8
≈5333.33(元)
答:现在每件5333.33元。
故答案为:5333.33。
【点评】本题考查了分数四则复合应用及折扣问题,几折就是百分之几十。
17.(2分)(2022 阜平县)三角形的面积不变,底与高成 反 比例关系;三角形的高不变,面积与底成 正 比例关系。
【考点】辨识成正比例的量与成反比例的量.
【专题】符号意识.
【答案】反,正。
【分析】两种相关联的量,如果它们的比值一定,两种量成正比例关系;如果它们的乘积一定,两种量成反比例关系。
【解答】解:因为三角形的面积=底×高÷2,
所以底×高=2×三角形的面积(一定),
符合反比例的意义,
所以三角形的面积一定,底与高成反比例关系;
因为三角形的面积÷底高(一定),是比值一定,所以它的底和高成正比例关系。
故答案为:反,正。
【点评】辨识两种量成正比例关系还是成反比例关系,就看它们是比值一定还是乘积一定。
18.(1分)(2024 晋源区)一个比例的两个外项互为倒数,如果其中一个内项为0.4,另一个内项是 2.5 。
【考点】比例的意义和基本性质.
【专题】比和比例.
【答案】2.5。
【分析】由“一个比例的两个外项互为倒数”,可知两个外项的乘积是1,根据比例的性质:两内项的积等于两外项的积,可知两个内项的积也是1;再根据“其中一个内项是0.4”,进而用两内项的积1除以一个内项0.4即得另一个内项的数值。
【解答】解:一个比例的两个外项互为倒数,乘积是1,根据两内项的积等于两外项的积,可知两个内项的积也是1,又其中一个内项是0.4,那么另一个内项是:1÷0.4=2.5;
故答案为:2.5。
【点评】此题考查比例性质的运用:在比例里,两内项的积等于两外项的积;也考查了互为倒数的两个数的乘积是1。
19.(2分)(2024春 潮州期中)一个圆柱和一个圆锥等底等高,它们的体积之和是72dm3,圆柱的体积是 54 dm3,圆锥的体积是 18 dm3。
【考点】圆锥的体积;圆柱的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】54;18。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,将圆锥的体积看作1份,则圆柱体积是3份,用它们的体积和除以(3+1),即可求出圆锥的体积,再乘3,即可求出圆柱的体积。
【解答】解:等底等高的圆柱的体积是圆锥体积的3倍,
72÷(3+1)
=72÷4
=18(立方分米)
18×3=54(立方分米)
故答案为:54;18。
【点评】此题考查圆柱与圆锥体积的计算。掌握等底等高的圆柱的体积与圆锥体积之间的数量关系是解答的关键。
20.(1分)(2022 市中区)张叔叔写一篇文章得到稿费4000元,其中800元是免税的,其余部分要按14%的税率缴税,张叔叔一共需缴税 448 元。
【考点】存款利息与纳税相关问题.
【专题】运算能力.
【答案】448元。
【分析】此题应先求出缴纳个人所得税的部分,即(4000﹣800)元,这部分钱按14%缴纳个人所得税,那么他应缴纳个人所得税:(4000﹣800)×14%,据此解答。
【解答】解:(4000﹣800)×14%
=3200×14%
=448(元)
答:张叔叔一共要缴税448元。
故答案为:448。
【点评】先求出缴纳个人所得税的部分,乘上税率即可解决问题。
21.(1分)(2023 牡丹区)按规定工资超过5000元的部分按3%缴纳个人所得税,李老师上月缴纳个人所得税45元,李老师的月工资是 6500 元。
【考点】存款利息与纳税相关问题.
【专题】运算能力.
【答案】6500。
【分析】用所缴纳的个人所得税除以税率就是应纳税的收入,然后再加上5000元就是月工资;据此解答即可。
【解答】解:45÷3%+5000
=1500+5000
=6500(元)
答:李老师的月工资是6500元。
故答案为:6500。
【点评】本题考查了“税款=应纳税的收入×税率”这一计算公式的灵活运用。
22.(2分)(2024 惠州)一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个 圆柱体 ,这个立体图形的体积是 141.3 cm3。
【考点】圆柱的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】圆柱体,141.3。
【分析】一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个圆柱体,它的底面半径是3cm,高是5cm,再根据圆柱体积=底面积×高,即可解答。
【解答】解:一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个圆柱体。
3.14×3×3×5
=28.26×5
=141.3(cm3)
答:一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个圆柱体,这个立体图形的体积是141.3cm3。
故答案为:圆柱体,141.3。
【点评】本题考查的是圆柱体积的计算,熟记公式是解答关键。
23.(1分)一副扑克牌有54张,最少要抽取 29 张牌,才能保证其中至少有3张牌有相同的点数。
【考点】抽屉原理.
【专题】压轴题;模型思想;应用意识.
【答案】29。
【分析】建立抽屉:一副扑克牌有54张,大小王不相同,那么(54﹣2)÷4=13,所以一共有13+2=15个抽屉;分别是:1、2、3、…K、小王、大王,由此利用抽屉原理考虑最差情况,即可进行解答。
【解答】解:建立抽屉:54张牌,根据点数特点可以分别看作15个抽屉,
考虑最差情况:小王、大王先抽取,剩下的每个抽屉都抽取了2张牌,共抽出13×2=26张牌,
此时再任意抽取1张,就有3张牌点数相同,所以最少要抽取:
2+13×2+1
=2+26+1
=29(张)
答:最少要抽29张牌,方能保证其中至少有3张牌有相同的点数。
故答案为:29。
【点评】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑.
四.计算题(共3小题,满分31分)
24.(10分)(2024 濉溪县)直接写得数。
1÷0.25= 5.6= 1+10%= 401×49≈
1.6×0.3= 0.33=
【考点】小数除法;分数的加法和减法;分数乘法;分数除法;数的估算;小数乘法.
【专题】运算能力.
【答案】4;;3.2;1.1;20000;0.48;;25;;0.027。
【分析】根据整数、小数、分数、百分数加、减、乘、除的计算方法和乘方的计算方法,依次口算结果。
【解答】解:
1÷0.25=4 5.6=3.2 1+10%=1.1 401×49≈20000
1.6×0.3=0.48 25 0.33=0.027
【点评】本题解题的关键是熟练掌握整数、小数、分数、百分数加、减、乘、除的计算方法和乘方的计算方法。
25.(9分)(2024春 夏邑县校级期中)解方程。
(1)x:5.4=8:0.6
(2)
(3)
【考点】解比例.
【专题】应用题;应用意识.
【答案】(1)x=72;(2)x=24;(3)x=30。
【分析】(1)根据比例的基本性质,把式子转化为0.6x=5.4×8,再化简方程,最后根据等式的性质,方程两边同时除以0.6即可;
(2)根据比例的基本性质,把式子转化为x9,再化简方程,最后根据等式的性质,方程两边同时除以即可;
(3)根据比例的基本性质,把式子转化为0.6x=12×1.5,再化简方程,最后根据等式的性质,方程两边同时除以0.6即可。
【解答】解:(1)x:5.4=8:0.6
0.6x=5.4×8
0.6x=43.2
0.6x÷0.6=43.2÷0.6
x=72
(2)
x9
x=6
x6
x=6×4
x=24
(3)
0.6x=12×1.5
0.6x=18
0.6x÷0.6=18÷0.6
x=30
【点评】解答此题要运用等式的基本性质。
26.(12分)(2024 渝北区)计算题。
(1)3.1 (2)[()]
(3) (4)[15﹣()×24]
【考点】分数的四则混合运算;运算定律与简便运算.
【专题】计算题;运算能力.
【答案】(1)0.5;(2);(3)1;(4)7。
【分析】(1)乘法和除法同时运算,然后再算减法和加法;
(2)先算小括号的加法,再算中括号的除法,然后算中括号的减法,最后算乘法;
(3)先约分,然后逆用乘法分配律即可简算;
(4)中括号利用乘法分配律,然后中括号外面减号约分即可简算。
【解答】解:(1)3.1
10.1
0.1
0.1
=0.4+0.1
=0.5
(2)[()]
=[(0.925+0.075)]
=[1]
=[]
(3)
()
1
=1
(4)[15﹣()×24]
=[15242424]÷0.5
=[15﹣9+4﹣6]÷0.5﹣1
=4÷0.5﹣1
=8﹣1
=7
【点评】本题考查了分数的四则混合运算以及简便运算方法。
五.操作题(共2小题,满分11分)
27.(5分)(2024秋 南昌县期末)图书馆在小兰家南偏东50°方向上,距离是450m。
(1)根据上面的描述,在平面图上标出图书馆的位置。
(2)小红家在图书馆的正东方向上,小红家不可能在小兰家 C 方向上。
A.东偏南
B.南偏东
C.南偏西
【考点】图上距离与实际距离的换算(比例尺的应用);用角度表示方向.
【专题】应用意识.
【答案】(1)如图所示:
(2)C。
【分析】(1)根据实际距离和比例尺,计算图书馆与学校的图上距离,然后根据图上确定方向的方法,结合题目所给信息,确定各地的位置即可。
(2)因为图上距离1厘米表示实际距离200米,于是即可求出两地之间的实际距离,进而依据两地之间的方向关系,即可描述出它们的位置关系。
【解答】解:(1)450÷150=3(厘米)
如图所示:
(2)小红家在图书馆的正东方向上,小红家不可能在小兰家南偏西方向上。
故答案为:C。
【点评】此题主要考查依据方向(角度)和距离判定物体位置的方法以及线段比例尺的意义。
28.(6分)(2024春 惠民县期中)计算圆柱的表面积和圆锥的体积。(单位:厘米)
(1)
(2)
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;应用意识.
【答案】(1)301.44平方厘米;(2)3140立方厘米。
【分析】(1)根据圆柱表面积=侧面积+底面积×2,即可解答;
(2)根据圆锥体积=底面积×高÷3,即可解答。
【解答】解:(1)3.14×8×8+3.14×(8÷2)×(8÷2)×2
=200.96+100.48
=301.44(平方厘米)
答:圆柱的表面积是301.44平方厘米。
(2)3.14×10×10×30÷3
=9420÷3
=3140(立方厘米)
答:圆锥体积是3140立方厘米。
【点评】本题考查的是圆柱表面积和圆锥体积的计算,熟记公式是解答关键。
六.应用题(共3小题,满分23分)
29.(4分)(2024 武汉模拟)从A城到B城,在比例尺是1:50000000的图上量得两地间的距离是6.3cm。一架飞机早上8时从A城飞往B城,如果每小时飞行700千米,中途休息1小时30分,请问到达B城是什么时间?
【考点】比例尺应用题.
【专题】运算能力.
【答案】14时。
【分析】已知图上距离和比例尺,可以求出实际距离,图上距离÷比例尺=实际距离,然后用实际距离÷飞机的速度=飞行的时间,最后用出发的时刻+中途休息的时间+飞行的时间=到达B城的时刻,据此列式解答。
【解答】解:6.3
=315000000(cm)
=3150(千米)
3150÷700=4.5(小时)
8时+1小时30分+4小时30分=14时
答:到达B城是14时。
【点评】此题主要考查了比例尺的应用,和时间的计算,解答此题的关键是先求出两地之间的实际距离。
30.(4分)(2023 七里河区模拟)某商场进了50件防晒衣,每件的进价为100元,售价为160元,在卖出60%后,由于天气转冷而滞销,店主将余下的打五折出售,并且全部售完。请问:该商店是亏了还是赚了?亏还是赚了多少钱?
【考点】百分数的实际应用.
【专题】应用意识.
【答案】赚了,1400元。
【分析】先用50乘60%再乘160,求出按售价160元卖的钱数;然后用50乘(1﹣60%)再乘(160×50%),求出余下的部分共卖的钱数;将两部分钱数求和后再与50×100元比较大小,即可知道该商店是亏了还是赚了,最后求出赔或赚的钱数即可。
【解答】解:五折=50%
50×60%×160+50×(1﹣60%)×(160×50%)
=4800+1600
=6400(元)
50×100=5000(元)
6400>5000
6400﹣5000=1400(元)
答:该商店赚了,赚了1400元。
【点评】本题考查了利用百分数乘法及比较数的大小解决盈亏问题,准确分析题目中的数量关系是关键。
31.(4分)(2022 北辰区)一辆货车箱是一个长方体,它的长是4米,宽是1.5米,高是4米,装满一车沙,卸后堆成一个高是8分米的圆锥体,沙堆底面面积是多少平方米?
【考点】圆锥的体积;长方体和正方体的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】90平方米。
【分析】车厢的长是4米,宽是1.5米,高是4米,装满沙子后,这些沙子的形状就是一个长和高都是4米、宽1.5米的长方体,根据长方体的体积公式“V=abh”即可求出这些沙子的体积;把这车沙子不论堆成什么形状它的体积不会改变,根据圆锥的体积公式“Vπr2h”,用这些沙子的体积乘3再除以高就是它的底面积。
【解答】解:8分米=0.8米
(4×1.5×4)×3÷0.8
=24×3÷0.8
=72÷0.8
=90(平方米)
答:它的底面积是90平方米。
【点评】此题是考查长方体、圆锥体的体积计算.关键抓住这些沙子不论堆成什么形状体积不变这一特征及圆锥体积计算公式的灵活运用。
32.(4分)六年级全体同学参加升旗仪式,按各列人数相等的规定排列站队,如果每列站25人,要排24列。 要排12列,每列站多少人?(答案不唯一) ?
根据以上信息,请你先补充一个条件,并提出一个能用反比例关系解答的问题,最后再解答。(条件和问题直接补充在横线上)
【考点】正、反比例应用题.
【专题】开放型;运算能力;应用意识.
【答案】要排12列,每列站多少人?(答案不唯一)50人。
【分析】如果两个相关联的量乘积一定,说明它们成反比例关系。所以根据=每列人数×列数=总人数(一定),进行补充条件。补充的条件如果列数已知,则求每列多少人;如果每列人数已知,则求排多少列。据此解答。
【解答】解:补充条件:要排12列,每列站多少人?(答案不唯一)
解:设每列站x人。
12x=24×25
12x=600
x=50
答:每列站50人。
故答案为:要排12列,每列站多少人?(答案不唯一)
【点评】解答此题的主要依据是:若两个量的乘积一定,则这两个量成反比例,于是可以列比例求解。
33.(4分)(2022秋 海门区期末)王老师准备在网上购买一套书(共5册)。A网店和B网店的价格信息如图。王老师在哪家网店购买比较合算?
A网店:每册19元,免运费
B网店:每套80元,运费8元
【考点】最优化问题.
【专题】压轴题;应用意识.
【答案】B网店。
【分析】根据A网店和B网店的价格,求出在两家网店购买的总价,再比较大小即可。
【解答】解:A 网店:19×5=95(元)
B网店:80+8=88(元)
88<95
所以在B网店购买合算。
答:王老师在B网店购买比较合算。
【点评】本题考查了简单的优化问题。
34.(3分)一文具店购进了一批钢笔,以每支19.5元的价格出售,当卖出56%时,老板发现还差54元就能收回全部成本,于是决定降价20%销售,很快就全部售出,最终共获得利润289.2元。问:文具店购进这批钢笔的价格是每支多少元?
【考点】利润和利息问题.
【专题】分数百分数应用题;应用意识.
【答案】12元。
【分析】已知全部售出后,总共获得利润289.2元,在这之前是还差54元才可以收回全部成本,说明又卖出的这部分的总额为289.2+54=343.2(元);又已知每支钢笔的原价是19.5元,降价20%是指按原价的(1﹣20%)出售,根据总价÷单价=数量,求出卖出的这部分钢笔的数量,而这一部分钢笔的数量相当于总数的(1﹣56%),据此求出这批钢笔的总支数;再用这批钢笔的售价减去利润,求出这批钢笔的进价,进而求出每支钢笔的进价。
【解答】解:这批钢笔的总数量:
(289.2+54)÷[19.2×(1﹣20%)]
=343.2÷15.6
=22(支)
22÷(1﹣56%)
=22÷0.44
=50(支)
每支钢笔的购进价:
[19.5×(50×56%)+(289.2+54)﹣289.2]÷50
=[546+343.2﹣289.2]÷50
=600÷50
=12(元)
答:文具店购进这批钢笔的价格是每支12元。
【点评】此题条件较复杂,需认真分析,先求出这批钢笔的数量是解决此题的关键。
第1页(共1页)
一.选择题(共5小题,满分5分,每小题1分)
1.(1分)(2022秋 海州区期末)连云港某天的最高气温是7℃,最低气温是﹣2℃,这天气温最高和最低相差( )
A.9℃ B.5℃ C.6℃ D.7℃
2.(1分)(2022春 沂源县期末)某商厦出售两台不同品牌的空调,其中一台赚了20%,另一台赔了20%,这两台空调的售价都是3600元,那么在这次销售中商厦( )
A.赚了 B.赔了
C.不赚不赔 D.不确定赔赚
3.(1分)(2022春 杭州期中)底面积相等的圆柱和圆锥,它们体积也相等,圆锥的高是9cm,圆柱的高是( )cm。
A.3 B.1.5 C.18 D.24
4.(1分)(2022 德宏州)等底等高的圆柱和圆锥体积之和是20m3,圆锥体积是( )
A.5m3 B.20m3 C.15m3 D.5m2
5.(1分)(2023 平果市)给一个正方体的六个面图上红、黄、蓝、绿四种颜色(每个面只涂一种颜色),不论怎么涂,至少有( )个面涂的颜色相同。
A.5 B.4 C.3 D.2
二.判断题(共4小题,满分4分,每小题1分)
6.(1分)(2023 兴庆区)数轴上,右边的数总比左边的数大,﹣1.5和1.5在数轴上与0的距离是相等的。
7.(1分)(2021春 华容区期中)满100减40,实际上就是打六折。
8.(1分)(2023春 金昌期中)在72:0.9=16:2中,0.9和16是比例的内项,72和2是比例的外项。
9.(1分)(2022 张家川县模拟)若xy,那么x和y成反比例。
三.填空题(共14小题,满分25分)
10.(1分)(2024 遵义)新蒲新区是一个适宜人居的城市,冬季白天的最高气温是14℃,到了晚上12时,气温下降了16℃,该地当晚12时的气温是 ℃。
11.(2分)(2022 双桥区)如图是买彩带米数和应付钱数之间关系图。买彩带米数和应付钱数成 比例关系;照这样计算,付40元,是买了 米彩带。
12.(2分)(2024 龙泉市)如图,将一个圆柱形包装盒的侧面沿着虚线剪开,得到一个平行四边形,这个包装盒的侧面积是 平方厘米,最多能容纳 立方厘米的物体。
13.(1分)(2021春 方城县期中)如果把一个高是10cm的圆柱切拼成一个近似的长方体后(如图),则表面积增加了60cm2,原来圆柱的体积是 cm3。
14.(4分)(2024 衡南县)9: =15÷ =60%= 折= 成。
15.(4分)(2023秋 西乡县月考)甲数是40,乙数是50,乙数是甲数的 %,甲数是乙数的 %。甲数比乙数少 %,乙数比甲数多 %。
16.(1分)(2024 镇江模拟)一种电器原来每件5000元,加价后再打八折,现在每件 元。
17.(2分)(2022 阜平县)三角形的面积不变,底与高成 比例关系;三角形的高不变,面积与底成 比例关系。
18.(1分)(2024 晋源区)一个比例的两个外项互为倒数,如果其中一个内项为0.4,另一个内项是 。
19.(2分)(2024春 潮州期中)一个圆柱和一个圆锥等底等高,它们的体积之和是72dm3,圆柱的体积是 dm3,圆锥的体积是 dm3。
20.(1分)(2022 市中区)张叔叔写一篇文章得到稿费4000元,其中800元是免税的,其余部分要按14%的税率缴税,张叔叔一共需缴税 元。
21.(1分)(2023 牡丹区)按规定工资超过5000元的部分按3%缴纳个人所得税,李老师上月缴纳个人所得税45元,李老师的月工资是 元。
22.(2分)(2024 惠州)一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个 ,这个立体图形的体积是 cm3。
23.(1分)一副扑克牌有54张,最少要抽取 张牌,才能保证其中至少有3张牌有相同的点数。
四.计算题(共3小题,满分31分)
24.(10分)(2024 濉溪县)直接写得数。
1÷0.25= 5.6= 1+10%= 401×49≈
1.6×0.3= 0.33=
25.(9分)(2024春 夏邑县校级期中)解方程。
(1)x:5.4=8:0.6
(2)
(3)
26.(12分)(2024 渝北区)计算题。
(1)3.1 (2)[()]
(3) (4)[15﹣()×24]
五.操作题(共2小题,满分11分)
27.(5分)(2024秋 南昌县期末)图书馆在小兰家南偏东50°方向上,距离是450m。
(1)根据上面的描述,在平面图上标出图书馆的位置。
(2)小红家在图书馆的正东方向上,小红家不可能在小兰家 方向上。
A.东偏南
B.南偏东
C.南偏西
28.(6分)(2024春 惠民县期中)计算圆柱的表面积和圆锥的体积。(单位:厘米)
(1)
(2)
六.应用题(共6小题,满分23分)
29.(4分)(2024 武汉模拟)从A城到B城,在比例尺是1:50000000的图上量得两地间的距离是6.3cm。一架飞机早上8时从A城飞往B城,如果每小时飞行700千米,中途休息1小时30分,请问到达B城是什么时间?
30.(4分)(2023 七里河区模拟)某商场进了50件防晒衣,每件的进价为100元,售价为160元,在卖出60%后,由于天气转冷而滞销,店主将余下的打五折出售,并且全部售完。请问:该商店是亏了还是赚了?亏还是赚了多少钱?
31.(4分)(2022 北辰区)一辆货车箱是一个长方体,它的长是4米,宽是1.5米,高是4米,装满一车沙,卸后堆成一个高是8分米的圆锥体,沙堆底面面积是多少平方米?
32.(4分)六年级全体同学参加升旗仪式,按各列人数相等的规定排列站队,如果每列站25人,要排24列。 ?
根据以上信息,请你先补充一个条件,并提出一个能用反比例关系解答的问题,最后再解答。(条件和问题直接补充在横线上)
33.(4分)(2022秋 海门区期末)王老师准备在网上购买一套书(共5册)。A网店和B网店的价格信息如图。王老师在哪家网店购买比较合算?
A网店:每册19元,免运费
B网店:每套80元,运费8元
34.(3分)一文具店购进了一批钢笔,以每支19.5元的价格出售,当卖出56%时,老板发现还差54元就能收回全部成本,于是决定降价20%销售,很快就全部售出,最终共获得利润289.2元。问:文具店购进这批钢笔的价格是每支多少元?
湖北省武汉市2024-2025学年六年级下学期期中综合测试数学试卷
参考答案与试题解析
一.选择题(共5小题,满分5分,每小题1分)
1.(1分)(2022秋 海州区期末)连云港某天的最高气温是7℃,最低气温是﹣2℃,这天气温最高和最低相差( )
A.9℃ B.5℃ C.6℃ D.7℃
【考点】正、负数的运算.
【专题】整数的认识;数据分析观念.
【答案】A
【分析】结合数轴理解可知,最高气温是7℃到0℃的距离是7,最低气温是﹣2℃到0℃的距离是2,那么7℃到﹣2℃的距离是7+2=9,也就是这天气温最高和最大相差9℃。据此解答。
【解答】解:7+2=9(℃)
连云港某天的最高气温是7℃,最低气温是﹣2℃,这天气温最高和最低相差9℃。
故选:A。
【点评】本题考查负数的认识,关键结果数轴观察两数之间的距离是多少来解答。
2.(1分)(2022春 沂源县期末)某商厦出售两台不同品牌的空调,其中一台赚了20%,另一台赔了20%,这两台空调的售价都是3600元,那么在这次销售中商厦( )
A.赚了 B.赔了
C.不赚不赔 D.不确定赔赚
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】B
【分析】先把赚钱空调的进价看成单位“1”,则售价是进价的(1+20%),由此用除法求出进价,再求出它赚了多少钱;
再把赔钱空调的进价看成单位“1”,则售价是进价的(1﹣20%),由此用除法求出进价,再求出它赔了多少钱;
再把赚的钱数和亏的钱数比较即可。
【解答】解:3600÷(1+20%)
=3600÷120%
=3000(元)
赚了:3600﹣3000=600(元)
3600÷(1﹣20%)
=3600÷80%
=4500(元)
亏了:4500﹣3600=900(元)
因为900>600,所以卖这两台空调是赔了。
故选:B。
【点评】解答此题的关键是分清两个不同的单位“1”,分别求出进价,进而求解。
3.(1分)(2022春 杭州期中)底面积相等的圆柱和圆锥,它们体积也相等,圆锥的高是9cm,圆柱的高是( )cm。
A.3 B.1.5 C.18 D.24
【考点】圆锥的体积;圆柱的体积.
【专题】空间观念;推理能力;应用意识.
【答案】A
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此解答即可。
【解答】解:93(厘米)
答:圆柱的高是3厘米。
故选:A。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
4.(1分)(2022 德宏州)等底等高的圆柱和圆锥体积之和是20m3,圆锥体积是( )
A.5m3 B.20m3 C.15m3 D.5m2
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】应用意识.
【答案】A
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积和相当于圆锥体积的(3+1)倍。根据已知一个数的几倍是多少,求这个数,用除法解答。
【解答】解:20÷(3+1)
=20÷4
=5(立方厘米)
答:圆锥的体积是5立方厘米。
故选:A。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
5.(1分)(2023 平果市)给一个正方体的六个面图上红、黄、蓝、绿四种颜色(每个面只涂一种颜色),不论怎么涂,至少有( )个面涂的颜色相同。
A.5 B.4 C.3 D.2
【考点】抽屉原理.
【专题】压轴题;模型思想;应用意识.
【答案】D
【分析】把红、黄、蓝、绿四种颜色看做4个抽屉,6个面看做6个元素,利用抽屉原理最差情况:要使涂的颜色相同的面数最少,只要使每个抽屉的元素数尽量平均,即可解答。
【解答】解:6÷4=1(个)......2(个)
1+1=2(个)
答:至少有2个面涂的颜色相同。
故选:D。
【点评】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑。
二.判断题(共4小题,满分4分,每小题1分)
6.(1分)(2023 兴庆区)数轴上,右边的数总比左边的数大,﹣1.5和1.5在数轴上与0的距离是相等的。 √
【考点】数轴的认识.
【专题】整数的认识;数据分析观念.
【答案】√
【分析】
像这样表示出正数、0和负数的直线,叫作数轴。
直线上0表示起点,0右边的数表示正数,左边的数表示负数;因此,数轴上,右边的数总是比左边的大;
用有正数和负数的直线可以表示距离和相反的方向;﹣1.5位于0的左边,距离0有1.5个单位的距离、1.5在数轴的右边,距离0有1.5个单位的距离。
【解答】解:由分析得:数轴上,右边的数总比左边的数大,﹣1.5和1.5在数轴上与0的距离是相等的;原题说法正确。
故答案为:√。
【点评】考查了对于数轴上正数、负数的位置,及正负数与0的距离的关系的理解,需要充分了解数轴的概念、特征。
7.(1分)(2021春 华容区期中)满100减40,实际上就是打六折。 √
【考点】百分数的实际应用.
【专题】应用意识.
【答案】√
【分析】把原价看作单位“1”,打几折就是现价是原价的百分之几十,把数代入计算即可。
【解答】解:(100﹣40)÷100
=60÷100
=60%
=六折
所以每满100元减40元,刚好满100元时才是打六折,原题说法正确。
故答案为:√。
【点评】本题主要考查百分数的应用,关键找到单位“1”,利用数量关系做题。
8.(1分)(2023春 金昌期中)在72:0.9=16:2中,0.9和16是比例的内项,72和2是比例的外项。 ×
【考点】比例的意义和基本性质.
【专题】比和比例;数据分析观念.
【答案】×
【分析】表示两个比相等的式子,叫做比例,据此解答。
【解答】解:因为72:0.9=80,16:2=8,比值相等,所以72:0.9与16:2不能组成比例,原题说法错误。
故答案为:×。
【点评】本题主要考查比例的意义,注意判断能否组成比例可以用求比值的方法,求出比值,比值相等两个比就能组成比例。
9.(1分)(2022 张家川县模拟)若xy,那么x和y成反比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:因为xy,所以xy
是x、y的乘积一定,
所以x、y成反比例。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
三.填空题(共14小题,满分25分)
10.(1分)(2024 遵义)新蒲新区是一个适宜人居的城市,冬季白天的最高气温是14℃,到了晚上12时,气温下降了16℃,该地当晚12时的气温是 ﹣2 ℃。
【考点】正、负数的运算.
【专题】运算顺序及法则;数据分析观念.
【答案】﹣2。
【分析】利用白天的温度减去下降的温度即可。
【解答】解:14℃﹣16℃=﹣2℃
答:该地当晚12时的气温是﹣2℃。
故答案为:﹣2。
【点评】本题考查了正负数的运算及应用。
11.(2分)(2022 双桥区)如图是买彩带米数和应付钱数之间关系图。买彩带米数和应付钱数成 正 比例关系;照这样计算,付40元,是买了 10 米彩带。
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】正,10。
【分析】买彩带米数和应付钱数之间关系图像是一条射线,所以买彩带米数和应付钱数之间关系成正比例关系。据此解答。
【解答】解:因为买彩带米数和应付钱数之间关系图像是一条射线,所以买彩带米数和应付钱数之间关系成正比例关系。
设付40元,是买了x米彩带,得:
1:4=x:40
4x=1×40
4x=40
4x÷4=40÷4
x=10
答:付40元,是买了10米彩带。
故答案为:正,10。
【点评】此题考查了正比例关系的图像积用比例解决问题,需灵活掌握。
12.(2分)(2024 龙泉市)如图,将一个圆柱形包装盒的侧面沿着虚线剪开,得到一个平行四边形,这个包装盒的侧面积是 502.4 平方厘米,最多能容纳 1004.8 立方厘米的物体。
【考点】圆柱的侧面积、表面积和体积.
【专题】应用题;应用意识.
【答案】(1)502.4;(2)1004.8。
【分析】(1)通过观察图形可知,这个圆柱的侧面展开后是一个底是25.12厘米,高是20厘米的平行四边形,根据平行四边形的面积公式:S=ah,把数据代入公式解答。
(2)根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式解答。
【解答】解:(1)25.12×20=502.4(平方厘米)
答:它的侧面积是502.4平方厘米。
(2)3.14×(25.12÷3.14÷2)2×20
=3.14×16×20
=50.24×20
=1004.8(立方厘米)
答:这个包装盒最多能容纳1004.8立方厘米的物体。
故答案为:(1)502.4;(2)1004.8。
【点评】此题主要考查圆柱的侧面积公式、圆柱的体积(容积)公式的灵活运用,关键是熟记公式。
13.(1分)(2021春 方城县期中)如果把一个高是10cm的圆柱切拼成一个近似的长方体后(如图),则表面积增加了60cm2,原来圆柱的体积是 282.6 cm3。
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;几何直观.
【答案】282.6。
【分析】根据圆柱体积公式的推导过程可知,把圆柱切拼成一个近似长方体体积不变,但是拼成的长方体的表面积比圆柱的表面积增加了两个长方形的面积,每个长方形的长等于圆柱的高,宽等于圆柱的底面半径,已知拼成后长方体的表面积比原来圆柱的表面积增加了60cm2,据此可以求出圆柱的底面半径,然后根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:60÷2÷10
=30÷10
=3(cm)
3.14×32×10
=3.14×9×10
=282.6(cm3)
答:原来圆柱的体积是282.6cm3。
故答案为:282.6。
【点评】此题考查的目的是理解掌握圆柱体积公式的推导过程,以及圆柱的表面积、体积公式的灵活运用,关键是熟记公式。
14.(4分)(2024 衡南县)9: 15 =15÷ 25 =60%= 六 折= 六 成。
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化;折扣;成数.
【专题】数感.
【答案】15,25,六,六。
【分析】把60%化成分母是100的分数并化简是,根据比与分数的关系3:5,再根据比的性质比的前、后项都乘3就是9:15;根据分数与除法的关系3÷5,再根据商不变的性质被除数、除数都乘5就是15÷25;根据折扣的意义60%就是六折;根据成数的意义60%就是六成。
【解答】解:9:15=15÷25=60%=六折=六成
故答案为:15,25,六,六。
【点评】此题主要是考查除法、比、百分数、折扣、成数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
15.(4分)(2023秋 西乡县月考)甲数是40,乙数是50,乙数是甲数的 125 %,甲数是乙数的 80 %。甲数比乙数少 20 %,乙数比甲数多 25 %。
【考点】百分数的加减乘除运算.
【专题】运算能力.
【答案】125,80,20,25。
【分析】(1)把甲数看作单位“1”,用乙数除以甲数即可解答;
(2)把乙数看作单位“1”,用甲数除以乙数即可解答;
(3)把乙数看作单位“1”,先求出乙数比甲数多的数,再除以乙数即可解答;
(4)把甲数看作单位“1”,先求出乙数比甲数多的数,再除以甲数即可解答。
【解答】解:(1)50÷40=125%
答:乙数是甲数125%。
(2)40÷50=80%
答:甲数是乙数80%。
(3)(50﹣40)÷50
=10÷50
=20%
答:甲数比乙数少20%。
(4)(50﹣40)÷40
=10÷40
=25%
答:乙数比甲数多25%。
故答案为:125,80,20,25。
【点评】本题主要考查了百分数除法的意义,解答本题的关键是明确以谁为标准量。
16.(1分)(2024 镇江模拟)一种电器原来每件5000元,加价后再打八折,现在每件 5333.33 元。
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】5333.33。
【分析】加价,是以原价5000元为单位“1”,加价后占原价的1,在加价后再打八折,现价是加价后的80%,据此列式计算。
【解答】解:5000×(1)×80%
=50000.8
≈5333.33(元)
答:现在每件5333.33元。
故答案为:5333.33。
【点评】本题考查了分数四则复合应用及折扣问题,几折就是百分之几十。
17.(2分)(2022 阜平县)三角形的面积不变,底与高成 反 比例关系;三角形的高不变,面积与底成 正 比例关系。
【考点】辨识成正比例的量与成反比例的量.
【专题】符号意识.
【答案】反,正。
【分析】两种相关联的量,如果它们的比值一定,两种量成正比例关系;如果它们的乘积一定,两种量成反比例关系。
【解答】解:因为三角形的面积=底×高÷2,
所以底×高=2×三角形的面积(一定),
符合反比例的意义,
所以三角形的面积一定,底与高成反比例关系;
因为三角形的面积÷底高(一定),是比值一定,所以它的底和高成正比例关系。
故答案为:反,正。
【点评】辨识两种量成正比例关系还是成反比例关系,就看它们是比值一定还是乘积一定。
18.(1分)(2024 晋源区)一个比例的两个外项互为倒数,如果其中一个内项为0.4,另一个内项是 2.5 。
【考点】比例的意义和基本性质.
【专题】比和比例.
【答案】2.5。
【分析】由“一个比例的两个外项互为倒数”,可知两个外项的乘积是1,根据比例的性质:两内项的积等于两外项的积,可知两个内项的积也是1;再根据“其中一个内项是0.4”,进而用两内项的积1除以一个内项0.4即得另一个内项的数值。
【解答】解:一个比例的两个外项互为倒数,乘积是1,根据两内项的积等于两外项的积,可知两个内项的积也是1,又其中一个内项是0.4,那么另一个内项是:1÷0.4=2.5;
故答案为:2.5。
【点评】此题考查比例性质的运用:在比例里,两内项的积等于两外项的积;也考查了互为倒数的两个数的乘积是1。
19.(2分)(2024春 潮州期中)一个圆柱和一个圆锥等底等高,它们的体积之和是72dm3,圆柱的体积是 54 dm3,圆锥的体积是 18 dm3。
【考点】圆锥的体积;圆柱的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】54;18。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,将圆锥的体积看作1份,则圆柱体积是3份,用它们的体积和除以(3+1),即可求出圆锥的体积,再乘3,即可求出圆柱的体积。
【解答】解:等底等高的圆柱的体积是圆锥体积的3倍,
72÷(3+1)
=72÷4
=18(立方分米)
18×3=54(立方分米)
故答案为:54;18。
【点评】此题考查圆柱与圆锥体积的计算。掌握等底等高的圆柱的体积与圆锥体积之间的数量关系是解答的关键。
20.(1分)(2022 市中区)张叔叔写一篇文章得到稿费4000元,其中800元是免税的,其余部分要按14%的税率缴税,张叔叔一共需缴税 448 元。
【考点】存款利息与纳税相关问题.
【专题】运算能力.
【答案】448元。
【分析】此题应先求出缴纳个人所得税的部分,即(4000﹣800)元,这部分钱按14%缴纳个人所得税,那么他应缴纳个人所得税:(4000﹣800)×14%,据此解答。
【解答】解:(4000﹣800)×14%
=3200×14%
=448(元)
答:张叔叔一共要缴税448元。
故答案为:448。
【点评】先求出缴纳个人所得税的部分,乘上税率即可解决问题。
21.(1分)(2023 牡丹区)按规定工资超过5000元的部分按3%缴纳个人所得税,李老师上月缴纳个人所得税45元,李老师的月工资是 6500 元。
【考点】存款利息与纳税相关问题.
【专题】运算能力.
【答案】6500。
【分析】用所缴纳的个人所得税除以税率就是应纳税的收入,然后再加上5000元就是月工资;据此解答即可。
【解答】解:45÷3%+5000
=1500+5000
=6500(元)
答:李老师的月工资是6500元。
故答案为:6500。
【点评】本题考查了“税款=应纳税的收入×税率”这一计算公式的灵活运用。
22.(2分)(2024 惠州)一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个 圆柱体 ,这个立体图形的体积是 141.3 cm3。
【考点】圆柱的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】圆柱体,141.3。
【分析】一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个圆柱体,它的底面半径是3cm,高是5cm,再根据圆柱体积=底面积×高,即可解答。
【解答】解:一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个圆柱体。
3.14×3×3×5
=28.26×5
=141.3(cm3)
答:一张长方形的纸,长是5cm,宽是3cm,以长为轴旋转一周形成一个圆柱体,这个立体图形的体积是141.3cm3。
故答案为:圆柱体,141.3。
【点评】本题考查的是圆柱体积的计算,熟记公式是解答关键。
23.(1分)一副扑克牌有54张,最少要抽取 29 张牌,才能保证其中至少有3张牌有相同的点数。
【考点】抽屉原理.
【专题】压轴题;模型思想;应用意识.
【答案】29。
【分析】建立抽屉:一副扑克牌有54张,大小王不相同,那么(54﹣2)÷4=13,所以一共有13+2=15个抽屉;分别是:1、2、3、…K、小王、大王,由此利用抽屉原理考虑最差情况,即可进行解答。
【解答】解:建立抽屉:54张牌,根据点数特点可以分别看作15个抽屉,
考虑最差情况:小王、大王先抽取,剩下的每个抽屉都抽取了2张牌,共抽出13×2=26张牌,
此时再任意抽取1张,就有3张牌点数相同,所以最少要抽取:
2+13×2+1
=2+26+1
=29(张)
答:最少要抽29张牌,方能保证其中至少有3张牌有相同的点数。
故答案为:29。
【点评】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑.
四.计算题(共3小题,满分31分)
24.(10分)(2024 濉溪县)直接写得数。
1÷0.25= 5.6= 1+10%= 401×49≈
1.6×0.3= 0.33=
【考点】小数除法;分数的加法和减法;分数乘法;分数除法;数的估算;小数乘法.
【专题】运算能力.
【答案】4;;3.2;1.1;20000;0.48;;25;;0.027。
【分析】根据整数、小数、分数、百分数加、减、乘、除的计算方法和乘方的计算方法,依次口算结果。
【解答】解:
1÷0.25=4 5.6=3.2 1+10%=1.1 401×49≈20000
1.6×0.3=0.48 25 0.33=0.027
【点评】本题解题的关键是熟练掌握整数、小数、分数、百分数加、减、乘、除的计算方法和乘方的计算方法。
25.(9分)(2024春 夏邑县校级期中)解方程。
(1)x:5.4=8:0.6
(2)
(3)
【考点】解比例.
【专题】应用题;应用意识.
【答案】(1)x=72;(2)x=24;(3)x=30。
【分析】(1)根据比例的基本性质,把式子转化为0.6x=5.4×8,再化简方程,最后根据等式的性质,方程两边同时除以0.6即可;
(2)根据比例的基本性质,把式子转化为x9,再化简方程,最后根据等式的性质,方程两边同时除以即可;
(3)根据比例的基本性质,把式子转化为0.6x=12×1.5,再化简方程,最后根据等式的性质,方程两边同时除以0.6即可。
【解答】解:(1)x:5.4=8:0.6
0.6x=5.4×8
0.6x=43.2
0.6x÷0.6=43.2÷0.6
x=72
(2)
x9
x=6
x6
x=6×4
x=24
(3)
0.6x=12×1.5
0.6x=18
0.6x÷0.6=18÷0.6
x=30
【点评】解答此题要运用等式的基本性质。
26.(12分)(2024 渝北区)计算题。
(1)3.1 (2)[()]
(3) (4)[15﹣()×24]
【考点】分数的四则混合运算;运算定律与简便运算.
【专题】计算题;运算能力.
【答案】(1)0.5;(2);(3)1;(4)7。
【分析】(1)乘法和除法同时运算,然后再算减法和加法;
(2)先算小括号的加法,再算中括号的除法,然后算中括号的减法,最后算乘法;
(3)先约分,然后逆用乘法分配律即可简算;
(4)中括号利用乘法分配律,然后中括号外面减号约分即可简算。
【解答】解:(1)3.1
10.1
0.1
0.1
=0.4+0.1
=0.5
(2)[()]
=[(0.925+0.075)]
=[1]
=[]
(3)
()
1
=1
(4)[15﹣()×24]
=[15242424]÷0.5
=[15﹣9+4﹣6]÷0.5﹣1
=4÷0.5﹣1
=8﹣1
=7
【点评】本题考查了分数的四则混合运算以及简便运算方法。
五.操作题(共2小题,满分11分)
27.(5分)(2024秋 南昌县期末)图书馆在小兰家南偏东50°方向上,距离是450m。
(1)根据上面的描述,在平面图上标出图书馆的位置。
(2)小红家在图书馆的正东方向上,小红家不可能在小兰家 C 方向上。
A.东偏南
B.南偏东
C.南偏西
【考点】图上距离与实际距离的换算(比例尺的应用);用角度表示方向.
【专题】应用意识.
【答案】(1)如图所示:
(2)C。
【分析】(1)根据实际距离和比例尺,计算图书馆与学校的图上距离,然后根据图上确定方向的方法,结合题目所给信息,确定各地的位置即可。
(2)因为图上距离1厘米表示实际距离200米,于是即可求出两地之间的实际距离,进而依据两地之间的方向关系,即可描述出它们的位置关系。
【解答】解:(1)450÷150=3(厘米)
如图所示:
(2)小红家在图书馆的正东方向上,小红家不可能在小兰家南偏西方向上。
故答案为:C。
【点评】此题主要考查依据方向(角度)和距离判定物体位置的方法以及线段比例尺的意义。
28.(6分)(2024春 惠民县期中)计算圆柱的表面积和圆锥的体积。(单位:厘米)
(1)
(2)
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;应用意识.
【答案】(1)301.44平方厘米;(2)3140立方厘米。
【分析】(1)根据圆柱表面积=侧面积+底面积×2,即可解答;
(2)根据圆锥体积=底面积×高÷3,即可解答。
【解答】解:(1)3.14×8×8+3.14×(8÷2)×(8÷2)×2
=200.96+100.48
=301.44(平方厘米)
答:圆柱的表面积是301.44平方厘米。
(2)3.14×10×10×30÷3
=9420÷3
=3140(立方厘米)
答:圆锥体积是3140立方厘米。
【点评】本题考查的是圆柱表面积和圆锥体积的计算,熟记公式是解答关键。
六.应用题(共3小题,满分23分)
29.(4分)(2024 武汉模拟)从A城到B城,在比例尺是1:50000000的图上量得两地间的距离是6.3cm。一架飞机早上8时从A城飞往B城,如果每小时飞行700千米,中途休息1小时30分,请问到达B城是什么时间?
【考点】比例尺应用题.
【专题】运算能力.
【答案】14时。
【分析】已知图上距离和比例尺,可以求出实际距离,图上距离÷比例尺=实际距离,然后用实际距离÷飞机的速度=飞行的时间,最后用出发的时刻+中途休息的时间+飞行的时间=到达B城的时刻,据此列式解答。
【解答】解:6.3
=315000000(cm)
=3150(千米)
3150÷700=4.5(小时)
8时+1小时30分+4小时30分=14时
答:到达B城是14时。
【点评】此题主要考查了比例尺的应用,和时间的计算,解答此题的关键是先求出两地之间的实际距离。
30.(4分)(2023 七里河区模拟)某商场进了50件防晒衣,每件的进价为100元,售价为160元,在卖出60%后,由于天气转冷而滞销,店主将余下的打五折出售,并且全部售完。请问:该商店是亏了还是赚了?亏还是赚了多少钱?
【考点】百分数的实际应用.
【专题】应用意识.
【答案】赚了,1400元。
【分析】先用50乘60%再乘160,求出按售价160元卖的钱数;然后用50乘(1﹣60%)再乘(160×50%),求出余下的部分共卖的钱数;将两部分钱数求和后再与50×100元比较大小,即可知道该商店是亏了还是赚了,最后求出赔或赚的钱数即可。
【解答】解:五折=50%
50×60%×160+50×(1﹣60%)×(160×50%)
=4800+1600
=6400(元)
50×100=5000(元)
6400>5000
6400﹣5000=1400(元)
答:该商店赚了,赚了1400元。
【点评】本题考查了利用百分数乘法及比较数的大小解决盈亏问题,准确分析题目中的数量关系是关键。
31.(4分)(2022 北辰区)一辆货车箱是一个长方体,它的长是4米,宽是1.5米,高是4米,装满一车沙,卸后堆成一个高是8分米的圆锥体,沙堆底面面积是多少平方米?
【考点】圆锥的体积;长方体和正方体的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】90平方米。
【分析】车厢的长是4米,宽是1.5米,高是4米,装满沙子后,这些沙子的形状就是一个长和高都是4米、宽1.5米的长方体,根据长方体的体积公式“V=abh”即可求出这些沙子的体积;把这车沙子不论堆成什么形状它的体积不会改变,根据圆锥的体积公式“Vπr2h”,用这些沙子的体积乘3再除以高就是它的底面积。
【解答】解:8分米=0.8米
(4×1.5×4)×3÷0.8
=24×3÷0.8
=72÷0.8
=90(平方米)
答:它的底面积是90平方米。
【点评】此题是考查长方体、圆锥体的体积计算.关键抓住这些沙子不论堆成什么形状体积不变这一特征及圆锥体积计算公式的灵活运用。
32.(4分)六年级全体同学参加升旗仪式,按各列人数相等的规定排列站队,如果每列站25人,要排24列。 要排12列,每列站多少人?(答案不唯一) ?
根据以上信息,请你先补充一个条件,并提出一个能用反比例关系解答的问题,最后再解答。(条件和问题直接补充在横线上)
【考点】正、反比例应用题.
【专题】开放型;运算能力;应用意识.
【答案】要排12列,每列站多少人?(答案不唯一)50人。
【分析】如果两个相关联的量乘积一定,说明它们成反比例关系。所以根据=每列人数×列数=总人数(一定),进行补充条件。补充的条件如果列数已知,则求每列多少人;如果每列人数已知,则求排多少列。据此解答。
【解答】解:补充条件:要排12列,每列站多少人?(答案不唯一)
解:设每列站x人。
12x=24×25
12x=600
x=50
答:每列站50人。
故答案为:要排12列,每列站多少人?(答案不唯一)
【点评】解答此题的主要依据是:若两个量的乘积一定,则这两个量成反比例,于是可以列比例求解。
33.(4分)(2022秋 海门区期末)王老师准备在网上购买一套书(共5册)。A网店和B网店的价格信息如图。王老师在哪家网店购买比较合算?
A网店:每册19元,免运费
B网店:每套80元,运费8元
【考点】最优化问题.
【专题】压轴题;应用意识.
【答案】B网店。
【分析】根据A网店和B网店的价格,求出在两家网店购买的总价,再比较大小即可。
【解答】解:A 网店:19×5=95(元)
B网店:80+8=88(元)
88<95
所以在B网店购买合算。
答:王老师在B网店购买比较合算。
【点评】本题考查了简单的优化问题。
34.(3分)一文具店购进了一批钢笔,以每支19.5元的价格出售,当卖出56%时,老板发现还差54元就能收回全部成本,于是决定降价20%销售,很快就全部售出,最终共获得利润289.2元。问:文具店购进这批钢笔的价格是每支多少元?
【考点】利润和利息问题.
【专题】分数百分数应用题;应用意识.
【答案】12元。
【分析】已知全部售出后,总共获得利润289.2元,在这之前是还差54元才可以收回全部成本,说明又卖出的这部分的总额为289.2+54=343.2(元);又已知每支钢笔的原价是19.5元,降价20%是指按原价的(1﹣20%)出售,根据总价÷单价=数量,求出卖出的这部分钢笔的数量,而这一部分钢笔的数量相当于总数的(1﹣56%),据此求出这批钢笔的总支数;再用这批钢笔的售价减去利润,求出这批钢笔的进价,进而求出每支钢笔的进价。
【解答】解:这批钢笔的总数量:
(289.2+54)÷[19.2×(1﹣20%)]
=343.2÷15.6
=22(支)
22÷(1﹣56%)
=22÷0.44
=50(支)
每支钢笔的购进价:
[19.5×(50×56%)+(289.2+54)﹣289.2]÷50
=[546+343.2﹣289.2]÷50
=600÷50
=12(元)
答:文具店购进这批钢笔的价格是每支12元。
【点评】此题条件较复杂,需认真分析,先求出这批钢笔的数量是解决此题的关键。
第1页(共1页)
同课章节目录
