【期中押题卷】湖北省武汉市2024-2025学年六年级下学期期中质量检测数学试卷人教版(含解析)
文档属性
| 名称 | 【期中押题卷】湖北省武汉市2024-2025学年六年级下学期期中质量检测数学试卷人教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 456.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 00:00:00 | ||
图片预览




文档简介
湖北省武汉市2024-2025学年六年级下学期期中质量检测数学试卷
一.填空题(共13小题,满分25分)
1.(2分)(2023秋 高新区期末)一幢大楼,地面以上有15层,地面以下有3层。以地面为准:规定向上为正,那么地面以上第2层记作 层,地面以下第1层记作 层。
2.(1分)(2023秋 高新区期末)某班女生比男生多20%,也就是男生比女生少 %。(百分号前面保留整数)
3.(3分)(2021春 淮上区期中)一幅平面图的比例尺是1:5000,说明图上距离是实际距离的 ;图上距离1厘米,表示实际距离 厘米,是 米。
4.(1分)(2024秋 大兴区期末)妈妈把2万元存入银行,定期3年,年利率1.50%。到期时妈妈可得利息 元。
5.(5分)(2023 正阳县)45% :60= (填小数)= (填成数)
6.(2分)(2023 武陵区)在一个长为13cm,宽和高都是4cm的长方体中削圆柱体,要使削出的圆柱体高都为4cm且体积最大,最多能削出 个,则其中一个圆柱体的表面积是 平方厘米。
7.(1分)(2024春 柘城县期中)一个圆锥的底面半径是3cm,体积是18.84cm3,这个圆锥的高是 cm。
8.(1分)(2022 市南区模拟)一个平行四边形的底是6cm,高是3cm,把它按3:1扩大后得到的平行四边形的面积是 。
9.(2分)如果y=7x,那么x和y成 比例关系;如果xy=5,那么x和y成 比例关系。
10.(1分)(2023秋 高邮市期末)300名学生去参加社会实践活动,一辆大巴车最多坐45人,至少需要 辆这样的大巴车。
11.(2分)(2022春 简阳市期中)把一段高3.3m,底面半径2m的圆柱形钢材切削成一个与它等底等高的圆锥,这个圆锥的体积是 m3,切削掉的部分熔化后还可以组成 个同样的圆锥。
12.(2分)(2022秋 邻水县期末)一幅地图的比例尺是1:1000000,表示图上距离1dm相当于实际距离 km,在这幅地图上量得A、B两地的距离是7.5cm,那么A、B两地实际相距 km。
13.(2分)(2024春 商河县期末)一个容积为120mL的水杯,小明加入1块铁块,溢出2ml水,如果加入3块完全一样的铁块,溢出18ml的水,每块铁块的体积是 cm3,杯中原有水 ml。
二.选择题(共5小题,满分5分,每小题1分)
14.(1分)(2023春 兴隆县期中)一袋上好佳薯片的外包装上写着50g±2g,这袋薯片最多或最少重( )g。
A.50,48 B.52,50 C.52,48
15.(1分)(2022 拱墅区)下列判断正确的选项是( )
A.汽车行驶的时间和速度成反比例。
B.圆的周长与直径成正比例。
C.正方体的表面积与它的棱长成正比例。
D.人的身高与体重成正比例。
16.(1分)如图(单位:cm),把一个无盖圆柱展开后得到一个长方形和一个圆,这个圆柱的高是( )cm。
A.2 B.4 C.6.28 D.12.56
17.(1分)(2023 平阴县)2022年北京冬季奥运会已经圆满结束。在此次冬奥会上,中国体育代表团所获得的金牌数和奖牌数均创历史新高,位列奖牌榜第三。中国体育代表团获得奖牌的数量如图:
北京冬季奥运会,中国体育代表团所获得的金牌数占所获奖牌总数的( )
A.9% B.30% C.60% D.90%
18.(1分)(2024 南京模拟)白兔的只数比黑兔多,黑兔与白兔只数的最简单的整数比是( )
A.10:9 B.9:10 C.1:10 D.1:9
三.计算题(共3小题,满分31分)
19.(10分)(2020秋 安化县期末)直接写出得数。
3÷1%=
20.(9分)(2024 宁波)解方程或解比例。
①x=5
②3.2×2.5﹣75%x=2
③
21.(12分)计算下面各题,怎样简便就怎样计算。
36+274+164 248﹣82﹣118 578﹣39+61
780÷26÷3 65×35+35×35 25×16×125
四.操作题(共1小题,满分8分,每小题8分)
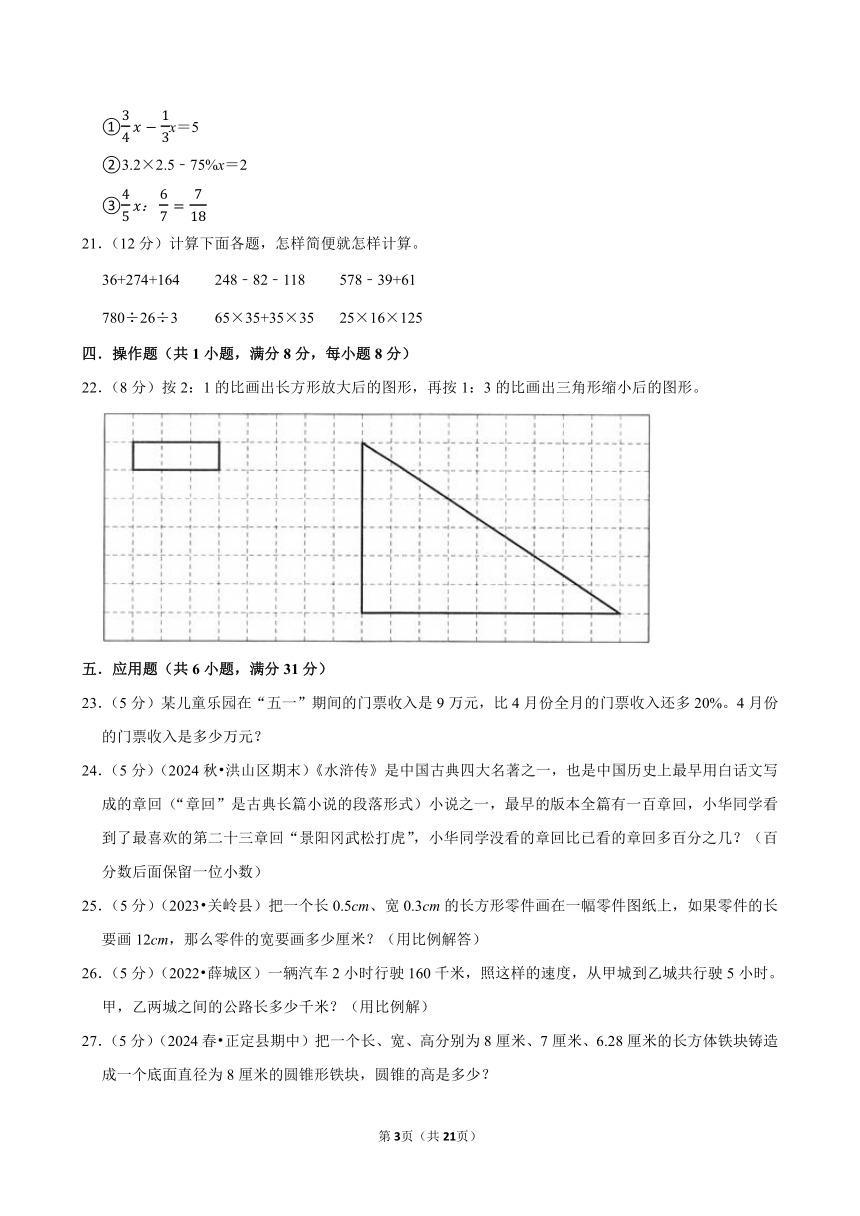
22.(8分)按2:1的比画出长方形放大后的图形,再按1:3的比画出三角形缩小后的图形。
五.应用题(共6小题,满分31分)
23.(5分)某儿童乐园在“五一”期间的门票收入是9万元,比4月份全月的门票收入还多20%。4月份的门票收入是多少万元?
24.(5分)(2024秋 洪山区期末)《水浒传》是中国古典四大名著之一,也是中国历史上最早用白话文写成的章回(“章回”是古典长篇小说的段落形式)小说之一,最早的版本全篇有一百章回,小华同学看到了最喜欢的第二十三章回“景阳冈武松打虎”,小华同学没看的章回比已看的章回多百分之几?(百分数后面保留一位小数)
25.(5分)(2023 关岭县)把一个长0.5cm、宽0.3cm的长方形零件画在一幅零件图纸上,如果零件的长要画12cm,那么零件的宽要画多少厘米?(用比例解答)
26.(5分)(2022 薛城区)一辆汽车2小时行驶160千米,照这样的速度,从甲城到乙城共行驶5小时。甲,乙两城之间的公路长多少千米?(用比例解)
27.(5分)(2024春 正定县期中)把一个长、宽、高分别为8厘米、7厘米、6.28厘米的长方体铁块铸造成一个底面直径为8厘米的圆锥形铁块,圆锥的高是多少?
28.(6分)(2023 芙蓉区模拟)比例尺是一个用于测量和绘制地图的工具,在生活中有着广泛的应用。它可以帮助人们估计和表示地理现象及地图上的物体大小。如在比例尺是1:5000000的地图上,量得从A城到B城长是8厘米。如果汽车平均每小时行驶80千米,从A城出发行驶几小时能到达B城?
湖北省武汉市2024-2025学年六年级下学期期中质量检测数学试卷
参考答案与试题解析
一.填空题(共13小题,满分25分)
1.(2分)(2023秋 高新区期末)一幢大楼,地面以上有15层,地面以下有3层。以地面为准:规定向上为正,那么地面以上第2层记作 +2 层,地面以下第1层记作 1 层。
【考点】负数的意义及其应用.
【专题】数感.
【答案】+2,1。
【分析】此题主要用正负数来表示具有意义相反的两种量:地面以上记为正,则地面以下就记为负,直接得出结论即可。
【解答】解:一幢大楼,地面以上有15层,地面以下有3层。以地面为准:规定向上为正,那么地面以上第2层记作+2层,地面以下第1层记作1层。
故答案为:+2,1。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
2.(1分)(2023秋 高新区期末)某班女生比男生多20%,也就是男生比女生少 17 %。(百分号前面保留整数)
【考点】百分数的实际应用.
【专题】综合填空题;运算能力.
【答案】17。
【分析】女生比男生多20%,则把男生看作单位“1”,女生是男生的(1+20%),设男生是1,根据百分数乘法的意义,用1×(1+20%)即可求出女生,再根据求一个数比另一个数少百分之几,用相差数除以另一个数再乘100%,则用女生减数男生的差除以女生再乘100%,即可求出男生就比女生少百分之几。
【解答】解:设男生是1,
女生:1×(1+20%)
=1×1.2
=1.2
(1.2﹣1)÷1.2×100%
=0.2÷1.2×100%
≈17%
答:某班女生比男生多20%,也就是男生比女生少17%。
故答案为:17。
【点评】本题主要考查百分数的应用,可用假设法解决问题,注意每个百分率对应的单位“1”不同。
3.(3分)(2021春 淮上区期中)一幅平面图的比例尺是1:5000,说明图上距离是实际距离的 ;图上距离1厘米,表示实际距离 5000 厘米,是 50 米。
【考点】比例尺.
【专题】比和比例;应用意识.
【答案】,5000,50。
【分析】(1)根据比例尺可知,用1除以5000即可解答;
(2)根据“比例尺=图上距离:实际距离”可知,图上1厘米,表示实际距离5000厘米,然后化成米作单位即可。
【解答】解:(1)1÷5000
(2)比例尺1:5000可得:图上距离1厘米,表示实际距离5000厘米,也就是50米。
答:说明图上距离是实际距离的;图上距离1厘米,表示实际距离5000厘米,是50米。
故答案为:,5000,50。
【点评】此题主要考查学生对比例尺意义的理解与认识。
4.(1分)(2024秋 大兴区期末)妈妈把2万元存入银行,定期3年,年利率1.50%。到期时妈妈可得利息 900 元。
【考点】存款利息与纳税相关问题.
【专题】应用意识.
【答案】900。
【分析】本金是2万元,存期是3年,年利率是1.50%,求利息,运用关系式:利息=本金×年利率×存期,代入数据,解决问题。
【解答】解:2万元=20000元
20000×1.50%×3
=20000×0.015×3
=300×3
=900(元)
答:到期后应得利息900元。
故答案为:900。
【点评】这种类型属于利息问题,运用关系式“利息=本金×年利率×存期”解决问题。
5.(5分)(2023 正阳县)45% 27 :60= 0.45 (填小数)= 四成五 (填成数)
【考点】比与分数、除法的关系.
【专题】数感.
【答案】(答案不唯一),27,0.45,四成五。
【分析】把45%化成分母是100的分数再化简是;根据比与分数的关系9:20,再根据比的基本性质比的前、后项都乘3就是27:60;把45%的小数点向左移动两位同时去掉百分号就是0.45;根据成数的意义45%就是四成五。
【解答】解:45%27:60=0.45=四成五
故答案为:(答案不唯一),27,0.45,四成五。
【点评】此题主要是考查小数、分数、除法、比、百分数、成数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
6.(2分)(2023 武陵区)在一个长为13cm,宽和高都是4cm的长方体中削圆柱体,要使削出的圆柱体高都为4cm且体积最大,最多能削出 3 个,则其中一个圆柱体的表面积是 75.36 平方厘米。
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;应用意识.
【答案】3;75.36。
【分析】根据圆柱的体积=底面积×高可知,要使削出的圆柱体高都为4厘米且体积最大,则圆柱的底面积要取最大值;已知长方体的宽和高都是4厘米,得出圆柱的底面直径是4厘米时,底面积最大。用13厘米除以4厘米,求出最多削出的个数;再根据圆柱的表面积=圆柱的侧面积+底面积×2,求出其中一个圆柱体的表面积。
【解答】解:由分析可得,13÷4≈3(个)
答:最多能削出3个。
4÷2=2(厘米)
3.14×4×4+3.14×22×2
=50.24+25.12
=75.36(平方厘米)
答:其中一个圆柱体的表面积是75.36平方厘米。
故答案为:3;75.36。
【点评】本题考查圆柱表面积的应用。关键是根据长方体的长、宽、高确定削出的圆柱体的底面直径,熟练掌握圆柱的表面积公式。
7.(1分)(2024春 柘城县期中)一个圆锥的底面半径是3cm,体积是18.84cm3,这个圆锥的高是 2 cm。
【考点】圆锥的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】2。
【分析】根据圆锥体积=底面积×高÷3,高=圆锥体积×3÷底面积,即可解答。
【解答】解:18.84×3÷(3.14×3×3)
=56.52÷28.26
=2(cm)
答:这个圆锥的高是2cm。
故答案为:2。
【点评】本题考查的是圆锥体积的计算,熟记公式是解答关键。
8.(1分)(2022 市南区模拟)一个平行四边形的底是6cm,高是3cm,把它按3:1扩大后得到的平行四边形的面积是 162平方厘米 。
【考点】图形的放大与缩小.
【专题】图形与变换;空间观念.
【答案】162平方厘米。
【分析】一个平行四边形底是6cm,高是3cm,把它按3:1放大后,它的底和高都要扩大到原来的3倍,求出扩大后的底和高是多少,利用平行四边形面积公式S=ah计算即可。
【解答】解:6×3=18(厘米)
3×3=9(厘米)
18×9=162(平方厘米)
答:把它按3:1扩大后得到的平行四边形的面积是162平方厘米。
故答案为:162平方厘米。
【点评】图形放大的倍数是指对应边放大的倍数;面积则放大这个倍数的平方倍。
9.(2分)如果y=7x,那么x和y成 正 比例关系;如果xy=5,那么x和y成 反 比例关系。
【考点】辨识成正比例的量与成反比例的量.
【专题】数据分析观念.
【答案】正,反。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:因为y=7x,所以y:x=7(一定),比值一定,所以x和y成正比例关系;
因为xy=5(一定),乘积一定,所以x和y成反比例关系。
故答案为:正,反。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
10.(1分)(2023秋 高邮市期末)300名学生去参加社会实践活动,一辆大巴车最多坐45人,至少需要 7 辆这样的大巴车。
【考点】有余数的除法应用题.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】7。
【分析】根据数量=总量÷单一量,即可解答。
【解答】解:300÷45=6(辆)……30(人)
6+1=7(辆)
答:至少需要7辆这样的大巴车。
故答案为:7。
【点评】本题考查的是有余数的除法应用题,根据实际情况用“进一法”取值是解答关键。
11.(2分)(2022春 简阳市期中)把一段高3.3m,底面半径2m的圆柱形钢材切削成一个与它等底等高的圆锥,这个圆锥的体积是 13.816 m3,切削掉的部分熔化后还可以组成 2 个同样的圆锥。
【考点】圆锥的体积;圆柱的体积.
【专题】空间观念;推理能力;应用意识.
【答案】13.816,2。
【分析】根据圆锥的体积公式:Vπr2h,把数据代入公式求出这个圆锥的体积,因为等底等高的圆柱的体积是圆锥体积的3倍,所以把圆柱形钢材切削成一个与它等底等高的圆锥,切削掉的部分的体积相当于圆锥体积的(3﹣1)倍,
【解答】解:3.14×22×3.3
3.14×4×3.3
=13.816(立方米)
3﹣1=2(个)
答:这个圆锥的体积是13.816立方米,切削掉的部分熔化后还可以组成2个同样的圆锥。
故答案为:13.816,2。
【点评】此题主要考查圆锥的体积公式及应用,等底等高的圆柱与圆锥体积之间的关系及应用。
12.(2分)(2022秋 邻水县期末)一幅地图的比例尺是1:1000000,表示图上距离1dm相当于实际距离 100 km,在这幅地图上量得A、B两地的距离是7.5cm,那么A、B两地实际相距 75 km。
【考点】图上距离与实际距离的换算(比例尺的应用).
【专题】运算能力.
【答案】100,75。
【分析】因为比例尺1:1000000表示图上距离1厘米代表实际距离1000000厘米,又因1000000厘米=10千米,所以比例尺1:1000000表示地图上1厘米的距离相当于地面上10千米的实际距离;
图上距离和比例尺已知,利用“实际距离=图上距离÷比例尺”即可求得两地的实际距离。
【解答】解:1000000cm=10km
1分米=10厘米
10×10=100(千米)
答:图上1dm表示实际距离100km;
7.5×1000000=75000000(cm)
75000000cm=75km
答:A、B两地的实际距离是75km。
故答案为:100,75。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
13.(2分)(2024春 商河县期末)一个容积为120mL的水杯,小明加入1块铁块,溢出2ml水,如果加入3块完全一样的铁块,溢出18ml的水,每块铁块的体积是 8 cm3,杯中原有水 114 ml。
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】8,114。
【分析】因为水杯内水的体积是一定,小明加入1块铁块,溢出2毫升水,如果加入3块完全一样的铁块,溢出18毫升的水,由此可知,(3﹣1)个铁块的体积是(18﹣2)立方厘米,据此可以求出每块铁块的体积,杯中水的体积等于杯子的容积加上2毫升再减去一块铁块的体积。
【解答】解:1毫升=1立方厘米
(18﹣2)÷(3﹣1)
=16÷2
=8(立方厘米)
120+2﹣8
=122﹣8
=114(毫升)
答:每块铁块的体积是8立方厘米,杯中原有水144毫升。
故答案为:8,114。
【点评】此题考查的目的是理解掌握不规则物体体积的测量方法及应用。
二.选择题(共5小题,满分5分,每小题1分)
14.(1分)(2023春 兴隆县期中)一袋上好佳薯片的外包装上写着50g±2g,这袋薯片最多或最少重( )g。
A.50,48 B.52,50 C.52,48
【考点】负数的意义及其应用;正、负数的运算.
【专题】数感.
【答案】C
【分析】正数、负数表示两种相反意义的量,“50g±2g”的含义,即50g是上好佳薯片的标准净重,实际每袋最多不超过(50+2)g,最少不低于(50﹣2)g,据此解答。
【解答】解:50+2=52(克)
50﹣2=48(克)
答:这袋薯片最多52克,最少48克。
故选:C。
【点评】掌握正负数的意义,知道以哪个数为标准,规定超出标准的为正,低于标准的为负。
15.(1分)(2022 拱墅区)下列判断正确的选项是( )
A.汽车行驶的时间和速度成反比例。
B.圆的周长与直径成正比例。
C.正方体的表面积与它的棱长成正比例。
D.人的身高与体重成正比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例;推理能力.
【答案】B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:A.根据路程=速度×时间,题目中没说路程一定,所以汽车行驶的时间和速度不成比例;
B.根据圆的周长公式:C=πd,圆周率一定,即圆的周长和圆的直径之间的商一定,所以圆的周长与直径成正比例;
C.根据正方体的表面积公式:S=6a2,可得S÷a2=6,即正方体的表面积与它的棱长的平方成正比例;
D.一个人的身高和体重是相关联的量,但是二者的数量关系既不是比值一定,也不是乘积一定,所以二者不成比例关系;
故选:B。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
16.(1分)如图(单位:cm),把一个无盖圆柱展开后得到一个长方形和一个圆,这个圆柱的高是( )cm。
A.2 B.4 C.6.28 D.12.56
【考点】圆柱的展开图.
【专题】应用意识.
【答案】C
【分析】根据圆柱展开图与圆柱的关系可知,圆柱的底面周长是长方形的一条边,圆柱的高是长方形的另一条边,据此求出圆的周长即可判断。
【解答】解:3.14×4=12.56(cm)
所以圆柱的高是6.28cm。
故选:C。
【点评】熟练掌握圆柱与圆柱展开图之间的关系是解题的关键。
17.(1分)(2023 平阴县)2022年北京冬季奥运会已经圆满结束。在此次冬奥会上,中国体育代表团所获得的金牌数和奖牌数均创历史新高,位列奖牌榜第三。中国体育代表团获得奖牌的数量如图:
北京冬季奥运会,中国体育代表团所获得的金牌数占所获奖牌总数的( )
A.9% B.30% C.60% D.90%
【考点】百分数的实际应用.
【专题】运算能力.
【答案】C
【分析】把奖牌总数看作单位“1”,根据求一个数是另一个数的几分之几,用除法解答。
【解答】解:9÷15=60%
答:中国体育代表团所获得的金牌数占所获奖牌总数的60%。
故选:C。
【点评】此题属于求一个数是另一个数的几分之几,关键是确定单位“1”作除数,求一个数是另一个数的几分之几,用除法解答即可。
18.(1分)(2024 南京模拟)白兔的只数比黑兔多,黑兔与白兔只数的最简单的整数比是( )
A.10:9 B.9:10 C.1:10 D.1:9
【考点】比的意义;求比值和化简比.
【专题】应用意识.
【答案】B
【分析】把黑兔的只数看作单位“1”,白兔的只数为(1),据此写出黑兔与白兔只数的比,再化简即可。
【解答】解:1:(1)
=1:
=9:10
答:黑兔与白兔只数的最简单的整数比是9:10。
故选:B。
【点评】本题主要考查了比的意义及化简比,解题的关键是把黑兔的只数看作单位“1”,得出白兔的只数。
三.计算题(共3小题,满分31分)
19.(10分)(2020秋 安化县期末)直接写出得数。
3÷1%=
【考点】分数乘法;分数除法;分数的四则混合运算.
【专题】计算题;应用意识.
【答案】0.3;13.5;0.16;;0.36;;300;。
【分析】分数乘整数或整数乘分数:由于任何整数(0除外)都可以化成分母是1的假分数,分数乘整数或整数乘分数,都可以转化成分数乘分数的形式,分数乘分数:用分子相乘的积作为分子,用分母相乘的积作为分母;同分母分数相加(减),分子进行相加(减)得数作分子,分母不变,异分母分数相加(减),必须先通分,然后,按照同分母分数相加(减)的法则进行运算,整数的运算定律同样适用于分数乘法中的简便计算,需要关注的是,根据数的特征正确运用运算定律,切勿随心所欲进行所谓的“简便计算”。
【解答】解:
0.3 13.5 0.16
0.36 3÷1%=300
【点评】本题考查的主要内容是分数乘法,分数除法和分数混合运算问题。
20.(9分)(2024 宁波)解方程或解比例。
①x=5
②3.2×2.5﹣75%x=2
③
【考点】解比例;分数方程求解;百分数方程求解.
【专题】简易方程;运算能力.
【答案】①x=12;②x=8;③x。
【分析】①先计算xx,根据等式的性质,方程的两边同时除以求解;
②先计算3.2×2.5=8,根据等式的性质,方程的两边同时加上75%x,把方程化为2+75%x=8,方程的两边同时减去2,然后方程的两边同时除以75%求解;
③根据比与除法的关系,把原式化为x,根据等式的性质,方程的两边同时乘,然后方程的两边同时除以求解。
【解答】解:①x=5
x=5
x5
x=12
②3.2×2.5﹣75%x=2
8﹣75%x=2
8﹣75%x+75%x=2+75%x
2+75%x=8
2+75%x﹣2=8﹣2
75%x=6
75%x÷75%=6÷75%
x=8
③
x
x
x
x
x
【点评】本题考查解方程,解题的关键是掌握等式的性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立。
21.(12分)计算下面各题,怎样简便就怎样计算。
36+274+164 248﹣82﹣118 578﹣39+61
780÷26÷3 65×35+35×35 25×16×125
【考点】运算定律与简便运算.
【专题】运算能力.
【答案】474;48;600;10;3500;50000。
【分析】(1)利用加法交换律计算;
(2)利用减法的性质计算;
(3)从左到右依次计算;
(4)利用除法的性质计算
(5)利用乘法分配律计算;
(6)将16化成2×8,再利用乘法结合律计算。
【解答】解:(1)36+274+164
=36+164+274
=200+274
=474
(2)248﹣82﹣118
=248﹣(82+118)
=248﹣200
=48
(3)578﹣39+61
=539+61
=600
(4)780÷26÷3
=780÷(26×3)
=780÷78
=10
(5)65×35+35×35
=(65+35)×35
=100×35
=3500
(6)25×16×125
=25×2×8×125
=(25×2)×(8×125)
=50×1000
=50000
【点评】解答本题需熟练掌握四则混合运算顺序,灵活使用运算律和运算性质。
四.操作题(共1小题,满分8分,每小题8分)
22.(8分)按2:1的比画出长方形放大后的图形,再按1:3的比画出三角形缩小后的图形。
【考点】图形的放大与缩小.
【专题】几何直观;应用意识.
【答案】
【分析】根据图形放大的方法,先分别求出放大2倍后,长方形的长、宽各是多少,再根据长方形的画法画出放大后的图形;根据图形缩小的方法,先分别求出缩小3倍后,三角形的底、和各是多少,然后根据三角形的画法画出缩小后的图形。据此解答即可。
【解答】解:3×2=6
1×2=2
9÷3=3
6÷3=2
作图如下:
【点评】此题考查的目的是理解掌握图形放大、缩小的方法及应用。
五.应用题(共6小题,满分31分)
23.(5分)某儿童乐园在“五一”期间的门票收入是9万元,比4月份全月的门票收入还多20%。4月份的门票收入是多少万元?
【考点】百分数的实际应用.
【专题】运算能力.
【答案】7.5万元。
【分析】五一”期间的门票收入是9万元,比4月份全月的门票收入还多20%,即“五一”期间的门票收入是4月份的(1+20%),用除法计算,即可得4月份的门票收入是多少万元。
【解答】解:9÷(1+20%)
=9÷1.2
=7.5(万元)
答:4月份的门票收入是7.5万元。
【点评】本题主要考查了百分数的实际应用,已知一个数的百分之几是多少,求这个数,用除法计算。
24.(5分)(2024秋 洪山区期末)《水浒传》是中国古典四大名著之一,也是中国历史上最早用白话文写成的章回(“章回”是古典长篇小说的段落形式)小说之一,最早的版本全篇有一百章回,小华同学看到了最喜欢的第二十三章回“景阳冈武松打虎”,小华同学没看的章回比已看的章回多百分之几?(百分数后面保留一位小数)
【考点】百分数的实际应用.
【专题】运算能力;应用意识.
【答案】234.8%。
【分析】用《水浒传》的总章回减小华同学看的章回,得出小华同学没看的章回,减小华同学看的章回,再除以小华同学看的章回,即可得解。
【解答】解:(100﹣23﹣23)÷23
=54÷23
≈234.8%
答:小华同学没看的章回比已看的章回多234.8%。
【点评】本题主要考查了百分数的实际应用,求一个数比另一个数多或少百分之几,用除法计算。
25.(5分)(2023 关岭县)把一个长0.5cm、宽0.3cm的长方形零件画在一幅零件图纸上,如果零件的长要画12cm,那么零件的宽要画多少厘米?(用比例解答)
【考点】正、反比例应用题.
【专题】运算能力.
【答案】7.2厘米。
【分析】长方形零件画在一幅零件图纸上,长和宽的比例尺是相同的,根据图上长的长度:实际长的长度=图上宽的长度:实际宽的长度列式解答。
【解答】解:设零件的宽要画x厘米,
12:0.5=x:0.3
0.5x÷0.5=3.6÷0.5
x=7.2
答:零件的宽要画7.2厘米。
【点评】此题考查正比例在生活中的应用。解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
26.(5分)(2022 薛城区)一辆汽车2小时行驶160千米,照这样的速度,从甲城到乙城共行驶5小时。甲,乙两城之间的公路长多少千米?(用比例解)
【考点】正、反比例应用题.
【专题】比和比例应用题.
【答案】400千米。
【分析】照这样的速度,说明速度一定,根据速度=路程÷时间,路程与时间成正比例;据此列出比例即可解答。
【解答】解:设甲,乙两城之间的公路长为x千米。
2x=160×5
2x=800
x=400
答:甲,乙两城之间的公路长为400千米。
【点评】根据速度=路程÷时间,判断路程与时间成正比例是解答关键。
27.(5分)(2024春 正定县期中)把一个长、宽、高分别为8厘米、7厘米、6.28厘米的长方体铁块铸造成一个底面直径为8厘米的圆锥形铁块,圆锥的高是多少?
【考点】圆锥的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】圆锥的高是21厘米。
【分析】熔铸成圆锥体,体积没变,等于长方体的体积,由此可以求出圆锥的体积为:8×7×6.28=351.68(立方厘米),知道底面直径,可求出圆锥的底面积,然后利用圆锥的体积公式可以计算得出圆锥的高。
【解答】解:8×7×6.28=351.68(立方厘米)
351.68×3÷[3.14×(8÷2)2]
=1055.04÷[3.14×16]
=1055.04÷50.24
=21(厘米)
答:圆锥的高是21厘米。
【点评】抓住熔铸前后的体积不变,是解决此类问题的关键。
28.(6分)(2023 芙蓉区模拟)比例尺是一个用于测量和绘制地图的工具,在生活中有着广泛的应用。它可以帮助人们估计和表示地理现象及地图上的物体大小。如在比例尺是1:5000000的地图上,量得从A城到B城长是8厘米。如果汽车平均每小时行驶80千米,从A城出发行驶几小时能到达B城?
【考点】比例尺应用题.
【专题】运算能力.
【答案】5小时。
【分析】先根据图上距离÷比例尺=实际距离,求出实际距离,再根据路程÷速度=时间进行解答即可。
【解答】解:840000000(厘米)
40000000厘米=400千米
400÷80=5(小时)
答:从A城出发行驶5小时能到达B城。
【点评】此题考查的目的是理解比例尺的意义及应用,掌握路程、速度、时间三者之间的关系。
第1页(共1页)
一.填空题(共13小题,满分25分)
1.(2分)(2023秋 高新区期末)一幢大楼,地面以上有15层,地面以下有3层。以地面为准:规定向上为正,那么地面以上第2层记作 层,地面以下第1层记作 层。
2.(1分)(2023秋 高新区期末)某班女生比男生多20%,也就是男生比女生少 %。(百分号前面保留整数)
3.(3分)(2021春 淮上区期中)一幅平面图的比例尺是1:5000,说明图上距离是实际距离的 ;图上距离1厘米,表示实际距离 厘米,是 米。
4.(1分)(2024秋 大兴区期末)妈妈把2万元存入银行,定期3年,年利率1.50%。到期时妈妈可得利息 元。
5.(5分)(2023 正阳县)45% :60= (填小数)= (填成数)
6.(2分)(2023 武陵区)在一个长为13cm,宽和高都是4cm的长方体中削圆柱体,要使削出的圆柱体高都为4cm且体积最大,最多能削出 个,则其中一个圆柱体的表面积是 平方厘米。
7.(1分)(2024春 柘城县期中)一个圆锥的底面半径是3cm,体积是18.84cm3,这个圆锥的高是 cm。
8.(1分)(2022 市南区模拟)一个平行四边形的底是6cm,高是3cm,把它按3:1扩大后得到的平行四边形的面积是 。
9.(2分)如果y=7x,那么x和y成 比例关系;如果xy=5,那么x和y成 比例关系。
10.(1分)(2023秋 高邮市期末)300名学生去参加社会实践活动,一辆大巴车最多坐45人,至少需要 辆这样的大巴车。
11.(2分)(2022春 简阳市期中)把一段高3.3m,底面半径2m的圆柱形钢材切削成一个与它等底等高的圆锥,这个圆锥的体积是 m3,切削掉的部分熔化后还可以组成 个同样的圆锥。
12.(2分)(2022秋 邻水县期末)一幅地图的比例尺是1:1000000,表示图上距离1dm相当于实际距离 km,在这幅地图上量得A、B两地的距离是7.5cm,那么A、B两地实际相距 km。
13.(2分)(2024春 商河县期末)一个容积为120mL的水杯,小明加入1块铁块,溢出2ml水,如果加入3块完全一样的铁块,溢出18ml的水,每块铁块的体积是 cm3,杯中原有水 ml。
二.选择题(共5小题,满分5分,每小题1分)
14.(1分)(2023春 兴隆县期中)一袋上好佳薯片的外包装上写着50g±2g,这袋薯片最多或最少重( )g。
A.50,48 B.52,50 C.52,48
15.(1分)(2022 拱墅区)下列判断正确的选项是( )
A.汽车行驶的时间和速度成反比例。
B.圆的周长与直径成正比例。
C.正方体的表面积与它的棱长成正比例。
D.人的身高与体重成正比例。
16.(1分)如图(单位:cm),把一个无盖圆柱展开后得到一个长方形和一个圆,这个圆柱的高是( )cm。
A.2 B.4 C.6.28 D.12.56
17.(1分)(2023 平阴县)2022年北京冬季奥运会已经圆满结束。在此次冬奥会上,中国体育代表团所获得的金牌数和奖牌数均创历史新高,位列奖牌榜第三。中国体育代表团获得奖牌的数量如图:
北京冬季奥运会,中国体育代表团所获得的金牌数占所获奖牌总数的( )
A.9% B.30% C.60% D.90%
18.(1分)(2024 南京模拟)白兔的只数比黑兔多,黑兔与白兔只数的最简单的整数比是( )
A.10:9 B.9:10 C.1:10 D.1:9
三.计算题(共3小题,满分31分)
19.(10分)(2020秋 安化县期末)直接写出得数。
3÷1%=
20.(9分)(2024 宁波)解方程或解比例。
①x=5
②3.2×2.5﹣75%x=2
③
21.(12分)计算下面各题,怎样简便就怎样计算。
36+274+164 248﹣82﹣118 578﹣39+61
780÷26÷3 65×35+35×35 25×16×125
四.操作题(共1小题,满分8分,每小题8分)
22.(8分)按2:1的比画出长方形放大后的图形,再按1:3的比画出三角形缩小后的图形。
五.应用题(共6小题,满分31分)
23.(5分)某儿童乐园在“五一”期间的门票收入是9万元,比4月份全月的门票收入还多20%。4月份的门票收入是多少万元?
24.(5分)(2024秋 洪山区期末)《水浒传》是中国古典四大名著之一,也是中国历史上最早用白话文写成的章回(“章回”是古典长篇小说的段落形式)小说之一,最早的版本全篇有一百章回,小华同学看到了最喜欢的第二十三章回“景阳冈武松打虎”,小华同学没看的章回比已看的章回多百分之几?(百分数后面保留一位小数)
25.(5分)(2023 关岭县)把一个长0.5cm、宽0.3cm的长方形零件画在一幅零件图纸上,如果零件的长要画12cm,那么零件的宽要画多少厘米?(用比例解答)
26.(5分)(2022 薛城区)一辆汽车2小时行驶160千米,照这样的速度,从甲城到乙城共行驶5小时。甲,乙两城之间的公路长多少千米?(用比例解)
27.(5分)(2024春 正定县期中)把一个长、宽、高分别为8厘米、7厘米、6.28厘米的长方体铁块铸造成一个底面直径为8厘米的圆锥形铁块,圆锥的高是多少?
28.(6分)(2023 芙蓉区模拟)比例尺是一个用于测量和绘制地图的工具,在生活中有着广泛的应用。它可以帮助人们估计和表示地理现象及地图上的物体大小。如在比例尺是1:5000000的地图上,量得从A城到B城长是8厘米。如果汽车平均每小时行驶80千米,从A城出发行驶几小时能到达B城?
湖北省武汉市2024-2025学年六年级下学期期中质量检测数学试卷
参考答案与试题解析
一.填空题(共13小题,满分25分)
1.(2分)(2023秋 高新区期末)一幢大楼,地面以上有15层,地面以下有3层。以地面为准:规定向上为正,那么地面以上第2层记作 +2 层,地面以下第1层记作 1 层。
【考点】负数的意义及其应用.
【专题】数感.
【答案】+2,1。
【分析】此题主要用正负数来表示具有意义相反的两种量:地面以上记为正,则地面以下就记为负,直接得出结论即可。
【解答】解:一幢大楼,地面以上有15层,地面以下有3层。以地面为准:规定向上为正,那么地面以上第2层记作+2层,地面以下第1层记作1层。
故答案为:+2,1。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
2.(1分)(2023秋 高新区期末)某班女生比男生多20%,也就是男生比女生少 17 %。(百分号前面保留整数)
【考点】百分数的实际应用.
【专题】综合填空题;运算能力.
【答案】17。
【分析】女生比男生多20%,则把男生看作单位“1”,女生是男生的(1+20%),设男生是1,根据百分数乘法的意义,用1×(1+20%)即可求出女生,再根据求一个数比另一个数少百分之几,用相差数除以另一个数再乘100%,则用女生减数男生的差除以女生再乘100%,即可求出男生就比女生少百分之几。
【解答】解:设男生是1,
女生:1×(1+20%)
=1×1.2
=1.2
(1.2﹣1)÷1.2×100%
=0.2÷1.2×100%
≈17%
答:某班女生比男生多20%,也就是男生比女生少17%。
故答案为:17。
【点评】本题主要考查百分数的应用,可用假设法解决问题,注意每个百分率对应的单位“1”不同。
3.(3分)(2021春 淮上区期中)一幅平面图的比例尺是1:5000,说明图上距离是实际距离的 ;图上距离1厘米,表示实际距离 5000 厘米,是 50 米。
【考点】比例尺.
【专题】比和比例;应用意识.
【答案】,5000,50。
【分析】(1)根据比例尺可知,用1除以5000即可解答;
(2)根据“比例尺=图上距离:实际距离”可知,图上1厘米,表示实际距离5000厘米,然后化成米作单位即可。
【解答】解:(1)1÷5000
(2)比例尺1:5000可得:图上距离1厘米,表示实际距离5000厘米,也就是50米。
答:说明图上距离是实际距离的;图上距离1厘米,表示实际距离5000厘米,是50米。
故答案为:,5000,50。
【点评】此题主要考查学生对比例尺意义的理解与认识。
4.(1分)(2024秋 大兴区期末)妈妈把2万元存入银行,定期3年,年利率1.50%。到期时妈妈可得利息 900 元。
【考点】存款利息与纳税相关问题.
【专题】应用意识.
【答案】900。
【分析】本金是2万元,存期是3年,年利率是1.50%,求利息,运用关系式:利息=本金×年利率×存期,代入数据,解决问题。
【解答】解:2万元=20000元
20000×1.50%×3
=20000×0.015×3
=300×3
=900(元)
答:到期后应得利息900元。
故答案为:900。
【点评】这种类型属于利息问题,运用关系式“利息=本金×年利率×存期”解决问题。
5.(5分)(2023 正阳县)45% 27 :60= 0.45 (填小数)= 四成五 (填成数)
【考点】比与分数、除法的关系.
【专题】数感.
【答案】(答案不唯一),27,0.45,四成五。
【分析】把45%化成分母是100的分数再化简是;根据比与分数的关系9:20,再根据比的基本性质比的前、后项都乘3就是27:60;把45%的小数点向左移动两位同时去掉百分号就是0.45;根据成数的意义45%就是四成五。
【解答】解:45%27:60=0.45=四成五
故答案为:(答案不唯一),27,0.45,四成五。
【点评】此题主要是考查小数、分数、除法、比、百分数、成数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
6.(2分)(2023 武陵区)在一个长为13cm,宽和高都是4cm的长方体中削圆柱体,要使削出的圆柱体高都为4cm且体积最大,最多能削出 3 个,则其中一个圆柱体的表面积是 75.36 平方厘米。
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;应用意识.
【答案】3;75.36。
【分析】根据圆柱的体积=底面积×高可知,要使削出的圆柱体高都为4厘米且体积最大,则圆柱的底面积要取最大值;已知长方体的宽和高都是4厘米,得出圆柱的底面直径是4厘米时,底面积最大。用13厘米除以4厘米,求出最多削出的个数;再根据圆柱的表面积=圆柱的侧面积+底面积×2,求出其中一个圆柱体的表面积。
【解答】解:由分析可得,13÷4≈3(个)
答:最多能削出3个。
4÷2=2(厘米)
3.14×4×4+3.14×22×2
=50.24+25.12
=75.36(平方厘米)
答:其中一个圆柱体的表面积是75.36平方厘米。
故答案为:3;75.36。
【点评】本题考查圆柱表面积的应用。关键是根据长方体的长、宽、高确定削出的圆柱体的底面直径,熟练掌握圆柱的表面积公式。
7.(1分)(2024春 柘城县期中)一个圆锥的底面半径是3cm,体积是18.84cm3,这个圆锥的高是 2 cm。
【考点】圆锥的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】2。
【分析】根据圆锥体积=底面积×高÷3,高=圆锥体积×3÷底面积,即可解答。
【解答】解:18.84×3÷(3.14×3×3)
=56.52÷28.26
=2(cm)
答:这个圆锥的高是2cm。
故答案为:2。
【点评】本题考查的是圆锥体积的计算,熟记公式是解答关键。
8.(1分)(2022 市南区模拟)一个平行四边形的底是6cm,高是3cm,把它按3:1扩大后得到的平行四边形的面积是 162平方厘米 。
【考点】图形的放大与缩小.
【专题】图形与变换;空间观念.
【答案】162平方厘米。
【分析】一个平行四边形底是6cm,高是3cm,把它按3:1放大后,它的底和高都要扩大到原来的3倍,求出扩大后的底和高是多少,利用平行四边形面积公式S=ah计算即可。
【解答】解:6×3=18(厘米)
3×3=9(厘米)
18×9=162(平方厘米)
答:把它按3:1扩大后得到的平行四边形的面积是162平方厘米。
故答案为:162平方厘米。
【点评】图形放大的倍数是指对应边放大的倍数;面积则放大这个倍数的平方倍。
9.(2分)如果y=7x,那么x和y成 正 比例关系;如果xy=5,那么x和y成 反 比例关系。
【考点】辨识成正比例的量与成反比例的量.
【专题】数据分析观念.
【答案】正,反。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:因为y=7x,所以y:x=7(一定),比值一定,所以x和y成正比例关系;
因为xy=5(一定),乘积一定,所以x和y成反比例关系。
故答案为:正,反。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
10.(1分)(2023秋 高邮市期末)300名学生去参加社会实践活动,一辆大巴车最多坐45人,至少需要 7 辆这样的大巴车。
【考点】有余数的除法应用题.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】7。
【分析】根据数量=总量÷单一量,即可解答。
【解答】解:300÷45=6(辆)……30(人)
6+1=7(辆)
答:至少需要7辆这样的大巴车。
故答案为:7。
【点评】本题考查的是有余数的除法应用题,根据实际情况用“进一法”取值是解答关键。
11.(2分)(2022春 简阳市期中)把一段高3.3m,底面半径2m的圆柱形钢材切削成一个与它等底等高的圆锥,这个圆锥的体积是 13.816 m3,切削掉的部分熔化后还可以组成 2 个同样的圆锥。
【考点】圆锥的体积;圆柱的体积.
【专题】空间观念;推理能力;应用意识.
【答案】13.816,2。
【分析】根据圆锥的体积公式:Vπr2h,把数据代入公式求出这个圆锥的体积,因为等底等高的圆柱的体积是圆锥体积的3倍,所以把圆柱形钢材切削成一个与它等底等高的圆锥,切削掉的部分的体积相当于圆锥体积的(3﹣1)倍,
【解答】解:3.14×22×3.3
3.14×4×3.3
=13.816(立方米)
3﹣1=2(个)
答:这个圆锥的体积是13.816立方米,切削掉的部分熔化后还可以组成2个同样的圆锥。
故答案为:13.816,2。
【点评】此题主要考查圆锥的体积公式及应用,等底等高的圆柱与圆锥体积之间的关系及应用。
12.(2分)(2022秋 邻水县期末)一幅地图的比例尺是1:1000000,表示图上距离1dm相当于实际距离 100 km,在这幅地图上量得A、B两地的距离是7.5cm,那么A、B两地实际相距 75 km。
【考点】图上距离与实际距离的换算(比例尺的应用).
【专题】运算能力.
【答案】100,75。
【分析】因为比例尺1:1000000表示图上距离1厘米代表实际距离1000000厘米,又因1000000厘米=10千米,所以比例尺1:1000000表示地图上1厘米的距离相当于地面上10千米的实际距离;
图上距离和比例尺已知,利用“实际距离=图上距离÷比例尺”即可求得两地的实际距离。
【解答】解:1000000cm=10km
1分米=10厘米
10×10=100(千米)
答:图上1dm表示实际距离100km;
7.5×1000000=75000000(cm)
75000000cm=75km
答:A、B两地的实际距离是75km。
故答案为:100,75。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
13.(2分)(2024春 商河县期末)一个容积为120mL的水杯,小明加入1块铁块,溢出2ml水,如果加入3块完全一样的铁块,溢出18ml的水,每块铁块的体积是 8 cm3,杯中原有水 114 ml。
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】8,114。
【分析】因为水杯内水的体积是一定,小明加入1块铁块,溢出2毫升水,如果加入3块完全一样的铁块,溢出18毫升的水,由此可知,(3﹣1)个铁块的体积是(18﹣2)立方厘米,据此可以求出每块铁块的体积,杯中水的体积等于杯子的容积加上2毫升再减去一块铁块的体积。
【解答】解:1毫升=1立方厘米
(18﹣2)÷(3﹣1)
=16÷2
=8(立方厘米)
120+2﹣8
=122﹣8
=114(毫升)
答:每块铁块的体积是8立方厘米,杯中原有水144毫升。
故答案为:8,114。
【点评】此题考查的目的是理解掌握不规则物体体积的测量方法及应用。
二.选择题(共5小题,满分5分,每小题1分)
14.(1分)(2023春 兴隆县期中)一袋上好佳薯片的外包装上写着50g±2g,这袋薯片最多或最少重( )g。
A.50,48 B.52,50 C.52,48
【考点】负数的意义及其应用;正、负数的运算.
【专题】数感.
【答案】C
【分析】正数、负数表示两种相反意义的量,“50g±2g”的含义,即50g是上好佳薯片的标准净重,实际每袋最多不超过(50+2)g,最少不低于(50﹣2)g,据此解答。
【解答】解:50+2=52(克)
50﹣2=48(克)
答:这袋薯片最多52克,最少48克。
故选:C。
【点评】掌握正负数的意义,知道以哪个数为标准,规定超出标准的为正,低于标准的为负。
15.(1分)(2022 拱墅区)下列判断正确的选项是( )
A.汽车行驶的时间和速度成反比例。
B.圆的周长与直径成正比例。
C.正方体的表面积与它的棱长成正比例。
D.人的身高与体重成正比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例;推理能力.
【答案】B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:A.根据路程=速度×时间,题目中没说路程一定,所以汽车行驶的时间和速度不成比例;
B.根据圆的周长公式:C=πd,圆周率一定,即圆的周长和圆的直径之间的商一定,所以圆的周长与直径成正比例;
C.根据正方体的表面积公式:S=6a2,可得S÷a2=6,即正方体的表面积与它的棱长的平方成正比例;
D.一个人的身高和体重是相关联的量,但是二者的数量关系既不是比值一定,也不是乘积一定,所以二者不成比例关系;
故选:B。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
16.(1分)如图(单位:cm),把一个无盖圆柱展开后得到一个长方形和一个圆,这个圆柱的高是( )cm。
A.2 B.4 C.6.28 D.12.56
【考点】圆柱的展开图.
【专题】应用意识.
【答案】C
【分析】根据圆柱展开图与圆柱的关系可知,圆柱的底面周长是长方形的一条边,圆柱的高是长方形的另一条边,据此求出圆的周长即可判断。
【解答】解:3.14×4=12.56(cm)
所以圆柱的高是6.28cm。
故选:C。
【点评】熟练掌握圆柱与圆柱展开图之间的关系是解题的关键。
17.(1分)(2023 平阴县)2022年北京冬季奥运会已经圆满结束。在此次冬奥会上,中国体育代表团所获得的金牌数和奖牌数均创历史新高,位列奖牌榜第三。中国体育代表团获得奖牌的数量如图:
北京冬季奥运会,中国体育代表团所获得的金牌数占所获奖牌总数的( )
A.9% B.30% C.60% D.90%
【考点】百分数的实际应用.
【专题】运算能力.
【答案】C
【分析】把奖牌总数看作单位“1”,根据求一个数是另一个数的几分之几,用除法解答。
【解答】解:9÷15=60%
答:中国体育代表团所获得的金牌数占所获奖牌总数的60%。
故选:C。
【点评】此题属于求一个数是另一个数的几分之几,关键是确定单位“1”作除数,求一个数是另一个数的几分之几,用除法解答即可。
18.(1分)(2024 南京模拟)白兔的只数比黑兔多,黑兔与白兔只数的最简单的整数比是( )
A.10:9 B.9:10 C.1:10 D.1:9
【考点】比的意义;求比值和化简比.
【专题】应用意识.
【答案】B
【分析】把黑兔的只数看作单位“1”,白兔的只数为(1),据此写出黑兔与白兔只数的比,再化简即可。
【解答】解:1:(1)
=1:
=9:10
答:黑兔与白兔只数的最简单的整数比是9:10。
故选:B。
【点评】本题主要考查了比的意义及化简比,解题的关键是把黑兔的只数看作单位“1”,得出白兔的只数。
三.计算题(共3小题,满分31分)
19.(10分)(2020秋 安化县期末)直接写出得数。
3÷1%=
【考点】分数乘法;分数除法;分数的四则混合运算.
【专题】计算题;应用意识.
【答案】0.3;13.5;0.16;;0.36;;300;。
【分析】分数乘整数或整数乘分数:由于任何整数(0除外)都可以化成分母是1的假分数,分数乘整数或整数乘分数,都可以转化成分数乘分数的形式,分数乘分数:用分子相乘的积作为分子,用分母相乘的积作为分母;同分母分数相加(减),分子进行相加(减)得数作分子,分母不变,异分母分数相加(减),必须先通分,然后,按照同分母分数相加(减)的法则进行运算,整数的运算定律同样适用于分数乘法中的简便计算,需要关注的是,根据数的特征正确运用运算定律,切勿随心所欲进行所谓的“简便计算”。
【解答】解:
0.3 13.5 0.16
0.36 3÷1%=300
【点评】本题考查的主要内容是分数乘法,分数除法和分数混合运算问题。
20.(9分)(2024 宁波)解方程或解比例。
①x=5
②3.2×2.5﹣75%x=2
③
【考点】解比例;分数方程求解;百分数方程求解.
【专题】简易方程;运算能力.
【答案】①x=12;②x=8;③x。
【分析】①先计算xx,根据等式的性质,方程的两边同时除以求解;
②先计算3.2×2.5=8,根据等式的性质,方程的两边同时加上75%x,把方程化为2+75%x=8,方程的两边同时减去2,然后方程的两边同时除以75%求解;
③根据比与除法的关系,把原式化为x,根据等式的性质,方程的两边同时乘,然后方程的两边同时除以求解。
【解答】解:①x=5
x=5
x5
x=12
②3.2×2.5﹣75%x=2
8﹣75%x=2
8﹣75%x+75%x=2+75%x
2+75%x=8
2+75%x﹣2=8﹣2
75%x=6
75%x÷75%=6÷75%
x=8
③
x
x
x
x
x
【点评】本题考查解方程,解题的关键是掌握等式的性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立。
21.(12分)计算下面各题,怎样简便就怎样计算。
36+274+164 248﹣82﹣118 578﹣39+61
780÷26÷3 65×35+35×35 25×16×125
【考点】运算定律与简便运算.
【专题】运算能力.
【答案】474;48;600;10;3500;50000。
【分析】(1)利用加法交换律计算;
(2)利用减法的性质计算;
(3)从左到右依次计算;
(4)利用除法的性质计算
(5)利用乘法分配律计算;
(6)将16化成2×8,再利用乘法结合律计算。
【解答】解:(1)36+274+164
=36+164+274
=200+274
=474
(2)248﹣82﹣118
=248﹣(82+118)
=248﹣200
=48
(3)578﹣39+61
=539+61
=600
(4)780÷26÷3
=780÷(26×3)
=780÷78
=10
(5)65×35+35×35
=(65+35)×35
=100×35
=3500
(6)25×16×125
=25×2×8×125
=(25×2)×(8×125)
=50×1000
=50000
【点评】解答本题需熟练掌握四则混合运算顺序,灵活使用运算律和运算性质。
四.操作题(共1小题,满分8分,每小题8分)
22.(8分)按2:1的比画出长方形放大后的图形,再按1:3的比画出三角形缩小后的图形。
【考点】图形的放大与缩小.
【专题】几何直观;应用意识.
【答案】
【分析】根据图形放大的方法,先分别求出放大2倍后,长方形的长、宽各是多少,再根据长方形的画法画出放大后的图形;根据图形缩小的方法,先分别求出缩小3倍后,三角形的底、和各是多少,然后根据三角形的画法画出缩小后的图形。据此解答即可。
【解答】解:3×2=6
1×2=2
9÷3=3
6÷3=2
作图如下:
【点评】此题考查的目的是理解掌握图形放大、缩小的方法及应用。
五.应用题(共6小题,满分31分)
23.(5分)某儿童乐园在“五一”期间的门票收入是9万元,比4月份全月的门票收入还多20%。4月份的门票收入是多少万元?
【考点】百分数的实际应用.
【专题】运算能力.
【答案】7.5万元。
【分析】五一”期间的门票收入是9万元,比4月份全月的门票收入还多20%,即“五一”期间的门票收入是4月份的(1+20%),用除法计算,即可得4月份的门票收入是多少万元。
【解答】解:9÷(1+20%)
=9÷1.2
=7.5(万元)
答:4月份的门票收入是7.5万元。
【点评】本题主要考查了百分数的实际应用,已知一个数的百分之几是多少,求这个数,用除法计算。
24.(5分)(2024秋 洪山区期末)《水浒传》是中国古典四大名著之一,也是中国历史上最早用白话文写成的章回(“章回”是古典长篇小说的段落形式)小说之一,最早的版本全篇有一百章回,小华同学看到了最喜欢的第二十三章回“景阳冈武松打虎”,小华同学没看的章回比已看的章回多百分之几?(百分数后面保留一位小数)
【考点】百分数的实际应用.
【专题】运算能力;应用意识.
【答案】234.8%。
【分析】用《水浒传》的总章回减小华同学看的章回,得出小华同学没看的章回,减小华同学看的章回,再除以小华同学看的章回,即可得解。
【解答】解:(100﹣23﹣23)÷23
=54÷23
≈234.8%
答:小华同学没看的章回比已看的章回多234.8%。
【点评】本题主要考查了百分数的实际应用,求一个数比另一个数多或少百分之几,用除法计算。
25.(5分)(2023 关岭县)把一个长0.5cm、宽0.3cm的长方形零件画在一幅零件图纸上,如果零件的长要画12cm,那么零件的宽要画多少厘米?(用比例解答)
【考点】正、反比例应用题.
【专题】运算能力.
【答案】7.2厘米。
【分析】长方形零件画在一幅零件图纸上,长和宽的比例尺是相同的,根据图上长的长度:实际长的长度=图上宽的长度:实际宽的长度列式解答。
【解答】解:设零件的宽要画x厘米,
12:0.5=x:0.3
0.5x÷0.5=3.6÷0.5
x=7.2
答:零件的宽要画7.2厘米。
【点评】此题考查正比例在生活中的应用。解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
26.(5分)(2022 薛城区)一辆汽车2小时行驶160千米,照这样的速度,从甲城到乙城共行驶5小时。甲,乙两城之间的公路长多少千米?(用比例解)
【考点】正、反比例应用题.
【专题】比和比例应用题.
【答案】400千米。
【分析】照这样的速度,说明速度一定,根据速度=路程÷时间,路程与时间成正比例;据此列出比例即可解答。
【解答】解:设甲,乙两城之间的公路长为x千米。
2x=160×5
2x=800
x=400
答:甲,乙两城之间的公路长为400千米。
【点评】根据速度=路程÷时间,判断路程与时间成正比例是解答关键。
27.(5分)(2024春 正定县期中)把一个长、宽、高分别为8厘米、7厘米、6.28厘米的长方体铁块铸造成一个底面直径为8厘米的圆锥形铁块,圆锥的高是多少?
【考点】圆锥的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】圆锥的高是21厘米。
【分析】熔铸成圆锥体,体积没变,等于长方体的体积,由此可以求出圆锥的体积为:8×7×6.28=351.68(立方厘米),知道底面直径,可求出圆锥的底面积,然后利用圆锥的体积公式可以计算得出圆锥的高。
【解答】解:8×7×6.28=351.68(立方厘米)
351.68×3÷[3.14×(8÷2)2]
=1055.04÷[3.14×16]
=1055.04÷50.24
=21(厘米)
答:圆锥的高是21厘米。
【点评】抓住熔铸前后的体积不变,是解决此类问题的关键。
28.(6分)(2023 芙蓉区模拟)比例尺是一个用于测量和绘制地图的工具,在生活中有着广泛的应用。它可以帮助人们估计和表示地理现象及地图上的物体大小。如在比例尺是1:5000000的地图上,量得从A城到B城长是8厘米。如果汽车平均每小时行驶80千米,从A城出发行驶几小时能到达B城?
【考点】比例尺应用题.
【专题】运算能力.
【答案】5小时。
【分析】先根据图上距离÷比例尺=实际距离,求出实际距离,再根据路程÷速度=时间进行解答即可。
【解答】解:840000000(厘米)
40000000厘米=400千米
400÷80=5(小时)
答:从A城出发行驶5小时能到达B城。
【点评】此题考查的目的是理解比例尺的意义及应用,掌握路程、速度、时间三者之间的关系。
第1页(共1页)
同课章节目录
