江苏省宜兴市外国语学校苏科版九年级数学下册6.3《相似图形》导学案(无答案)
文档属性
| 名称 | 江苏省宜兴市外国语学校苏科版九年级数学下册6.3《相似图形》导学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 90.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-04 20:31:22 | ||
图片预览

文档简介
宜兴外国语学校初二数学学科导学提纲
课题:6.3《相似图形》 设计人:吴黎云 审核:初三数学备课组
姓名____________班级____________ 使用时间:
课前参与:
1.概念:形状相同的图形是相似形。
交流:(1)你能举出生活中所见过的相似图形吗?
(2)全等图形和相似图形之间有什么联系与区别?
2、找一找:下面各组图形中,哪些是相似图形?哪些不是?
3、归纳:各角分别相等,各边对应成比例的两个三角形,称为相似三角形。
相似三角形中对应边的比叫做相似比。
例如:如图,在△ABC和△A′B′C′中,
各角分别相等:∠A=∠A′,∠B=∠B′,∠C=∠C′;
各边成比例:
则△ABC与△A′B′C′相似。
记作:△ABC∽△ A′B′C′,
读作:△ABC相似于△ A′B′C′
其中k叫做它们的相似比
注意:对应顶点的字母写在对应的位置上
反之:若△ABC与△A′B′C′相似,
则∠A=∠A′,∠B=∠B′,∠C=∠C′;
4、思考:如果相似比 k=1,这两个三角形有怎样的关系? 。
5、探索:(类比思想)
我们知道:各角对应相等、各边对应成比例的两个三角形,叫做相似三角形。相似三角形中对应边的比叫做相似比。假如把三角形换成四边形、或者五边形,甚至多边形呢?
归纳:如果两个边数相同的多边形的角对应相等,边对应成比例,那么这两个多边形叫做相似多边形。相似多边形对应边的比叫做相似比。
通过预习,你还有什么疑惑?请写下来:
课中参与
例1、判断:
所有的直角三角形都相似( )
所有的等腰直角三角形都相似( )
所有的等边三角形都相似( )
所有的四边形都相似( )
所有的正方形都相似( )
所有的矩形都相似( )
所有的菱形都相似( )
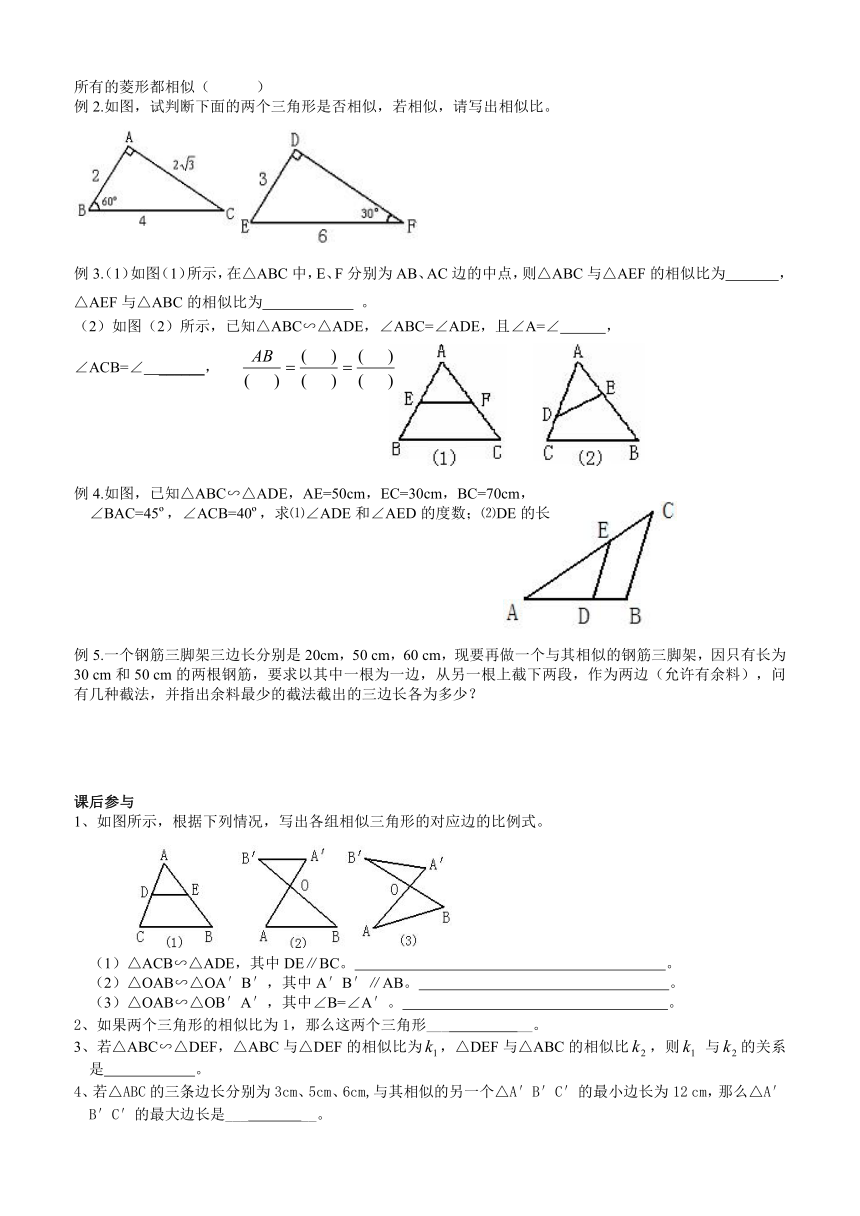
例2.如图,试判断下面的两个三角形是否相似,若相似,请写出相似比。
例3.(1)如图(1)所示,在△ABC中,E、F分别为AB、AC边的中点,则△ABC与△AEF的相似比为 ,△AEF与△ABC的相似比为 。
(2)如图(2)所示,已知△ABC∽△ADE,∠ABC=∠ADE,且∠A=∠ ,
∠ACB=∠ ______,
例4.如图,已知△ABC∽△ADE,AE=50cm,EC=30cm,BC=70cm,
∠BAC=45o,∠ACB=40o,求⑴∠ADE和∠AED的度数;⑵DE的长
例5.一个钢筋三脚架三边长分别是20cm,50 cm,60 cm,现要再做一个与其相似的钢筋三脚架,因只有长为30 cm和50 cm的两根钢筋,要求以其中一根为一边,从另一根上截下两段,作为两边(允许有余料),问有几种截法,并指出余料最少的截法截出的三边长各为多少?
课后参与
1、如图所示,根据下列情况,写出各组相似三角形的对应边的比例式。
(1)△ACB∽△ADE,其中DE∥BC。 。
(2)△OAB∽△OA′B′,其中A′B′∥AB。 。
(3)△OAB∽△OB′A′,其中∠B=∠A′。 。
2、如果两个三角形的相似比为1,那么这两个三角形___ __。
3、若△ABC∽△DEF,△ABC与△DEF的相似比为,△DEF与△ABC的相似比,则 与的关系是 。
4、若△ABC的三条边长分别为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12 cm,那么△A′B′C′的最大边长是___ __。
5、已知△ABC∽△DEF,AB=6,DE=2,EF=5,则AC的取值范围是 。
6、如果一个三角形的三边长分别是5、12和13,与其相似的三角形的最长边长是39,那么
较大三角形的周长是 ,较小三角形与较大三角形周长的比 。
7、若△ABC与△A′B′C′相似,一组对应边的长为AB=3 cm,A′B′=4 cm,那么
△A′B′C′与△ABC的相似比是___ _ 。
8、下列命题错误的是( )
A.两个全等的三角形一定相似 B.两个直角三角形一定相似
C.两个相似三角形的对应角相等,对应边成比例 D.相似的两个三角形不一定全等
9、如图,△ABC∽△ACD,则下列各式中,正确的是( ) 。
A、 B、
C、 D、
10、△ABC与△相似,相似比为2:3,△与△ 相
似,相似比为6:5,则△ABC与△的相似比是( )
A. 2:5 B. 4:5 C. 5:9 D. 3:5
11、语句:“①所有度数相等的角都相似;②所有边长相等的菱形都相似;③所有的正方形都相似;④所有的圆都相似”中准确的有( ). (A)4句 (B)3句 (C)2句 (D)1句
12、若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠C’的度
数是 A.55° B.100° C.25° D.不能确定( )
13、如图,△ABC∽△ADE,且∠ADE=∠B,则下列比例式正确的是( )
A、 B、 C、 D、
14、如图,在△ABC中,D,E分别是AB,AC上的点,DE=1cm,BC=3 cm,
AB=6 cm,EC=3 cm,如果△ADE∽△ABC,求AD,AC的长。
15、已知等腰直角三角形ABC与等腰直角三角形A ′ B ′C '相似,相似比为3:1,斜边AB=5cm, (1)求△ A ′B ′C ′的斜边A ′B ′的长; (2)求斜边A ′B ′上的高。
16、有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长5cm,其他两边的长都是3.5cm,求该草坪其他两边的实际长度。
17、已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的一边为8,求其余两边.
18、如图,等腰△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,
∠BAC=40o,若△ABD∽△ECA,求∠DAE的度数。
19、如图,等腰△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,若
△ADB∽△EAC,试说明
课题:6.3《相似图形》 设计人:吴黎云 审核:初三数学备课组
姓名____________班级____________ 使用时间:
课前参与:
1.概念:形状相同的图形是相似形。
交流:(1)你能举出生活中所见过的相似图形吗?
(2)全等图形和相似图形之间有什么联系与区别?
2、找一找:下面各组图形中,哪些是相似图形?哪些不是?
3、归纳:各角分别相等,各边对应成比例的两个三角形,称为相似三角形。
相似三角形中对应边的比叫做相似比。
例如:如图,在△ABC和△A′B′C′中,
各角分别相等:∠A=∠A′,∠B=∠B′,∠C=∠C′;
各边成比例:
则△ABC与△A′B′C′相似。
记作:△ABC∽△ A′B′C′,
读作:△ABC相似于△ A′B′C′
其中k叫做它们的相似比
注意:对应顶点的字母写在对应的位置上
反之:若△ABC与△A′B′C′相似,
则∠A=∠A′,∠B=∠B′,∠C=∠C′;
4、思考:如果相似比 k=1,这两个三角形有怎样的关系? 。
5、探索:(类比思想)
我们知道:各角对应相等、各边对应成比例的两个三角形,叫做相似三角形。相似三角形中对应边的比叫做相似比。假如把三角形换成四边形、或者五边形,甚至多边形呢?
归纳:如果两个边数相同的多边形的角对应相等,边对应成比例,那么这两个多边形叫做相似多边形。相似多边形对应边的比叫做相似比。
通过预习,你还有什么疑惑?请写下来:
课中参与
例1、判断:
所有的直角三角形都相似( )
所有的等腰直角三角形都相似( )
所有的等边三角形都相似( )
所有的四边形都相似( )
所有的正方形都相似( )
所有的矩形都相似( )
所有的菱形都相似( )
例2.如图,试判断下面的两个三角形是否相似,若相似,请写出相似比。
例3.(1)如图(1)所示,在△ABC中,E、F分别为AB、AC边的中点,则△ABC与△AEF的相似比为 ,△AEF与△ABC的相似比为 。
(2)如图(2)所示,已知△ABC∽△ADE,∠ABC=∠ADE,且∠A=∠ ,
∠ACB=∠ ______,
例4.如图,已知△ABC∽△ADE,AE=50cm,EC=30cm,BC=70cm,
∠BAC=45o,∠ACB=40o,求⑴∠ADE和∠AED的度数;⑵DE的长
例5.一个钢筋三脚架三边长分别是20cm,50 cm,60 cm,现要再做一个与其相似的钢筋三脚架,因只有长为30 cm和50 cm的两根钢筋,要求以其中一根为一边,从另一根上截下两段,作为两边(允许有余料),问有几种截法,并指出余料最少的截法截出的三边长各为多少?
课后参与
1、如图所示,根据下列情况,写出各组相似三角形的对应边的比例式。
(1)△ACB∽△ADE,其中DE∥BC。 。
(2)△OAB∽△OA′B′,其中A′B′∥AB。 。
(3)△OAB∽△OB′A′,其中∠B=∠A′。 。
2、如果两个三角形的相似比为1,那么这两个三角形___ __。
3、若△ABC∽△DEF,△ABC与△DEF的相似比为,△DEF与△ABC的相似比,则 与的关系是 。
4、若△ABC的三条边长分别为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12 cm,那么△A′B′C′的最大边长是___ __。
5、已知△ABC∽△DEF,AB=6,DE=2,EF=5,则AC的取值范围是 。
6、如果一个三角形的三边长分别是5、12和13,与其相似的三角形的最长边长是39,那么
较大三角形的周长是 ,较小三角形与较大三角形周长的比 。
7、若△ABC与△A′B′C′相似,一组对应边的长为AB=3 cm,A′B′=4 cm,那么
△A′B′C′与△ABC的相似比是___ _ 。
8、下列命题错误的是( )
A.两个全等的三角形一定相似 B.两个直角三角形一定相似
C.两个相似三角形的对应角相等,对应边成比例 D.相似的两个三角形不一定全等
9、如图,△ABC∽△ACD,则下列各式中,正确的是( ) 。
A、 B、
C、 D、
10、△ABC与△相似,相似比为2:3,△与△ 相
似,相似比为6:5,则△ABC与△的相似比是( )
A. 2:5 B. 4:5 C. 5:9 D. 3:5
11、语句:“①所有度数相等的角都相似;②所有边长相等的菱形都相似;③所有的正方形都相似;④所有的圆都相似”中准确的有( ). (A)4句 (B)3句 (C)2句 (D)1句
12、若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠C’的度
数是 A.55° B.100° C.25° D.不能确定( )
13、如图,△ABC∽△ADE,且∠ADE=∠B,则下列比例式正确的是( )
A、 B、 C、 D、
14、如图,在△ABC中,D,E分别是AB,AC上的点,DE=1cm,BC=3 cm,
AB=6 cm,EC=3 cm,如果△ADE∽△ABC,求AD,AC的长。
15、已知等腰直角三角形ABC与等腰直角三角形A ′ B ′C '相似,相似比为3:1,斜边AB=5cm, (1)求△ A ′B ′C ′的斜边A ′B ′的长; (2)求斜边A ′B ′上的高。
16、有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长5cm,其他两边的长都是3.5cm,求该草坪其他两边的实际长度。
17、已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的一边为8,求其余两边.
18、如图,等腰△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,
∠BAC=40o,若△ABD∽△ECA,求∠DAE的度数。
19、如图,等腰△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,若
△ADB∽△EAC,试说明
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
