2025年中考数学专题训练:一元一次方程的应用(含解析)
文档属性
| 名称 | 2025年中考数学专题训练:一元一次方程的应用(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年中考数学专题训练:一元一次方程的应用
一、单选题
1.某市按以下规定收取每月的燃气费,用燃气不超过30立方米,按每立方米1.2元收费;如果超过30立方米,超过部分按每立方米2元收费.已知3月份张老师家的燃气费平均每立方米元,那么3月份张老师家应缴燃气费( )
A.48元 B.60元 C.72元 D.90元
2.嘉嘉设计了一个“幻方”游戏,现在将1、、3、、5、、7、分别填入图中的圆圈内,使横、竖以及内外两个正方形顶点上的4个数字之和都相等,则的值为( )
A.或4 B.或1 C.或 D.1或
3.《四元玉鉴》中提出了下列问题:今有布帛二色,共织三丈六尺,已知白布每尺价八文,彩布每尺价十文,若白布减五尺,彩布增三尺,二者总价相等,问白布、彩布各几何尺?这段话的意思是:现在有白色和彩色两种布帛,总共织了三丈六尺(一丈等于十尺,三丈六尺就是36尺).已知白色布每尺价格是8文钱,彩色布每尺价格是10文钱,如果白色布的长度减少5尺,彩色布的长度增加3尺,那么白色布和彩色布的价钱就相等.问白色布和彩色布各有多少尺?设白色布有尺,可列方程为( )
A. B.
C. D.
4.为弘扬中华优秀传统文化,某校组织了传统文化知识竞赛,共设20道选择题,各题分值相同,每题均为必答题.下表统计了3名参赛学生甲,乙,丙的得分情况,则另一名参赛学生丁的得分可能是( )
参赛学生 答对题数 答错题数 得分/分
甲 20 0 100
乙 18 2 88
丙 10 10 40
A.54分 B.64分 C.78分 D.93分
5.小明一家人去电影院看电影《哪吒(2)》,路上预计用时25分钟,但由于堵车,结果实际车速比预计的每小时慢10千米,且路上多用了5分钟.设预计车速为x千米/时,根据题意可列方程为( )
A. B.
C. D.
6.《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人公车,九人步.问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘.问共有多少人?多少辆车?设共有x人,可列方程为( )
A. B.
C. D.
7.《九章算术》中记载,浮箭漏出现于汉武帝时期.如图,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺刻度计算时间.已知在箭尺有一定读数的情况下,供水小时,箭尺读数为;供水小时,箭尺读数为.设开始高度为,根据题意可列方程为( )
A. B.
C. D.
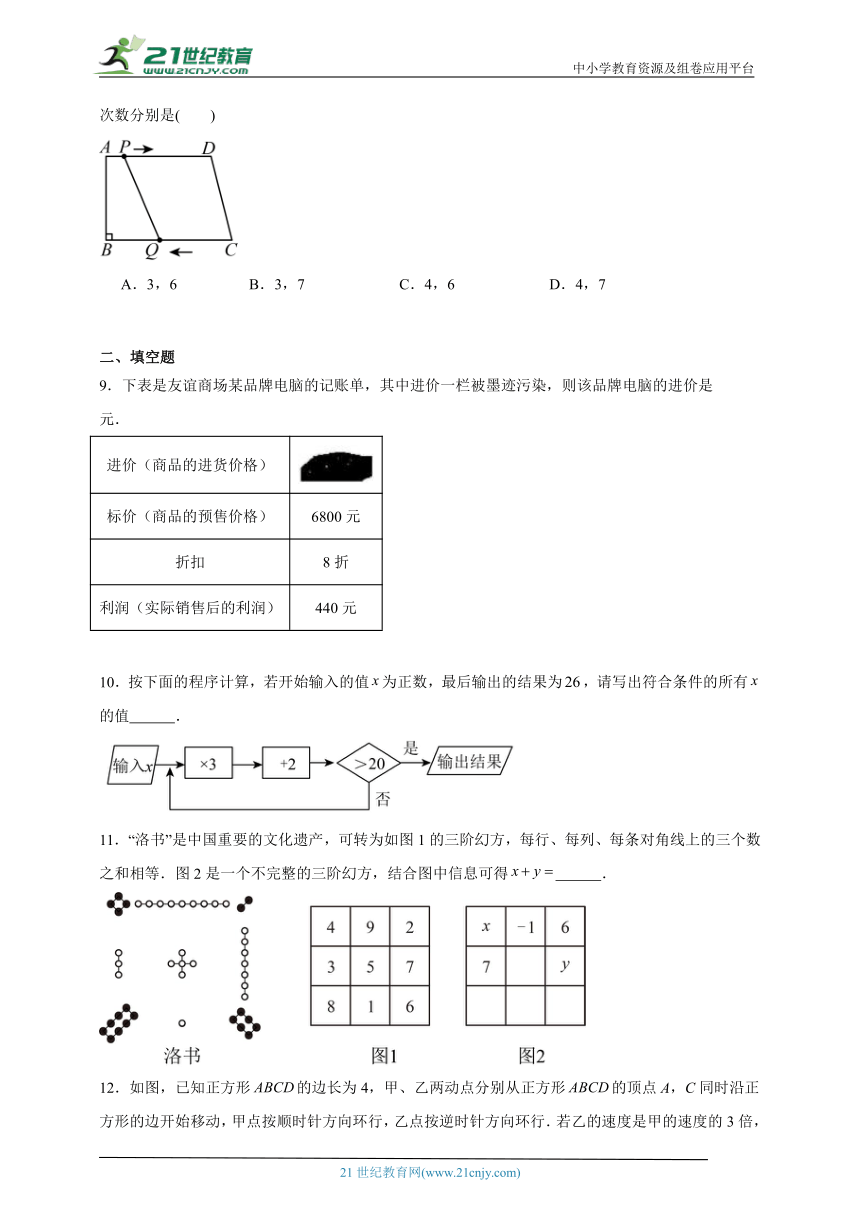
8.如图.在四边形中,,,,..点P从点A出发,以的速度向点D运动,点Q从点C同时出发,以的速度在线段上来回运动,当点P当到达点D时,两点停止运动.在此运动过程中,出现和的次数分别是( )
A.3,6 B.3,7 C.4,6 D.4,7
二、填空题
9.下表是友谊商场某品牌电脑的记账单,其中进价一栏被墨迹污染,则该品牌电脑的进价是 元.
进价(商品的进货价格)
标价(商品的预售价格) 6800元
折扣 8折
利润(实际销售后的利润) 440元
10.按下面的程序计算,若开始输入的值为正数,最后输出的结果为,请写出符合条件的所有的值 .
11.“洛书”是中国重要的文化遗产,可转为如图1的三阶幻方,每行、每列、每条对角线上的三个数之和相等.图2是一个不完整的三阶幻方,结合图中信息可得 .
12.如图,已知正方形的边长为4,甲、乙两动点分别从正方形的顶点A,C同时沿正方形的边开始移动,甲点按顺时针方向环行,乙点按逆时针方向环行.若乙的速度是甲的速度的3倍,则它们第2025次相遇在 边上.
13.在一次劳动课上,有30名同学在甲处劳动,有12名同学在乙处劳动,现在另调25人也去这两处劳动,使得在甲处劳动的人数是在乙处劳动的人数的2倍,如果设调往甲处人,那么依题意可列方程为 .
14.如图,分别为直线上两点,且射线绕点以3度/秒的速度顺时针旋转至停止,射线绕点F以12度/秒的速度逆时针旋转至射线后立即以8度/秒的速度顺时针返回.当与重合时,两条射线都停止运动,设旋转时间为(秒),当时,的值为 秒.
三、解答题
15.我国古代文房四宝(笔、墨、纸、砚)是文人墨客必备的文具.某文房阁直接从作坊购进毛笔、砚台两款文具进行销售,进货价和销售价如下表:
毛笔 砚台
进货价/(元/件) 30 40
销售价/(元/件) 45 60
(1)该文房阁第一次用1300元购进毛笔、砚台两款文具共40件,求两款文具分别购进的件数;
(2)第一次购进的两款文具售完后,该文房阁计划最多用5600元再次购进毛笔、砚台两款文具共150件,该文房阁应如何设计进货方案,才能使第二次所购毛笔、砚台全部销售完后能获得最大销售利润?最大销售利润是多少元?
16.鲁班锁是我国古代传统建筑物的固定结合器,也是一种广泛流传的益智玩具,如图.其中六根鲁班锁中一个构件的一个面的尺寸如图所示.已知,求这个面的面积.
17.某中学组织部分学生赴博物馆参加研学活动,委托甲、乙两家旅行社承担此次活动的出行事宜.由于接待能力有限,甲旅行社一次最多只能接待人(即额定数量),超过额定数量的人,再由乙旅行社接待.甲旅行社收费标准:团队固定费300元,再额外收取每人150元;乙旅行社收费标准;每人收取180元.该中学第一批组织了35名学生参加,总费用为5700元.
(1)求甲旅行社一次最多能接待的人数;
(2)为节约开支,要控制人均费用不超过165元,试求每批组织人数的合理范围.
18.【建立概念】对于两个不相等的有理数,,我们规定符号表示,,中的较大值,如,.
【概念理解】请解答下列问题:
(1)________;
(2)如果,求的取值范围;
【拓展应用】
(3)如果,求的值.
19.甲乙两名同事计划周末登“虞山”,两人从山下同一地点出发,相约之前到达山顶某景区,甲先出发,中途在休息一段时间后保持原速继续登山;乙晚出发分钟,比甲早到达山顶.从开始计时,时长记为分钟,甲、乙两人登山的路程记为、.甲、乙两人登山的路程、与时长之间的函数关系如图所示.
(1)乙到达山顶的时间为_______;
(2)记甲的速度为,乙的速度为.
①甲、乙两人的速度之比的值为_______;
②已知甲的速度米/分钟,在乙登山的过程中,若,求的值.
20.【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形进行完美地结合.研究数轴我们发现了很多重要的规律.如数轴上点、在数轴上分别表示有理数、,则、两点之间的距离表示为.
【综合运用】已知点、、为数轴上三个点,表示的数分别是,,,满足,且为的倒数.
(1)______,______,______;
(2)若动点从点出发沿数轴正方向运动,动点同时从点出发也沿数轴正方向运动,点的速度是每秒3个单位长度,点的速度是每秒2个单位长度.设运动的时间为秒.
①用含的式子表示:秒后,点表示的数为______;
②当时,求的值.
(3)在(2)的条件下,、出发的同时,动点从点出发沿数轴正方向运动,速度为每秒5个单位长度,点追上点后立即返回沿数轴负方向运动.求点追上点后再经过几秒,?
《2025年中考数学专题训练:一元一次方程的应用》参考答案
题号 1 2 3 4 5 6 7 8
答案 C A B B D B C A
1.C
【分析】本题考查一元一次方程的应用,理解收费规定建立方程是解题的关键. 根据3月份张老师家的燃气费平均每立方米元,可知用户用量超过30立方米,设3月份燃气用量为x,则根据平均每立方米元,可得出方程,解出x后,即可得出答案.
【详解】解:∵3月份张老师家的燃气费平均每立方米元,
∴用户燃气用量超过30立方米,
设3月份燃气用量为x,
由题意得,,
解得:,
则3月份张老师家应交燃气费为:(元)
答:3月份张老师家应交燃气费72元.
故选:C
2.A
【分析】本题考查了一元一次方程.由于八个数的和是,所以需满足内外两个正方形顶点上的4个数字之和都是,横、竖的和也是.列方程可得结论.
【详解】解:设小正方形顶点上的数为x,大正方形顶点上的数为y,
,
∵横、竖以及内外两圈上的4个数字之和都相等,
∴内外两个正方形顶点上的4个数字之和都是,横、竖的和也是,
则,得,
,得,
,,
∵当时,,则,
当时,,则,
故选:A.
3.B
【分析】本题考查了一元一次方程的应用,读懂题意,找出等量关系是解题的关键.由题意可知,现在有白色和彩色两种布帛共有36尺,设白色布有尺,那么彩色布帛有尺,如果白色布的长度减少5尺,彩色布的长度增加3尺,那么白色布有尺,彩色布有尺,然后根据白色布每尺价格乘以白色布数量等于彩色布每尺价格乘以彩色布数量列出方程即可.
【详解】解:设白色布有尺,那么彩色布帛有尺,由题意可知,
故选:B.
4.B
【分析】本题考查了一元一次方程的应用,由记录表格可知,答对一道题得5分,答错一道题扣1分,设答对x道题,则得分分,逐一对选项求解,根据x为正整数,即可得到答案.
【详解】解:由甲同学得分情况可知,答对一道题得分,
由乙同学得分情况可知,答错一道题扣分,
丙同学得分也符合;
设学生丁答对x道题,则答错道题,
∴得分,且x为正整数,
A、,解得:,不符合题意;
B、,解得:,符合题意;
C、,解得:,不合题意;
D、6x-20=62,解得:,不符合题意;
故选:B.
5.D
【分析】本题主要考查了由实际问题列一元一次方程,找准等量关系、正确列出一元一次方程是解题的关键.
设预计车速为x千米/时,由实际车速比预计的每小时慢了10千米可得出实际车速为千米时,利用路程速度时间,结合路程不变,即可得出关于x的一元一次方程即可解答.
【详解】解:设预计车速为x千米/时,则实际车速为千米时,
依题意得:,
故选:D.
6.B
【分析】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.根据车的辆数不变,即可列出方程求解.
【详解】解: 由“每3人共乘一车,最终剩余2辆车”可知车辆有辆,由“每2人共乘一车,最终剩余9个人无车可乘”可知车辆有辆,
所以可列方程.
故选:B.
7.C
【分析】本题主要考查了一元一次方程的应用,设开始高度为,根据题意列出方程即可,读懂题意,找出等量关系,列出方程是解题的关键.
【详解】解:设开始高度为,
根据题意得,,
故选:.
8.A
【分析】本题考查了平行四边形的性质,矩形的性质,勾股定理,根据题意分别求得和的情形,分类讨论,即可求解.
【详解】解:设点P的运动时间为t,
∵,点P从点A出发,以的速度向点D运动,当点P当到达点D时,P、Q两点停止运动.
∴秒,,则,
∵,点Q从点C同时出发,以的速度在线段上来回运动,
∴,
当时,则四边形是平行四边形,
∴,
当时,点Q从C到B运动,,
∴,解得:,
当时,点Q从B到C运动,,
∴,
解得:,
当时,点Q从C到B运动,,
∴,解得:,
当,点Q从B到C运动,,
∴,解得:(舍去),
∴能出现三次,
如图所示,过点P,D分别作的垂线,垂足分别为F,E,
∵,,
∴四边形是矩形,
∴,,,
∴中,,
当时,
在中,,
∴,
当时,点Q从C到B运动,,
∴,解得:或,
当时,点Q从B到C运动,,
∴,解得:或,
当时,点Q从C到B运动,,
∴,解得:或,
当,点Q从B到C运动,,
∴,解得:(舍去)或(舍去),
∴能出现6次,
故选:A.
9.5000
【分析】本题考查了一元一次方程的应用,设该品牌电脑的进价是x元,利用利润=标价×折扣率-进价,可列出关于x的一元一次方程,解之即可得出结论.
【详解】解:设该品牌电脑的进价是x元,
根据题意得:,
解得:,
∴该品牌电脑的进价是5000元.
故答案为:5000.
10.或/8或2
【分析】本题考查了程序流程图与有理数计算,一元一次方程的应用,根据输出结果,由运算程序求出所有的值即可,熟练掌握运算法则是解题的关键.
【详解】解:若第一次输入,输出结果为时,则,解得:;
若第二次输出结果为时,则,解得:;
若第三次输出结果为时,则,解得:(不符合题意);
∴所有正数的值为或,
故答案为:或.
11.
【分析】本题考查了一元一次方程的应用,根据题意列出方程,求解即可.
【详解】解:如图:
由图可知:,
∴,,
如图:
由图可知:,
∴,
∴和为6,
如图:
∴,
故答案为:.
12./
【分析】本题考查了运动中的规律、一元一次方程的实际应用等知识点,发现相遇点所在的边循环出现成为解题的关键.
设甲的速度是1,则乙的速度为3,根据题意,,解得,,第一次相遇点在的中点上;第二次相遇时,满足,解得,,第二次相遇点在的中点上;第三次相遇时,满足,解得,,第二次相遇点在的中点上;第四次相遇时,满足,解得,,第二次相遇点在的中点上;依次循环,根据与相同,据此即可解答.
【详解】解:设甲的速度是1,则乙的速度为3,
根据题意:
,解得,,第一次相遇点在的中点上;
第二次相遇时,满足,解得,,第二次相遇点在的中点上;
第三次相遇时,满足,解得,,第二次相遇点在的中点上;
第四次相遇时,满足,解得,,第二次相遇点在的中点上;
依次循环,根据与相同,即它们第2025次相遇在边上.
故答案为:.
13.
【分析】本题考查根据实际问题列方程,根据在甲处劳动的人数是在乙处劳动的人数的2倍,列出方程即可.
【详解】解:设调往甲处人,则调往乙处人,由题意,得:
;
故答案为:
14.12或24
【分析】本题考查平行线的性质,分和两种情况,根据平行线的性质,列出方程进行求解即可.正确的画图,利用分类讨论的思想进行求解,是解题的关键.
【详解】解:由题意,得:与重合所需时间为,旋转至射线所需时间为:;,
∵,
∴,
当时,如图,
∵,
∴,即:,
解得:;
当时,如图:
同理:,即:,
解得:;
综上:或;
故答案为:12或24.
15.(1)购进毛笔30件,购进砚台10件
(2)应该购进毛笔40件,购进砚台110件,才能获得最大利润,最大利润为2800元
【分析】本题考查了一元一次方程,不等式的应用,一次函数的应用,熟练利用题意得到不等关系或等量关系是解题的关键.
(1)设购进毛笔件,则购进砚台件,根据进货价为1300元列方程即可解答;
(2)设第二次购进毛笔件,则购进砚台件,获得的利润为元,表示出第二次所购毛笔、砚台全部销售完后能获得销售利润,再利用最多用5600元再次购进毛笔、砚台列不等式求得自变量的取值范围,即可解答.
【详解】(1)解:设购进毛笔件,则购进砚台件,
根据题意可得,
解得,
件,
答:购进毛笔30件,购进砚台10件;
(2)解:设第二次购进毛笔件,则购进砚台件,获得的利润为元,
根据题意可得,
最多用5600元再次购进毛笔、砚台两款文具共150件,
,
解得,
的最小值为40,
,
随的增大而减小,
则取最小值40时,最大利润为元,
件,
答:应该购进毛笔40件,购进砚台110件,才能获得最大利润,最大利润为2800元.
16.
【分析】本题考查了一元一次方程的应用,整式混合运算的实际应用,由已知可设,,,进而根据得,即得,即可得,,,再根据图形列式计算即可求解,正确识图是解题的关键.
【详解】解:∵,,
可设,,,
由图可得,,
∴,
解得,
∴,,,
∴这个面的面积.
17.(1)甲旅行社一次最多能接纳的人数为30人;
(2)每批组织人数的合理范围为.
【分析】本题考查了一元一次方程和一元一次不等式的应用,根据题意,掌握列出一元一次方程和一元一次不等式是解题的关键.
()当时,名学生的总费用为,得,依题意可得方程,解方程即可求解;
()分两种情况:和,列出不等式解答即可求解;
【详解】(1)解:若,则名学生的总费用为元,
∵,
∴,
依题意得,,
解得,
答:甲旅行社一次最多能接纳的人数为人;
(2)解:当时,;
解得;
当时,,
解得;
∴每批组织人数的合理范围为.
18.();();()的值为或.
【分析】本题考查了一元一次不等式的应用、一元一次方程的应用,理解符号的定义是解题的关键.
()根据规定符号表示,,中的较大值即可求解;
()根据规定符号可得,然后解不等式即可得;
()根据题意分;两种情况结合绝对值的意义进行分析解答即可.
【详解】解:()∵,
∴,
故答案为:;
()∵,
∴,
∴;
()时,即,
∵,
∴,
∴,
解得:;
时,即,
∵,
∴,
∴,
解得:;
综上可知:的值为或.
19.(1)
(2)①;②或
【分析】本题考查函数的图象的应用,一元一次方程的应用,掌握速度、时间和路程之间的关系是解题的关键.
(1)根据乙出发的时刻和到达景区所用的时间计算即可;
(2)①根据速度路程时间分别用含的代数式将甲、乙的速度表示出来并求出二者的比值即可;
②根据甲的速度和甲、乙的速度比值求出乙的速度,由路程速度时间分别求出、的关于的函数关系式并代入,得到关于的方程并求解即可.
【详解】(1)解:∵分钟小时,
∴乙到达山顶的时间为.
故答案为:.
(2)解:①(米分钟),
(米分钟),
∴,
故答案为:;
②∵,,
∴,(米分钟),
则,
当时,;
当时,;
当时,.
由在乙登山的过程中,即时,
当时,,
解得(舍),
当时,,
解得或(舍去),
当时,,
解得,
综上所述,或.
20.(1),13,7
(2)①;②或6;
(3)点M追上点Q后再经过2秒或秒,.
【分析】(1)根据平方和绝对值的非负性,倒数的定义即可解答;
(2)①根据题意直接列出代数式即可;
②由,结合两点间的距离公式即可得到关于t的方程,求解即可;
(3)点M未追上点Q时,表示出点M表示的数,根据点M追上点Q时,点M,Q表示的数相同,可求出运动的时间和此时点M表示的数,从而可求出点M返回沿负方向运动时所表示的数,根据两点间的距离公式,根据可列出方程,求解即可.
【详解】(1)解:∵a为的倒数,
∴,
∵,,且,
∴,,
∴,.
故答案为:,13,7;
(2)解:①当运动t秒时,点P表示的数为,点Q表示的数为.
故答案为:;
②当时,,
∴,
解得或6;
(3)解:点M未追上点Q时,点M表示的数为,
当点M追上点Q时,,
解得,
即当它们运动2秒时,点M追上点Q,此时点M表示的数为,
∵点M追上点Q后立即返回沿数轴负方向运动,
∴点M表示的数为,
当时,,
∴,
解得或,
∴,,
∴点M追上点Q后再经过秒或2秒,.
【点睛】本题考查绝对值的几何意义,列代数式,数轴上两点间的距离,一元一次方程解决实际问题,掌握绝对值的几何意义,熟练运用方程思想是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年中考数学专题训练:一元一次方程的应用
一、单选题
1.某市按以下规定收取每月的燃气费,用燃气不超过30立方米,按每立方米1.2元收费;如果超过30立方米,超过部分按每立方米2元收费.已知3月份张老师家的燃气费平均每立方米元,那么3月份张老师家应缴燃气费( )
A.48元 B.60元 C.72元 D.90元
2.嘉嘉设计了一个“幻方”游戏,现在将1、、3、、5、、7、分别填入图中的圆圈内,使横、竖以及内外两个正方形顶点上的4个数字之和都相等,则的值为( )
A.或4 B.或1 C.或 D.1或
3.《四元玉鉴》中提出了下列问题:今有布帛二色,共织三丈六尺,已知白布每尺价八文,彩布每尺价十文,若白布减五尺,彩布增三尺,二者总价相等,问白布、彩布各几何尺?这段话的意思是:现在有白色和彩色两种布帛,总共织了三丈六尺(一丈等于十尺,三丈六尺就是36尺).已知白色布每尺价格是8文钱,彩色布每尺价格是10文钱,如果白色布的长度减少5尺,彩色布的长度增加3尺,那么白色布和彩色布的价钱就相等.问白色布和彩色布各有多少尺?设白色布有尺,可列方程为( )
A. B.
C. D.
4.为弘扬中华优秀传统文化,某校组织了传统文化知识竞赛,共设20道选择题,各题分值相同,每题均为必答题.下表统计了3名参赛学生甲,乙,丙的得分情况,则另一名参赛学生丁的得分可能是( )
参赛学生 答对题数 答错题数 得分/分
甲 20 0 100
乙 18 2 88
丙 10 10 40
A.54分 B.64分 C.78分 D.93分
5.小明一家人去电影院看电影《哪吒(2)》,路上预计用时25分钟,但由于堵车,结果实际车速比预计的每小时慢10千米,且路上多用了5分钟.设预计车速为x千米/时,根据题意可列方程为( )
A. B.
C. D.
6.《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人公车,九人步.问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘.问共有多少人?多少辆车?设共有x人,可列方程为( )
A. B.
C. D.
7.《九章算术》中记载,浮箭漏出现于汉武帝时期.如图,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺刻度计算时间.已知在箭尺有一定读数的情况下,供水小时,箭尺读数为;供水小时,箭尺读数为.设开始高度为,根据题意可列方程为( )
A. B.
C. D.
8.如图.在四边形中,,,,..点P从点A出发,以的速度向点D运动,点Q从点C同时出发,以的速度在线段上来回运动,当点P当到达点D时,两点停止运动.在此运动过程中,出现和的次数分别是( )
A.3,6 B.3,7 C.4,6 D.4,7
二、填空题
9.下表是友谊商场某品牌电脑的记账单,其中进价一栏被墨迹污染,则该品牌电脑的进价是 元.
进价(商品的进货价格)
标价(商品的预售价格) 6800元
折扣 8折
利润(实际销售后的利润) 440元
10.按下面的程序计算,若开始输入的值为正数,最后输出的结果为,请写出符合条件的所有的值 .
11.“洛书”是中国重要的文化遗产,可转为如图1的三阶幻方,每行、每列、每条对角线上的三个数之和相等.图2是一个不完整的三阶幻方,结合图中信息可得 .
12.如图,已知正方形的边长为4,甲、乙两动点分别从正方形的顶点A,C同时沿正方形的边开始移动,甲点按顺时针方向环行,乙点按逆时针方向环行.若乙的速度是甲的速度的3倍,则它们第2025次相遇在 边上.
13.在一次劳动课上,有30名同学在甲处劳动,有12名同学在乙处劳动,现在另调25人也去这两处劳动,使得在甲处劳动的人数是在乙处劳动的人数的2倍,如果设调往甲处人,那么依题意可列方程为 .
14.如图,分别为直线上两点,且射线绕点以3度/秒的速度顺时针旋转至停止,射线绕点F以12度/秒的速度逆时针旋转至射线后立即以8度/秒的速度顺时针返回.当与重合时,两条射线都停止运动,设旋转时间为(秒),当时,的值为 秒.
三、解答题
15.我国古代文房四宝(笔、墨、纸、砚)是文人墨客必备的文具.某文房阁直接从作坊购进毛笔、砚台两款文具进行销售,进货价和销售价如下表:
毛笔 砚台
进货价/(元/件) 30 40
销售价/(元/件) 45 60
(1)该文房阁第一次用1300元购进毛笔、砚台两款文具共40件,求两款文具分别购进的件数;
(2)第一次购进的两款文具售完后,该文房阁计划最多用5600元再次购进毛笔、砚台两款文具共150件,该文房阁应如何设计进货方案,才能使第二次所购毛笔、砚台全部销售完后能获得最大销售利润?最大销售利润是多少元?
16.鲁班锁是我国古代传统建筑物的固定结合器,也是一种广泛流传的益智玩具,如图.其中六根鲁班锁中一个构件的一个面的尺寸如图所示.已知,求这个面的面积.
17.某中学组织部分学生赴博物馆参加研学活动,委托甲、乙两家旅行社承担此次活动的出行事宜.由于接待能力有限,甲旅行社一次最多只能接待人(即额定数量),超过额定数量的人,再由乙旅行社接待.甲旅行社收费标准:团队固定费300元,再额外收取每人150元;乙旅行社收费标准;每人收取180元.该中学第一批组织了35名学生参加,总费用为5700元.
(1)求甲旅行社一次最多能接待的人数;
(2)为节约开支,要控制人均费用不超过165元,试求每批组织人数的合理范围.
18.【建立概念】对于两个不相等的有理数,,我们规定符号表示,,中的较大值,如,.
【概念理解】请解答下列问题:
(1)________;
(2)如果,求的取值范围;
【拓展应用】
(3)如果,求的值.
19.甲乙两名同事计划周末登“虞山”,两人从山下同一地点出发,相约之前到达山顶某景区,甲先出发,中途在休息一段时间后保持原速继续登山;乙晚出发分钟,比甲早到达山顶.从开始计时,时长记为分钟,甲、乙两人登山的路程记为、.甲、乙两人登山的路程、与时长之间的函数关系如图所示.
(1)乙到达山顶的时间为_______;
(2)记甲的速度为,乙的速度为.
①甲、乙两人的速度之比的值为_______;
②已知甲的速度米/分钟,在乙登山的过程中,若,求的值.
20.【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形进行完美地结合.研究数轴我们发现了很多重要的规律.如数轴上点、在数轴上分别表示有理数、,则、两点之间的距离表示为.
【综合运用】已知点、、为数轴上三个点,表示的数分别是,,,满足,且为的倒数.
(1)______,______,______;
(2)若动点从点出发沿数轴正方向运动,动点同时从点出发也沿数轴正方向运动,点的速度是每秒3个单位长度,点的速度是每秒2个单位长度.设运动的时间为秒.
①用含的式子表示:秒后,点表示的数为______;
②当时,求的值.
(3)在(2)的条件下,、出发的同时,动点从点出发沿数轴正方向运动,速度为每秒5个单位长度,点追上点后立即返回沿数轴负方向运动.求点追上点后再经过几秒,?
《2025年中考数学专题训练:一元一次方程的应用》参考答案
题号 1 2 3 4 5 6 7 8
答案 C A B B D B C A
1.C
【分析】本题考查一元一次方程的应用,理解收费规定建立方程是解题的关键. 根据3月份张老师家的燃气费平均每立方米元,可知用户用量超过30立方米,设3月份燃气用量为x,则根据平均每立方米元,可得出方程,解出x后,即可得出答案.
【详解】解:∵3月份张老师家的燃气费平均每立方米元,
∴用户燃气用量超过30立方米,
设3月份燃气用量为x,
由题意得,,
解得:,
则3月份张老师家应交燃气费为:(元)
答:3月份张老师家应交燃气费72元.
故选:C
2.A
【分析】本题考查了一元一次方程.由于八个数的和是,所以需满足内外两个正方形顶点上的4个数字之和都是,横、竖的和也是.列方程可得结论.
【详解】解:设小正方形顶点上的数为x,大正方形顶点上的数为y,
,
∵横、竖以及内外两圈上的4个数字之和都相等,
∴内外两个正方形顶点上的4个数字之和都是,横、竖的和也是,
则,得,
,得,
,,
∵当时,,则,
当时,,则,
故选:A.
3.B
【分析】本题考查了一元一次方程的应用,读懂题意,找出等量关系是解题的关键.由题意可知,现在有白色和彩色两种布帛共有36尺,设白色布有尺,那么彩色布帛有尺,如果白色布的长度减少5尺,彩色布的长度增加3尺,那么白色布有尺,彩色布有尺,然后根据白色布每尺价格乘以白色布数量等于彩色布每尺价格乘以彩色布数量列出方程即可.
【详解】解:设白色布有尺,那么彩色布帛有尺,由题意可知,
故选:B.
4.B
【分析】本题考查了一元一次方程的应用,由记录表格可知,答对一道题得5分,答错一道题扣1分,设答对x道题,则得分分,逐一对选项求解,根据x为正整数,即可得到答案.
【详解】解:由甲同学得分情况可知,答对一道题得分,
由乙同学得分情况可知,答错一道题扣分,
丙同学得分也符合;
设学生丁答对x道题,则答错道题,
∴得分,且x为正整数,
A、,解得:,不符合题意;
B、,解得:,符合题意;
C、,解得:,不合题意;
D、6x-20=62,解得:,不符合题意;
故选:B.
5.D
【分析】本题主要考查了由实际问题列一元一次方程,找准等量关系、正确列出一元一次方程是解题的关键.
设预计车速为x千米/时,由实际车速比预计的每小时慢了10千米可得出实际车速为千米时,利用路程速度时间,结合路程不变,即可得出关于x的一元一次方程即可解答.
【详解】解:设预计车速为x千米/时,则实际车速为千米时,
依题意得:,
故选:D.
6.B
【分析】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.根据车的辆数不变,即可列出方程求解.
【详解】解: 由“每3人共乘一车,最终剩余2辆车”可知车辆有辆,由“每2人共乘一车,最终剩余9个人无车可乘”可知车辆有辆,
所以可列方程.
故选:B.
7.C
【分析】本题主要考查了一元一次方程的应用,设开始高度为,根据题意列出方程即可,读懂题意,找出等量关系,列出方程是解题的关键.
【详解】解:设开始高度为,
根据题意得,,
故选:.
8.A
【分析】本题考查了平行四边形的性质,矩形的性质,勾股定理,根据题意分别求得和的情形,分类讨论,即可求解.
【详解】解:设点P的运动时间为t,
∵,点P从点A出发,以的速度向点D运动,当点P当到达点D时,P、Q两点停止运动.
∴秒,,则,
∵,点Q从点C同时出发,以的速度在线段上来回运动,
∴,
当时,则四边形是平行四边形,
∴,
当时,点Q从C到B运动,,
∴,解得:,
当时,点Q从B到C运动,,
∴,
解得:,
当时,点Q从C到B运动,,
∴,解得:,
当,点Q从B到C运动,,
∴,解得:(舍去),
∴能出现三次,
如图所示,过点P,D分别作的垂线,垂足分别为F,E,
∵,,
∴四边形是矩形,
∴,,,
∴中,,
当时,
在中,,
∴,
当时,点Q从C到B运动,,
∴,解得:或,
当时,点Q从B到C运动,,
∴,解得:或,
当时,点Q从C到B运动,,
∴,解得:或,
当,点Q从B到C运动,,
∴,解得:(舍去)或(舍去),
∴能出现6次,
故选:A.
9.5000
【分析】本题考查了一元一次方程的应用,设该品牌电脑的进价是x元,利用利润=标价×折扣率-进价,可列出关于x的一元一次方程,解之即可得出结论.
【详解】解:设该品牌电脑的进价是x元,
根据题意得:,
解得:,
∴该品牌电脑的进价是5000元.
故答案为:5000.
10.或/8或2
【分析】本题考查了程序流程图与有理数计算,一元一次方程的应用,根据输出结果,由运算程序求出所有的值即可,熟练掌握运算法则是解题的关键.
【详解】解:若第一次输入,输出结果为时,则,解得:;
若第二次输出结果为时,则,解得:;
若第三次输出结果为时,则,解得:(不符合题意);
∴所有正数的值为或,
故答案为:或.
11.
【分析】本题考查了一元一次方程的应用,根据题意列出方程,求解即可.
【详解】解:如图:
由图可知:,
∴,,
如图:
由图可知:,
∴,
∴和为6,
如图:
∴,
故答案为:.
12./
【分析】本题考查了运动中的规律、一元一次方程的实际应用等知识点,发现相遇点所在的边循环出现成为解题的关键.
设甲的速度是1,则乙的速度为3,根据题意,,解得,,第一次相遇点在的中点上;第二次相遇时,满足,解得,,第二次相遇点在的中点上;第三次相遇时,满足,解得,,第二次相遇点在的中点上;第四次相遇时,满足,解得,,第二次相遇点在的中点上;依次循环,根据与相同,据此即可解答.
【详解】解:设甲的速度是1,则乙的速度为3,
根据题意:
,解得,,第一次相遇点在的中点上;
第二次相遇时,满足,解得,,第二次相遇点在的中点上;
第三次相遇时,满足,解得,,第二次相遇点在的中点上;
第四次相遇时,满足,解得,,第二次相遇点在的中点上;
依次循环,根据与相同,即它们第2025次相遇在边上.
故答案为:.
13.
【分析】本题考查根据实际问题列方程,根据在甲处劳动的人数是在乙处劳动的人数的2倍,列出方程即可.
【详解】解:设调往甲处人,则调往乙处人,由题意,得:
;
故答案为:
14.12或24
【分析】本题考查平行线的性质,分和两种情况,根据平行线的性质,列出方程进行求解即可.正确的画图,利用分类讨论的思想进行求解,是解题的关键.
【详解】解:由题意,得:与重合所需时间为,旋转至射线所需时间为:;,
∵,
∴,
当时,如图,
∵,
∴,即:,
解得:;
当时,如图:
同理:,即:,
解得:;
综上:或;
故答案为:12或24.
15.(1)购进毛笔30件,购进砚台10件
(2)应该购进毛笔40件,购进砚台110件,才能获得最大利润,最大利润为2800元
【分析】本题考查了一元一次方程,不等式的应用,一次函数的应用,熟练利用题意得到不等关系或等量关系是解题的关键.
(1)设购进毛笔件,则购进砚台件,根据进货价为1300元列方程即可解答;
(2)设第二次购进毛笔件,则购进砚台件,获得的利润为元,表示出第二次所购毛笔、砚台全部销售完后能获得销售利润,再利用最多用5600元再次购进毛笔、砚台列不等式求得自变量的取值范围,即可解答.
【详解】(1)解:设购进毛笔件,则购进砚台件,
根据题意可得,
解得,
件,
答:购进毛笔30件,购进砚台10件;
(2)解:设第二次购进毛笔件,则购进砚台件,获得的利润为元,
根据题意可得,
最多用5600元再次购进毛笔、砚台两款文具共150件,
,
解得,
的最小值为40,
,
随的增大而减小,
则取最小值40时,最大利润为元,
件,
答:应该购进毛笔40件,购进砚台110件,才能获得最大利润,最大利润为2800元.
16.
【分析】本题考查了一元一次方程的应用,整式混合运算的实际应用,由已知可设,,,进而根据得,即得,即可得,,,再根据图形列式计算即可求解,正确识图是解题的关键.
【详解】解:∵,,
可设,,,
由图可得,,
∴,
解得,
∴,,,
∴这个面的面积.
17.(1)甲旅行社一次最多能接纳的人数为30人;
(2)每批组织人数的合理范围为.
【分析】本题考查了一元一次方程和一元一次不等式的应用,根据题意,掌握列出一元一次方程和一元一次不等式是解题的关键.
()当时,名学生的总费用为,得,依题意可得方程,解方程即可求解;
()分两种情况:和,列出不等式解答即可求解;
【详解】(1)解:若,则名学生的总费用为元,
∵,
∴,
依题意得,,
解得,
答:甲旅行社一次最多能接纳的人数为人;
(2)解:当时,;
解得;
当时,,
解得;
∴每批组织人数的合理范围为.
18.();();()的值为或.
【分析】本题考查了一元一次不等式的应用、一元一次方程的应用,理解符号的定义是解题的关键.
()根据规定符号表示,,中的较大值即可求解;
()根据规定符号可得,然后解不等式即可得;
()根据题意分;两种情况结合绝对值的意义进行分析解答即可.
【详解】解:()∵,
∴,
故答案为:;
()∵,
∴,
∴;
()时,即,
∵,
∴,
∴,
解得:;
时,即,
∵,
∴,
∴,
解得:;
综上可知:的值为或.
19.(1)
(2)①;②或
【分析】本题考查函数的图象的应用,一元一次方程的应用,掌握速度、时间和路程之间的关系是解题的关键.
(1)根据乙出发的时刻和到达景区所用的时间计算即可;
(2)①根据速度路程时间分别用含的代数式将甲、乙的速度表示出来并求出二者的比值即可;
②根据甲的速度和甲、乙的速度比值求出乙的速度,由路程速度时间分别求出、的关于的函数关系式并代入,得到关于的方程并求解即可.
【详解】(1)解:∵分钟小时,
∴乙到达山顶的时间为.
故答案为:.
(2)解:①(米分钟),
(米分钟),
∴,
故答案为:;
②∵,,
∴,(米分钟),
则,
当时,;
当时,;
当时,.
由在乙登山的过程中,即时,
当时,,
解得(舍),
当时,,
解得或(舍去),
当时,,
解得,
综上所述,或.
20.(1),13,7
(2)①;②或6;
(3)点M追上点Q后再经过2秒或秒,.
【分析】(1)根据平方和绝对值的非负性,倒数的定义即可解答;
(2)①根据题意直接列出代数式即可;
②由,结合两点间的距离公式即可得到关于t的方程,求解即可;
(3)点M未追上点Q时,表示出点M表示的数,根据点M追上点Q时,点M,Q表示的数相同,可求出运动的时间和此时点M表示的数,从而可求出点M返回沿负方向运动时所表示的数,根据两点间的距离公式,根据可列出方程,求解即可.
【详解】(1)解:∵a为的倒数,
∴,
∵,,且,
∴,,
∴,.
故答案为:,13,7;
(2)解:①当运动t秒时,点P表示的数为,点Q表示的数为.
故答案为:;
②当时,,
∴,
解得或6;
(3)解:点M未追上点Q时,点M表示的数为,
当点M追上点Q时,,
解得,
即当它们运动2秒时,点M追上点Q,此时点M表示的数为,
∵点M追上点Q后立即返回沿数轴负方向运动,
∴点M表示的数为,
当时,,
∴,
解得或,
∴,,
∴点M追上点Q后再经过秒或2秒,.
【点睛】本题考查绝对值的几何意义,列代数式,数轴上两点间的距离,一元一次方程解决实际问题,掌握绝对值的几何意义,熟练运用方程思想是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
