2025年中考数学专题训练:统计与概率(含解析)
文档属性
| 名称 | 2025年中考数学专题训练:统计与概率(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 731.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 09:39:07 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年中考数学专题训练:统计与概率
一、单选题
1.下列调查方式中,合适的是( ).
A.要了解某市百万居民的生活状况,采取普查方式
B.要了解一批节能灯使用寿命,采用普查方式
C.要了解某中校学生视力情况,采用普查方式
D.要了解智能自动驾驶汽车零部件情况,采用抽样调查
2.某班8名同学在一次“1分钟仰卧起坐”测试中,成绩(单位:次)分别为:38,45,41,37,40,38,40,38.这组数据的众数、中位数分别是( ).
A.39,40 B.38,39 C.38,38 D.39,38
3.如图,向甲、乙两个正方形飞镖盘中各随机投掷一枚飞镖,投中阴影区域的概率分别为和,则下列关系正确的是( )
A. B.
C. D.无法确定的大小
4.为了更好地了解和感受河南历史,淇淇和茜茜分别游览了“只有河南·戏剧幻城”.景区拥有三个主剧场,分别是《李家村剧场》、《幻城剧场》、《火车站剧场》.淇淇、茜茜随机选择一个主剧场观看,则她俩恰好选择同一剧场的概率为( )
A. B. C. D.
5.某服装销售专柜统计该专柜三月份的服装销售量.按服装的不同颜色统计了相关销量数据如下表所示:
颜色 红色 黄色 蓝色 绿色
数量(件) 243 135 196 151
根据表中数据,该专柜决定四月份多购进红色服装,影响该专柜决策的统计量是( )
A.众数 B.中位数 C.平均数 D.方差
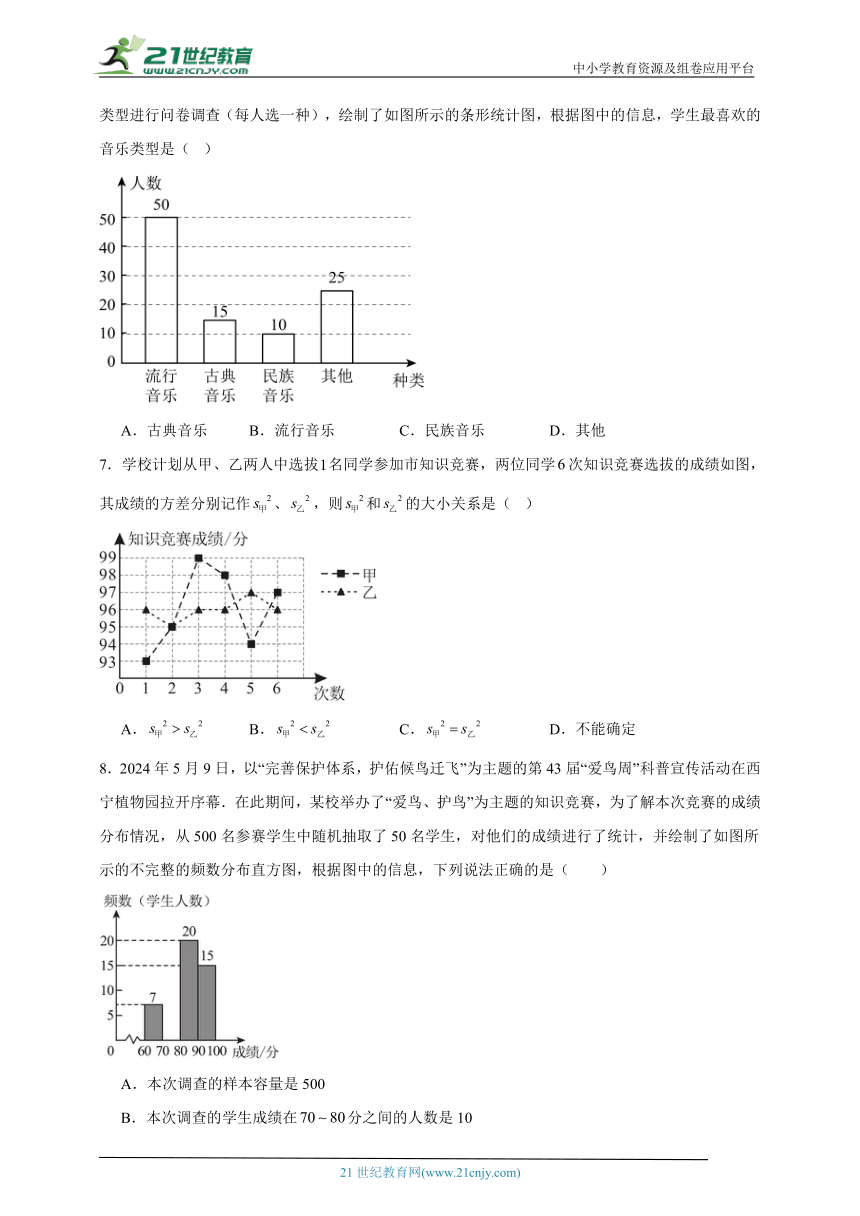
6.为提高学生的音乐素养,培养学生的音乐兴趣,某校随机抽取了部分学生,对他们最喜欢的音乐类型进行问卷调查(每人选一种),绘制了如图所示的条形统计图,根据图中的信息,学生最喜欢的音乐类型是( )
A.古典音乐 B.流行音乐 C.民族音乐 D.其他
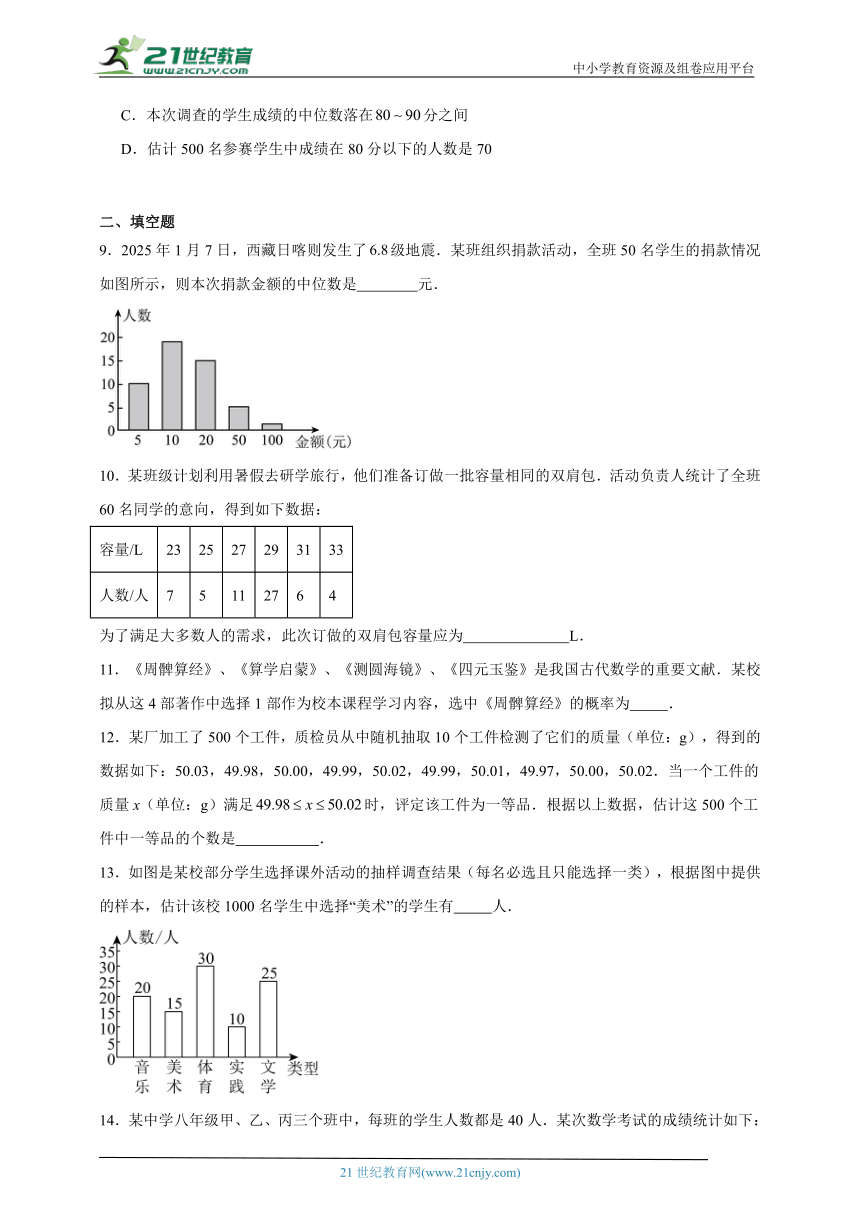
7.学校计划从甲、乙两人中选拔名同学参加市知识竞赛,两位同学次知识竞赛选拔的成绩如图,其成绩的方差分别记作、,则和的大小关系是( )
A. B. C. D.不能确定
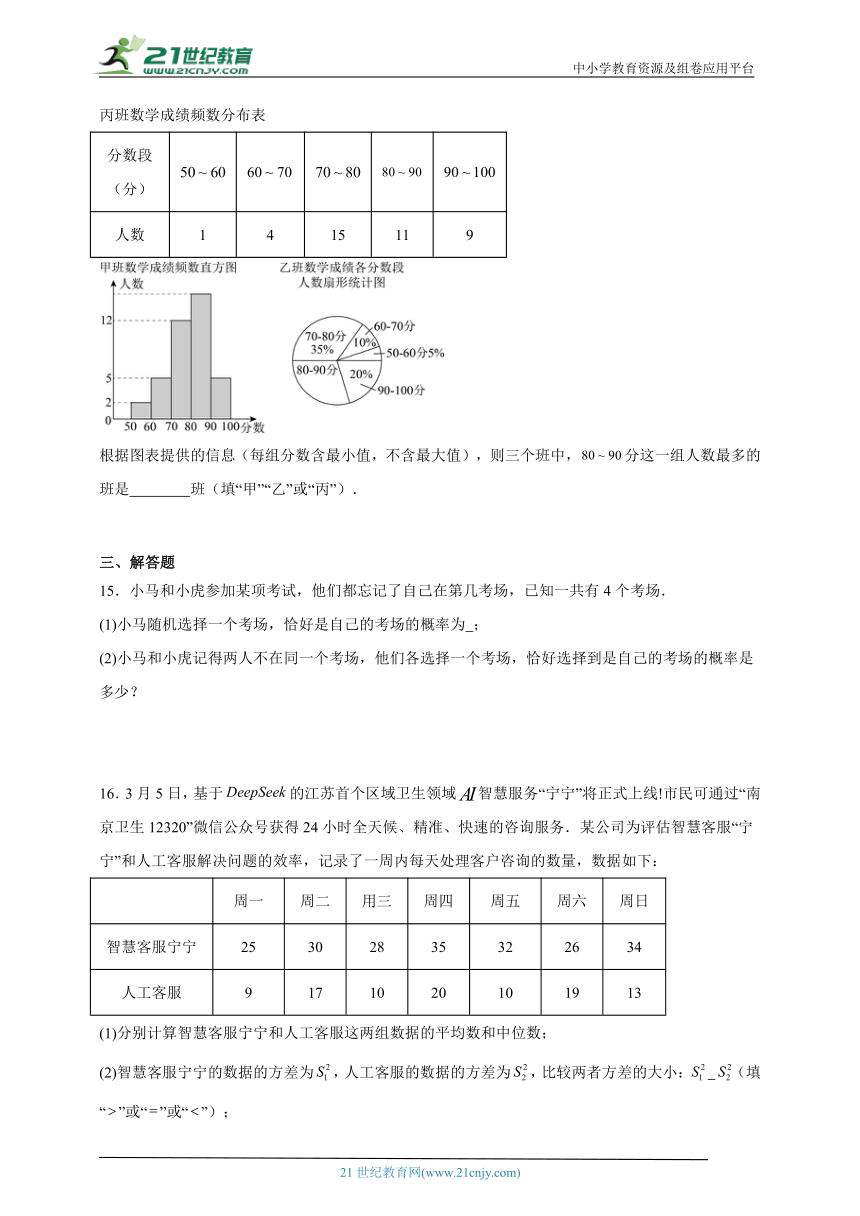
8.2024年5月9日,以“完善保护体系,护佑候鸟迁飞”为主题的第43届“爱鸟周”科普宣传活动在西宁植物园拉开序幕.在此期间,某校举办了“爱鸟、护鸟”为主题的知识竞赛,为了解本次竞赛的成绩分布情况,从500名参赛学生中随机抽取了50名学生,对他们的成绩进行了统计,并绘制了如图所示的不完整的频数分布直方图,根据图中的信息,下列说法正确的是( )
A.本次调查的样本容量是500
B.本次调查的学生成绩在分之间的人数是10
C.本次调查的学生成绩的中位数落在分之间
D.估计500名参赛学生中成绩在80分以下的人数是70
二、填空题
9.2025年1月7日,西藏日喀则发生了级地震.某班组织捐款活动,全班50名学生的捐款情况如图所示,则本次捐款金额的中位数是 元.
10.某班级计划利用暑假去研学旅行,他们准备订做一批容量相同的双肩包.活动负责人统计了全班60名同学的意向,得到如下数据:
容量/L 23 25 27 29 31 33
人数/人 7 5 11 27 6 4
为了满足大多数人的需求,此次订做的双肩包容量应为 L.
11.《周髀算经》、《算学启蒙》、《测圆海镜》、《四元玉鉴》是我国古代数学的重要文献.某校拟从这4部著作中选择1部作为校本课程学习内容,选中《周髀算经》的概率为 .
12.某厂加工了500个工件,质检员从中随机抽取10个工件检测了它们的质量(单位:g),得到的数据如下:50.03,49.98,50.00,49.99,50.02,49.99,50.01,49.97,50.00,50.02.当一个工件的质量x(单位:g)满足时,评定该工件为一等品.根据以上数据,估计这500个工件中一等品的个数是 .
13.如图是某校部分学生选择课外活动的抽样调查结果(每名必选且只能选择一类),根据图中提供的样本,估计该校1000名学生中选择“美术”的学生有 人.
14.某中学八年级甲、乙、丙三个班中,每班的学生人数都是40人.某次数学考试的成绩统计如下:
丙班数学成绩频数分布表
分数段(分)
人数 1 4 15 11 9
根据图表提供的信息(每组分数含最小值,不含最大值),则三个班中,分这一组人数最多的班是 班(填“甲”“乙”或“丙”).
三、解答题
15.小马和小虎参加某项考试,他们都忘记了自己在第几考场,已知一共有4个考场.
(1)小马随机选择一个考场,恰好是自己的考场的概率为 ;
(2)小马和小虎记得两人不在同一个考场,他们各选择一个考场,恰好选择到是自己的考场的概率是多少?
16.3月5日,基于的江苏首个区域卫生领域智慧服务“宁宁”将正式上线!市民可通过“南京卫生12320”微信公众号获得24小时全天候、精准、快速的咨询服务.某公司为评估智慧客服“宁宁”和人工客服解决问题的效率,记录了一周内每天处理客户咨询的数量,数据如下:
周一 周二 用三 周四 周五 周六 周日
智慧客服宁宁 25 30 28 35 32 26 34
人工客服 9 17 10 20 10 19 13
(1)分别计算智慧客服宁宁和人工客服这两组数据的平均数和中位数;
(2)智慧客服宁宁的数据的方差为,人工客服的数据的方差为,比较两者方差的大小: (填“”或“”或“”);
(3)根据以上数据,对智慧客服宁宁和人工客服的工作数量进行评价(至少两条).
17.为贯彻五育并举方针,将劳动教育纳入必修课程,区劳技中心开设了多门劳动综合课.开设一段时间后,为了解对课程的喜爱情况,中心对下列课程进行了抽样调查:家庭电路;简单烹饪;布艺手缝;收纳整理;编织.收回所有的问卷后,将有关数据进行整理,绘制了如下两幅不完整的统计图.
根据图中信息,回答下面问题:
(1)本次调查的学生人数为______;并补全条形统计图.
(2)在一个学期中,全区共有10800名学生参加综合课程的培训,估计喜欢“简单烹饪”的学生人数;
(3)小明同学从,,三门课程中选择一门参加劳动实践,小红同学从,,三门课程中随机选择一门参加劳动实践,用表格或树状图求他们选择相同课程的概率.
18.下面是七年级甲、乙两位同学期末考试的成绩情况.
甲、乙两位同学期末考试各科得分情况统计表
姓名 语文 数学 英语 道法 历史 生物 地理
甲 75 85 86 88 90 96 96
乙 80 83 87 90 90 92 94
甲、乙两位同学期末考试成绩情况统计表
姓名 平均数 中位数 众数
甲 88 88 a
乙 88 b 90
甲、乙两位同学期末考试各科成绩折线统计图
根据以上信息,回答下列问题:
(1)上述统计表中, , ;
(2)从折线统计图看,两个同学的得分的方差 (填“”或“”);
(3)哪个同学成绩比较好?请结合统计图表中的信息给出你的理由.
19.为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在九年级组织的足球联赛中,甲、乙两名队员表现突出,在他们参与的六场比赛中关于进球个数、抢断次数和失误次数三个方面的统计结果如下:
甲、乙两名队员技术统计表
平均每场进球个数 平均每场抢断次数 平均每场失误次数
甲队员 2 4 1
乙队员 2 5 3
根据以上信息,回答下列问题:
(1)求甲队员这六场球进球个数的中位数.
(2)你认为这六场比赛中,甲、乙两名队员谁的表现更好,请说明理由.(说出一条理由即可)
(3)若规定“综合得分”为:平均每场进球个数平均每场抢断次数平均每场失误次数,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
《2025年中考数学专题训练:统计与概率》参考答案
题号 1 2 3 4 5 6 7 8
答案 C B A D A B A C
1.C
【分析】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,据此进行判断即可.
【详解】解:A、要了解某市百万居民的生活状况,适合采用抽样调查,不符合题意;
B、要了解一批节能灯使用寿命,适合采用抽样调查,不符合题意;
C、要了解某中校学生视力情况,适合采用普查,符合题意;
D、要了解智能自动驾驶汽车零部件情况,适合采用普查,不符合题意;
故选C.
2.B
【分析】本题考查了求中位数“将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数”、求众数“众数就是一组数据中出现次数最多的那个数据”,熟记中位数和众数的定义是解题关键.根据中位数和众数的定义求解即可得.
【详解】解:在这组数据中,38出现的次数最多,
所以这组数据的众数是38,
将这组数据从小到大进行排序为37,38,38,38,40,40,41,45,第4个数和第5个数分别是38和40,
所以这组数据的中位数是,
故选:B.
3.A
【分析】本题考查几何概率模型,由图及题意可知,甲正方形中,阴影部分的面积占正方形面积的比为;乙正方形中,阴影部分的面积占正方形面积的比也为;即可得到答案.熟记几何概率模型问题的解法是解决问题的关键.
【详解】解:如图所示:
甲正方形中,阴影部分的面积占正方形面积的比为;乙正方形中,阴影部分的面积占正方形面积的比也为;
由几何概率模型可知,投中阴影区域的概率,
故选:A.
4.D
【分析】本题考查概率的应用,掌握画树状图或列表求概率的方法是解题的关键.通过画树状图或列表罗列出所有等可能的情况,再从中找出符合条件的情况数,最后利用概率公式求解.
【详解】解:设《李家村剧场》、《幻城剧场》、《火车站剧场》分别为A、B、C,
列表如下:
A B C
A
B
C
∴共有9种可能结果,其中她俩恰好选择同一剧场的有3种,
∴P(她俩恰好选择同一剧场).
故选:D.
5.A
【分析】本题考查了运用众数做决策,出现次数最多的数为众数,结合红色销售的数量为243件,销量最多,且该专柜决定四月份多购进红色服装,因此影响该专柜决策的统计量是众数,即可作答.
【详解】解:∵三月份的服装销售量中,红色销售的数量为243件,销量最多,且该专柜决定四月份多购进红色服装,
∴影响该专柜决策的统计量是众数,
故选:A.
6.B
【分析】本题考查从条形图获取消息和处理消息,掌握从条形图获取消息和处理消息是解题关键.根据条形图获取人数最多的音乐类型进行求解即可.
【详解】解:根据条形图知,喜欢流行音乐类型的有人,人数最多.
故选:B.
7.A
【分析】本题考查了方差的意义,解答本题的关键是熟练掌握方差的意义:方差是反映一组数据的波动大小的一个量,方差越大,则平均值的离散程度越大,稳定性也越小;反之,则其平均值的离散程度越小,稳定性越好.根据方差的意义解答即可.
【详解】解:∵图可知甲的成绩波动程度比乙的成绩的波动程度大,
∴,
故选:A.
8.C
【分析】本题考查了频数分布直方图,样本容量,用样本估计总体等知识,根据样本容量,中位数的定义,用样本估计总体逐一判断即可,掌握相关知识是解题的关键.
【详解】解:A、本次调查的样本容量是50,故选项不符合题意;
B、本次调查的学生成绩在分之间的人数是,故选项不符合题意;
C、把本次调查的学生成绩按从小到大的顺序排列,排在中间的两个数都在分之间,所以本次调查的学生成绩的中位数落在分之间,故选项符合题意;
D、估计500名参赛学生中成绩在80分以下的人数是人,故选项不符合题意;
故选:C.
9.10
【分析】本题主要考查了中位线的定义,熟练掌握中位线的定义,是解题的关键.根据中位线定义:一组数据中处于中间位置的数为中位数,进行求解即可.
【详解】解:将50名学生的捐款数从小到大进行排序,排在中间位置的两个数都是10,因此本次捐款金额的中位数是10.
故答案为:10.
10.29
【分析】本题考查了众数.众数是一组数据中出现次数最多的数,众数可能没有,可能有1个,也可能有多个.根据众数的定义求解即可.
【详解】解:出现27次,出现次数最多,
∴众数是,
故答案为:29.
11.
【分析】本题主要考查概率,熟练掌握概率公式是解题的关键;因此此题可根据概率公式直接进行求解.
【详解】解:从这4部著作中选择1部作为校本课程学习内容,共有4种可能性,所以选中《周髀算经》的概率为;
故答案为.
12.400
【分析】本题考查用样本估计总体,根据题意,先写出10个数据中的一等品,然后即可估计这200个工件中一等品的个数.
【详解】解:∵满足时,评定该工件为一等品,
∴抽取10个工件的一等品有49.98,50.00,49.99,50.02,49.99,50.01,50.00,50.02,共计8个,
∴估计这500个工件中一等品的个数是,
故答案为:400.
13.150
【分析】本题考查了样本估计总体,根据抽样调查中,得出选择“美术”的学生的占比,即可得出该校1000名学生中选择“美术”的学生的人数,即可作答.
【详解】解:依题意,在抽样调查中,选择“美术”的学生的占比,
则(人),
故答案为:150.
14.甲
【分析】本题主要考查了频数分布表,频数分布直方图,扇形统计图等知识点,熟练掌握各种统计图表并从中正确获取信息是解题的关键.
由“丙班数学成绩频数分布表”可得丙班中分这一组的人数,由“甲班数学成绩频数直方图”可得甲班中分这一组的人数,由“乙班数学成绩各分数段人数扇形统计图”可得乙班中分这一组的人数,然后比较即可得出答案.
【详解】解:由“丙班数学成绩频数分布表”可得,丙班中分这一组的人数为人,
由“甲班数学成绩频数直方图”可得,甲班中分这一组的人数为人,
由“乙班数学成绩各分数段人数扇形统计图”可得,乙班中分这一组的人数为人,
在三个班中,分这一组人数最多的班是甲班,
故答案为:甲.
15.(1)
(2)
【分析】本题主要考查了列表法与树状图法求概率,解题的关键是根据题意,画树状图得出所有等可能结果.
(1)直接根据概率公式求解即可;
(2)设四个考查为A、B、C、D,其中小马应在A考场、小虎应在B考场,画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】(1)解:小马随机选择一个考场,恰好是自己的考场的概率为,
故答案为:.
(2)解:设四个考场为A、B、C、D,其中小马应在A考场、小虎应在B考场,画树状图,如图所示:
由图可知,共有12种等可能结果,其中恰好选择到是自己的考场的只有1种结果,
∴恰好选择到是自己的考场的概率为.
16.(1)客服宁宁的平均数为30,中位数为30;人工客服的平均数为14,中位数为13
(2)
(3)见解析
【分析】本题主要考查方差,解题的关键是掌握中位数、平均数、方差的定义和意义.
(1)根据平均数和中位数的定义列式求解即可;
(2)根据方差的计算公式计算即可;
(3)根据平均数、中位数或方差的意义求解即可.
【详解】(1)解:智慧客服宁宁的平均数为,
将数据重新排列为,
∴其中位数为30,
人工客服的平均数为,
将数据重新排列为,
∴其中位数为13;
(2)解:,
,
∵,
∴,
故答案为:;
(3)解:智慧客服宁宁的服务效率高于人工客服,
∵智慧客服宁宁服务人数的平均数和中位数均大于人工客服,
∴智慧客服宁宁服务人数多于人工客服.
17.(1)200;图见解析
(2)1080人
(3)
【分析】本题考查列表法或树状图法求解概率,频率分布直方图以及扇形统计图,用样本估计总体,正确读懂统计图是解题的关键.
(1)根据A家庭电路总人数为30人,占,用30除以即可得总人数,再求出D和B的人数,即可补全统计图;
(2)用总人数乘以喜欢“简单烹饪”的百分比即可得出喜欢“简单烹饪”的人数;
(3)列表,共有9种等可能结果,其中选课相同的结果一共有2种,再由概率公式求解即可.
【详解】(1)解:(人),即本次调查的学生人数为200人,
∴喜欢D的人数为(人),
∴喜欢B的人数为(人),
补全统计图如下所示:
(2)解:(人),
答:估计喜欢“简单烹饪”的学生人数为1080人;
(3)解:列表如下:
小明小红 A B D
B
D
E
由表格可知,两名同学选课一共有9种等可能结果,其中选课相同的结果一共有2种,
∴他们选择相同课程的概率.
18.(1)96,90
(2)
(3)乙同学成绩比较好,理由见解析
【分析】本题考查频数分布表,折线统计图,中位数与众数、方差.
(1)根据中位数和众数的定义即可得;
(2)先利用方差公式求出方差,再根据方差的意义即可得;
(3)从中位数和方差的意义进行分析即可得.
【详解】(1)解:在甲同学各科成绩中,96出现的次数最多,为2次,
则其众数,
将乙同学各科成绩按从小到大进行排序后,第4个数即为中位数,
则,
故答案为:96,90;
(2)解:甲同学的得分的方差为:
,
乙同学的得分的方差为:
,
∵,
∴,
故答案为:;
(3)解:乙同学成绩比较好,理由如下:
∵甲、乙两同学成绩的平均数相同,由折线统计图可知,乙同学的稳定性较好,
∴乙同学成绩比较好.
19.(1)2
(2)乙队员表现更好,见解析(答案不唯一)
(3)甲队员表现更好,具体评价见解析
【分析】本题考查了折线统计图,统计表,中位数,加权平均数等知识,
(1)根据中位数的定义求解即可;
(2)根据甲、乙两名队员技术统计表选一项比较判断即可;
(3)分别求出甲、乙的综合得分,然后判断即可.
【详解】(1)解:∵六次进球个数从小到大排列:1,2,2,2,2,3,
∴甲队员的中位数是.
(2)从技术统计表中可知,平均每场抢断次数,乙的抢断次数多于甲,所以乙队员表现更好(答案不唯一).
(3)甲队员的综合得分为:(分)
乙队员的综合得分为:(分)
因为,所以甲队员表现更好.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年中考数学专题训练:统计与概率
一、单选题
1.下列调查方式中,合适的是( ).
A.要了解某市百万居民的生活状况,采取普查方式
B.要了解一批节能灯使用寿命,采用普查方式
C.要了解某中校学生视力情况,采用普查方式
D.要了解智能自动驾驶汽车零部件情况,采用抽样调查
2.某班8名同学在一次“1分钟仰卧起坐”测试中,成绩(单位:次)分别为:38,45,41,37,40,38,40,38.这组数据的众数、中位数分别是( ).
A.39,40 B.38,39 C.38,38 D.39,38
3.如图,向甲、乙两个正方形飞镖盘中各随机投掷一枚飞镖,投中阴影区域的概率分别为和,则下列关系正确的是( )
A. B.
C. D.无法确定的大小
4.为了更好地了解和感受河南历史,淇淇和茜茜分别游览了“只有河南·戏剧幻城”.景区拥有三个主剧场,分别是《李家村剧场》、《幻城剧场》、《火车站剧场》.淇淇、茜茜随机选择一个主剧场观看,则她俩恰好选择同一剧场的概率为( )
A. B. C. D.
5.某服装销售专柜统计该专柜三月份的服装销售量.按服装的不同颜色统计了相关销量数据如下表所示:
颜色 红色 黄色 蓝色 绿色
数量(件) 243 135 196 151
根据表中数据,该专柜决定四月份多购进红色服装,影响该专柜决策的统计量是( )
A.众数 B.中位数 C.平均数 D.方差
6.为提高学生的音乐素养,培养学生的音乐兴趣,某校随机抽取了部分学生,对他们最喜欢的音乐类型进行问卷调查(每人选一种),绘制了如图所示的条形统计图,根据图中的信息,学生最喜欢的音乐类型是( )
A.古典音乐 B.流行音乐 C.民族音乐 D.其他
7.学校计划从甲、乙两人中选拔名同学参加市知识竞赛,两位同学次知识竞赛选拔的成绩如图,其成绩的方差分别记作、,则和的大小关系是( )
A. B. C. D.不能确定
8.2024年5月9日,以“完善保护体系,护佑候鸟迁飞”为主题的第43届“爱鸟周”科普宣传活动在西宁植物园拉开序幕.在此期间,某校举办了“爱鸟、护鸟”为主题的知识竞赛,为了解本次竞赛的成绩分布情况,从500名参赛学生中随机抽取了50名学生,对他们的成绩进行了统计,并绘制了如图所示的不完整的频数分布直方图,根据图中的信息,下列说法正确的是( )
A.本次调查的样本容量是500
B.本次调查的学生成绩在分之间的人数是10
C.本次调查的学生成绩的中位数落在分之间
D.估计500名参赛学生中成绩在80分以下的人数是70
二、填空题
9.2025年1月7日,西藏日喀则发生了级地震.某班组织捐款活动,全班50名学生的捐款情况如图所示,则本次捐款金额的中位数是 元.
10.某班级计划利用暑假去研学旅行,他们准备订做一批容量相同的双肩包.活动负责人统计了全班60名同学的意向,得到如下数据:
容量/L 23 25 27 29 31 33
人数/人 7 5 11 27 6 4
为了满足大多数人的需求,此次订做的双肩包容量应为 L.
11.《周髀算经》、《算学启蒙》、《测圆海镜》、《四元玉鉴》是我国古代数学的重要文献.某校拟从这4部著作中选择1部作为校本课程学习内容,选中《周髀算经》的概率为 .
12.某厂加工了500个工件,质检员从中随机抽取10个工件检测了它们的质量(单位:g),得到的数据如下:50.03,49.98,50.00,49.99,50.02,49.99,50.01,49.97,50.00,50.02.当一个工件的质量x(单位:g)满足时,评定该工件为一等品.根据以上数据,估计这500个工件中一等品的个数是 .
13.如图是某校部分学生选择课外活动的抽样调查结果(每名必选且只能选择一类),根据图中提供的样本,估计该校1000名学生中选择“美术”的学生有 人.
14.某中学八年级甲、乙、丙三个班中,每班的学生人数都是40人.某次数学考试的成绩统计如下:
丙班数学成绩频数分布表
分数段(分)
人数 1 4 15 11 9
根据图表提供的信息(每组分数含最小值,不含最大值),则三个班中,分这一组人数最多的班是 班(填“甲”“乙”或“丙”).
三、解答题
15.小马和小虎参加某项考试,他们都忘记了自己在第几考场,已知一共有4个考场.
(1)小马随机选择一个考场,恰好是自己的考场的概率为 ;
(2)小马和小虎记得两人不在同一个考场,他们各选择一个考场,恰好选择到是自己的考场的概率是多少?
16.3月5日,基于的江苏首个区域卫生领域智慧服务“宁宁”将正式上线!市民可通过“南京卫生12320”微信公众号获得24小时全天候、精准、快速的咨询服务.某公司为评估智慧客服“宁宁”和人工客服解决问题的效率,记录了一周内每天处理客户咨询的数量,数据如下:
周一 周二 用三 周四 周五 周六 周日
智慧客服宁宁 25 30 28 35 32 26 34
人工客服 9 17 10 20 10 19 13
(1)分别计算智慧客服宁宁和人工客服这两组数据的平均数和中位数;
(2)智慧客服宁宁的数据的方差为,人工客服的数据的方差为,比较两者方差的大小: (填“”或“”或“”);
(3)根据以上数据,对智慧客服宁宁和人工客服的工作数量进行评价(至少两条).
17.为贯彻五育并举方针,将劳动教育纳入必修课程,区劳技中心开设了多门劳动综合课.开设一段时间后,为了解对课程的喜爱情况,中心对下列课程进行了抽样调查:家庭电路;简单烹饪;布艺手缝;收纳整理;编织.收回所有的问卷后,将有关数据进行整理,绘制了如下两幅不完整的统计图.
根据图中信息,回答下面问题:
(1)本次调查的学生人数为______;并补全条形统计图.
(2)在一个学期中,全区共有10800名学生参加综合课程的培训,估计喜欢“简单烹饪”的学生人数;
(3)小明同学从,,三门课程中选择一门参加劳动实践,小红同学从,,三门课程中随机选择一门参加劳动实践,用表格或树状图求他们选择相同课程的概率.
18.下面是七年级甲、乙两位同学期末考试的成绩情况.
甲、乙两位同学期末考试各科得分情况统计表
姓名 语文 数学 英语 道法 历史 生物 地理
甲 75 85 86 88 90 96 96
乙 80 83 87 90 90 92 94
甲、乙两位同学期末考试成绩情况统计表
姓名 平均数 中位数 众数
甲 88 88 a
乙 88 b 90
甲、乙两位同学期末考试各科成绩折线统计图
根据以上信息,回答下列问题:
(1)上述统计表中, , ;
(2)从折线统计图看,两个同学的得分的方差 (填“”或“”);
(3)哪个同学成绩比较好?请结合统计图表中的信息给出你的理由.
19.为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在九年级组织的足球联赛中,甲、乙两名队员表现突出,在他们参与的六场比赛中关于进球个数、抢断次数和失误次数三个方面的统计结果如下:
甲、乙两名队员技术统计表
平均每场进球个数 平均每场抢断次数 平均每场失误次数
甲队员 2 4 1
乙队员 2 5 3
根据以上信息,回答下列问题:
(1)求甲队员这六场球进球个数的中位数.
(2)你认为这六场比赛中,甲、乙两名队员谁的表现更好,请说明理由.(说出一条理由即可)
(3)若规定“综合得分”为:平均每场进球个数平均每场抢断次数平均每场失误次数,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
《2025年中考数学专题训练:统计与概率》参考答案
题号 1 2 3 4 5 6 7 8
答案 C B A D A B A C
1.C
【分析】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,据此进行判断即可.
【详解】解:A、要了解某市百万居民的生活状况,适合采用抽样调查,不符合题意;
B、要了解一批节能灯使用寿命,适合采用抽样调查,不符合题意;
C、要了解某中校学生视力情况,适合采用普查,符合题意;
D、要了解智能自动驾驶汽车零部件情况,适合采用普查,不符合题意;
故选C.
2.B
【分析】本题考查了求中位数“将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数”、求众数“众数就是一组数据中出现次数最多的那个数据”,熟记中位数和众数的定义是解题关键.根据中位数和众数的定义求解即可得.
【详解】解:在这组数据中,38出现的次数最多,
所以这组数据的众数是38,
将这组数据从小到大进行排序为37,38,38,38,40,40,41,45,第4个数和第5个数分别是38和40,
所以这组数据的中位数是,
故选:B.
3.A
【分析】本题考查几何概率模型,由图及题意可知,甲正方形中,阴影部分的面积占正方形面积的比为;乙正方形中,阴影部分的面积占正方形面积的比也为;即可得到答案.熟记几何概率模型问题的解法是解决问题的关键.
【详解】解:如图所示:
甲正方形中,阴影部分的面积占正方形面积的比为;乙正方形中,阴影部分的面积占正方形面积的比也为;
由几何概率模型可知,投中阴影区域的概率,
故选:A.
4.D
【分析】本题考查概率的应用,掌握画树状图或列表求概率的方法是解题的关键.通过画树状图或列表罗列出所有等可能的情况,再从中找出符合条件的情况数,最后利用概率公式求解.
【详解】解:设《李家村剧场》、《幻城剧场》、《火车站剧场》分别为A、B、C,
列表如下:
A B C
A
B
C
∴共有9种可能结果,其中她俩恰好选择同一剧场的有3种,
∴P(她俩恰好选择同一剧场).
故选:D.
5.A
【分析】本题考查了运用众数做决策,出现次数最多的数为众数,结合红色销售的数量为243件,销量最多,且该专柜决定四月份多购进红色服装,因此影响该专柜决策的统计量是众数,即可作答.
【详解】解:∵三月份的服装销售量中,红色销售的数量为243件,销量最多,且该专柜决定四月份多购进红色服装,
∴影响该专柜决策的统计量是众数,
故选:A.
6.B
【分析】本题考查从条形图获取消息和处理消息,掌握从条形图获取消息和处理消息是解题关键.根据条形图获取人数最多的音乐类型进行求解即可.
【详解】解:根据条形图知,喜欢流行音乐类型的有人,人数最多.
故选:B.
7.A
【分析】本题考查了方差的意义,解答本题的关键是熟练掌握方差的意义:方差是反映一组数据的波动大小的一个量,方差越大,则平均值的离散程度越大,稳定性也越小;反之,则其平均值的离散程度越小,稳定性越好.根据方差的意义解答即可.
【详解】解:∵图可知甲的成绩波动程度比乙的成绩的波动程度大,
∴,
故选:A.
8.C
【分析】本题考查了频数分布直方图,样本容量,用样本估计总体等知识,根据样本容量,中位数的定义,用样本估计总体逐一判断即可,掌握相关知识是解题的关键.
【详解】解:A、本次调查的样本容量是50,故选项不符合题意;
B、本次调查的学生成绩在分之间的人数是,故选项不符合题意;
C、把本次调查的学生成绩按从小到大的顺序排列,排在中间的两个数都在分之间,所以本次调查的学生成绩的中位数落在分之间,故选项符合题意;
D、估计500名参赛学生中成绩在80分以下的人数是人,故选项不符合题意;
故选:C.
9.10
【分析】本题主要考查了中位线的定义,熟练掌握中位线的定义,是解题的关键.根据中位线定义:一组数据中处于中间位置的数为中位数,进行求解即可.
【详解】解:将50名学生的捐款数从小到大进行排序,排在中间位置的两个数都是10,因此本次捐款金额的中位数是10.
故答案为:10.
10.29
【分析】本题考查了众数.众数是一组数据中出现次数最多的数,众数可能没有,可能有1个,也可能有多个.根据众数的定义求解即可.
【详解】解:出现27次,出现次数最多,
∴众数是,
故答案为:29.
11.
【分析】本题主要考查概率,熟练掌握概率公式是解题的关键;因此此题可根据概率公式直接进行求解.
【详解】解:从这4部著作中选择1部作为校本课程学习内容,共有4种可能性,所以选中《周髀算经》的概率为;
故答案为.
12.400
【分析】本题考查用样本估计总体,根据题意,先写出10个数据中的一等品,然后即可估计这200个工件中一等品的个数.
【详解】解:∵满足时,评定该工件为一等品,
∴抽取10个工件的一等品有49.98,50.00,49.99,50.02,49.99,50.01,50.00,50.02,共计8个,
∴估计这500个工件中一等品的个数是,
故答案为:400.
13.150
【分析】本题考查了样本估计总体,根据抽样调查中,得出选择“美术”的学生的占比,即可得出该校1000名学生中选择“美术”的学生的人数,即可作答.
【详解】解:依题意,在抽样调查中,选择“美术”的学生的占比,
则(人),
故答案为:150.
14.甲
【分析】本题主要考查了频数分布表,频数分布直方图,扇形统计图等知识点,熟练掌握各种统计图表并从中正确获取信息是解题的关键.
由“丙班数学成绩频数分布表”可得丙班中分这一组的人数,由“甲班数学成绩频数直方图”可得甲班中分这一组的人数,由“乙班数学成绩各分数段人数扇形统计图”可得乙班中分这一组的人数,然后比较即可得出答案.
【详解】解:由“丙班数学成绩频数分布表”可得,丙班中分这一组的人数为人,
由“甲班数学成绩频数直方图”可得,甲班中分这一组的人数为人,
由“乙班数学成绩各分数段人数扇形统计图”可得,乙班中分这一组的人数为人,
在三个班中,分这一组人数最多的班是甲班,
故答案为:甲.
15.(1)
(2)
【分析】本题主要考查了列表法与树状图法求概率,解题的关键是根据题意,画树状图得出所有等可能结果.
(1)直接根据概率公式求解即可;
(2)设四个考查为A、B、C、D,其中小马应在A考场、小虎应在B考场,画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】(1)解:小马随机选择一个考场,恰好是自己的考场的概率为,
故答案为:.
(2)解:设四个考场为A、B、C、D,其中小马应在A考场、小虎应在B考场,画树状图,如图所示:
由图可知,共有12种等可能结果,其中恰好选择到是自己的考场的只有1种结果,
∴恰好选择到是自己的考场的概率为.
16.(1)客服宁宁的平均数为30,中位数为30;人工客服的平均数为14,中位数为13
(2)
(3)见解析
【分析】本题主要考查方差,解题的关键是掌握中位数、平均数、方差的定义和意义.
(1)根据平均数和中位数的定义列式求解即可;
(2)根据方差的计算公式计算即可;
(3)根据平均数、中位数或方差的意义求解即可.
【详解】(1)解:智慧客服宁宁的平均数为,
将数据重新排列为,
∴其中位数为30,
人工客服的平均数为,
将数据重新排列为,
∴其中位数为13;
(2)解:,
,
∵,
∴,
故答案为:;
(3)解:智慧客服宁宁的服务效率高于人工客服,
∵智慧客服宁宁服务人数的平均数和中位数均大于人工客服,
∴智慧客服宁宁服务人数多于人工客服.
17.(1)200;图见解析
(2)1080人
(3)
【分析】本题考查列表法或树状图法求解概率,频率分布直方图以及扇形统计图,用样本估计总体,正确读懂统计图是解题的关键.
(1)根据A家庭电路总人数为30人,占,用30除以即可得总人数,再求出D和B的人数,即可补全统计图;
(2)用总人数乘以喜欢“简单烹饪”的百分比即可得出喜欢“简单烹饪”的人数;
(3)列表,共有9种等可能结果,其中选课相同的结果一共有2种,再由概率公式求解即可.
【详解】(1)解:(人),即本次调查的学生人数为200人,
∴喜欢D的人数为(人),
∴喜欢B的人数为(人),
补全统计图如下所示:
(2)解:(人),
答:估计喜欢“简单烹饪”的学生人数为1080人;
(3)解:列表如下:
小明小红 A B D
B
D
E
由表格可知,两名同学选课一共有9种等可能结果,其中选课相同的结果一共有2种,
∴他们选择相同课程的概率.
18.(1)96,90
(2)
(3)乙同学成绩比较好,理由见解析
【分析】本题考查频数分布表,折线统计图,中位数与众数、方差.
(1)根据中位数和众数的定义即可得;
(2)先利用方差公式求出方差,再根据方差的意义即可得;
(3)从中位数和方差的意义进行分析即可得.
【详解】(1)解:在甲同学各科成绩中,96出现的次数最多,为2次,
则其众数,
将乙同学各科成绩按从小到大进行排序后,第4个数即为中位数,
则,
故答案为:96,90;
(2)解:甲同学的得分的方差为:
,
乙同学的得分的方差为:
,
∵,
∴,
故答案为:;
(3)解:乙同学成绩比较好,理由如下:
∵甲、乙两同学成绩的平均数相同,由折线统计图可知,乙同学的稳定性较好,
∴乙同学成绩比较好.
19.(1)2
(2)乙队员表现更好,见解析(答案不唯一)
(3)甲队员表现更好,具体评价见解析
【分析】本题考查了折线统计图,统计表,中位数,加权平均数等知识,
(1)根据中位数的定义求解即可;
(2)根据甲、乙两名队员技术统计表选一项比较判断即可;
(3)分别求出甲、乙的综合得分,然后判断即可.
【详解】(1)解:∵六次进球个数从小到大排列:1,2,2,2,2,3,
∴甲队员的中位数是.
(2)从技术统计表中可知,平均每场抢断次数,乙的抢断次数多于甲,所以乙队员表现更好(答案不唯一).
(3)甲队员的综合得分为:(分)
乙队员的综合得分为:(分)
因为,所以甲队员表现更好.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
