第八章 成对数据的统计分析 章末综合巩固试题 2024-2025学年数学人教A版(2019) 选择性必修第三册
文档属性
| 名称 | 第八章 成对数据的统计分析 章末综合巩固试题 2024-2025学年数学人教A版(2019) 选择性必修第三册 | 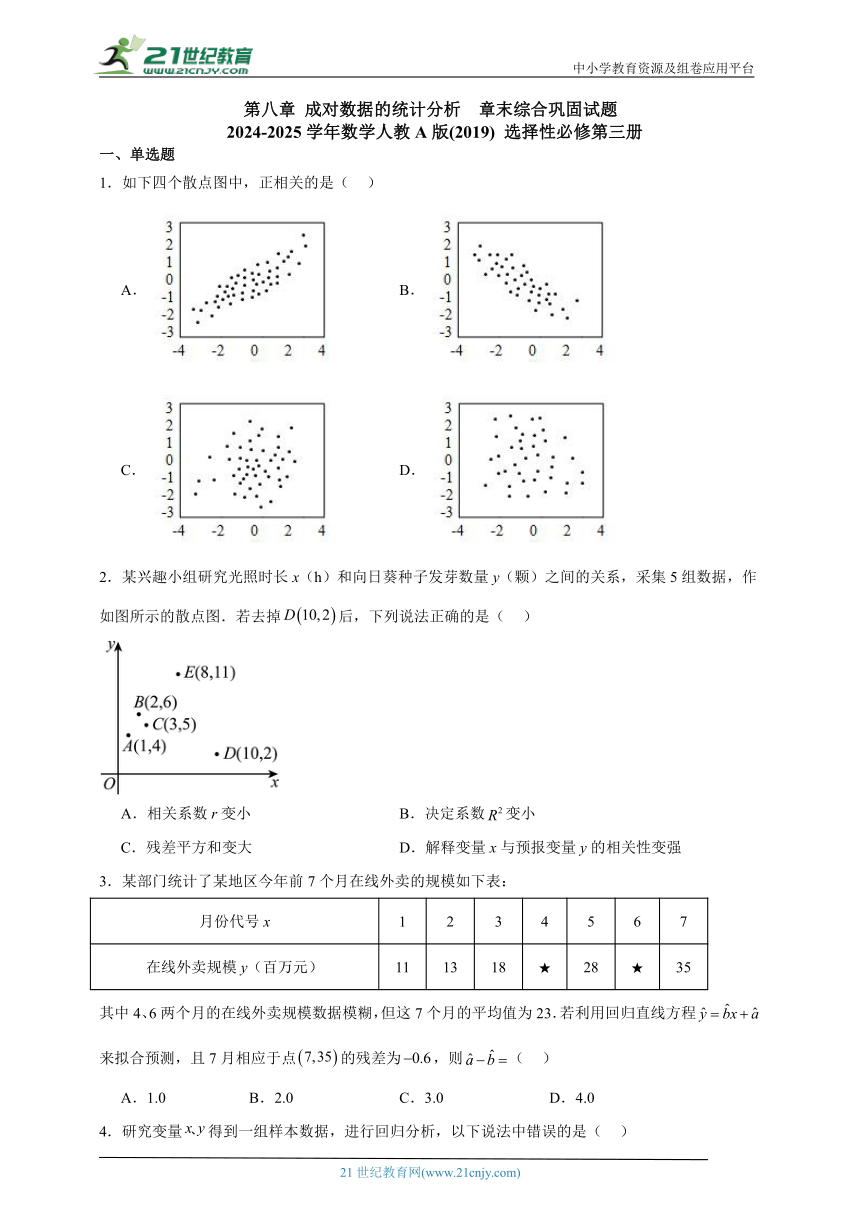 | |
| 格式 | docx | ||
| 文件大小 | 832.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 10:10:25 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
第八章 成对数据的统计分析 章末综合巩固试题
2024-2025学年数学人教A版(2019) 选择性必修第三册
一、单选题
1.如下四个散点图中,正相关的是( )
A. B.
C. D.
2.某兴趣小组研究光照时长x(h)和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉后,下列说法正确的是( )
A.相关系数r变小 B.决定系数变小
C.残差平方和变大 D.解释变量x与预报变量y的相关性变强
3.某部门统计了某地区今年前7个月在线外卖的规模如下表:
月份代号x 1 2 3 4 5 6 7
在线外卖规模y(百万元) 11 13 18 ★ 28 ★ 35
其中4、6两个月的在线外卖规模数据模糊,但这7个月的平均值为23.若利用回归直线方程来拟合预测,且7月相应于点的残差为,则( )
A.1.0 B.2.0 C.3.0 D.4.0
4.研究变量得到一组样本数据,进行回归分析,以下说法中错误的是( )
A.若变量和之间的相关系数为,则变量和之间的负相关很强
B.用决定系数来比较两个模型拟合效果,越大,表示残差平方和越小,即模型的拟合效果越好
C.在经验回归方程中,当解释变量每增加1个单位时,响应变量平均减少2个单位
D.经验回归直线至少经过点中的一个
5.为了发展学生的兴趣和个性特长,培养全面发展的人才.某学校在不加重学生负担的前提下.提供个性、全面的选修课程.为了解学生对于选修课《学生领导力的开发》的选择意愿情况,对部分高二学生进行了抽样调查,制作出如图所示的两个等高条形图,根据条形图,下列结论正确的是( )
A.样本中不愿意选该门课的人数较多
B.样本中男生人数多于女生人数
C.样本中女生人数多于男生人数
D.该等高条形图无法确定样本中男生人数是否多于女生人数
6.千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了地区A的100天日落和夜晚天气,得到如下2×2列联表(单位:天),并计算得到,下列小波对地区A天气的判断不正确的是( )
日落云里走 夜晚天气 下雨 未下雨
出现 25 5
未出现 25 45
参考公式:
临界值参照表:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
A.夜晚下雨的概率约为
B.未出现“日落云里走”,夜晚下雨的概率约为
C.据小概率值的独立性检验,认为“日落云里走”是否出现与夜晚天气有关
D.出现“日落云里走”, 据小概率值的独立性检验,可以认为夜晚会下雨
7.某学校一同学研究温差(℃)与本校当天新增感冒人数(人)的关系,该同学记录了5天的数据:
x 5 6 8 9 12
y 17 20 25 28 35
经过拟合,发现基本符合经验回归方程,则下列结论错误的是( )
A.样本中心点为
B.
C.时,残差为
D.若去掉样本点,则样本的相关系数增大
8.用模型拟合一组数,若,,设,得变换后的线性回归方程为,则( )
A.12 B. C. D.7
二、多选题
9.数据的平均数为,方差为,数据的平均数为,方差为,其中满足关系式:,则( )
A.
B.数据的平均数为
C.若数据,则
D.若,数据不全相等,则样本点的成对样本数据的样本相关系数为
10.某班级学生开展课外数学探究活动,将一杯冷水从冰箱中取出后静置,在的室温下测量水温单位随时间(单位:)的变化关系,在测量了15个数据后,根据这些实验数据得到如下的散点图:
现需要选择合适的回归方程进行回归分析,则根据散点图,合适的回归方程类型有( )
A. B.
C. D.
11.针对当下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”做了一次调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的,女生喜欢抖音的人数占女生人数的,若有的把握认为是否喜欢抖音和性别有关,则调查人数中男生有可能( )
附:
A. B. C. D.
三、填空题
12.为研究变量x,y的相关关系,收集得到如下数据:
x 1 2 3 4 5
y 60
若由最小二乘法求得y关于x的线性回归方程为,并据此计算在样本点处的残差为0,则 .
13.现调查某地区某种野生动物的数量,将该地区分成面积相近的200个地块,从这些地块中简单随机抽样的方法抽取20个作为样本,调查得到样本数据,其中分别表示第个样本的植物覆盖面积(单位:公顷)和这种野生动物的数量,构造向量,,其中,,并计算得,,,,,由选择性必修二教材中的知识,我们知道对数据的相关系数,则上述数据的相关系数 .
14.有两个分类变量和,其中一组观测值为如下的2×2列联表:
总计
15
50
总计 20 45 65
其中,均为大于5的整数,则 时,在犯错误的概率不超过的前提下为“和之间有关系”.附:
四、解答题
15.大学生刘铭去某工厂实习,实习结束时从自己制作的某种零件中随机选取了10个样品,测量每个零件的横截面积(单位:)和耗材量(单位:),得到如下数据:
样本号 1 2 3 4 5 6 7 8 9 10 总和
零件的横截面积 0.03 0.05 0.04 0.07 0.07 0.04 0.05 0.06 0.06 0.05 0.52
耗材量 0.24 0.40 0.23 0.55 0.50 0.34 0.35 0.45 0.43 0.41 3.9
并计算得,.
(1)估算刘铭同学制作的这种零件平均每个零件的横截面积以及平均一个零件的耗材量;
(2)求刘铭同学制作的这种零件的横截面积和耗材量的样本相关系数(精确到0.01).
附:相关系数;.
16.2024年3月4日,丰城市农业局在市委组织下召开推进湖塘-董家富硒梨产业高质量发展专题会议,安排部署加快推进特色优势产业富硒梨高质量发展工作,集中资源、力量打造“富硒梨”公共品牌.丰城市为做好富硒梨产业的高质量发展,项目组统计了某果场近5年富硒梨产业综合总产值的各项数据如下:年份x,综合产值y(单位:万元)
年份 2019 2020 2021 2022 2023
年份代码 1 2 3 4 5
综合产值 23.1 37.0 62.1 111.6 150.8
(1)根据表格中的数据,可用一元线性回归模型刻画变量y与变量x之间的线性相关关系,请用相关系数加以说明(精确到0.01);
(2)求出y关于x的经验回归方程,并预测2024年底该果场富硒梨产业的综合总产值.
参考公式:相关系数回归方程中斜率和截距的最小二乘法估计公式分别为:;
参考数据:
17.将氢储存在甲基环乙烷和甲苯等有机液体中是储氢和运输氢的重要方向.2023年12月俄罗斯科学院西伯利亚分院科研人员用镍和锡取代铂,研发出一种新型高效的脱氢催化剂,脱氢效率达,且对储氢载体没有破坏作用,可重复使用.近年来,我国氢能源汽车产业迅速发展,下表是某市氢能源乘用车的年销售量与年份的统计表:
年份 2018 2019 2020 2021 2022
销量(万台) 2 3.5 2.5 8 9
(1)求氢能源乘用车的销量关于年份的线性回归方程,并预测2024年氢能源乘用车的销量;
(2)为了研究不同性别的学生对氢能源的了解情况,某校组织了一次有关氢能源的知识竞赛活动,随机抽取了男生和女生各60名,得到如表所示的数据:
了解 不了解 合计
男生 25
女生 20
合计
(ⅰ)根据已知条件,填写上述列联表;
(ⅱ)依据的独立性检验,能否认为该校学生对氢能源的了解情况与性别有关?
参考公式:1.回归方程中斜率和截距的最小二乘法估计公式分别为;
2..
0.050 0.010 0.001
3.841 6.635 10.828
18.某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本(元)与生产该产品的数量(千件)有关,经统计得到如下数据:
x 1 2 3 4 5 6 7 8
y 56.5 31 22.75 17.8 15.95 14.5 13 12.5
根据以上数据绘制了散点图观察散点图,两个变量间关系考虑用反比例函数模型和指数函数模型分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为,与x的相关系数.
(1)用反比例函数模型求y关于x的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.001),并用其估计产量为10千件时每件产品的非原料成本;
(3)根据企业长期研究表明,非原料成本y服从正态分布,用样本平均数作为的估计值,用样本标准差s作为的估计值,若非原料成本y在之外,说明该成本异常,并称落在之外的成本为异样成本,此时需寻找出现异样成本的原因.利用估计值判断上述非原料成本数据是否需要寻找出现异样成本的原因?
参考数据(其中):
0.34 0.115 1.53 184 5777.555 93.06 30.705 13.9
参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计公式分别为:,,相关系数.
19.某校20名学生的数学成绩和知识竞赛成绩如下表:
学生编号i 1 2 3 4 5 6 7 8 9 10
数学成绩 100 99 96 93 90 88 85 83 80 77
知识竞赛成绩 290 160 220 200 65 70 90 100 60 270
学生编号i 11 12 13 14 15 16 17 18 19 20
数学成绩 75 74 72 70 68 66 60 50 39 35
知识竞赛成绩 45 35 40 50 25 30 20 15 10 5
计算可得数学成绩的平均值是,知识竞赛成绩的平均值是,并且,,.
(1)求这组学生的数学成绩和知识竞赛成绩的样本相关系数(精确到0.01);
(2)设,变量和变量的一组样本数据为,其中两两不相同,两两不相同.记在中的排名是第位,在中的排名是第位,.定义变量和变量的“斯皮尔曼相关系数”(记为)为变量的排名和变量的排名的样本相关系数.
(i)记,.证明:;
(ii)用(i)的公式求得这组学生的数学成绩和知识竞赛成绩的“斯皮尔曼相关系数”约为0.91,简述“斯皮尔曼相关系数”在分析线性相关性时的优势.
注:参考公式与参考数据.
;;.
参考答案
1.A
根据散点图中点的分布情况,判断是否具有相关性和正负相关关系.
对于A,散点图中的点从左向右是上升的,且在一条直线附近,是正相关;
对于B,散点图中的点从左向右是下降的,且在一条直线附近,是负相关;
对于C、D,散点图中的点不成带状分布,没有明显的相关关系;
故选:A.
方法点睛:该题考查的是有关正负相关的判断问题,解题方法如下:
(1)观察图中散点图是不是成带状区域;
(2)判断其从左往右上升正相关,下降负相关.
2.D
从图中分析得到去掉后,回归效果更好,再由相关系数,决定系数,残差平方和和相关性的概念和性质作出判断即可.
从图中可以看出较其他点,偏离直线远,故去掉后,回归效果更好,
对于A,相关系数越接近于1,模型的拟合效果越好,若去掉后,相关系数r变大,故A错误;
对于B,决定系数越接近于1,模型的拟合效果越好,若去掉后,决定系数变大,故B错误;
对于C,残差平方和越小,模型的拟合效果越好,若去掉后,残差平方和变小,故C错误;
对于D,若去掉后,解释变量x与预报变量y的相关性变强,且是正相关,故D正确.
故选:D.
3.B
根据给定条件,求出,再借助回归直线的特征及残差列出方程组即可求解作答.
依题意,,而,于是得,
而当时,,即,联立解得,
所以.
故选:B
4.D
根据相关系数、决定系数和线性回归方程逐项理解判断.
对A:若变量和之间的相关系数为,则变量和之间的负相关很强,A正确;
对B:用决定系数来比较两个模型拟合效果,越大,表示残差平方和越小,即模型的拟合效果越好,B正确;
对C:在经验回归方程中,当解释变量每增加1个单位时,响应变量平均减少2个单位,C正确;
对D:经验回归直线必过样本中心点,但不一定过样本点,D错误.
故选:D.
5.B
根据等高条形图直接判断各个选项即可.
对于A,由图乙可知,样本中男生,女生都大部分愿意选择该门课,
则样本中愿意选该门课的人数较多,A错误;
对于BCD,由图甲可知,在愿意和不愿意的人中,都是男生占比较大,
所以可以确定,样本中男生人数多于女生人数,B正确,CD错误.
故选:B.
6.D
应用古典概型的概率求法求概率判断A、B,应用卡方计算公式求卡方值,与临界值比较,应用独立检验的基本思想得到结论,判断C、D.
由列联表知:100天中有50天下雨,50天未下雨,因此夜晚下雨的概率约为,A正确;
未出现“日落云里走”,夜晚下雨的概率约为,B正确;
,因此据小概率值的独立性检验,认为“日落云里走”是否出现与夜晚天气有关,C正确,D错误.
故选:D
7.D
由回归直线必过样本中心可判断A项、B项,由残差公式可判断C项,由相关系数公式可判断D项.
对于A项,因为,,
所以样本中心点为,故A项正确;
对于B项,由回归直线必过样本中心可得:,解得:,故B项正确;
对于C项,由B项知,,
令,则,
所以残差为,故C项正确;
对于D项,由相关系数公式可知,去掉样本点后,x与y的样本相关系数r不变,故D项错误.
故选:D.
8.B
由已知,可根据,先计算出,然后把样本中心点带入线性回归方程为中计算出,从而得到线性回归方程,然后将方程化为指数形式,通过待定系数法分别对应出、的值,即可完成求解.
由已知,,所以,
,,所以
,
由题意,满足线性回归方程为,所以,所以,
此时线性回归方程为,即,
可将此式子化为指数形式,即为,
因为模型为模型,所以,,
所以.
故选:B.
9.AD
利用平均数的定义相关公式以及方差的定义相关公式即可判断选项ABC,结合样本相关系数的概念即可判断选项D.
对于A,,故A正确;
对于B,,
其平均数为,故B错误;
对于C,,
因为,故,
而当时,,满足条件,
但此时可以不都相等,故C错误;
对于D,由样本相关系数的概念可知,D正确.
故选:AD
10.AC
散点图的特点是单调递增,增长速度越来越慢,且,根据特点对选项一一判断即可.
散点图的特点是单调递增,增长速度越来越慢,且
对A选项,符合散点图的特点;
对B选项,有不符合散点图的特点;
对C选项,符合散点图的特点;
对D选项,的增长速度不变,不符合散点图的特点;
故选:AC
11.BC
先设男生人数为,,列出列联表,利用独立性检验计算观测值,再结合观测值列关系即得答案.
解:由题意被调查的男女生人数相同,设男生的人数为:,,由题意可列出列联表:
男生 女生 合计
喜欢抖音
不喜欢抖音
合计
.
由于有的把握认为是否喜欢抖音和性别有关,
所以;
解得:,因为,
故的可能取值为:9、10、11、12、13,即男生的人数可以是45,50,55,60,65.
则选项中被调查学生中男生的人数可能45或60.
故选:BC.
12.290
先利用残差的计算公式求出,再根据回归直线过样本点的中心求出,即可得解.
因为在样本点处的残差为0,
所以,得,
则y关于x的线性回归方程为.
因为,所以,
所以.
故答案为:
13.
根据题干中相关系数的定义进行计算.
由题干数据,,可得,
根据夹角公式的定义,,而,
根据
,
于是.
故答案为:
14.9
由题意,计算,列出不等式求出的取值范围,再根据题意求得的值.
解:由题意知:,
则,
解得:或,
因为:且,,
综上得:,,
所以:.
故答案为:9.
本题考查独立性检验的应用问题.
15.(1)横截面积为,耗材量为.
(2)0.94
(1)根据表格中的数据,结合平均数的计算公式,即可求解;
(2)由表格中的参考数据和相关系数的公式,准确计算,即可求解.
(1)解:样本中10个这种零件的横截面积的平均值,
样本中10个这种零件的耗材量的平均值,
由此可估算刘铭同学制作的这种零件平均每个零件的横截面积为,平均一个零件的耗材量为.
(2)解:由表格中的参考数据和相关系数的公式,可得
,
所以这种零件的横截面积和耗材量的样本相关系数.
16.(1)说明见解析
(2),175.64万元
(1)首先算出,进一步分别算出,由此即可求得相关系数,进一步即可说明;
(2)依次求出的值即可得回归方程,进一步代入即可预测.
(1)由题设,
则,,,
所以,两个变量有强相关性,
故可用一元线性回归模型刻画变量y与变量x之间的线性相关关系.
(2)由(1),,,
所以,
当,则万元.
17.(1),12.4万台;
(2)(ⅰ)表格见解析;(ⅱ)该校学生对氢能源的了解情况与性别有关.
(1)利用已知数据和公式求线性回归方程,由方程进行数据预测;
(2)(ⅰ)根据男生和女生各60名补全列联表.
(ⅱ)计算,与临界值比较下结论.
(1)年份的平均数,销量的平均数,
所以,
,
所以,
所以,
所以氢能源乘用车的销量关于年份的线性回归方程为,
令,得,
所以预测2024年氢能源乘用车的销量约为12.4万台.
(2)(ⅰ)根据男生和女生各60名,补全列联表为:
了解 不了解 合计
男生 35 25 60
女生 20 40 60
合计 55 65 120
(ⅱ)零假设:该校学生对氢能源的了解情况与性别无关,
根据列联表中的数据可得,
,
依据的独立性检验,可以推断不成立,
即该校学生对氢能源的了解情况与性别有关.
18.(1)
(2)反比例函数模型拟合效果更好,产量为10千件时每件产品的非原料成本约为11元,
(3)见解析
(1)令,则可转化为,求出样本中心,回归方程的斜率,转化求回归方程即可,
(2)求出与的相关系数,通过比较,可得用反比例函数模型拟合效果更好,然后将代入回归方程中可求结果
(3)利用已知数据求出样本标准差s,从而可得非原料成本y服从正态分布,再计算,然后各个数据是否在此范围内,从而可得结论
(1)令,则可转化为,
因为,
所以,
所以,所以,
所以y关于x的回归方程为
(2)与的相关系数为
因为,所以用反比例函数模型拟合效果更好,
把代入回归方程得(元),
所以产量为10千件时每件产品的非原料成本约为11元
(3)因为,所以,
因为样本标准差为,
所以,
所以非原料成本y服从正态分布,
所以
因为在之外,所以需要此非原料成本数据寻找出现异样成本的原因
19.(1)证明见解析
(2)答案见解析
(1)利用相关系数的公式进行计算即可;
(2)(i)根据题意即相关系数的公式进行计算即可证明;(ii)只要能说出斯皮尔曼相关系数与一般的样本相关系数相比的优势即可.
(1)由题意,这组学生数学成绩和知识竞赛成绩的样本相关系数为
;
(2)(i)证明:因为和都是1,2,,的一个排列,所以
,
,
从而和的平均数都是.
因此,,
同理可得,
由于
,
所以.
(ii)这组学生的数学成绩和知识竞赛成绩的斯皮尔曼相关系数是0.91,
答案①:斯皮尔曼相关系数对于异常值不太敏感,如果数据中有明显的异常值,那么用斯皮尔曼相关系数比用样本相关系数更能刻画某种线性关系;
答案②:斯皮尔曼相关系数刻画的是样本数据排名的样本相关系数,与具体的数值无关,只与排名有关.如果一组数据有异常值,但排名依然符合一定的线性关系,则可以采用斯皮尔曼相关系数刻画线性关系.
方法点睛;新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的;遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 成对数据的统计分析 章末综合巩固试题
2024-2025学年数学人教A版(2019) 选择性必修第三册
一、单选题
1.如下四个散点图中,正相关的是( )
A. B.
C. D.
2.某兴趣小组研究光照时长x(h)和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉后,下列说法正确的是( )
A.相关系数r变小 B.决定系数变小
C.残差平方和变大 D.解释变量x与预报变量y的相关性变强
3.某部门统计了某地区今年前7个月在线外卖的规模如下表:
月份代号x 1 2 3 4 5 6 7
在线外卖规模y(百万元) 11 13 18 ★ 28 ★ 35
其中4、6两个月的在线外卖规模数据模糊,但这7个月的平均值为23.若利用回归直线方程来拟合预测,且7月相应于点的残差为,则( )
A.1.0 B.2.0 C.3.0 D.4.0
4.研究变量得到一组样本数据,进行回归分析,以下说法中错误的是( )
A.若变量和之间的相关系数为,则变量和之间的负相关很强
B.用决定系数来比较两个模型拟合效果,越大,表示残差平方和越小,即模型的拟合效果越好
C.在经验回归方程中,当解释变量每增加1个单位时,响应变量平均减少2个单位
D.经验回归直线至少经过点中的一个
5.为了发展学生的兴趣和个性特长,培养全面发展的人才.某学校在不加重学生负担的前提下.提供个性、全面的选修课程.为了解学生对于选修课《学生领导力的开发》的选择意愿情况,对部分高二学生进行了抽样调查,制作出如图所示的两个等高条形图,根据条形图,下列结论正确的是( )
A.样本中不愿意选该门课的人数较多
B.样本中男生人数多于女生人数
C.样本中女生人数多于男生人数
D.该等高条形图无法确定样本中男生人数是否多于女生人数
6.千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了地区A的100天日落和夜晚天气,得到如下2×2列联表(单位:天),并计算得到,下列小波对地区A天气的判断不正确的是( )
日落云里走 夜晚天气 下雨 未下雨
出现 25 5
未出现 25 45
参考公式:
临界值参照表:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
A.夜晚下雨的概率约为
B.未出现“日落云里走”,夜晚下雨的概率约为
C.据小概率值的独立性检验,认为“日落云里走”是否出现与夜晚天气有关
D.出现“日落云里走”, 据小概率值的独立性检验,可以认为夜晚会下雨
7.某学校一同学研究温差(℃)与本校当天新增感冒人数(人)的关系,该同学记录了5天的数据:
x 5 6 8 9 12
y 17 20 25 28 35
经过拟合,发现基本符合经验回归方程,则下列结论错误的是( )
A.样本中心点为
B.
C.时,残差为
D.若去掉样本点,则样本的相关系数增大
8.用模型拟合一组数,若,,设,得变换后的线性回归方程为,则( )
A.12 B. C. D.7
二、多选题
9.数据的平均数为,方差为,数据的平均数为,方差为,其中满足关系式:,则( )
A.
B.数据的平均数为
C.若数据,则
D.若,数据不全相等,则样本点的成对样本数据的样本相关系数为
10.某班级学生开展课外数学探究活动,将一杯冷水从冰箱中取出后静置,在的室温下测量水温单位随时间(单位:)的变化关系,在测量了15个数据后,根据这些实验数据得到如下的散点图:
现需要选择合适的回归方程进行回归分析,则根据散点图,合适的回归方程类型有( )
A. B.
C. D.
11.针对当下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”做了一次调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的,女生喜欢抖音的人数占女生人数的,若有的把握认为是否喜欢抖音和性别有关,则调查人数中男生有可能( )
附:
A. B. C. D.
三、填空题
12.为研究变量x,y的相关关系,收集得到如下数据:
x 1 2 3 4 5
y 60
若由最小二乘法求得y关于x的线性回归方程为,并据此计算在样本点处的残差为0,则 .
13.现调查某地区某种野生动物的数量,将该地区分成面积相近的200个地块,从这些地块中简单随机抽样的方法抽取20个作为样本,调查得到样本数据,其中分别表示第个样本的植物覆盖面积(单位:公顷)和这种野生动物的数量,构造向量,,其中,,并计算得,,,,,由选择性必修二教材中的知识,我们知道对数据的相关系数,则上述数据的相关系数 .
14.有两个分类变量和,其中一组观测值为如下的2×2列联表:
总计
15
50
总计 20 45 65
其中,均为大于5的整数,则 时,在犯错误的概率不超过的前提下为“和之间有关系”.附:
四、解答题
15.大学生刘铭去某工厂实习,实习结束时从自己制作的某种零件中随机选取了10个样品,测量每个零件的横截面积(单位:)和耗材量(单位:),得到如下数据:
样本号 1 2 3 4 5 6 7 8 9 10 总和
零件的横截面积 0.03 0.05 0.04 0.07 0.07 0.04 0.05 0.06 0.06 0.05 0.52
耗材量 0.24 0.40 0.23 0.55 0.50 0.34 0.35 0.45 0.43 0.41 3.9
并计算得,.
(1)估算刘铭同学制作的这种零件平均每个零件的横截面积以及平均一个零件的耗材量;
(2)求刘铭同学制作的这种零件的横截面积和耗材量的样本相关系数(精确到0.01).
附:相关系数;.
16.2024年3月4日,丰城市农业局在市委组织下召开推进湖塘-董家富硒梨产业高质量发展专题会议,安排部署加快推进特色优势产业富硒梨高质量发展工作,集中资源、力量打造“富硒梨”公共品牌.丰城市为做好富硒梨产业的高质量发展,项目组统计了某果场近5年富硒梨产业综合总产值的各项数据如下:年份x,综合产值y(单位:万元)
年份 2019 2020 2021 2022 2023
年份代码 1 2 3 4 5
综合产值 23.1 37.0 62.1 111.6 150.8
(1)根据表格中的数据,可用一元线性回归模型刻画变量y与变量x之间的线性相关关系,请用相关系数加以说明(精确到0.01);
(2)求出y关于x的经验回归方程,并预测2024年底该果场富硒梨产业的综合总产值.
参考公式:相关系数回归方程中斜率和截距的最小二乘法估计公式分别为:;
参考数据:
17.将氢储存在甲基环乙烷和甲苯等有机液体中是储氢和运输氢的重要方向.2023年12月俄罗斯科学院西伯利亚分院科研人员用镍和锡取代铂,研发出一种新型高效的脱氢催化剂,脱氢效率达,且对储氢载体没有破坏作用,可重复使用.近年来,我国氢能源汽车产业迅速发展,下表是某市氢能源乘用车的年销售量与年份的统计表:
年份 2018 2019 2020 2021 2022
销量(万台) 2 3.5 2.5 8 9
(1)求氢能源乘用车的销量关于年份的线性回归方程,并预测2024年氢能源乘用车的销量;
(2)为了研究不同性别的学生对氢能源的了解情况,某校组织了一次有关氢能源的知识竞赛活动,随机抽取了男生和女生各60名,得到如表所示的数据:
了解 不了解 合计
男生 25
女生 20
合计
(ⅰ)根据已知条件,填写上述列联表;
(ⅱ)依据的独立性检验,能否认为该校学生对氢能源的了解情况与性别有关?
参考公式:1.回归方程中斜率和截距的最小二乘法估计公式分别为;
2..
0.050 0.010 0.001
3.841 6.635 10.828
18.某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本(元)与生产该产品的数量(千件)有关,经统计得到如下数据:
x 1 2 3 4 5 6 7 8
y 56.5 31 22.75 17.8 15.95 14.5 13 12.5
根据以上数据绘制了散点图观察散点图,两个变量间关系考虑用反比例函数模型和指数函数模型分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为,与x的相关系数.
(1)用反比例函数模型求y关于x的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.001),并用其估计产量为10千件时每件产品的非原料成本;
(3)根据企业长期研究表明,非原料成本y服从正态分布,用样本平均数作为的估计值,用样本标准差s作为的估计值,若非原料成本y在之外,说明该成本异常,并称落在之外的成本为异样成本,此时需寻找出现异样成本的原因.利用估计值判断上述非原料成本数据是否需要寻找出现异样成本的原因?
参考数据(其中):
0.34 0.115 1.53 184 5777.555 93.06 30.705 13.9
参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计公式分别为:,,相关系数.
19.某校20名学生的数学成绩和知识竞赛成绩如下表:
学生编号i 1 2 3 4 5 6 7 8 9 10
数学成绩 100 99 96 93 90 88 85 83 80 77
知识竞赛成绩 290 160 220 200 65 70 90 100 60 270
学生编号i 11 12 13 14 15 16 17 18 19 20
数学成绩 75 74 72 70 68 66 60 50 39 35
知识竞赛成绩 45 35 40 50 25 30 20 15 10 5
计算可得数学成绩的平均值是,知识竞赛成绩的平均值是,并且,,.
(1)求这组学生的数学成绩和知识竞赛成绩的样本相关系数(精确到0.01);
(2)设,变量和变量的一组样本数据为,其中两两不相同,两两不相同.记在中的排名是第位,在中的排名是第位,.定义变量和变量的“斯皮尔曼相关系数”(记为)为变量的排名和变量的排名的样本相关系数.
(i)记,.证明:;
(ii)用(i)的公式求得这组学生的数学成绩和知识竞赛成绩的“斯皮尔曼相关系数”约为0.91,简述“斯皮尔曼相关系数”在分析线性相关性时的优势.
注:参考公式与参考数据.
;;.
参考答案
1.A
根据散点图中点的分布情况,判断是否具有相关性和正负相关关系.
对于A,散点图中的点从左向右是上升的,且在一条直线附近,是正相关;
对于B,散点图中的点从左向右是下降的,且在一条直线附近,是负相关;
对于C、D,散点图中的点不成带状分布,没有明显的相关关系;
故选:A.
方法点睛:该题考查的是有关正负相关的判断问题,解题方法如下:
(1)观察图中散点图是不是成带状区域;
(2)判断其从左往右上升正相关,下降负相关.
2.D
从图中分析得到去掉后,回归效果更好,再由相关系数,决定系数,残差平方和和相关性的概念和性质作出判断即可.
从图中可以看出较其他点,偏离直线远,故去掉后,回归效果更好,
对于A,相关系数越接近于1,模型的拟合效果越好,若去掉后,相关系数r变大,故A错误;
对于B,决定系数越接近于1,模型的拟合效果越好,若去掉后,决定系数变大,故B错误;
对于C,残差平方和越小,模型的拟合效果越好,若去掉后,残差平方和变小,故C错误;
对于D,若去掉后,解释变量x与预报变量y的相关性变强,且是正相关,故D正确.
故选:D.
3.B
根据给定条件,求出,再借助回归直线的特征及残差列出方程组即可求解作答.
依题意,,而,于是得,
而当时,,即,联立解得,
所以.
故选:B
4.D
根据相关系数、决定系数和线性回归方程逐项理解判断.
对A:若变量和之间的相关系数为,则变量和之间的负相关很强,A正确;
对B:用决定系数来比较两个模型拟合效果,越大,表示残差平方和越小,即模型的拟合效果越好,B正确;
对C:在经验回归方程中,当解释变量每增加1个单位时,响应变量平均减少2个单位,C正确;
对D:经验回归直线必过样本中心点,但不一定过样本点,D错误.
故选:D.
5.B
根据等高条形图直接判断各个选项即可.
对于A,由图乙可知,样本中男生,女生都大部分愿意选择该门课,
则样本中愿意选该门课的人数较多,A错误;
对于BCD,由图甲可知,在愿意和不愿意的人中,都是男生占比较大,
所以可以确定,样本中男生人数多于女生人数,B正确,CD错误.
故选:B.
6.D
应用古典概型的概率求法求概率判断A、B,应用卡方计算公式求卡方值,与临界值比较,应用独立检验的基本思想得到结论,判断C、D.
由列联表知:100天中有50天下雨,50天未下雨,因此夜晚下雨的概率约为,A正确;
未出现“日落云里走”,夜晚下雨的概率约为,B正确;
,因此据小概率值的独立性检验,认为“日落云里走”是否出现与夜晚天气有关,C正确,D错误.
故选:D
7.D
由回归直线必过样本中心可判断A项、B项,由残差公式可判断C项,由相关系数公式可判断D项.
对于A项,因为,,
所以样本中心点为,故A项正确;
对于B项,由回归直线必过样本中心可得:,解得:,故B项正确;
对于C项,由B项知,,
令,则,
所以残差为,故C项正确;
对于D项,由相关系数公式可知,去掉样本点后,x与y的样本相关系数r不变,故D项错误.
故选:D.
8.B
由已知,可根据,先计算出,然后把样本中心点带入线性回归方程为中计算出,从而得到线性回归方程,然后将方程化为指数形式,通过待定系数法分别对应出、的值,即可完成求解.
由已知,,所以,
,,所以
,
由题意,满足线性回归方程为,所以,所以,
此时线性回归方程为,即,
可将此式子化为指数形式,即为,
因为模型为模型,所以,,
所以.
故选:B.
9.AD
利用平均数的定义相关公式以及方差的定义相关公式即可判断选项ABC,结合样本相关系数的概念即可判断选项D.
对于A,,故A正确;
对于B,,
其平均数为,故B错误;
对于C,,
因为,故,
而当时,,满足条件,
但此时可以不都相等,故C错误;
对于D,由样本相关系数的概念可知,D正确.
故选:AD
10.AC
散点图的特点是单调递增,增长速度越来越慢,且,根据特点对选项一一判断即可.
散点图的特点是单调递增,增长速度越来越慢,且
对A选项,符合散点图的特点;
对B选项,有不符合散点图的特点;
对C选项,符合散点图的特点;
对D选项,的增长速度不变,不符合散点图的特点;
故选:AC
11.BC
先设男生人数为,,列出列联表,利用独立性检验计算观测值,再结合观测值列关系即得答案.
解:由题意被调查的男女生人数相同,设男生的人数为:,,由题意可列出列联表:
男生 女生 合计
喜欢抖音
不喜欢抖音
合计
.
由于有的把握认为是否喜欢抖音和性别有关,
所以;
解得:,因为,
故的可能取值为:9、10、11、12、13,即男生的人数可以是45,50,55,60,65.
则选项中被调查学生中男生的人数可能45或60.
故选:BC.
12.290
先利用残差的计算公式求出,再根据回归直线过样本点的中心求出,即可得解.
因为在样本点处的残差为0,
所以,得,
则y关于x的线性回归方程为.
因为,所以,
所以.
故答案为:
13.
根据题干中相关系数的定义进行计算.
由题干数据,,可得,
根据夹角公式的定义,,而,
根据
,
于是.
故答案为:
14.9
由题意,计算,列出不等式求出的取值范围,再根据题意求得的值.
解:由题意知:,
则,
解得:或,
因为:且,,
综上得:,,
所以:.
故答案为:9.
本题考查独立性检验的应用问题.
15.(1)横截面积为,耗材量为.
(2)0.94
(1)根据表格中的数据,结合平均数的计算公式,即可求解;
(2)由表格中的参考数据和相关系数的公式,准确计算,即可求解.
(1)解:样本中10个这种零件的横截面积的平均值,
样本中10个这种零件的耗材量的平均值,
由此可估算刘铭同学制作的这种零件平均每个零件的横截面积为,平均一个零件的耗材量为.
(2)解:由表格中的参考数据和相关系数的公式,可得
,
所以这种零件的横截面积和耗材量的样本相关系数.
16.(1)说明见解析
(2),175.64万元
(1)首先算出,进一步分别算出,由此即可求得相关系数,进一步即可说明;
(2)依次求出的值即可得回归方程,进一步代入即可预测.
(1)由题设,
则,,,
所以,两个变量有强相关性,
故可用一元线性回归模型刻画变量y与变量x之间的线性相关关系.
(2)由(1),,,
所以,
当,则万元.
17.(1),12.4万台;
(2)(ⅰ)表格见解析;(ⅱ)该校学生对氢能源的了解情况与性别有关.
(1)利用已知数据和公式求线性回归方程,由方程进行数据预测;
(2)(ⅰ)根据男生和女生各60名补全列联表.
(ⅱ)计算,与临界值比较下结论.
(1)年份的平均数,销量的平均数,
所以,
,
所以,
所以,
所以氢能源乘用车的销量关于年份的线性回归方程为,
令,得,
所以预测2024年氢能源乘用车的销量约为12.4万台.
(2)(ⅰ)根据男生和女生各60名,补全列联表为:
了解 不了解 合计
男生 35 25 60
女生 20 40 60
合计 55 65 120
(ⅱ)零假设:该校学生对氢能源的了解情况与性别无关,
根据列联表中的数据可得,
,
依据的独立性检验,可以推断不成立,
即该校学生对氢能源的了解情况与性别有关.
18.(1)
(2)反比例函数模型拟合效果更好,产量为10千件时每件产品的非原料成本约为11元,
(3)见解析
(1)令,则可转化为,求出样本中心,回归方程的斜率,转化求回归方程即可,
(2)求出与的相关系数,通过比较,可得用反比例函数模型拟合效果更好,然后将代入回归方程中可求结果
(3)利用已知数据求出样本标准差s,从而可得非原料成本y服从正态分布,再计算,然后各个数据是否在此范围内,从而可得结论
(1)令,则可转化为,
因为,
所以,
所以,所以,
所以y关于x的回归方程为
(2)与的相关系数为
因为,所以用反比例函数模型拟合效果更好,
把代入回归方程得(元),
所以产量为10千件时每件产品的非原料成本约为11元
(3)因为,所以,
因为样本标准差为,
所以,
所以非原料成本y服从正态分布,
所以
因为在之外,所以需要此非原料成本数据寻找出现异样成本的原因
19.(1)证明见解析
(2)答案见解析
(1)利用相关系数的公式进行计算即可;
(2)(i)根据题意即相关系数的公式进行计算即可证明;(ii)只要能说出斯皮尔曼相关系数与一般的样本相关系数相比的优势即可.
(1)由题意,这组学生数学成绩和知识竞赛成绩的样本相关系数为
;
(2)(i)证明:因为和都是1,2,,的一个排列,所以
,
,
从而和的平均数都是.
因此,,
同理可得,
由于
,
所以.
(ii)这组学生的数学成绩和知识竞赛成绩的斯皮尔曼相关系数是0.91,
答案①:斯皮尔曼相关系数对于异常值不太敏感,如果数据中有明显的异常值,那么用斯皮尔曼相关系数比用样本相关系数更能刻画某种线性关系;
答案②:斯皮尔曼相关系数刻画的是样本数据排名的样本相关系数,与具体的数值无关,只与排名有关.如果一组数据有异常值,但排名依然符合一定的线性关系,则可以采用斯皮尔曼相关系数刻画线性关系.
方法点睛;新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的;遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
