7.1.2 全概率公式 同步巩固练 2024-2025学年数学人教A版(2019) 选择性必修第三册
文档属性
| 名称 | 7.1.2 全概率公式 同步巩固练 2024-2025学年数学人教A版(2019) 选择性必修第三册 |  | |
| 格式 | docx | ||
| 文件大小 | 429.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 10:10:50 | ||
图片预览



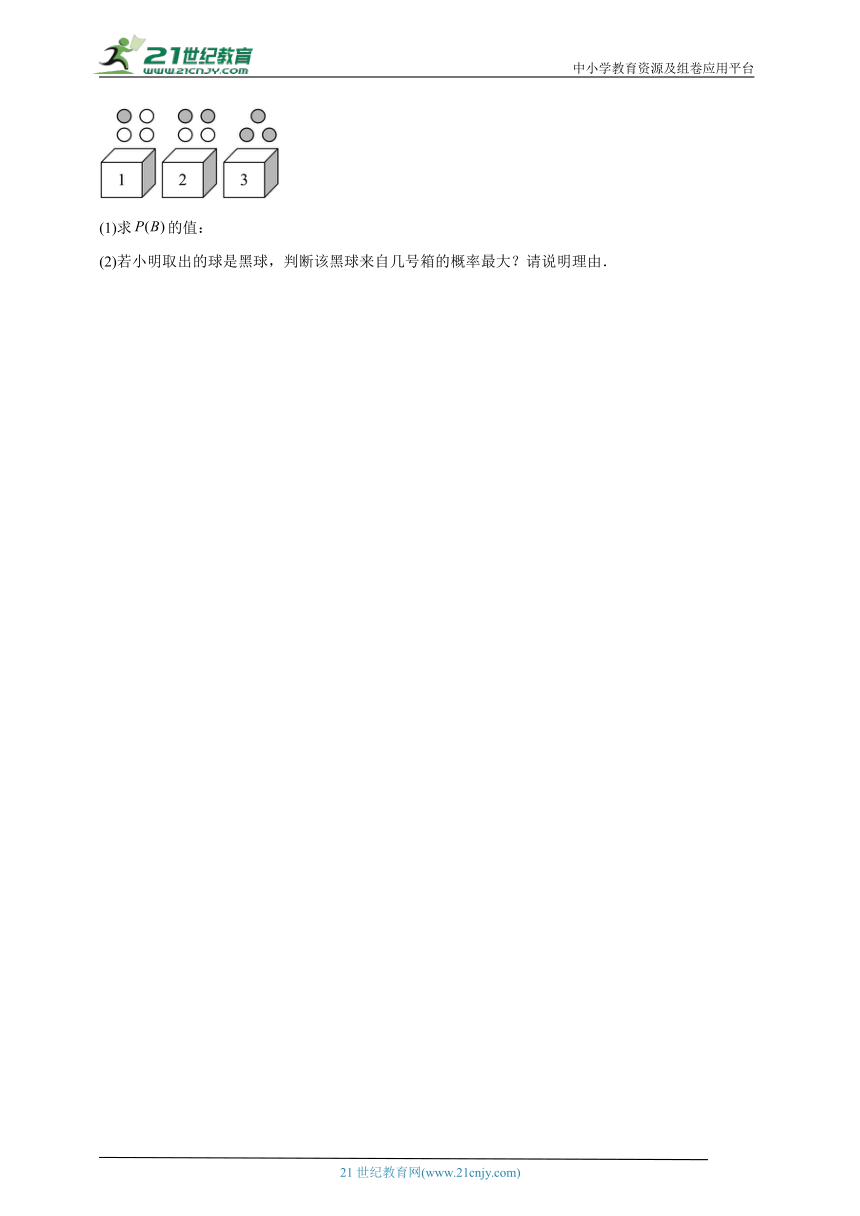

文档简介
中小学教育资源及组卷应用平台
7.1.2 全概率公式 同步巩固练
2024-2025学年数学人教A版(2019) 选择性必修第三册
一、单选题
1.某人外出出差,委托邻居给家里盆栽浇一次水,若不浇水,盆栽枯萎的概率为0.8;若浇水,盆栽枯萎的概率为0.1.若邻居浇水的概率为,该人回来盆栽没有枯萎的概率为0.83,则实数的值为( )
A.0.9 B.0.85 C.0.8 D.0.75
2.长时间玩手机可能影响视力.据调查,某校学生大约的人近视,而该校大约有的学生每天玩手机超过1小时,这些人的近视率约为,现从每天玩手机不超过1小时的学生中任意调查一名学生,则他近视的概率为( )
A. B. C. D.
3.根据曲靖一中食堂人脸识别支付系统后台数据分析发现,高三年级小孔同学一周只去食堂一楼和二楼吃饭.周一去食堂一楼和二楼的概率分别为和,若他周一去了食堂一楼,那么周二去食堂二楼的概率为,若他周一去了食堂二楼,那么周二去食堂一楼的概率为,现已知小孔同学周二去了食堂二楼,则周一去食堂一楼的概率为( ).
A. B. C. D.
4.居民的某疾病发病率为,现进行普查化验,医学研究表明,化验结果是可能存有误差的.已知患有该疾病的人其化验结果呈阳性,而没有患该疾病的人其化验结果呈阳性.现有某人的化验结果呈阳性,则他真的患该疾病的概率是( )
A.0.99 B.0.9 C.0.5 D.0.1
5.某次考试共有8道单选题,某学生掌握了其中5道题,2道题有思路,1道题完全没有思路.掌握了的题目他可以选择唯一正确的答案,有思路的题目每道做对的概率为,没有思路的题目,只好任意猜一个答案,猜对的概率为.已知这个学生随机选一道题作答且做对了,则该题为有思路的题目的概率为( )
A. B. C. D.
6.“狼来了”的故事大家小时候应该都听说过:小孩第一次喊“狼来了”,大家信了,但去了之后发现没有狼;第二次喊“狼来了”,大家又信了,但去了之后又发现没有狼;第三次狼真的来了,但是这个小孩再喊狼来了就没人信了.从数学的角度解释这一变化,假设小孩是诚实的,则他出于某种特殊的原因说谎的概率为;小孩是不诚实的,则他说谎的概率是.最初人们不知道这个小孩诚实与否,所以在大家心目中每个小孩是诚实的概率是.已知第一次他说谎了,那么他是诚实的小孩的概率是( )
A. B. C. D.
7.设有5个袋子中放有白球,黑球,其中1号袋中白球占,另外2,3,4,5号4个袋子中白球都占,今从中随机取1个袋子,从所取的袋子中随机取1个球,结果是白球,则这个球是来自1号袋子中的概率为( )
A. B. C. D.
8.一道考题有4个,要求学生将其中的一个正确选择出来.某考生知道正确的概率为,而乱猜正确的概率为.在乱猜时,4个都有机会被他选择,如果他答对了,则他确实知道正确的概率是( )
A. B.
C. D.
二、填空题
9.已知在自然人群中,男性色盲患者出现的概率为7%,女性色盲患者出现的概率为0.5%.今从男女人数相等的人群中随机地挑选一人,恰好是色盲患者,则此人是男性的概率是 .
10.甲箱中有个白球,个黑球,乙箱中有个白球,个黑球,先从甲箱中任取一球放入乙箱中,再从乙箱中任取一球,从乙箱中取出白球的概率是 .
11.已知是一个随机试验中的两个事件,若,则
12.某校面向高一全体学生共开设3门体育类选修课,每人限选一门.已知这三门体育类 选修课的选修人数之比为,考核优秀率分别为20%、16%和12%,现从该年级所有选择体育类选修课的同学中任取一名,其成绩是优秀的概率为 .
三、解答题
13.现有10个球,其中5个球由甲工厂生产,3个球由乙工厂生产,2个球由丙工厂生产.这三个工厂生产该类产品的合格率依次是,,.现从这10个球中任取1个球,设事件为“取得的球是合格品”,事件分别表示“取得的球是甲、乙、丙三个工厂生产的”.
(1)求;
(2)求.
14.三批同种规格的产品,第一批占25%,次品率为6%;第二批占30%,次品率为5%;第三批占45%,次品率为5%.将三批产品混合,从混合产品中任取一件.
(1)求这件产品是次品的概率;
(2)已知取到的是次品,求它取自第一批产品的概率.
15.某学校安排甲、乙、丙三个班级同时到学校礼堂参加联欢晚会,已知甲班艺术生占比8%,乙班艺术生占比6%,丙班艺术生占比5%.学生自由选择座位,先到者先选.甲、乙、丙三个班人数分别占总人数的,,.若主持人随机从场下学生中选一人参与互动.
(1)求选到的学生是艺术生的概率;
(2)如果选到的学生是艺术生,判断其来自哪个班的可能性最大.
16.某次社会实践活动中,甲、乙两个班的同学共同在一个社区进行新冠疫情防控宣传.参加活动的甲、乙两班的人数之比为5∶3,其中甲班中女生占,乙班中女生占.求该社区居民遇到一位进行新冠疫情防控宣传的同学恰好是女生的概率.
17.现有两台车床加工同一型号的零件,第1台车床加工的零件次品率为6%,第2台车床加工的零件次品率为5%,加工出来的零件混放在一起已知第1台车床加工的零件数与第2台车床加工的零件数之比为2:3,从这些零件中任取一个.
(1)求这个零件是次品的概率;
(2)已知这个零件是次品,求它是第一台车床加工的概率.
18.学习小组设计了如下试验模型:有完全相同的甲、乙两个袋子,袋子里有形状和大小完全相同的小球,其中甲袋中有2个红球和8个白球,乙袋中有6个红球和4个白球.从这两个袋子中选择1个袋子,再从该袋子中随机摸出1个球,称为一次摸球.多次摸球直到摸出白球时试验结束.假设首次摸球选到甲袋或乙袋的概率均为.
(1)求首次摸球就试验结束的概率;
(2)在首次摸球摸出红球的条件下.
①求选到的袋子为乙袋的概率;
②将首次摸球摸出的红球放回原来袋子,继续进行第二次摸球时有如下两种方案:方案一,从原来袋子中摸球;方案二,从另外一个袋子中摸球,请通过计算,说明选择哪个方案使得第二次摸球就试验结束的概率更大.
19.如图,有三个外形相同的箱子,分别编号为1,2,3,其中1号箱装有1个黑球和3个白球,2号箱装有2个黑球和2个白球,3号箱装有3个黑球,这些球除颜色外完全相同.小明先从三个箱子中任取一箱,再从取出的箱中任意摸出一球,记事件()表示“球取自第i号箱”,事件B表示“取得黑球”.
(1)求的值:
(2)若小明取出的球是黑球,判断该黑球来自几号箱的概率最大?请说明理由.
参考答案
1.A
根据给定条件,由全概率公式列式,求解计算即可求出结果.
记为事件“盆栽没有枯萎”,为事件“邻居给盆栽浇水”,由题意可得,,由对立事件的概率公式可得.
由全概率公式可得
,解得.
故选:A
2.C
根据给定条件,结合全概率公式列式求解作答.
令=“玩手机时间超过1小时的学生”,=“玩手机时间不超过1小时的学生”,=“任意调查一人,此人近视”,
,且互斥,,
依题意有,解得
从每天玩手机不超过1小时的学生中任意调查一名学生,则他近视的概率为.
故选:C
3.A
利用贝叶斯概率公式求解即可.
记小孔同学周一去食堂一楼为事件A,周二去食堂一楼为事件B,
则本题所求.
故选:A.
4.C
记事件某人患病,事件化验结果呈阳性,利用全概率公式求出的值,再利用条件概率公式可求得所求事件的概率.
记事件某人患病,事件化验结果呈阳性,
由题意可知,,,
所以,
,
现在某人的化验结果呈阳性,则他真的患该疾病的概率是:
.
故选:C.
5.B
根据全概率公式和条件概率公式,即可求解.
设事件表示选到会做的题,事件表示选到有思路的题,事件表示选到完全没有思路的题;
设事件表示答对该题,则,
设事件表示答对某个题,
则,
设事件表示将有思路的题目做对,则,
故选:B
6.D
设出事件,利用全概率公式和贝叶斯公式进行求解.
设事件表示“小孩诚实”,事件表示“小孩说谎”,
则,,,,
则,
,
故,
故.
故选:D
7.A
根据题意结合贝叶斯公式求解即可.
设事件表示“取到第号袋子”(=1,2,3,4,5),事件表示“取到白球”,
则由贝叶斯公式得,
故选:A
8.B
根据全概率公式,结合贝叶斯公式进行求解即可.
[设A=“考生答对”,B=“考生知道正确”,
由全概率公式:
.
又由贝叶斯公式: .
故选:B
9.
以事件表示“选出的是男性”,则事件表示“选出的是女性”,以事件表示“选出的人是色盲患者”.由已知得,,.根据贝叶斯公式可求得答案.
解:以事件表示“选出的是男性”,则事件表示“选出的是女性”,以事件表示“选出的人是色盲患者”.
由题意,知,,.
由贝叶斯公式,可知此色盲患者是男性的概率为
.
故答案为:.
10./
根据全概率公式直接求解即可.
记事件为“从甲箱中取出一个白球放入乙箱”,事件为“从乙箱中取出白球”,
则,,,,
.
故答案为:.
11.3
由条件概率计算公式计算得,,求的值.
因为,所以,即,
同理,由得,
因为,所以,
,所以,
所以.
故答案为:3.
12.0.18
根据给定条件,利用全概率公式列式计算即得.
设事件“任取一名同学,成绩为优秀”,“抽取的选修第门选修课的同学”(),
则,且两两互斥,依题意,,
,
所以成绩是优秀的概率为
.
故答案为:0.18
13.(1);
(2)0.81.
(1)根据给定条件,利用古典概率公式计算即得.
(2)由(1)的结论,利用全概率公式列式计算即得.
(1)依题意,.
(2)依题意,,
由(1)知,
由全概率公式得
.
14.(1)
(2)
(1)取到第批产品为事件,,取到次品为事件,由全概率公式求解;
(2)由条件概率公式结合乘法公式求解.
(1)设取到第批产品为事件,,取到次品为事件.
.
(2).
15.(1)
(2)来自丙班的可能性最大
(1)依据题意根据全概率公式计算即可;
(2)根据条件概率公式分别计算,即可判断.
(1)设“任选一名学生恰好是艺术生”,
“所选学生来自甲班”,“所选学生来自乙班”,
“所选学生来自丙班”.由题可知:
,,,
,,
.
(2);
所以其来自丙班的可能性最高.
16.
用事件分别表示“居民所遇到的一位同学是甲班的与乙班的”,事件B表示“居民所遇到的一位同学是女生”,根据题意利用全概率公式运算求解.
用事件分别表示“居民所遇到的一位同学是甲班的与乙班的”,事件B表示“居民所遇到的一位同学是女生”,
则,且互斥,,
由题意可知,且,
由全概率公式可知.
17.(1)
(2)
(1)根据题意,结合全概率公式,准确计算,即可求解;
(2)根据题意,结合条件概率的计算公式,即可求解.
(1)解:记事件:第一台车床加工的零件,记事件:第二台车床加工的零件,
记事件:这个零件是次品,
由题意可得,,,,
由全概率公式可得:
.
(2)解:由(1)知,已知这个零件是次品,它是第一台车床加工的概率为
.
18.(1);
(2)①;②选择方案二使得第二次摸球就试验结束的概率更大.
(1)利用全概率公式计算可得;
(2)①利用条件概率概率公式计算可得;②分别求出两种方案中摸到白球的概率,再比较即可.
(1)设摸球一次,“取到甲袋”为事件,“取到乙袋”为事件,“摸出白球”为事件,“摸出红球”为事件.
所以.
所以摸球一次就试验结束的概率为.
(2)①因为,是对立事件,.
所以,
所以选到的袋子为乙袋的概率为.
②由①,得,
所以方案一中取到白球的概率为.
方案二中取到白球的概率为,
因为.
所以方案二中取到白球的概率更大,即选择方案二使得第二次摸球就试验结束的概率更大.
19.(1)
(2)可判断该黑球来自3号箱的概率最大.
(1)因先从三个箱子中任取一箱,再从取出的箱中任意摸出一球为黑球,其中有三种可能,即黑球取自于1号,2号或者3号箱,故事件属于全概率事件,分别计算出和,代入全概率公式即得;
(2)由“小明取出的球是黑球,判断该黑球来自几号箱”是求条件概率,根据条件概率公式分别计算再比较即得.
(1)由已知得:,而
由全概率公式可得:
(2)因“小明取出的球是黑球,该黑球来自1号箱”可表示为:,其概率为,
“小明取出的球是黑球,该黑球来自2号箱”可表示为:,其概率为,
“小明取出的球是黑球,该黑球来自3号箱”可表示为:,其概率为.
综上,最大,即若小明取出的球是黑球,可判断该黑球来自3号箱的概率最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.1.2 全概率公式 同步巩固练
2024-2025学年数学人教A版(2019) 选择性必修第三册
一、单选题
1.某人外出出差,委托邻居给家里盆栽浇一次水,若不浇水,盆栽枯萎的概率为0.8;若浇水,盆栽枯萎的概率为0.1.若邻居浇水的概率为,该人回来盆栽没有枯萎的概率为0.83,则实数的值为( )
A.0.9 B.0.85 C.0.8 D.0.75
2.长时间玩手机可能影响视力.据调查,某校学生大约的人近视,而该校大约有的学生每天玩手机超过1小时,这些人的近视率约为,现从每天玩手机不超过1小时的学生中任意调查一名学生,则他近视的概率为( )
A. B. C. D.
3.根据曲靖一中食堂人脸识别支付系统后台数据分析发现,高三年级小孔同学一周只去食堂一楼和二楼吃饭.周一去食堂一楼和二楼的概率分别为和,若他周一去了食堂一楼,那么周二去食堂二楼的概率为,若他周一去了食堂二楼,那么周二去食堂一楼的概率为,现已知小孔同学周二去了食堂二楼,则周一去食堂一楼的概率为( ).
A. B. C. D.
4.居民的某疾病发病率为,现进行普查化验,医学研究表明,化验结果是可能存有误差的.已知患有该疾病的人其化验结果呈阳性,而没有患该疾病的人其化验结果呈阳性.现有某人的化验结果呈阳性,则他真的患该疾病的概率是( )
A.0.99 B.0.9 C.0.5 D.0.1
5.某次考试共有8道单选题,某学生掌握了其中5道题,2道题有思路,1道题完全没有思路.掌握了的题目他可以选择唯一正确的答案,有思路的题目每道做对的概率为,没有思路的题目,只好任意猜一个答案,猜对的概率为.已知这个学生随机选一道题作答且做对了,则该题为有思路的题目的概率为( )
A. B. C. D.
6.“狼来了”的故事大家小时候应该都听说过:小孩第一次喊“狼来了”,大家信了,但去了之后发现没有狼;第二次喊“狼来了”,大家又信了,但去了之后又发现没有狼;第三次狼真的来了,但是这个小孩再喊狼来了就没人信了.从数学的角度解释这一变化,假设小孩是诚实的,则他出于某种特殊的原因说谎的概率为;小孩是不诚实的,则他说谎的概率是.最初人们不知道这个小孩诚实与否,所以在大家心目中每个小孩是诚实的概率是.已知第一次他说谎了,那么他是诚实的小孩的概率是( )
A. B. C. D.
7.设有5个袋子中放有白球,黑球,其中1号袋中白球占,另外2,3,4,5号4个袋子中白球都占,今从中随机取1个袋子,从所取的袋子中随机取1个球,结果是白球,则这个球是来自1号袋子中的概率为( )
A. B. C. D.
8.一道考题有4个,要求学生将其中的一个正确选择出来.某考生知道正确的概率为,而乱猜正确的概率为.在乱猜时,4个都有机会被他选择,如果他答对了,则他确实知道正确的概率是( )
A. B.
C. D.
二、填空题
9.已知在自然人群中,男性色盲患者出现的概率为7%,女性色盲患者出现的概率为0.5%.今从男女人数相等的人群中随机地挑选一人,恰好是色盲患者,则此人是男性的概率是 .
10.甲箱中有个白球,个黑球,乙箱中有个白球,个黑球,先从甲箱中任取一球放入乙箱中,再从乙箱中任取一球,从乙箱中取出白球的概率是 .
11.已知是一个随机试验中的两个事件,若,则
12.某校面向高一全体学生共开设3门体育类选修课,每人限选一门.已知这三门体育类 选修课的选修人数之比为,考核优秀率分别为20%、16%和12%,现从该年级所有选择体育类选修课的同学中任取一名,其成绩是优秀的概率为 .
三、解答题
13.现有10个球,其中5个球由甲工厂生产,3个球由乙工厂生产,2个球由丙工厂生产.这三个工厂生产该类产品的合格率依次是,,.现从这10个球中任取1个球,设事件为“取得的球是合格品”,事件分别表示“取得的球是甲、乙、丙三个工厂生产的”.
(1)求;
(2)求.
14.三批同种规格的产品,第一批占25%,次品率为6%;第二批占30%,次品率为5%;第三批占45%,次品率为5%.将三批产品混合,从混合产品中任取一件.
(1)求这件产品是次品的概率;
(2)已知取到的是次品,求它取自第一批产品的概率.
15.某学校安排甲、乙、丙三个班级同时到学校礼堂参加联欢晚会,已知甲班艺术生占比8%,乙班艺术生占比6%,丙班艺术生占比5%.学生自由选择座位,先到者先选.甲、乙、丙三个班人数分别占总人数的,,.若主持人随机从场下学生中选一人参与互动.
(1)求选到的学生是艺术生的概率;
(2)如果选到的学生是艺术生,判断其来自哪个班的可能性最大.
16.某次社会实践活动中,甲、乙两个班的同学共同在一个社区进行新冠疫情防控宣传.参加活动的甲、乙两班的人数之比为5∶3,其中甲班中女生占,乙班中女生占.求该社区居民遇到一位进行新冠疫情防控宣传的同学恰好是女生的概率.
17.现有两台车床加工同一型号的零件,第1台车床加工的零件次品率为6%,第2台车床加工的零件次品率为5%,加工出来的零件混放在一起已知第1台车床加工的零件数与第2台车床加工的零件数之比为2:3,从这些零件中任取一个.
(1)求这个零件是次品的概率;
(2)已知这个零件是次品,求它是第一台车床加工的概率.
18.学习小组设计了如下试验模型:有完全相同的甲、乙两个袋子,袋子里有形状和大小完全相同的小球,其中甲袋中有2个红球和8个白球,乙袋中有6个红球和4个白球.从这两个袋子中选择1个袋子,再从该袋子中随机摸出1个球,称为一次摸球.多次摸球直到摸出白球时试验结束.假设首次摸球选到甲袋或乙袋的概率均为.
(1)求首次摸球就试验结束的概率;
(2)在首次摸球摸出红球的条件下.
①求选到的袋子为乙袋的概率;
②将首次摸球摸出的红球放回原来袋子,继续进行第二次摸球时有如下两种方案:方案一,从原来袋子中摸球;方案二,从另外一个袋子中摸球,请通过计算,说明选择哪个方案使得第二次摸球就试验结束的概率更大.
19.如图,有三个外形相同的箱子,分别编号为1,2,3,其中1号箱装有1个黑球和3个白球,2号箱装有2个黑球和2个白球,3号箱装有3个黑球,这些球除颜色外完全相同.小明先从三个箱子中任取一箱,再从取出的箱中任意摸出一球,记事件()表示“球取自第i号箱”,事件B表示“取得黑球”.
(1)求的值:
(2)若小明取出的球是黑球,判断该黑球来自几号箱的概率最大?请说明理由.
参考答案
1.A
根据给定条件,由全概率公式列式,求解计算即可求出结果.
记为事件“盆栽没有枯萎”,为事件“邻居给盆栽浇水”,由题意可得,,由对立事件的概率公式可得.
由全概率公式可得
,解得.
故选:A
2.C
根据给定条件,结合全概率公式列式求解作答.
令=“玩手机时间超过1小时的学生”,=“玩手机时间不超过1小时的学生”,=“任意调查一人,此人近视”,
,且互斥,,
依题意有,解得
从每天玩手机不超过1小时的学生中任意调查一名学生,则他近视的概率为.
故选:C
3.A
利用贝叶斯概率公式求解即可.
记小孔同学周一去食堂一楼为事件A,周二去食堂一楼为事件B,
则本题所求.
故选:A.
4.C
记事件某人患病,事件化验结果呈阳性,利用全概率公式求出的值,再利用条件概率公式可求得所求事件的概率.
记事件某人患病,事件化验结果呈阳性,
由题意可知,,,
所以,
,
现在某人的化验结果呈阳性,则他真的患该疾病的概率是:
.
故选:C.
5.B
根据全概率公式和条件概率公式,即可求解.
设事件表示选到会做的题,事件表示选到有思路的题,事件表示选到完全没有思路的题;
设事件表示答对该题,则,
设事件表示答对某个题,
则,
设事件表示将有思路的题目做对,则,
故选:B
6.D
设出事件,利用全概率公式和贝叶斯公式进行求解.
设事件表示“小孩诚实”,事件表示“小孩说谎”,
则,,,,
则,
,
故,
故.
故选:D
7.A
根据题意结合贝叶斯公式求解即可.
设事件表示“取到第号袋子”(=1,2,3,4,5),事件表示“取到白球”,
则由贝叶斯公式得,
故选:A
8.B
根据全概率公式,结合贝叶斯公式进行求解即可.
[设A=“考生答对”,B=“考生知道正确”,
由全概率公式:
.
又由贝叶斯公式: .
故选:B
9.
以事件表示“选出的是男性”,则事件表示“选出的是女性”,以事件表示“选出的人是色盲患者”.由已知得,,.根据贝叶斯公式可求得答案.
解:以事件表示“选出的是男性”,则事件表示“选出的是女性”,以事件表示“选出的人是色盲患者”.
由题意,知,,.
由贝叶斯公式,可知此色盲患者是男性的概率为
.
故答案为:.
10./
根据全概率公式直接求解即可.
记事件为“从甲箱中取出一个白球放入乙箱”,事件为“从乙箱中取出白球”,
则,,,,
.
故答案为:.
11.3
由条件概率计算公式计算得,,求的值.
因为,所以,即,
同理,由得,
因为,所以,
,所以,
所以.
故答案为:3.
12.0.18
根据给定条件,利用全概率公式列式计算即得.
设事件“任取一名同学,成绩为优秀”,“抽取的选修第门选修课的同学”(),
则,且两两互斥,依题意,,
,
所以成绩是优秀的概率为
.
故答案为:0.18
13.(1);
(2)0.81.
(1)根据给定条件,利用古典概率公式计算即得.
(2)由(1)的结论,利用全概率公式列式计算即得.
(1)依题意,.
(2)依题意,,
由(1)知,
由全概率公式得
.
14.(1)
(2)
(1)取到第批产品为事件,,取到次品为事件,由全概率公式求解;
(2)由条件概率公式结合乘法公式求解.
(1)设取到第批产品为事件,,取到次品为事件.
.
(2).
15.(1)
(2)来自丙班的可能性最大
(1)依据题意根据全概率公式计算即可;
(2)根据条件概率公式分别计算,即可判断.
(1)设“任选一名学生恰好是艺术生”,
“所选学生来自甲班”,“所选学生来自乙班”,
“所选学生来自丙班”.由题可知:
,,,
,,
.
(2);
所以其来自丙班的可能性最高.
16.
用事件分别表示“居民所遇到的一位同学是甲班的与乙班的”,事件B表示“居民所遇到的一位同学是女生”,根据题意利用全概率公式运算求解.
用事件分别表示“居民所遇到的一位同学是甲班的与乙班的”,事件B表示“居民所遇到的一位同学是女生”,
则,且互斥,,
由题意可知,且,
由全概率公式可知.
17.(1)
(2)
(1)根据题意,结合全概率公式,准确计算,即可求解;
(2)根据题意,结合条件概率的计算公式,即可求解.
(1)解:记事件:第一台车床加工的零件,记事件:第二台车床加工的零件,
记事件:这个零件是次品,
由题意可得,,,,
由全概率公式可得:
.
(2)解:由(1)知,已知这个零件是次品,它是第一台车床加工的概率为
.
18.(1);
(2)①;②选择方案二使得第二次摸球就试验结束的概率更大.
(1)利用全概率公式计算可得;
(2)①利用条件概率概率公式计算可得;②分别求出两种方案中摸到白球的概率,再比较即可.
(1)设摸球一次,“取到甲袋”为事件,“取到乙袋”为事件,“摸出白球”为事件,“摸出红球”为事件.
所以.
所以摸球一次就试验结束的概率为.
(2)①因为,是对立事件,.
所以,
所以选到的袋子为乙袋的概率为.
②由①,得,
所以方案一中取到白球的概率为.
方案二中取到白球的概率为,
因为.
所以方案二中取到白球的概率更大,即选择方案二使得第二次摸球就试验结束的概率更大.
19.(1)
(2)可判断该黑球来自3号箱的概率最大.
(1)因先从三个箱子中任取一箱,再从取出的箱中任意摸出一球为黑球,其中有三种可能,即黑球取自于1号,2号或者3号箱,故事件属于全概率事件,分别计算出和,代入全概率公式即得;
(2)由“小明取出的球是黑球,判断该黑球来自几号箱”是求条件概率,根据条件概率公式分别计算再比较即得.
(1)由已知得:,而
由全概率公式可得:
(2)因“小明取出的球是黑球,该黑球来自1号箱”可表示为:,其概率为,
“小明取出的球是黑球,该黑球来自2号箱”可表示为:,其概率为,
“小明取出的球是黑球,该黑球来自3号箱”可表示为:,其概率为.
综上,最大,即若小明取出的球是黑球,可判断该黑球来自3号箱的概率最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
