7.3.1 离散型随机变量的均值 同步巩固练 2024-2025学年数学人教A版(2019) 选择性必修第三册
文档属性
| 名称 | 7.3.1 离散型随机变量的均值 同步巩固练 2024-2025学年数学人教A版(2019) 选择性必修第三册 |  | |
| 格式 | docx | ||
| 文件大小 | 520.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 10:10:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.3.1 离散型随机变量的均值 同步巩固练
2024-2025学年数学人教A版(2019) 选择性必修第三册
一、单选题
1.已知随机变量服从两点分布,,则其成功概率为( )
A.0.3 B.0.4 C.0.5 D.0.6
2.已知离散型随机变量X的分布列如下表:
X 0 1 2
P 0.64 q2 1-2q
则E(X)=( )
A.0.56 B.0.64 C.0.72 D.0.8
3.设为正实数,若随机变量的分布列为,则( )
A.3 B.1 C. D.
4.设随机变量的分布列为:
0 1 2
P
则的数学期望的最小值是( )
A. B.0 C.2 D.随p的变化而变化
5.设随机变量X的分布列如下表所示,且,则等于( )
X 0 1 2 3
P 0.1 a b 0.1
A. B. C. D.
6.某篮球运动员一次投篮得分的分布列为:
若他在一次投篮中得分的期望,则的最大值为( )
A. B. C. D.
7.已知随机变量X的分布列为
X 1 2 3
P
且,若,则等于( )
A. B. C. D.
8.已知随机变量的分布列是,则( )
1 2 3
A. B. C. D.
9.设的分布列如表所示,又设,则等于( )
1 2 3 4
A. B. C. D.
10.将个球(形状相同,编号不同)随机地投入编号为、、、的个盒子,以表示其中至少有一个球的盒子的最小号码(表示第号,第号盒子是空的,第个盒子至少个球),则、分别等于( )
A.、 B.、 C.、 D.、
二、填空题
11.已知随机变量X的取值为0,1,若,则X的均值为 .
12.已知,则 .
13.已知随机变量服从两点分布,且,设,那么 .
14.已知随机变量的分布为,且,若,则实数 .
15.已知随机变量的分布列如下表所示,若,则 .
三、解答题
16.某校高三年级嘟嘟老师准备利用高中数学知识对甲、乙、丙三名学生在即将到来的全省适应性考试成绩进行预测,为此,他收集了三位同学近三个月的数学月考、周测成绩(满分150分),若考试成绩超过100分则称为“破百”.
甲:74,85,81,90,103,89,92,97,109,95;
乙:95,92,97,99,89,103,105,108,101,113;
丙:92,102,97,105,89,94,92,97.
假设用频率估计概率,且甲、乙、丙三名同学的考试成绩相互独立.
(1)分别估计甲、乙、丙三名同学“破百”的概率;
(2)设这甲、乙、丙三名同学在这次决赛上“破百”的人数为,求的分布列和数学期望.
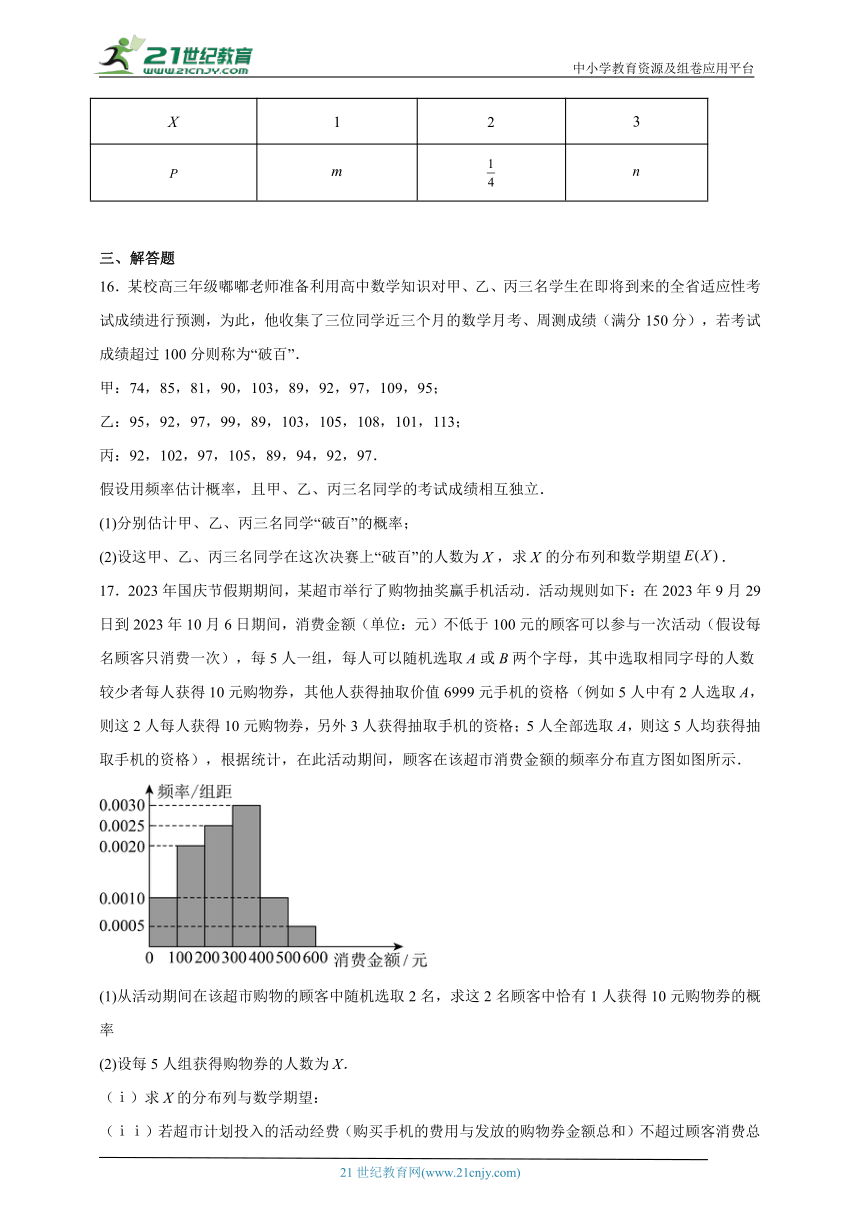
17.2023年国庆节假期期间,某超市举行了购物抽奖赢手机活动.活动规则如下:在2023年9月29日到2023年10月6日期间,消费金额(单位:元)不低于100元的顾客可以参与一次活动(假设每名顾客只消费一次),每5人一组,每人可以随机选取A或B两个字母,其中选取相同字母的人数较少者每人获得10元购物券,其他人获得抽取价值6999元手机的资格(例如5人中有2人选取A,则这2人每人获得10元购物券,另外3人获得抽取手机的资格;5人全部选取A,则这5人均获得抽取手机的资格),根据统计,在此活动期间,顾客在该超市消费金额的频率分布直方图如图所示.
(1)从活动期间在该超市购物的顾客中随机选取2名,求这2名顾客中恰有1人获得10元购物券的概率
(2)设每5人组获得购物券的人数为X.
(ⅰ)求X的分布列与数学期望:
(ⅰⅰ)若超市计划投入的活动经费(购买手机的费用与发放的购物券金额总和)不超过顾客消费总金额的10%,则每1000名顾客最多送出多少部手机?(同一组中的数据用该组区间的中点值为代表)
18.已知随机变量的分布列为:
5 6 7 8 9
0.1 0.2 0.3
(1)若,求、的值;
(2)记事件:;事件:为偶数.已知,求,的值.
19.某超市每天以4元/千克购进某种有机蔬菜,然后以7元/千克出售.若每天下午6点以前所购进的有机蔬菜没有全部销售完,则对未售出的有机蔬菜降价处理,以2元/千克出售,并且降价后能够把剩余所有的有机蔬菜全部处理完毕,且当天不再进货.该超市整理了过去两个月(按60天计算)每天下午6点前这种有机蔬菜的日销售量(单位:千克),得到如下统计数据.(注:视频率为概率,).
每天下午6点前的销售量/千克 250 300 350 400 450
天数 10 10 5
(1)求1天下午6点前的销售量不少于350千克的概率;
(2)在接下来的2天中,设为下午6点前的销售量不少于350千克的天数,求的分布列和数学期望;
(3)若该超市以当天的利润期望值为决策依据,当购进350千克的期望值比购进400千克的期望值大时,求的最小值.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C A A D A C D B
1.D
根据两点分布的期望即可求解.
随机变量服从两点分布,设成功的概率为,
.
故选:D.
2.A
由概率之和为1可求出的值,再根据分布列直接计算均值..
由题可得,解得或,
当时,,不符合题意,舍去,
;
所以可得分布列为
X 0 1 2
P 0.64 0.16 0.2
,
故选:A.
3.C
先由概率和为1,求出a,再求.
因为随机变量的分布列为,
所以,解得:a=3.
所以.
故选:C
4.A
根据分布列和概率的性质求出p的范围,再求数学期望关于p的函数即可求其最小值.
由分布列的性质得,解得,
,
∴的最小值为.
故选:A.
5.A
根数学期望的公式,结合概率的性质求解即可
由分布列的性质可得,,即①,
,
,即②,
联立①②解得,,
故.
故选:A.
6.D
根据离散型随机变量数学期望求解公式可得,利用基本不等式可求得结果.
由题意得:,
(当且仅当时取等号),.
即的最大值为.
故选:D.
7.A
结合题意,先计算出,再表示,建立等式,解出即可.
结合题意:,
因为,所以,解得:,
故选:A.
8.C
根据分布列的性质求出,即可求出,再根据期望的性质计算可得;
解:依题意可得,解得,
所以,
所以;
故选:C
9.D
根据分布列求出,再根据期望的性质计算可得.
解:依题意可得,
所以.
故选:D.
10.B
由题意可知,随机变量的可能取值有、、、,计算出随机变量在不同取值下的概率,可求得,利用数学期望的性质可求得.
由题意可知,随机变量的可能取值有、、、,
,,
,,
所以,,
因此,.
故选:B.
方法点睛:求随机变量的期望和方差的基本方法如下:
(1)已知随机变量的分布列,直接利用期望和方差公式直接求解;
(2)已知随机变量的期望、方差,求的期望与方差,利用期望和方差的性质(,)进行计算;
(3)若能分析出所给的随机变量服从常用的分布(如:两点分布、二项分布等),可直接利用常用分布列的期望和方差公式进行计算.
11./
X服从两点分布,结合两点分布的均值公式,即可求解.
由题意可得,X服从两点分布,
,
故.
故答案为:.
12.
直接根据均值公式结合已知条件,解方程即可得出所求的答案.
由,可得.
故答案为:
13.
先求出,再由随机变量的线性关系的期望性质,即可求解.
,
故答案为:
本题考查两点分布的期望和期望的性质,属于基础题.
14.
由期望性质可得答案.
因,则.
又,则.
故选:.
15./
利用分布列的性质结合期望公式可得出关于、的方程组,解出这两个量的值,结合表格可求得的值.
由分布列的性质和期望公式可得,解得,
因此,.
故答案为:.
16.(1)甲同学“破百”的概率为,乙同学“破百”的概率为,丙同学“破百”的概率为
(2)分布列见解析;期望为
(1)利用古典概型的概率公式直接计算得解;
(2)写出的可能取值,计算对应的概率,根据期望公式求解即可.
(1)甲同学“破百”的概率为,
乙同学“破百”的概率为,
丙同学“破百”的概率为.
(2)的可能取值为0,1,2,3,则:
,
,
,
,
所以的分布列为
0 1 2 3
所以,期望.
17.(1)
(2)(ⅰ)分布列见解析, (ⅱ)3
(1)根据古典概型计算公式,结合频率分布直方图进行求解即可;
(2)(ⅰ)根据古典概型计算公式,结合数学期望公式进行求解即可;
(ⅱ)根据频率分布直方图,通过计算平均数进行判断即可.
(1)由频率分布直方图可知,每名顾客获得抽奖资格的概率为.
参与抽奖的顾客获得10元购物券的概率为,
则每名顾客获得10元购物券的概率,
则这2名顾客中恰有1人获得10元购物券的概率.
(2)(ⅰ)的所有可能取值为0,1,2,
,,,
则的分布列为
0 1 2
则的数学期望.
(ⅱ)由频率分布直方图可知,顾客消费金额的平均值(元),
则1000名顾客的消费总金额为(元).
设每1000名顾客最多送出部手机,
则,
又,所以,故每1000名顾客最多送出3部手机.
18.(1),;
(2),.
(1)由随机变量分布列的性质和联立方程,解出即可;
(2)由事件:,可得,又事件:为偶数,得,再根据条件概率可求得的值.
(1)由随机变量分布列的性质,
有, 得,即,
又
,
解得,.
(2)由事件:,
得,
又事件:为偶数,得,
所以,解得.
由(1)知,所以.
所以,.
19.(1)
(2)分布答案见解析,
(3)
(1)由表格中的数据,结合对立事件的概率公式,即可求解;
(2)根据题意,得到随机变量的可能值为,结合独立重复试验的概率计算公式,求得相应的概率,列出分布列,利用期望公式,即可求解;
(3)分别求得购进350千克和400千克时利润的期望值,列出不等式,求得,再由且,得到,即可求解.
(1)解:由表格中的数据,可得1天下午6点前的销售量不小于350千克的概率为.
(2)解:依题意,1天下午6点前的销售量不少于350千克的概率,
随机变量的可能值为,
可得,
所以随机变量的分布为:
0 1 2
所以的数学期望.
(3)解:购进350千克时利润的期望值:,
购进400千克时利润的期望值:,
由,解得,
因为且,因此,
所以的最小值是.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.3.1 离散型随机变量的均值 同步巩固练
2024-2025学年数学人教A版(2019) 选择性必修第三册
一、单选题
1.已知随机变量服从两点分布,,则其成功概率为( )
A.0.3 B.0.4 C.0.5 D.0.6
2.已知离散型随机变量X的分布列如下表:
X 0 1 2
P 0.64 q2 1-2q
则E(X)=( )
A.0.56 B.0.64 C.0.72 D.0.8
3.设为正实数,若随机变量的分布列为,则( )
A.3 B.1 C. D.
4.设随机变量的分布列为:
0 1 2
P
则的数学期望的最小值是( )
A. B.0 C.2 D.随p的变化而变化
5.设随机变量X的分布列如下表所示,且,则等于( )
X 0 1 2 3
P 0.1 a b 0.1
A. B. C. D.
6.某篮球运动员一次投篮得分的分布列为:
若他在一次投篮中得分的期望,则的最大值为( )
A. B. C. D.
7.已知随机变量X的分布列为
X 1 2 3
P
且,若,则等于( )
A. B. C. D.
8.已知随机变量的分布列是,则( )
1 2 3
A. B. C. D.
9.设的分布列如表所示,又设,则等于( )
1 2 3 4
A. B. C. D.
10.将个球(形状相同,编号不同)随机地投入编号为、、、的个盒子,以表示其中至少有一个球的盒子的最小号码(表示第号,第号盒子是空的,第个盒子至少个球),则、分别等于( )
A.、 B.、 C.、 D.、
二、填空题
11.已知随机变量X的取值为0,1,若,则X的均值为 .
12.已知,则 .
13.已知随机变量服从两点分布,且,设,那么 .
14.已知随机变量的分布为,且,若,则实数 .
15.已知随机变量的分布列如下表所示,若,则 .
三、解答题
16.某校高三年级嘟嘟老师准备利用高中数学知识对甲、乙、丙三名学生在即将到来的全省适应性考试成绩进行预测,为此,他收集了三位同学近三个月的数学月考、周测成绩(满分150分),若考试成绩超过100分则称为“破百”.
甲:74,85,81,90,103,89,92,97,109,95;
乙:95,92,97,99,89,103,105,108,101,113;
丙:92,102,97,105,89,94,92,97.
假设用频率估计概率,且甲、乙、丙三名同学的考试成绩相互独立.
(1)分别估计甲、乙、丙三名同学“破百”的概率;
(2)设这甲、乙、丙三名同学在这次决赛上“破百”的人数为,求的分布列和数学期望.
17.2023年国庆节假期期间,某超市举行了购物抽奖赢手机活动.活动规则如下:在2023年9月29日到2023年10月6日期间,消费金额(单位:元)不低于100元的顾客可以参与一次活动(假设每名顾客只消费一次),每5人一组,每人可以随机选取A或B两个字母,其中选取相同字母的人数较少者每人获得10元购物券,其他人获得抽取价值6999元手机的资格(例如5人中有2人选取A,则这2人每人获得10元购物券,另外3人获得抽取手机的资格;5人全部选取A,则这5人均获得抽取手机的资格),根据统计,在此活动期间,顾客在该超市消费金额的频率分布直方图如图所示.
(1)从活动期间在该超市购物的顾客中随机选取2名,求这2名顾客中恰有1人获得10元购物券的概率
(2)设每5人组获得购物券的人数为X.
(ⅰ)求X的分布列与数学期望:
(ⅰⅰ)若超市计划投入的活动经费(购买手机的费用与发放的购物券金额总和)不超过顾客消费总金额的10%,则每1000名顾客最多送出多少部手机?(同一组中的数据用该组区间的中点值为代表)
18.已知随机变量的分布列为:
5 6 7 8 9
0.1 0.2 0.3
(1)若,求、的值;
(2)记事件:;事件:为偶数.已知,求,的值.
19.某超市每天以4元/千克购进某种有机蔬菜,然后以7元/千克出售.若每天下午6点以前所购进的有机蔬菜没有全部销售完,则对未售出的有机蔬菜降价处理,以2元/千克出售,并且降价后能够把剩余所有的有机蔬菜全部处理完毕,且当天不再进货.该超市整理了过去两个月(按60天计算)每天下午6点前这种有机蔬菜的日销售量(单位:千克),得到如下统计数据.(注:视频率为概率,).
每天下午6点前的销售量/千克 250 300 350 400 450
天数 10 10 5
(1)求1天下午6点前的销售量不少于350千克的概率;
(2)在接下来的2天中,设为下午6点前的销售量不少于350千克的天数,求的分布列和数学期望;
(3)若该超市以当天的利润期望值为决策依据,当购进350千克的期望值比购进400千克的期望值大时,求的最小值.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C A A D A C D B
1.D
根据两点分布的期望即可求解.
随机变量服从两点分布,设成功的概率为,
.
故选:D.
2.A
由概率之和为1可求出的值,再根据分布列直接计算均值..
由题可得,解得或,
当时,,不符合题意,舍去,
;
所以可得分布列为
X 0 1 2
P 0.64 0.16 0.2
,
故选:A.
3.C
先由概率和为1,求出a,再求.
因为随机变量的分布列为,
所以,解得:a=3.
所以.
故选:C
4.A
根据分布列和概率的性质求出p的范围,再求数学期望关于p的函数即可求其最小值.
由分布列的性质得,解得,
,
∴的最小值为.
故选:A.
5.A
根数学期望的公式,结合概率的性质求解即可
由分布列的性质可得,,即①,
,
,即②,
联立①②解得,,
故.
故选:A.
6.D
根据离散型随机变量数学期望求解公式可得,利用基本不等式可求得结果.
由题意得:,
(当且仅当时取等号),.
即的最大值为.
故选:D.
7.A
结合题意,先计算出,再表示,建立等式,解出即可.
结合题意:,
因为,所以,解得:,
故选:A.
8.C
根据分布列的性质求出,即可求出,再根据期望的性质计算可得;
解:依题意可得,解得,
所以,
所以;
故选:C
9.D
根据分布列求出,再根据期望的性质计算可得.
解:依题意可得,
所以.
故选:D.
10.B
由题意可知,随机变量的可能取值有、、、,计算出随机变量在不同取值下的概率,可求得,利用数学期望的性质可求得.
由题意可知,随机变量的可能取值有、、、,
,,
,,
所以,,
因此,.
故选:B.
方法点睛:求随机变量的期望和方差的基本方法如下:
(1)已知随机变量的分布列,直接利用期望和方差公式直接求解;
(2)已知随机变量的期望、方差,求的期望与方差,利用期望和方差的性质(,)进行计算;
(3)若能分析出所给的随机变量服从常用的分布(如:两点分布、二项分布等),可直接利用常用分布列的期望和方差公式进行计算.
11./
X服从两点分布,结合两点分布的均值公式,即可求解.
由题意可得,X服从两点分布,
,
故.
故答案为:.
12.
直接根据均值公式结合已知条件,解方程即可得出所求的答案.
由,可得.
故答案为:
13.
先求出,再由随机变量的线性关系的期望性质,即可求解.
,
故答案为:
本题考查两点分布的期望和期望的性质,属于基础题.
14.
由期望性质可得答案.
因,则.
又,则.
故选:.
15./
利用分布列的性质结合期望公式可得出关于、的方程组,解出这两个量的值,结合表格可求得的值.
由分布列的性质和期望公式可得,解得,
因此,.
故答案为:.
16.(1)甲同学“破百”的概率为,乙同学“破百”的概率为,丙同学“破百”的概率为
(2)分布列见解析;期望为
(1)利用古典概型的概率公式直接计算得解;
(2)写出的可能取值,计算对应的概率,根据期望公式求解即可.
(1)甲同学“破百”的概率为,
乙同学“破百”的概率为,
丙同学“破百”的概率为.
(2)的可能取值为0,1,2,3,则:
,
,
,
,
所以的分布列为
0 1 2 3
所以,期望.
17.(1)
(2)(ⅰ)分布列见解析, (ⅱ)3
(1)根据古典概型计算公式,结合频率分布直方图进行求解即可;
(2)(ⅰ)根据古典概型计算公式,结合数学期望公式进行求解即可;
(ⅱ)根据频率分布直方图,通过计算平均数进行判断即可.
(1)由频率分布直方图可知,每名顾客获得抽奖资格的概率为.
参与抽奖的顾客获得10元购物券的概率为,
则每名顾客获得10元购物券的概率,
则这2名顾客中恰有1人获得10元购物券的概率.
(2)(ⅰ)的所有可能取值为0,1,2,
,,,
则的分布列为
0 1 2
则的数学期望.
(ⅱ)由频率分布直方图可知,顾客消费金额的平均值(元),
则1000名顾客的消费总金额为(元).
设每1000名顾客最多送出部手机,
则,
又,所以,故每1000名顾客最多送出3部手机.
18.(1),;
(2),.
(1)由随机变量分布列的性质和联立方程,解出即可;
(2)由事件:,可得,又事件:为偶数,得,再根据条件概率可求得的值.
(1)由随机变量分布列的性质,
有, 得,即,
又
,
解得,.
(2)由事件:,
得,
又事件:为偶数,得,
所以,解得.
由(1)知,所以.
所以,.
19.(1)
(2)分布答案见解析,
(3)
(1)由表格中的数据,结合对立事件的概率公式,即可求解;
(2)根据题意,得到随机变量的可能值为,结合独立重复试验的概率计算公式,求得相应的概率,列出分布列,利用期望公式,即可求解;
(3)分别求得购进350千克和400千克时利润的期望值,列出不等式,求得,再由且,得到,即可求解.
(1)解:由表格中的数据,可得1天下午6点前的销售量不小于350千克的概率为.
(2)解:依题意,1天下午6点前的销售量不少于350千克的概率,
随机变量的可能值为,
可得,
所以随机变量的分布为:
0 1 2
所以的数学期望.
(3)解:购进350千克时利润的期望值:,
购进400千克时利润的期望值:,
由,解得,
因为且,因此,
所以的最小值是.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
