【期中押题卷】湖南省长沙市2024-2025学年五年级下学期期中综合测试数学试卷人教版(含解析)
文档属性
| 名称 | 【期中押题卷】湖南省长沙市2024-2025学年五年级下学期期中综合测试数学试卷人教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 530.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湖南省长沙市2024-2025学年五年级下学期期中综合测试数学试卷
一.填空题(共8小题,满分22分)
1.(2分)(2023春 临平区期中)36的因数有 ,50以内的9的倍数有 。
2.(2分)5、10、15、20,……这样数数,数出来都是 的倍数,第14个数是 。
3.(1分)(2021春 清河县期末)把一根长36厘米的长方体木料平均锯成6段,表面积比原来增加了125平方厘米,则这根木料原来的体积是 立方厘米。
4.(3分)(2023春 淮安期末)1÷ = ÷32= (填小数)
5.(4分)(2022秋 杜尔伯特县期末)4÷5 填小数。
6.(4分)(2021 梁山县)
①3时40分= 时 ②4.05m2= dm2
③6.03公顷= 平方米 ④7吨70千克= 吨
7.(4分)(2022春 电白区期末)把、0.06、、0.65按照从大到小的顺序排列:
> > > 。
8.(2分)(2022春 石景山区期末)如图是一个正方体的平面展开图,与A面相对的是 面,与C面相对的是 面。
二.选择题(共8小题,满分8分,每小题1分)
9.(1分)(2023 宝安区)下列说法错误的是( )
A.把2769020000四舍五入到亿位约是28亿
B.三个连续奇数的和是141,这三个数的平均数是47
C.一个正方体的棱长扩大到原来的2倍,它的表面积会扩大到原来的4倍,体积会扩大到原来的8倍
D.一个两位数的偶数,它既是3的倍数,又是5的倍数,这个数最小是15
10.(1分)(2022春 金湾区期末)26□既是2的倍数,又是3的倍数,□里可以填( )
A.0 B.1 C.2 D.4
11.(1分)(2022 南京模拟)著名的“哥德巴赫猜想”被喻为“数学皇冠上的明珠”,猜想认为:任何大于2的偶数都是两个质数之和。下列4个算式中,符合这个猜想的是( )
A.32=13+19 B.13=2+11 C.16=7+9 D.4=1+3
12.(1分)(2023 兴庆区)用一根长52cm的铁丝围成一个长方体,它的长是6cm,宽是4cm,高是( )
A.5cm B.4cm C.3cm D.7cm
13.(1分)(2024秋 南陵县期末)黄河被称为“中华母亲河”,黄河全长5400多( )
A.米 B.分米 C.千米
14.(1分)(2023春 靖远县期中)一个长7dm,宽6dm,高4dm的长方体纸箱,最多能放( )个棱长2dm的正方体。
A.18 B.24 C.21
15.(1分)(2023秋 湘西州期末)元旦节当天,老师拿出6颗幸运星,奖给小云3颗,奖给小花3颗,小云的幸运星占6颗幸运星的______。小云有8支水彩笔,其中有3支是黄色的,2支是红色的、3支是绿色的,红色的水彩笔占8支水彩笔的______,你的选择是( )
A. B. C. D.
16.(1分)(2023春 广州期末)把 约分得到最简分数后,下面说法正确的是( )
A.分数单位变小了 B.分数单位的个数增加
C.分数的大小不变
三.判断题(共5小题,满分5分,每小题1分)
17.(1分)(2024 埇桥区)因为,所以的分数单位大于的分数单位。
18.(1分)(2022春 昌黎县期末)把的分子加上5,要使分数的大小不变,分母要乘2。
19.(1分)(2021秋 郴州月考)36和48的最小公倍数是96。
20.(1分)(2022秋 岑溪市校级期中)用两个完全一样的正方形拼成一个长方形,长方形的周长是正方形周长的2倍。
21.(1分)(2023秋 天门期末)把一袋苹果分成6份,其中的2份是。
四.解答题(共3小题,满分22分)
22.(6分)(2022春 陇县期末)只列式,不计算。
分母是8的最简真分数的和是多少?
列式: 。
23.(4分)(2021春 张家川县期末)把下面各组中的两个分数先通分,再比较大小。
(1)和 (2)和
24.(12分)(2021秋 吉林期末)求出下列每组数的最大公因数和最小公倍数。
①3和22
②17和51
五.解答题(共1小题,满分6分,每小题6分)
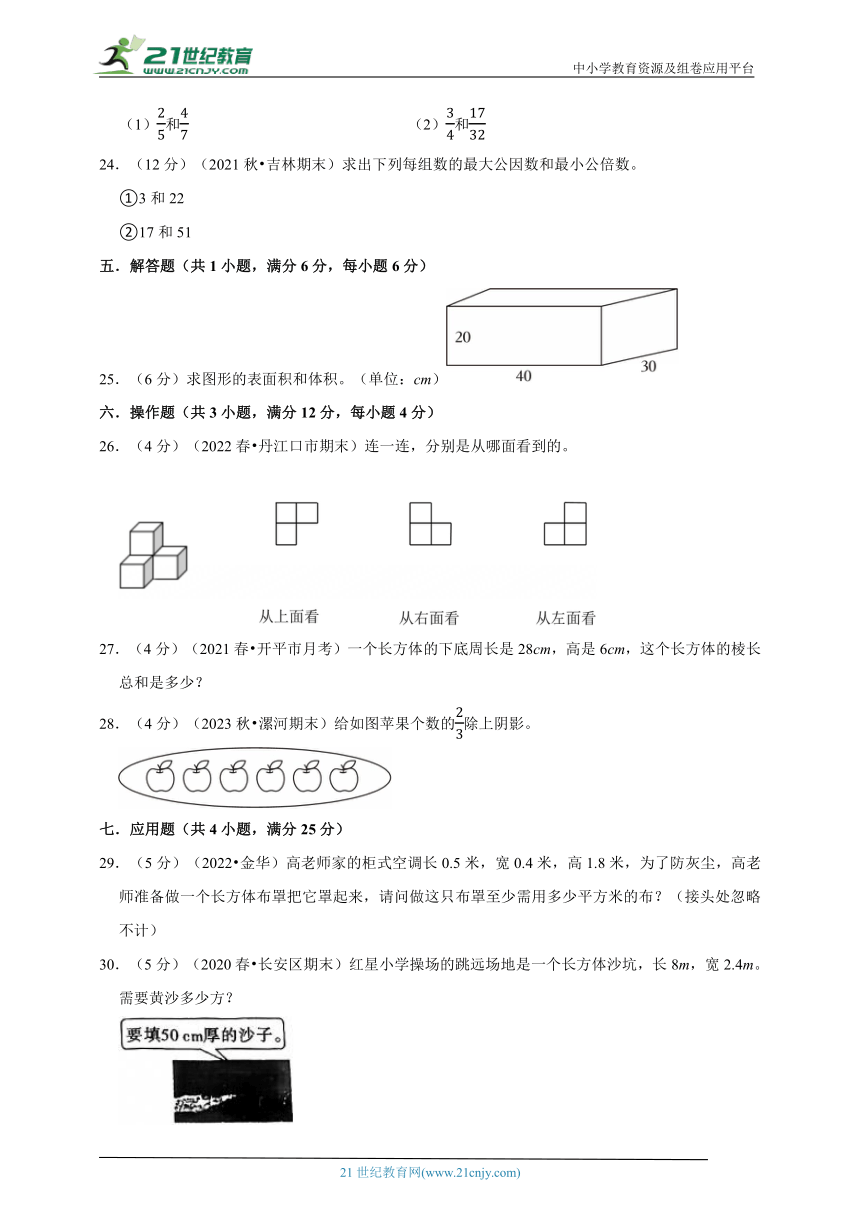
25.(6分)求图形的表面积和体积。(单位:cm)
六.操作题(共3小题,满分12分,每小题4分)
26.(4分)(2022春 丹江口市期末)连一连,分别是从哪面看到的。
27.(4分)(2021春 开平市月考)一个长方体的下底周长是28cm,高是6cm,这个长方体的棱长总和是多少?
28.(4分)(2023秋 漯河期末)给如图苹果个数的除上阴影。
七.应用题(共4小题,满分25分)
29.(5分)(2022 金华)高老师家的柜式空调长0.5米,宽0.4米,高1.8米,为了防灰尘,高老师准备做一个长方体布罩把它罩起来,请问做这只布罩至少需用多少平方米的布?(接头处忽略不计)
30.(5分)(2020春 长安区期末)红星小学操场的跳远场地是一个长方体沙坑,长8m,宽2.4m。需要黄沙多少方?
31.(5分)(2024春 上思县期中)一种长方形木块的长是12厘米,宽是10厘米,用这种木块铺成一个正方形(不允许切割),这个正方形的边长最少是多少厘米?至少要用多少块这样的木块?
32.(10分)一个长方体玻璃鱼缸,底面长50cm,宽40cm,高30cm。
(1)在鱼缸里注入40L水,水深多少厘米?
(2)再往鱼缸里放入鹅卵石、水草和鱼,水面上升了2.5cm,这些鹅卵石、水草和鱼的体积一共是多少立方厘米?
湖南省长沙市2024-2025学年五年级下学期期中综合测试数学试卷
参考答案与试题解析
一.填空题(共8小题,满分22分)
1.(2分)(2023春 临平区期中)36的因数有 1、2、3、4、6、9、12、18、36 ,50以内的9的倍数有 9、18、27、36、45 。
【考点】找一个数的因数的方法;找一个数的倍数的方法.
【专题】数的整除;数感.
【答案】1、2、3、4、6、9、12、18、36;9、18、27、36、45。
【分析】根据找一个数因数的方法,进行列举即可;
根据找一个数倍数的方法,用这个数分别乘自然数1、2、3、4……从中找出符合要求的倍数,进行列举即可。
【解答】解:36的因数有:1、2、3、4、6、9、12、18、36;
50以内9的倍数有:9、18、27、36、45。
故答案为:1、2、3、4、6、9、12、18、36;9、18、27、36、45。
【点评】解答此题应根据找一个数因数和倍数的方法进行解答。
2.(2分)5、10、15、20,……这样数数,数出来都是 5 的倍数,第14个数是 70 。
【考点】5的倍数特征;找一个数的倍数的方法;2的倍数特征.
【专题】数感.
【答案】5;70。
【分析】根据5的倍数特征,个位上是0或5的数都是5的倍数,所以五个五个地数数,数出来的数都是5的倍数;
第14个数就是(14×5),据此解答。
【解答】解:14×5=70
所以这样数数,数出来的数都是5的倍数,第14个数是70。
故答案为:5;70。
【点评】此题考查的目的是理解掌握整数的认识,以及5的倍数的特征及应用。
3.(1分)(2021春 清河县期末)把一根长36厘米的长方体木料平均锯成6段,表面积比原来增加了125平方厘米,则这根木料原来的体积是 450 立方厘米。
【考点】长方体和正方体的表面积;长方体和正方体的体积.
【专题】空间观念;推理能力;应用意识.
【答案】450。
【分析】根据题意可知,把这根长方体木料平均锯成6段,表面积比原来增加了125平方厘米,表面积增加的是10截面的面积,据此可以求出长方体的底面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【解答】解:125÷10×36
=12.5×36
=450(立方厘米)
答:这根木料原来的体积是450立方厘米。
故答案为:450。
【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式,重点是求出长方体的底面积。
4.(3分)(2023春 淮安期末)1÷ 8 = 4 ÷32= 0.125 (填小数)
【考点】小数与分数的互化.
【专题】小数的认识;分数和百分数;数感.
【答案】见试题解答内容
【分析】解答此题的关键是,写成除法算式是1÷8,根据商不变的性质,被除数和除数同时乘4可得:1÷8=4÷32;计算出结果是小数为1÷8=0.125,据此即可填空。
【解答】解:1÷8=4÷32=0.125(填小数)
故答案为:8,4,0.125。
【点评】此题考查运用小数、分数、除法之间的关系和性质解决问题。
5.(4分)(2022秋 杜尔伯特县期末)4÷5 0.8 填小数。
【考点】分数的基本性质;小数与分数的互化.
【专题】运算能力.
【答案】25,3.2,10,0.8。
【分析】解答此题的突破口是4÷5,根据分数与除法的关系,4÷5,根据分数的基本性质,分子、分母都乘2就是;分子、分母都乘5就是,分子、分母都除以1.25就是,4÷5=0.8.由此进行转化并填空。
【解答】解:4÷50.8
故答案为:25,3.2,10,0.8。
【点评】此题主要是考查除式、小数、分数之间的关系及转化,利用它们之间的关系和性质进行转化即可。
6.(4分)(2021 梁山县)
①3时40分= 时 ②4.05m2= 405 dm2
③6.03公顷= 60300 平方米 ④7吨70千克= 7.07 吨
【考点】时、分、秒及其关系、单位换算与计算;小面积单位间的进率及单位换算;大面积单位间的进率及单位换算;质量的单位换算.
【专题】推理能力.
【答案】①;
②405;
③60300;
④7.07。
【分析】①根据时间单位间的换算关系:1时=60分;
②③面积单位间的换算关系:1平方米=100平方分米;1公顷=10000平方米;
④质量单位间的换算关系:1吨=1000千克。
换算即可。
【解答】解:
①3时40分时 ②4.05m2=405dm2
③6.03公顷=60300平方米 ④7吨70千克=7.07吨
故答案为:;405;60300;7.07。
【点评】本题主要考查质量单位、时间单位及面积单位间的换算关系。
7.(4分)(2022春 电白区期末)把、0.06、、0.65按照从大到小的顺序排列:
0.65 > > > 0.06 。
【考点】小数与分数的互化;小数大小的比较.
【专题】数感;运算能力.
【答案】0.65,,,0.06。
【分析】把,化成小数,再根据小数大小比较的方法进行比较解答。
【解答】解:0.429
0.625
因为0.65>0.625>0.429>0.06,所以把、0.06、、0.65按照从大到小的顺序排列是:0.650.06。
故答案为:0.65,,,0.06。
【点评】在分数、小数进行大小比较时,一般要把分数化成小数再比较大小,除不尽的保留三位小数。
8.(2分)(2022春 石景山区期末)如图是一个正方体的平面展开图,与A面相对的是 D 面,与C面相对的是 E 面。
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】D,E。
【分析】根据正方体展开图的11种特征,此图属于正方体展开图的“1﹣3﹣2”型,折成正方体后,字母A与D相对,B与F相对,C与E相对。
【解答】解:如图:
是一个正方体的平面展开图,与A面相对的是D面,与C面相对的是E面。
故答案为:D,E。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住规律,能快速解答此类题。
二.选择题(共8小题,满分8分,每小题1分)
9.(1分)(2023 宝安区)下列说法错误的是( )
A.把2769020000四舍五入到亿位约是28亿
B.三个连续奇数的和是141,这三个数的平均数是47
C.一个正方体的棱长扩大到原来的2倍,它的表面积会扩大到原来的4倍,体积会扩大到原来的8倍
D.一个两位数的偶数,它既是3的倍数,又是5的倍数,这个数最小是15
【考点】奇数与偶数的初步认识;2、3、5的倍数特征;长方体和正方体的表面积;长方体和正方体的体积;平均数的含义及求平均数的方法;亿以上数的改写与近似.
【专题】数感.
【答案】D
【分析】根据大数的改写、平均数、奇数和偶数、正方体的认识、倍数知识等,结合题意分析解答即可。
【解答】解:A.把2769020000四舍五入到亿位约是28亿,本选项说法正确;
B.三个连续奇数的和是141,这三个数的平均数是47,本选项说法正确;
C.一个正方体的棱长扩大到原来的2倍,它的表面积会扩大到原来的4倍,体积会扩大到原来的8倍,本选项说法正确;
D.一个两位数的偶数,它既是3的倍数,又是5的倍数,这个数最小是30,所以本选项说法错误。
故选:D。
【点评】本题考查了大数的改写、平均数、奇数和偶数、正方体的认识、倍数知识等,结合题意分析解答即可。
10.(1分)(2022春 金湾区期末)26□既是2的倍数,又是3的倍数,□里可以填( )
A.0 B.1 C.2 D.4
【考点】2、3、5的倍数特征.
【专题】数感.
【答案】D
【分析】根据2、3的倍数的特征,个位上是0、2、4、6、8的数都是2的倍数;一个数各位上的数字之和是3的倍数,这个数有多少3的倍数,同时是2和3的倍数的数,个位上是偶数且各位上的数字之和是3的倍数。据此解答。
【解答】解:2+6=8,8至少加上1是3的倍数,如果个位上是1就不是2的倍数,所以□里只能填4。
故选:D。
【点评】此题考查的目的是理解掌握2、3的倍数的特征及应用。
11.(1分)(2022 南京模拟)著名的“哥德巴赫猜想”被喻为“数学皇冠上的明珠”,猜想认为:任何大于2的偶数都是两个质数之和。下列4个算式中,符合这个猜想的是( )
A.32=13+19 B.13=2+11 C.16=7+9 D.4=1+3
【考点】合数与质数的初步认识;奇数与偶数的初步认识.
【专题】数感.
【答案】A
【分析】根据质数的含义:除了1和它本身没有其它因数的数,叫做质数,自然数中是2的倍数的数是偶数;由此根据题目要求找出大于2的偶数并且都是两个质数之和即可。
【解答】解:在32=13+19,13=2+11,16=7+9,4=1+3中,32=13+19符合这个猜想;
故选:A。
【点评】解决本题主要根据猜想按要求写数,要注意写出的两个数都要是质数。
12.(1分)(2023 兴庆区)用一根长52cm的铁丝围成一个长方体,它的长是6cm,宽是4cm,高是( )
A.5cm B.4cm C.3cm D.7cm
【考点】长方体的特征.
【专题】应用意识.
【答案】C
【分析】已知用一根铁丝围成一个长方体,那么长方体的棱长总和等于这根铁丝的长度。
根据长方体的棱长总和=(长+宽+高)×4可知,长方体的高=棱长总和÷4﹣长﹣宽,代入数据计算即可求解。
【解答】解:52÷4﹣6﹣4
=13﹣6﹣4
=3(cm)
高是3cm。
故选:C。
【点评】本题考查长方体棱长总和公式的灵活运用。
13.(1分)(2024秋 南陵县期末)黄河被称为“中华母亲河”,黄河全长5400多( )
A.米 B.分米 C.千米
【考点】根据情景选择合适的计量单位.
【专题】长度、面积、体积单位;应用意识.
【答案】C
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解答】解:黄河被称为“中华母亲河”,黄河全长5400多千米。
故选:C。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
14.(1分)(2023春 靖远县期中)一个长7dm,宽6dm,高4dm的长方体纸箱,最多能放( )个棱长2dm的正方体。
A.18 B.24 C.21
【考点】长方体和正方体的体积.
【专题】综合填空题;立体图形的认识与计算;几何直观.
【答案】A
【分析】以长为边,最多能装7÷2≈3(块),以宽为边,最多能装6÷2=3(块),以高为边,最多能装4÷2=2(块),再把每条棱上放的块数相乘即可计算。
【解答】解:7÷2≈3(块)
6÷2=3(块)
4÷2=2(块)所以最多能装:3×3×2=18(块)
答:最多能装18块。
故选:A。
【点评】此类问题,先求出每条棱长上最多能装下的木块的个数,再把每条棱上放的块数相乘即可计算出最多能装下的块数。
15.(1分)(2023秋 湘西州期末)元旦节当天,老师拿出6颗幸运星,奖给小云3颗,奖给小花3颗,小云的幸运星占6颗幸运星的______。小云有8支水彩笔,其中有3支是黄色的,2支是红色的、3支是绿色的,红色的水彩笔占8支水彩笔的______,你的选择是( )
A. B. C. D.
【考点】分数与除法的关系.
【专题】分数和百分数;数据分析观念.
【答案】C
【分析】利用小云的颗数除以6即可,利用红色的数量除以8即可。注意分数要约分。
【解答】解:3÷6
2
答:小云的幸运星占6颗幸运星的,红色的水彩笔占8支水彩笔的。
故选:C。
【点评】本题考查了一个数占另一个数的几分之几的问题应用。
16.(1分)(2023春 广州期末)把 约分得到最简分数后,下面说法正确的是( )
A.分数单位变小了 B.分数单位的个数增加
C.分数的大小不变
【考点】最简分数;约分.
【专题】整数的认识;分数和百分数;数感.
【答案】C
【分析】约分后得到最简分数是,分数单位变大了,没有增加分数单位的个数,分数大小没有改变。
【解答】解:,
化成最简分数后分数单位是,分数大小不变。
故选:C。
【点评】掌握分数约分的意义是解题关键。
三.判断题(共5小题,满分5分,每小题1分)
17.(1分)(2024 埇桥区)因为,所以的分数单位大于的分数单位。 ×
【考点】分数大小的比较.
【专题】综合判断题;数据分析观念.
【答案】×
【分析】分数单位是把单位“1”平均分成若干份,表示其中的一份的数。
【解答】解:的分数单位是,的分数单位是,;故原题说法错误。
故答案为:×。
【点评】此题考查了分数单位的知识,要求学生掌握。
18.(1分)(2022春 昌黎县期末)把的分子加上5,要使分数的大小不变,分母要乘2。 √
【考点】分数的基本性质.
【专题】分数和百分数;数据分析观念.
【答案】√
【分析】分子加上5后是原来的几倍,根据分数的基本性质,那么分母也是原来的几倍,分数的大小才不变。
【解答】解:分子:5+5=10,10÷5=2,要想分数的大小不变,那么分母也要扩大到原来的2倍,分母乘2,原题说法正确。
故答案为:√。
【点评】本题主要考查分数的基本性质,根据这一性质解答即可。
19.(1分)(2021秋 郴州月考)36和48的最小公倍数是96。 × (判断题)
【考点】求几个数的最小公倍数的方法.
【专题】数据分析观念.
【答案】×
【分析】求几个数的最小公倍数的方法:这几个数的公有的因数和它们独有的质因数的连乘积就是它们的最小公倍数,由此可以解得。
【解答】解:36=2×2×3×3
48=2×2×2×2×3
所以36和48的最小公倍数是2×2×2×2×3×3=144,所以原题计算错误。
故答案为:×。
【点评】此题考查了求几个数的最小公倍数的方法,由此可以解决。
20.(1分)(2022秋 岑溪市校级期中)用两个完全一样的正方形拼成一个长方形,长方形的周长是正方形周长的2倍。 ×
【考点】图形的拼组.
【专题】应用意识.
【答案】×
【分析】根据题意可知,用两个完全一样的正方形拼成一个长方形,拼成后长方形的周长比两个正方形的周长之和少了2个正方形的边长;据此解答。
【解答】解:如图:
用两个完全一样的正方形拼成一个长方形,拼成的长方形的周长比原来两个正方形的周长之和减少了2个正方形的边长,所以原题的说法错误。
故答案为:×。
【点评】本题考查了学生对拼组后图形周长的计算方法的掌握情况,注意拼组后图形的周长不是两个正方形周长的和。
21.(1分)(2023秋 天门期末)把一袋苹果分成6份,其中的2份是。 ×
【考点】分数的意义和读写.
【专题】数感.
【答案】×
【分析】把一袋苹果看作一个整体,把它平均分成6份,每份是它的,其中2份是。
【解答】解:把一袋苹果平均分成6份,其中的2份是。
这里没说平均分,说法错误。
故答案为:×。
【点评】此题是考查分数的意义。把一个整体平均分成若干份,用分数表示,分母是平均分成的份数,分子是要表示的份数。
四.解答题(共3小题,满分22分)
22.(6分)(2022春 陇县期末)只列式,不计算。
分母是8的最简真分数的和是多少?
列式: 2 。
【考点】最简分数.
【专题】运算能力.
【答案】2。
【分析】分母是8的最简真分数有:、、、,求出它们的和即可。
【解答】解:
=()+()
=1+1
=2
故答案为:2。
【点评】本题考查了分数加法,解答本题需理解最简真分数的意义:①分子小于分母,②分子和分母是互质数。
23.(4分)(2021春 张家川县期末)把下面各组中的两个分数先通分,再比较大小。
(1)和 (2)和
【考点】通分;分数大小的比较.
【专题】运算能力.
【答案】(1)<;(2)>。
【分析】把异分母分数分别化成和原来分数相等的同分母分数,叫做通分,用分母的最小公倍数作为公分母,通分后再根据分母相同的分数比较大小的方法进行比较即可。
【解答】解:(1)因为,
所以
(2)因为
所以
【点评】熟练掌握通分的方法以及同分母分数比较大小的方法是解题的关键。
24.(12分)(2021秋 吉林期末)求出下列每组数的最大公因数和最小公倍数。
①3和22
②17和51
【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【专题】推理能力.
【答案】①1,66;②17,51。
【分析】两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积;两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数。
【解答】解:①因为3和22互质,所以3和22的最大公因数是1,最小公倍数是3×22=66;
②因为51÷17=3,所以17和51的最大公因数是17,最小公倍数是51。
【点评】熟练掌握两个数互质、两个数为倍数关系的最大公因数和最小公倍数的求法是解题的关键。
五.解答题(共1小题,满分6分,每小题6分)
25.(6分)求图形的表面积和体积。(单位:cm)
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】空间观念;应用意识.
【答案】5200平方厘米,24000立方厘米。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:(40×30+40×20+30×20)×2
=(1200+800+600)×2
=2600×2
=5200(平方厘米)
40×30×20
=1200×20
=24000(立方厘米)
答:它的表面积是5200平方厘米,体积是24000立方厘米。
【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
六.操作题(共3小题,满分12分,每小题4分)
26.(4分)(2022春 丹江口市期末)连一连,分别是从哪面看到的。
【考点】从不同方向观察物体和几何体.
【专题】空间观念;几何直观.
【答案】
【分析】根据观察几何体,可知上面图形为,右面图形为,左面图形为。
【解答】解:如图:
【点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
27.(4分)(2021春 开平市月考)一个长方体的下底周长是28cm,高是6cm,这个长方体的棱长总和是多少?
【考点】长方体的特征.
【专题】运算能力;应用意识.
【答案】80cm。
【分析】已知长方体的底面周长是28厘米的正方形,高4厘米,由此可知长方体的4个侧面是完全相同的长方形,这个长方体的棱长总和是(28×2+6×4)厘米。
【解答】解:28×2+6×4
=56+24
=80(cm)
答:这个长方体的棱长总和是80cm。
【点评】此题主要考查长方体的棱长总和的计算。
28.(4分)(2023秋 漯河期末)给如图苹果个数的除上阴影。
【考点】分数的意义和读写.
【专题】作图题;几何直观.
【答案】
【分析】把整个图形看作单位“1”,平均分成了3份,阴影部分占3份,用分数表示是;涂色2份即可解答。
【解答】解:
【点评】此题考查了分数的意义,要求学生掌握。
七.应用题(共4小题,满分25分)
29.(5分)(2022 金华)高老师家的柜式空调长0.5米,宽0.4米,高1.8米,为了防灰尘,高老师准备做一个长方体布罩把它罩起来,请问做这只布罩至少需用多少平方米的布?(接头处忽略不计)
【考点】长方体、正方体表面积与体积计算的应用.
【专题】应用意识.
【答案】3.44平方米。
【分析】这个长方体布罩应该没有下面,所以只需要计算上、左右、前后,五个面的面积。
【解答】解:0.5×0.4+0.5×1.8×2+0.4×1.8×2
=0.2+1.8+1.44
=3.44(平方米)
答:做这只布罩至少需用3.44平方米的布。
【点评】本题解题关键是能够联系生活实际,理解这个长方体布罩应该没有下面,所以只需要计算上、左右、前后,五个面的面积,再根据长方体表面积的计算方法,列式计算。
30.(5分)(2020春 长安区期末)红星小学操场的跳远场地是一个长方体沙坑,长8m,宽2.4m。需要黄沙多少方?
【考点】长方体和正方体的体积.
【专题】空间观念;应用意识.
【答案】9.6方。
【分析】根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:50厘米=0.5米
8×2.4×0.5
=19.2×0.5
=9.6(立方米)
9.6立方米=9.6方
答:需要填黄沙9.6方。
【点评】此题主要考查长方体体积公式的灵活应用,关键是熟记公式。
31.(5分)(2024春 上思县期中)一种长方形木块的长是12厘米,宽是10厘米,用这种木块铺成一个正方形(不允许切割),这个正方形的边长最少是多少厘米?至少要用多少块这样的木块?
【考点】公因数和公倍数应用题.
【专题】约数倍数应用题;应用意识.
【答案】60厘米,30块。
【分析】求出12和10的最小公倍数,再用最小公倍数分别除以12和10,再相乘,即可解答。
【解答】解:12=2×2×3
10=2×5
12和10的最小公倍数是2×2×3×5=60。
(60÷12)×(60÷10)
=5×6
=30(块)
答:这个正方形的边长最少是60厘米,至少要用30块这样的木块。
【点评】本题考查的是求最小公倍数应用题,掌握求最小公倍数的方法是解答关键。
32.(10分)一个长方体玻璃鱼缸,底面长50cm,宽40cm,高30cm。
(1)在鱼缸里注入40L水,水深多少厘米?
(2)再往鱼缸里放入鹅卵石、水草和鱼,水面上升了2.5cm,这些鹅卵石、水草和鱼的体积一共是多少立方厘米?
【考点】长方体和正方体的体积.
【专题】应用题;应用意识.
【答案】(1)20厘米;(2)5000cm3。
【分析】(1)首先求出40L水的体积是40000cm3,再用水的体积除以鱼缸的底面积可得水深;
(2)根据这些鹅卵石、水草和鱼的体积等于上升部分水的体积,结合长方体的体积=长×宽×高计算即可解答。
【解答】解:(1)40L=40000cm3
50×40=2000(平方厘米)
40000÷2000=20(厘米)
答:在鱼缸里注入40L水,水深20厘米。
(2)50×40×2.5=5000(cm3)
答:这些鹅卵石、水草和鱼的体积一共是5000cm3。
【点评】本题考查的是长方体体积计算公式的运用,灵活运用所学的知识是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
湖南省长沙市2024-2025学年五年级下学期期中综合测试数学试卷
一.填空题(共8小题,满分22分)
1.(2分)(2023春 临平区期中)36的因数有 ,50以内的9的倍数有 。
2.(2分)5、10、15、20,……这样数数,数出来都是 的倍数,第14个数是 。
3.(1分)(2021春 清河县期末)把一根长36厘米的长方体木料平均锯成6段,表面积比原来增加了125平方厘米,则这根木料原来的体积是 立方厘米。
4.(3分)(2023春 淮安期末)1÷ = ÷32= (填小数)
5.(4分)(2022秋 杜尔伯特县期末)4÷5 填小数。
6.(4分)(2021 梁山县)
①3时40分= 时 ②4.05m2= dm2
③6.03公顷= 平方米 ④7吨70千克= 吨
7.(4分)(2022春 电白区期末)把、0.06、、0.65按照从大到小的顺序排列:
> > > 。
8.(2分)(2022春 石景山区期末)如图是一个正方体的平面展开图,与A面相对的是 面,与C面相对的是 面。
二.选择题(共8小题,满分8分,每小题1分)
9.(1分)(2023 宝安区)下列说法错误的是( )
A.把2769020000四舍五入到亿位约是28亿
B.三个连续奇数的和是141,这三个数的平均数是47
C.一个正方体的棱长扩大到原来的2倍,它的表面积会扩大到原来的4倍,体积会扩大到原来的8倍
D.一个两位数的偶数,它既是3的倍数,又是5的倍数,这个数最小是15
10.(1分)(2022春 金湾区期末)26□既是2的倍数,又是3的倍数,□里可以填( )
A.0 B.1 C.2 D.4
11.(1分)(2022 南京模拟)著名的“哥德巴赫猜想”被喻为“数学皇冠上的明珠”,猜想认为:任何大于2的偶数都是两个质数之和。下列4个算式中,符合这个猜想的是( )
A.32=13+19 B.13=2+11 C.16=7+9 D.4=1+3
12.(1分)(2023 兴庆区)用一根长52cm的铁丝围成一个长方体,它的长是6cm,宽是4cm,高是( )
A.5cm B.4cm C.3cm D.7cm
13.(1分)(2024秋 南陵县期末)黄河被称为“中华母亲河”,黄河全长5400多( )
A.米 B.分米 C.千米
14.(1分)(2023春 靖远县期中)一个长7dm,宽6dm,高4dm的长方体纸箱,最多能放( )个棱长2dm的正方体。
A.18 B.24 C.21
15.(1分)(2023秋 湘西州期末)元旦节当天,老师拿出6颗幸运星,奖给小云3颗,奖给小花3颗,小云的幸运星占6颗幸运星的______。小云有8支水彩笔,其中有3支是黄色的,2支是红色的、3支是绿色的,红色的水彩笔占8支水彩笔的______,你的选择是( )
A. B. C. D.
16.(1分)(2023春 广州期末)把 约分得到最简分数后,下面说法正确的是( )
A.分数单位变小了 B.分数单位的个数增加
C.分数的大小不变
三.判断题(共5小题,满分5分,每小题1分)
17.(1分)(2024 埇桥区)因为,所以的分数单位大于的分数单位。
18.(1分)(2022春 昌黎县期末)把的分子加上5,要使分数的大小不变,分母要乘2。
19.(1分)(2021秋 郴州月考)36和48的最小公倍数是96。
20.(1分)(2022秋 岑溪市校级期中)用两个完全一样的正方形拼成一个长方形,长方形的周长是正方形周长的2倍。
21.(1分)(2023秋 天门期末)把一袋苹果分成6份,其中的2份是。
四.解答题(共3小题,满分22分)
22.(6分)(2022春 陇县期末)只列式,不计算。
分母是8的最简真分数的和是多少?
列式: 。
23.(4分)(2021春 张家川县期末)把下面各组中的两个分数先通分,再比较大小。
(1)和 (2)和
24.(12分)(2021秋 吉林期末)求出下列每组数的最大公因数和最小公倍数。
①3和22
②17和51
五.解答题(共1小题,满分6分,每小题6分)
25.(6分)求图形的表面积和体积。(单位:cm)
六.操作题(共3小题,满分12分,每小题4分)
26.(4分)(2022春 丹江口市期末)连一连,分别是从哪面看到的。
27.(4分)(2021春 开平市月考)一个长方体的下底周长是28cm,高是6cm,这个长方体的棱长总和是多少?
28.(4分)(2023秋 漯河期末)给如图苹果个数的除上阴影。
七.应用题(共4小题,满分25分)
29.(5分)(2022 金华)高老师家的柜式空调长0.5米,宽0.4米,高1.8米,为了防灰尘,高老师准备做一个长方体布罩把它罩起来,请问做这只布罩至少需用多少平方米的布?(接头处忽略不计)
30.(5分)(2020春 长安区期末)红星小学操场的跳远场地是一个长方体沙坑,长8m,宽2.4m。需要黄沙多少方?
31.(5分)(2024春 上思县期中)一种长方形木块的长是12厘米,宽是10厘米,用这种木块铺成一个正方形(不允许切割),这个正方形的边长最少是多少厘米?至少要用多少块这样的木块?
32.(10分)一个长方体玻璃鱼缸,底面长50cm,宽40cm,高30cm。
(1)在鱼缸里注入40L水,水深多少厘米?
(2)再往鱼缸里放入鹅卵石、水草和鱼,水面上升了2.5cm,这些鹅卵石、水草和鱼的体积一共是多少立方厘米?
湖南省长沙市2024-2025学年五年级下学期期中综合测试数学试卷
参考答案与试题解析
一.填空题(共8小题,满分22分)
1.(2分)(2023春 临平区期中)36的因数有 1、2、3、4、6、9、12、18、36 ,50以内的9的倍数有 9、18、27、36、45 。
【考点】找一个数的因数的方法;找一个数的倍数的方法.
【专题】数的整除;数感.
【答案】1、2、3、4、6、9、12、18、36;9、18、27、36、45。
【分析】根据找一个数因数的方法,进行列举即可;
根据找一个数倍数的方法,用这个数分别乘自然数1、2、3、4……从中找出符合要求的倍数,进行列举即可。
【解答】解:36的因数有:1、2、3、4、6、9、12、18、36;
50以内9的倍数有:9、18、27、36、45。
故答案为:1、2、3、4、6、9、12、18、36;9、18、27、36、45。
【点评】解答此题应根据找一个数因数和倍数的方法进行解答。
2.(2分)5、10、15、20,……这样数数,数出来都是 5 的倍数,第14个数是 70 。
【考点】5的倍数特征;找一个数的倍数的方法;2的倍数特征.
【专题】数感.
【答案】5;70。
【分析】根据5的倍数特征,个位上是0或5的数都是5的倍数,所以五个五个地数数,数出来的数都是5的倍数;
第14个数就是(14×5),据此解答。
【解答】解:14×5=70
所以这样数数,数出来的数都是5的倍数,第14个数是70。
故答案为:5;70。
【点评】此题考查的目的是理解掌握整数的认识,以及5的倍数的特征及应用。
3.(1分)(2021春 清河县期末)把一根长36厘米的长方体木料平均锯成6段,表面积比原来增加了125平方厘米,则这根木料原来的体积是 450 立方厘米。
【考点】长方体和正方体的表面积;长方体和正方体的体积.
【专题】空间观念;推理能力;应用意识.
【答案】450。
【分析】根据题意可知,把这根长方体木料平均锯成6段,表面积比原来增加了125平方厘米,表面积增加的是10截面的面积,据此可以求出长方体的底面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【解答】解:125÷10×36
=12.5×36
=450(立方厘米)
答:这根木料原来的体积是450立方厘米。
故答案为:450。
【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式,重点是求出长方体的底面积。
4.(3分)(2023春 淮安期末)1÷ 8 = 4 ÷32= 0.125 (填小数)
【考点】小数与分数的互化.
【专题】小数的认识;分数和百分数;数感.
【答案】见试题解答内容
【分析】解答此题的关键是,写成除法算式是1÷8,根据商不变的性质,被除数和除数同时乘4可得:1÷8=4÷32;计算出结果是小数为1÷8=0.125,据此即可填空。
【解答】解:1÷8=4÷32=0.125(填小数)
故答案为:8,4,0.125。
【点评】此题考查运用小数、分数、除法之间的关系和性质解决问题。
5.(4分)(2022秋 杜尔伯特县期末)4÷5 0.8 填小数。
【考点】分数的基本性质;小数与分数的互化.
【专题】运算能力.
【答案】25,3.2,10,0.8。
【分析】解答此题的突破口是4÷5,根据分数与除法的关系,4÷5,根据分数的基本性质,分子、分母都乘2就是;分子、分母都乘5就是,分子、分母都除以1.25就是,4÷5=0.8.由此进行转化并填空。
【解答】解:4÷50.8
故答案为:25,3.2,10,0.8。
【点评】此题主要是考查除式、小数、分数之间的关系及转化,利用它们之间的关系和性质进行转化即可。
6.(4分)(2021 梁山县)
①3时40分= 时 ②4.05m2= 405 dm2
③6.03公顷= 60300 平方米 ④7吨70千克= 7.07 吨
【考点】时、分、秒及其关系、单位换算与计算;小面积单位间的进率及单位换算;大面积单位间的进率及单位换算;质量的单位换算.
【专题】推理能力.
【答案】①;
②405;
③60300;
④7.07。
【分析】①根据时间单位间的换算关系:1时=60分;
②③面积单位间的换算关系:1平方米=100平方分米;1公顷=10000平方米;
④质量单位间的换算关系:1吨=1000千克。
换算即可。
【解答】解:
①3时40分时 ②4.05m2=405dm2
③6.03公顷=60300平方米 ④7吨70千克=7.07吨
故答案为:;405;60300;7.07。
【点评】本题主要考查质量单位、时间单位及面积单位间的换算关系。
7.(4分)(2022春 电白区期末)把、0.06、、0.65按照从大到小的顺序排列:
0.65 > > > 0.06 。
【考点】小数与分数的互化;小数大小的比较.
【专题】数感;运算能力.
【答案】0.65,,,0.06。
【分析】把,化成小数,再根据小数大小比较的方法进行比较解答。
【解答】解:0.429
0.625
因为0.65>0.625>0.429>0.06,所以把、0.06、、0.65按照从大到小的顺序排列是:0.650.06。
故答案为:0.65,,,0.06。
【点评】在分数、小数进行大小比较时,一般要把分数化成小数再比较大小,除不尽的保留三位小数。
8.(2分)(2022春 石景山区期末)如图是一个正方体的平面展开图,与A面相对的是 D 面,与C面相对的是 E 面。
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】D,E。
【分析】根据正方体展开图的11种特征,此图属于正方体展开图的“1﹣3﹣2”型,折成正方体后,字母A与D相对,B与F相对,C与E相对。
【解答】解:如图:
是一个正方体的平面展开图,与A面相对的是D面,与C面相对的是E面。
故答案为:D,E。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住规律,能快速解答此类题。
二.选择题(共8小题,满分8分,每小题1分)
9.(1分)(2023 宝安区)下列说法错误的是( )
A.把2769020000四舍五入到亿位约是28亿
B.三个连续奇数的和是141,这三个数的平均数是47
C.一个正方体的棱长扩大到原来的2倍,它的表面积会扩大到原来的4倍,体积会扩大到原来的8倍
D.一个两位数的偶数,它既是3的倍数,又是5的倍数,这个数最小是15
【考点】奇数与偶数的初步认识;2、3、5的倍数特征;长方体和正方体的表面积;长方体和正方体的体积;平均数的含义及求平均数的方法;亿以上数的改写与近似.
【专题】数感.
【答案】D
【分析】根据大数的改写、平均数、奇数和偶数、正方体的认识、倍数知识等,结合题意分析解答即可。
【解答】解:A.把2769020000四舍五入到亿位约是28亿,本选项说法正确;
B.三个连续奇数的和是141,这三个数的平均数是47,本选项说法正确;
C.一个正方体的棱长扩大到原来的2倍,它的表面积会扩大到原来的4倍,体积会扩大到原来的8倍,本选项说法正确;
D.一个两位数的偶数,它既是3的倍数,又是5的倍数,这个数最小是30,所以本选项说法错误。
故选:D。
【点评】本题考查了大数的改写、平均数、奇数和偶数、正方体的认识、倍数知识等,结合题意分析解答即可。
10.(1分)(2022春 金湾区期末)26□既是2的倍数,又是3的倍数,□里可以填( )
A.0 B.1 C.2 D.4
【考点】2、3、5的倍数特征.
【专题】数感.
【答案】D
【分析】根据2、3的倍数的特征,个位上是0、2、4、6、8的数都是2的倍数;一个数各位上的数字之和是3的倍数,这个数有多少3的倍数,同时是2和3的倍数的数,个位上是偶数且各位上的数字之和是3的倍数。据此解答。
【解答】解:2+6=8,8至少加上1是3的倍数,如果个位上是1就不是2的倍数,所以□里只能填4。
故选:D。
【点评】此题考查的目的是理解掌握2、3的倍数的特征及应用。
11.(1分)(2022 南京模拟)著名的“哥德巴赫猜想”被喻为“数学皇冠上的明珠”,猜想认为:任何大于2的偶数都是两个质数之和。下列4个算式中,符合这个猜想的是( )
A.32=13+19 B.13=2+11 C.16=7+9 D.4=1+3
【考点】合数与质数的初步认识;奇数与偶数的初步认识.
【专题】数感.
【答案】A
【分析】根据质数的含义:除了1和它本身没有其它因数的数,叫做质数,自然数中是2的倍数的数是偶数;由此根据题目要求找出大于2的偶数并且都是两个质数之和即可。
【解答】解:在32=13+19,13=2+11,16=7+9,4=1+3中,32=13+19符合这个猜想;
故选:A。
【点评】解决本题主要根据猜想按要求写数,要注意写出的两个数都要是质数。
12.(1分)(2023 兴庆区)用一根长52cm的铁丝围成一个长方体,它的长是6cm,宽是4cm,高是( )
A.5cm B.4cm C.3cm D.7cm
【考点】长方体的特征.
【专题】应用意识.
【答案】C
【分析】已知用一根铁丝围成一个长方体,那么长方体的棱长总和等于这根铁丝的长度。
根据长方体的棱长总和=(长+宽+高)×4可知,长方体的高=棱长总和÷4﹣长﹣宽,代入数据计算即可求解。
【解答】解:52÷4﹣6﹣4
=13﹣6﹣4
=3(cm)
高是3cm。
故选:C。
【点评】本题考查长方体棱长总和公式的灵活运用。
13.(1分)(2024秋 南陵县期末)黄河被称为“中华母亲河”,黄河全长5400多( )
A.米 B.分米 C.千米
【考点】根据情景选择合适的计量单位.
【专题】长度、面积、体积单位;应用意识.
【答案】C
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解答】解:黄河被称为“中华母亲河”,黄河全长5400多千米。
故选:C。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
14.(1分)(2023春 靖远县期中)一个长7dm,宽6dm,高4dm的长方体纸箱,最多能放( )个棱长2dm的正方体。
A.18 B.24 C.21
【考点】长方体和正方体的体积.
【专题】综合填空题;立体图形的认识与计算;几何直观.
【答案】A
【分析】以长为边,最多能装7÷2≈3(块),以宽为边,最多能装6÷2=3(块),以高为边,最多能装4÷2=2(块),再把每条棱上放的块数相乘即可计算。
【解答】解:7÷2≈3(块)
6÷2=3(块)
4÷2=2(块)所以最多能装:3×3×2=18(块)
答:最多能装18块。
故选:A。
【点评】此类问题,先求出每条棱长上最多能装下的木块的个数,再把每条棱上放的块数相乘即可计算出最多能装下的块数。
15.(1分)(2023秋 湘西州期末)元旦节当天,老师拿出6颗幸运星,奖给小云3颗,奖给小花3颗,小云的幸运星占6颗幸运星的______。小云有8支水彩笔,其中有3支是黄色的,2支是红色的、3支是绿色的,红色的水彩笔占8支水彩笔的______,你的选择是( )
A. B. C. D.
【考点】分数与除法的关系.
【专题】分数和百分数;数据分析观念.
【答案】C
【分析】利用小云的颗数除以6即可,利用红色的数量除以8即可。注意分数要约分。
【解答】解:3÷6
2
答:小云的幸运星占6颗幸运星的,红色的水彩笔占8支水彩笔的。
故选:C。
【点评】本题考查了一个数占另一个数的几分之几的问题应用。
16.(1分)(2023春 广州期末)把 约分得到最简分数后,下面说法正确的是( )
A.分数单位变小了 B.分数单位的个数增加
C.分数的大小不变
【考点】最简分数;约分.
【专题】整数的认识;分数和百分数;数感.
【答案】C
【分析】约分后得到最简分数是,分数单位变大了,没有增加分数单位的个数,分数大小没有改变。
【解答】解:,
化成最简分数后分数单位是,分数大小不变。
故选:C。
【点评】掌握分数约分的意义是解题关键。
三.判断题(共5小题,满分5分,每小题1分)
17.(1分)(2024 埇桥区)因为,所以的分数单位大于的分数单位。 ×
【考点】分数大小的比较.
【专题】综合判断题;数据分析观念.
【答案】×
【分析】分数单位是把单位“1”平均分成若干份,表示其中的一份的数。
【解答】解:的分数单位是,的分数单位是,;故原题说法错误。
故答案为:×。
【点评】此题考查了分数单位的知识,要求学生掌握。
18.(1分)(2022春 昌黎县期末)把的分子加上5,要使分数的大小不变,分母要乘2。 √
【考点】分数的基本性质.
【专题】分数和百分数;数据分析观念.
【答案】√
【分析】分子加上5后是原来的几倍,根据分数的基本性质,那么分母也是原来的几倍,分数的大小才不变。
【解答】解:分子:5+5=10,10÷5=2,要想分数的大小不变,那么分母也要扩大到原来的2倍,分母乘2,原题说法正确。
故答案为:√。
【点评】本题主要考查分数的基本性质,根据这一性质解答即可。
19.(1分)(2021秋 郴州月考)36和48的最小公倍数是96。 × (判断题)
【考点】求几个数的最小公倍数的方法.
【专题】数据分析观念.
【答案】×
【分析】求几个数的最小公倍数的方法:这几个数的公有的因数和它们独有的质因数的连乘积就是它们的最小公倍数,由此可以解得。
【解答】解:36=2×2×3×3
48=2×2×2×2×3
所以36和48的最小公倍数是2×2×2×2×3×3=144,所以原题计算错误。
故答案为:×。
【点评】此题考查了求几个数的最小公倍数的方法,由此可以解决。
20.(1分)(2022秋 岑溪市校级期中)用两个完全一样的正方形拼成一个长方形,长方形的周长是正方形周长的2倍。 ×
【考点】图形的拼组.
【专题】应用意识.
【答案】×
【分析】根据题意可知,用两个完全一样的正方形拼成一个长方形,拼成后长方形的周长比两个正方形的周长之和少了2个正方形的边长;据此解答。
【解答】解:如图:
用两个完全一样的正方形拼成一个长方形,拼成的长方形的周长比原来两个正方形的周长之和减少了2个正方形的边长,所以原题的说法错误。
故答案为:×。
【点评】本题考查了学生对拼组后图形周长的计算方法的掌握情况,注意拼组后图形的周长不是两个正方形周长的和。
21.(1分)(2023秋 天门期末)把一袋苹果分成6份,其中的2份是。 ×
【考点】分数的意义和读写.
【专题】数感.
【答案】×
【分析】把一袋苹果看作一个整体,把它平均分成6份,每份是它的,其中2份是。
【解答】解:把一袋苹果平均分成6份,其中的2份是。
这里没说平均分,说法错误。
故答案为:×。
【点评】此题是考查分数的意义。把一个整体平均分成若干份,用分数表示,分母是平均分成的份数,分子是要表示的份数。
四.解答题(共3小题,满分22分)
22.(6分)(2022春 陇县期末)只列式,不计算。
分母是8的最简真分数的和是多少?
列式: 2 。
【考点】最简分数.
【专题】运算能力.
【答案】2。
【分析】分母是8的最简真分数有:、、、,求出它们的和即可。
【解答】解:
=()+()
=1+1
=2
故答案为:2。
【点评】本题考查了分数加法,解答本题需理解最简真分数的意义:①分子小于分母,②分子和分母是互质数。
23.(4分)(2021春 张家川县期末)把下面各组中的两个分数先通分,再比较大小。
(1)和 (2)和
【考点】通分;分数大小的比较.
【专题】运算能力.
【答案】(1)<;(2)>。
【分析】把异分母分数分别化成和原来分数相等的同分母分数,叫做通分,用分母的最小公倍数作为公分母,通分后再根据分母相同的分数比较大小的方法进行比较即可。
【解答】解:(1)因为,
所以
(2)因为
所以
【点评】熟练掌握通分的方法以及同分母分数比较大小的方法是解题的关键。
24.(12分)(2021秋 吉林期末)求出下列每组数的最大公因数和最小公倍数。
①3和22
②17和51
【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【专题】推理能力.
【答案】①1,66;②17,51。
【分析】两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积;两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数。
【解答】解:①因为3和22互质,所以3和22的最大公因数是1,最小公倍数是3×22=66;
②因为51÷17=3,所以17和51的最大公因数是17,最小公倍数是51。
【点评】熟练掌握两个数互质、两个数为倍数关系的最大公因数和最小公倍数的求法是解题的关键。
五.解答题(共1小题,满分6分,每小题6分)
25.(6分)求图形的表面积和体积。(单位:cm)
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】空间观念;应用意识.
【答案】5200平方厘米,24000立方厘米。
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:(40×30+40×20+30×20)×2
=(1200+800+600)×2
=2600×2
=5200(平方厘米)
40×30×20
=1200×20
=24000(立方厘米)
答:它的表面积是5200平方厘米,体积是24000立方厘米。
【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
六.操作题(共3小题,满分12分,每小题4分)
26.(4分)(2022春 丹江口市期末)连一连,分别是从哪面看到的。
【考点】从不同方向观察物体和几何体.
【专题】空间观念;几何直观.
【答案】
【分析】根据观察几何体,可知上面图形为,右面图形为,左面图形为。
【解答】解:如图:
【点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
27.(4分)(2021春 开平市月考)一个长方体的下底周长是28cm,高是6cm,这个长方体的棱长总和是多少?
【考点】长方体的特征.
【专题】运算能力;应用意识.
【答案】80cm。
【分析】已知长方体的底面周长是28厘米的正方形,高4厘米,由此可知长方体的4个侧面是完全相同的长方形,这个长方体的棱长总和是(28×2+6×4)厘米。
【解答】解:28×2+6×4
=56+24
=80(cm)
答:这个长方体的棱长总和是80cm。
【点评】此题主要考查长方体的棱长总和的计算。
28.(4分)(2023秋 漯河期末)给如图苹果个数的除上阴影。
【考点】分数的意义和读写.
【专题】作图题;几何直观.
【答案】
【分析】把整个图形看作单位“1”,平均分成了3份,阴影部分占3份,用分数表示是;涂色2份即可解答。
【解答】解:
【点评】此题考查了分数的意义,要求学生掌握。
七.应用题(共4小题,满分25分)
29.(5分)(2022 金华)高老师家的柜式空调长0.5米,宽0.4米,高1.8米,为了防灰尘,高老师准备做一个长方体布罩把它罩起来,请问做这只布罩至少需用多少平方米的布?(接头处忽略不计)
【考点】长方体、正方体表面积与体积计算的应用.
【专题】应用意识.
【答案】3.44平方米。
【分析】这个长方体布罩应该没有下面,所以只需要计算上、左右、前后,五个面的面积。
【解答】解:0.5×0.4+0.5×1.8×2+0.4×1.8×2
=0.2+1.8+1.44
=3.44(平方米)
答:做这只布罩至少需用3.44平方米的布。
【点评】本题解题关键是能够联系生活实际,理解这个长方体布罩应该没有下面,所以只需要计算上、左右、前后,五个面的面积,再根据长方体表面积的计算方法,列式计算。
30.(5分)(2020春 长安区期末)红星小学操场的跳远场地是一个长方体沙坑,长8m,宽2.4m。需要黄沙多少方?
【考点】长方体和正方体的体积.
【专题】空间观念;应用意识.
【答案】9.6方。
【分析】根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:50厘米=0.5米
8×2.4×0.5
=19.2×0.5
=9.6(立方米)
9.6立方米=9.6方
答:需要填黄沙9.6方。
【点评】此题主要考查长方体体积公式的灵活应用,关键是熟记公式。
31.(5分)(2024春 上思县期中)一种长方形木块的长是12厘米,宽是10厘米,用这种木块铺成一个正方形(不允许切割),这个正方形的边长最少是多少厘米?至少要用多少块这样的木块?
【考点】公因数和公倍数应用题.
【专题】约数倍数应用题;应用意识.
【答案】60厘米,30块。
【分析】求出12和10的最小公倍数,再用最小公倍数分别除以12和10,再相乘,即可解答。
【解答】解:12=2×2×3
10=2×5
12和10的最小公倍数是2×2×3×5=60。
(60÷12)×(60÷10)
=5×6
=30(块)
答:这个正方形的边长最少是60厘米,至少要用30块这样的木块。
【点评】本题考查的是求最小公倍数应用题,掌握求最小公倍数的方法是解答关键。
32.(10分)一个长方体玻璃鱼缸,底面长50cm,宽40cm,高30cm。
(1)在鱼缸里注入40L水,水深多少厘米?
(2)再往鱼缸里放入鹅卵石、水草和鱼,水面上升了2.5cm,这些鹅卵石、水草和鱼的体积一共是多少立方厘米?
【考点】长方体和正方体的体积.
【专题】应用题;应用意识.
【答案】(1)20厘米;(2)5000cm3。
【分析】(1)首先求出40L水的体积是40000cm3,再用水的体积除以鱼缸的底面积可得水深;
(2)根据这些鹅卵石、水草和鱼的体积等于上升部分水的体积,结合长方体的体积=长×宽×高计算即可解答。
【解答】解:(1)40L=40000cm3
50×40=2000(平方厘米)
40000÷2000=20(厘米)
答:在鱼缸里注入40L水,水深20厘米。
(2)50×40×2.5=5000(cm3)
答:这些鹅卵石、水草和鱼的体积一共是5000cm3。
【点评】本题考查的是长方体体积计算公式的运用,灵活运用所学的知识是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
