八年级数学下册苏科版试题-9.4《矩形、菱形、正方形》复习题-正方形(含解析)
文档属性
| 名称 | 八年级数学下册苏科版试题-9.4《矩形、菱形、正方形》复习题-正方形(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 13:27:59 | ||
图片预览




文档简介
9.4《矩形、菱形、正方形》复习题--正方形
【类型一:正方形的性质】
1.如图,在正方形ABCD的对角线BD上取点E使BE=BA,连接AE,过点E作EF⊥AE交BC于点F,则∠EFC的大小为 .
2.已知:如图,E是边长为2的正方形ABCD对角线BD上的一点,EF⊥BD交DC于点F,且DE=CF.则线段EF的长为 .
3.如图,正方形ABCD的对角线交于点O,以AB为边向外作等边△ABE,连接OE.交AB于点F.若AB=4,则OE的长为 .
4.如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,求GH的长.
5.如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF⊥DG于F.
(1)求证:△AED≌△DFC;
(2)求证:AE=FC+EF.
【类型二:正方形的判定】
6.如图,已知 ABCD的对角线AC、BD交于点O,添加条件后, ABCD不一定是正方形的选项为( )
A.AB=AD,AC=BD B.AB=BC,AC⊥BD
C.∠BAD=90°,AC⊥BD D.∠AOD=90°,AO=DO
7.如图,△ABC中,D为AC边上一点,BD平分∠ABC,过点D作DE∥BC,与AB交于点E,作DF∥AB,与BC交于点F,连接EF.则以下结论中错误的是( )
A.四边形BFDE是菱形
B.BD与EF互相垂直且平分
C.当AB=BC时,四边形DEFC是菱形
D.若∠ABC=90°时,则四边形BFDE是正方形
8.如图, ABCD中,点E、F分别在边AD、BC上,点G、H在边BD上,且AE=CF,BG=DH,关于四边形EGFH,下列说法正确的个数是( )
①四边形EGFH一定是平行四边形且有无数个;
②四边形EGFH可以是矩形且有无数个;
③四边形EGFH可以是菱形且有无数个;
④四边形EGFH可以是正方形且有无数个.
A.1个 B.2个 C.3个 D.4个
9.如图,AD是等腰三角形ABC的底边BC上的高,O是AC的中点,延长DO到点E,使AE∥BC,连接CE.
(1)求证:四边形ADCE是矩形;
(2)若AB=2,BC=2,求证:四边形ADCE是正方形.
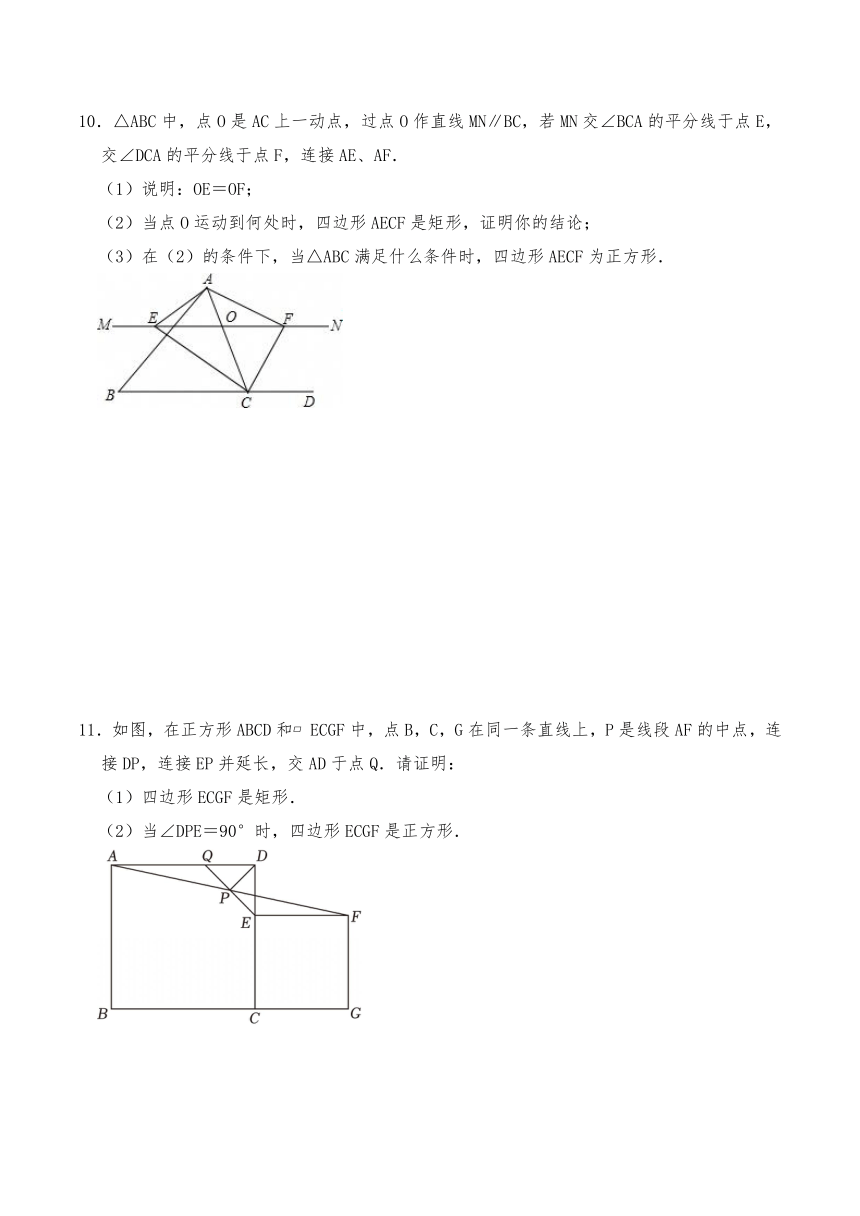
10.△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
(1)说明:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,证明你的结论;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF为正方形.
11.如图,在正方形ABCD和 ECGF中,点B,C,G在同一条直线上,P是线段AF的中点,连接DP,连接EP并延长,交AD于点Q.请证明:
(1)四边形ECGF是矩形.
(2)当∠DPE=90°时,四边形ECGF是正方形.
【类型三:正方形的旋转问题】
12.如图,将正方形ABCD绕点A按逆时针方向旋转到正方形AB'C'D',旋转角为a(0°<α<180°),连接B'D、C'D,若B'D=C'D,则∠α= .
13.如图,边长为1的正方形ABCD绕点C逆时针旋转45°后得到正方形A′B′CD′,边A′D′与AB交于点E,则阴影部分的面积是( )
A. B. C. D.
14.已知正方形ABCD中,点E在边DC上,DE=2,EC=1,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则EF的长为 .
15.如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转60°,使点B落在点B′的位置,连接BB′,过点D作DE⊥BB′,交BB′的延长线于点E,则B′E的长为( )
A. B. C. D.
【类型四:正方形的翻折问题】
16.如图,在矩形ABCD中,AB=m,BC=8,点M是AD的中点,点N是射线DC上一点,且CN=6,连接BN,将△DMN沿MN翻折至△D'MN,使D恰好落在BN上,则m= .
17.【模型呈现】在正方形学习过程中,我们发现下面的结论:如图1,正方形ABCD中,点P为线段BC上一个动点,若线段MN垂直AP于点E,交线段AB于点M,交线段CD于点N,则AP=MN.
(1)如图②,将边长为40的正方形ABCD折叠,使得点B落在CD上的点E处.若折痕FG=41,则CE= .
【继续探索】
(2)如图③,正方形ABCD中,点P为线段BC上一动点,若MN垂直平分线段AP,分别交AB,AP,BD,
DC于点M,E,F,N.求证:EF=ME+FN.
(3)如图④,在正方形ABCD中,E、F分别为AD,BC上的点,作DM⊥EF于M,在MF上截取MN=DM,
连接BN,G为BN中点,连接CG,CM.请依题意补全图形,若CG=2,则CM= .
【类型五:正方形的动点问题】
18.如图,正方形ABCD中,P为BD上一动点,过点P作PQ⊥AP交CD边于点Q.点P从点B出发,沿BD方向移动,若移动的路径长为6,则AQ的中点M移动的路径长为 .
19.在正方形ABCD中,O是AD的中点,点P从A点出发沿A→B→C→D的路线匀速运动,移动到点D时停止.
(1)如图1,若正方形的边长为12,点P的运动速度为2单位长度/秒,设t秒时,正方形ABCD与∠POD重叠部分的面积为y.
①当t=5时,y= ;当t=10时,y= .
②求t为何值时,以点O、A、P、C为顶点的四边形是平行四边形?
(2)如图2,若点Q从D出发沿D→C→B→A的路线匀速运动.P、Q两点同时出发,点P的速度大于点Q的速度,当P到终点时,Q也停止运动.设t秒时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积为S,S与t的函数图象如图3所示.
①P,Q两点在第 秒相遇;正方形ABCD的边长是 .
②点P的速度为 单位长度/秒;点Q的速度为 单位长度/秒.
③当t为何值时,重叠部分面积S等于32?
【类型六:正方形与函数综合】
20.若一个三角形有一边上的中线与这边的长相等,则称这个三角形为该边上的“完美三角形”.如图在直角坐标系中,正方形ABCO的两边OA、OC分别在坐标轴上,点B的坐标是(3,3).在正方形ABCO的边上找一点P,使得△POC是OC边上的“完美三角形”,点P的坐标为
21.如图,在平面直角坐标系xOy中,矩形OABC的顶点A(8,0),顶点C(0,6),点D为BC边上一动点,设CD的长为m,以AD为一边在与点B的同侧作正方形ADEF,在点D运动过程中,探究以下问题:
(1)①当点D与点C重合时,点E的坐标为 ;
②用含m的代数式表示点E的坐标为 .
(2)三角形ABF的面积是否改变?如果不变,求出此定值;如果改变,请说明理由;
(3)当△BEF为等腰三角形时,直接写出所有m的值.
22.如图,正方形OABC的顶点O在坐标原点,定点A的坐标为(4,3).
(1)求正方形OABC顶点C的坐标为 ,顶点B的坐标为 ;
(2)现有一动点P从C点出发,沿线段CB向终点B运动,P的速度为每秒1个单位长度,同时另一动点Q从点A出发沿A→O→C向终点C运动,速度为每秒k个单位长度.设运动时间为2秒时,将三角形CPQ沿它的一边翻折,若翻折前后的两个三角形组成的四边形为菱形,求k的值.
【类型七:正方形综合题】
23.如图1,点C在线段AB上,分别以AC、BC为边在线段AB的同侧作正方形ACDE和BCFG,连接AF、BD.
(1)若AF=5,则BD= ;
(2)如果点C在线段AB的延长线上,如图2,其他条件不变,求证:AF=BD.
24.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
(1)求证:BE=DE;
(2)判断DF与ON的位置关系,并说明理由;
(3)△BEF的周长为 .
25.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)∠EAF= °(直接写出结果不写解答过程);
(2)①求证:四边形ABCD是正方形.
②若BE=EC=3,求DF的长.
26.点E、F分别在正方形ABCD的边BC、AB所在直线上,点M在直线DE上,且DM=EF,EF⊥DE,MN⊥直线BC,垂足分别是E、N.
(1)当点E在边BC上时,如图①,求证:MN+BE=CD;
(2)当点E在BC的延长线上时,如图②;当点E在CB的延长线上时,如图③,请直接写出线段MN,BE,CD之间的数量关系,不需要证明.
27.数学课上,李老师给出这么一道数学问题:如图①,正方形ABCD中,点E是对角线AC上任意一点,过点E作EF⊥AC,垂足为E,交BC所在直线于点F.探索AF与DE之间的数量关系,并说明理由.
小明在解决这一问题之前,先进行特殊思考:如图②,当E是对角线AC的中点时,他发现AF与DE之间的数量关系是 .若点E在其它位置时,这个结论是否都成立呢?小明继续探究,他用“平移法”将AF沿AD方向平移得到DG,将原来分散的两条线段集中到同一个三角形中,如图③,这样就可以将问题转化为探究DG与DE之间的数量关系.
(1)请你按照小明的思路,完成解题过程;
(2)你能用与小明不同的方法来解决李老师给出的“数学问题”吗?请写出解题过程.
28.在如图所示的平面直角坐标系中,正方形AOBC边长为2,点C的坐标为(2,2).
(1)如图1,动点D在OB边上,将△BCD沿直线DC折叠,点B落在点B′处,连接DB′并延长,交AO于点E.
①当B′D=OD时,点D的坐标是 ;
②若点E是线段OA的中点,求此时点D与点B′的坐标;
(2)如图2,动点D,G分别在边OB,AC上,将四边形DBCG沿直线DG折叠,使点B的对应点B′始终落在边OA上(点B′不与点O,A重合),点C落在点C′处,B′C′交AC于点E.设OB′=t,四边形AB′DG的面积为S,直接写出S与t的关系式.
29.如图,正方形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(4,4),一次函数的图象与边OC、AB分别交于点D、E,并且满足.点M是线段DE上的一个动点.
(1)连接BD、OE,求证:四边形ODBE是平行四边形;
(2)作BP⊥DE交OA于P,当△OMP面积为2.6时,求M点的坐标;
(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
30.在数学综合与实践活动课上,同学们用两个完全相同的矩形纸片展开探究活动:
【实践探究】
(1)小红将两个矩形纸片摆成图1的形状,连接AG、AC,则∠ACG= °;
【解决问题】
(2)将矩形AQGF绕点A顺时针转动,边AF与边CD交于点M,连接BM,AB=10,AD=6.
①如图2,当BM=AB时,求证:AM平分∠DMB;
②如图3,当点F落在DC上时,连接BQ交AF于点O,则AO= ;
【迁移应用】
(3)如图4,正方形ABCD的边长为5,E是BC边上一点(不与点B、C重合),连接AE,将线段AE绕点E顺时针旋转90°至FE,作射线FC交AB的延长线于点G,则BG= ;
(4)如图5,在菱形ABCD中,∠A=120°,E是CD边上一点(不与点C、D重合),连接BE,将线段BE绕点E顺时针旋转120°至FE,作射线FD交BC的延长线于点G.若BG=6,则CG= .
参考答案
【类型一:正方形的性质】
1.
【分析】由四边形ABCD是正方形,EF⊥AE得∠BAD=∠AEF=∠C=90°,则∠DAE+∠BAE=90°,∠BEF+∠BEA=90°,∠ABD=∠ADB=∠CBD=∠CDB=45°,而BE=BA,则DA=BE,∠BAE=∠BEA=67.5°,所以∠DAE=∠BEF,可证明△DAE≌△BEF,得∠AED=∠EFB,则∠EFC=∠BEA=67.5°,于是得到问题的答案.
【解答】解:∵四边形ABCD是正方形,EF⊥AE,
∴DA=BA=BC=DC,∠BAD=∠AEF=∠C=90°,
∴∠DAE+∠BAE=90°,∠BEF+∠BEA=90°,∠ABD=∠ADB=∠CBD=∠CDB=45°,
∵BE=BA,
∴DA=BE,∠BAE=∠BEA(180°﹣45°)=67.5°,
∴∠DAE=∠BEF,
在△DAE和△BEF中,
,
∴△DAE≌△BEF(ASA),
∴∠AED=∠EFB,
∴∠EFC=180°﹣∠EFB=180°﹣∠AED=∠BEA=67.5°,
故答案为:67.5°.
2.
【分析】由边长为2的正方形ABCD中∠BDC=45°,EF⊥BD,DE=CF,得BDDC=2,设DE=x,则DFDEx,由DF+FC=DC,得x+x=2,即可得EF=DE=x=22.
【解答】解:由边长为2的正方形ABCD中∠BDC=45°,EF⊥BD,DE=CF,
得BDDC=2,
设CF=DE=x,则DFDEx,
由DF+FC=DC,
得x+x=2,
得EF=DE=x=22.
故答案为:22.
3.
【分析】根据正方形的性质得AB=BC=4,OA=OC=OB=OD,∠ABC=90°,则点O在线段AB的垂直平分线上,再根据等边三角形的性质得EA=EB=AB=2,则点E在线段AB的垂直平分线上,由此的OE是线段AB的垂直平分线,则AF=BF=2,然后由勾股定理分别求出OF=2,EF,进而可得OE的长.
【解答】解:∵四边形ABCD是正方形,AB=4,
∴AB=BC=4,OA=OC=OB=OD,∠ABC=90°,
在Rt△ABC中,由勾股定理得:AC,
∴OA=OBAC,
∴点O在线段AB的垂直平分线上,
∵△ABE是等边三角形,
∴EA=EB=AB=2,
∴点E在线段AB的垂直平分线上,
∴OE是线段AB的垂直平分线
∴OE⊥AB,AF=BFAB=2,
在Rt△AOF中,由勾股定理得:OF2,
在Rt△AEF中,由勾股定理得:EF,
∴OE=OF+EF.
故答案为:.
4.解:∵四边形ABCD是正方形,
∴AB=DA,∠BAE=∠ADF=90°,
在△BAE和△ADF中
,
∴△BAE≌△ADF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=90°,
∴∠BGF=90°,
∵点H为BF的中点,
∴GHBF,
又∵BC=CD=5,DF=2,∠C=90°,
∴CF=3,
∴BF,
∴GH.
5.证明:(1)∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
∴∠ADE+∠CDF=90°,
∵AE⊥DG,CF⊥DG,
∴∠AED=∠DFC=90°,
∴∠DAE+∠ADE=90°,
∴∠DAE=∠CDF,
在△AEE和△DFC中,
,
∴△AED≌△DFC(AAS);
(2)∵△AED≌△DFC,
∴AE=DF,ED=FC,
∵DF=ED+EF=FC+EF.
∴AE=FC+EF.
【类型二:正方形的判定】
6.
【分析】根据题意逐一对选项分析即可得出答案.
【解答】解:A、因为AB=AD,所以 ABCD为菱形,因为AC=BD,所以 ABCD为正方形,不符合题意;
B、因为AB=BC,所以 ABCD为菱形,但AC⊥BD不能证明 ABCD为正方形,符合题意;
C、因为∠BAD=90°,所以 ABCD为矩形,又因为AC⊥BD所以 ABCD为正方形,不符合题意;
D、因为∠AOD=90°,所以 ABCD为菱形,又因为AO=DO所以 ABCD为正方形,不符合题意;
故选:B.
7.
【分析】根据菱形的判定得出四边形BFDE是菱形,再根据菱形的性质得出BD与EF互相垂直且平分,进而利用菱形的判定和正方形的判定解答即可.
【解答】解:∵DE∥BC,DF∥AB,
∴四边形BFDE是平行四边形,∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠EBD=∠DBF,
∴∠EBD=∠EDB,
∴BE=DE,
∴ BFDE是菱形,故A正确;
∴BD与EF互相垂直且平分,故B正确;
∵∠ABC=90°时,则四边形BFDE是正方形,故D正确;
当AB=BC,不能得出四边形DEFC是菱形,故C错误;
故选:C.
8.
【分析】先利用SAS证明△BFH≌△DEG,由全等三角形的性质得出FH=EG,∠BHF=∠DGE,证出FH∥EG,得出四边形EGFH是平行四边形.再根据矩形、菱形、正方形的判定分别判断即可.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠FBH=∠EDG,
∵AE=CF,BG=DH,
∴DE=BF,BH=DG,
在△BFH和△DEG中,
,
∴△BFH≌△DEG(SAS),
∴FH=EG,∠BHF=∠DGE,
∴FH∥EG,
∴四边形EGFH是平行四边形,
点E、F分别在边AD、BC上移动时, EGFH有无数个,故①说法正确;
如果EF=GH,则 EGFH是矩形且有无数个,故②说法正确;
如果FG=FH,则 EGFH是菱形且有无数个,故③说法正确;
假设过BD的中点O的直线交AD、BC于点M、N,只有当OG=OM时,生产的四边形是正方形,点M、N即为符合题意得点E、F,且仅有这一种可能,故④说法错误.
故选:C.
9.证明:(1)∵AD是等腰三角形ABC底边BC上的高,
∴AD⊥BC,BD=CD,
∴D为BC的中点,
又∵O是AC的中点,
∴DO∥AB,
∵DE∥AB,AE∥BD,
∴四边形AEDB是平行四边形,
∴AE=BD=CD,
∵AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵∠ADC=90°,
∴四边形ADCE是矩形;
(2)∵AD是等腰三角形ABC的底边BC上的高,
∴BD=CD,
∴AD,
∴AD=CD,
∴四边形ADCE是正方形.
10.(1)证明:∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠DCF,
又∵CE平分∠BCO,CF平分∠DCO,
∴∠OCE=∠BCE,∠OCF=∠DCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形;
(3)解:当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(2)知,当点O运动到AC的中点时,四边形AECF是矩形,
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形.
11.(1)解:∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠GCE=90°,
∵四边形ECGF是平行四边形,
∴平行四边形ECGF是矩形;
(2)证明:在正方形ABCD和 ECGF中,点B,C,G在同一条直线上,
∴AD∥BG,EF∥BG,∠ADC=90°,
∴AD∥EF,
∴∠QAP=∠EFP,
∵P是线段AF的中点,
∴AP=PF,
又∠APQ=∠FPE,
∴△APQ≌△FPE(ASA),
∴AQ=EF,QP=PE,
∵∠DPE=90°,
∴∠DPQ=90°,
在△PDQ和△PDE中,
,
∴△PDQ≌△PDE(SAS),
∴QD=DE,
∵AD=DC,
∴AQ=EC,
∴EC=EF,
∴矩形ECGF是正方形.
【类型三:正方形的旋转问题】
12.
【分析】作DH⊥B′C′于H,交AD′于G,如图,根据旋转的性质得AD′=AD,∠DAD′=α,再根据等腰三角形的性质由B'D=C'D得到B′H=C′H,则AG=D′G,然后证明△ADD′为等边三角形得到∠DAG=60°,从而得到α的度数.
【解答】解:作DH⊥B′C′于H,交AD′于G,如图,
∵正方形ABCD绕点A按逆时针方向旋转到正方形AB'C'D',旋转角为a,
∴AD′=AD,∠DAD′=α,
∵B'D=C'D,
∴B′H=C′H,
∵四边形AB'C'D'为正方形,
∴AG=D′G,
连接DD′,如图,
∵DG垂直平分AD′,
∴DD′=DA,
∴DD′=AD=AD′,
∴△ADD′为等边三角形,
∴∠DAG=60°,
即α=60°.
故答案为60°.
13.
【分析】连接A′C,证明A′,B,C三点共线,勾股定理求出A′C的长,进而求出A′B的长,利用分割法求出阴影部分的面积即可.
【解答】解:连接A′C,
∵边长为1的正方形ABCD绕点C逆时针旋转45°后得到正方形A′B′CD′,
∴BC=1,∠BCD=90°,∠DCD′=45°,∠A′CD′=∠D′A′C=45°,A′D′=CD′=1,
∴∠BCD′=∠BCD﹣∠DCD′=45°,,
∵∠BCD′=∠A′CD′=45°,
∴A′,B,C三点共线,
∴,∠A′BE=90°,
∵∠D′A′B=45°,
∴,
∴,
∴;
故选:D.
14.
【分析】根据正方形的性质可得AB=AD,∠ABC=∠D=90°,再根据旋转的性质可得AF=AE,然后利用“HL”证明Rt△ABF和Rt△ADE全等,根据全等三角形对应边相等可得BF=DE,再求出正方形的边长为3,然后分点F在线段BC上和CB的延长线上两种情况讨论求解.
【解答】解:在正方形ABCD中,AB=AD,∠ABC=∠D=90°,
由旋转的性质得,AF=AE,
在Rt△ABF和Rt△ADE中,,
∴Rt△ABF≌Rt△ADE(HL),
∴BF=DE=2,
∵DE=2,EC=1,
∴正方形的边长为2+1=3,
①点F在线段BC上时,FC=3﹣2=1,
∴EF;
②点F在CB的延长线上时,FC=3+2=5,
∴EF′,
综上所述,EF的长为或,
故答案为:或.
15.
【分析】分别延长AD和BE交于点F,由直角三角形的性质求出EF的长,根据△ABB'是等边三角形,求出B'E=BF﹣BB'﹣EF即可.
【解答】解:分别延长AD和BE交于点F,
由题知,AB=2,∠ABF=60°,
∴BF=2AB=4,AFAB=2,∠F=90°﹣∠ABF=30°,
∴DF=AF﹣AD=22,
∴EFDF=(2)3,
由题知,△ABB'是等边三角形,
∴B'E=BF﹣BB'﹣EF=4﹣2﹣(3)1,
故选:A.
方法二:分别延长BA和ED交于点F,
由题知,AD=2,∠ABE=60°,DE⊥BB′,
∴∠F=90°﹣∠ABE=30°,
∴AFAD=2,
∴BF=AF+AB=22,
∴BEBF1,
由题知,△ABB'是等边三角形,
∴B'E=BE﹣BB'1﹣21,
故选:A.
【类型四:正方形的翻折问题】
16.
【分析】分两种情况:如图,当点N在线段CD时,当点N在CD的延长线时,连接BM,根据矩形的性质得到∠C=∠D=∠A=90°,AD=BC=8,AB=CD=m,由点M是AD的中点,得到AM=DMAD=4,根据折叠的性质得到DM=D′M,∠MD′N=∠D=90°,∠DMN=∠D′MN,根据全等三角形的性质得到∠AMB=∠D′MB,根据勾股定理即可得到结论.
【解答】解:如图,当点N在线段CD时,
连接BM,
∵四边形ABCD是矩形,
∴∠C=∠D=∠A=90°,AD=BC=8,AB=CD=m,
∵点M是AD的中点,
∴AM=DMAD=4,
∵将△DMN沿MN翻折至△D'MN,使D恰好落在BN上,
∴DM=D′M,∠MD′N=∠D=90°,∠DMN=∠D′MN,ND′=ND,
∴∠MDB=90°,
在△AMB与△D′MB中,
,
∴△AMB≌△D′MB(SSS),
∴BD′=AB=m,∠AMB=∠D′MB,
∴∠BMN=∠BMD′+∠NMD′=90°,
∴AB2+AM2=BM2,DM2+DN2=MN2,BM2+MN2=BN2,
∴m2+42+42+(m﹣6)2=(m+m﹣6)2,
∴m=8(负值舍去),
如图,当点N在CD的延长线时,
连接BM,
∵四边形ABCD是矩形,
∴∠C=∠D=∠A=90°,AD=BC=8,AB=CD=m,
∵点M是AD的中点,
∴AM=DMAD=4,
∵将△DMN沿MN翻折至△D'MN,使D恰好落在BN上,
∴DM=D′M,∠MD′N=∠D=90°,∠DMN=∠D′MN,
∴∠MDB=90°,
在△AMB与△D′MB中,
,
∴△AMB≌△D′MB(SSS),
∴BD′=AB=m,∠AMB=∠D′MB,
∴∠BMN=∠BMD′+∠NMD′=90°,
∴AB2+AM2=BM2,DM2+DN2=MN2,BM2+MN2=BN2,
∴m2+42+42+(m+6)2=(m+m+6)2,
解得m=2(负值舍去),
综上所述,m=8或2,
故答案为:8或2.
17.(1)解:∵四边形ABCD是正方形,
∴∠A=∠ABC=∠C=90°,AB=CB,
作FP⊥CB于P,连接BE,
则四边形AFPB是矩形,
∴∠BCE=∠FPG=90°,
由翻折知,GF⊥BE,
∴∠PFG=∠CBE,
∵AB=CB=FP,
∴△FPG≌△BCE(ASA),
∴BE=FG=41,
在Rt△CBE中,由勾股定理得CE9,
故答案为:9;
(2)证明:如图2,连接FA,FP,FC,
∵正方形ABCD是轴对称图形,F为对角线BD上一点,
∴FA=FC,
又∵FE垂直平分AP,
∴FA=FP,
∴FP=FC,
∴∠FPC=∠FCP,
∵∠FAB=∠FCP,
∴∠FAB=∠FPC,
∴∠FAB+∠FPB=180°,
∴∠ABC+∠AFP=180°,
∴∠AFP=90°,
∴FEAP,
由【模型呈现】知,AP=MN,
∴MN=ME+EF+FN=AP=2EF,
∴EF=ME+FN;
(3)解:根据题意补全图形如图所示:
连接MG并延长使得MG=GH,
∵点G为BN的中点,
∴BG=NG,
又∵∠BGH=∠NGM,
∴△BGH≌△NGM(SAS),
∴HG=MG,BH=NM,∠BHG=∠NMG,则BH∥NM,
∴∠CBH=∠BFE,
∵四边形ABCD是正方形,
∴AD∥BC,∠ADC=90°,
∴∠BFE=∠DEM,∠CDM+∠EDM=90°,
又∵DM⊥EF,
∴∠DEM+∠EDM=90°,
∴∠CDM=∠DEM,
∴∠CDM=∠BFE,
∴∠CBH=∠CDM,
∵MN=DM,
∴BH=DM,
由正方形的性质可知,CB=CD,
∴△CBH≌△CDM(SAS),
∴CH=CM,∠BCH=∠DCM,∠BCD=90°,
则∠BCH+∠BCM=∠DCM+∠BCM=∠BCD=90°,
∴△MCH是等腰直角三角形,
∵HG=MG,
∴CG⊥MH,则△CGM也是等腰直角三角形,则CG=MG,
∴CMCG=2.
故答案为:2.
【类型五:正方形的动点问题】
18.
【分析】根据题意,画出运动后 的M点位置,再根据三角形中位线定理即可求得.
【解答】解:连接AC,交BD于点O,连接PC,过P点作 PE⊥AD,PF⊥CD垂足分别为E、F,延长FP,交AB于G,
∵正方形ABCD,
∴∠ADC=90°,∠EDB=∠CDB=45°,
∵∠PED=∠PFD=90°,
∴∠EPD=∠EDP=45°,
∴PE=DE,则四边形PEDF为正方形,
∴PE=PF,∠EPF=90°,
∵∠APQ=∠APE+∠EPQ=90°,∠EPF=∠FPQ+∠EPQ=90°,
∴∠APE=∠QPF,
在△PAE和△PQF中,
,
∴△PAE≌△PQF(AAS),
∴PA=PQ;
∵正方形ABCD,
∴∠ABC=∠C=90°,∠EDB=∠CDB=∠ABD=∠CBD=45°,
∴GF∥BC,
∴∠BGP=90°,
∴△BGP 为等腰直角三角形,
∵BP=6,
∴,
∴,
∵正方形ABCD,
∴AB=BC,∠ABP=∠CBP=45°,BP=BP,O是AC中点,
∴△ABP≌△CBP,
∴PA=PC=PQ
,∵PF⊥CQ,
∴,
∵O是AC中点,M是AQ中点,
,
故答案为:.
19.解:(1)①当t=5时,AP=10,
∵O是正方形ABCD边AD的中点,
∴OA=ODAD=6,
∴S△AOPOA AP6×10=30,
∴y=S正方形ABCD﹣S△AOP=122﹣30=114;
当t=10时,如图1,
则AB+BP=20,
∴BP=20﹣AB=20﹣12=8,
∴PC=BC﹣BP=12﹣8=4,
∴y=S梯形CDOP(PC+OD) CD(4+6)×12=60;
故答案为:114;60.
②如图2,AB+BP=2t,
∴PC=24﹣2t,
∵OA∥CP,
∴当OA=CP时,以点O、A、P、C为顶点的四边形是平行四边形,
∴6=24﹣2t,
解得:t=9,
∴当t=9时,以点O、A、P、C为顶点的四边形是平行四边形.
(2)①由图3可知:当t=4时,S=0,即P,Q两点在第4秒相遇;
当t=0时,S正方形ABCD=AB2=64,
∴AB=8,即正方形ABCD的边长是8;
故答案为:4;8.
②由图3可知:点P、Q相遇于点C,且点P的速度大于点Q的速度,
∴点P的速度为点Q的速度的2倍,
设点Q的速度为a单位长度/秒,则点P的速度为2a单位长度/秒,
∴4(a+2a)=24,
解得:a=2,
∴点P的速度为4单位长度/秒,点Q的速度为2单位长度/秒;
故答案为:4;2.
③∵O是AD的中点,
∴OA=OD=4,
设t秒时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积S等于32,
分三种情况讨论:
当0≤t≤2时,点P在AB边上,点Q在CD边上,如图,
则AP=4t,DQ=2t,OA=OD=4,
∴S=S正方形ABCD﹣S△OAP﹣S△ODQ=644×4t4×2t=64﹣12t,
由题意得:64﹣12t=32,
解得:t2(不符合题意,舍去);
当2<t≤4时,点P在BC边上,点Q在CD边上,如图,
则AB+BP=4t,AB=8,
∴BP=4t﹣8,
∵DQ=2t,OA=OD=4,
∴S=S正方形ABCD﹣S梯形OABP﹣S△ODQ=64(4t﹣8+4)×84×2t=80﹣20t,
由题意得:80﹣20t=32,
解得:t,符合题意;
当4<t≤6时,点P在CD边上,点Q在BC边上,如图,
∵AB+BC+CP=4t,AB=BC=CD=AD=8,
∴DP=24﹣4t,
∵DC+CQ=2t,
∴BQ=16﹣2t,
∴S=S正方形ABCD﹣S梯形OABQ﹣S△ODP=64(4+16﹣2t)×84×(24﹣4t)=16t﹣64,
由题意得:16t﹣64=32,
解得:t=6(符合题意);
综上,当t或6时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积等于32.
【类型六:正方形与函数综合】
20.
【分析】根据正方形的性质得出C(3,0),A(0,3),进而利用勾股定理解答即可.
【解答】解:∵四边形ABCO是正方形,点B的坐标是(3,3),
∴C(3,0),A(0,3),
∴OC中点D的坐标为(1.5,0),
如图所示,当点P在AB上时,设P(m,3);
∵△POC是OC边上的“完美三角形”,
∴P1D=OC=3,
∴(m﹣1.5)2+(3﹣0)2=32,
解得m=1.5,
∴点P的坐标为(1.5,3).
如图2所示,当点P在BC上时,设P(3,n);
∵△POC是OC边上的“中线三角形”,
∴P2D=OC=3,
∴(n﹣0)2+(3﹣1)2=32,
解得m(负值舍去),
∴点P的坐标为(3,),
如图3所示,当点P在OA上时,设P(0,s);
∵△POC是OC边上的“中线三角形”,
∴P3D=OC=3,
∴(s﹣0)2+(0﹣1)2=32,
解得s(负值舍去),
∴点P的坐标为(0,);
综上所述,点P的坐标为(1.5,3)或(3,)或(0,).
21.解:(1)①如图1﹣1中,过点E作EH⊥BC于H.
∵四边形ABCO是矩形,A(8,0),C(0,6),
∴OA=BC=8,AB=OC=6,
∵∠BCO=∠ACE=90°,
∴∠ACB=∠ECH,
∵CE=CB,∠EHC=∠ABC=90°,
∴△EHC≌△CBA(AAS),
∴EH=CB=8,CH=AB=6,
∴E(6,14).
故答案为:(6,14);
②如图1﹣2中,过点E作EH⊥BC于H.
同法可证:△EHD≌△DBA(AAS),
∴EH=DB=8﹣m,DH=AB=6,
∴CH=6+m,
∴E(6+m,14﹣m).
故答案为:(6+m,14﹣m);
(2)△ABF的面积不会改变,理由如下:
如图2,过点F作FH⊥AB,交AB的延长线于H,
∵矩形OABC的顶点B坐标为(8,6),
∴AB=6,BC=8,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∴∠DAB+∠FAB=90°,且∠DAB+∠BDA=90°,
∴∠BDA=∠FAB,
∵AD=AF,∠ABD=∠AHF=90°,
∴△ABD≌△FHA(AAS),
∴HF=AB=6,
∴△ABF的面积AB×HF=18;
(3)若BE=EF,当点B与点D重合时,AD=AB=6,此时m=8.
当点B与点D不重合时,如图3,过点E作EH⊥DB于H,
∵∠EDH+∠ADB=90°,∠ADB+∠DAB=90°,
∴∠EDH=∠DAB,
AD=DE,∠EHD=∠ABD=90°,
∴△ADB≌△DEH(AAS),
∴DH=AB=6,
∵BE=EF,EF=DE,
∴DE=BE,
∵EH⊥DB
∴DH=BH=6,
∴DB=12,
∵DB<BC,
∴此种情形不存在.
若EB=BF,
∵BE=BF,
∴∠BEF=∠BFE,
∴∠DEB=∠AFB,
∵DE=AF,BE=BF,
∴△DEB≌△AFB(AAS),
∴DB=AB=36,
∴CD=BC﹣BD=8﹣6=2,即m=2;
若BF=EF,如图4,过点F作FH⊥AB于H,
∵∠DAB+∠FAB=90°,∠DAB+∠BDA=90°,
∴∠BDA=∠FAB,
∵AD=AF,∠ABD=∠AHF=90°,
∴△ABD≌△FHA(AAS),
∴AH=DB,
∵EF=BF,EF=AF,
∴BF=AF,
∵FH⊥AB,
∴AH=BH=3,
∴DB=3,
∴CD=BC﹣BD=8﹣3=5,即m=5,
综上所述,满足条件的m的值为8或2或5.
22.解:(1)过点A作AD⊥x轴于D,过点B作BE⊥AD交DA的延长线于E,过点C作CF⊥x轴于点F,
∴∠ADO=∠OFC=∠BEA=90°,
∴∠DAO+∠AOD=90°,
∵四边形ABCO是正方形,
∴∠OAB=∠AOC=90°,OA=OC=AB,
∴∠COF+∠AOD=90°,∠BAE+∠DAO=90°,
∴∠FOC=∠DAO,∠BAE=∠AOD,
∴△COF≌△AOD≌△BAE(AAS),
∴OF=AD=BE,CF=OD=AE,
∵点A的坐标为(4,3),
∴OF=AD=BE=3,CF=OD=AE=4,
∴点C的坐标为(﹣3,4);
∴ED=4+3=7,点B到y轴的距离为OD﹣BE=4﹣3=1,
∴点B的坐标为(1,7);
故答案为:﹣3,4,1,7;
(2)由题意,得AO=CO=BC=AB5,
当 t=2 时,CP=2.
将三角形CPQ沿它的一边翻折,若翻折前后的两个三角形组成的四边形为菱形,
只需三角形CPQ是等腰三角形即可.
①当点Q在OA上时,
∵PQ AB>PC,
∴只存在一点Q,使QC=QP.
过点Q作QD⊥PC于点D,如图,
则CD=PD=1,
∵QA=BD,
∴2k=5﹣1=4,
∴k=2;
②当点Q在OC上时,
∵∠BCO=90°,
∴只存在一点Q,使CP=CQ=2,
∴2k=10﹣2=8,
∴k=4.
综上所述,k的值为2或4.
【类型七:正方形综合题】
23.(1)解:四边形ACDE和四边形BCFG是正方形,
∴AC=CD,∠DCA=∠DCB=90°,BC=CF,
在△AFC和△DBC中,
∴在△AFC≌△DBC(SAS),
∴BD=AF=5;
故答案为:5;
(2)证明:连接AF,
∵四边形ACDE、BCFG是正方形,
∴AC=DC,CB=CF,
同(1)可证△ACF≌△DCB(SAS),
∴AF=DB,
24.解:(1)∵四边形ABCD是正方形,
∴CA平分∠BCD,BC=DC,
∴∠BCE=∠DCE=45°,
∵CE=CE,
∴△BCE≌△DCE(SAS),
∴BE=DE.
(2)DF⊥ON,理由如下:
∵△BCE≌△DCE,
∴∠EBC=∠EDC,
∵∠EBC=∠CBN,
∴∠EDC=∠CBN,
∵∠EDC+∠1=90°,∠1=∠2,
∴∠2+∠CBN=90°,
∴∠EFB=90°,即DF⊥ON;
(3)如图所示,过C作CG⊥ON于G,过D作DH⊥CG于H,则∠CGB=∠AOB=90°,四边形DFGH是矩形,
又∵∠ABC=90°,
∴∠ABO+∠BAO=90°=∠ABO+∠CBG,
∴∠BAO=∠CBG,
又∵AB=BC,
∴△ABO≌△BCG(AAS),
∴BG=AO12,CG=BO=5,
同理可得△CDH≌△BCG,
∴DH=CG=5,CH=BG=12,
∴HG=5+12=17,
∴DF=HG=17,GF=DH=5,
∴BF=BG﹣GF=12﹣5=7,
∴△BEF的周长=BF+EF+BE=BF+EF+DE=BF+DF=7+17=24,
故答案为:24.
25.(1)解:∵∠C=90°,
∴∠CFE+∠CEF=90°,
∴∠DFE+∠BEF=360°﹣90°=270°,
∵AF平分∠DFE,AE平分∠BEF,
∴∠AFEDFE,∠AEFBEF,
∴∠AEF+∠AFE(∠DFE+∠BEF)270°=135°,
∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,
故答案为:45;
(2)①证明:作AG⊥EF于G,如图1所示:
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
②解:设DF=x,
∵BE=EC=3,
∴BC=6,
由①得四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE与Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=EG=6,
同理,GF=DF=x,
在Rt△CEF中,EC2+FC2=EF2,
即32+(6﹣x)2=(x+3)2,
解得:x=2,
∴DF的长为2.
26.(1)证明:当点E在边BC上时,如图①,
过M点作MG⊥DC于G点,
∵四边形ABCD是正方形,
∴∠C=∠B=90°,
∴∠1+∠2=90,
∴∠DEF=90°,
∴∠2+∠3=90,
∴∠1=∠3,
又∵∠MGD=∠B=90°,DM=EF,
∴△DGM≌△EBF(AAS),
∴DG=EB,
∵MG⊥DC,MN⊥BC,∠C=90°,
∴∠MGC=∠MNC=∠C=90°,
∴四边形GMNC是矩形,
∴MN=GC,
∴MN+BE=GC+DG=CD.
(2)当点E在BC的延长线上时,如图②,
延长DC,过M点作MG⊥DC的延长线于G点,
则四边形MNCG是矩形,
∴MN=CG,
∵∠DCE=90°,∠DEF=90°,
∴∠1+∠2=90,∠2+∠3=90,
∴∠1=∠3,
∵∠DGM=∠EBF=90°,DM=EF,
∴△DGM≌△EBF(AAS),
∴DG=EB,
∵DG=DC+CG,
∴EB=DC+MN.
当点E在CB的延长线上时,如图③,
过D点作DG⊥MN于G点,
则四边形GDCN是矩形,
∴DC=GN,
∵∠N=90°,
∴∠1+∠2=90°,
∵∠MEF=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∵∠MGD=∠EBF=90°,MD=EF,
∴△MGD≌△EBF(AAS),
∴MG=EB,
∵MN=MG+GN,
∴MN=BE+DC.
27.解:AFDE,理由如下:
∵四边形ABCD是正方形,E是对角线AC的中点,
∴AC⊥BD,AE=BE=CE=DE.
∵AB2=AE2+BE2,
∴AB2=2DE2,
∵B点与F点重合,
∴AF2=2DE2,
∴;
(1)如图③,延长BC,作DG∥AF,交BC的延长线于点G,连接EG,
∵四边形ABCD是正方形,
∴∠ABC=∠BCD﹣90°,AB=BC=CD=AD,AD∥BC,
∵DG∥AF,AD∥BC,
∴四边形AFGD为平行四边形,
∴AF=DG,AD=FG,
∴FG=CD.
∵∠ABC=90°,AB=BC,
∴∠ACB=45°,∠ACD=45°,
∵EF⊥AC,
∴∠FEC=90°,
∴∠EFC=∠ECF=45°,
∴EF=EC.
∴∠EFC=∠ECD.
∴△CDE≌△FGE(SAS).
∴ED=EG,∠FEG=∠CED.
∴∠DEG=∠FEC=90°,
∴△DEG是等腰直角三角,
∴DG2=DE2+EG2=2DE2,
∴,
∴AFDE,
故答案为:AFDE.
(2)如图④,作DG⊥DE,并截取DG=DE,连接AG、GE,
∵四边形ABCD是正方形,
∴∠ADC=90°,CD=AD,
∴∠DAC=∠DCA=45°,
同理,∠ACB=45°,
∵GD⊥DE,
∴∠GDE=90°,
又∵DG=DE,
∴△DEG是等腰直角三角形,
∴EG2=DE2+DG2=2DE2,
∴EGDE,
∵∠ADC=∠GDE=90°,
∴∠GDA=∠EDC,
∴△GDA≌Δ EDC(SAS),
∴∠GAD=∠ECD=45°,AG=EC,
∴∠GAE=90°,
∵EF⊥AC,
∴∠FEC=∠FEA=90°,
∴∠EFC=∠ECF=45°,
∴EF=EC.
∴EF=AG,
∵∠GAE=∠FEA=90°,
∴AG∥EF,
∴四边形AGEF为平行四边形,
∴AF=EG.
∵AFDE.
28.解:(1)①∵正方形AOBC边长为2,点C的坐标为(2,2),
∴OB=BC=AC=OA=2,
∵将△BCD沿直线DC折叠,
∴B′D=BD,
又∵B′D=OD,
∴BD=OD,
∴,
∴点D的坐标是(1,0),
故答案为:(1,0);
②连接CE.
∵折叠,
∴CB′=CB=AC=2.
在Rt△EAC和Rt△E′BC中,
,
∴Rt△EAC≌Rt△E′BC(HL),
∴EB′=AE,
∵E为OA中点,
∴AE=OEOA=1,
∴EB′=AE=1.
设D(x,0),则OD=x,DB=DB′=2﹣x,DE=3﹣x.
∵∠EOD=90°,
∴12+x2=(3﹣x)2,
解得:x,
∴D(,0),
∵EB′:DB′=1:(2)=3:2,
∴S△OEB′:S△ODB′=3:2,
又∵S△OED1,
∴S△OEB′S△OED,S△ODB′S△OED,
∴1×xB′,yB′
∴xB′,yB′,
∴B′(,).
(2)如图,连接B'G,B'B,BG,
设OB'=t,则AB'=OA﹣OB'=2﹣t.设BD=B'D=m,则OD=OB﹣BD=2﹣m,
在RtΔOB'D中,OB'+OD2=B'D2,
∴t2+(2﹣m)2=m2,
解得.
∴,
设CG=n,则AG=AC﹣CG=2﹣n,
在 Rt△AB'G中,B'G2=AB'2+AG2=(2﹣t)2+(2﹣n)2,
在Rt△BCG中,BG2=CG2+BC2=n2+22=n2+4,
由折叠可知DG垂直平分B'B,
∴B'G=BG,
∴B'G2=BG2,
即(2﹣t)2+(2﹣n)2=n2+4,
解得,
∴S梯形DBCG,
∴S=S正方形OABC﹣S△BOD﹣S梯形DBCG.
29.(1)证明:正方形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(4,4),
∴OC=AB=OA=BC=4,OC∥AB,
∵3,
∴BE=3,AE=1,
∴E(4,1),
代入yx+b得﹣2+b=1,解得b=3,
∴yx+3,
∴D(0,3),
∴OD=BE=3,
∵OD∥BE,
∴四边形ODBE是平行四边形;
(2)解:过点D作DH⊥AB于H,
∴∠DHE=∠BAP=90°,四边形ODHA是矩形,
∴DH=OA=AB=4,BH=CD=1,
∵DH⊥AB,BP⊥DE,
∴∠EDH+DEH=∠PBA+DEH=90°,
∴∠EDH=∠PBA,
∴△DHE≌△BAP(ASA),
∴PA=EH=BE﹣BH=2,
∴OP=OA﹣PA=2,
设M的坐标为(m,m+3),
∴S△OMP2×(m+3)=2.6,解得m,
∴M点的坐标为(,);
(3)解:当四边形OMDN是菱形时,如图,
∵M的纵坐标是1.5,把y=1.5代入1.5x+3,解得:x=3,
则M的坐标是(3,1.5),
∴点N的坐标为(﹣3,1.5);
当四边形OMND是菱形时,如图,
∵OM=OD=3,则设M的横坐标是m,则纵坐标是m+3,
则m2+(m+3)2=9,
解得:m或0(舍去).
则M的坐标是(,),
∴点N的坐标为(,).
综上,点N的坐标为(﹣3,1.5)或(,).
30.(1)解:∵长方形纸片ABCD和AFGQ是两个完全相同的长方形,
∴AC=AG,∠BAC=∠GAF,
∴∠BAC+∠CAD=∠GAF+∠CAD,
∴∠GAC=∠BAD=90°,
∴△ACG是等腰直角三角形,
∴∠ACG=45°,
故答案为:45;
(2)①证明:∵BM=AB,
∴∠BMA=∠BAM,
∵四边形ABCD是矩形,
∴AB∥DC,
∴∠DMA=∠MAB;
∴∠BMA=∠DMA,
∴AM平分∠DMB;
②解:过点B作BE⊥AF于点E,
∵AF=AB=10,AD=6,
∴DF8,
∴CF=DC﹣DF=2,
∵AB=AF,
∴∠AFB=∠ABF,
∵AB∥CD,
∴∠ABF=∠CFB,
∴∠AFB=∠CFB,
∵BF=BF,∠C=∠BEF=90°,
∴△BCF≌△BEF(AAS),
∴CF=EF=2,BC=BE,
∴AE=8,
∵AD=AQ=BC,
∴AQ=BE,
∵∠QAO=∠BEO,∠AOQ=∠BOE,
∴△AOQ≌△EOB(AAS),
∴AO=OEAE=4,
故答案为:4;
(3)解:如图,过点F作FH⊥CD交CD于点H,
∵四边形ABCD是正方形,
∴CB=AB,∠ABC=90°,
∴∠H=∠ABC=90°,
由旋转的性质得:∠AEF=90°,EF=AE,
∵∠BEA+∠BAE=∠BEA+∠FEH=90°,
∴∠BAE=∠FEH,
在△AEB和△EFH中,
,
∴△AEB≌△EFH(AAS),
∴FH=BE,AB=EH,
∴EH=CB,
∴CH+CE=CE+BE,
∴CH=BE,
∴FH=CH,
∴∠FCH=45°,
∴∠BCG=45°,
∵∠CBG=90°,
∴△CBG是等腰直角三角形,
∴BG=BC=5;
故答案为:5;
(4)解:过点F作∠EFH=∠BEC,与ED的延长线交于点H,
∵四边形ABCD是菱形,
∴CB=CD,∠A=∠BCD=120°,
由旋转得∠BEF=120°,EF=BE,
∴∠BEC+∠CBE=∠BEC+∠FEH=60°,
∴∠CBE=∠FEH,
∴△BEC≌△EFH(AAS),
∴∠H=∠BCD=120°,EH=BC,FH=CE,
∴CD=EH,
∴DH=CE,
∴DH=FH,
∴∠FDH=∠DFH=30°,
∴∠CDG=30°,
∵∠DCG=180°﹣∠BCD=60°,
∴∠G=90°,
∴△DCG是直角三角形,
∵∠CDG=30°,
∴CGCDBC,
∵BG=6,
∴3CG=6,
∴CG=2.
故答案为:2.
【类型一:正方形的性质】
1.如图,在正方形ABCD的对角线BD上取点E使BE=BA,连接AE,过点E作EF⊥AE交BC于点F,则∠EFC的大小为 .
2.已知:如图,E是边长为2的正方形ABCD对角线BD上的一点,EF⊥BD交DC于点F,且DE=CF.则线段EF的长为 .
3.如图,正方形ABCD的对角线交于点O,以AB为边向外作等边△ABE,连接OE.交AB于点F.若AB=4,则OE的长为 .
4.如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,求GH的长.
5.如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF⊥DG于F.
(1)求证:△AED≌△DFC;
(2)求证:AE=FC+EF.
【类型二:正方形的判定】
6.如图,已知 ABCD的对角线AC、BD交于点O,添加条件后, ABCD不一定是正方形的选项为( )
A.AB=AD,AC=BD B.AB=BC,AC⊥BD
C.∠BAD=90°,AC⊥BD D.∠AOD=90°,AO=DO
7.如图,△ABC中,D为AC边上一点,BD平分∠ABC,过点D作DE∥BC,与AB交于点E,作DF∥AB,与BC交于点F,连接EF.则以下结论中错误的是( )
A.四边形BFDE是菱形
B.BD与EF互相垂直且平分
C.当AB=BC时,四边形DEFC是菱形
D.若∠ABC=90°时,则四边形BFDE是正方形
8.如图, ABCD中,点E、F分别在边AD、BC上,点G、H在边BD上,且AE=CF,BG=DH,关于四边形EGFH,下列说法正确的个数是( )
①四边形EGFH一定是平行四边形且有无数个;
②四边形EGFH可以是矩形且有无数个;
③四边形EGFH可以是菱形且有无数个;
④四边形EGFH可以是正方形且有无数个.
A.1个 B.2个 C.3个 D.4个
9.如图,AD是等腰三角形ABC的底边BC上的高,O是AC的中点,延长DO到点E,使AE∥BC,连接CE.
(1)求证:四边形ADCE是矩形;
(2)若AB=2,BC=2,求证:四边形ADCE是正方形.
10.△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
(1)说明:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,证明你的结论;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF为正方形.
11.如图,在正方形ABCD和 ECGF中,点B,C,G在同一条直线上,P是线段AF的中点,连接DP,连接EP并延长,交AD于点Q.请证明:
(1)四边形ECGF是矩形.
(2)当∠DPE=90°时,四边形ECGF是正方形.
【类型三:正方形的旋转问题】
12.如图,将正方形ABCD绕点A按逆时针方向旋转到正方形AB'C'D',旋转角为a(0°<α<180°),连接B'D、C'D,若B'D=C'D,则∠α= .
13.如图,边长为1的正方形ABCD绕点C逆时针旋转45°后得到正方形A′B′CD′,边A′D′与AB交于点E,则阴影部分的面积是( )
A. B. C. D.
14.已知正方形ABCD中,点E在边DC上,DE=2,EC=1,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则EF的长为 .
15.如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转60°,使点B落在点B′的位置,连接BB′,过点D作DE⊥BB′,交BB′的延长线于点E,则B′E的长为( )
A. B. C. D.
【类型四:正方形的翻折问题】
16.如图,在矩形ABCD中,AB=m,BC=8,点M是AD的中点,点N是射线DC上一点,且CN=6,连接BN,将△DMN沿MN翻折至△D'MN,使D恰好落在BN上,则m= .
17.【模型呈现】在正方形学习过程中,我们发现下面的结论:如图1,正方形ABCD中,点P为线段BC上一个动点,若线段MN垂直AP于点E,交线段AB于点M,交线段CD于点N,则AP=MN.
(1)如图②,将边长为40的正方形ABCD折叠,使得点B落在CD上的点E处.若折痕FG=41,则CE= .
【继续探索】
(2)如图③,正方形ABCD中,点P为线段BC上一动点,若MN垂直平分线段AP,分别交AB,AP,BD,
DC于点M,E,F,N.求证:EF=ME+FN.
(3)如图④,在正方形ABCD中,E、F分别为AD,BC上的点,作DM⊥EF于M,在MF上截取MN=DM,
连接BN,G为BN中点,连接CG,CM.请依题意补全图形,若CG=2,则CM= .
【类型五:正方形的动点问题】
18.如图,正方形ABCD中,P为BD上一动点,过点P作PQ⊥AP交CD边于点Q.点P从点B出发,沿BD方向移动,若移动的路径长为6,则AQ的中点M移动的路径长为 .
19.在正方形ABCD中,O是AD的中点,点P从A点出发沿A→B→C→D的路线匀速运动,移动到点D时停止.
(1)如图1,若正方形的边长为12,点P的运动速度为2单位长度/秒,设t秒时,正方形ABCD与∠POD重叠部分的面积为y.
①当t=5时,y= ;当t=10时,y= .
②求t为何值时,以点O、A、P、C为顶点的四边形是平行四边形?
(2)如图2,若点Q从D出发沿D→C→B→A的路线匀速运动.P、Q两点同时出发,点P的速度大于点Q的速度,当P到终点时,Q也停止运动.设t秒时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积为S,S与t的函数图象如图3所示.
①P,Q两点在第 秒相遇;正方形ABCD的边长是 .
②点P的速度为 单位长度/秒;点Q的速度为 单位长度/秒.
③当t为何值时,重叠部分面积S等于32?
【类型六:正方形与函数综合】
20.若一个三角形有一边上的中线与这边的长相等,则称这个三角形为该边上的“完美三角形”.如图在直角坐标系中,正方形ABCO的两边OA、OC分别在坐标轴上,点B的坐标是(3,3).在正方形ABCO的边上找一点P,使得△POC是OC边上的“完美三角形”,点P的坐标为
21.如图,在平面直角坐标系xOy中,矩形OABC的顶点A(8,0),顶点C(0,6),点D为BC边上一动点,设CD的长为m,以AD为一边在与点B的同侧作正方形ADEF,在点D运动过程中,探究以下问题:
(1)①当点D与点C重合时,点E的坐标为 ;
②用含m的代数式表示点E的坐标为 .
(2)三角形ABF的面积是否改变?如果不变,求出此定值;如果改变,请说明理由;
(3)当△BEF为等腰三角形时,直接写出所有m的值.
22.如图,正方形OABC的顶点O在坐标原点,定点A的坐标为(4,3).
(1)求正方形OABC顶点C的坐标为 ,顶点B的坐标为 ;
(2)现有一动点P从C点出发,沿线段CB向终点B运动,P的速度为每秒1个单位长度,同时另一动点Q从点A出发沿A→O→C向终点C运动,速度为每秒k个单位长度.设运动时间为2秒时,将三角形CPQ沿它的一边翻折,若翻折前后的两个三角形组成的四边形为菱形,求k的值.
【类型七:正方形综合题】
23.如图1,点C在线段AB上,分别以AC、BC为边在线段AB的同侧作正方形ACDE和BCFG,连接AF、BD.
(1)若AF=5,则BD= ;
(2)如果点C在线段AB的延长线上,如图2,其他条件不变,求证:AF=BD.
24.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
(1)求证:BE=DE;
(2)判断DF与ON的位置关系,并说明理由;
(3)△BEF的周长为 .
25.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)∠EAF= °(直接写出结果不写解答过程);
(2)①求证:四边形ABCD是正方形.
②若BE=EC=3,求DF的长.
26.点E、F分别在正方形ABCD的边BC、AB所在直线上,点M在直线DE上,且DM=EF,EF⊥DE,MN⊥直线BC,垂足分别是E、N.
(1)当点E在边BC上时,如图①,求证:MN+BE=CD;
(2)当点E在BC的延长线上时,如图②;当点E在CB的延长线上时,如图③,请直接写出线段MN,BE,CD之间的数量关系,不需要证明.
27.数学课上,李老师给出这么一道数学问题:如图①,正方形ABCD中,点E是对角线AC上任意一点,过点E作EF⊥AC,垂足为E,交BC所在直线于点F.探索AF与DE之间的数量关系,并说明理由.
小明在解决这一问题之前,先进行特殊思考:如图②,当E是对角线AC的中点时,他发现AF与DE之间的数量关系是 .若点E在其它位置时,这个结论是否都成立呢?小明继续探究,他用“平移法”将AF沿AD方向平移得到DG,将原来分散的两条线段集中到同一个三角形中,如图③,这样就可以将问题转化为探究DG与DE之间的数量关系.
(1)请你按照小明的思路,完成解题过程;
(2)你能用与小明不同的方法来解决李老师给出的“数学问题”吗?请写出解题过程.
28.在如图所示的平面直角坐标系中,正方形AOBC边长为2,点C的坐标为(2,2).
(1)如图1,动点D在OB边上,将△BCD沿直线DC折叠,点B落在点B′处,连接DB′并延长,交AO于点E.
①当B′D=OD时,点D的坐标是 ;
②若点E是线段OA的中点,求此时点D与点B′的坐标;
(2)如图2,动点D,G分别在边OB,AC上,将四边形DBCG沿直线DG折叠,使点B的对应点B′始终落在边OA上(点B′不与点O,A重合),点C落在点C′处,B′C′交AC于点E.设OB′=t,四边形AB′DG的面积为S,直接写出S与t的关系式.
29.如图,正方形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(4,4),一次函数的图象与边OC、AB分别交于点D、E,并且满足.点M是线段DE上的一个动点.
(1)连接BD、OE,求证:四边形ODBE是平行四边形;
(2)作BP⊥DE交OA于P,当△OMP面积为2.6时,求M点的坐标;
(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
30.在数学综合与实践活动课上,同学们用两个完全相同的矩形纸片展开探究活动:
【实践探究】
(1)小红将两个矩形纸片摆成图1的形状,连接AG、AC,则∠ACG= °;
【解决问题】
(2)将矩形AQGF绕点A顺时针转动,边AF与边CD交于点M,连接BM,AB=10,AD=6.
①如图2,当BM=AB时,求证:AM平分∠DMB;
②如图3,当点F落在DC上时,连接BQ交AF于点O,则AO= ;
【迁移应用】
(3)如图4,正方形ABCD的边长为5,E是BC边上一点(不与点B、C重合),连接AE,将线段AE绕点E顺时针旋转90°至FE,作射线FC交AB的延长线于点G,则BG= ;
(4)如图5,在菱形ABCD中,∠A=120°,E是CD边上一点(不与点C、D重合),连接BE,将线段BE绕点E顺时针旋转120°至FE,作射线FD交BC的延长线于点G.若BG=6,则CG= .
参考答案
【类型一:正方形的性质】
1.
【分析】由四边形ABCD是正方形,EF⊥AE得∠BAD=∠AEF=∠C=90°,则∠DAE+∠BAE=90°,∠BEF+∠BEA=90°,∠ABD=∠ADB=∠CBD=∠CDB=45°,而BE=BA,则DA=BE,∠BAE=∠BEA=67.5°,所以∠DAE=∠BEF,可证明△DAE≌△BEF,得∠AED=∠EFB,则∠EFC=∠BEA=67.5°,于是得到问题的答案.
【解答】解:∵四边形ABCD是正方形,EF⊥AE,
∴DA=BA=BC=DC,∠BAD=∠AEF=∠C=90°,
∴∠DAE+∠BAE=90°,∠BEF+∠BEA=90°,∠ABD=∠ADB=∠CBD=∠CDB=45°,
∵BE=BA,
∴DA=BE,∠BAE=∠BEA(180°﹣45°)=67.5°,
∴∠DAE=∠BEF,
在△DAE和△BEF中,
,
∴△DAE≌△BEF(ASA),
∴∠AED=∠EFB,
∴∠EFC=180°﹣∠EFB=180°﹣∠AED=∠BEA=67.5°,
故答案为:67.5°.
2.
【分析】由边长为2的正方形ABCD中∠BDC=45°,EF⊥BD,DE=CF,得BDDC=2,设DE=x,则DFDEx,由DF+FC=DC,得x+x=2,即可得EF=DE=x=22.
【解答】解:由边长为2的正方形ABCD中∠BDC=45°,EF⊥BD,DE=CF,
得BDDC=2,
设CF=DE=x,则DFDEx,
由DF+FC=DC,
得x+x=2,
得EF=DE=x=22.
故答案为:22.
3.
【分析】根据正方形的性质得AB=BC=4,OA=OC=OB=OD,∠ABC=90°,则点O在线段AB的垂直平分线上,再根据等边三角形的性质得EA=EB=AB=2,则点E在线段AB的垂直平分线上,由此的OE是线段AB的垂直平分线,则AF=BF=2,然后由勾股定理分别求出OF=2,EF,进而可得OE的长.
【解答】解:∵四边形ABCD是正方形,AB=4,
∴AB=BC=4,OA=OC=OB=OD,∠ABC=90°,
在Rt△ABC中,由勾股定理得:AC,
∴OA=OBAC,
∴点O在线段AB的垂直平分线上,
∵△ABE是等边三角形,
∴EA=EB=AB=2,
∴点E在线段AB的垂直平分线上,
∴OE是线段AB的垂直平分线
∴OE⊥AB,AF=BFAB=2,
在Rt△AOF中,由勾股定理得:OF2,
在Rt△AEF中,由勾股定理得:EF,
∴OE=OF+EF.
故答案为:.
4.解:∵四边形ABCD是正方形,
∴AB=DA,∠BAE=∠ADF=90°,
在△BAE和△ADF中
,
∴△BAE≌△ADF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=90°,
∴∠BGF=90°,
∵点H为BF的中点,
∴GHBF,
又∵BC=CD=5,DF=2,∠C=90°,
∴CF=3,
∴BF,
∴GH.
5.证明:(1)∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
∴∠ADE+∠CDF=90°,
∵AE⊥DG,CF⊥DG,
∴∠AED=∠DFC=90°,
∴∠DAE+∠ADE=90°,
∴∠DAE=∠CDF,
在△AEE和△DFC中,
,
∴△AED≌△DFC(AAS);
(2)∵△AED≌△DFC,
∴AE=DF,ED=FC,
∵DF=ED+EF=FC+EF.
∴AE=FC+EF.
【类型二:正方形的判定】
6.
【分析】根据题意逐一对选项分析即可得出答案.
【解答】解:A、因为AB=AD,所以 ABCD为菱形,因为AC=BD,所以 ABCD为正方形,不符合题意;
B、因为AB=BC,所以 ABCD为菱形,但AC⊥BD不能证明 ABCD为正方形,符合题意;
C、因为∠BAD=90°,所以 ABCD为矩形,又因为AC⊥BD所以 ABCD为正方形,不符合题意;
D、因为∠AOD=90°,所以 ABCD为菱形,又因为AO=DO所以 ABCD为正方形,不符合题意;
故选:B.
7.
【分析】根据菱形的判定得出四边形BFDE是菱形,再根据菱形的性质得出BD与EF互相垂直且平分,进而利用菱形的判定和正方形的判定解答即可.
【解答】解:∵DE∥BC,DF∥AB,
∴四边形BFDE是平行四边形,∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠EBD=∠DBF,
∴∠EBD=∠EDB,
∴BE=DE,
∴ BFDE是菱形,故A正确;
∴BD与EF互相垂直且平分,故B正确;
∵∠ABC=90°时,则四边形BFDE是正方形,故D正确;
当AB=BC,不能得出四边形DEFC是菱形,故C错误;
故选:C.
8.
【分析】先利用SAS证明△BFH≌△DEG,由全等三角形的性质得出FH=EG,∠BHF=∠DGE,证出FH∥EG,得出四边形EGFH是平行四边形.再根据矩形、菱形、正方形的判定分别判断即可.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠FBH=∠EDG,
∵AE=CF,BG=DH,
∴DE=BF,BH=DG,
在△BFH和△DEG中,
,
∴△BFH≌△DEG(SAS),
∴FH=EG,∠BHF=∠DGE,
∴FH∥EG,
∴四边形EGFH是平行四边形,
点E、F分别在边AD、BC上移动时, EGFH有无数个,故①说法正确;
如果EF=GH,则 EGFH是矩形且有无数个,故②说法正确;
如果FG=FH,则 EGFH是菱形且有无数个,故③说法正确;
假设过BD的中点O的直线交AD、BC于点M、N,只有当OG=OM时,生产的四边形是正方形,点M、N即为符合题意得点E、F,且仅有这一种可能,故④说法错误.
故选:C.
9.证明:(1)∵AD是等腰三角形ABC底边BC上的高,
∴AD⊥BC,BD=CD,
∴D为BC的中点,
又∵O是AC的中点,
∴DO∥AB,
∵DE∥AB,AE∥BD,
∴四边形AEDB是平行四边形,
∴AE=BD=CD,
∵AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵∠ADC=90°,
∴四边形ADCE是矩形;
(2)∵AD是等腰三角形ABC的底边BC上的高,
∴BD=CD,
∴AD,
∴AD=CD,
∴四边形ADCE是正方形.
10.(1)证明:∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠DCF,
又∵CE平分∠BCO,CF平分∠DCO,
∴∠OCE=∠BCE,∠OCF=∠DCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形;
(3)解:当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(2)知,当点O运动到AC的中点时,四边形AECF是矩形,
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形.
11.(1)解:∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠GCE=90°,
∵四边形ECGF是平行四边形,
∴平行四边形ECGF是矩形;
(2)证明:在正方形ABCD和 ECGF中,点B,C,G在同一条直线上,
∴AD∥BG,EF∥BG,∠ADC=90°,
∴AD∥EF,
∴∠QAP=∠EFP,
∵P是线段AF的中点,
∴AP=PF,
又∠APQ=∠FPE,
∴△APQ≌△FPE(ASA),
∴AQ=EF,QP=PE,
∵∠DPE=90°,
∴∠DPQ=90°,
在△PDQ和△PDE中,
,
∴△PDQ≌△PDE(SAS),
∴QD=DE,
∵AD=DC,
∴AQ=EC,
∴EC=EF,
∴矩形ECGF是正方形.
【类型三:正方形的旋转问题】
12.
【分析】作DH⊥B′C′于H,交AD′于G,如图,根据旋转的性质得AD′=AD,∠DAD′=α,再根据等腰三角形的性质由B'D=C'D得到B′H=C′H,则AG=D′G,然后证明△ADD′为等边三角形得到∠DAG=60°,从而得到α的度数.
【解答】解:作DH⊥B′C′于H,交AD′于G,如图,
∵正方形ABCD绕点A按逆时针方向旋转到正方形AB'C'D',旋转角为a,
∴AD′=AD,∠DAD′=α,
∵B'D=C'D,
∴B′H=C′H,
∵四边形AB'C'D'为正方形,
∴AG=D′G,
连接DD′,如图,
∵DG垂直平分AD′,
∴DD′=DA,
∴DD′=AD=AD′,
∴△ADD′为等边三角形,
∴∠DAG=60°,
即α=60°.
故答案为60°.
13.
【分析】连接A′C,证明A′,B,C三点共线,勾股定理求出A′C的长,进而求出A′B的长,利用分割法求出阴影部分的面积即可.
【解答】解:连接A′C,
∵边长为1的正方形ABCD绕点C逆时针旋转45°后得到正方形A′B′CD′,
∴BC=1,∠BCD=90°,∠DCD′=45°,∠A′CD′=∠D′A′C=45°,A′D′=CD′=1,
∴∠BCD′=∠BCD﹣∠DCD′=45°,,
∵∠BCD′=∠A′CD′=45°,
∴A′,B,C三点共线,
∴,∠A′BE=90°,
∵∠D′A′B=45°,
∴,
∴,
∴;
故选:D.
14.
【分析】根据正方形的性质可得AB=AD,∠ABC=∠D=90°,再根据旋转的性质可得AF=AE,然后利用“HL”证明Rt△ABF和Rt△ADE全等,根据全等三角形对应边相等可得BF=DE,再求出正方形的边长为3,然后分点F在线段BC上和CB的延长线上两种情况讨论求解.
【解答】解:在正方形ABCD中,AB=AD,∠ABC=∠D=90°,
由旋转的性质得,AF=AE,
在Rt△ABF和Rt△ADE中,,
∴Rt△ABF≌Rt△ADE(HL),
∴BF=DE=2,
∵DE=2,EC=1,
∴正方形的边长为2+1=3,
①点F在线段BC上时,FC=3﹣2=1,
∴EF;
②点F在CB的延长线上时,FC=3+2=5,
∴EF′,
综上所述,EF的长为或,
故答案为:或.
15.
【分析】分别延长AD和BE交于点F,由直角三角形的性质求出EF的长,根据△ABB'是等边三角形,求出B'E=BF﹣BB'﹣EF即可.
【解答】解:分别延长AD和BE交于点F,
由题知,AB=2,∠ABF=60°,
∴BF=2AB=4,AFAB=2,∠F=90°﹣∠ABF=30°,
∴DF=AF﹣AD=22,
∴EFDF=(2)3,
由题知,△ABB'是等边三角形,
∴B'E=BF﹣BB'﹣EF=4﹣2﹣(3)1,
故选:A.
方法二:分别延长BA和ED交于点F,
由题知,AD=2,∠ABE=60°,DE⊥BB′,
∴∠F=90°﹣∠ABE=30°,
∴AFAD=2,
∴BF=AF+AB=22,
∴BEBF1,
由题知,△ABB'是等边三角形,
∴B'E=BE﹣BB'1﹣21,
故选:A.
【类型四:正方形的翻折问题】
16.
【分析】分两种情况:如图,当点N在线段CD时,当点N在CD的延长线时,连接BM,根据矩形的性质得到∠C=∠D=∠A=90°,AD=BC=8,AB=CD=m,由点M是AD的中点,得到AM=DMAD=4,根据折叠的性质得到DM=D′M,∠MD′N=∠D=90°,∠DMN=∠D′MN,根据全等三角形的性质得到∠AMB=∠D′MB,根据勾股定理即可得到结论.
【解答】解:如图,当点N在线段CD时,
连接BM,
∵四边形ABCD是矩形,
∴∠C=∠D=∠A=90°,AD=BC=8,AB=CD=m,
∵点M是AD的中点,
∴AM=DMAD=4,
∵将△DMN沿MN翻折至△D'MN,使D恰好落在BN上,
∴DM=D′M,∠MD′N=∠D=90°,∠DMN=∠D′MN,ND′=ND,
∴∠MDB=90°,
在△AMB与△D′MB中,
,
∴△AMB≌△D′MB(SSS),
∴BD′=AB=m,∠AMB=∠D′MB,
∴∠BMN=∠BMD′+∠NMD′=90°,
∴AB2+AM2=BM2,DM2+DN2=MN2,BM2+MN2=BN2,
∴m2+42+42+(m﹣6)2=(m+m﹣6)2,
∴m=8(负值舍去),
如图,当点N在CD的延长线时,
连接BM,
∵四边形ABCD是矩形,
∴∠C=∠D=∠A=90°,AD=BC=8,AB=CD=m,
∵点M是AD的中点,
∴AM=DMAD=4,
∵将△DMN沿MN翻折至△D'MN,使D恰好落在BN上,
∴DM=D′M,∠MD′N=∠D=90°,∠DMN=∠D′MN,
∴∠MDB=90°,
在△AMB与△D′MB中,
,
∴△AMB≌△D′MB(SSS),
∴BD′=AB=m,∠AMB=∠D′MB,
∴∠BMN=∠BMD′+∠NMD′=90°,
∴AB2+AM2=BM2,DM2+DN2=MN2,BM2+MN2=BN2,
∴m2+42+42+(m+6)2=(m+m+6)2,
解得m=2(负值舍去),
综上所述,m=8或2,
故答案为:8或2.
17.(1)解:∵四边形ABCD是正方形,
∴∠A=∠ABC=∠C=90°,AB=CB,
作FP⊥CB于P,连接BE,
则四边形AFPB是矩形,
∴∠BCE=∠FPG=90°,
由翻折知,GF⊥BE,
∴∠PFG=∠CBE,
∵AB=CB=FP,
∴△FPG≌△BCE(ASA),
∴BE=FG=41,
在Rt△CBE中,由勾股定理得CE9,
故答案为:9;
(2)证明:如图2,连接FA,FP,FC,
∵正方形ABCD是轴对称图形,F为对角线BD上一点,
∴FA=FC,
又∵FE垂直平分AP,
∴FA=FP,
∴FP=FC,
∴∠FPC=∠FCP,
∵∠FAB=∠FCP,
∴∠FAB=∠FPC,
∴∠FAB+∠FPB=180°,
∴∠ABC+∠AFP=180°,
∴∠AFP=90°,
∴FEAP,
由【模型呈现】知,AP=MN,
∴MN=ME+EF+FN=AP=2EF,
∴EF=ME+FN;
(3)解:根据题意补全图形如图所示:
连接MG并延长使得MG=GH,
∵点G为BN的中点,
∴BG=NG,
又∵∠BGH=∠NGM,
∴△BGH≌△NGM(SAS),
∴HG=MG,BH=NM,∠BHG=∠NMG,则BH∥NM,
∴∠CBH=∠BFE,
∵四边形ABCD是正方形,
∴AD∥BC,∠ADC=90°,
∴∠BFE=∠DEM,∠CDM+∠EDM=90°,
又∵DM⊥EF,
∴∠DEM+∠EDM=90°,
∴∠CDM=∠DEM,
∴∠CDM=∠BFE,
∴∠CBH=∠CDM,
∵MN=DM,
∴BH=DM,
由正方形的性质可知,CB=CD,
∴△CBH≌△CDM(SAS),
∴CH=CM,∠BCH=∠DCM,∠BCD=90°,
则∠BCH+∠BCM=∠DCM+∠BCM=∠BCD=90°,
∴△MCH是等腰直角三角形,
∵HG=MG,
∴CG⊥MH,则△CGM也是等腰直角三角形,则CG=MG,
∴CMCG=2.
故答案为:2.
【类型五:正方形的动点问题】
18.
【分析】根据题意,画出运动后 的M点位置,再根据三角形中位线定理即可求得.
【解答】解:连接AC,交BD于点O,连接PC,过P点作 PE⊥AD,PF⊥CD垂足分别为E、F,延长FP,交AB于G,
∵正方形ABCD,
∴∠ADC=90°,∠EDB=∠CDB=45°,
∵∠PED=∠PFD=90°,
∴∠EPD=∠EDP=45°,
∴PE=DE,则四边形PEDF为正方形,
∴PE=PF,∠EPF=90°,
∵∠APQ=∠APE+∠EPQ=90°,∠EPF=∠FPQ+∠EPQ=90°,
∴∠APE=∠QPF,
在△PAE和△PQF中,
,
∴△PAE≌△PQF(AAS),
∴PA=PQ;
∵正方形ABCD,
∴∠ABC=∠C=90°,∠EDB=∠CDB=∠ABD=∠CBD=45°,
∴GF∥BC,
∴∠BGP=90°,
∴△BGP 为等腰直角三角形,
∵BP=6,
∴,
∴,
∵正方形ABCD,
∴AB=BC,∠ABP=∠CBP=45°,BP=BP,O是AC中点,
∴△ABP≌△CBP,
∴PA=PC=PQ
,∵PF⊥CQ,
∴,
∵O是AC中点,M是AQ中点,
,
故答案为:.
19.解:(1)①当t=5时,AP=10,
∵O是正方形ABCD边AD的中点,
∴OA=ODAD=6,
∴S△AOPOA AP6×10=30,
∴y=S正方形ABCD﹣S△AOP=122﹣30=114;
当t=10时,如图1,
则AB+BP=20,
∴BP=20﹣AB=20﹣12=8,
∴PC=BC﹣BP=12﹣8=4,
∴y=S梯形CDOP(PC+OD) CD(4+6)×12=60;
故答案为:114;60.
②如图2,AB+BP=2t,
∴PC=24﹣2t,
∵OA∥CP,
∴当OA=CP时,以点O、A、P、C为顶点的四边形是平行四边形,
∴6=24﹣2t,
解得:t=9,
∴当t=9时,以点O、A、P、C为顶点的四边形是平行四边形.
(2)①由图3可知:当t=4时,S=0,即P,Q两点在第4秒相遇;
当t=0时,S正方形ABCD=AB2=64,
∴AB=8,即正方形ABCD的边长是8;
故答案为:4;8.
②由图3可知:点P、Q相遇于点C,且点P的速度大于点Q的速度,
∴点P的速度为点Q的速度的2倍,
设点Q的速度为a单位长度/秒,则点P的速度为2a单位长度/秒,
∴4(a+2a)=24,
解得:a=2,
∴点P的速度为4单位长度/秒,点Q的速度为2单位长度/秒;
故答案为:4;2.
③∵O是AD的中点,
∴OA=OD=4,
设t秒时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积S等于32,
分三种情况讨论:
当0≤t≤2时,点P在AB边上,点Q在CD边上,如图,
则AP=4t,DQ=2t,OA=OD=4,
∴S=S正方形ABCD﹣S△OAP﹣S△ODQ=644×4t4×2t=64﹣12t,
由题意得:64﹣12t=32,
解得:t2(不符合题意,舍去);
当2<t≤4时,点P在BC边上,点Q在CD边上,如图,
则AB+BP=4t,AB=8,
∴BP=4t﹣8,
∵DQ=2t,OA=OD=4,
∴S=S正方形ABCD﹣S梯形OABP﹣S△ODQ=64(4t﹣8+4)×84×2t=80﹣20t,
由题意得:80﹣20t=32,
解得:t,符合题意;
当4<t≤6时,点P在CD边上,点Q在BC边上,如图,
∵AB+BC+CP=4t,AB=BC=CD=AD=8,
∴DP=24﹣4t,
∵DC+CQ=2t,
∴BQ=16﹣2t,
∴S=S正方形ABCD﹣S梯形OABQ﹣S△ODP=64(4+16﹣2t)×84×(24﹣4t)=16t﹣64,
由题意得:16t﹣64=32,
解得:t=6(符合题意);
综上,当t或6时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积等于32.
【类型六:正方形与函数综合】
20.
【分析】根据正方形的性质得出C(3,0),A(0,3),进而利用勾股定理解答即可.
【解答】解:∵四边形ABCO是正方形,点B的坐标是(3,3),
∴C(3,0),A(0,3),
∴OC中点D的坐标为(1.5,0),
如图所示,当点P在AB上时,设P(m,3);
∵△POC是OC边上的“完美三角形”,
∴P1D=OC=3,
∴(m﹣1.5)2+(3﹣0)2=32,
解得m=1.5,
∴点P的坐标为(1.5,3).
如图2所示,当点P在BC上时,设P(3,n);
∵△POC是OC边上的“中线三角形”,
∴P2D=OC=3,
∴(n﹣0)2+(3﹣1)2=32,
解得m(负值舍去),
∴点P的坐标为(3,),
如图3所示,当点P在OA上时,设P(0,s);
∵△POC是OC边上的“中线三角形”,
∴P3D=OC=3,
∴(s﹣0)2+(0﹣1)2=32,
解得s(负值舍去),
∴点P的坐标为(0,);
综上所述,点P的坐标为(1.5,3)或(3,)或(0,).
21.解:(1)①如图1﹣1中,过点E作EH⊥BC于H.
∵四边形ABCO是矩形,A(8,0),C(0,6),
∴OA=BC=8,AB=OC=6,
∵∠BCO=∠ACE=90°,
∴∠ACB=∠ECH,
∵CE=CB,∠EHC=∠ABC=90°,
∴△EHC≌△CBA(AAS),
∴EH=CB=8,CH=AB=6,
∴E(6,14).
故答案为:(6,14);
②如图1﹣2中,过点E作EH⊥BC于H.
同法可证:△EHD≌△DBA(AAS),
∴EH=DB=8﹣m,DH=AB=6,
∴CH=6+m,
∴E(6+m,14﹣m).
故答案为:(6+m,14﹣m);
(2)△ABF的面积不会改变,理由如下:
如图2,过点F作FH⊥AB,交AB的延长线于H,
∵矩形OABC的顶点B坐标为(8,6),
∴AB=6,BC=8,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∴∠DAB+∠FAB=90°,且∠DAB+∠BDA=90°,
∴∠BDA=∠FAB,
∵AD=AF,∠ABD=∠AHF=90°,
∴△ABD≌△FHA(AAS),
∴HF=AB=6,
∴△ABF的面积AB×HF=18;
(3)若BE=EF,当点B与点D重合时,AD=AB=6,此时m=8.
当点B与点D不重合时,如图3,过点E作EH⊥DB于H,
∵∠EDH+∠ADB=90°,∠ADB+∠DAB=90°,
∴∠EDH=∠DAB,
AD=DE,∠EHD=∠ABD=90°,
∴△ADB≌△DEH(AAS),
∴DH=AB=6,
∵BE=EF,EF=DE,
∴DE=BE,
∵EH⊥DB
∴DH=BH=6,
∴DB=12,
∵DB<BC,
∴此种情形不存在.
若EB=BF,
∵BE=BF,
∴∠BEF=∠BFE,
∴∠DEB=∠AFB,
∵DE=AF,BE=BF,
∴△DEB≌△AFB(AAS),
∴DB=AB=36,
∴CD=BC﹣BD=8﹣6=2,即m=2;
若BF=EF,如图4,过点F作FH⊥AB于H,
∵∠DAB+∠FAB=90°,∠DAB+∠BDA=90°,
∴∠BDA=∠FAB,
∵AD=AF,∠ABD=∠AHF=90°,
∴△ABD≌△FHA(AAS),
∴AH=DB,
∵EF=BF,EF=AF,
∴BF=AF,
∵FH⊥AB,
∴AH=BH=3,
∴DB=3,
∴CD=BC﹣BD=8﹣3=5,即m=5,
综上所述,满足条件的m的值为8或2或5.
22.解:(1)过点A作AD⊥x轴于D,过点B作BE⊥AD交DA的延长线于E,过点C作CF⊥x轴于点F,
∴∠ADO=∠OFC=∠BEA=90°,
∴∠DAO+∠AOD=90°,
∵四边形ABCO是正方形,
∴∠OAB=∠AOC=90°,OA=OC=AB,
∴∠COF+∠AOD=90°,∠BAE+∠DAO=90°,
∴∠FOC=∠DAO,∠BAE=∠AOD,
∴△COF≌△AOD≌△BAE(AAS),
∴OF=AD=BE,CF=OD=AE,
∵点A的坐标为(4,3),
∴OF=AD=BE=3,CF=OD=AE=4,
∴点C的坐标为(﹣3,4);
∴ED=4+3=7,点B到y轴的距离为OD﹣BE=4﹣3=1,
∴点B的坐标为(1,7);
故答案为:﹣3,4,1,7;
(2)由题意,得AO=CO=BC=AB5,
当 t=2 时,CP=2.
将三角形CPQ沿它的一边翻折,若翻折前后的两个三角形组成的四边形为菱形,
只需三角形CPQ是等腰三角形即可.
①当点Q在OA上时,
∵PQ AB>PC,
∴只存在一点Q,使QC=QP.
过点Q作QD⊥PC于点D,如图,
则CD=PD=1,
∵QA=BD,
∴2k=5﹣1=4,
∴k=2;
②当点Q在OC上时,
∵∠BCO=90°,
∴只存在一点Q,使CP=CQ=2,
∴2k=10﹣2=8,
∴k=4.
综上所述,k的值为2或4.
【类型七:正方形综合题】
23.(1)解:四边形ACDE和四边形BCFG是正方形,
∴AC=CD,∠DCA=∠DCB=90°,BC=CF,
在△AFC和△DBC中,
∴在△AFC≌△DBC(SAS),
∴BD=AF=5;
故答案为:5;
(2)证明:连接AF,
∵四边形ACDE、BCFG是正方形,
∴AC=DC,CB=CF,
同(1)可证△ACF≌△DCB(SAS),
∴AF=DB,
24.解:(1)∵四边形ABCD是正方形,
∴CA平分∠BCD,BC=DC,
∴∠BCE=∠DCE=45°,
∵CE=CE,
∴△BCE≌△DCE(SAS),
∴BE=DE.
(2)DF⊥ON,理由如下:
∵△BCE≌△DCE,
∴∠EBC=∠EDC,
∵∠EBC=∠CBN,
∴∠EDC=∠CBN,
∵∠EDC+∠1=90°,∠1=∠2,
∴∠2+∠CBN=90°,
∴∠EFB=90°,即DF⊥ON;
(3)如图所示,过C作CG⊥ON于G,过D作DH⊥CG于H,则∠CGB=∠AOB=90°,四边形DFGH是矩形,
又∵∠ABC=90°,
∴∠ABO+∠BAO=90°=∠ABO+∠CBG,
∴∠BAO=∠CBG,
又∵AB=BC,
∴△ABO≌△BCG(AAS),
∴BG=AO12,CG=BO=5,
同理可得△CDH≌△BCG,
∴DH=CG=5,CH=BG=12,
∴HG=5+12=17,
∴DF=HG=17,GF=DH=5,
∴BF=BG﹣GF=12﹣5=7,
∴△BEF的周长=BF+EF+BE=BF+EF+DE=BF+DF=7+17=24,
故答案为:24.
25.(1)解:∵∠C=90°,
∴∠CFE+∠CEF=90°,
∴∠DFE+∠BEF=360°﹣90°=270°,
∵AF平分∠DFE,AE平分∠BEF,
∴∠AFEDFE,∠AEFBEF,
∴∠AEF+∠AFE(∠DFE+∠BEF)270°=135°,
∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,
故答案为:45;
(2)①证明:作AG⊥EF于G,如图1所示:
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
②解:设DF=x,
∵BE=EC=3,
∴BC=6,
由①得四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE与Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=EG=6,
同理,GF=DF=x,
在Rt△CEF中,EC2+FC2=EF2,
即32+(6﹣x)2=(x+3)2,
解得:x=2,
∴DF的长为2.
26.(1)证明:当点E在边BC上时,如图①,
过M点作MG⊥DC于G点,
∵四边形ABCD是正方形,
∴∠C=∠B=90°,
∴∠1+∠2=90,
∴∠DEF=90°,
∴∠2+∠3=90,
∴∠1=∠3,
又∵∠MGD=∠B=90°,DM=EF,
∴△DGM≌△EBF(AAS),
∴DG=EB,
∵MG⊥DC,MN⊥BC,∠C=90°,
∴∠MGC=∠MNC=∠C=90°,
∴四边形GMNC是矩形,
∴MN=GC,
∴MN+BE=GC+DG=CD.
(2)当点E在BC的延长线上时,如图②,
延长DC,过M点作MG⊥DC的延长线于G点,
则四边形MNCG是矩形,
∴MN=CG,
∵∠DCE=90°,∠DEF=90°,
∴∠1+∠2=90,∠2+∠3=90,
∴∠1=∠3,
∵∠DGM=∠EBF=90°,DM=EF,
∴△DGM≌△EBF(AAS),
∴DG=EB,
∵DG=DC+CG,
∴EB=DC+MN.
当点E在CB的延长线上时,如图③,
过D点作DG⊥MN于G点,
则四边形GDCN是矩形,
∴DC=GN,
∵∠N=90°,
∴∠1+∠2=90°,
∵∠MEF=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∵∠MGD=∠EBF=90°,MD=EF,
∴△MGD≌△EBF(AAS),
∴MG=EB,
∵MN=MG+GN,
∴MN=BE+DC.
27.解:AFDE,理由如下:
∵四边形ABCD是正方形,E是对角线AC的中点,
∴AC⊥BD,AE=BE=CE=DE.
∵AB2=AE2+BE2,
∴AB2=2DE2,
∵B点与F点重合,
∴AF2=2DE2,
∴;
(1)如图③,延长BC,作DG∥AF,交BC的延长线于点G,连接EG,
∵四边形ABCD是正方形,
∴∠ABC=∠BCD﹣90°,AB=BC=CD=AD,AD∥BC,
∵DG∥AF,AD∥BC,
∴四边形AFGD为平行四边形,
∴AF=DG,AD=FG,
∴FG=CD.
∵∠ABC=90°,AB=BC,
∴∠ACB=45°,∠ACD=45°,
∵EF⊥AC,
∴∠FEC=90°,
∴∠EFC=∠ECF=45°,
∴EF=EC.
∴∠EFC=∠ECD.
∴△CDE≌△FGE(SAS).
∴ED=EG,∠FEG=∠CED.
∴∠DEG=∠FEC=90°,
∴△DEG是等腰直角三角,
∴DG2=DE2+EG2=2DE2,
∴,
∴AFDE,
故答案为:AFDE.
(2)如图④,作DG⊥DE,并截取DG=DE,连接AG、GE,
∵四边形ABCD是正方形,
∴∠ADC=90°,CD=AD,
∴∠DAC=∠DCA=45°,
同理,∠ACB=45°,
∵GD⊥DE,
∴∠GDE=90°,
又∵DG=DE,
∴△DEG是等腰直角三角形,
∴EG2=DE2+DG2=2DE2,
∴EGDE,
∵∠ADC=∠GDE=90°,
∴∠GDA=∠EDC,
∴△GDA≌Δ EDC(SAS),
∴∠GAD=∠ECD=45°,AG=EC,
∴∠GAE=90°,
∵EF⊥AC,
∴∠FEC=∠FEA=90°,
∴∠EFC=∠ECF=45°,
∴EF=EC.
∴EF=AG,
∵∠GAE=∠FEA=90°,
∴AG∥EF,
∴四边形AGEF为平行四边形,
∴AF=EG.
∵AFDE.
28.解:(1)①∵正方形AOBC边长为2,点C的坐标为(2,2),
∴OB=BC=AC=OA=2,
∵将△BCD沿直线DC折叠,
∴B′D=BD,
又∵B′D=OD,
∴BD=OD,
∴,
∴点D的坐标是(1,0),
故答案为:(1,0);
②连接CE.
∵折叠,
∴CB′=CB=AC=2.
在Rt△EAC和Rt△E′BC中,
,
∴Rt△EAC≌Rt△E′BC(HL),
∴EB′=AE,
∵E为OA中点,
∴AE=OEOA=1,
∴EB′=AE=1.
设D(x,0),则OD=x,DB=DB′=2﹣x,DE=3﹣x.
∵∠EOD=90°,
∴12+x2=(3﹣x)2,
解得:x,
∴D(,0),
∵EB′:DB′=1:(2)=3:2,
∴S△OEB′:S△ODB′=3:2,
又∵S△OED1,
∴S△OEB′S△OED,S△ODB′S△OED,
∴1×xB′,yB′
∴xB′,yB′,
∴B′(,).
(2)如图,连接B'G,B'B,BG,
设OB'=t,则AB'=OA﹣OB'=2﹣t.设BD=B'D=m,则OD=OB﹣BD=2﹣m,
在RtΔOB'D中,OB'+OD2=B'D2,
∴t2+(2﹣m)2=m2,
解得.
∴,
设CG=n,则AG=AC﹣CG=2﹣n,
在 Rt△AB'G中,B'G2=AB'2+AG2=(2﹣t)2+(2﹣n)2,
在Rt△BCG中,BG2=CG2+BC2=n2+22=n2+4,
由折叠可知DG垂直平分B'B,
∴B'G=BG,
∴B'G2=BG2,
即(2﹣t)2+(2﹣n)2=n2+4,
解得,
∴S梯形DBCG,
∴S=S正方形OABC﹣S△BOD﹣S梯形DBCG.
29.(1)证明:正方形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(4,4),
∴OC=AB=OA=BC=4,OC∥AB,
∵3,
∴BE=3,AE=1,
∴E(4,1),
代入yx+b得﹣2+b=1,解得b=3,
∴yx+3,
∴D(0,3),
∴OD=BE=3,
∵OD∥BE,
∴四边形ODBE是平行四边形;
(2)解:过点D作DH⊥AB于H,
∴∠DHE=∠BAP=90°,四边形ODHA是矩形,
∴DH=OA=AB=4,BH=CD=1,
∵DH⊥AB,BP⊥DE,
∴∠EDH+DEH=∠PBA+DEH=90°,
∴∠EDH=∠PBA,
∴△DHE≌△BAP(ASA),
∴PA=EH=BE﹣BH=2,
∴OP=OA﹣PA=2,
设M的坐标为(m,m+3),
∴S△OMP2×(m+3)=2.6,解得m,
∴M点的坐标为(,);
(3)解:当四边形OMDN是菱形时,如图,
∵M的纵坐标是1.5,把y=1.5代入1.5x+3,解得:x=3,
则M的坐标是(3,1.5),
∴点N的坐标为(﹣3,1.5);
当四边形OMND是菱形时,如图,
∵OM=OD=3,则设M的横坐标是m,则纵坐标是m+3,
则m2+(m+3)2=9,
解得:m或0(舍去).
则M的坐标是(,),
∴点N的坐标为(,).
综上,点N的坐标为(﹣3,1.5)或(,).
30.(1)解:∵长方形纸片ABCD和AFGQ是两个完全相同的长方形,
∴AC=AG,∠BAC=∠GAF,
∴∠BAC+∠CAD=∠GAF+∠CAD,
∴∠GAC=∠BAD=90°,
∴△ACG是等腰直角三角形,
∴∠ACG=45°,
故答案为:45;
(2)①证明:∵BM=AB,
∴∠BMA=∠BAM,
∵四边形ABCD是矩形,
∴AB∥DC,
∴∠DMA=∠MAB;
∴∠BMA=∠DMA,
∴AM平分∠DMB;
②解:过点B作BE⊥AF于点E,
∵AF=AB=10,AD=6,
∴DF8,
∴CF=DC﹣DF=2,
∵AB=AF,
∴∠AFB=∠ABF,
∵AB∥CD,
∴∠ABF=∠CFB,
∴∠AFB=∠CFB,
∵BF=BF,∠C=∠BEF=90°,
∴△BCF≌△BEF(AAS),
∴CF=EF=2,BC=BE,
∴AE=8,
∵AD=AQ=BC,
∴AQ=BE,
∵∠QAO=∠BEO,∠AOQ=∠BOE,
∴△AOQ≌△EOB(AAS),
∴AO=OEAE=4,
故答案为:4;
(3)解:如图,过点F作FH⊥CD交CD于点H,
∵四边形ABCD是正方形,
∴CB=AB,∠ABC=90°,
∴∠H=∠ABC=90°,
由旋转的性质得:∠AEF=90°,EF=AE,
∵∠BEA+∠BAE=∠BEA+∠FEH=90°,
∴∠BAE=∠FEH,
在△AEB和△EFH中,
,
∴△AEB≌△EFH(AAS),
∴FH=BE,AB=EH,
∴EH=CB,
∴CH+CE=CE+BE,
∴CH=BE,
∴FH=CH,
∴∠FCH=45°,
∴∠BCG=45°,
∵∠CBG=90°,
∴△CBG是等腰直角三角形,
∴BG=BC=5;
故答案为:5;
(4)解:过点F作∠EFH=∠BEC,与ED的延长线交于点H,
∵四边形ABCD是菱形,
∴CB=CD,∠A=∠BCD=120°,
由旋转得∠BEF=120°,EF=BE,
∴∠BEC+∠CBE=∠BEC+∠FEH=60°,
∴∠CBE=∠FEH,
∴△BEC≌△EFH(AAS),
∴∠H=∠BCD=120°,EH=BC,FH=CE,
∴CD=EH,
∴DH=CE,
∴DH=FH,
∴∠FDH=∠DFH=30°,
∴∠CDG=30°,
∵∠DCG=180°﹣∠BCD=60°,
∴∠G=90°,
∴△DCG是直角三角形,
∵∠CDG=30°,
∴CGCDBC,
∵BG=6,
∴3CG=6,
∴CG=2.
故答案为:2.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
