八年级数学下册试题 第9章《中心对称图形-平行四边形》复习题--四边形中的尺规作图和格点作图--苏科版(含解析)
文档属性
| 名称 | 八年级数学下册试题 第9章《中心对称图形-平行四边形》复习题--四边形中的尺规作图和格点作图--苏科版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 13:28:50 | ||
图片预览


文档简介
第9章《中心对称图形-平行四边形》复习题--四边形中的尺规作图和格点作图
解答题
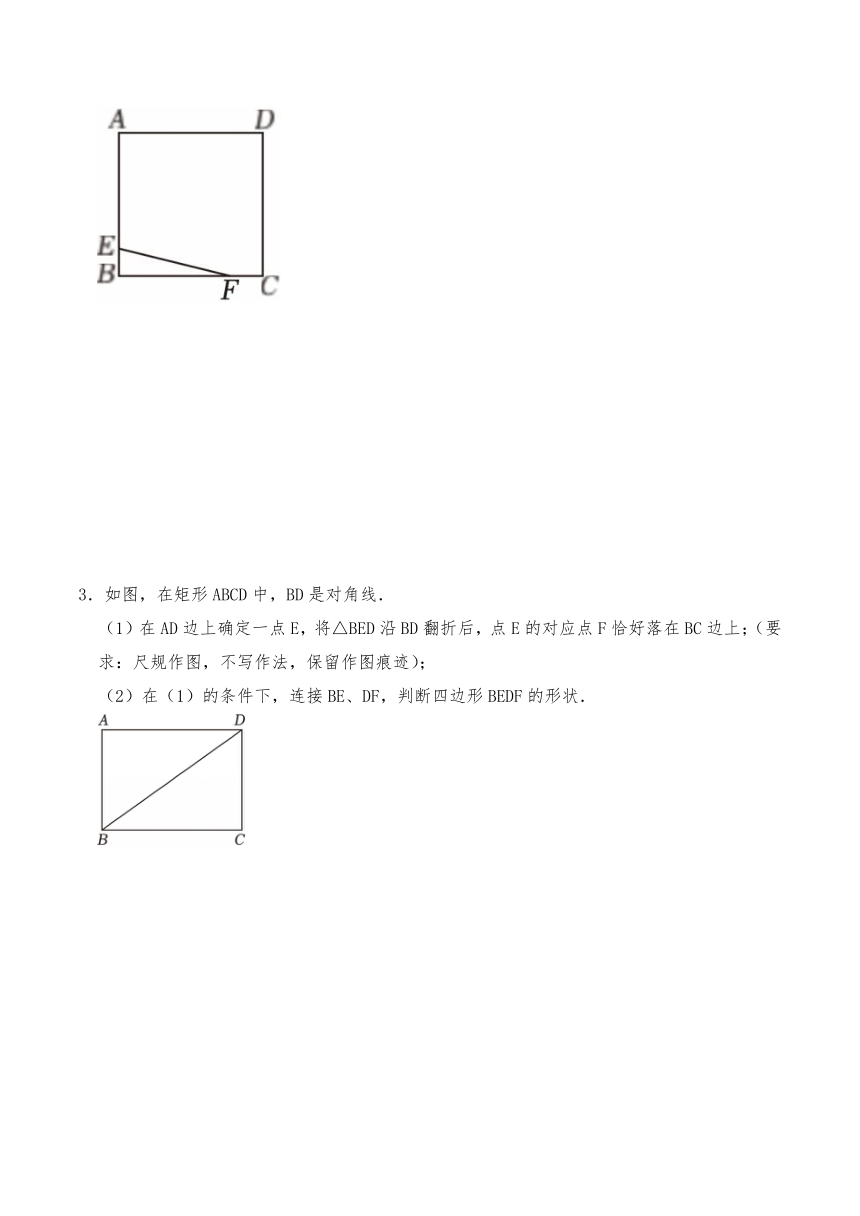
1.(1)图1是在Rt△ABC中,∠B=90°,用直尺和圆规作矩形ABCD,作法是“以点A为圆心,BC长为半径画弧;以点C为圆心,AB长为半径画弧,两弧交于点D“,请判断所作的四边形ABCD是不是矩形,并说明理由.
(2)如图2,在矩形ABCD的边AB上任取一点E,O是AC中点,在BC、CD、DA上各找一点F、G、H,使得四边形EFGH是菱形.(要求:利用直尺和圆规,作出图形,保留作图痕迹)
2.已知:如图,正方形ABCD中,点E、F分别是边AB和BC上的点,且满足BE=CF.
(1)不用圆规,请只用不带刻度的直尺作图:在边CD和DA上分别作出点G和点H,DG=AH=BE=CF(保留作图痕迹,不写作法作法);
(2)判断:四边形EFGH的形状是 .
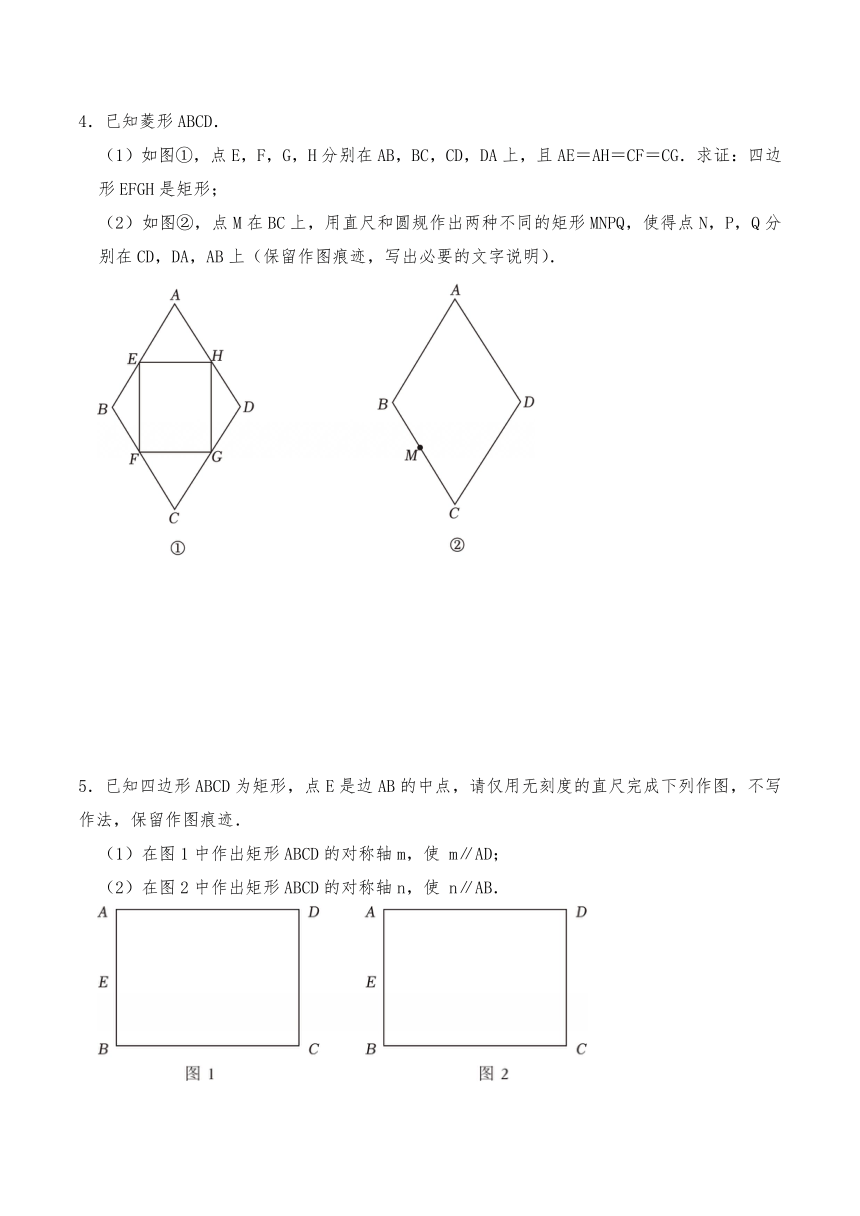
3.如图,在矩形ABCD中,BD是对角线.
(1)在AD边上确定一点E,将△BED沿BD翻折后,点E的对应点F恰好落在BC边上;(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,连接BE、DF,判断四边形BEDF的形状.
4.已知菱形ABCD.
(1)如图①,点E,F,G,H分别在AB,BC,CD,DA上,且AE=AH=CF=CG.求证:四边形EFGH是矩形;
(2)如图②,点M在BC上,用直尺和圆规作出两种不同的矩形MNPQ,使得点N,P,Q分别在CD,DA,AB上(保留作图痕迹,写出必要的文字说明).
5.已知四边形ABCD为矩形,点E是边AB的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
(1)在图1中作出矩形ABCD的对称轴m,使 m∥AD;
(2)在图2中作出矩形ABCD的对称轴n,使 n∥AB.
6.如图,四边形ABCD是平行四边形,E为AB上一点.
(1)如图①,只用无刻度直尺在CD上作出点F,使得四边形AECF为平行四边形;
(2)如图②,用直尺和圆规作出矩形EFGH,使得点F、G、H分别在BC、CD、DA上.(保留作图痕迹,写出必要的文字说明)
7.如图,已知△ABC,AP平分∠BAC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMPN,使点M,N分别在边AB、CA上,并根据你的作法证明你的结论;
(2)若∠C=90°,AB=8,BP=4,求(1)中所作菱形AMPN的面积.
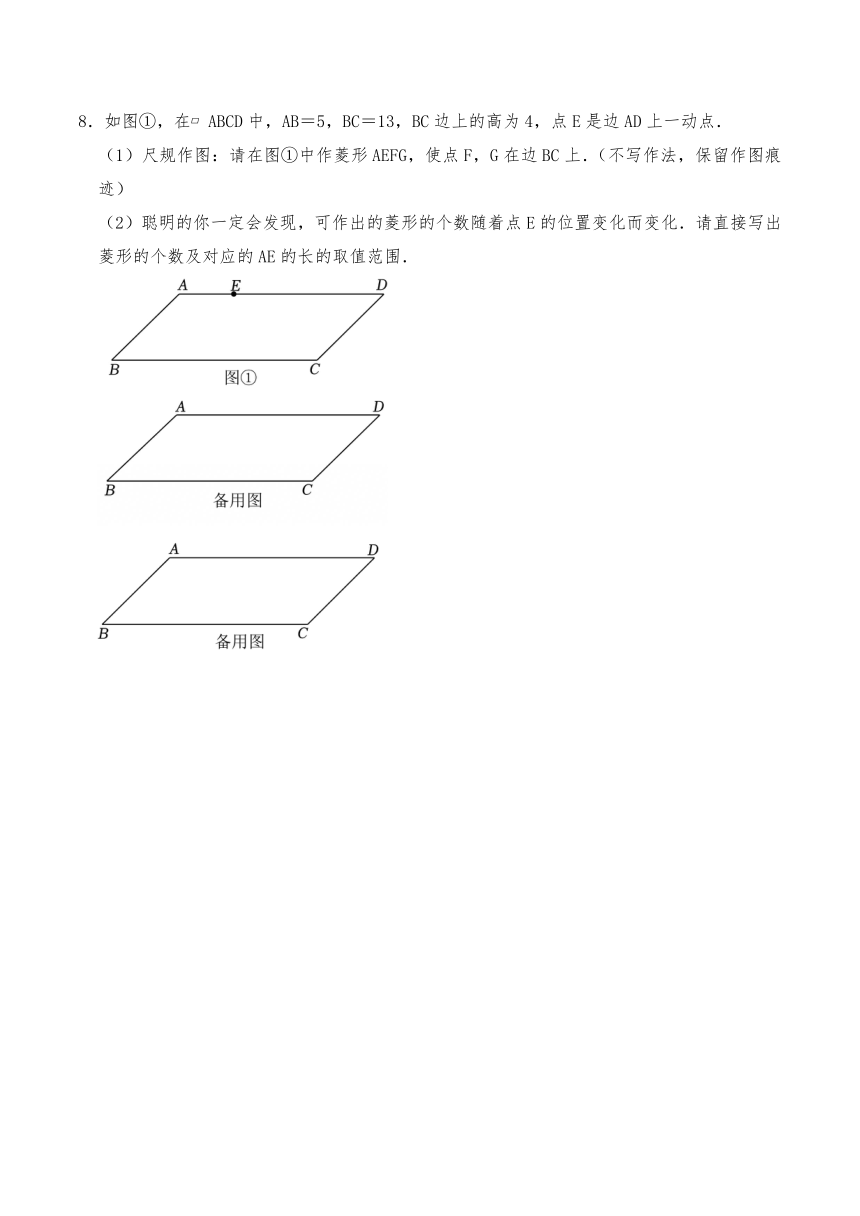
8.如图①,在 ABCD中,AB=5,BC=13,BC边上的高为4,点E是边AD上一动点.
(1)尺规作图:请在图①中作菱形AEFG,使点F,G在边BC上.(不写作法,保留作图痕迹)
(2)聪明的你一定会发现,可作出的菱形的个数随着点E的位置变化而变化.请直接写出菱形的个数及对应的AE的长的取值范围.
9.按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE;
(2)如图2,BE是菱形ABCD的边AD上的高,请只用直尺(不带刻度)作出菱形ABCD的边AB上的高DF.
10.如图,四边形ABCD是矩形.
(1)请用无刻度的直尺和圆规在图中作一个菱形FBED,其中F在直线AD上,E在直线BC上;
(不要求写作法,但要保留作图痕迹)
(2)在(1)的条件下,若AB=3,AD=9,求所作菱形的面积.
11.如图,在矩形ABCD中,AC是对角线.
(1)利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边BC于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母);
(2)连接AF、CE,求证四边形AECF为菱形.
12.已知正方形ABCD,P是CD的中点,请仅用无刻度的直尺按下列要求画图.(保留画图痕迹,不写画法)
(1)在图①中,画PQ⊥AB,垂足为Q;
(2)在图②中,画BH⊥AP,垂足为H.
13.如图①,在 ABCD中,AB=5,BC=13,BC边上的高为4.求作菱形AEFG,使点E在边AD上,点F,G在边BC上.
小宁的作法1.如图②,在边AD上取一点E.
2.以点A为圆心,AE长为半径画弧,交BC于点G.
3.在BC上截取GF=AE,连接EF,则四边形AEFG为所求作的菱形.
(1)证明小宁所作的四边形AEFG是菱形.
(2)小宁进一步探索,发现可作出的菱形的个数随着点E的位置变化而变化.请你继续探索,直接写出菱形的个数及对应的AE的长的取值范围.
14.已知∠MAN,按要求完成下列尺规作图(不写作法,保留作图痕迹).
(1)如图①,B,C分别在射线AM、AN上,求作 ABDC;
(2)如图②,点O是∠MAN内一点,求作线段PQ,使P、Q分别在射线AM、AN上,且点O是PQ的中点.
15.如图,AE∥BF.
(1)请用直尺和圆规完成以下基本作图:在射线BF上截取BC=AB,作∠ABC的平分线,交AE于点D,连接CD;(保留作图痕迹,不写作法)
(2)求证:四边形ABCD是菱形.
16.如图,点O是∠MAN内一点,求作线段PQ,使P、Q分别在射线AM、AN上,且点O是PQ的中点(要求:用无刻度的直尺和圆规作图,保留作图痕迹).
小亮的作法如下:作OT∥AN,交AM于点T,在射线TO上截取OE=OT,在AN上截取AQ,使得AQ=TE,连接QO,延长QO交AM于点P,线段PQ即为所求.
(1)请证明小亮作法的正确性;
(2)请你再设计另一种尺规作图的方法(保留作图痕迹,不写作法).
17.已知直线l和直线外一点A,只利用圆规完成以下作图.(保留作图痕迹,不写画法)
(1)图①中,作点B,使AB∥l;
(2)图②中,作点B、C、D,使A、B、C、D为矩形的四个顶点.
18.(2024春 玄武区校级期中)如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,△ABC中,A是格线上的点,仅用无刻度的直尺在给定网格中完成画图.
(1)在图(1)中,作 ABDC;
(2)在图(2)中,将线段CB绕C逆时针旋转90°至CE(点E为点B的对应点);过点E作EF⊥AB于F.(可以写出必要的文字说明)
19.规定:每个顶点都在格点的四边形叫做格点四边形.在10×6的正方形网格中画出符合要求的格点四边形(设每个小正方形的边长为1).
(1)在图甲中画出一个以AB为边的平行四边形,且它的面积为8.
(2)在图乙中画出一个以AB为对角线的矩形,且它的面积为6.
参考答案
解答题
1.解:(1)如图1中,四边形ABCD是矩形.
理由:∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∵∠B=90°,
∴四边形ABCD是矩形;
(2)四边形EFGH即为所求.
2.解:(1)如图1所示:DG=AH=BE=CF;
;
(2)四边形EFGH是正方形,理由如下:
如图2,
∵正方形ABCD中,
∴AB∥CD,OB=OD,
∴∠EBO=∠GDO,
∵∠EOB=∠GOD,
∴△EOB≌△GOD(ASA),
∴BE=DG,
同理AH=CF,
∵BE=CF,
∴EF=FG=GH=HE,
∵正方形ABCD中,∠BAD=∠ABC=∠BCD=∠CDA,AB=BC=CD=DA,
∵DG=AH=BE=CF,
∴AE=BF=CG=DH,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∴∠AEH=∠BFE,
∵∠AEH+∠BEF=∠BFE+∠BEF=90°,
∴四边形EFGH是正方形.
故答案为:正方形.
3.解:(1)所作的图形如图:
;
(2)证明:四边形BEDF是菱形.理由如下:
∵四边形ABCD为矩形,
∴AD∥BC,
由翻折知,BE=BF,
由作图知,BE=DE,
∴DE=BF,
∴四边形BEDF是平行四边形,
∵BE=BF,
∴四边形BEDF是菱形.
4.(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠A=∠C,∠B=∠D,∠A+∠B=180°,
∵AE=AH=CF=CG,
∴BE=BF=DH=DG,
∴△AEH≌△CFG(SAS),△BEF≌△DHG(SAS),
∴∠AEH=∠AHE,∠BEF=∠BFE,
∵∠A+∠AEH+∠AHE+∠B+∠BEF+∠BFE=360°,
∴2∠AEH+2∠BEF=180°,
∴∠AEH+∠BEF=90°,
∴∠HEF=90°,
同理∠EFG=∠FGH=90°,
∴四边形EFGH是矩形;
(2)解:连接对角线AC和BD交于点O,以O为圆心,OM为半径画圆分别交CD、DA、AB上使得点 N(N1)、P、Q(Q1),则QP∥BD∥MN,QM∥AC∥PN,且AC⊥BD,
∴四边形MNPQ为矩形,连接Q1N1,MP,
∵Q1N1,MP为直径,
∴∠PQ1M=∠MN1P=∠Q1MN1=90°,
∴四边形MN1PQ1为矩形,
即四边形MNPQ与MN1PQ1均为矩形.
5.解:(1)如图1中,直线m即为所求;
(2)如图2中,直线n即为所求;
6.解:(1)如图1,点F,四边形AECF即为所求作.
(2)如图2,四边形EFGH即为所求作.
理由:由△AOE≌△COF,可得OE=OF,
由△AOH≌△COF.可得OH=OF,
∴四边形EFGH是平行四边形,
∵OG=OF,
∴FH=EG,
∴四边形EFGH是矩形.
7.解:(1)作线段AP的垂直平分线交AB于点M,交AC于点N,连接PM、PN得四边形AMPN即为所求菱形,
证明:∵MN是AP的垂直平分线,
∴AN=PN,AM=PM,∠AON=∠AOM=90°,
∵AP平分∠BAC,
∴∠NAO=∠MAO,
∵AO=AO
∴△AON≌△AOM(ASA),
∴AN=AM,
∴AN=PN=PM=AM,
∴四边形AMPN是菱形;
(2)∵四边形AMPN是菱形,
∴AN=PN=PM=AM,PM∥AC,
∵∠C=90°,AB=8,BP=4,
∴∠BPM=∠C=90°,
设AN=PN=PM=AM=x,则BM=8﹣x,
由勾股定理得:BM2=PM2+BP2,
∴(8﹣x)2=x2+42,
解得:x=3,
∴BM=8﹣3=5,
∵PM∥AC,
∴,即,
解得:BC,
∴PC=BC﹣BP4,
∴菱形AMPN的面积=AN PC=3.
8.解:(1)如图①,菱形AEFG即为所求;
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形,
∵AE=AG,
∴四边形AEFG是菱形;
(2)如图②中,过点A作AT⊥BC于点T,
在Rt△ABT中,BT3,
∵BC=13,
∴CT=13﹣3=10,
在TC上取一点G,使得AG=CG,设AG=CG=x,
则有x2=42+(10﹣x)2,
∴x,
观察图形可知:
①当0<AE<4时,菱形的个数为0;
②当AE=4时,菱形的个数为1;
③当4<AE≤5时,菱形的个数为2;
④当5<AE时,菱形的个数为1;
⑤当AE≤13时,菱形的个数为0.
9.解:(1)连接AC、BD交于点O,作直线EO交AD于F,点F即为所求.
(2)连接AC交BF于点T,作直线DT交AB于F,线段DF即为所求.
10.解:(1)如图,作线段BD的垂直平分线,交AD于点F,交BC于点E,连接BF,DE,
则四边形FBED即为所求.
(2)∵四边形FBED为菱形,
∴BE=DE.
∵四边形ABCD是矩形,
∴BC=AD=9,CD=AB=3,∠C=90°.
设BE=DE=x,
则CE=9﹣x.
在Rt△CDE中,由勾股定理得,DE2=CE2+CD2,
即x2=(9﹣x)2+32,
解得x=5,
∴BE=5,
∴菱形FBED的面积为BE CD=5×3=15.
11.(1)解:如图,EF为所作;
(2)证明:∵EF垂直平分AC,
∴EF⊥AC,OA=OC,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DAC=∠BCA,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴AC与EF互相垂直平分,
∴四边形AECF为菱形.
12.解:(1)如图①,PQ为所作;
(2)如图②,BH为所作.
13.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形,
∵AE=AG,
∴四边形AEFG是菱形.
(2)解:如图①中,过点A作AT⊥BC于点T,
在Rt△ABT中,BT3,
∵BC=13,
∴CT=13﹣3=10,
在TC上取一点G,使得AG=CG,设AG=CG=x,
则有x2=42+(10﹣x)2,
∴x,
观察图象可知:
①当0<AE<4时,菱形的个数为0;
②当AE=4时,菱形的个数为1;
③当4<AE≤5时,菱形的个数为2;
④当5<AE时,菱形的个数为1;
⑤当AE≤13时,菱形的个数为0.
14.解:(1)如图①,平行四边形ABDC为所作;
(2)如图②,PQ为所作.
15.(1)解:如图所示.
(2)证明:∵AE∥BF,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD.
∵BC=AB,
∴BC=AD,
∴四边形ABCD为平行四边形.
∵BC=AB,
∴四边形ABCD为菱形.
16.解:(1)如图1,作∠POT=∠AQO,则OT∥AN,交AM于点T,在射线TO上截取OE=OT,在AN上截取AQ,使得AQ=TE,连接QO,延长QO交AM于点P,线段PQ即为所求,
证明:由作图过程可知:OT∥AN,AQ=TE,
∴四边形ATEQ是平行四边形,
∴AT∥QE,AT=QE,
∴∠OTP=∠OEQ,
∵OT=OE,∠TOP=∠EOQ,
∴△OTP≌△OEQ(ASA),
∴OP=OQ;
(2)解:如图2,线段PQ即为所求,点O是PQ的中点.
17.解:(1)如图①,点B为所作;
(2)如图②,矩形ABCD为所作.
18.解:(1)如图1中,平行四边形ABCD即为所求;
(2)如图2中,直线EF即为所求.
方法:取CD是中点J,连接BJ,延长BJ交直线AC于点T,则DT∥BC,DT⊥EC,取格点W,连接CW交DT于点Q,作直线EQ交AB一点F,直线EF即为所求.
19.解:(1)如图甲所示,平行四边形ABCD即为所求(答案不唯一).
(2)如图乙所示,矩形AEBF即为所求(答案不唯一).
解答题
1.(1)图1是在Rt△ABC中,∠B=90°,用直尺和圆规作矩形ABCD,作法是“以点A为圆心,BC长为半径画弧;以点C为圆心,AB长为半径画弧,两弧交于点D“,请判断所作的四边形ABCD是不是矩形,并说明理由.
(2)如图2,在矩形ABCD的边AB上任取一点E,O是AC中点,在BC、CD、DA上各找一点F、G、H,使得四边形EFGH是菱形.(要求:利用直尺和圆规,作出图形,保留作图痕迹)
2.已知:如图,正方形ABCD中,点E、F分别是边AB和BC上的点,且满足BE=CF.
(1)不用圆规,请只用不带刻度的直尺作图:在边CD和DA上分别作出点G和点H,DG=AH=BE=CF(保留作图痕迹,不写作法作法);
(2)判断:四边形EFGH的形状是 .
3.如图,在矩形ABCD中,BD是对角线.
(1)在AD边上确定一点E,将△BED沿BD翻折后,点E的对应点F恰好落在BC边上;(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,连接BE、DF,判断四边形BEDF的形状.
4.已知菱形ABCD.
(1)如图①,点E,F,G,H分别在AB,BC,CD,DA上,且AE=AH=CF=CG.求证:四边形EFGH是矩形;
(2)如图②,点M在BC上,用直尺和圆规作出两种不同的矩形MNPQ,使得点N,P,Q分别在CD,DA,AB上(保留作图痕迹,写出必要的文字说明).
5.已知四边形ABCD为矩形,点E是边AB的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
(1)在图1中作出矩形ABCD的对称轴m,使 m∥AD;
(2)在图2中作出矩形ABCD的对称轴n,使 n∥AB.
6.如图,四边形ABCD是平行四边形,E为AB上一点.
(1)如图①,只用无刻度直尺在CD上作出点F,使得四边形AECF为平行四边形;
(2)如图②,用直尺和圆规作出矩形EFGH,使得点F、G、H分别在BC、CD、DA上.(保留作图痕迹,写出必要的文字说明)
7.如图,已知△ABC,AP平分∠BAC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMPN,使点M,N分别在边AB、CA上,并根据你的作法证明你的结论;
(2)若∠C=90°,AB=8,BP=4,求(1)中所作菱形AMPN的面积.
8.如图①,在 ABCD中,AB=5,BC=13,BC边上的高为4,点E是边AD上一动点.
(1)尺规作图:请在图①中作菱形AEFG,使点F,G在边BC上.(不写作法,保留作图痕迹)
(2)聪明的你一定会发现,可作出的菱形的个数随着点E的位置变化而变化.请直接写出菱形的个数及对应的AE的长的取值范围.
9.按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE;
(2)如图2,BE是菱形ABCD的边AD上的高,请只用直尺(不带刻度)作出菱形ABCD的边AB上的高DF.
10.如图,四边形ABCD是矩形.
(1)请用无刻度的直尺和圆规在图中作一个菱形FBED,其中F在直线AD上,E在直线BC上;
(不要求写作法,但要保留作图痕迹)
(2)在(1)的条件下,若AB=3,AD=9,求所作菱形的面积.
11.如图,在矩形ABCD中,AC是对角线.
(1)利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边BC于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母);
(2)连接AF、CE,求证四边形AECF为菱形.
12.已知正方形ABCD,P是CD的中点,请仅用无刻度的直尺按下列要求画图.(保留画图痕迹,不写画法)
(1)在图①中,画PQ⊥AB,垂足为Q;
(2)在图②中,画BH⊥AP,垂足为H.
13.如图①,在 ABCD中,AB=5,BC=13,BC边上的高为4.求作菱形AEFG,使点E在边AD上,点F,G在边BC上.
小宁的作法1.如图②,在边AD上取一点E.
2.以点A为圆心,AE长为半径画弧,交BC于点G.
3.在BC上截取GF=AE,连接EF,则四边形AEFG为所求作的菱形.
(1)证明小宁所作的四边形AEFG是菱形.
(2)小宁进一步探索,发现可作出的菱形的个数随着点E的位置变化而变化.请你继续探索,直接写出菱形的个数及对应的AE的长的取值范围.
14.已知∠MAN,按要求完成下列尺规作图(不写作法,保留作图痕迹).
(1)如图①,B,C分别在射线AM、AN上,求作 ABDC;
(2)如图②,点O是∠MAN内一点,求作线段PQ,使P、Q分别在射线AM、AN上,且点O是PQ的中点.
15.如图,AE∥BF.
(1)请用直尺和圆规完成以下基本作图:在射线BF上截取BC=AB,作∠ABC的平分线,交AE于点D,连接CD;(保留作图痕迹,不写作法)
(2)求证:四边形ABCD是菱形.
16.如图,点O是∠MAN内一点,求作线段PQ,使P、Q分别在射线AM、AN上,且点O是PQ的中点(要求:用无刻度的直尺和圆规作图,保留作图痕迹).
小亮的作法如下:作OT∥AN,交AM于点T,在射线TO上截取OE=OT,在AN上截取AQ,使得AQ=TE,连接QO,延长QO交AM于点P,线段PQ即为所求.
(1)请证明小亮作法的正确性;
(2)请你再设计另一种尺规作图的方法(保留作图痕迹,不写作法).
17.已知直线l和直线外一点A,只利用圆规完成以下作图.(保留作图痕迹,不写画法)
(1)图①中,作点B,使AB∥l;
(2)图②中,作点B、C、D,使A、B、C、D为矩形的四个顶点.
18.(2024春 玄武区校级期中)如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,△ABC中,A是格线上的点,仅用无刻度的直尺在给定网格中完成画图.
(1)在图(1)中,作 ABDC;
(2)在图(2)中,将线段CB绕C逆时针旋转90°至CE(点E为点B的对应点);过点E作EF⊥AB于F.(可以写出必要的文字说明)
19.规定:每个顶点都在格点的四边形叫做格点四边形.在10×6的正方形网格中画出符合要求的格点四边形(设每个小正方形的边长为1).
(1)在图甲中画出一个以AB为边的平行四边形,且它的面积为8.
(2)在图乙中画出一个以AB为对角线的矩形,且它的面积为6.
参考答案
解答题
1.解:(1)如图1中,四边形ABCD是矩形.
理由:∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∵∠B=90°,
∴四边形ABCD是矩形;
(2)四边形EFGH即为所求.
2.解:(1)如图1所示:DG=AH=BE=CF;
;
(2)四边形EFGH是正方形,理由如下:
如图2,
∵正方形ABCD中,
∴AB∥CD,OB=OD,
∴∠EBO=∠GDO,
∵∠EOB=∠GOD,
∴△EOB≌△GOD(ASA),
∴BE=DG,
同理AH=CF,
∵BE=CF,
∴EF=FG=GH=HE,
∵正方形ABCD中,∠BAD=∠ABC=∠BCD=∠CDA,AB=BC=CD=DA,
∵DG=AH=BE=CF,
∴AE=BF=CG=DH,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∴∠AEH=∠BFE,
∵∠AEH+∠BEF=∠BFE+∠BEF=90°,
∴四边形EFGH是正方形.
故答案为:正方形.
3.解:(1)所作的图形如图:
;
(2)证明:四边形BEDF是菱形.理由如下:
∵四边形ABCD为矩形,
∴AD∥BC,
由翻折知,BE=BF,
由作图知,BE=DE,
∴DE=BF,
∴四边形BEDF是平行四边形,
∵BE=BF,
∴四边形BEDF是菱形.
4.(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠A=∠C,∠B=∠D,∠A+∠B=180°,
∵AE=AH=CF=CG,
∴BE=BF=DH=DG,
∴△AEH≌△CFG(SAS),△BEF≌△DHG(SAS),
∴∠AEH=∠AHE,∠BEF=∠BFE,
∵∠A+∠AEH+∠AHE+∠B+∠BEF+∠BFE=360°,
∴2∠AEH+2∠BEF=180°,
∴∠AEH+∠BEF=90°,
∴∠HEF=90°,
同理∠EFG=∠FGH=90°,
∴四边形EFGH是矩形;
(2)解:连接对角线AC和BD交于点O,以O为圆心,OM为半径画圆分别交CD、DA、AB上使得点 N(N1)、P、Q(Q1),则QP∥BD∥MN,QM∥AC∥PN,且AC⊥BD,
∴四边形MNPQ为矩形,连接Q1N1,MP,
∵Q1N1,MP为直径,
∴∠PQ1M=∠MN1P=∠Q1MN1=90°,
∴四边形MN1PQ1为矩形,
即四边形MNPQ与MN1PQ1均为矩形.
5.解:(1)如图1中,直线m即为所求;
(2)如图2中,直线n即为所求;
6.解:(1)如图1,点F,四边形AECF即为所求作.
(2)如图2,四边形EFGH即为所求作.
理由:由△AOE≌△COF,可得OE=OF,
由△AOH≌△COF.可得OH=OF,
∴四边形EFGH是平行四边形,
∵OG=OF,
∴FH=EG,
∴四边形EFGH是矩形.
7.解:(1)作线段AP的垂直平分线交AB于点M,交AC于点N,连接PM、PN得四边形AMPN即为所求菱形,
证明:∵MN是AP的垂直平分线,
∴AN=PN,AM=PM,∠AON=∠AOM=90°,
∵AP平分∠BAC,
∴∠NAO=∠MAO,
∵AO=AO
∴△AON≌△AOM(ASA),
∴AN=AM,
∴AN=PN=PM=AM,
∴四边形AMPN是菱形;
(2)∵四边形AMPN是菱形,
∴AN=PN=PM=AM,PM∥AC,
∵∠C=90°,AB=8,BP=4,
∴∠BPM=∠C=90°,
设AN=PN=PM=AM=x,则BM=8﹣x,
由勾股定理得:BM2=PM2+BP2,
∴(8﹣x)2=x2+42,
解得:x=3,
∴BM=8﹣3=5,
∵PM∥AC,
∴,即,
解得:BC,
∴PC=BC﹣BP4,
∴菱形AMPN的面积=AN PC=3.
8.解:(1)如图①,菱形AEFG即为所求;
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形,
∵AE=AG,
∴四边形AEFG是菱形;
(2)如图②中,过点A作AT⊥BC于点T,
在Rt△ABT中,BT3,
∵BC=13,
∴CT=13﹣3=10,
在TC上取一点G,使得AG=CG,设AG=CG=x,
则有x2=42+(10﹣x)2,
∴x,
观察图形可知:
①当0<AE<4时,菱形的个数为0;
②当AE=4时,菱形的个数为1;
③当4<AE≤5时,菱形的个数为2;
④当5<AE时,菱形的个数为1;
⑤当AE≤13时,菱形的个数为0.
9.解:(1)连接AC、BD交于点O,作直线EO交AD于F,点F即为所求.
(2)连接AC交BF于点T,作直线DT交AB于F,线段DF即为所求.
10.解:(1)如图,作线段BD的垂直平分线,交AD于点F,交BC于点E,连接BF,DE,
则四边形FBED即为所求.
(2)∵四边形FBED为菱形,
∴BE=DE.
∵四边形ABCD是矩形,
∴BC=AD=9,CD=AB=3,∠C=90°.
设BE=DE=x,
则CE=9﹣x.
在Rt△CDE中,由勾股定理得,DE2=CE2+CD2,
即x2=(9﹣x)2+32,
解得x=5,
∴BE=5,
∴菱形FBED的面积为BE CD=5×3=15.
11.(1)解:如图,EF为所作;
(2)证明:∵EF垂直平分AC,
∴EF⊥AC,OA=OC,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DAC=∠BCA,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴AC与EF互相垂直平分,
∴四边形AECF为菱形.
12.解:(1)如图①,PQ为所作;
(2)如图②,BH为所作.
13.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形,
∵AE=AG,
∴四边形AEFG是菱形.
(2)解:如图①中,过点A作AT⊥BC于点T,
在Rt△ABT中,BT3,
∵BC=13,
∴CT=13﹣3=10,
在TC上取一点G,使得AG=CG,设AG=CG=x,
则有x2=42+(10﹣x)2,
∴x,
观察图象可知:
①当0<AE<4时,菱形的个数为0;
②当AE=4时,菱形的个数为1;
③当4<AE≤5时,菱形的个数为2;
④当5<AE时,菱形的个数为1;
⑤当AE≤13时,菱形的个数为0.
14.解:(1)如图①,平行四边形ABDC为所作;
(2)如图②,PQ为所作.
15.(1)解:如图所示.
(2)证明:∵AE∥BF,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD.
∵BC=AB,
∴BC=AD,
∴四边形ABCD为平行四边形.
∵BC=AB,
∴四边形ABCD为菱形.
16.解:(1)如图1,作∠POT=∠AQO,则OT∥AN,交AM于点T,在射线TO上截取OE=OT,在AN上截取AQ,使得AQ=TE,连接QO,延长QO交AM于点P,线段PQ即为所求,
证明:由作图过程可知:OT∥AN,AQ=TE,
∴四边形ATEQ是平行四边形,
∴AT∥QE,AT=QE,
∴∠OTP=∠OEQ,
∵OT=OE,∠TOP=∠EOQ,
∴△OTP≌△OEQ(ASA),
∴OP=OQ;
(2)解:如图2,线段PQ即为所求,点O是PQ的中点.
17.解:(1)如图①,点B为所作;
(2)如图②,矩形ABCD为所作.
18.解:(1)如图1中,平行四边形ABCD即为所求;
(2)如图2中,直线EF即为所求.
方法:取CD是中点J,连接BJ,延长BJ交直线AC于点T,则DT∥BC,DT⊥EC,取格点W,连接CW交DT于点Q,作直线EQ交AB一点F,直线EF即为所求.
19.解:(1)如图甲所示,平行四边形ABCD即为所求(答案不唯一).
(2)如图乙所示,矩形AEBF即为所求(答案不唯一).
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
