八年级数学下册试题 第9章《中心对称图形-平行四边形》复习题--四边形中的动点和存在性问题--苏科版(含解析)
文档属性
| 名称 | 八年级数学下册试题 第9章《中心对称图形-平行四边形》复习题--四边形中的动点和存在性问题--苏科版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 13:39:13 | ||
图片预览



文档简介
第9章《中心对称图形-平行四边形》复习题--四边形中的动点和存在性问题
【类型一:点和运动和函数图像的结合】
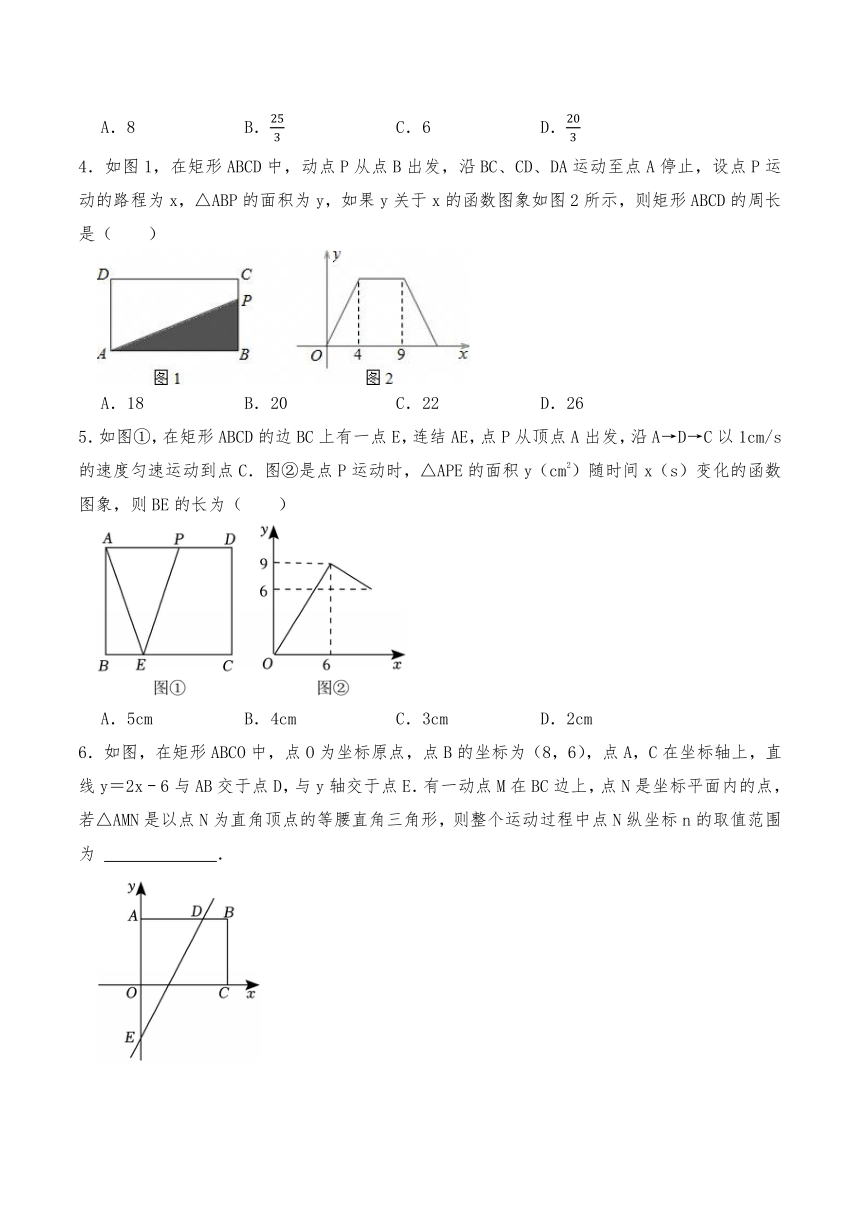
1.如图,在平面直角坐标系中,将 ABCD放置在第一象限,且AB∥x轴.直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,则 ABCD的面积为( )
A.10 B. C.5 D.
2.如图1,在菱形ABCD中,点P沿A﹣B﹣C方向从点A移动到点C,设点P的移动路程为x,线段AP的长为y,点P在运动过程中y与x的变化关系如图2所示,点P运动到BC边上时,当x=18,y的值最小为12,则a的值是 .
3.如图1,点P从菱形ABCD的顶点A出发,沿A→C→B以1cm/s的速度匀速运动到点B,点P运动时△PAD的面积y(cm2)随时间x(s)变化的关系如图2,则a的值为( )
A.8 B. C.6 D.
4.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则矩形ABCD的周长是( )
A.18 B.20 C.22 D.26
5.如图①,在矩形ABCD的边BC上有一点E,连结AE,点P从顶点A出发,沿A→D→C以1cm/s的速度匀速运动到点C.图②是点P运动时,△APE的面积y(cm2)随时间x(s)变化的函数图象,则BE的长为( )
A.5cm B.4cm C.3cm D.2cm
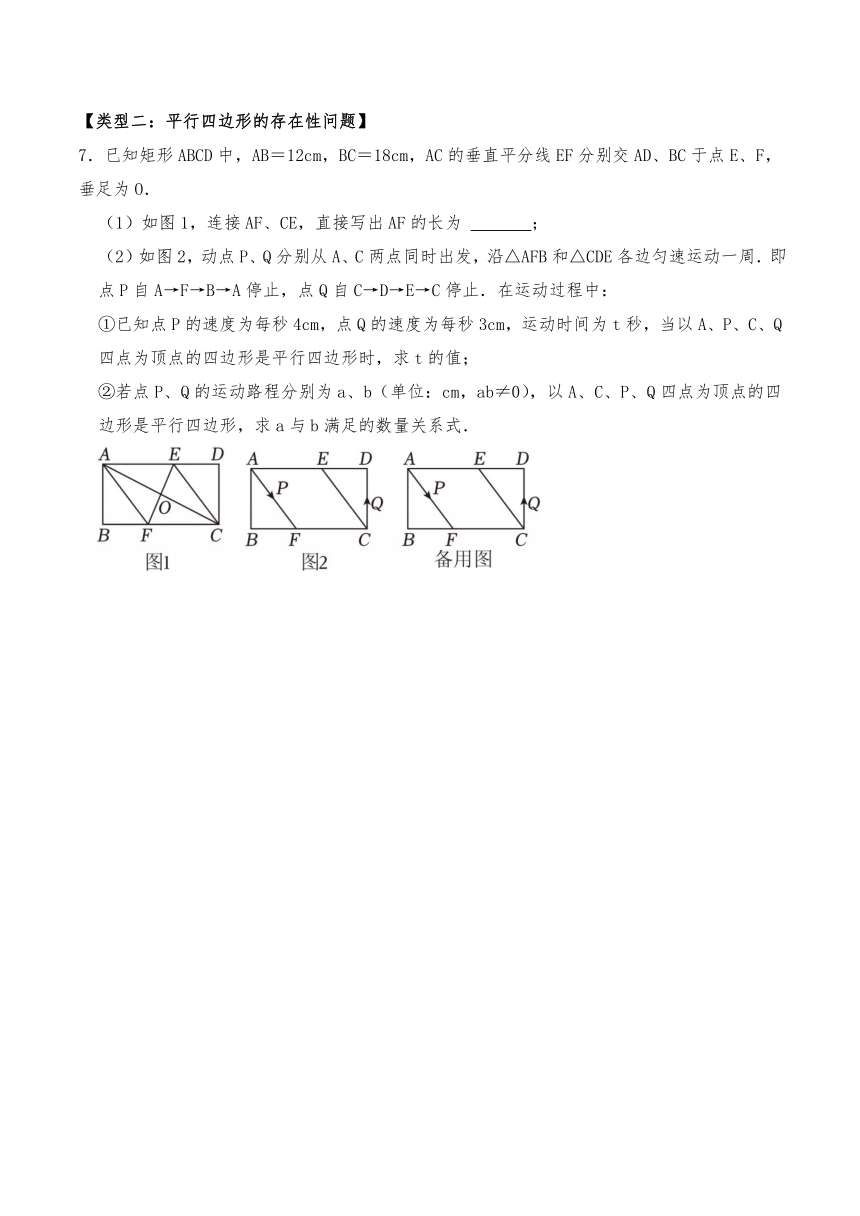
6.如图,在矩形ABCO中,点O为坐标原点,点B的坐标为(8,6),点A,C在坐标轴上,直线y=2x﹣6与AB交于点D,与y轴交于点E.有一动点M在BC边上,点N是坐标平面内的点,若△AMN是以点N为直角顶点的等腰直角三角形,则整个运动过程中点N纵坐标n的取值范围为 .
【类型二:平行四边形的存在性问题】
7.已知矩形ABCD中,AB=12cm,BC=18cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE,直接写出AF的长为 ;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中:
①已知点P的速度为每秒4cm,点Q的速度为每秒3cm,运动时间为t秒,当以A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值;
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),以A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
8.在四边形ABCD中,AD∥BC,AB=12cm,AD=8cm,BC=24cm,∠ABC=90°,P,Q同时沿着四边形的边逆时针运动,点P从点D出发,以1cm/s的速度运动,点Q从点B出发,以2cm/s的速度运动,设运动时间为t秒.
(1)CD= cm;
(2)若点Q运动到点C时就停止,点P也随之停止运动,用含t的代数式表示四边形PQCD的面积S(cm2);
(3)若其中一个动点回到其出发点时,另一个动点也随之停止运动,则当t= 时,以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形.
9.如图,在平面直角坐标系中,点A的坐标是,将线段OA绕着点O顺时针方向旋转60°后得到线段OB,连接AB,直线AB交x轴于点C.
(1)求直线AB的解析式.
(2)若点D是点C关于直线OB的对称点,△BOC沿着直线CB平移得到△B1O1C1,求的最小值,及此时B1的坐标.
(3)点E是坐标平面内一点,且满足S△EOB=S△AOB,在y轴上是否存在一点F,使得以点B、O、E、F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
10.将一长方形纸片OABC放在直角坐标系中,O为原点,点C在x轴上,OA=9,OC=15.
(1)如图1,在OA上取一点E,将△EOC沿EC折叠,使点O落在AB边上的点D,求线段AE.
(2)如图2,在OA,OC边上选取适当的点M,F,将△MOF沿MF折叠,使点O落在AB边上的点D′处,过点D,作D′G垂直于CO于点G,交MF于点T.
①求证:TG=AM;
②设T(x,y),求y与x满足的等量关系式,并将y用含x的代数式表示.
(3)在(2)的条件下,当x=6时,点P在直线MF上,问:在坐标轴上是否存在点Q,使以M,D′,Q,P为顶点的四边形是平行四边形?若存在,请直接写出Q点坐标;若不存在,请说明理由.
【类型四:菱形的存在性问题】
11.如图1,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设点E的运动时间为t(s).
(1)如图2,连接EF,若EF经过边AC的中点D.
①求证:四边形AFCE是平行四边形;
②求此时t的值.
(2)是否存在t,使得以点A,E,C,F为顶点的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
12.已知,如图,O为坐标原点,在四边形OABC中,BC∥OA,BC=24,A(26,0),C(0,12),点D是OA的中点,动点P在线段BC上以每秒2个单位长度的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当P运动 秒,四边形PDAB是平行四边形.
(2)在直线CB上是否存在一点Q,使得以O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由.
13.如图,正方形OABC的顶点O在坐标原点,定点A的坐标为(4,3).
(1)求正方形OABC顶点C的坐标为( , )顶点B的坐标为( , );
(2)现有一动点P从C点出发,沿线段CB向终点B运动,P的速度为每秒1个单位长度,同时另一动点Q从点A出发沿A→O→C向终点C运动,速度为每秒k个单位长度.设运动时间为2秒时,将三角形CPQ沿它的一边翻折,若翻折前后的两个三角形组成的四边形为菱形,求k的值.
14.如图,在平面直角坐标系中,点A(4,0),B(6,3),C(0,3).
(1)若动点P从原点O出发,以每秒3个单位长度沿着x轴正方向运动,动点Q从点B出发,以每秒1个单位长度向点C运动,当点Q到达点C处时,两点都停止运动.设运动时间为t(秒).若以A、B、P、Q四个点为顶点的四边形是平行四边形,求此时t的值;
(2)点M在x轴上,平面内是否存在点N,当以A、C、M、N为顶点的四边形是菱形时,请直接写出所有满足条件的点N的坐标.
15.将一个矩形纸片OABC放置在平面直角坐标系中,OA,OC分别在x轴,y轴的正半轴上,点B坐标为(4,10).
(Ⅰ)如图①,将矩形纸片OABC折叠,使点B落在y轴上的点D处,折痕为线段AE,求点D坐标;
(Ⅱ)如图②,点E,F分别在OC,AB边上.将矩形纸片OABC沿线段EF折叠,使得点B与点D(0,2)重合,求点C的对应点G的坐标;
(Ⅲ)在(Ⅱ)的条件下,若点P是坐标系内任意一点,点Q在y轴上,使以点D,F,P,Q为顶点的四边形是菱形,请直接写出满足条件的点P的坐标.
16.如图,正方形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(4,4),一次函数的图象与边OC、AB分别交于点D、E,并且满足.点M是线段DE上的一个动点.
(1)连接BD、OE,求证:四边形ODBE是平行四边形;
(2)作BP⊥DE交OA于P,当△OMP面积为2.6时,求M点的坐标;
(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
【类型四:矩形的存在性问题】
17.如图,一次函数y=kx+b(k≠0)的图象与x轴交于点,与y轴交于点B,且与正比例函数的图象交于点C(m,6).
(1)求m的值和一次函数y=kx+b(k≠0)的解析式;
(2)点P为坐标平面内的点,在x轴上是否存在点M,使得四边形ABMP是矩形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,且OA=6,OC=4.点D为OA的中点,连接CD,DE为∠ADC的平分线,交BC于点E.
(1)求点B和点E的坐标;
(2)点P为射线DE上一动点,点Q为平面内任意一点,
①连接BD,CP,若S△CDP=S△BCD,请求出点P的坐标;
②是否存在P,Q两点,使得四边形OBPQ为矩形?若存在,请求出P点的坐标;若不存在,请说明理由.
19.如图,平面直角坐标系中,矩形OBCD的顶点B(0,b)、顶点C(c,b),且b、c满足,点A(﹣6,0).
(1)顶点C的坐标为 ;线段AB的长度是 ;
(2)已知点E是线段AB上的动点,点F是线段AC上的动点,点H(2,8),当EF+FH的值最小时,求F点的坐标;
(3)在第(2)问的条件下,点P是坐标轴上的点,点Q是平面内一点,请问存在以点A、F、P、Q为顶点的四边形是以AF为边的矩形吗?若存在,求出点Q的坐标;若不存在,请说明理由.
【类型五:正方形的存在性问题】
20.平面直角坐标系内如图放矩形OABC已知点B(8,6),D(0,4).将矩形OABC沿EF折叠,便点A与点D重合.折痕交BC于点E,交OA于点F.
(1)求点F的坐标;
(2)若动点P,Q同时从点A出发,点P以每秒1个单位长度的速度向点O运动,点Q以每秒2个单位长度的速度沿射线AB方向运动,当点P运动到点O时停止运动,点Q也同时停止运动.设△PQF的面积为S,点P,Q的运动时间为t秒,求S与t的函数关系式并直接写出自变量的取值范围;
(3)在(2)的条件下,R是射线CB上的一点,点M为平面内一点,是否存在点M,使以P,Q,R,M为顶点的四边形是正方形?若存在,请求出点M的坐标;若不存在.请说明理由.
【类型六:四边形动点综合题】
21.在Rt△ABC中,∠ABC=90°,AB=8,BC=4.如图,将直角顶点B放在原点,点A放在y轴正半轴上,当点B在x轴上向右移动时,点A也随之在y轴上向下移动,当点A到达原点时,点B停止移动,在移动过程中,AC= ,点C到原点的最大距离为 .
22.如图,在平面直角坐标系中,点A(6,4)、B(7,2),点C在x轴上运动,点D在直线y=x上运动,则四边形ABCD周长的最小值是 .
23.已知B,C是平面直角坐标系中与x轴平行且距离x轴1个单位长度的直线上的两个动点(点B在点C左侧),且 BC=2,若有点A(0,5)和点D(3,3),则当AB+BC+CD的值最小时,点C的坐标为 .
24.在正方形ABCD中,O是AD的中点,点P从A点出发沿A→B→C→D的路线匀速运动,移动到点D时停止.
(1)如图1,若正方形的边长为12,点P的运动速度为2单位长度/秒,设t秒时,正方形ABCD与∠POD重叠部分的面积为y.
①当t=5时,y= ;当t=10时,y= .
②求t为何值时,以点O、A、P、C为顶点的四边形是平行四边形?
(2)如图2,若点Q从D出发沿D→C→B→A的路线匀速运动.P、Q两点同时出发,点P的速度大于点Q的速度,当P到终点时,Q也停止运动.设t秒时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积为S,S与t的函数图象如图3所示.
①P,Q两点在第 秒相遇;正方形ABCD的边长是 .
②点P的速度为 单位长度/秒;点Q的速度为 单位长度/秒.
③当t为何值时,重叠部分面积S等于32?
25.如图,在平面直角坐标系xOy中,矩形OABC的顶点A(8,0),顶点C(0,6),点D为BC边上一动点,设CD的长为m,以AD为一边在与点B的同侧作正方形ADEF,在点D运动过程中,探究以下问题:
(1)①当点D与点C重合时,点E的坐标为 ;
②用含m的代数式表示点E的坐标为 .
(2)三角形ABF的面积是否改变?如果不变,求出此定值;如果改变,请说明理由;
(3)当△BEF为等腰三角形时,直接写出所有m的值.
26.如图1,在平面直角坐标系中,矩形OABC的顶点,动点P从A出发,以每秒1个单位的速度沿射线AB方向移动,作△PAO关于直线PO的对称△PA′O,设点P的运动时间为t(s).
(1)如图2.当C(0,2),且点A′落在OB上时,求此时A′的坐标;
(2)若直线PA′与直线BC相交于点M,且t<2时,∠POM=45°.
①求点C的坐标;
②当t≥2时,∠POM的大小是否发生变化,请说明理由.
27.如图, ABCD的顶点B与坐标原点重合,点C在x轴上,点A的坐标为(3,4),AD=8.动点P从点D出发沿DA以1个单位每秒的速度向终点A运动,同时点Q从点B出发,以3个单位每秒的速度沿射线BC运动,当点P到达终点时,点Q也随之停止运动,设点P的运动时间为t秒(t>0).
(1)求CD的长;
(2)连结PQ,是否存在t的值,使得PQ与CD互相平分?若存在,求出t的值;若不存在,请说明理由;
(3)若点P关于直线DQ对称的点恰好落在直线CD上,请直接写出点P的坐标.
28.已知:如图,在矩形ABCD中,AB=7,BC=3.在AD上取一点E,AE=1,点F是AB边上的一个动点,以EF为一边作菱形EFMN,使点N落在CD边上,点M落在矩形ABCD内或其边上.若AF=x,△BFM的面积为S.
(1)如图1,当四边形EFMN是正方形时,x的值为 ,S的值为 ;
(2)如图2,当四边形EFMN是菱形时,
①求证:∠DNE=∠MFB;
②求S与x的函数关系式;
(3)当x 时,△BFM的面积S最大;当x= 时,△BFM的面积S最小;
(4)在点F运动的过程中,请直接写出点M运动的路线长: .
参考答案
【类型一:点和运动和函数图像的结合】
1.
【分析】通过图象中(3,0),(7,2),(8,2)可得直线运动到A,D,B三点时所移动距离,从而求出AB长度,再通过添加辅助线构造直角三角形求出平行四边形的高而求解.
【解答】解:由图象可知,直线经过A时移动距离为3,经过D时移动距离为7,经过B时移动距离为8,
∴AB=8﹣3=5.
如图,当直线经过点D时,交AB于点E,作DF垂直于AB于点F,由图2可知DE2,
∵直线与AB夹角为45°,
∴DF=EF=2,
∴ABCD面积为AB DF=5×2=10.
故选:A.
2.
【分析】根据菱形的性质,再结合P运动时y随x的变化的关系图象,运用勾股定理即可求解.
【解答】解:如图1,过A点作AE⊥BC于E,
根据图2知:当点P与点E重合时,AB+BP=18,AP=12,
∴AB+BE=18,AE=12,
设AB=m,则BE=18﹣m,
在Rt△ABE中,AE2+BE2=AB2,
∴122+(18﹣m)2=m2,
解得:m=13,
∴AB=BC=CD=AD=13,BE=5,
∴EC=BC﹣BE=13﹣5=8,
当点P到达点C时,AP=AC=a,
在Rt△ACE中,AC2=AE2+EC2,即a2=122+82=208,
∵a>0,
∴a=4,
故答案为:4.
3.
【分析】过点C作CE⊥AD,再根据图象的三角形的面积可得CE=8,再利用菱形的性质和勾股定理列方程可求a即可.
【解答】解:过点C作CE⊥AD,垂足为E,
∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∴点P在边BC上运动时,y的值不变,
∴AD=BC=10+a﹣10=a,
即菱形的边长是a,
∴AD CE=4a,即CE=8,
当点P在AC上运动时,y逐渐增大,
∴AC=10,
∴AE6,
在Rt△DCE中,DC=a,DE=a﹣6,CE=8,
∴a2=82+(a﹣6)2,
解得:a.
故选:B.
4.
【分析】根据函数的图象、结合图形求出AB、BC的值,即可得出矩形ABCD的周长.
【解答】解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变,
函数图象上横轴表示点P运动的路程,x=4时,y开始不变,说明BC=4,x=9时,接着变化,说明CD=9﹣4=5,
∴AB=5,BC=4,
∴矩形ABCD的周长=2(AB+BC)=18.
故选:A.
5.
【分析】抓住关键点,函数图象最高点的纵坐标为9,横坐标为6,得△APE的最大面积为9,此时P、D重合,AD=AP=6,,通过图象知道点P到终点时,△APE的面积是6,此时P、C重合,,得EC,即可求得BE的长.
【解答】解:∵四边形ABCD是矩形,
∴AD=BC,
由图象可知,当P、D重合,AD=AP=6cm,,
可得:AB=3cm,
当时P、C重合,,可得:EC=4cm,
则:BE=BC﹣EC=6﹣4=2cm.
故选:D.
6.
【分析】根据等腰直角三角形的性质解答即可.
【解答】解:当点M在B点时,如图,
AN1=BN1,∠AN1B=90°,∠N1AB=∠N1BA=45°,
∵AB=8,N1T⊥AB,
∴AT=N1T=AB=4,
∴N1的纵坐标为6+4=10,
同理,N2的纵坐标为6﹣4=2,
当M在C点时,如图,
AN3=CN3,∠AN3C=90°,∠N3AC=∠N3CA=45°,
过点N3作N3S⊥AO于点S,延长SN3交CB于点M,
则Rt△N3SA≌Rt△CMN3,
则N3S=CM,SA=MN3,
设点N3纵坐标为6+y,则BM=SA=MN3=y,
那么N3S=8﹣y=CM=6+y,
解得:y=1,
则点N3纵坐标为6+y=7,
同理可得,N4纵坐标为6﹣y=﹣1,
当点N为直角顶点时,t的取值范围为7≤n≤10或﹣1≤n≤2.
【类型二:平行四边形的存在性问题】
7.解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE,
∵EF垂直平分AC,垂足为O,
∴OA=OC,
∴△AOE≌△COF(AAS),
∴OE=OF,
∴四边形AFCE为平行四边形,
又∵EF⊥AC,
∴四边形AFCE为菱形,
设菱形的边长AF=CF=x cm,则BF=(18﹣x)cm,
在Rt△ABF中,AB=12cm,
由勾股定理得122+(18﹣x)2=x2,
解得x=13,
∴AF=13cm.
故答案为:13cm;
(2)①显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上或P在BF,Q在CD时不构成平行四边形,也不能构成平行四边形.
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒4cm,点Q的速度为每秒3cm,运动时间为t秒,
∴PC=4t,QA=CD+AD﹣3t=30﹣3t,即QA=30﹣3t,
∴4t=30﹣3t,
解得t,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t.
②由题意得,四边形APCQ是平行四边形时,点P、Q在互相平行的对应边上.
分三种情况:
i)如图1,当P点在AF上、Q点在CE上时,AP=CQ,即a=30﹣b,得a+b=30;
ii)如图2,当P点在BF上、Q点在DE上时,AQ=CP,即30﹣b=a,得a+b=30;
iii)如图3,当P点在AB上、Q点在CD上时,AP=CQ,即30﹣a=b,得a+b=30.
综上所述,a与b满足的数量关系式是a+b=30(ab≠0).
8.解:(1)过点D作DE⊥BC交BC于点E,如图1,
∵∠ABC=90°,AD∥BC,
∴∠A=∠BED=∠ABC=90°,
则四边形ABED为矩形,
∴BE=AD=8cm,AB=DE=12cm,
∴EC=BC﹣BE=24﹣8=16(cm),
∴DC20(cm),
故答案为:20;
(2)若点Q运动到点C时就停止,点P也随之停止运动,
如图2,当点P在AD上运动,即0≤t≤8时,
则DP=t cm,BQ=2t cm,AP=(8﹣t)cm,
∴S=S四边形PQCD=S梯形ABCD﹣S梯形APQB(8+24)×12(8﹣t+2t)×12=144﹣6t(cm2);
如图3,当点P在AB上运动,即8≤t≤12时,
则AP=(t﹣8)cm,BQ=2t cm,BP=12﹣(t﹣8)=(20﹣t)cm,
∴S=S四边形PQCD=S精形ABCD﹣S△PQB﹣S△APD(8+24)×122t (20﹣t)8 (t﹣8)=t2﹣24t+224(cm2),
综上,S=144﹣6t(0≤t≤8)或S=t2﹣24t+224(8≤t≤12);
(3)①如图4,当AP=BQ时,8﹣t=2t,此时ts,四边形ABQP是平行四边形;
②如图5,当PD=QC时,t=24﹣2t,此时t=8s,四边形PQCD为平行四边形;
③如图6,当AQ=BP时,四边形ABPQ是平行四边形,8﹣(2t﹣24﹣20)=t﹣8﹣12,此时t=24s;
④如图7,当PC=QD时,24﹣(t﹣8﹣12)=2t﹣24﹣20,此时ts,四边形PCDQ为平行四边形;
综上所述,当ts或t=8s或t=24s或ts时,以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形,
故答案为:s或8s或24s或s.
9.解:(1)∵点A的坐标是,将线段OA绕着点O顺时针方向旋转60°后得到线段OB,
∴△AOB是等边三角形,且,
∴∠OAB=60°,∠ACO=30°,
∴,,
∴点C的坐标是(6,0),
设直线AB的解析式为,
则,
∴,
∴直线AB的解析式为;
(2)如图1,连接CD,BD,OO1,O1C1,OD,
由平移可得:∠ACO=∠B1C1O1=30°,OC=O1C1=6,
由(1)可得:△ABO为等边三角形,
∴∠ACB=60°,
∴∠BOC=90°﹣60°=30°,
∵点D是点C关于直线OB的对称点,
∴OD=OC,BC=BD,∠BOC=∠BOD=30°,
∴∠DOC=60°,
∴△DOC为等边三角形,∠OKC=180°﹣60°﹣30°=90°,
∴DO=OC=6,,
∴当C1与K重合时,
∴,此时最小,
即的最小值为6;
如图2,,,
∴,
过B1作B1G⊥OC于G,
∴,,
∴,
∴;
(3)如图3,点E是坐标平面内一点,且满足S△EOB=S△AOB,
∴E在过A点与OB平行的直线上或在OB下方,与OB平行,与A到OB的距离相等的平行线CJ上,
∵以点B、O、E、F为顶点的四边形是平行四边形,
∴F与A重合,当OB为对角线时,
∴,
由(1)(2)可得:OB=AB=BC,,C(6,0),
∴,
∴由平移可得:;
同理:F与J重合,当OE为对角线时,
此时,
∴,,
如图4,F与J重合,当BE为对角线时,
同理:,
由平移可得:;
当E在AI上时,如图5,F与A重合,当BF为对角线时,
∴,,
如图6,F与A重合,当OF为对角线时,
∴;;
当F与J重合,当OB为对角线时,如图7,
∴;;
综上:或或或.
10.(1)解:∵长方形OABC,
∴BC=OA=9,AB=OC=15,
由折叠的性质可知,CD=OC=15,DE=OE,
由勾股定理得,,
∴AD=3,
设AE=x,则DE=OE=9﹣x,
由勾股定理得,DE2﹣AE2=AD2,即(9﹣x)2﹣x2=32,
解得,x=4,
∴线段AE的长为4;
(2)①证明:由折叠的性质可知,∠D′MF=∠OMF,D′M=OM,
∵D′G⊥OC,AO⊥OC,
∴AO∥D′G,四边形AOGD′是矩形,
∴∠OMF=∠D′TM,AO=GD′,
∴∠D′MF=∠D′TM,
∴D′T=D′M=OM,
∴GD′﹣D′T=AO﹣OM,
∴TG=AM;
②解:∵T(x,y),
∴AM=TG=y,AD′=x,D′T=D′M=OM=9﹣y,
由勾股定理得,AM2+AD′2=D′M2,即y2+x2=(9﹣y)2,
整理得,;
(3)解:在坐标轴上存在点Q,使以M,D′,Q,P为顶点的四边形是平行四边形,Q点坐标为(0,13)或(0,0)或;理由如下:
当x=6时,,
∴,,
∴,D′(6,9),
∵以M,D′,Q,P为顶点的四边形是平行四边形,
∴当MD′为对角线时,MQ∥D′P,如图2,四边形MQD′P是平行四边形,P、T重合,
∴,
由平移的性质可得,Q(0,13);
当MD′为边,MP为对角线时,MQ∥D′P,如图2,四边形MQ′PD′平行四边形,P、T重合,则,
由平移的性质可得,Q′(0,0);
当MD′为边,MP为边时,MP∥D′Q,如图2,四边形MP″Q″D′是平行四边形,
设直线MP的解析式为y=kx+b,将点T,点M的坐标代入得:
,
解得,,
∴直线MP的解析式为,
∴直线D′Q″的解析式为,
将D′(6,9)代入得:,
解得:c=13,
∴直线D′Q″的解析式为,
令y=0,则,
解得,,
∴;
综上所述,在坐标轴上存在点Q,使以M,D′,Q,P为顶点的四边形是平行四边形,Q点坐标为(0,13)或(0,0)或.
【类型四:菱形的存在性问题】
11.解:(1)∵AG∥BC,
∴∠EAC=∠FCA,∠AED=∠CFD.
∵EF经过边AC的中点D,
∴AD=CD,
∴△ADE≌△CDF(AAS),
∴AE=CF.
∵AE∥FC,
∴四边形AFCE是平行四边形;
②此时AE=CF,
由运动知,AE=tcm,CF=(6﹣2t)cm.
∴t=6﹣2t,
解得t=2;
(2)存在;
∵点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,
∴当点F在线段BC上时,四边形AFCE不可能为菱形;
当点F在BC的延长线上时,
∵AE∥CF,
∴当AE=CF时,四边形ACFE是平行四边形,
∴t=2t﹣6,
解得t=6,
此时AE=AC=6,
∴当t=6时,四边形ACFE是菱形.
12.解:(1)∵A(26,0),C(0,12),
∴OA=26,OC=8,
∵点D时OA的中点,
∴OD=1OA=13,
由运动知,PC=2t,
∵BC=24,
∴BP=BC﹣PC=24﹣2t,
∵四边形PDAB是平行四边形,
∴PB=AD=13,
∴24﹣2t=13,
解得t=5.5,
∴当t值为5.5时,四边形PDAB是平行四边形.
故答案为:5.5;
(2)存在,分三种情况:
①当Q点在P点的右边时,如图,
∵四边形ODQP是菱形,
∴OD=OP=PQ=13,
∴在Rt△OPC中,由勾股定理得:PC=5,
∴2t=5,
解得t=2.5,
∴Q(18,12);
②当Q点在P点左侧且在BC线段上时,如图,
同理①得PC=18,
即2t=18,
解得t=9,
∴Q(5,12);
③当Q点在P点左侧且在BC延长线上时,如图3,
同理①求出QC=5,PC=13﹣5=8,
即2t=8,
解得t=4,
∴Q(﹣5,12);
综上,t=2.5时,Q(18,12),t=9时,Q(5,12),t=4时,Q(﹣5,12).
13.解:(1)过点A作AD⊥x轴于D,过点B作BE⊥AD交DA的延长线于E,过点C作CF⊥x轴于点F,
∴∠ADO=∠OFC=∠BEA=90°,
∴∠DAO+∠AOD=90°,
∵四边形ABCO是正方形,
∴∠OAB=∠AOC=90°,OA=OC=AB,
∴∠COF+∠AOD=90°,∠BAE+∠DAO=90°,
∴∠FOC=∠DAO,∠BAE=∠AOD,
∴△COF≌△AOD≌△BAE(AAS),
∴OF=AD=BE,CF=OD=AE,
∵点A的坐标为(4,3),
∴OF=AD=BE=3,CF=OD=AE=4,
∴点C的坐标为(﹣3,4);
∴ED=4+3=7,点B到y轴的距离为OD﹣BE=4﹣3=1,
∴点B的坐标为(1,7);
故答案为:﹣3,4,1,7;
(2)由题意,得AO=CO=BC=AB5,
当 t=2 时,CP=2.
将三角形CPQ沿它的一边翻折,若翻折前后的两个三角形组成的四边形为菱形,
只需三角形CPQ是等腰三角形即可.
①当点Q在OA上时,
∵PQ AB>PC,
∴只存在一点Q,使QC=QP.
过点Q作QD⊥PC于点D,如图,
则CD=PD=1,
∵QA=BD,
∴2k=5﹣1=4,
∴k=2;
②当点Q在OC上时,
∵∠BCO=90°,
∴只存在一点Q,使CP=CQ=2,
∴2k=10﹣2=8,
∴k=4.
综上所述,k的值为2或4.
14.解:(1)若点P在点A的左侧,四边形PABQ为平行四边形,PA=QB,
由题意得4﹣3t=t,
解得t=1,
若点P在点A的右侧,四边形PAQB为平行四边形,PA=QB,
∴3t﹣4=t,
解得t=2,
综上:t=1或2时,以A,B,P,Q为顶点的四边形为平行四边形.
(2)N点坐标为(﹣5,3),(5,3),(0,﹣3),.
∵点A(4,0),C(0,3),
∴AO=4,OC=3,
∴AC5,
如图,以AC为边,四边形ACMN是菱形,
∵C(0,3),
∴N(0,﹣3);
如图,以AC为边,四边形ACNM是菱形,
∵CN=AC=5,CN∥AM,
∴N(5,3);
如图,以AC为边,四边形ACNM是菱形,
∵CN=AC=5,CN∥AM,
∴N(﹣5,3);
如图,以AC为对角线,四边形ACNM是菱形,
设CM=AM=CN=x,
∴OM=4﹣x,
∵OC2+OM2=CM2,
∴32+(4﹣x)2=x2,
∴,
∴CN,
∴N(,3);
综上所述,以A、C、M、N为顶点的四边形是菱形时,点N的坐标为(﹣5,3),(5,3),(0,﹣3),.
15.解:(Ⅰ)∵四边形OABC是矩形,
∴∠BAO=∠BCO=90°,OA=CB,CO=BA.
∵点B坐标为(4,10),
∴OA=CB=4,CO=BA=10;
由折叠可知,△ADE≌△ABE,
∴DA=BA=10.
在Rt△AOD中,OD2,
∴点D的坐标为(0,2 );
(Ⅱ)如图,过点G作GH⊥y轴于点H,
∵点D (0,2),
∴DO=2,
∵四边形OABC是矩形,
∴∠B=90°;
由折叠知,四边形BCEF与四边形DGEF全等,
∴∠EGD=∠B=90°,GD=CB=4,CE=EG.
设CE=EG=x,则ED=CO﹣CE﹣DO=10﹣2﹣x=8﹣x.
在Rt△EGD中,EG2+GD2=ED2,
∴x2+42=(8﹣x)2,
解得:x=3.
∴EG=3,ED=5.
∴S△EGDEG GDED GH,
∴3×45×GH,
∴GH,
在Rt△GHD中,HD,
∴HO=HD+DO2.
∴点G的坐标为(,).
(Ⅲ)由折叠可知,∠BFE=∠DFE,
∵BF∥ED,
∴∠BFE=∠FED,
∴∠FED=∠DFE,
∴BF=DF=ED=5,
∴AF=AB﹣BF=10﹣5=5,
∴F(4,5),
设Q(0,y),P(m,n),
∵D (0,2),
∴DQ=|y﹣2|,DF=5,FQ2=42+(y﹣5)2,DF的中点坐标为(2,),
∵点Q在y轴上,使以点D,F,P,Q为顶点的四边形是菱形,
∴分三种情况:DQ=DF或FQ=DF或DQ=FQ,
①当DQ=DF时,|y﹣2|=5,
解得:y=7或﹣3,
∴Q(0,7)或(0,﹣3),
∴P(4,0)或(4,10),
②当FQ=DF时,42+(y﹣5)2=25,
解得y=8或y=2(舍去),
∴Q(0,8),
∴P(﹣4,5),
③当DQ=FQ时,|y﹣2|2=42+(y﹣5)2,
解得:y,
∴Q(0,),
∵2,,
∴m=4,n,
∴P(4,),
综上所述,点P的坐标为(4,10),(4,0),(﹣4,5),(4,).
16.(1)证明:正方形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(4,4),
∴OC=AB=OA=BC=4,OC∥AB,
∵3,
∴BE=3,AE=1,
∴E(4,1),
代入yx+b得﹣2+b=1,解得b=3,
∴yx+3,
∴D(0,3),
∴OD=BE=3,
∵OD∥BE,
∴四边形ODBE是平行四边形;
(2)解:过点D作DH⊥AB于H,
∴∠DHE=∠BAP=90°,四边形ODHA是矩形,
∴DH=OA=AB=4,BH=CD=1,
∵DH⊥AB,BP⊥DE,
∴∠EDH+DEH=∠PBA+DEH=90°,
∴∠EDH=∠PBA,
∴△DHE≌△BAP(ASA),
∴PA=EH=BE﹣BH=2,
∴OP=OA﹣PA=2,
设M的坐标为(m,m+3),
∴S△OMP2×(m+3)=2.6,解得m,
∴M点的坐标为(,);
(3)解:当四边形OMDN是菱形时,如图,
∵M的纵坐标是1.5,把y=1.5代入1.5x+3,解得:x=3,
则M的坐标是(3,1.5),
∴点N的坐标为(﹣3,1.5);
当四边形OMND是菱形时,如图,
∵OM=OD=3,则设M的横坐标是m,则纵坐标是m+3,
则m2+(m+3)2=9,
解得:m或0(舍去).
则M的坐标是(,),
∴点N的坐标为(,).
综上,点N的坐标为(﹣3,1.5)或(,).
【类型四:矩形的存在性问题】
17.解:(1)∵将点C(m,6)代入,
∴,
∴,
∴,
将,代入一次函数的解析式为y=kx+b(k≠0)得:,
解得,
∴一次函数的表达式为;
(2)在x轴上存在点M,平面内存在一点P,使得四边形ABMP是矩形,
设M(m,0),
∵四边形ABMP是矩形,
∴∠ABM=90°,
∴AB2+BM2=AM2,
∴,
∴,
∴点M的坐标为.
18.解:(1)∵四边形OABC为矩形,
∴BC∥OA,BC=OA,AB∥OC,AB=OC,
∴∠CED=∠ADE,
∵OA=6,OC=4,
∴BC=6,AB=4,
∴B(6,4),
∵DE为∠ADC的平分线,
∴∠CDE=∠ADE,
∴∠CED=∠CDE,
∴CE=CD,
∵D为OA中点,
∴ODOA=3,
∴D(3,0),
由勾股定理可得CD=5,
∴CE=5,
∴E(5,4).
(2)①∵四边形OABC为矩形,点D为OA的中点,
∴S△BCDS四边形OABCOA OC=12,
∴S△CDP=S△BCD=12,
延长ED,交y轴于点M,
∵D(3,0),E(5,4),
∴yDE=2x﹣6,
∴M(0,﹣6),
∴CM=10,
∵S△CDP=S△PCM﹣S△DCMCM (xP﹣xD)=12,
∴10×(xP﹣3)=12,
∴xP,
∴P(,).
②存在,
∵点P是射线DE上的动点,
∴设P(x,2x﹣6),
∵O(0,0),B(6,4),
∴OB2=62+42=52,
OP2=x2+(2x﹣6)2=5x2﹣24x+36,
BP2=(x﹣6)2+(2x﹣6﹣4)2=5x2﹣52x+136,
要使四边形OBPQ是矩形,则△OBP为直角三角形,∠OBP=90°,
∴OB2+BP2=OP2,即52+5x2﹣52x+136=5x2﹣24x+36,
解得x,
∴P(,).
19.解:(1)∵,
∴,
解得:b=8,
∴c=10,
∴C(10,8),
∴OA=6,OB=8,
∴
=10;
故答案为:C(10,8),10;
(2)如图,
∵C(10,8),
∴BC=AB=10,
∴∠BAC=∠ACB,
∵四边形OBCD是矩形,
∴BC∥x轴,
∴∠BCA=∠CAD,
∴∠BAC=∠CAD,
∴AC平分∠BAD,
如图,作E关于AC对称点G,连接GF,
∴AE=AG,
在△AEF和△AGF中
,
∴△AEF≌△AGF(SAS),
∴GF=EF,
当G、F、H三点共线,且GH⊥x轴时,GH最小,
∴EF+FH最小,
∵H(2,8),
∴OG=2,
设直线AC的解析式为y=kx+b,则有
,
解得,
∴直线AC的解析式为,
当x=2时,
,
∴F(2,4);
(3)存在,理由如下:
如图,
①如图,当P在x轴上时,
此时矩形为AQ1P1F,
如图,作OM∥AC,将直线OM绕O逆时针旋转90°得直线ON,
∴ON∥P1F,
直线OM的解析式为,
设M(a,b)(a>0),
∴,
由旋转得:N(﹣b,a),
设直线ON的解析式为y=kx,则有,
﹣bk=a,
∴,
解得:k=﹣2,
∴直线ON的解析式为y=﹣2x,
∴设直线P1F的解析式为y=﹣2x+m,
∴﹣2×2+m=4,
解得:m=8,
∴直线P1F的解析式为y=﹣2x+8,
当y=0时,
﹣2x+8=0,
解得:x=4,
∴P1(4,0),
同理可求:
直线P1Q1的解析式为,
直线AQ1的解析式为y=﹣2x﹣12,
联立直线P1Q1和直线AQ1的解析式得
,
解得,
∴Q1(﹣4,﹣4);
②当P在y轴上时,
此时矩形为AFP2Q2,
由①可求P(0,8),
同理可求:
直线P2Q2的解析式为,
联立直线P2Q2和直线AQ1的解析式得
,
解得,
∴Q2(﹣8,4);
同理可求:直线P2Q3解析式为yx﹣12,直线FQ3解析式为y=﹣2x+8,
联立得,
解得,
∴Q3(8,﹣8);
综上所述:Q点坐标为(﹣4,﹣4)或(﹣8,4)或(8,﹣8).
【类型五:正方形的存在性问题】
20.解:(1)由折叠可得AF=DF,
∵点B(8,6),点D(0,4),四边形OABC为矩形,
∴OA⊥AB,OC=AB=6,OA=BC=8,OD=4,
设AF=DF=x,则OF=OA﹣AF=8﹣x,
在Rt△ODF中,由勾股定理可得OD2+OF2=DF2,
即42+(8﹣x)2=x2,
解得x=5,
∴OF=8﹣x=3,
∴点F的坐标为(3,0);
(2)①如图,当点P在点F右侧时,
根据题意AQ=2t,AP=t(0<t≤5),
∴FP=AF﹣AP=5﹣t,
∴;
②如图,当点P在点F左侧时,
根据题意AQ=2t,AP=t(5<t≤8),
∴FP=AP﹣AF=t﹣5,
∴;
综上所述,;
(3)若以P,Q,R,M为顶点的四边形是正方形时,则点P、R、Q三点围成的三角形为等腰直角三角形,
分情况讨论:①如图,
∵四边形PQRM是正方形,
∴PQ=QR,∠PQR=90°,
∴∠PQA+∠BQR=∠BQR+∠QRB,
∴∠PQA=∠QRB,
在△PAQ和△QBR中,
,
∴△PAQ≌△QBR(AAS),
∴AQ=BR,BQ=AP=t,
∴AB=AQ+BQ=2t+t=3t=6,
∴BQ=AP=t=2,
∴BR=AQ=2×2=4,P(8﹣2,0),
即P(6,0),
∴CR=BC﹣BR=4,Q(8,4),
∴R(4,6),
∵四边形PQRM是正方形,
∴M(4+6﹣8,6+0﹣4),即M(2,2);
②如图,过点R作RK⊥OA于点K,则四边形OCRK、RKAB均为矩形,
∴RK=AB=6,∠BRK=∠RKA=90°,
∵四边形PRQM是正方形,
∴PR=QR,∠PRQ=90°,
∴∠KRB﹣∠PRB=∠PRQ+∠PRB,
∴∠KRP=∠BRQ,
在△PKR和△QBR中,
,
∴△PKR≌△QBR(AAS),
∴RB=RK=6,KP=BQ=AQ﹣AB=2t﹣6,
∴OK=CR=BC﹣BR=8﹣6=2,
∴R(2,6),AK=OA﹣OK=6=2t﹣6+t,
∴AP=t=4,
∴P(8﹣4,0),
即P(4,0),KP=BQ=2t﹣6=2,
∴Q(8,6+2),即Q(8,8),
∵四边形PMQR是正方形,
∴M(4+8﹣2,8+0﹣6),即M(10,2);
③如图,
∵四边形PQRM是正方形,
∴PQ=QR,∠PQR=90°,
∴∠PQA+∠BQR=∠BQR+∠QRB,
∴∠PQA=∠QRB,
在△PAQ和△QBR中,
,
∴△PAQ≌△QBR(AAS),
∴AQ=BR=2t,BQ=AP=t,
又∵AQ=AB+BQ=6+t=2t,
∴AP=t=6,
∴BR=2×6=12,P(8﹣6,0),
即P(2,0),AQ=2t=12,
∴CR=BC+BR=8+12=20,Q(8,12),
∴R(20,6),
∵四边形PMRQ是正方形,
∴M(2+20﹣8,6+0﹣12),即M(14,﹣6).
综上所述,存在M(2,2)或M(10,2)或M(14,﹣6)时,P,Q,R,M为顶点的四边形是正方形.
【类型六:四边形动点综合题】
21.
【分析】根据题意首先取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,进而求出答案.
【解答】解:∵∠ABC=90°,AB=8,BC=4,并且在移动过程中,△ABC的大小、形状没变,
∴AC,
=4.
如图所示:
取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,
Rt△A1OB1中,∵A1B1=AB=8,点OE为斜边中线,
∴OE=B1EA1B1=4,
又∵B1C1=BC=4,
∴C1E,
=4 ,
∴点C到原点的最大距离为:OE+C1E=4+4.
故答案为:4;4+4,
22.
【分析】作点A关于直线y=x的对称轴A′,作B关于x轴的对称轴点B′,连接A′B′交OD于D′,交x轴于C′,连接AD′、A′D′、BC′、B′C′、则A′B′+AB就是四边形ABCD周长的最小值,据此展开计算即可.
【解答】解:作点A关于直线y=x的对称轴A′,作B关于x轴的对称轴点B′,连接A′B′交OD于D′,交x轴于C′,连接AD′、A′D′、BC′、B′C′、则A′B′+AB就是四边形ABCD周长的最小值.
∵B(7,2),
∴B′(7,﹣2),
由A(6,4),直线OD解析式是y=x,设直线AA′解析式为y=﹣x+b,
∴4=﹣6+b,解得b=10,
∴直线AA′解析式为y=﹣x+10,
联立,解得,
∴线段AA′的中点坐标为(5,5),
由中点坐标公式得A′(4,6),
∴A′B′,
AB.
∴四边形ABCD周长的最小值是.
故答案为:.
23.
【分析】分当B,C是直线y=1上的两个点时,当B,C是直线y=﹣1上的两个点时,这两种情况讨论,利用轴对称的性质,利用待定系数法求出函数解析式,进而求出C的坐标.
【解答】解:分两种情况:
①当B,C是直线y=1上的两个点时,
取点D(3,3)关于直线y=1的对称点D′(3,﹣1),将点A(0,5)向右平移2个单位得点A'(2,5),连接A'D′交直线y=1交于一点C,如图,此时,AB+BC+CD的值最小,
∵AA'∥BC,AA'=BC=2,
∴四边形AA'CB为平行四边形,则A'C=AB,
∵点D与点D′关于直线y=1对称,
∴CD=CD′,
∴AB+BC+CD=A'C+CD'+BC=A'D′+2,
∴AB+BC+CD的最小值为A'D′+2的值,
设直线A'D′的解析式为y=kx+b,图象过点A'(2,5),D′(3,﹣1),
∴,
解得,
∴直线A'D′的解析式为y=﹣6x+17,
当y=1时,1=﹣6x+17,
解得x,
∴点C的坐标为(,1);
②当B,C是直线y=﹣1上的两个点时,
取点D(3,3)关于直线y=﹣1的对称点D′(3,﹣5),将点A(0,5)向右平移2个单位得点A'(2,5),连接A'D′交直线y=﹣1交于一点C,如图,此时,AB+BC+CD的值最小,
∵AA'∥BC,AA'=BC=2,
∴四边形AA'CB为平行四边形,则A'C=AB,
∵点D与点D′关于直线y=﹣1对称,
∴CD=CD′,
∴AB+BC+CD=A'C+CD'+BC=A'D′+2,
∴AB+BC+CD的最小值为A'D′+2的值,
设直线A'D′的解析式为y=k'x+b',图象过点A'(2,5),D′(3,﹣5),
∴,
解得,
∴直线A'D′的解析式为y=﹣10x+25,
当y=﹣1时,﹣1=﹣10x+25,
解得x,
∴点C的坐标为(,﹣1);
故答案为:(,1)或(,﹣1)
24.解:(1)①当t=5时,AP=10,
∵O是正方形ABCD边AD的中点,
∴OA=ODAD=6,
∴S△AOPOA AP6×10=30,
∴y=S正方形ABCD﹣S△AOP=122﹣30=114;
当t=10时,如图1,
则AB+BP=20,
∴BP=20﹣AB=20﹣12=8,
∴PC=BC﹣BP=12﹣8=4,
∴y=S梯形CDOP(PC+OD) CD(4+6)×12=60;
故答案为:114;60.
②如图2,AB+BP=2t,
∴PC=24﹣2t,
∵OA∥CP,
∴当OA=CP时,以点O、A、P、C为顶点的四边形是平行四边形,
∴6=24﹣2t,
解得:t=9,
∴当t=9时,以点O、A、P、C为顶点的四边形是平行四边形.
(2)①由图3可知:当t=4时,S=0,即P,Q两点在第4秒相遇;
当t=0时,S正方形ABCD=AB2=64,
∴AB=8,即正方形ABCD的边长是8;
故答案为:4;8.
②由图3可知:点P、Q相遇于点C,且点P的速度大于点Q的速度,
∴点P的速度为点Q的速度的2倍,
设点Q的速度为a单位长度/秒,则点P的速度为2a单位长度/秒,
∴4(a+2a)=24,
解得:a=2,
∴点P的速度为4单位长度/秒,点Q的速度为2单位长度/秒;
故答案为:4;2.
③∵O是AD的中点,
∴OA=OD=4,
设t秒时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积S等于32,
分三种情况讨论:
当0≤t≤2时,点P在AB边上,点Q在CD边上,如图,
则AP=4t,DQ=2t,OA=OD=4,
∴S=S正方形ABCD﹣S△OAP﹣S△ODQ=644×4t4×2t=64﹣12t,
由题意得:64﹣12t=32,
解得:t2(不符合题意,舍去);
当2<t≤4时,点P在BC边上,点Q在CD边上,如图,
则AB+BP=4t,AB=8,
∴BP=4t﹣8,
∵DQ=2t,OA=OD=4,
∴S=S正方形ABCD﹣S梯形OABP﹣S△ODQ=64(4t﹣8+4)×84×2t=80﹣20t,
由题意得:80﹣20t=32,
解得:t,符合题意;
当4<t≤6时,点P在CD边上,点Q在BC边上,如图,
∵AB+BC+CP=4t,AB=BC=CD=AD=8,
∴DP=24﹣4t,
∵DC+CQ=2t,
∴BQ=16﹣2t,
∴S=S正方形ABCD﹣S梯形OABQ﹣S△ODP=64(4+16﹣2t)×84×(24﹣4t)=16t﹣64,
由题意得:16t﹣64=32,
解得:t=6(符合题意);
综上,当t或6时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积等于32.
25.解:(1)①如图1﹣1中,过点E作EH⊥BC于H.
∵四边形ABCO是矩形,A(8,0),C(0,6),
∴OA=BC=8,AB=OC=6,
∵∠BCO=∠ACE=90°,
∴∠ACB=∠ECH,
∵CE=CB,∠EHC=∠ABC=90°,
∴△EHC≌△CBA(AAS),
∴EH=CB=8,CH=AB=6,
∴E(6,14).
故答案为:(6,14);
②如图1﹣2中,过点E作EH⊥BC于H.
同法可证:△EHD≌△DBA(AAS),
∴EH=DB=8﹣m,DH=AB=6,
∴CH=6+m,
∴E(6+m,14﹣m).
故答案为:(6+m,14﹣m);
(2)△ABF的面积不会改变,理由如下:
如图2,过点F作FH⊥AB,交AB的延长线于H,
∵矩形OABC的顶点B坐标为(8,6),
∴AB=6,BC=8,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∴∠DAB+∠FAB=90°,且∠DAB+∠BDA=90°,
∴∠BDA=∠FAB,
∵AD=AF,∠ABD=∠AHF=90°,
∴△ABD≌△FHA(AAS),
∴HF=AB=6,
∴△ABF的面积AB×HF=18;
(3)若BE=EF,当点B与点D重合时,AD=AB=6,此时m=8.
当点B与点D不重合时,如图3,过点E作EH⊥DB于H,
∵∠EDH+∠ADB=90°,∠ADB+∠DAB=90°,
∴∠EDH=∠DAB,
AD=DE,∠EHD=∠ABD=90°,
∴△ADB≌△DEH(AAS),
∴DH=AB=6,
∵BE=EF,EF=DE,
∴DE=BE,
∵EH⊥DB
∴DH=BH=6,
∴DB=12,
∵DB<BC,
∴此种情形不存在.
若EB=BF,
∵BE=BF,
∴∠BEF=∠BFE,
∴∠DEB=∠AFB,
∵DE=AF,BE=BF,
∴△DEB≌△AFB(AAS),
∴DB=AB=36,
∴CD=BC﹣BD=8﹣6=2,即m=2;
若BF=EF,如图4,过点F作FH⊥AB于H,
∵∠DAB+∠FAB=90°,∠DAB+∠BDA=90°,
∴∠BDA=∠FAB,
∵AD=AF,∠ABD=∠AHF=90°,
∴△ABD≌△FHA(AAS),
∴AH=DB,
∵EF=BF,EF=AF,
∴BF=AF,
∵FH⊥AB,
∴AH=BH=3,
∴DB=3,
∴CD=BC﹣BD=8﹣3=5,即m=5,
综上所述,满足条件的m的值为8或2或5.
26.解:(1)过点A'作AQ⊥AB于点Q,
∵矩形OABC中,,C(0,2),
∴,AB=2,
∴,
由对称得,AP=A′P,
则,
设AP=A′P=x,则BP=AB﹣x=2﹣x,
由勾股定理得:A'B2+A'P2=BP2,
即 ,
解得:,
∴,
∵∠PA'B=90°,S△A'BP,
即,
解得:,
∴点A'的横坐标为,
设OB的函数表达式为y=kx,将 代入得:,
∴OB的函数表达式为,
将 代入得:,
∴;
(2)①连接OM,
∵∠POM=45°,∠AOC=90°,
∴∠1+∠4=45°,∠2+∠3=45°,
∵△PAO和△PA′O对称,
∴∠3=∠4,
∴∠1=∠2,
又∵∠C=∠OA'M=∠OAP,OM=OM,
∴△OMC≌△OMA'(AAS),
∴OC=OA'=OA,
则四边形OABC为正方形,
∴;
②(Ⅰ)当 时,
∵△OMC≌△OM,△OAP≌△OAP,
∴,
(Ⅱ)当时,Rt△OMA'≌Rt△OMC(HL),
∴∠1=∠2,
∵OC∥AP,
∴∠3=∠OPA,
由折叠的性质可得:∠4=∠OPA,∠A′=∠OAP=90°,
∴∠3=∠4,
∵∠1+∠2+∠3+∠4=90°,∠1=∠2,∠3=∠4,
∴∠2+∠3=45°,
即∠POM=45°,
综上所述:∠POM的大小不会改变.
27.解:(1)过点A作AE⊥OC于点E,如图,
∵点A的坐标为(3,4),
∴OE=3,AE=4,
∴OA=AB5,
∵四边形ABCD为平行四边形,
∴CD=AB=5.
(2)存在t的值,使得PQ与CD互相平分,t的值为4,理由:
连接PC,DQ,如图,
若PQ与CD互相平分,
∴四边形PCQD为平行四边形,
∴PD=CQ,
由题意得:PD=t,BQ=3t,
∵四边形ABCD为平行四边形,
∴BC=AD=8,
∴CQ=BQ﹣BC=3t﹣8,
∴t=3t﹣8,
∴t=4.
∴存在t的值,使得PQ与CD互相平分,t的值为4.
(3)①当点Q在BC上时,如图,
∵点P关于直线DQ对称的点恰好落在直线CD上,
∴∠ADQ=∠CDQ,
∵AB∥CD,
∴∠DQC=∠ADQ,
∴∠DQC=∠CDQ,
∴CQ=CD,
∵CQ=BC﹣BQ=8﹣3t,
∴8﹣3t=5,
∴t=1.
∴PD=1,
∴AP=7,
∴P(10,4);
②当点Q在BC的延长线上时,如图,
∵点P关于直线DQ对称的点恰好落在直线CD上,
∴∠PDF=∠P′DF,
∵AD∥BC,
∴∠CQD=∠PDF,
∴∠P′DF=∠CDQ,
∴∠CDQ=∠CQD,
∴CQ=CD,
∵CQ=3t﹣8,
∴3t﹣8=5,
∴t.
∴DP,
∴AP=AD﹣DP=8,
∴P(,4).
综上,点P关于直线DQ对称的点恰好落在直线CD上,点P的坐标为(10,4)或(,4).
28.(1)解:如图1中,
∵四边形EFMN是正方形,
∴EF=EN,∠FEN=∠A=∠D=90°,
∴∠AEF+∠AFE=90°,∠AEF+∠DEN=90°,
∴∠AFE=∠DEN,
∴△AEF≌△DNE(AAS),
∴AF=DE,
∵AD=3.AE=1,
∴DE=2,
∴x=AF=2.
过点M作MH⊥FB于点H.同法可证△MHF≌△FAE,
可得MH=AF=2,
∴S FB MH5×2=5.
故答案为:2,5;
(2)①证明:如图2中,
如图,连接FN,作MQ⊥FB于Q,则∠MQF=90°,∠MQF=∠A
∵四边形FEMN是菱形,
∴EN=FM,EN∥FM,
∴∠ENF=∠NFM,
∵矩形ABCD中,DC∥AB,
∴∠DNF=∠NFQ,
∴∠DNF﹣∠ENF=∠NFQ﹣∠NFM,即∠DNE=∠MFQ,
②解:∵∠D=∠FQM=90°,∠QNE=∠MFQ,NE=FM,
∴△DNE≌△QFM(AAS),
∴MQ=DE=2,
∵AB=7,AF=x,
∴S△FBMFB×MQ(7﹣x)×2=7﹣x.
∴S与x的函数关系式S=7﹣x;
(3)①如图3中,当点N与D重合时,x的值最小,△FBM的面积最大,
在Rt△AEF中,x,
∴S的最大值=7.
②如图4中,当点M在BC上时,x的值最大,△FBM的面积最小,
此时易证CN=AF=x,
∵EN=EF,
∴1+x2=22+(7﹣x)2,
∴x,
∴S的最小值为7.
故答案为:,.
(4)如图3中,在△BFM的面积S由最大变为最小的过程中,点M的运动轨迹是平行AB的线段,点M运动的路线长=BF的长=7,
故答案为:7.
【类型一:点和运动和函数图像的结合】
1.如图,在平面直角坐标系中,将 ABCD放置在第一象限,且AB∥x轴.直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,则 ABCD的面积为( )
A.10 B. C.5 D.
2.如图1,在菱形ABCD中,点P沿A﹣B﹣C方向从点A移动到点C,设点P的移动路程为x,线段AP的长为y,点P在运动过程中y与x的变化关系如图2所示,点P运动到BC边上时,当x=18,y的值最小为12,则a的值是 .
3.如图1,点P从菱形ABCD的顶点A出发,沿A→C→B以1cm/s的速度匀速运动到点B,点P运动时△PAD的面积y(cm2)随时间x(s)变化的关系如图2,则a的值为( )
A.8 B. C.6 D.
4.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则矩形ABCD的周长是( )
A.18 B.20 C.22 D.26
5.如图①,在矩形ABCD的边BC上有一点E,连结AE,点P从顶点A出发,沿A→D→C以1cm/s的速度匀速运动到点C.图②是点P运动时,△APE的面积y(cm2)随时间x(s)变化的函数图象,则BE的长为( )
A.5cm B.4cm C.3cm D.2cm
6.如图,在矩形ABCO中,点O为坐标原点,点B的坐标为(8,6),点A,C在坐标轴上,直线y=2x﹣6与AB交于点D,与y轴交于点E.有一动点M在BC边上,点N是坐标平面内的点,若△AMN是以点N为直角顶点的等腰直角三角形,则整个运动过程中点N纵坐标n的取值范围为 .
【类型二:平行四边形的存在性问题】
7.已知矩形ABCD中,AB=12cm,BC=18cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE,直接写出AF的长为 ;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中:
①已知点P的速度为每秒4cm,点Q的速度为每秒3cm,运动时间为t秒,当以A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值;
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),以A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
8.在四边形ABCD中,AD∥BC,AB=12cm,AD=8cm,BC=24cm,∠ABC=90°,P,Q同时沿着四边形的边逆时针运动,点P从点D出发,以1cm/s的速度运动,点Q从点B出发,以2cm/s的速度运动,设运动时间为t秒.
(1)CD= cm;
(2)若点Q运动到点C时就停止,点P也随之停止运动,用含t的代数式表示四边形PQCD的面积S(cm2);
(3)若其中一个动点回到其出发点时,另一个动点也随之停止运动,则当t= 时,以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形.
9.如图,在平面直角坐标系中,点A的坐标是,将线段OA绕着点O顺时针方向旋转60°后得到线段OB,连接AB,直线AB交x轴于点C.
(1)求直线AB的解析式.
(2)若点D是点C关于直线OB的对称点,△BOC沿着直线CB平移得到△B1O1C1,求的最小值,及此时B1的坐标.
(3)点E是坐标平面内一点,且满足S△EOB=S△AOB,在y轴上是否存在一点F,使得以点B、O、E、F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
10.将一长方形纸片OABC放在直角坐标系中,O为原点,点C在x轴上,OA=9,OC=15.
(1)如图1,在OA上取一点E,将△EOC沿EC折叠,使点O落在AB边上的点D,求线段AE.
(2)如图2,在OA,OC边上选取适当的点M,F,将△MOF沿MF折叠,使点O落在AB边上的点D′处,过点D,作D′G垂直于CO于点G,交MF于点T.
①求证:TG=AM;
②设T(x,y),求y与x满足的等量关系式,并将y用含x的代数式表示.
(3)在(2)的条件下,当x=6时,点P在直线MF上,问:在坐标轴上是否存在点Q,使以M,D′,Q,P为顶点的四边形是平行四边形?若存在,请直接写出Q点坐标;若不存在,请说明理由.
【类型四:菱形的存在性问题】
11.如图1,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设点E的运动时间为t(s).
(1)如图2,连接EF,若EF经过边AC的中点D.
①求证:四边形AFCE是平行四边形;
②求此时t的值.
(2)是否存在t,使得以点A,E,C,F为顶点的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
12.已知,如图,O为坐标原点,在四边形OABC中,BC∥OA,BC=24,A(26,0),C(0,12),点D是OA的中点,动点P在线段BC上以每秒2个单位长度的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当P运动 秒,四边形PDAB是平行四边形.
(2)在直线CB上是否存在一点Q,使得以O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由.
13.如图,正方形OABC的顶点O在坐标原点,定点A的坐标为(4,3).
(1)求正方形OABC顶点C的坐标为( , )顶点B的坐标为( , );
(2)现有一动点P从C点出发,沿线段CB向终点B运动,P的速度为每秒1个单位长度,同时另一动点Q从点A出发沿A→O→C向终点C运动,速度为每秒k个单位长度.设运动时间为2秒时,将三角形CPQ沿它的一边翻折,若翻折前后的两个三角形组成的四边形为菱形,求k的值.
14.如图,在平面直角坐标系中,点A(4,0),B(6,3),C(0,3).
(1)若动点P从原点O出发,以每秒3个单位长度沿着x轴正方向运动,动点Q从点B出发,以每秒1个单位长度向点C运动,当点Q到达点C处时,两点都停止运动.设运动时间为t(秒).若以A、B、P、Q四个点为顶点的四边形是平行四边形,求此时t的值;
(2)点M在x轴上,平面内是否存在点N,当以A、C、M、N为顶点的四边形是菱形时,请直接写出所有满足条件的点N的坐标.
15.将一个矩形纸片OABC放置在平面直角坐标系中,OA,OC分别在x轴,y轴的正半轴上,点B坐标为(4,10).
(Ⅰ)如图①,将矩形纸片OABC折叠,使点B落在y轴上的点D处,折痕为线段AE,求点D坐标;
(Ⅱ)如图②,点E,F分别在OC,AB边上.将矩形纸片OABC沿线段EF折叠,使得点B与点D(0,2)重合,求点C的对应点G的坐标;
(Ⅲ)在(Ⅱ)的条件下,若点P是坐标系内任意一点,点Q在y轴上,使以点D,F,P,Q为顶点的四边形是菱形,请直接写出满足条件的点P的坐标.
16.如图,正方形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(4,4),一次函数的图象与边OC、AB分别交于点D、E,并且满足.点M是线段DE上的一个动点.
(1)连接BD、OE,求证:四边形ODBE是平行四边形;
(2)作BP⊥DE交OA于P,当△OMP面积为2.6时,求M点的坐标;
(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
【类型四:矩形的存在性问题】
17.如图,一次函数y=kx+b(k≠0)的图象与x轴交于点,与y轴交于点B,且与正比例函数的图象交于点C(m,6).
(1)求m的值和一次函数y=kx+b(k≠0)的解析式;
(2)点P为坐标平面内的点,在x轴上是否存在点M,使得四边形ABMP是矩形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,且OA=6,OC=4.点D为OA的中点,连接CD,DE为∠ADC的平分线,交BC于点E.
(1)求点B和点E的坐标;
(2)点P为射线DE上一动点,点Q为平面内任意一点,
①连接BD,CP,若S△CDP=S△BCD,请求出点P的坐标;
②是否存在P,Q两点,使得四边形OBPQ为矩形?若存在,请求出P点的坐标;若不存在,请说明理由.
19.如图,平面直角坐标系中,矩形OBCD的顶点B(0,b)、顶点C(c,b),且b、c满足,点A(﹣6,0).
(1)顶点C的坐标为 ;线段AB的长度是 ;
(2)已知点E是线段AB上的动点,点F是线段AC上的动点,点H(2,8),当EF+FH的值最小时,求F点的坐标;
(3)在第(2)问的条件下,点P是坐标轴上的点,点Q是平面内一点,请问存在以点A、F、P、Q为顶点的四边形是以AF为边的矩形吗?若存在,求出点Q的坐标;若不存在,请说明理由.
【类型五:正方形的存在性问题】
20.平面直角坐标系内如图放矩形OABC已知点B(8,6),D(0,4).将矩形OABC沿EF折叠,便点A与点D重合.折痕交BC于点E,交OA于点F.
(1)求点F的坐标;
(2)若动点P,Q同时从点A出发,点P以每秒1个单位长度的速度向点O运动,点Q以每秒2个单位长度的速度沿射线AB方向运动,当点P运动到点O时停止运动,点Q也同时停止运动.设△PQF的面积为S,点P,Q的运动时间为t秒,求S与t的函数关系式并直接写出自变量的取值范围;
(3)在(2)的条件下,R是射线CB上的一点,点M为平面内一点,是否存在点M,使以P,Q,R,M为顶点的四边形是正方形?若存在,请求出点M的坐标;若不存在.请说明理由.
【类型六:四边形动点综合题】
21.在Rt△ABC中,∠ABC=90°,AB=8,BC=4.如图,将直角顶点B放在原点,点A放在y轴正半轴上,当点B在x轴上向右移动时,点A也随之在y轴上向下移动,当点A到达原点时,点B停止移动,在移动过程中,AC= ,点C到原点的最大距离为 .
22.如图,在平面直角坐标系中,点A(6,4)、B(7,2),点C在x轴上运动,点D在直线y=x上运动,则四边形ABCD周长的最小值是 .
23.已知B,C是平面直角坐标系中与x轴平行且距离x轴1个单位长度的直线上的两个动点(点B在点C左侧),且 BC=2,若有点A(0,5)和点D(3,3),则当AB+BC+CD的值最小时,点C的坐标为 .
24.在正方形ABCD中,O是AD的中点,点P从A点出发沿A→B→C→D的路线匀速运动,移动到点D时停止.
(1)如图1,若正方形的边长为12,点P的运动速度为2单位长度/秒,设t秒时,正方形ABCD与∠POD重叠部分的面积为y.
①当t=5时,y= ;当t=10时,y= .
②求t为何值时,以点O、A、P、C为顶点的四边形是平行四边形?
(2)如图2,若点Q从D出发沿D→C→B→A的路线匀速运动.P、Q两点同时出发,点P的速度大于点Q的速度,当P到终点时,Q也停止运动.设t秒时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积为S,S与t的函数图象如图3所示.
①P,Q两点在第 秒相遇;正方形ABCD的边长是 .
②点P的速度为 单位长度/秒;点Q的速度为 单位长度/秒.
③当t为何值时,重叠部分面积S等于32?
25.如图,在平面直角坐标系xOy中,矩形OABC的顶点A(8,0),顶点C(0,6),点D为BC边上一动点,设CD的长为m,以AD为一边在与点B的同侧作正方形ADEF,在点D运动过程中,探究以下问题:
(1)①当点D与点C重合时,点E的坐标为 ;
②用含m的代数式表示点E的坐标为 .
(2)三角形ABF的面积是否改变?如果不变,求出此定值;如果改变,请说明理由;
(3)当△BEF为等腰三角形时,直接写出所有m的值.
26.如图1,在平面直角坐标系中,矩形OABC的顶点,动点P从A出发,以每秒1个单位的速度沿射线AB方向移动,作△PAO关于直线PO的对称△PA′O,设点P的运动时间为t(s).
(1)如图2.当C(0,2),且点A′落在OB上时,求此时A′的坐标;
(2)若直线PA′与直线BC相交于点M,且t<2时,∠POM=45°.
①求点C的坐标;
②当t≥2时,∠POM的大小是否发生变化,请说明理由.
27.如图, ABCD的顶点B与坐标原点重合,点C在x轴上,点A的坐标为(3,4),AD=8.动点P从点D出发沿DA以1个单位每秒的速度向终点A运动,同时点Q从点B出发,以3个单位每秒的速度沿射线BC运动,当点P到达终点时,点Q也随之停止运动,设点P的运动时间为t秒(t>0).
(1)求CD的长;
(2)连结PQ,是否存在t的值,使得PQ与CD互相平分?若存在,求出t的值;若不存在,请说明理由;
(3)若点P关于直线DQ对称的点恰好落在直线CD上,请直接写出点P的坐标.
28.已知:如图,在矩形ABCD中,AB=7,BC=3.在AD上取一点E,AE=1,点F是AB边上的一个动点,以EF为一边作菱形EFMN,使点N落在CD边上,点M落在矩形ABCD内或其边上.若AF=x,△BFM的面积为S.
(1)如图1,当四边形EFMN是正方形时,x的值为 ,S的值为 ;
(2)如图2,当四边形EFMN是菱形时,
①求证:∠DNE=∠MFB;
②求S与x的函数关系式;
(3)当x 时,△BFM的面积S最大;当x= 时,△BFM的面积S最小;
(4)在点F运动的过程中,请直接写出点M运动的路线长: .
参考答案
【类型一:点和运动和函数图像的结合】
1.
【分析】通过图象中(3,0),(7,2),(8,2)可得直线运动到A,D,B三点时所移动距离,从而求出AB长度,再通过添加辅助线构造直角三角形求出平行四边形的高而求解.
【解答】解:由图象可知,直线经过A时移动距离为3,经过D时移动距离为7,经过B时移动距离为8,
∴AB=8﹣3=5.
如图,当直线经过点D时,交AB于点E,作DF垂直于AB于点F,由图2可知DE2,
∵直线与AB夹角为45°,
∴DF=EF=2,
∴ABCD面积为AB DF=5×2=10.
故选:A.
2.
【分析】根据菱形的性质,再结合P运动时y随x的变化的关系图象,运用勾股定理即可求解.
【解答】解:如图1,过A点作AE⊥BC于E,
根据图2知:当点P与点E重合时,AB+BP=18,AP=12,
∴AB+BE=18,AE=12,
设AB=m,则BE=18﹣m,
在Rt△ABE中,AE2+BE2=AB2,
∴122+(18﹣m)2=m2,
解得:m=13,
∴AB=BC=CD=AD=13,BE=5,
∴EC=BC﹣BE=13﹣5=8,
当点P到达点C时,AP=AC=a,
在Rt△ACE中,AC2=AE2+EC2,即a2=122+82=208,
∵a>0,
∴a=4,
故答案为:4.
3.
【分析】过点C作CE⊥AD,再根据图象的三角形的面积可得CE=8,再利用菱形的性质和勾股定理列方程可求a即可.
【解答】解:过点C作CE⊥AD,垂足为E,
∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∴点P在边BC上运动时,y的值不变,
∴AD=BC=10+a﹣10=a,
即菱形的边长是a,
∴AD CE=4a,即CE=8,
当点P在AC上运动时,y逐渐增大,
∴AC=10,
∴AE6,
在Rt△DCE中,DC=a,DE=a﹣6,CE=8,
∴a2=82+(a﹣6)2,
解得:a.
故选:B.
4.
【分析】根据函数的图象、结合图形求出AB、BC的值,即可得出矩形ABCD的周长.
【解答】解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变,
函数图象上横轴表示点P运动的路程,x=4时,y开始不变,说明BC=4,x=9时,接着变化,说明CD=9﹣4=5,
∴AB=5,BC=4,
∴矩形ABCD的周长=2(AB+BC)=18.
故选:A.
5.
【分析】抓住关键点,函数图象最高点的纵坐标为9,横坐标为6,得△APE的最大面积为9,此时P、D重合,AD=AP=6,,通过图象知道点P到终点时,△APE的面积是6,此时P、C重合,,得EC,即可求得BE的长.
【解答】解:∵四边形ABCD是矩形,
∴AD=BC,
由图象可知,当P、D重合,AD=AP=6cm,,
可得:AB=3cm,
当时P、C重合,,可得:EC=4cm,
则:BE=BC﹣EC=6﹣4=2cm.
故选:D.
6.
【分析】根据等腰直角三角形的性质解答即可.
【解答】解:当点M在B点时,如图,
AN1=BN1,∠AN1B=90°,∠N1AB=∠N1BA=45°,
∵AB=8,N1T⊥AB,
∴AT=N1T=AB=4,
∴N1的纵坐标为6+4=10,
同理,N2的纵坐标为6﹣4=2,
当M在C点时,如图,
AN3=CN3,∠AN3C=90°,∠N3AC=∠N3CA=45°,
过点N3作N3S⊥AO于点S,延长SN3交CB于点M,
则Rt△N3SA≌Rt△CMN3,
则N3S=CM,SA=MN3,
设点N3纵坐标为6+y,则BM=SA=MN3=y,
那么N3S=8﹣y=CM=6+y,
解得:y=1,
则点N3纵坐标为6+y=7,
同理可得,N4纵坐标为6﹣y=﹣1,
当点N为直角顶点时,t的取值范围为7≤n≤10或﹣1≤n≤2.
【类型二:平行四边形的存在性问题】
7.解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE,
∵EF垂直平分AC,垂足为O,
∴OA=OC,
∴△AOE≌△COF(AAS),
∴OE=OF,
∴四边形AFCE为平行四边形,
又∵EF⊥AC,
∴四边形AFCE为菱形,
设菱形的边长AF=CF=x cm,则BF=(18﹣x)cm,
在Rt△ABF中,AB=12cm,
由勾股定理得122+(18﹣x)2=x2,
解得x=13,
∴AF=13cm.
故答案为:13cm;
(2)①显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上或P在BF,Q在CD时不构成平行四边形,也不能构成平行四边形.
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒4cm,点Q的速度为每秒3cm,运动时间为t秒,
∴PC=4t,QA=CD+AD﹣3t=30﹣3t,即QA=30﹣3t,
∴4t=30﹣3t,
解得t,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t.
②由题意得,四边形APCQ是平行四边形时,点P、Q在互相平行的对应边上.
分三种情况:
i)如图1,当P点在AF上、Q点在CE上时,AP=CQ,即a=30﹣b,得a+b=30;
ii)如图2,当P点在BF上、Q点在DE上时,AQ=CP,即30﹣b=a,得a+b=30;
iii)如图3,当P点在AB上、Q点在CD上时,AP=CQ,即30﹣a=b,得a+b=30.
综上所述,a与b满足的数量关系式是a+b=30(ab≠0).
8.解:(1)过点D作DE⊥BC交BC于点E,如图1,
∵∠ABC=90°,AD∥BC,
∴∠A=∠BED=∠ABC=90°,
则四边形ABED为矩形,
∴BE=AD=8cm,AB=DE=12cm,
∴EC=BC﹣BE=24﹣8=16(cm),
∴DC20(cm),
故答案为:20;
(2)若点Q运动到点C时就停止,点P也随之停止运动,
如图2,当点P在AD上运动,即0≤t≤8时,
则DP=t cm,BQ=2t cm,AP=(8﹣t)cm,
∴S=S四边形PQCD=S梯形ABCD﹣S梯形APQB(8+24)×12(8﹣t+2t)×12=144﹣6t(cm2);
如图3,当点P在AB上运动,即8≤t≤12时,
则AP=(t﹣8)cm,BQ=2t cm,BP=12﹣(t﹣8)=(20﹣t)cm,
∴S=S四边形PQCD=S精形ABCD﹣S△PQB﹣S△APD(8+24)×122t (20﹣t)8 (t﹣8)=t2﹣24t+224(cm2),
综上,S=144﹣6t(0≤t≤8)或S=t2﹣24t+224(8≤t≤12);
(3)①如图4,当AP=BQ时,8﹣t=2t,此时ts,四边形ABQP是平行四边形;
②如图5,当PD=QC时,t=24﹣2t,此时t=8s,四边形PQCD为平行四边形;
③如图6,当AQ=BP时,四边形ABPQ是平行四边形,8﹣(2t﹣24﹣20)=t﹣8﹣12,此时t=24s;
④如图7,当PC=QD时,24﹣(t﹣8﹣12)=2t﹣24﹣20,此时ts,四边形PCDQ为平行四边形;
综上所述,当ts或t=8s或t=24s或ts时,以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形,
故答案为:s或8s或24s或s.
9.解:(1)∵点A的坐标是,将线段OA绕着点O顺时针方向旋转60°后得到线段OB,
∴△AOB是等边三角形,且,
∴∠OAB=60°,∠ACO=30°,
∴,,
∴点C的坐标是(6,0),
设直线AB的解析式为,
则,
∴,
∴直线AB的解析式为;
(2)如图1,连接CD,BD,OO1,O1C1,OD,
由平移可得:∠ACO=∠B1C1O1=30°,OC=O1C1=6,
由(1)可得:△ABO为等边三角形,
∴∠ACB=60°,
∴∠BOC=90°﹣60°=30°,
∵点D是点C关于直线OB的对称点,
∴OD=OC,BC=BD,∠BOC=∠BOD=30°,
∴∠DOC=60°,
∴△DOC为等边三角形,∠OKC=180°﹣60°﹣30°=90°,
∴DO=OC=6,,
∴当C1与K重合时,
∴,此时最小,
即的最小值为6;
如图2,,,
∴,
过B1作B1G⊥OC于G,
∴,,
∴,
∴;
(3)如图3,点E是坐标平面内一点,且满足S△EOB=S△AOB,
∴E在过A点与OB平行的直线上或在OB下方,与OB平行,与A到OB的距离相等的平行线CJ上,
∵以点B、O、E、F为顶点的四边形是平行四边形,
∴F与A重合,当OB为对角线时,
∴,
由(1)(2)可得:OB=AB=BC,,C(6,0),
∴,
∴由平移可得:;
同理:F与J重合,当OE为对角线时,
此时,
∴,,
如图4,F与J重合,当BE为对角线时,
同理:,
由平移可得:;
当E在AI上时,如图5,F与A重合,当BF为对角线时,
∴,,
如图6,F与A重合,当OF为对角线时,
∴;;
当F与J重合,当OB为对角线时,如图7,
∴;;
综上:或或或.
10.(1)解:∵长方形OABC,
∴BC=OA=9,AB=OC=15,
由折叠的性质可知,CD=OC=15,DE=OE,
由勾股定理得,,
∴AD=3,
设AE=x,则DE=OE=9﹣x,
由勾股定理得,DE2﹣AE2=AD2,即(9﹣x)2﹣x2=32,
解得,x=4,
∴线段AE的长为4;
(2)①证明:由折叠的性质可知,∠D′MF=∠OMF,D′M=OM,
∵D′G⊥OC,AO⊥OC,
∴AO∥D′G,四边形AOGD′是矩形,
∴∠OMF=∠D′TM,AO=GD′,
∴∠D′MF=∠D′TM,
∴D′T=D′M=OM,
∴GD′﹣D′T=AO﹣OM,
∴TG=AM;
②解:∵T(x,y),
∴AM=TG=y,AD′=x,D′T=D′M=OM=9﹣y,
由勾股定理得,AM2+AD′2=D′M2,即y2+x2=(9﹣y)2,
整理得,;
(3)解:在坐标轴上存在点Q,使以M,D′,Q,P为顶点的四边形是平行四边形,Q点坐标为(0,13)或(0,0)或;理由如下:
当x=6时,,
∴,,
∴,D′(6,9),
∵以M,D′,Q,P为顶点的四边形是平行四边形,
∴当MD′为对角线时,MQ∥D′P,如图2,四边形MQD′P是平行四边形,P、T重合,
∴,
由平移的性质可得,Q(0,13);
当MD′为边,MP为对角线时,MQ∥D′P,如图2,四边形MQ′PD′平行四边形,P、T重合,则,
由平移的性质可得,Q′(0,0);
当MD′为边,MP为边时,MP∥D′Q,如图2,四边形MP″Q″D′是平行四边形,
设直线MP的解析式为y=kx+b,将点T,点M的坐标代入得:
,
解得,,
∴直线MP的解析式为,
∴直线D′Q″的解析式为,
将D′(6,9)代入得:,
解得:c=13,
∴直线D′Q″的解析式为,
令y=0,则,
解得,,
∴;
综上所述,在坐标轴上存在点Q,使以M,D′,Q,P为顶点的四边形是平行四边形,Q点坐标为(0,13)或(0,0)或.
【类型四:菱形的存在性问题】
11.解:(1)∵AG∥BC,
∴∠EAC=∠FCA,∠AED=∠CFD.
∵EF经过边AC的中点D,
∴AD=CD,
∴△ADE≌△CDF(AAS),
∴AE=CF.
∵AE∥FC,
∴四边形AFCE是平行四边形;
②此时AE=CF,
由运动知,AE=tcm,CF=(6﹣2t)cm.
∴t=6﹣2t,
解得t=2;
(2)存在;
∵点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,
∴当点F在线段BC上时,四边形AFCE不可能为菱形;
当点F在BC的延长线上时,
∵AE∥CF,
∴当AE=CF时,四边形ACFE是平行四边形,
∴t=2t﹣6,
解得t=6,
此时AE=AC=6,
∴当t=6时,四边形ACFE是菱形.
12.解:(1)∵A(26,0),C(0,12),
∴OA=26,OC=8,
∵点D时OA的中点,
∴OD=1OA=13,
由运动知,PC=2t,
∵BC=24,
∴BP=BC﹣PC=24﹣2t,
∵四边形PDAB是平行四边形,
∴PB=AD=13,
∴24﹣2t=13,
解得t=5.5,
∴当t值为5.5时,四边形PDAB是平行四边形.
故答案为:5.5;
(2)存在,分三种情况:
①当Q点在P点的右边时,如图,
∵四边形ODQP是菱形,
∴OD=OP=PQ=13,
∴在Rt△OPC中,由勾股定理得:PC=5,
∴2t=5,
解得t=2.5,
∴Q(18,12);
②当Q点在P点左侧且在BC线段上时,如图,
同理①得PC=18,
即2t=18,
解得t=9,
∴Q(5,12);
③当Q点在P点左侧且在BC延长线上时,如图3,
同理①求出QC=5,PC=13﹣5=8,
即2t=8,
解得t=4,
∴Q(﹣5,12);
综上,t=2.5时,Q(18,12),t=9时,Q(5,12),t=4时,Q(﹣5,12).
13.解:(1)过点A作AD⊥x轴于D,过点B作BE⊥AD交DA的延长线于E,过点C作CF⊥x轴于点F,
∴∠ADO=∠OFC=∠BEA=90°,
∴∠DAO+∠AOD=90°,
∵四边形ABCO是正方形,
∴∠OAB=∠AOC=90°,OA=OC=AB,
∴∠COF+∠AOD=90°,∠BAE+∠DAO=90°,
∴∠FOC=∠DAO,∠BAE=∠AOD,
∴△COF≌△AOD≌△BAE(AAS),
∴OF=AD=BE,CF=OD=AE,
∵点A的坐标为(4,3),
∴OF=AD=BE=3,CF=OD=AE=4,
∴点C的坐标为(﹣3,4);
∴ED=4+3=7,点B到y轴的距离为OD﹣BE=4﹣3=1,
∴点B的坐标为(1,7);
故答案为:﹣3,4,1,7;
(2)由题意,得AO=CO=BC=AB5,
当 t=2 时,CP=2.
将三角形CPQ沿它的一边翻折,若翻折前后的两个三角形组成的四边形为菱形,
只需三角形CPQ是等腰三角形即可.
①当点Q在OA上时,
∵PQ AB>PC,
∴只存在一点Q,使QC=QP.
过点Q作QD⊥PC于点D,如图,
则CD=PD=1,
∵QA=BD,
∴2k=5﹣1=4,
∴k=2;
②当点Q在OC上时,
∵∠BCO=90°,
∴只存在一点Q,使CP=CQ=2,
∴2k=10﹣2=8,
∴k=4.
综上所述,k的值为2或4.
14.解:(1)若点P在点A的左侧,四边形PABQ为平行四边形,PA=QB,
由题意得4﹣3t=t,
解得t=1,
若点P在点A的右侧,四边形PAQB为平行四边形,PA=QB,
∴3t﹣4=t,
解得t=2,
综上:t=1或2时,以A,B,P,Q为顶点的四边形为平行四边形.
(2)N点坐标为(﹣5,3),(5,3),(0,﹣3),.
∵点A(4,0),C(0,3),
∴AO=4,OC=3,
∴AC5,
如图,以AC为边,四边形ACMN是菱形,
∵C(0,3),
∴N(0,﹣3);
如图,以AC为边,四边形ACNM是菱形,
∵CN=AC=5,CN∥AM,
∴N(5,3);
如图,以AC为边,四边形ACNM是菱形,
∵CN=AC=5,CN∥AM,
∴N(﹣5,3);
如图,以AC为对角线,四边形ACNM是菱形,
设CM=AM=CN=x,
∴OM=4﹣x,
∵OC2+OM2=CM2,
∴32+(4﹣x)2=x2,
∴,
∴CN,
∴N(,3);
综上所述,以A、C、M、N为顶点的四边形是菱形时,点N的坐标为(﹣5,3),(5,3),(0,﹣3),.
15.解:(Ⅰ)∵四边形OABC是矩形,
∴∠BAO=∠BCO=90°,OA=CB,CO=BA.
∵点B坐标为(4,10),
∴OA=CB=4,CO=BA=10;
由折叠可知,△ADE≌△ABE,
∴DA=BA=10.
在Rt△AOD中,OD2,
∴点D的坐标为(0,2 );
(Ⅱ)如图,过点G作GH⊥y轴于点H,
∵点D (0,2),
∴DO=2,
∵四边形OABC是矩形,
∴∠B=90°;
由折叠知,四边形BCEF与四边形DGEF全等,
∴∠EGD=∠B=90°,GD=CB=4,CE=EG.
设CE=EG=x,则ED=CO﹣CE﹣DO=10﹣2﹣x=8﹣x.
在Rt△EGD中,EG2+GD2=ED2,
∴x2+42=(8﹣x)2,
解得:x=3.
∴EG=3,ED=5.
∴S△EGDEG GDED GH,
∴3×45×GH,
∴GH,
在Rt△GHD中,HD,
∴HO=HD+DO2.
∴点G的坐标为(,).
(Ⅲ)由折叠可知,∠BFE=∠DFE,
∵BF∥ED,
∴∠BFE=∠FED,
∴∠FED=∠DFE,
∴BF=DF=ED=5,
∴AF=AB﹣BF=10﹣5=5,
∴F(4,5),
设Q(0,y),P(m,n),
∵D (0,2),
∴DQ=|y﹣2|,DF=5,FQ2=42+(y﹣5)2,DF的中点坐标为(2,),
∵点Q在y轴上,使以点D,F,P,Q为顶点的四边形是菱形,
∴分三种情况:DQ=DF或FQ=DF或DQ=FQ,
①当DQ=DF时,|y﹣2|=5,
解得:y=7或﹣3,
∴Q(0,7)或(0,﹣3),
∴P(4,0)或(4,10),
②当FQ=DF时,42+(y﹣5)2=25,
解得y=8或y=2(舍去),
∴Q(0,8),
∴P(﹣4,5),
③当DQ=FQ时,|y﹣2|2=42+(y﹣5)2,
解得:y,
∴Q(0,),
∵2,,
∴m=4,n,
∴P(4,),
综上所述,点P的坐标为(4,10),(4,0),(﹣4,5),(4,).
16.(1)证明:正方形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(4,4),
∴OC=AB=OA=BC=4,OC∥AB,
∵3,
∴BE=3,AE=1,
∴E(4,1),
代入yx+b得﹣2+b=1,解得b=3,
∴yx+3,
∴D(0,3),
∴OD=BE=3,
∵OD∥BE,
∴四边形ODBE是平行四边形;
(2)解:过点D作DH⊥AB于H,
∴∠DHE=∠BAP=90°,四边形ODHA是矩形,
∴DH=OA=AB=4,BH=CD=1,
∵DH⊥AB,BP⊥DE,
∴∠EDH+DEH=∠PBA+DEH=90°,
∴∠EDH=∠PBA,
∴△DHE≌△BAP(ASA),
∴PA=EH=BE﹣BH=2,
∴OP=OA﹣PA=2,
设M的坐标为(m,m+3),
∴S△OMP2×(m+3)=2.6,解得m,
∴M点的坐标为(,);
(3)解:当四边形OMDN是菱形时,如图,
∵M的纵坐标是1.5,把y=1.5代入1.5x+3,解得:x=3,
则M的坐标是(3,1.5),
∴点N的坐标为(﹣3,1.5);
当四边形OMND是菱形时,如图,
∵OM=OD=3,则设M的横坐标是m,则纵坐标是m+3,
则m2+(m+3)2=9,
解得:m或0(舍去).
则M的坐标是(,),
∴点N的坐标为(,).
综上,点N的坐标为(﹣3,1.5)或(,).
【类型四:矩形的存在性问题】
17.解:(1)∵将点C(m,6)代入,
∴,
∴,
∴,
将,代入一次函数的解析式为y=kx+b(k≠0)得:,
解得,
∴一次函数的表达式为;
(2)在x轴上存在点M,平面内存在一点P,使得四边形ABMP是矩形,
设M(m,0),
∵四边形ABMP是矩形,
∴∠ABM=90°,
∴AB2+BM2=AM2,
∴,
∴,
∴点M的坐标为.
18.解:(1)∵四边形OABC为矩形,
∴BC∥OA,BC=OA,AB∥OC,AB=OC,
∴∠CED=∠ADE,
∵OA=6,OC=4,
∴BC=6,AB=4,
∴B(6,4),
∵DE为∠ADC的平分线,
∴∠CDE=∠ADE,
∴∠CED=∠CDE,
∴CE=CD,
∵D为OA中点,
∴ODOA=3,
∴D(3,0),
由勾股定理可得CD=5,
∴CE=5,
∴E(5,4).
(2)①∵四边形OABC为矩形,点D为OA的中点,
∴S△BCDS四边形OABCOA OC=12,
∴S△CDP=S△BCD=12,
延长ED,交y轴于点M,
∵D(3,0),E(5,4),
∴yDE=2x﹣6,
∴M(0,﹣6),
∴CM=10,
∵S△CDP=S△PCM﹣S△DCMCM (xP﹣xD)=12,
∴10×(xP﹣3)=12,
∴xP,
∴P(,).
②存在,
∵点P是射线DE上的动点,
∴设P(x,2x﹣6),
∵O(0,0),B(6,4),
∴OB2=62+42=52,
OP2=x2+(2x﹣6)2=5x2﹣24x+36,
BP2=(x﹣6)2+(2x﹣6﹣4)2=5x2﹣52x+136,
要使四边形OBPQ是矩形,则△OBP为直角三角形,∠OBP=90°,
∴OB2+BP2=OP2,即52+5x2﹣52x+136=5x2﹣24x+36,
解得x,
∴P(,).
19.解:(1)∵,
∴,
解得:b=8,
∴c=10,
∴C(10,8),
∴OA=6,OB=8,
∴
=10;
故答案为:C(10,8),10;
(2)如图,
∵C(10,8),
∴BC=AB=10,
∴∠BAC=∠ACB,
∵四边形OBCD是矩形,
∴BC∥x轴,
∴∠BCA=∠CAD,
∴∠BAC=∠CAD,
∴AC平分∠BAD,
如图,作E关于AC对称点G,连接GF,
∴AE=AG,
在△AEF和△AGF中
,
∴△AEF≌△AGF(SAS),
∴GF=EF,
当G、F、H三点共线,且GH⊥x轴时,GH最小,
∴EF+FH最小,
∵H(2,8),
∴OG=2,
设直线AC的解析式为y=kx+b,则有
,
解得,
∴直线AC的解析式为,
当x=2时,
,
∴F(2,4);
(3)存在,理由如下:
如图,
①如图,当P在x轴上时,
此时矩形为AQ1P1F,
如图,作OM∥AC,将直线OM绕O逆时针旋转90°得直线ON,
∴ON∥P1F,
直线OM的解析式为,
设M(a,b)(a>0),
∴,
由旋转得:N(﹣b,a),
设直线ON的解析式为y=kx,则有,
﹣bk=a,
∴,
解得:k=﹣2,
∴直线ON的解析式为y=﹣2x,
∴设直线P1F的解析式为y=﹣2x+m,
∴﹣2×2+m=4,
解得:m=8,
∴直线P1F的解析式为y=﹣2x+8,
当y=0时,
﹣2x+8=0,
解得:x=4,
∴P1(4,0),
同理可求:
直线P1Q1的解析式为,
直线AQ1的解析式为y=﹣2x﹣12,
联立直线P1Q1和直线AQ1的解析式得
,
解得,
∴Q1(﹣4,﹣4);
②当P在y轴上时,
此时矩形为AFP2Q2,
由①可求P(0,8),
同理可求:
直线P2Q2的解析式为,
联立直线P2Q2和直线AQ1的解析式得
,
解得,
∴Q2(﹣8,4);
同理可求:直线P2Q3解析式为yx﹣12,直线FQ3解析式为y=﹣2x+8,
联立得,
解得,
∴Q3(8,﹣8);
综上所述:Q点坐标为(﹣4,﹣4)或(﹣8,4)或(8,﹣8).
【类型五:正方形的存在性问题】
20.解:(1)由折叠可得AF=DF,
∵点B(8,6),点D(0,4),四边形OABC为矩形,
∴OA⊥AB,OC=AB=6,OA=BC=8,OD=4,
设AF=DF=x,则OF=OA﹣AF=8﹣x,
在Rt△ODF中,由勾股定理可得OD2+OF2=DF2,
即42+(8﹣x)2=x2,
解得x=5,
∴OF=8﹣x=3,
∴点F的坐标为(3,0);
(2)①如图,当点P在点F右侧时,
根据题意AQ=2t,AP=t(0<t≤5),
∴FP=AF﹣AP=5﹣t,
∴;
②如图,当点P在点F左侧时,
根据题意AQ=2t,AP=t(5<t≤8),
∴FP=AP﹣AF=t﹣5,
∴;
综上所述,;
(3)若以P,Q,R,M为顶点的四边形是正方形时,则点P、R、Q三点围成的三角形为等腰直角三角形,
分情况讨论:①如图,
∵四边形PQRM是正方形,
∴PQ=QR,∠PQR=90°,
∴∠PQA+∠BQR=∠BQR+∠QRB,
∴∠PQA=∠QRB,
在△PAQ和△QBR中,
,
∴△PAQ≌△QBR(AAS),
∴AQ=BR,BQ=AP=t,
∴AB=AQ+BQ=2t+t=3t=6,
∴BQ=AP=t=2,
∴BR=AQ=2×2=4,P(8﹣2,0),
即P(6,0),
∴CR=BC﹣BR=4,Q(8,4),
∴R(4,6),
∵四边形PQRM是正方形,
∴M(4+6﹣8,6+0﹣4),即M(2,2);
②如图,过点R作RK⊥OA于点K,则四边形OCRK、RKAB均为矩形,
∴RK=AB=6,∠BRK=∠RKA=90°,
∵四边形PRQM是正方形,
∴PR=QR,∠PRQ=90°,
∴∠KRB﹣∠PRB=∠PRQ+∠PRB,
∴∠KRP=∠BRQ,
在△PKR和△QBR中,
,
∴△PKR≌△QBR(AAS),
∴RB=RK=6,KP=BQ=AQ﹣AB=2t﹣6,
∴OK=CR=BC﹣BR=8﹣6=2,
∴R(2,6),AK=OA﹣OK=6=2t﹣6+t,
∴AP=t=4,
∴P(8﹣4,0),
即P(4,0),KP=BQ=2t﹣6=2,
∴Q(8,6+2),即Q(8,8),
∵四边形PMQR是正方形,
∴M(4+8﹣2,8+0﹣6),即M(10,2);
③如图,
∵四边形PQRM是正方形,
∴PQ=QR,∠PQR=90°,
∴∠PQA+∠BQR=∠BQR+∠QRB,
∴∠PQA=∠QRB,
在△PAQ和△QBR中,
,
∴△PAQ≌△QBR(AAS),
∴AQ=BR=2t,BQ=AP=t,
又∵AQ=AB+BQ=6+t=2t,
∴AP=t=6,
∴BR=2×6=12,P(8﹣6,0),
即P(2,0),AQ=2t=12,
∴CR=BC+BR=8+12=20,Q(8,12),
∴R(20,6),
∵四边形PMRQ是正方形,
∴M(2+20﹣8,6+0﹣12),即M(14,﹣6).
综上所述,存在M(2,2)或M(10,2)或M(14,﹣6)时,P,Q,R,M为顶点的四边形是正方形.
【类型六:四边形动点综合题】
21.
【分析】根据题意首先取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,进而求出答案.
【解答】解:∵∠ABC=90°,AB=8,BC=4,并且在移动过程中,△ABC的大小、形状没变,
∴AC,
=4.
如图所示:
取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,
Rt△A1OB1中,∵A1B1=AB=8,点OE为斜边中线,
∴OE=B1EA1B1=4,
又∵B1C1=BC=4,
∴C1E,
=4 ,
∴点C到原点的最大距离为:OE+C1E=4+4.
故答案为:4;4+4,
22.
【分析】作点A关于直线y=x的对称轴A′,作B关于x轴的对称轴点B′,连接A′B′交OD于D′,交x轴于C′,连接AD′、A′D′、BC′、B′C′、则A′B′+AB就是四边形ABCD周长的最小值,据此展开计算即可.
【解答】解:作点A关于直线y=x的对称轴A′,作B关于x轴的对称轴点B′,连接A′B′交OD于D′,交x轴于C′,连接AD′、A′D′、BC′、B′C′、则A′B′+AB就是四边形ABCD周长的最小值.
∵B(7,2),
∴B′(7,﹣2),
由A(6,4),直线OD解析式是y=x,设直线AA′解析式为y=﹣x+b,
∴4=﹣6+b,解得b=10,
∴直线AA′解析式为y=﹣x+10,
联立,解得,
∴线段AA′的中点坐标为(5,5),
由中点坐标公式得A′(4,6),
∴A′B′,
AB.
∴四边形ABCD周长的最小值是.
故答案为:.
23.
【分析】分当B,C是直线y=1上的两个点时,当B,C是直线y=﹣1上的两个点时,这两种情况讨论,利用轴对称的性质,利用待定系数法求出函数解析式,进而求出C的坐标.
【解答】解:分两种情况:
①当B,C是直线y=1上的两个点时,
取点D(3,3)关于直线y=1的对称点D′(3,﹣1),将点A(0,5)向右平移2个单位得点A'(2,5),连接A'D′交直线y=1交于一点C,如图,此时,AB+BC+CD的值最小,
∵AA'∥BC,AA'=BC=2,
∴四边形AA'CB为平行四边形,则A'C=AB,
∵点D与点D′关于直线y=1对称,
∴CD=CD′,
∴AB+BC+CD=A'C+CD'+BC=A'D′+2,
∴AB+BC+CD的最小值为A'D′+2的值,
设直线A'D′的解析式为y=kx+b,图象过点A'(2,5),D′(3,﹣1),
∴,
解得,
∴直线A'D′的解析式为y=﹣6x+17,
当y=1时,1=﹣6x+17,
解得x,
∴点C的坐标为(,1);
②当B,C是直线y=﹣1上的两个点时,
取点D(3,3)关于直线y=﹣1的对称点D′(3,﹣5),将点A(0,5)向右平移2个单位得点A'(2,5),连接A'D′交直线y=﹣1交于一点C,如图,此时,AB+BC+CD的值最小,
∵AA'∥BC,AA'=BC=2,
∴四边形AA'CB为平行四边形,则A'C=AB,
∵点D与点D′关于直线y=﹣1对称,
∴CD=CD′,
∴AB+BC+CD=A'C+CD'+BC=A'D′+2,
∴AB+BC+CD的最小值为A'D′+2的值,
设直线A'D′的解析式为y=k'x+b',图象过点A'(2,5),D′(3,﹣5),
∴,
解得,
∴直线A'D′的解析式为y=﹣10x+25,
当y=﹣1时,﹣1=﹣10x+25,
解得x,
∴点C的坐标为(,﹣1);
故答案为:(,1)或(,﹣1)
24.解:(1)①当t=5时,AP=10,
∵O是正方形ABCD边AD的中点,
∴OA=ODAD=6,
∴S△AOPOA AP6×10=30,
∴y=S正方形ABCD﹣S△AOP=122﹣30=114;
当t=10时,如图1,
则AB+BP=20,
∴BP=20﹣AB=20﹣12=8,
∴PC=BC﹣BP=12﹣8=4,
∴y=S梯形CDOP(PC+OD) CD(4+6)×12=60;
故答案为:114;60.
②如图2,AB+BP=2t,
∴PC=24﹣2t,
∵OA∥CP,
∴当OA=CP时,以点O、A、P、C为顶点的四边形是平行四边形,
∴6=24﹣2t,
解得:t=9,
∴当t=9时,以点O、A、P、C为顶点的四边形是平行四边形.
(2)①由图3可知:当t=4时,S=0,即P,Q两点在第4秒相遇;
当t=0时,S正方形ABCD=AB2=64,
∴AB=8,即正方形ABCD的边长是8;
故答案为:4;8.
②由图3可知:点P、Q相遇于点C,且点P的速度大于点Q的速度,
∴点P的速度为点Q的速度的2倍,
设点Q的速度为a单位长度/秒,则点P的速度为2a单位长度/秒,
∴4(a+2a)=24,
解得:a=2,
∴点P的速度为4单位长度/秒,点Q的速度为2单位长度/秒;
故答案为:4;2.
③∵O是AD的中点,
∴OA=OD=4,
设t秒时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积S等于32,
分三种情况讨论:
当0≤t≤2时,点P在AB边上,点Q在CD边上,如图,
则AP=4t,DQ=2t,OA=OD=4,
∴S=S正方形ABCD﹣S△OAP﹣S△ODQ=644×4t4×2t=64﹣12t,
由题意得:64﹣12t=32,
解得:t2(不符合题意,舍去);
当2<t≤4时,点P在BC边上,点Q在CD边上,如图,
则AB+BP=4t,AB=8,
∴BP=4t﹣8,
∵DQ=2t,OA=OD=4,
∴S=S正方形ABCD﹣S梯形OABP﹣S△ODQ=64(4t﹣8+4)×84×2t=80﹣20t,
由题意得:80﹣20t=32,
解得:t,符合题意;
当4<t≤6时,点P在CD边上,点Q在BC边上,如图,
∵AB+BC+CP=4t,AB=BC=CD=AD=8,
∴DP=24﹣4t,
∵DC+CQ=2t,
∴BQ=16﹣2t,
∴S=S正方形ABCD﹣S梯形OABQ﹣S△ODP=64(4+16﹣2t)×84×(24﹣4t)=16t﹣64,
由题意得:16t﹣64=32,
解得:t=6(符合题意);
综上,当t或6时,正方形ABCD与∠POQ(包括边缘及内部)重叠部分的面积等于32.
25.解:(1)①如图1﹣1中,过点E作EH⊥BC于H.
∵四边形ABCO是矩形,A(8,0),C(0,6),
∴OA=BC=8,AB=OC=6,
∵∠BCO=∠ACE=90°,
∴∠ACB=∠ECH,
∵CE=CB,∠EHC=∠ABC=90°,
∴△EHC≌△CBA(AAS),
∴EH=CB=8,CH=AB=6,
∴E(6,14).
故答案为:(6,14);
②如图1﹣2中,过点E作EH⊥BC于H.
同法可证:△EHD≌△DBA(AAS),
∴EH=DB=8﹣m,DH=AB=6,
∴CH=6+m,
∴E(6+m,14﹣m).
故答案为:(6+m,14﹣m);
(2)△ABF的面积不会改变,理由如下:
如图2,过点F作FH⊥AB,交AB的延长线于H,
∵矩形OABC的顶点B坐标为(8,6),
∴AB=6,BC=8,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∴∠DAB+∠FAB=90°,且∠DAB+∠BDA=90°,
∴∠BDA=∠FAB,
∵AD=AF,∠ABD=∠AHF=90°,
∴△ABD≌△FHA(AAS),
∴HF=AB=6,
∴△ABF的面积AB×HF=18;
(3)若BE=EF,当点B与点D重合时,AD=AB=6,此时m=8.
当点B与点D不重合时,如图3,过点E作EH⊥DB于H,
∵∠EDH+∠ADB=90°,∠ADB+∠DAB=90°,
∴∠EDH=∠DAB,
AD=DE,∠EHD=∠ABD=90°,
∴△ADB≌△DEH(AAS),
∴DH=AB=6,
∵BE=EF,EF=DE,
∴DE=BE,
∵EH⊥DB
∴DH=BH=6,
∴DB=12,
∵DB<BC,
∴此种情形不存在.
若EB=BF,
∵BE=BF,
∴∠BEF=∠BFE,
∴∠DEB=∠AFB,
∵DE=AF,BE=BF,
∴△DEB≌△AFB(AAS),
∴DB=AB=36,
∴CD=BC﹣BD=8﹣6=2,即m=2;
若BF=EF,如图4,过点F作FH⊥AB于H,
∵∠DAB+∠FAB=90°,∠DAB+∠BDA=90°,
∴∠BDA=∠FAB,
∵AD=AF,∠ABD=∠AHF=90°,
∴△ABD≌△FHA(AAS),
∴AH=DB,
∵EF=BF,EF=AF,
∴BF=AF,
∵FH⊥AB,
∴AH=BH=3,
∴DB=3,
∴CD=BC﹣BD=8﹣3=5,即m=5,
综上所述,满足条件的m的值为8或2或5.
26.解:(1)过点A'作AQ⊥AB于点Q,
∵矩形OABC中,,C(0,2),
∴,AB=2,
∴,
由对称得,AP=A′P,
则,
设AP=A′P=x,则BP=AB﹣x=2﹣x,
由勾股定理得:A'B2+A'P2=BP2,
即 ,
解得:,
∴,
∵∠PA'B=90°,S△A'BP,
即,
解得:,
∴点A'的横坐标为,
设OB的函数表达式为y=kx,将 代入得:,
∴OB的函数表达式为,
将 代入得:,
∴;
(2)①连接OM,
∵∠POM=45°,∠AOC=90°,
∴∠1+∠4=45°,∠2+∠3=45°,
∵△PAO和△PA′O对称,
∴∠3=∠4,
∴∠1=∠2,
又∵∠C=∠OA'M=∠OAP,OM=OM,
∴△OMC≌△OMA'(AAS),
∴OC=OA'=OA,
则四边形OABC为正方形,
∴;
②(Ⅰ)当 时,
∵△OMC≌△OM,△OAP≌△OAP,
∴,
(Ⅱ)当时,Rt△OMA'≌Rt△OMC(HL),
∴∠1=∠2,
∵OC∥AP,
∴∠3=∠OPA,
由折叠的性质可得:∠4=∠OPA,∠A′=∠OAP=90°,
∴∠3=∠4,
∵∠1+∠2+∠3+∠4=90°,∠1=∠2,∠3=∠4,
∴∠2+∠3=45°,
即∠POM=45°,
综上所述:∠POM的大小不会改变.
27.解:(1)过点A作AE⊥OC于点E,如图,
∵点A的坐标为(3,4),
∴OE=3,AE=4,
∴OA=AB5,
∵四边形ABCD为平行四边形,
∴CD=AB=5.
(2)存在t的值,使得PQ与CD互相平分,t的值为4,理由:
连接PC,DQ,如图,
若PQ与CD互相平分,
∴四边形PCQD为平行四边形,
∴PD=CQ,
由题意得:PD=t,BQ=3t,
∵四边形ABCD为平行四边形,
∴BC=AD=8,
∴CQ=BQ﹣BC=3t﹣8,
∴t=3t﹣8,
∴t=4.
∴存在t的值,使得PQ与CD互相平分,t的值为4.
(3)①当点Q在BC上时,如图,
∵点P关于直线DQ对称的点恰好落在直线CD上,
∴∠ADQ=∠CDQ,
∵AB∥CD,
∴∠DQC=∠ADQ,
∴∠DQC=∠CDQ,
∴CQ=CD,
∵CQ=BC﹣BQ=8﹣3t,
∴8﹣3t=5,
∴t=1.
∴PD=1,
∴AP=7,
∴P(10,4);
②当点Q在BC的延长线上时,如图,
∵点P关于直线DQ对称的点恰好落在直线CD上,
∴∠PDF=∠P′DF,
∵AD∥BC,
∴∠CQD=∠PDF,
∴∠P′DF=∠CDQ,
∴∠CDQ=∠CQD,
∴CQ=CD,
∵CQ=3t﹣8,
∴3t﹣8=5,
∴t.
∴DP,
∴AP=AD﹣DP=8,
∴P(,4).
综上,点P关于直线DQ对称的点恰好落在直线CD上,点P的坐标为(10,4)或(,4).
28.(1)解:如图1中,
∵四边形EFMN是正方形,
∴EF=EN,∠FEN=∠A=∠D=90°,
∴∠AEF+∠AFE=90°,∠AEF+∠DEN=90°,
∴∠AFE=∠DEN,
∴△AEF≌△DNE(AAS),
∴AF=DE,
∵AD=3.AE=1,
∴DE=2,
∴x=AF=2.
过点M作MH⊥FB于点H.同法可证△MHF≌△FAE,
可得MH=AF=2,
∴S FB MH5×2=5.
故答案为:2,5;
(2)①证明:如图2中,
如图,连接FN,作MQ⊥FB于Q,则∠MQF=90°,∠MQF=∠A
∵四边形FEMN是菱形,
∴EN=FM,EN∥FM,
∴∠ENF=∠NFM,
∵矩形ABCD中,DC∥AB,
∴∠DNF=∠NFQ,
∴∠DNF﹣∠ENF=∠NFQ﹣∠NFM,即∠DNE=∠MFQ,
②解:∵∠D=∠FQM=90°,∠QNE=∠MFQ,NE=FM,
∴△DNE≌△QFM(AAS),
∴MQ=DE=2,
∵AB=7,AF=x,
∴S△FBMFB×MQ(7﹣x)×2=7﹣x.
∴S与x的函数关系式S=7﹣x;
(3)①如图3中,当点N与D重合时,x的值最小,△FBM的面积最大,
在Rt△AEF中,x,
∴S的最大值=7.
②如图4中,当点M在BC上时,x的值最大,△FBM的面积最小,
此时易证CN=AF=x,
∵EN=EF,
∴1+x2=22+(7﹣x)2,
∴x,
∴S的最小值为7.
故答案为:,.
(4)如图3中,在△BFM的面积S由最大变为最小的过程中,点M的运动轨迹是平行AB的线段,点M运动的路线长=BF的长=7,
故答案为:7.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
