八年级数学下册试题 第9章《中心对称图形-平行四边形》复习题--四边形中的翻折和旋转问题--苏科版(含解析)
文档属性
| 名称 | 八年级数学下册试题 第9章《中心对称图形-平行四边形》复习题--四边形中的翻折和旋转问题--苏科版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 13:30:08 | ||
图片预览


文档简介
第9章《中心对称图形-平行四边形》复习题--四边形中的翻折和旋转问题
一.四边形的翻折问题
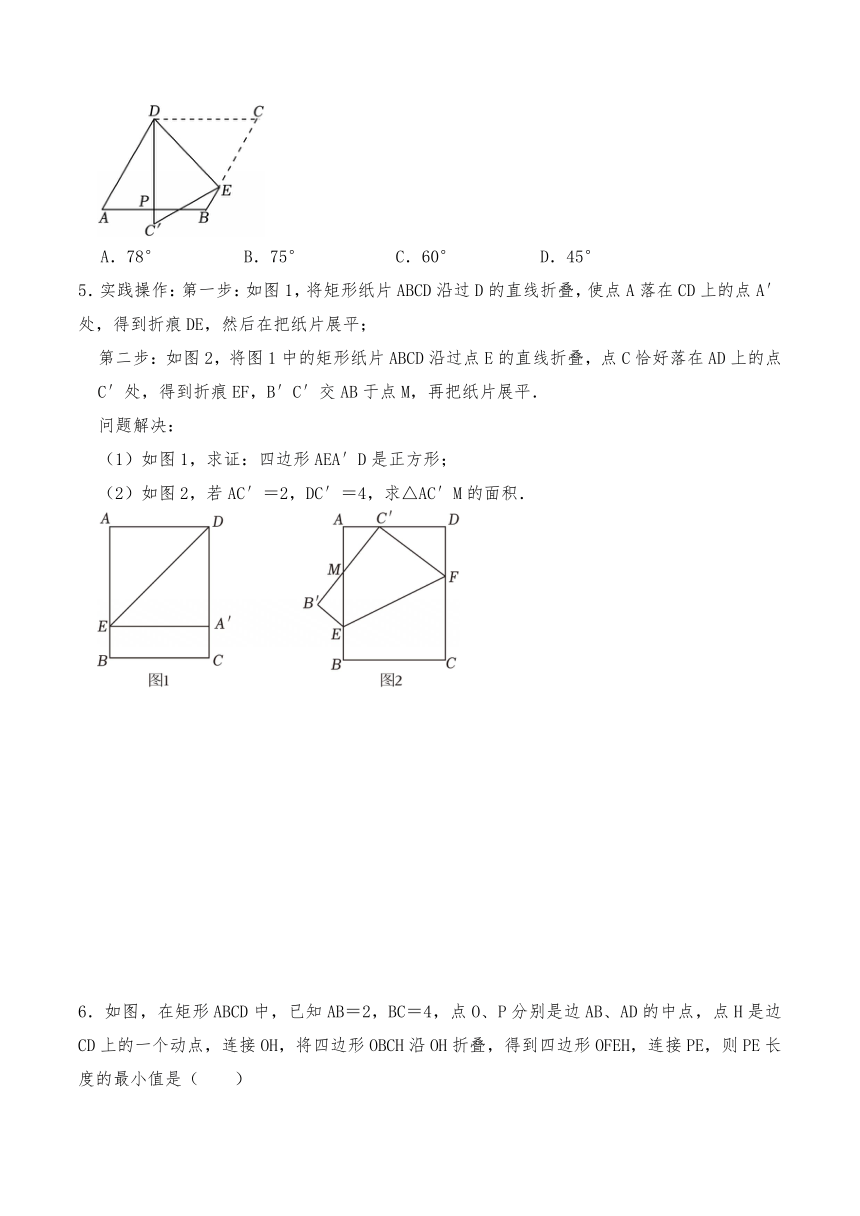
1.如图,将 ABCD沿对角线AC折叠,使点B落在B'处,若∠1=∠2=42°,则∠B= .
2.如图,在矩形ABCD中,将△BCD沿对角线BD对折得到△BED,BE交AD于点F.若AB=1,BC=2,则AF的长为 .
3.如图,矩形ABCO如图放置在平面直角坐标系中,其中AB=6,∠AOB=30°,若将其沿着OB对折后,A′为点A的对应点,则A′的坐标为( )
A. B.
C.(﹣3,9) D.
4.如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
A.78° B.75° C.60° D.45°
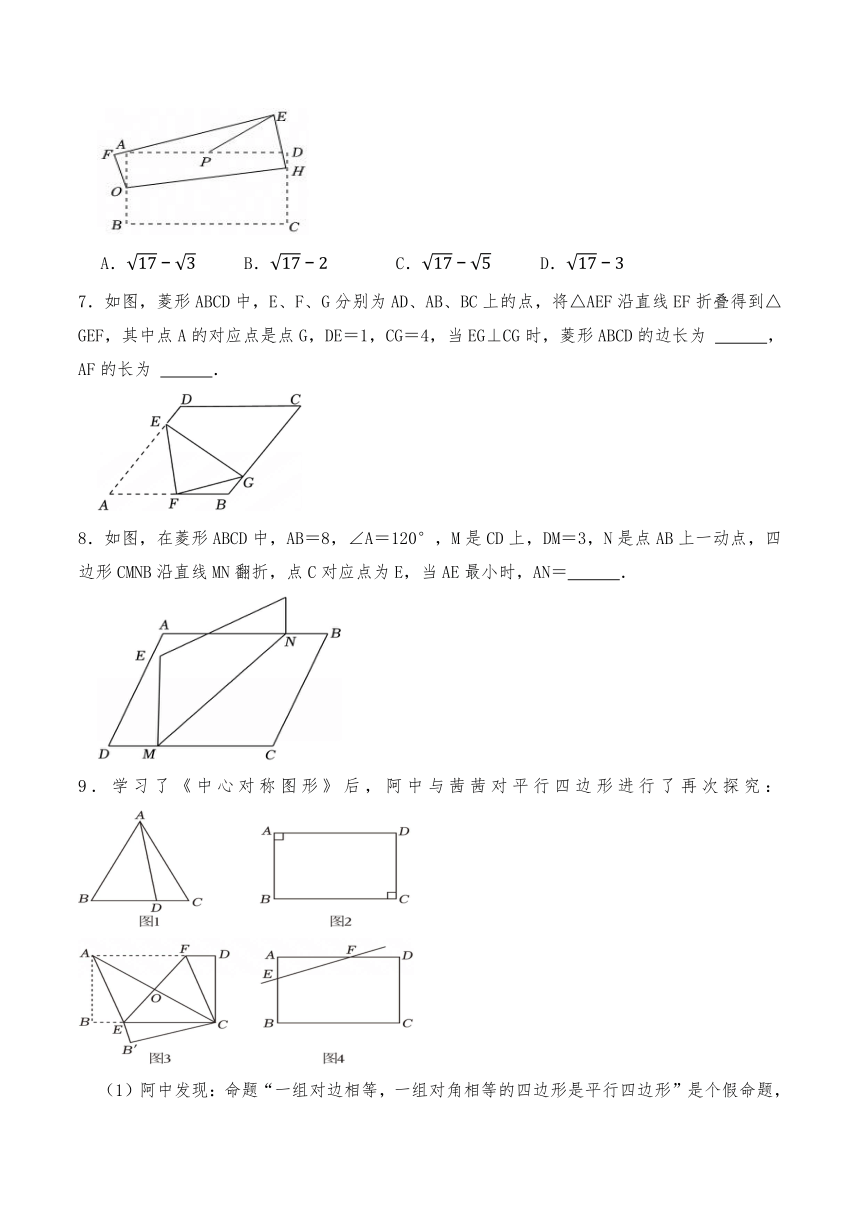
5.实践操作:第一步:如图1,将矩形纸片ABCD沿过D的直线折叠,使点A落在CD上的点A′处,得到折痕DE,然后在把纸片展平;
第二步:如图2,将图1中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C′处,得到折痕EF,B′C′交AB于点M,再把纸片展平.
问题解决:
(1)如图1,求证:四边形AEA′D是正方形;
(2)如图2,若AC′=2,DC′=4,求△AC′M的面积.
6.如图,在矩形ABCD中,已知AB=2,BC=4,点O、P分别是边AB、AD的中点,点H是边CD上的一个动点,连接OH,将四边形OBCH沿OH折叠,得到四边形OFEH,连接PE,则PE长度的最小值是( )
A. B. C. D.
7.如图,菱形ABCD中,E、F、G分别为AD、AB、BC上的点,将△AEF沿直线EF折叠得到△GEF,其中点A的对应点是点G,DE=1,CG=4,当EG⊥CG时,菱形ABCD的边长为 ,AF的长为 .
8.如图,在菱形ABCD中,AB=8,∠A=120°,M是CD上,DM=3,N是点AB上一动点,四边形CMNB沿直线MN翻折,点C对应点为E,当AE最小时,AN= .
9.学习了《中心对称图形》后,阿中与茜茜对平行四边形进行了再次探究:
(1)阿中发现:命题“一组对边相等,一组对角相等的四边形是平行四边形”是个假命题,如何举反例说明呢?茜茜稍作思考说:“取一张如图1所示的等腰三角形纸片ABC,其中AB=AC,在BC边上取一点D(不是中点),连接AD,沿AD剪开纸片,重新拼接……”,
请你完成茜茜的举反例过程,画出相应的图形,并配以必要的说明;
(2)阿中进一步探究发现:“一组对边相等且一组对角是直角的四边形是矩形”,请你完成证明过程;
已知:如图2,四边形ABCD中,AB=CD,∠A=∠C=90°,求证:四边形ABCD是矩形.
(3)茜茜发现折叠矩形可以得到菱形:如图3,将矩形ABCD折叠,使得A、C两点重合,点B落在点B′,折痕分别交边BC、AD于E、F两点,交AC于O两点,则四边形AECF是菱形.请在框图中补全茜茜的证明思路.
茜茜的证明思路
由折叠易知EF是AC的垂直平分线,可以先证△AOF≌① △COE ,得到② OE=OF ,又由OA=OC,可得四边形AECF是平行四边形,再由③ EF⊥AC ,于是 AECF是菱形.
(4)茜茜给阿中出了一道思考题:“如图4,在矩形ABCD中,AB=2,AD=3,点E、F分别是边AB、AD上的点,将矩形ABCD沿着直线EF折叠,使点A与矩形ABCD内部的点P重合,问BP的最小值是多少?”请聪明的你用矩形纸片操作探究一下,直接写出BP的最小值.
10.实践操作
在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
初步思考
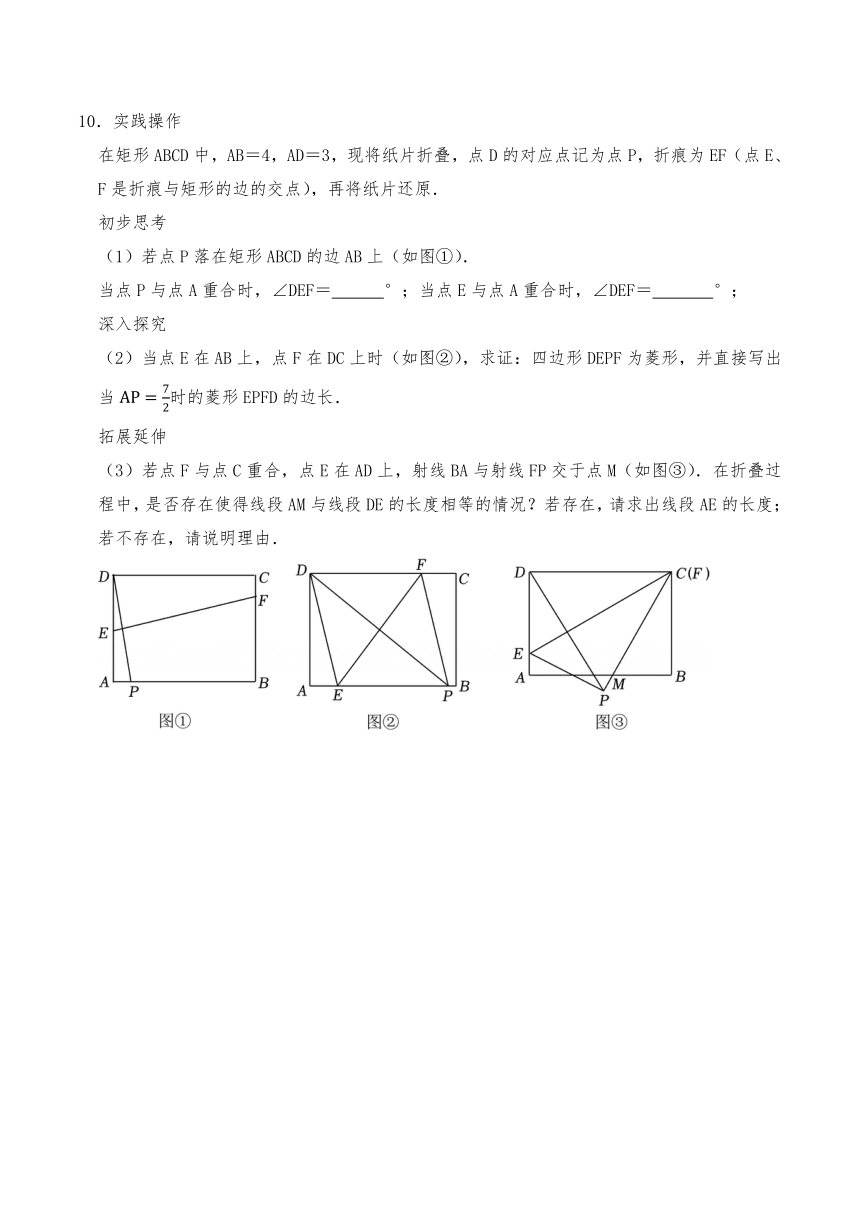
(1)若点P落在矩形ABCD的边AB上(如图①).
当点P与点A重合时,∠DEF= °;当点E与点A重合时,∠DEF= °;
深入探究
(2)当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当时的菱形EPFD的边长.
拓展延伸
(3)若点F与点C重合,点E在AD上,射线BA与射线FP交于点M(如图③).在折叠过程中,是否存在使得线段AM与线段DE的长度相等的情况?若存在,请求出线段AE的长度;若不存在,请说明理由.
11.综合与实践
动手实践:数学课上老师让学生们折矩形纸片,下面几幅图是学生们折出的一部分图形(沿直线l折叠),由于折痕所在的直线不同,折出的图形也不同,各个图形中所隐含的“基本图形也不同,我们可以通过发现基本图形研究这些图形中的几何问题.
问题解决:
(1)如图1,将矩形纸片ABCD沿直线MN折叠,使得点C与点A重合,点D落在点D1的位置,连接MC,AN,AC,线段AC交MN于点O,则△CDM与△AD1M的关系为 ,线段AC与线段MN的关系为 ,小强量得∠MNC=50°,则∠DAN= ,小丽说:“四边形ANCM是菱形”,请你帮她证明.
拓展延伸:
(2)如图2,矩形纸片ABCD中,BC=2AB=6cm,BM=4cm,小明将矩形纸片ABCD沿直线AM折叠,点B落在点B1的位置,MB1交AD于点N,请你直接写出线段ND的长: .
综合探究;
(3)如图3,ABCD是一张矩形纸片,AD=1,AB=5,在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使线段MB与线段DN交于点P,得到△MNP,请你确定△MNP面积的取值范围 .
12.在矩形ABCD中,AB=6,BC=12,点E是矩形ABCD边CD上一点,连接BE,将△CEB沿BE翻折,
(1)如图1,点C刚好落在边AD上的点F处,求AF长.
(2)如图2,点C落在矩形外一点F处,连接AF,若CE=4,求△ABF的面积.
(3)如图3,点C落在点F处,∠ABF的角平分线与EF的延长线交于点M,当点E从点C运动到点D时,求点M运动的路径长
二.四边形的旋转问题
1.如图,在 ABCD中,∠A=65°,将 ABCD绕顶点B顺时针旋转到 A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1的大小为 .
2.如图,将矩形ABCD绕点A顺时针旋转到矩形AB'C'D'的位置,旋转角为α(0°<α<90°),若∠1=114°,则α= °.
3.如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD交于点O.点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),DF长度的最小值为 .
4.如图,将正方形ABCD绕点A按逆时针方向旋转到正方形AB'C'D',旋转角为a(0°<α<180°),连接B'D、C'D,若B'D=C'D,则∠α= .
5.如图1,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,连接DF、DG.
(1)如图2,点E落在对角线BD上,AD与EF相交于点H,
①连接AF,求证:四边形ABDF是平行四边形;
②求线段AH的长度;
(2)在矩形AEFG绕点A旋转一周的过程中,△DFG面积的最大值为 .
6.如图,在矩形ABCD中,AB=4,BC=3,将△ABC绕点C顺时针旋转α(α<90°)得到△EFC,延长EF分别交AB、CD于M、N,当N为EM中点时,DN的长为( )
A. B. C. D.
7.如图,在正方形ABCD中,E、F分别为对角线AC上的两点,且∠EBF=45°,若AE=3,CF=4,则EF的长为 .
8.如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为 .
9.如图,在矩形ABCD中,AB=3,BC=2,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为α(0°<α<180°),得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,△BEP的面积最大值是 .
10.如图,在矩形ABCD中,AB=4,BC=8,点O是BD的中点,点E在BC边上,BE=3.已知点P是AD边上动点(DP≤4),线段OP绕点O逆时针旋转一定的度数,使点P落在线段AE上的点Q处.连接PQ,则PQ2的最小值是 .
11.如图,在 ABCD中,AB=4,∠B=60°,BC=3,E为AB上一点,且BE=1,F为BC边上的一个动点,连接EF,将其绕点E逆时针旋转30°至直线EG,使得∠EGF=120°,连接AG,则AG的最小值为( )
A. B.2 C. D.
12.如图,将四边形ABCD绕点A旋转,使得点B的对应点B’恰好落在射线BD上,旋转后的四边形为AB/C/D/ ,连接BC’交AD于点E.
(1)如图①,若四边形ABCD为正方形,则四边形ABDC/是 .(填序号)
①平行四边形;
②矩形;
③菱形;
(2)如图②,若四边形ABCD为矩形,若AB=6,BC=8,B/C/交AD于点F,求EF的长.
(3)如图③,若BC’与AD互相平分,求证:AB∥CD.
13.如图,在矩形ABCD中,AB=3,AD=4,以点C为旋转中心,将矩形ABCD沿顺时针方向旋转,得到矩形EFCG,点A、B、D的对应点分别是点E、F、G.
(1)如图1,当点F落在矩形ABCD的对角线AC上时,求线段AF的长;
(2)如图2,当点F落在矩形ABCD的边CD的延长线上时,连接AE,取AE的中点M,求证:;
(3)如图3,当点F落在矩形ABCD的对角线BD的延长线上时,求△CDF的面积.
14.如图1,四边形ABCD是边长为6的正方形,点E在线段CD上运动,连接AE,将线段AE绕点A顺时针旋转45°得到AF.
【探索发现】
(1)爱思考的小鹿发现:过点F作FH⊥AC时,AH一定等于AD,小鹿发现的结论正确吗?如果正确请帮小鹿完成证明过程,如不正确请说明理由;
【结论运用】
(2)当点F落在BC上时,此时DE的长为 ;
【深入理解】
(3)若点G在直线BC上运动,当以点C、H、G、F为顶点的四边形是平行四边形时,求DE的长;
【拓展延伸】
(4)如图2.在平面直角坐标系xOy中,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转45°得到线段AC.若点C的坐标为(m,3),则m的值为 .
参考答案
一.四边形的翻折问题
1.
【分析】由平行线的性质可得∠1=∠B'AB=42°,由折叠的性质可得∠BAC=∠B'AC=21°,即可求解.
【解答】解:∵四边形ABCD
∴AB∥CD,
∴∠1=∠B'AB=42°
∵将 ABCD沿对角线AC折叠
∴∠BAC=∠B'AC=21°
∴∠B=180°﹣∠2﹣∠BAC=117°
故答案为:117°
2.
【分析】先由长方形的性质可知,AB=CD,BE=BC,再根据图形翻折变换的性质可知,CD=DE=AB,利用全等三角形的判定定理可得△ABF≌△EDF,故BF=DF,AF+BF=AD,设AF=x,由勾股定理即可求出x的值.
【解答】解:∵四边形ABCD是长方形,AB=1,BC=2,
∴AB=CD=1,AD=BC=2,
∵△BED是△BCD沿BD翻折而成,
∴CD=DE=AB=1,∠E=90°,
又∵∠AFB=∠EFD,
∴△ABF≌△EDF(AAS),
∴BF=DF,AF+BF=AD=2,
在Rt△ABF中,设AF=x,则BF=2﹣x,由勾股定理得BF2=AB2+AF2,即(2﹣x)2=12+x2,
解得x,
故答案为:.
3.
【分析】作AD⊥x轴,根据含 30°角直角三形的性质,及勾 股定理,求出AO,根据折叠的性质,求出AO,∠AOD,在Rt△ADO中,求出DO,AD,根据 第二象限内点的特征,即可求解,
【解答】解:过点A作AD⊥x轴,交x轴于点D,
在Rt△BAO 中,AB=6,∠AOB=30°,
∴BO=2AB=2×6=12,,
由折叠的性质可得:,
∠A'OB=∠AOB=30°,
即:∠AOD=2∠AOB=2×30°=60°,
在Rt△ADO 中,,,
∵点A在第二象限,,
故选:D.
4.
【分析】连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°,利用三角形的内角和定理即可求出所求角的度数.
【解答】解:连接BD,
∵四边形ABCD为菱形,∠A=60°,
∴△ABD为等边三角形,∠ADC=120°,∠C=60°,
∵P为AB的中点,
∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,
∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,
在△DEC中,∠DEC=180°﹣(∠CDE+∠C)=75°.
故选:B.
5.解:(1)∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,
∴AD=A′D,AE=A′E,∠ADE=∠A′DE=45°,
∵AB∥CD,
∴∠AED=∠A′DE=∠ADE,
∴AD=AE,
∴AD=AE=A′E=A′D,
∴四边形AEA′D是菱形,
∵∠A=90°,
∴四边形AEA′D是正方形;
(2)如图,连接C′E,由(1)知,AD=AE,
∵四边形ABCD是矩形,
∴AD=BC,∠EAC′=∠B=90°,
由折叠知,B′C′=BC,∠B=∠B′,
∴AE=B′C′,∠EAC′=∠B′,
又∵EC′=C′E,
∴Rt△EC′A≌Rt△C′EB′(HL),
∴∠C′EA=∠EC′B′,
∴MC′=ME,
设AM=x,
∵AC′=2,DC′=4,
∴AE=AD=2+4=6,
∴C'M=BM=6﹣x,
在Rt△MC'A中,
由勾股定理,得AC'2+AM2=MC'2,
即22+x2=(6﹣x)2,
解得x,
即AM,
∴△AC′M的面积AC' AM2.
6.
【分析】连接EO、PO、OC.根据三边关系,PE≥OE﹣OP,求出OE,OP即可解决问题.
【解答】解:如图,连接EO、PO、OC.
∵四边形ABCD是矩形,
∴∠B=∠OAP=90°,
∵AB=2,BC=4,点O、P分别是边AB、AD的中点,
∴OB=OA=1,PA=2,
在Rt△OBC中,
由勾股定理,得OC,
在Rt△AOP中,
由勾股定理,得OP,
∵OE=OC,PE≥OE﹣OP,
∴PE的最小值为.
故选:C.
7.
【分析】作DM⊥BC于M,作FN⊥AD于N,设AE为x,证明四边形DMGE为矩形,在Rt△DCM中,利用勾股定理求出x,即可求出边长;证明△AFN∽△DCM,设AN=3y,表示出FN,AF,利用AE=4,列出方程,求出y值,即可解答.
【解答】解:作DM⊥BC于M,作FN⊥AD于N,如图,
设AE=x,则AD=x+1=DC,
由折叠得,EC=AE=x,
∵EG⊥CG,
∴四边形DMGE为矩形,
∴DM=EC=x,GM=DE=1,
∴CM=4﹣1=3,
在Rt△DCM中,CM2+DM2=DC2,即32+x2=(x+1)2,
∴x=4,
∴AD=5,即棱形边长为5;
∵∠A=∠C,
∴△AFN∽△DCM,
∴AN:CM=FN:DM,
设AN=3y,则FN=4y,AF=5y,
由折叠得,∠AEF=∠GEF=45°,
∴EN=4y,
∵AE=4,即AN+EN=4,
∴y,
∴AF=5.
故答案为:5;.
8.7.
9.(1)解:等腰三角形纸片ABC,其中AB=AC,在BC边上取一点D(不是中点),连接AD,沿AD 剪开纸片,重新拼接如图所示,
∴AB=CD,∠B=∠C,而BD≠AC,
∴四边形ABDC不是平行四边形,
∴命题“一组对边相等,一组对角相等的四边形是平行四边形”是个假命题;
(2)证明:连接BD,
∵AB=CD,∠A=∠C=90°,且BD=BD,
∴Rt△ABD≌Rt△CDB(HL),
∴AD=BC,
∵AB=CD,
∴四边形ABCD是平行四边形,
∵∠A=90°,
∴四边形ABCD是矩形;
(3)证明:由折叠知EF是AC的垂直平分线,
∴AO=OC,∠AOF=∠COE=90°,
∵矩形ABCD,
∴AF∥CE,
∴∠FAO=∠ECO,
∴△AOF≌△COE,
∴OE=OF,
∵OA=OC,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴ AECF是菱形,
故答案为:△COE;OE=OF;EF⊥AC;
(4)解:如图,连接BF,BD,
∵PB≥FB﹣FP,FA=FP,
∴PB≥FB﹣FA,此时PB的最小值=FB﹣FA
∵(FB﹣FA)﹣(BD﹣AD)=FB﹣FA﹣BD+AF+DF=FB+DF﹣BD>0,
∴BD﹣AD<FB﹣FA,
∴当F与D重合时,FB﹣FA的值最小,由折叠得:AD=PD=3,
由勾股定理得:BD,
∵PB≥BD﹣PD,
当P,A,C共线时,BP有最小值,
∴BP3,
则BP的最小值是3.
10.初步思考
(1)当点P与点A重合时,如图1,
∴EF是AD的中垂线,
∴∠DEF=90°,
当点E与点A重合时,如图2,
此时∠DEF∠DAB=45°,
故答案为:90,45;
深入探究
(2)当点E在AB上,点F在DC上时,如图3,
∵EF是PD的中垂线,
∴DO=PO,EF⊥PD,
∵四边形ABCD是矩形,
∴DC∥AB,
∴∠FDO=∠EPO,
∵∠DOF=∠EOP,
∴△DOF≌△POE(ASA),
∴DF=PE,
∵DF∥PE,
∴四边形DEPF是平行四边形,
∵EF⊥PD,
∴ DEPF为菱形,
当AP时,设菱形的边长为x,则AEx,DE=x,
在Rt△ADE中,由勾股定理得:
AD2+AE2=DE2,
∴32+(x)2=x2,
∴x,
∴时的菱形EPFD的边长为:;
拓展延伸
(3)存在,
情况一:如图4,连接EM,
∵DE=EP=AM,
∴△EAM≌△MPE(HL),
设AE=x,则AM=DE=3﹣x,则BM=x+1,
∵MP=EA=x,CP=CD=4,
∴MC=4﹣x,
∴(x+1)2+32=(4﹣x)2,
解得:x;
情况二,如图5,
∵DE=EP=AM,
∴△GAM≌△GPE(AAS),
设AE=x,则DE=3﹣x,则AM=PE=DE=3﹣x,MP=AE=x,
则MC=MP+PC=x+4,BC=3,BM=7﹣x,
∴(7﹣x)2+32=(x+4)2,
解得:x,
综上,线段AE的长为:或.
11.解:(1)如图1中,
∵矩形纸片ABCD沿直线MN折叠,使得点C与点A重合,点D落在点D1的位置,
∴AM=MC,AD1=CD,MD1=MD,
∴△AMD1≌△CMD(SSS),
∵MN垂直平分线段AC,
∴OA=OC,
∵AD∥CB,
∴∠AMO=∠CNO,
∵∠AOM=∠CON,
∴△AMO≌△CNO(AAS),
∴OM=ON,AM=CM,
∴线段AC与线段MN互相垂直平分.
∵MA=MC,NA=NC,
∴AM=CM=CN=AN,
∴四边形ANCM是菱形,
∴∠ANM=∠MNC=50°,
∴∠ANC=100°,
∵AD∥BC,
∴∠DAN=180°﹣100°=80°,
故答案为:△CDM≌△AD1M,线段AC与线段MN互相垂直平分,80°.
(2)如图2中,
∵四边形ABCD是矩形,
∴AD=BC=∠B=90°,
由翻折的性质可知,∠AMB=∠AMN,∠B1=∠B=90°,
∵AD∥BC,
∴∠AMB=∠MAN,
∴∠AMN=∠NAM,
∴AN=NM,设AN=MN=x,
在Rt△ANB1中,∵AB1=AB=3,NB1=4﹣x,AN=x,
∴x2=32+(4﹣x)2,
解得x,
∴AN,
∴DN=AD﹣AN=6.
故答案为.
(3)如图3,当点B与点D重合时,△MNP的面积最大,作MH⊥BN于H,则MH=AB=1,
由题意得:MP=MQ,设MP=MQ=k,则AM=5﹣k;
由勾股定理得:(5﹣k)2+12=k2,
解得:k=2.6;由(1)知:
NP=MP=2.6,MH=1,
∴S△MNK NP MH=1.3,
∴△MNP的面积的最大值为1.3.
因为PN的最小值为1,
∴△MNP的面积的最小值为1×1=0.5,
∴0.5<S△MNP≤1.3.
故答案为:0.5<S△MNP≤1.3.
12.解:(1)由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∵四边形ABCD为矩形,
∴∠A=90°,
∴AF6.
(2)过点F作FG⊥AB,交AB的延长线于点G,延长GF交CD的延长线于点H,如图,
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵FG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
设HD=AG=x,则HE=x+2,BG=x+6,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,FE=CE=4.
∴∠EFH+∠GFB=90°.
∵∠GFB+∠GBF=90°,
∴∠EFH=∠GBF.
∵∠H=∠G=90°,
∴△EFH∽△FBG,
∴,
∴GF=3EH=3x+6,FHBGx+2,
∵GH=12,
∴3x+6x+2=12,
∴x.
∴FG=36,
∴△ABF的面积AB FG.
(3)过点M作MG⊥AB,交AB的延长线于点G,延长GM交CD的延长线于点H,如图
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵MG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∴∠G=∠BFM=90°.
∵BM为∠GBF的平分线,
∴∠GBM=∠FBM.
在△BGM和△BFM中,
,
∴△BGM≌△BFM(AAS),
∴BG=BF=12,
∴AG=BG=AB=6,
∵点M在GH上,
∴点M到AD的距离等于AG=6,即点M在GH上运动,
∴点E与点C重合时,点M与点H重合.
当点E与点D重合时,如图,
∵△BGM≌△BFM,
∴MG=MF,
由题意得:△BCE≌△BFE,
∴CD=DF=6.
∵四边形ADHG为矩形,
∴DH=AG=6.
设MG=MF=x,则MD=x+6,MH=GH﹣GM=12﹣x.
∵∠H=90°,
∴MD2=MH2+DH2,
∴(x+6)2=(12﹣x)2+62.
∴x=4.
∴MH=GH﹣GM=8.
∴当点E从点C运动到点D时,点M运动的路径长为线段HM的长等于8.
二.四边形的旋转问题
1.
【分析】由旋转的性质得出BC=BC1,由等腰三角形的性质得出∠BCC1=∠C1,由旋转角∠ABA1=∠CBC1,根据等腰三角形的性质计算即可.
【解答】解:∵ ABCD绕顶点B顺时针旋转到 A1BC1D1,
∴BC=BC1,
∴∠BCC1=∠C1,
∵∠A=65°,
∴∠A=∠BCD=∠C1=65°,
∴∠BCC1=∠C1=65°,
∴∠CBC1=180°﹣2×65°=50°,
∴∠ABA1=50°,
故答案为:50°.
2.
【分析】先利用旋转的性质得到∠ADC=∠D=90°,∠DAD′=α,再利用四边形内角和计算出∠BAD=66°,然后利用互余计算出∠DAD′,从而得到α的值.
【解答】解:∵矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,
∴∠ADC=∠D'=90°,∠DAD′=α,
∵∠ABC=90°,
∴∠BAD'=180°﹣∠2,
又∵∠2=∠1=114°,
∴∠BAD'=180°﹣114°=66°,
∴∠DAD′=∠BAD﹣∠BAD'=90°﹣66°=24°,
即α=24°.
故答案为:24.
3.
【分析】连接BE,作BH⊥AD,由旋转的性质可得△DCF≌△BCE,把求DF的最小值转化为求BE的最小值,再根据垂线段最短可得答案.
【解答】解:连接BE,作BH⊥AD交DA的延长线于H,
菱形ABCD中,∠ABC=60°,
∴∠BCD=120°.
∵∠ECF=120°,
∴∠BCD=∠ECF,
∴∠BCE=∠DCF
由旋转可得:EC=FC,
在△BEC和△DFC中,
,
∴△DCF≌△BCE(SAS),
∴DF=BE,
即求DF的最小值转化为求BE的最小值.
∵在Rt△AHB中,∠BAH=60°,AB=2,
∴BH=2sin60°,
当E与H重合时,BE最小值是,
∴DF的最小值是.
故答案为:.
4.
【分析】作DH⊥B′C′于H,交AD′于G,如图,根据旋转的性质得AD′=AD,∠DAD′=α,再根据等腰三角形的性质由B'D=C'D得到B′H=C′H,则AG=D′G,然后证明△ADD′为等边三角形得到∠DAG=60°,从而得到α的度数.
【解答】解:作DH⊥B′C′于H,交AD′于G,如图,
∵正方形ABCD绕点A按逆时针方向旋转到正方形AB'C'D',旋转角为a,
∴AD′=AD,∠DAD′=α,
∵B'D=C'D,
∴B′H=C′H,
∵四边形AB'C'D'为正方形,
∴AG=D′G,
连接DD′,如图,
∵DG垂直平分AD′,
∴DD′=DA,
∴DD′=AD=AD′,
∴△ADD′为等边三角形,
∴∠DAG=60°,
即α=60°.
故答案为60°.
5.(1)①证明:如图,
∵四边形形ABCD是矩形,
∴AD=BC,∠BAD=∠ABC=90°,
∵旋转,
∴AE=AB,EF=BC=AD,∠1=∠ABC=∠BAD=90°,
在△ABD和△EAF中,
,
∴△ABD≌△EAF(SAS),
∴∠2=∠EAF,BD=AF,
∵AB=AE,
∴∠3=∠2=∠EAF,
∴AF∥BD,
又∵AF=BD,
∴四边形ABDF是平行四边形;
②解:设HD=x,则AH=4﹣x,
∵四边形ABDF是平行四边形,
∴AB∥DF,AB=DF,
∴∠ADF=∠BAD=90°,
又∵∠1=90°,
∴∠ADF=∠1,
∵AE=AB,AB=DF,
∴AE=DF,
在△AEH和△FDH中,
,
∴△AEH≌△FDH(SAS),
∴HE=HD=x,
∵∠1=90°,
∴EA2+EH2=AH2,
又∵AH=4﹣x,EA=AB=3,EH=x,
∴32+x2=(4﹣x)2,
∴x,
∴AH=4﹣x.
(2)解:∵将矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,
∴旋转过程中,GF是定值,
当D,A,G三点共时,三角形DFG的面积最大,如图,
此时DG=8,
∴S△DFG12,
故答案为:12.
6.
【分析】连接MC,根据全等三角形的性质结合平行线的性质可得出NM=NC,进而得出∠MCE=90°,最后利用勾股定理即可解决问题.
【解答】解:连接MC,
由旋转可知,
BC=FC,∠EFC=∠B=90°,CE=AC,CF=BC=3,
∴∠MFC=90°.
在Rt△MBC和Rt△MFC中,
,
∴Rt△MBC≌Rt△MFC(HL),
∴∠BMC=∠NMC.
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠BMC=∠MCN,
∴∠NMC=∠MCN,
∴NM=NC.
∵点N是ME的中点,
∴EN=MN,
∴EN=NC.
在Rt△ABC中,
AC,
∴EC=AC=5.
令NC=x,
则FN=4﹣EN=4﹣x,
在Rt△CFN中,
(4﹣x)2+32=x2,
解得x,
∴DN=4.
故选:C.
7.
【分析】将△BFC绕点B逆时针旋转90°,即△BMA,连接ME,由于旋转得,∠MBA=∠FBC,∠MAB=∠FCB,AM=FC=3,MB=FB,∠MBF=90°,在正方形ABCD中,∠MAB=∠FCB=45°,∠BAC=45°,∠ABC=90°,可得∠MAE=90°,
证△MBE≌△FBE,可得ME=EF,在Rt△MAE中,ME2=AE2+AM2,因为MA=FC=4,AE=3,ME=EF,可得EF的长.
【解答】解:将△BFC绕点B逆时针旋转90°,即△BMA,连接ME,
,
由于旋转得,∠MBA=∠FBC,∠MAB=∠FCB,AM=FC=3,MB=FB,∠MBF=90°,
∵四边形ABCD是正方形,
∴∠MAB=∠FCB=45°,∠BAC=45°,∠ABC=90°,
∴∠MAE=∠MAB+∠BAC=90°,
∵∠EBF=45°,∠MBF=90°,
∴∠MBE=∠MBF﹣∠EBF=45°,
∴∠MBE=∠FBE,
在△MBE和△FBE中,
∴△MBE≌△FBE(SAS),
∴ME=EF,
∵∠MAE=90°,
∴ME2=AE2+AM2,
∵MA=FC=4,AE=3,
∴ME=5,
∵ME=EF,
∴EF=5,
故答案为:5.
8.
【分析】以EC为边作等边三角形ECH,过点H作HN⊥BC于N,HM⊥AB于M,可证四边形MHNB是矩形,可证MH=BN,由“SAS”可证△FEH≌△GEC,可得FH=GC,当FH⊥AB时,FH有最小值,即GC有最小值,即可求解.
【解答】解:如图,以EC为边作等边三角形ECH,过点H作HN⊥BC于N,HM⊥AB于M,
又∵∠ABC=90°,
∴四边形MHNB是矩形,
∴MH=BN,
∵BE=2,
∴EC=4,
∵△EHC是等边三角形,HN⊥EC,
∴EC=EH=4,EN=NC=2,∠HEC=60°,
∴BN=4=MH,
∵△FGE是等边三角形,
∴FE=GE,∠FEG=60°=∠HEC,
∴∠FEH=∠GEC,
在△FEH和△GEC中,
,
∴△FEH≌△GEC(SAS),
∴FH=GC,
∴当FH⊥AB时,FH有最小值,即GC有最小值,
∴点F与点M重合时,FH=HM=4,
∴CG的最小值为4.
故答案为:4.
9.
【分析】连接PA,作AM⊥PE于M.当AM与AB共线,且BM=BA+AM时,△BPE面积最大,利用S△APES矩形AGFEPE AM,求出AM,再根据S△BPEPE BM计算即可得出答案.
【解答】解:连接PA,作AM⊥PE于M.
当AM与AB共线,且BM=BA+AM时,△BPE面积最大,
由题意:PF=PG,
∵AG=EF=2,∠G=∠F=90°,
∴PA=PE,
∵S△APES矩形AGFEPE AM,
∴AM,
则S△BPEPE BM(3),
∴△PBE的面积的最大值为,
故答案为:.
10..
11.
【分析】根据∠ABC=60°,∠EGF=120°得到∠EGF+∠B=180°,从而得到E、B、F、G四点共圆,结合∠EGF=120°,∠GEF=30°,得到∠GFE=30°,继而得到GF=GE,得到∠EBG=∠FBG=30°,故BG平分∠ABC,作AM⊥BG于点M,根据垂线段最短原理,得到当G与M重合时,最短,结合AB=4,根据AM=ABsin30°=2,解答即可.
【解答】解:∵∠ABC=60°,∠EGF=120°,
∴∠EGF+∠B=180°,
∴E、B、F、G四点共圆,
∵∠EGF=120°,∠GEF=30°,
∴∠GFE=30°,
∴∠GFE=∠GEF,
∴GF=GE,
∴∠EBG=∠FBG=30°,
∴BG平分∠ABC,
作AM⊥BG于点M,根据垂线段最短原理,得到当G与M重合时,最短,
∵AB=4,
∴,
故选:B.
12.(1)解:由旋转可知:AB=DC′,AB∥DC′,
∴四边形ABDC′是平行四边形,
故答案为:①;
(2)解:连接AC′,C′D,AC,AC与BD相交于点O,
∵四边形ABCD是矩形,
∴,,AC=BD,
∴OA=OB,
∴∠OBA=∠OAB,
∵AB=AB',
∴∠OBA=∠AB'O,
∵∠OAB=∠C'AB',
∴∠AB'O=∠C'AB',
∴AC′∥BD,
∵AC′=AC=BD,
∴四边形ABDC′是平行四边形,
∴AE=DE=4,
由旋转可知:AB=AB',
∴∠ABB′=∠AB'B,
∵∠AB′C′=∠ABC=90°,
∴∠CBD=∠DB′F,
∵AD∥BC,
∴∠CBD=∠B′DF,
∴∠B′DF=∠DB′F,
∴FD=FB′,
∴AF=AD﹣FD=8﹣FB′,
在Rt△AB′F中,根据勾股定理得:AF2=AB′2+FB′2,
∴(8﹣FB′)2=62+FB′2,
∴FB′,
∵DE=AE=4,
∴EF=DE﹣FD=DE﹣FB′=4;
(3)证明:连接AC′,C′D,连接AC交BD于点O,
∵BC′与AD互相平分,
∴四边形ABDC′是平行四边形,
∴AC′∥BD,AC′=BD,
∴∠AB'B=∠C'AB',AC=AC′=BD,
∵AB=AB',
∴∠AB'B=∠ABB',
∵∠C'AB'=∠CAB,
∴,
∴OA=OB,
∴AC﹣OA=BD﹣OB,
∴OC=OD,
∴,
∵∠AOB=∠COD,
∴∠OCD=∠CAB,
∴AB∥CD.
13.(1)解:∵四边形ABCD为矩形,
∴∠B=90°,AD=BC,
∴AC5,
∵将矩形ABCD沿顺时针方向旋转,
∴BC=CF=4,
∴AF=AC﹣CF=5﹣4=1;
(2)证明:连接AC,CE,
∵将矩形ABCD沿顺时针方向旋转,得到矩形EFCG,
∴AB=CG,BC=EG,∠B=∠G=90°,
∴△ABC≌△CGE(SAS),
∴∠ACB=∠CEG,
∴∠CEG+∠ECG=∠ECG+∠ACB=90°,
∴∠ACE=90°,
∵M为AE的中点,
∴CMAE;
(3)解:过点C作CH⊥BD于点H,
∵BC=AD=4,AB=CD=3,
∴BD5,
∵S△BCD,
∴CH,
∴DH,HF,
∴DF=HF﹣DH,
∴.
14.解:(1)小鹿发现的结论正确,
证明:∵四边形ABCD为正方形,FH⊥AC,
∴∠D=∠AHF=90°,∠DAC=45°,
由旋转可知AE=AF,∠EAF=45°,
则∠FAH+∠CAE=∠EAD+∠CAE,
∴∠FAH=∠EAD,
∴△FAH≌△EAD(AAS),
∴AH=AD;
(2)∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠B=∠D=∠BAD=∠BCD=90°,∠CAD=∠CAB=45°,
由旋转可知AE=AF,∠EAF=45°,
∴Rt△ABF≌Rt△ADE(HL),∠BAF+∠DAE=45°
∴∠BAF=∠DAE=22.5°,BF=DE,则CF=CE,
∴AC是EF的垂直平分线,∠FAC=∠BAC﹣∠BAF=22.5°,
∴∠BAF=∠FAC,
∴AF平分∠BAC,
∴BF=HF,同理DE=HE,即EF=HE+HF=2DE,
设DE=x,则CE=CF=6﹣x,EF=2x,
由勾股定理可得:CE2+CF2=EF2,即:2(6﹣x)2=4x2,
解得:(负值舍去),
∴;
故答案为:;
(3)由(1)可知,FH⊥AC,且AH=AD=6,点H为定点,
即当点E在线段CD上运动时,点F在过定点H的垂线上,则∠FHC=90°,
由正方形的性质可知,点G在直线BC上运动是,∠HCG=45°或∠HCG=135°,
则点C、H、G、F为顶点的四边形是平行四边形时,∠FHC与∠HCG不能为对角,也不为邻角,
∴点C、H、G、F为顶点的四边形是平行四边形时,CG与FH是对角线,
∵四边形CFGH是平行四边形,
∴FH=2OH,
∵FH⊥AC,∠GCH=45°,
∴CH=OH,
∵,
∴,
∴,
∵△FAH≌△EAD
∴;
(4)如图,过点C作CD⊥y轴,在x轴上取OA=OE,过点C作CH⊥AE于H点,过点H作HF∥y轴,过点H作HG⊥y轴于G点,则△AOE为等腰直角三角形,
∴∠OAE=45°,则△AGH为等腰直角三角形,则,
由旋转可知,AB=AC,∠BAC=45°,
则∠OAE+∠EAB=∠EAB+∠BAC,即:∠OAB=∠HAC,
又∵∠AHC=∠AOB=90°,
∴△AHC≌△AOB(AAS),
∴AO=AH
∵HF∥y轴,则∠AHF=∠OAE=45°,
∴△HCF为等腰直角三角形,四边形DFHG为矩形,
∴CF=FH=DG,GH=DF,
∵A(0,2),C(m,3),
∴AO=AH=2,OD=3,CD=m,
∴AD=OD﹣AO=1,,
∴,
∴,
故答案为:.
一.四边形的翻折问题
1.如图,将 ABCD沿对角线AC折叠,使点B落在B'处,若∠1=∠2=42°,则∠B= .
2.如图,在矩形ABCD中,将△BCD沿对角线BD对折得到△BED,BE交AD于点F.若AB=1,BC=2,则AF的长为 .
3.如图,矩形ABCO如图放置在平面直角坐标系中,其中AB=6,∠AOB=30°,若将其沿着OB对折后,A′为点A的对应点,则A′的坐标为( )
A. B.
C.(﹣3,9) D.
4.如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
A.78° B.75° C.60° D.45°
5.实践操作:第一步:如图1,将矩形纸片ABCD沿过D的直线折叠,使点A落在CD上的点A′处,得到折痕DE,然后在把纸片展平;
第二步:如图2,将图1中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C′处,得到折痕EF,B′C′交AB于点M,再把纸片展平.
问题解决:
(1)如图1,求证:四边形AEA′D是正方形;
(2)如图2,若AC′=2,DC′=4,求△AC′M的面积.
6.如图,在矩形ABCD中,已知AB=2,BC=4,点O、P分别是边AB、AD的中点,点H是边CD上的一个动点,连接OH,将四边形OBCH沿OH折叠,得到四边形OFEH,连接PE,则PE长度的最小值是( )
A. B. C. D.
7.如图,菱形ABCD中,E、F、G分别为AD、AB、BC上的点,将△AEF沿直线EF折叠得到△GEF,其中点A的对应点是点G,DE=1,CG=4,当EG⊥CG时,菱形ABCD的边长为 ,AF的长为 .
8.如图,在菱形ABCD中,AB=8,∠A=120°,M是CD上,DM=3,N是点AB上一动点,四边形CMNB沿直线MN翻折,点C对应点为E,当AE最小时,AN= .
9.学习了《中心对称图形》后,阿中与茜茜对平行四边形进行了再次探究:
(1)阿中发现:命题“一组对边相等,一组对角相等的四边形是平行四边形”是个假命题,如何举反例说明呢?茜茜稍作思考说:“取一张如图1所示的等腰三角形纸片ABC,其中AB=AC,在BC边上取一点D(不是中点),连接AD,沿AD剪开纸片,重新拼接……”,
请你完成茜茜的举反例过程,画出相应的图形,并配以必要的说明;
(2)阿中进一步探究发现:“一组对边相等且一组对角是直角的四边形是矩形”,请你完成证明过程;
已知:如图2,四边形ABCD中,AB=CD,∠A=∠C=90°,求证:四边形ABCD是矩形.
(3)茜茜发现折叠矩形可以得到菱形:如图3,将矩形ABCD折叠,使得A、C两点重合,点B落在点B′,折痕分别交边BC、AD于E、F两点,交AC于O两点,则四边形AECF是菱形.请在框图中补全茜茜的证明思路.
茜茜的证明思路
由折叠易知EF是AC的垂直平分线,可以先证△AOF≌① △COE ,得到② OE=OF ,又由OA=OC,可得四边形AECF是平行四边形,再由③ EF⊥AC ,于是 AECF是菱形.
(4)茜茜给阿中出了一道思考题:“如图4,在矩形ABCD中,AB=2,AD=3,点E、F分别是边AB、AD上的点,将矩形ABCD沿着直线EF折叠,使点A与矩形ABCD内部的点P重合,问BP的最小值是多少?”请聪明的你用矩形纸片操作探究一下,直接写出BP的最小值.
10.实践操作
在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
初步思考
(1)若点P落在矩形ABCD的边AB上(如图①).
当点P与点A重合时,∠DEF= °;当点E与点A重合时,∠DEF= °;
深入探究
(2)当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当时的菱形EPFD的边长.
拓展延伸
(3)若点F与点C重合,点E在AD上,射线BA与射线FP交于点M(如图③).在折叠过程中,是否存在使得线段AM与线段DE的长度相等的情况?若存在,请求出线段AE的长度;若不存在,请说明理由.
11.综合与实践
动手实践:数学课上老师让学生们折矩形纸片,下面几幅图是学生们折出的一部分图形(沿直线l折叠),由于折痕所在的直线不同,折出的图形也不同,各个图形中所隐含的“基本图形也不同,我们可以通过发现基本图形研究这些图形中的几何问题.
问题解决:
(1)如图1,将矩形纸片ABCD沿直线MN折叠,使得点C与点A重合,点D落在点D1的位置,连接MC,AN,AC,线段AC交MN于点O,则△CDM与△AD1M的关系为 ,线段AC与线段MN的关系为 ,小强量得∠MNC=50°,则∠DAN= ,小丽说:“四边形ANCM是菱形”,请你帮她证明.
拓展延伸:
(2)如图2,矩形纸片ABCD中,BC=2AB=6cm,BM=4cm,小明将矩形纸片ABCD沿直线AM折叠,点B落在点B1的位置,MB1交AD于点N,请你直接写出线段ND的长: .
综合探究;
(3)如图3,ABCD是一张矩形纸片,AD=1,AB=5,在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使线段MB与线段DN交于点P,得到△MNP,请你确定△MNP面积的取值范围 .
12.在矩形ABCD中,AB=6,BC=12,点E是矩形ABCD边CD上一点,连接BE,将△CEB沿BE翻折,
(1)如图1,点C刚好落在边AD上的点F处,求AF长.
(2)如图2,点C落在矩形外一点F处,连接AF,若CE=4,求△ABF的面积.
(3)如图3,点C落在点F处,∠ABF的角平分线与EF的延长线交于点M,当点E从点C运动到点D时,求点M运动的路径长
二.四边形的旋转问题
1.如图,在 ABCD中,∠A=65°,将 ABCD绕顶点B顺时针旋转到 A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1的大小为 .
2.如图,将矩形ABCD绕点A顺时针旋转到矩形AB'C'D'的位置,旋转角为α(0°<α<90°),若∠1=114°,则α= °.
3.如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD交于点O.点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),DF长度的最小值为 .
4.如图,将正方形ABCD绕点A按逆时针方向旋转到正方形AB'C'D',旋转角为a(0°<α<180°),连接B'D、C'D,若B'D=C'D,则∠α= .
5.如图1,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,连接DF、DG.
(1)如图2,点E落在对角线BD上,AD与EF相交于点H,
①连接AF,求证:四边形ABDF是平行四边形;
②求线段AH的长度;
(2)在矩形AEFG绕点A旋转一周的过程中,△DFG面积的最大值为 .
6.如图,在矩形ABCD中,AB=4,BC=3,将△ABC绕点C顺时针旋转α(α<90°)得到△EFC,延长EF分别交AB、CD于M、N,当N为EM中点时,DN的长为( )
A. B. C. D.
7.如图,在正方形ABCD中,E、F分别为对角线AC上的两点,且∠EBF=45°,若AE=3,CF=4,则EF的长为 .
8.如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为 .
9.如图,在矩形ABCD中,AB=3,BC=2,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为α(0°<α<180°),得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,△BEP的面积最大值是 .
10.如图,在矩形ABCD中,AB=4,BC=8,点O是BD的中点,点E在BC边上,BE=3.已知点P是AD边上动点(DP≤4),线段OP绕点O逆时针旋转一定的度数,使点P落在线段AE上的点Q处.连接PQ,则PQ2的最小值是 .
11.如图,在 ABCD中,AB=4,∠B=60°,BC=3,E为AB上一点,且BE=1,F为BC边上的一个动点,连接EF,将其绕点E逆时针旋转30°至直线EG,使得∠EGF=120°,连接AG,则AG的最小值为( )
A. B.2 C. D.
12.如图,将四边形ABCD绕点A旋转,使得点B的对应点B’恰好落在射线BD上,旋转后的四边形为AB/C/D/ ,连接BC’交AD于点E.
(1)如图①,若四边形ABCD为正方形,则四边形ABDC/是 .(填序号)
①平行四边形;
②矩形;
③菱形;
(2)如图②,若四边形ABCD为矩形,若AB=6,BC=8,B/C/交AD于点F,求EF的长.
(3)如图③,若BC’与AD互相平分,求证:AB∥CD.
13.如图,在矩形ABCD中,AB=3,AD=4,以点C为旋转中心,将矩形ABCD沿顺时针方向旋转,得到矩形EFCG,点A、B、D的对应点分别是点E、F、G.
(1)如图1,当点F落在矩形ABCD的对角线AC上时,求线段AF的长;
(2)如图2,当点F落在矩形ABCD的边CD的延长线上时,连接AE,取AE的中点M,求证:;
(3)如图3,当点F落在矩形ABCD的对角线BD的延长线上时,求△CDF的面积.
14.如图1,四边形ABCD是边长为6的正方形,点E在线段CD上运动,连接AE,将线段AE绕点A顺时针旋转45°得到AF.
【探索发现】
(1)爱思考的小鹿发现:过点F作FH⊥AC时,AH一定等于AD,小鹿发现的结论正确吗?如果正确请帮小鹿完成证明过程,如不正确请说明理由;
【结论运用】
(2)当点F落在BC上时,此时DE的长为 ;
【深入理解】
(3)若点G在直线BC上运动,当以点C、H、G、F为顶点的四边形是平行四边形时,求DE的长;
【拓展延伸】
(4)如图2.在平面直角坐标系xOy中,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转45°得到线段AC.若点C的坐标为(m,3),则m的值为 .
参考答案
一.四边形的翻折问题
1.
【分析】由平行线的性质可得∠1=∠B'AB=42°,由折叠的性质可得∠BAC=∠B'AC=21°,即可求解.
【解答】解:∵四边形ABCD
∴AB∥CD,
∴∠1=∠B'AB=42°
∵将 ABCD沿对角线AC折叠
∴∠BAC=∠B'AC=21°
∴∠B=180°﹣∠2﹣∠BAC=117°
故答案为:117°
2.
【分析】先由长方形的性质可知,AB=CD,BE=BC,再根据图形翻折变换的性质可知,CD=DE=AB,利用全等三角形的判定定理可得△ABF≌△EDF,故BF=DF,AF+BF=AD,设AF=x,由勾股定理即可求出x的值.
【解答】解:∵四边形ABCD是长方形,AB=1,BC=2,
∴AB=CD=1,AD=BC=2,
∵△BED是△BCD沿BD翻折而成,
∴CD=DE=AB=1,∠E=90°,
又∵∠AFB=∠EFD,
∴△ABF≌△EDF(AAS),
∴BF=DF,AF+BF=AD=2,
在Rt△ABF中,设AF=x,则BF=2﹣x,由勾股定理得BF2=AB2+AF2,即(2﹣x)2=12+x2,
解得x,
故答案为:.
3.
【分析】作AD⊥x轴,根据含 30°角直角三形的性质,及勾 股定理,求出AO,根据折叠的性质,求出AO,∠AOD,在Rt△ADO中,求出DO,AD,根据 第二象限内点的特征,即可求解,
【解答】解:过点A作AD⊥x轴,交x轴于点D,
在Rt△BAO 中,AB=6,∠AOB=30°,
∴BO=2AB=2×6=12,,
由折叠的性质可得:,
∠A'OB=∠AOB=30°,
即:∠AOD=2∠AOB=2×30°=60°,
在Rt△ADO 中,,,
∵点A在第二象限,,
故选:D.
4.
【分析】连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°,利用三角形的内角和定理即可求出所求角的度数.
【解答】解:连接BD,
∵四边形ABCD为菱形,∠A=60°,
∴△ABD为等边三角形,∠ADC=120°,∠C=60°,
∵P为AB的中点,
∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,
∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,
在△DEC中,∠DEC=180°﹣(∠CDE+∠C)=75°.
故选:B.
5.解:(1)∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,
∴AD=A′D,AE=A′E,∠ADE=∠A′DE=45°,
∵AB∥CD,
∴∠AED=∠A′DE=∠ADE,
∴AD=AE,
∴AD=AE=A′E=A′D,
∴四边形AEA′D是菱形,
∵∠A=90°,
∴四边形AEA′D是正方形;
(2)如图,连接C′E,由(1)知,AD=AE,
∵四边形ABCD是矩形,
∴AD=BC,∠EAC′=∠B=90°,
由折叠知,B′C′=BC,∠B=∠B′,
∴AE=B′C′,∠EAC′=∠B′,
又∵EC′=C′E,
∴Rt△EC′A≌Rt△C′EB′(HL),
∴∠C′EA=∠EC′B′,
∴MC′=ME,
设AM=x,
∵AC′=2,DC′=4,
∴AE=AD=2+4=6,
∴C'M=BM=6﹣x,
在Rt△MC'A中,
由勾股定理,得AC'2+AM2=MC'2,
即22+x2=(6﹣x)2,
解得x,
即AM,
∴△AC′M的面积AC' AM2.
6.
【分析】连接EO、PO、OC.根据三边关系,PE≥OE﹣OP,求出OE,OP即可解决问题.
【解答】解:如图,连接EO、PO、OC.
∵四边形ABCD是矩形,
∴∠B=∠OAP=90°,
∵AB=2,BC=4,点O、P分别是边AB、AD的中点,
∴OB=OA=1,PA=2,
在Rt△OBC中,
由勾股定理,得OC,
在Rt△AOP中,
由勾股定理,得OP,
∵OE=OC,PE≥OE﹣OP,
∴PE的最小值为.
故选:C.
7.
【分析】作DM⊥BC于M,作FN⊥AD于N,设AE为x,证明四边形DMGE为矩形,在Rt△DCM中,利用勾股定理求出x,即可求出边长;证明△AFN∽△DCM,设AN=3y,表示出FN,AF,利用AE=4,列出方程,求出y值,即可解答.
【解答】解:作DM⊥BC于M,作FN⊥AD于N,如图,
设AE=x,则AD=x+1=DC,
由折叠得,EC=AE=x,
∵EG⊥CG,
∴四边形DMGE为矩形,
∴DM=EC=x,GM=DE=1,
∴CM=4﹣1=3,
在Rt△DCM中,CM2+DM2=DC2,即32+x2=(x+1)2,
∴x=4,
∴AD=5,即棱形边长为5;
∵∠A=∠C,
∴△AFN∽△DCM,
∴AN:CM=FN:DM,
设AN=3y,则FN=4y,AF=5y,
由折叠得,∠AEF=∠GEF=45°,
∴EN=4y,
∵AE=4,即AN+EN=4,
∴y,
∴AF=5.
故答案为:5;.
8.7.
9.(1)解:等腰三角形纸片ABC,其中AB=AC,在BC边上取一点D(不是中点),连接AD,沿AD 剪开纸片,重新拼接如图所示,
∴AB=CD,∠B=∠C,而BD≠AC,
∴四边形ABDC不是平行四边形,
∴命题“一组对边相等,一组对角相等的四边形是平行四边形”是个假命题;
(2)证明:连接BD,
∵AB=CD,∠A=∠C=90°,且BD=BD,
∴Rt△ABD≌Rt△CDB(HL),
∴AD=BC,
∵AB=CD,
∴四边形ABCD是平行四边形,
∵∠A=90°,
∴四边形ABCD是矩形;
(3)证明:由折叠知EF是AC的垂直平分线,
∴AO=OC,∠AOF=∠COE=90°,
∵矩形ABCD,
∴AF∥CE,
∴∠FAO=∠ECO,
∴△AOF≌△COE,
∴OE=OF,
∵OA=OC,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴ AECF是菱形,
故答案为:△COE;OE=OF;EF⊥AC;
(4)解:如图,连接BF,BD,
∵PB≥FB﹣FP,FA=FP,
∴PB≥FB﹣FA,此时PB的最小值=FB﹣FA
∵(FB﹣FA)﹣(BD﹣AD)=FB﹣FA﹣BD+AF+DF=FB+DF﹣BD>0,
∴BD﹣AD<FB﹣FA,
∴当F与D重合时,FB﹣FA的值最小,由折叠得:AD=PD=3,
由勾股定理得:BD,
∵PB≥BD﹣PD,
当P,A,C共线时,BP有最小值,
∴BP3,
则BP的最小值是3.
10.初步思考
(1)当点P与点A重合时,如图1,
∴EF是AD的中垂线,
∴∠DEF=90°,
当点E与点A重合时,如图2,
此时∠DEF∠DAB=45°,
故答案为:90,45;
深入探究
(2)当点E在AB上,点F在DC上时,如图3,
∵EF是PD的中垂线,
∴DO=PO,EF⊥PD,
∵四边形ABCD是矩形,
∴DC∥AB,
∴∠FDO=∠EPO,
∵∠DOF=∠EOP,
∴△DOF≌△POE(ASA),
∴DF=PE,
∵DF∥PE,
∴四边形DEPF是平行四边形,
∵EF⊥PD,
∴ DEPF为菱形,
当AP时,设菱形的边长为x,则AEx,DE=x,
在Rt△ADE中,由勾股定理得:
AD2+AE2=DE2,
∴32+(x)2=x2,
∴x,
∴时的菱形EPFD的边长为:;
拓展延伸
(3)存在,
情况一:如图4,连接EM,
∵DE=EP=AM,
∴△EAM≌△MPE(HL),
设AE=x,则AM=DE=3﹣x,则BM=x+1,
∵MP=EA=x,CP=CD=4,
∴MC=4﹣x,
∴(x+1)2+32=(4﹣x)2,
解得:x;
情况二,如图5,
∵DE=EP=AM,
∴△GAM≌△GPE(AAS),
设AE=x,则DE=3﹣x,则AM=PE=DE=3﹣x,MP=AE=x,
则MC=MP+PC=x+4,BC=3,BM=7﹣x,
∴(7﹣x)2+32=(x+4)2,
解得:x,
综上,线段AE的长为:或.
11.解:(1)如图1中,
∵矩形纸片ABCD沿直线MN折叠,使得点C与点A重合,点D落在点D1的位置,
∴AM=MC,AD1=CD,MD1=MD,
∴△AMD1≌△CMD(SSS),
∵MN垂直平分线段AC,
∴OA=OC,
∵AD∥CB,
∴∠AMO=∠CNO,
∵∠AOM=∠CON,
∴△AMO≌△CNO(AAS),
∴OM=ON,AM=CM,
∴线段AC与线段MN互相垂直平分.
∵MA=MC,NA=NC,
∴AM=CM=CN=AN,
∴四边形ANCM是菱形,
∴∠ANM=∠MNC=50°,
∴∠ANC=100°,
∵AD∥BC,
∴∠DAN=180°﹣100°=80°,
故答案为:△CDM≌△AD1M,线段AC与线段MN互相垂直平分,80°.
(2)如图2中,
∵四边形ABCD是矩形,
∴AD=BC=∠B=90°,
由翻折的性质可知,∠AMB=∠AMN,∠B1=∠B=90°,
∵AD∥BC,
∴∠AMB=∠MAN,
∴∠AMN=∠NAM,
∴AN=NM,设AN=MN=x,
在Rt△ANB1中,∵AB1=AB=3,NB1=4﹣x,AN=x,
∴x2=32+(4﹣x)2,
解得x,
∴AN,
∴DN=AD﹣AN=6.
故答案为.
(3)如图3,当点B与点D重合时,△MNP的面积最大,作MH⊥BN于H,则MH=AB=1,
由题意得:MP=MQ,设MP=MQ=k,则AM=5﹣k;
由勾股定理得:(5﹣k)2+12=k2,
解得:k=2.6;由(1)知:
NP=MP=2.6,MH=1,
∴S△MNK NP MH=1.3,
∴△MNP的面积的最大值为1.3.
因为PN的最小值为1,
∴△MNP的面积的最小值为1×1=0.5,
∴0.5<S△MNP≤1.3.
故答案为:0.5<S△MNP≤1.3.
12.解:(1)由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∵四边形ABCD为矩形,
∴∠A=90°,
∴AF6.
(2)过点F作FG⊥AB,交AB的延长线于点G,延长GF交CD的延长线于点H,如图,
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵FG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
设HD=AG=x,则HE=x+2,BG=x+6,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,FE=CE=4.
∴∠EFH+∠GFB=90°.
∵∠GFB+∠GBF=90°,
∴∠EFH=∠GBF.
∵∠H=∠G=90°,
∴△EFH∽△FBG,
∴,
∴GF=3EH=3x+6,FHBGx+2,
∵GH=12,
∴3x+6x+2=12,
∴x.
∴FG=36,
∴△ABF的面积AB FG.
(3)过点M作MG⊥AB,交AB的延长线于点G,延长GM交CD的延长线于点H,如图
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵MG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∴∠G=∠BFM=90°.
∵BM为∠GBF的平分线,
∴∠GBM=∠FBM.
在△BGM和△BFM中,
,
∴△BGM≌△BFM(AAS),
∴BG=BF=12,
∴AG=BG=AB=6,
∵点M在GH上,
∴点M到AD的距离等于AG=6,即点M在GH上运动,
∴点E与点C重合时,点M与点H重合.
当点E与点D重合时,如图,
∵△BGM≌△BFM,
∴MG=MF,
由题意得:△BCE≌△BFE,
∴CD=DF=6.
∵四边形ADHG为矩形,
∴DH=AG=6.
设MG=MF=x,则MD=x+6,MH=GH﹣GM=12﹣x.
∵∠H=90°,
∴MD2=MH2+DH2,
∴(x+6)2=(12﹣x)2+62.
∴x=4.
∴MH=GH﹣GM=8.
∴当点E从点C运动到点D时,点M运动的路径长为线段HM的长等于8.
二.四边形的旋转问题
1.
【分析】由旋转的性质得出BC=BC1,由等腰三角形的性质得出∠BCC1=∠C1,由旋转角∠ABA1=∠CBC1,根据等腰三角形的性质计算即可.
【解答】解:∵ ABCD绕顶点B顺时针旋转到 A1BC1D1,
∴BC=BC1,
∴∠BCC1=∠C1,
∵∠A=65°,
∴∠A=∠BCD=∠C1=65°,
∴∠BCC1=∠C1=65°,
∴∠CBC1=180°﹣2×65°=50°,
∴∠ABA1=50°,
故答案为:50°.
2.
【分析】先利用旋转的性质得到∠ADC=∠D=90°,∠DAD′=α,再利用四边形内角和计算出∠BAD=66°,然后利用互余计算出∠DAD′,从而得到α的值.
【解答】解:∵矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,
∴∠ADC=∠D'=90°,∠DAD′=α,
∵∠ABC=90°,
∴∠BAD'=180°﹣∠2,
又∵∠2=∠1=114°,
∴∠BAD'=180°﹣114°=66°,
∴∠DAD′=∠BAD﹣∠BAD'=90°﹣66°=24°,
即α=24°.
故答案为:24.
3.
【分析】连接BE,作BH⊥AD,由旋转的性质可得△DCF≌△BCE,把求DF的最小值转化为求BE的最小值,再根据垂线段最短可得答案.
【解答】解:连接BE,作BH⊥AD交DA的延长线于H,
菱形ABCD中,∠ABC=60°,
∴∠BCD=120°.
∵∠ECF=120°,
∴∠BCD=∠ECF,
∴∠BCE=∠DCF
由旋转可得:EC=FC,
在△BEC和△DFC中,
,
∴△DCF≌△BCE(SAS),
∴DF=BE,
即求DF的最小值转化为求BE的最小值.
∵在Rt△AHB中,∠BAH=60°,AB=2,
∴BH=2sin60°,
当E与H重合时,BE最小值是,
∴DF的最小值是.
故答案为:.
4.
【分析】作DH⊥B′C′于H,交AD′于G,如图,根据旋转的性质得AD′=AD,∠DAD′=α,再根据等腰三角形的性质由B'D=C'D得到B′H=C′H,则AG=D′G,然后证明△ADD′为等边三角形得到∠DAG=60°,从而得到α的度数.
【解答】解:作DH⊥B′C′于H,交AD′于G,如图,
∵正方形ABCD绕点A按逆时针方向旋转到正方形AB'C'D',旋转角为a,
∴AD′=AD,∠DAD′=α,
∵B'D=C'D,
∴B′H=C′H,
∵四边形AB'C'D'为正方形,
∴AG=D′G,
连接DD′,如图,
∵DG垂直平分AD′,
∴DD′=DA,
∴DD′=AD=AD′,
∴△ADD′为等边三角形,
∴∠DAG=60°,
即α=60°.
故答案为60°.
5.(1)①证明:如图,
∵四边形形ABCD是矩形,
∴AD=BC,∠BAD=∠ABC=90°,
∵旋转,
∴AE=AB,EF=BC=AD,∠1=∠ABC=∠BAD=90°,
在△ABD和△EAF中,
,
∴△ABD≌△EAF(SAS),
∴∠2=∠EAF,BD=AF,
∵AB=AE,
∴∠3=∠2=∠EAF,
∴AF∥BD,
又∵AF=BD,
∴四边形ABDF是平行四边形;
②解:设HD=x,则AH=4﹣x,
∵四边形ABDF是平行四边形,
∴AB∥DF,AB=DF,
∴∠ADF=∠BAD=90°,
又∵∠1=90°,
∴∠ADF=∠1,
∵AE=AB,AB=DF,
∴AE=DF,
在△AEH和△FDH中,
,
∴△AEH≌△FDH(SAS),
∴HE=HD=x,
∵∠1=90°,
∴EA2+EH2=AH2,
又∵AH=4﹣x,EA=AB=3,EH=x,
∴32+x2=(4﹣x)2,
∴x,
∴AH=4﹣x.
(2)解:∵将矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,
∴旋转过程中,GF是定值,
当D,A,G三点共时,三角形DFG的面积最大,如图,
此时DG=8,
∴S△DFG12,
故答案为:12.
6.
【分析】连接MC,根据全等三角形的性质结合平行线的性质可得出NM=NC,进而得出∠MCE=90°,最后利用勾股定理即可解决问题.
【解答】解:连接MC,
由旋转可知,
BC=FC,∠EFC=∠B=90°,CE=AC,CF=BC=3,
∴∠MFC=90°.
在Rt△MBC和Rt△MFC中,
,
∴Rt△MBC≌Rt△MFC(HL),
∴∠BMC=∠NMC.
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠BMC=∠MCN,
∴∠NMC=∠MCN,
∴NM=NC.
∵点N是ME的中点,
∴EN=MN,
∴EN=NC.
在Rt△ABC中,
AC,
∴EC=AC=5.
令NC=x,
则FN=4﹣EN=4﹣x,
在Rt△CFN中,
(4﹣x)2+32=x2,
解得x,
∴DN=4.
故选:C.
7.
【分析】将△BFC绕点B逆时针旋转90°,即△BMA,连接ME,由于旋转得,∠MBA=∠FBC,∠MAB=∠FCB,AM=FC=3,MB=FB,∠MBF=90°,在正方形ABCD中,∠MAB=∠FCB=45°,∠BAC=45°,∠ABC=90°,可得∠MAE=90°,
证△MBE≌△FBE,可得ME=EF,在Rt△MAE中,ME2=AE2+AM2,因为MA=FC=4,AE=3,ME=EF,可得EF的长.
【解答】解:将△BFC绕点B逆时针旋转90°,即△BMA,连接ME,
,
由于旋转得,∠MBA=∠FBC,∠MAB=∠FCB,AM=FC=3,MB=FB,∠MBF=90°,
∵四边形ABCD是正方形,
∴∠MAB=∠FCB=45°,∠BAC=45°,∠ABC=90°,
∴∠MAE=∠MAB+∠BAC=90°,
∵∠EBF=45°,∠MBF=90°,
∴∠MBE=∠MBF﹣∠EBF=45°,
∴∠MBE=∠FBE,
在△MBE和△FBE中,
∴△MBE≌△FBE(SAS),
∴ME=EF,
∵∠MAE=90°,
∴ME2=AE2+AM2,
∵MA=FC=4,AE=3,
∴ME=5,
∵ME=EF,
∴EF=5,
故答案为:5.
8.
【分析】以EC为边作等边三角形ECH,过点H作HN⊥BC于N,HM⊥AB于M,可证四边形MHNB是矩形,可证MH=BN,由“SAS”可证△FEH≌△GEC,可得FH=GC,当FH⊥AB时,FH有最小值,即GC有最小值,即可求解.
【解答】解:如图,以EC为边作等边三角形ECH,过点H作HN⊥BC于N,HM⊥AB于M,
又∵∠ABC=90°,
∴四边形MHNB是矩形,
∴MH=BN,
∵BE=2,
∴EC=4,
∵△EHC是等边三角形,HN⊥EC,
∴EC=EH=4,EN=NC=2,∠HEC=60°,
∴BN=4=MH,
∵△FGE是等边三角形,
∴FE=GE,∠FEG=60°=∠HEC,
∴∠FEH=∠GEC,
在△FEH和△GEC中,
,
∴△FEH≌△GEC(SAS),
∴FH=GC,
∴当FH⊥AB时,FH有最小值,即GC有最小值,
∴点F与点M重合时,FH=HM=4,
∴CG的最小值为4.
故答案为:4.
9.
【分析】连接PA,作AM⊥PE于M.当AM与AB共线,且BM=BA+AM时,△BPE面积最大,利用S△APES矩形AGFEPE AM,求出AM,再根据S△BPEPE BM计算即可得出答案.
【解答】解:连接PA,作AM⊥PE于M.
当AM与AB共线,且BM=BA+AM时,△BPE面积最大,
由题意:PF=PG,
∵AG=EF=2,∠G=∠F=90°,
∴PA=PE,
∵S△APES矩形AGFEPE AM,
∴AM,
则S△BPEPE BM(3),
∴△PBE的面积的最大值为,
故答案为:.
10..
11.
【分析】根据∠ABC=60°,∠EGF=120°得到∠EGF+∠B=180°,从而得到E、B、F、G四点共圆,结合∠EGF=120°,∠GEF=30°,得到∠GFE=30°,继而得到GF=GE,得到∠EBG=∠FBG=30°,故BG平分∠ABC,作AM⊥BG于点M,根据垂线段最短原理,得到当G与M重合时,最短,结合AB=4,根据AM=ABsin30°=2,解答即可.
【解答】解:∵∠ABC=60°,∠EGF=120°,
∴∠EGF+∠B=180°,
∴E、B、F、G四点共圆,
∵∠EGF=120°,∠GEF=30°,
∴∠GFE=30°,
∴∠GFE=∠GEF,
∴GF=GE,
∴∠EBG=∠FBG=30°,
∴BG平分∠ABC,
作AM⊥BG于点M,根据垂线段最短原理,得到当G与M重合时,最短,
∵AB=4,
∴,
故选:B.
12.(1)解:由旋转可知:AB=DC′,AB∥DC′,
∴四边形ABDC′是平行四边形,
故答案为:①;
(2)解:连接AC′,C′D,AC,AC与BD相交于点O,
∵四边形ABCD是矩形,
∴,,AC=BD,
∴OA=OB,
∴∠OBA=∠OAB,
∵AB=AB',
∴∠OBA=∠AB'O,
∵∠OAB=∠C'AB',
∴∠AB'O=∠C'AB',
∴AC′∥BD,
∵AC′=AC=BD,
∴四边形ABDC′是平行四边形,
∴AE=DE=4,
由旋转可知:AB=AB',
∴∠ABB′=∠AB'B,
∵∠AB′C′=∠ABC=90°,
∴∠CBD=∠DB′F,
∵AD∥BC,
∴∠CBD=∠B′DF,
∴∠B′DF=∠DB′F,
∴FD=FB′,
∴AF=AD﹣FD=8﹣FB′,
在Rt△AB′F中,根据勾股定理得:AF2=AB′2+FB′2,
∴(8﹣FB′)2=62+FB′2,
∴FB′,
∵DE=AE=4,
∴EF=DE﹣FD=DE﹣FB′=4;
(3)证明:连接AC′,C′D,连接AC交BD于点O,
∵BC′与AD互相平分,
∴四边形ABDC′是平行四边形,
∴AC′∥BD,AC′=BD,
∴∠AB'B=∠C'AB',AC=AC′=BD,
∵AB=AB',
∴∠AB'B=∠ABB',
∵∠C'AB'=∠CAB,
∴,
∴OA=OB,
∴AC﹣OA=BD﹣OB,
∴OC=OD,
∴,
∵∠AOB=∠COD,
∴∠OCD=∠CAB,
∴AB∥CD.
13.(1)解:∵四边形ABCD为矩形,
∴∠B=90°,AD=BC,
∴AC5,
∵将矩形ABCD沿顺时针方向旋转,
∴BC=CF=4,
∴AF=AC﹣CF=5﹣4=1;
(2)证明:连接AC,CE,
∵将矩形ABCD沿顺时针方向旋转,得到矩形EFCG,
∴AB=CG,BC=EG,∠B=∠G=90°,
∴△ABC≌△CGE(SAS),
∴∠ACB=∠CEG,
∴∠CEG+∠ECG=∠ECG+∠ACB=90°,
∴∠ACE=90°,
∵M为AE的中点,
∴CMAE;
(3)解:过点C作CH⊥BD于点H,
∵BC=AD=4,AB=CD=3,
∴BD5,
∵S△BCD,
∴CH,
∴DH,HF,
∴DF=HF﹣DH,
∴.
14.解:(1)小鹿发现的结论正确,
证明:∵四边形ABCD为正方形,FH⊥AC,
∴∠D=∠AHF=90°,∠DAC=45°,
由旋转可知AE=AF,∠EAF=45°,
则∠FAH+∠CAE=∠EAD+∠CAE,
∴∠FAH=∠EAD,
∴△FAH≌△EAD(AAS),
∴AH=AD;
(2)∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠B=∠D=∠BAD=∠BCD=90°,∠CAD=∠CAB=45°,
由旋转可知AE=AF,∠EAF=45°,
∴Rt△ABF≌Rt△ADE(HL),∠BAF+∠DAE=45°
∴∠BAF=∠DAE=22.5°,BF=DE,则CF=CE,
∴AC是EF的垂直平分线,∠FAC=∠BAC﹣∠BAF=22.5°,
∴∠BAF=∠FAC,
∴AF平分∠BAC,
∴BF=HF,同理DE=HE,即EF=HE+HF=2DE,
设DE=x,则CE=CF=6﹣x,EF=2x,
由勾股定理可得:CE2+CF2=EF2,即:2(6﹣x)2=4x2,
解得:(负值舍去),
∴;
故答案为:;
(3)由(1)可知,FH⊥AC,且AH=AD=6,点H为定点,
即当点E在线段CD上运动时,点F在过定点H的垂线上,则∠FHC=90°,
由正方形的性质可知,点G在直线BC上运动是,∠HCG=45°或∠HCG=135°,
则点C、H、G、F为顶点的四边形是平行四边形时,∠FHC与∠HCG不能为对角,也不为邻角,
∴点C、H、G、F为顶点的四边形是平行四边形时,CG与FH是对角线,
∵四边形CFGH是平行四边形,
∴FH=2OH,
∵FH⊥AC,∠GCH=45°,
∴CH=OH,
∵,
∴,
∴,
∵△FAH≌△EAD
∴;
(4)如图,过点C作CD⊥y轴,在x轴上取OA=OE,过点C作CH⊥AE于H点,过点H作HF∥y轴,过点H作HG⊥y轴于G点,则△AOE为等腰直角三角形,
∴∠OAE=45°,则△AGH为等腰直角三角形,则,
由旋转可知,AB=AC,∠BAC=45°,
则∠OAE+∠EAB=∠EAB+∠BAC,即:∠OAB=∠HAC,
又∵∠AHC=∠AOB=90°,
∴△AHC≌△AOB(AAS),
∴AO=AH
∵HF∥y轴,则∠AHF=∠OAE=45°,
∴△HCF为等腰直角三角形,四边形DFHG为矩形,
∴CF=FH=DG,GH=DF,
∵A(0,2),C(m,3),
∴AO=AH=2,OD=3,CD=m,
∴AD=OD﹣AO=1,,
∴,
∴,
故答案为:.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
