11.4点到直线的距离
图片预览





文档简介
课件18张PPT。3.3.3点 到 直 线 的 距 离3.3.3点到直线的距离
3.3.4两条平行线间的距离难点:点到直线距离公式的推导回顾:1、平面内任意两点距离公式平面内有任意两点A(x1,y1)和B(x2,y2),
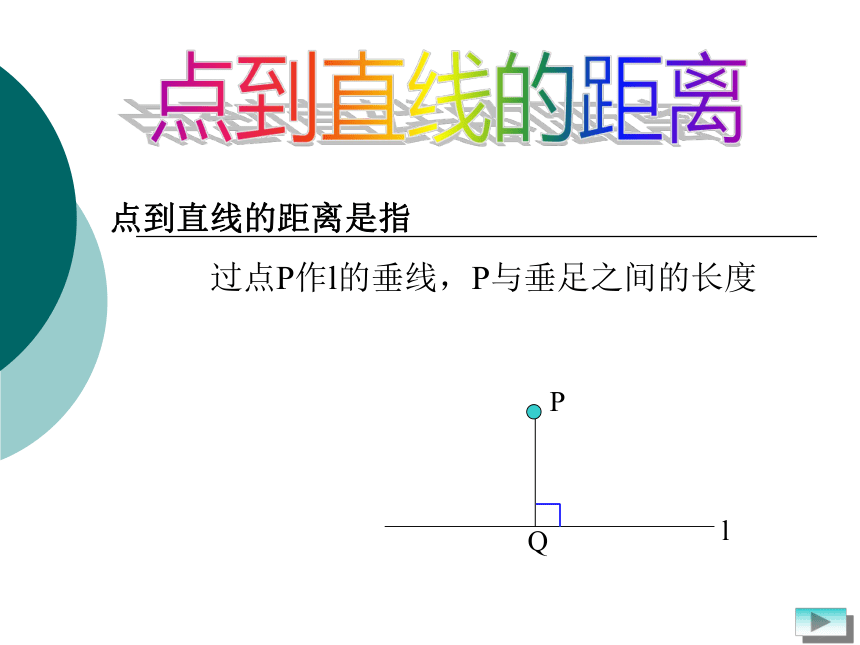
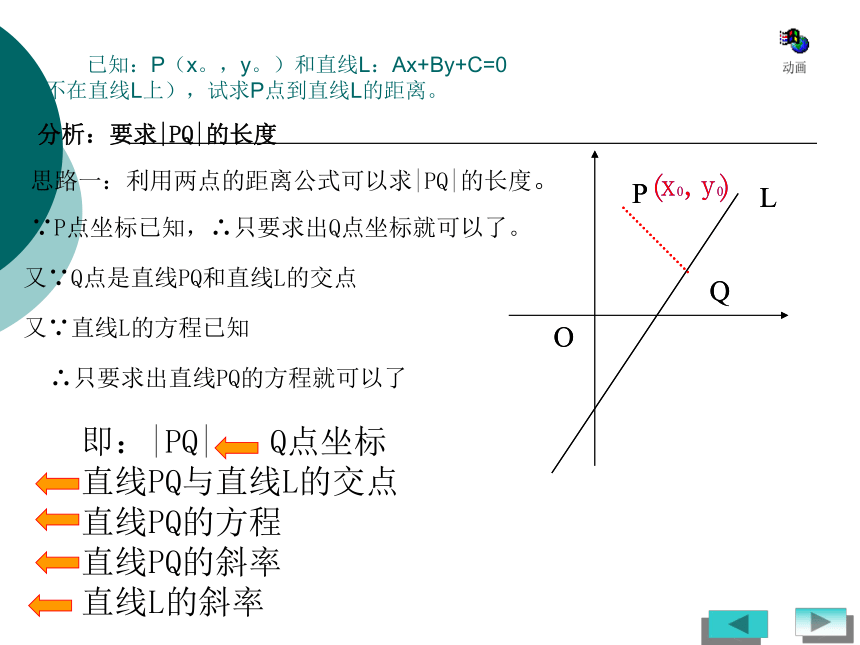
则AB的距离|AB|= .引入:点到直线的距离过点P作l的垂线,P与垂足之间的长度点到直线的距离是指PlQ一、点到直线的距离公式1思考: 已知:P(x。,y。)和直线L:Ax+By+C=0 (P不在直线L上),试求P点到直线L的距离。2推导过程 已知:P(x。,y。)和直线L:Ax+By+C=0 (P不在直线L上),试求P点到直线L的距离。思路一:利用两点的距离公式可以求|PQ|的长度。分析:要求|PQ|的长度∵P点坐标已知,∴只要求出Q点坐标就可以了。又∵Q点是直线PQ和直线L的交点又∵直线L的方程已知∴只要求出直线PQ的方程就可以了即:|PQ| Q点坐标
直线PQ与直线L的交点
直线PQ的方程
直线PQ的斜率
直线L的斜率 已知:P(x。,y。)和直线L:Ax+By+C=0 (P不在直线L上),试求P点到直线L的距离。思路二:利用面积求|PQ|的长度。分析:要求|PQ|的长度1、首先求出两条与坐标轴平行的线段的长度2、利用勾股定理求这两点间的距离3、利用面积|PQ|的长度RS求R的坐标求S的坐标求|PR|求|PS|利用勾股定理求|RS|面积法求|RQ|1.此公式的作用是求点到直线的距离;2.此公式是在A、B≠0的前提下推导的;3.如果A=0或B=0,此公式恰好也成立;4.如果A=0或B=0,一般不用此公式;5.用此公式时直线要先化成一般式。例1 求点P(-1,2)到直线①2x+y-10=0; ②3x=2的距离。解: ①根据点到直线的距离公式,得②如图,直线3x=2平行于y轴,用公式验证,结果怎样?例2 求平行线2x-7y+8=0与2x-7y-6=0的距离。两平行线间的距离处处相等在l2上任取一点,例如P(3,0)P到l1的距离等于l1与l2的距离直线到直线的距离转化为点到直线的距离求两条平行直线Ax+By+ =0与
Ax+By+ =0的距离。解:在直线上Ax+By+ =0任取一点,如P(x0,y0)则两平行线的距离就是点P(x0,y0)
到直线Ax+By+ =0 的距离。(如图)因此,d=练习:1、直线x+y-1=0与直线x+y-2=0之间的
距离: 。
2、直线2x+3y-1=0与直线4x+6y-1=0之间的距离: 。
3、与直线x+y-1=0平行,且距离为2的直线方程为: 。例3求过点(0,-1),且与点A(-3,-4),
B(6,3)两点距离相等的直线方程。例4正方形中心在点O( -1,0),一条边
所在直线方程x+y=0,求其他三边所在
的直线方程。 思考:过点(0,0)的直线和过点(1,1)
的直线互相平行,若他们之间的距离
为d,求d的取值范围,及此时这两条
直线方程。点 到 直 线 的 距 离1.此公式的作用是求点到直线的距离;2.此公式是在A、B≠0的前提下推导的;3.如果A=0或B=0,此公式恰好也成立;4.如果A=0或B=0,一般不用此公式;5.用此公式时直线要先化成一般式。要求:1.掌握点到直线的距离公式的推导过程;2.能用点到直线的距离公式进行计算;3.能求有关平行线间的距离。探索与思考:如果已知点到直线的距离及直线的有关特征,怎样求直线的方程。思考题:直线l在两坐标轴上的截距相等,点P(4,3)到l的距离为3 ,求直线l的方程。
则AB的距离|AB|= .引入:点到直线的距离过点P作l的垂线,P与垂足之间的长度点到直线的距离是指PlQ一、点到直线的距离公式1思考: 已知:P(x。,y。)和直线L:Ax+By+C=0 (P不在直线L上),试求P点到直线L的距离。2推导过程 已知:P(x。,y。)和直线L:Ax+By+C=0 (P不在直线L上),试求P点到直线L的距离。思路一:利用两点的距离公式可以求|PQ|的长度。分析:要求|PQ|的长度∵P点坐标已知,∴只要求出Q点坐标就可以了。又∵Q点是直线PQ和直线L的交点又∵直线L的方程已知∴只要求出直线PQ的方程就可以了即:|PQ| Q点坐标
直线PQ与直线L的交点
直线PQ的方程
直线PQ的斜率
直线L的斜率 已知:P(x。,y。)和直线L:Ax+By+C=0 (P不在直线L上),试求P点到直线L的距离。思路二:利用面积求|PQ|的长度。分析:要求|PQ|的长度1、首先求出两条与坐标轴平行的线段的长度2、利用勾股定理求这两点间的距离3、利用面积|PQ|的长度RS求R的坐标求S的坐标求|PR|求|PS|利用勾股定理求|RS|面积法求|RQ|1.此公式的作用是求点到直线的距离;2.此公式是在A、B≠0的前提下推导的;3.如果A=0或B=0,此公式恰好也成立;4.如果A=0或B=0,一般不用此公式;5.用此公式时直线要先化成一般式。例1 求点P(-1,2)到直线①2x+y-10=0; ②3x=2的距离。解: ①根据点到直线的距离公式,得②如图,直线3x=2平行于y轴,用公式验证,结果怎样?例2 求平行线2x-7y+8=0与2x-7y-6=0的距离。两平行线间的距离处处相等在l2上任取一点,例如P(3,0)P到l1的距离等于l1与l2的距离直线到直线的距离转化为点到直线的距离求两条平行直线Ax+By+ =0与
Ax+By+ =0的距离。解:在直线上Ax+By+ =0任取一点,如P(x0,y0)则两平行线的距离就是点P(x0,y0)
到直线Ax+By+ =0 的距离。(如图)因此,d=练习:1、直线x+y-1=0与直线x+y-2=0之间的
距离: 。
2、直线2x+3y-1=0与直线4x+6y-1=0之间的距离: 。
3、与直线x+y-1=0平行,且距离为2的直线方程为: 。例3求过点(0,-1),且与点A(-3,-4),
B(6,3)两点距离相等的直线方程。例4正方形中心在点O( -1,0),一条边
所在直线方程x+y=0,求其他三边所在
的直线方程。 思考:过点(0,0)的直线和过点(1,1)
的直线互相平行,若他们之间的距离
为d,求d的取值范围,及此时这两条
直线方程。点 到 直 线 的 距 离1.此公式的作用是求点到直线的距离;2.此公式是在A、B≠0的前提下推导的;3.如果A=0或B=0,此公式恰好也成立;4.如果A=0或B=0,一般不用此公式;5.用此公式时直线要先化成一般式。要求:1.掌握点到直线的距离公式的推导过程;2.能用点到直线的距离公式进行计算;3.能求有关平行线间的距离。探索与思考:如果已知点到直线的距离及直线的有关特征,怎样求直线的方程。思考题:直线l在两坐标轴上的截距相等,点P(4,3)到l的距离为3 ,求直线l的方程。
