15.1.1同底数幂的乘法
图片预览









文档简介
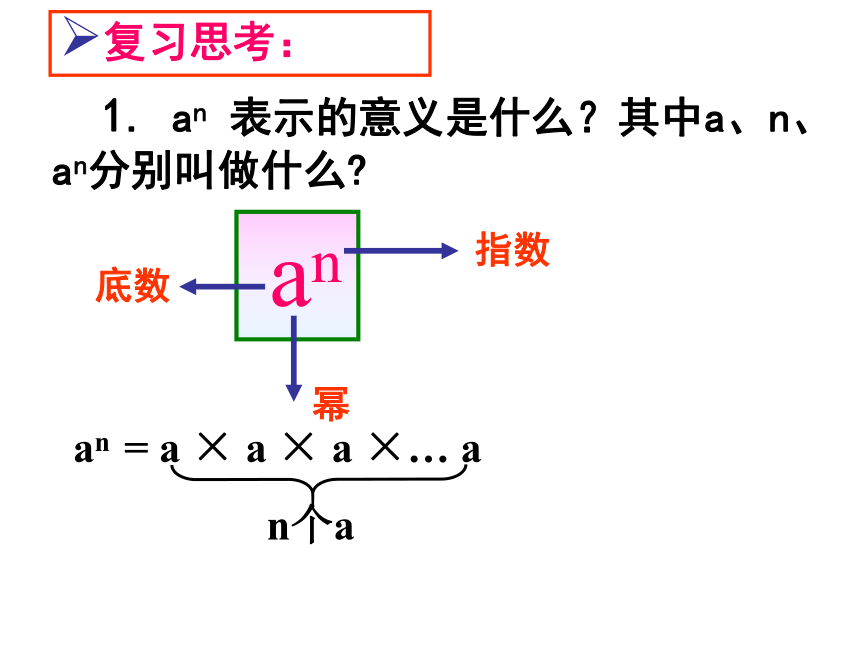
课件32张PPT。同底数幂的乘法 1. an 表示的意义是什么?其中a、n、an分别叫做什么? an底数幂指数复习思考:an = a × a × a ×… a
n个a
一种电子计算机每秒可进行1014次运算,它工作103秒可进行多少次运算?创设情境 提出问题(根据乘方的意义)(根据乘方的意义)(根据乘法结合律)解决问题 式子103×102的意义是什么? 思考: 这个式子中的两个因式有何特点?请同学们先根据自己的理解,解答下列各题.
103 ×102 = (10×10×10)×(10×10) =10( ) ;
23 ×22 = = 2( ) ;
5(2×2×2)×(2×2)5 a3×a2 = = a( ) .5(a a a)(a a)=2×2×2×2×2= a a a a a3个a2个a5个a1、你能写出一个同底数幂相乘的式子吗?试一试,议一议 2、你能发现同底数幂相乘的规律吗?
并把你的发现在小组内交流一下。再思考:请同学们观察下面各题左右两边,底数、指数有什么关系?
103 ×102 = 10( )
23 ×22 = 2( )
a3× a2 = a( ) 5 55 猜想:am · an= ? (当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确. 3+2 3+2 3+2 = 10( );
= 2( );
= a( ) 。
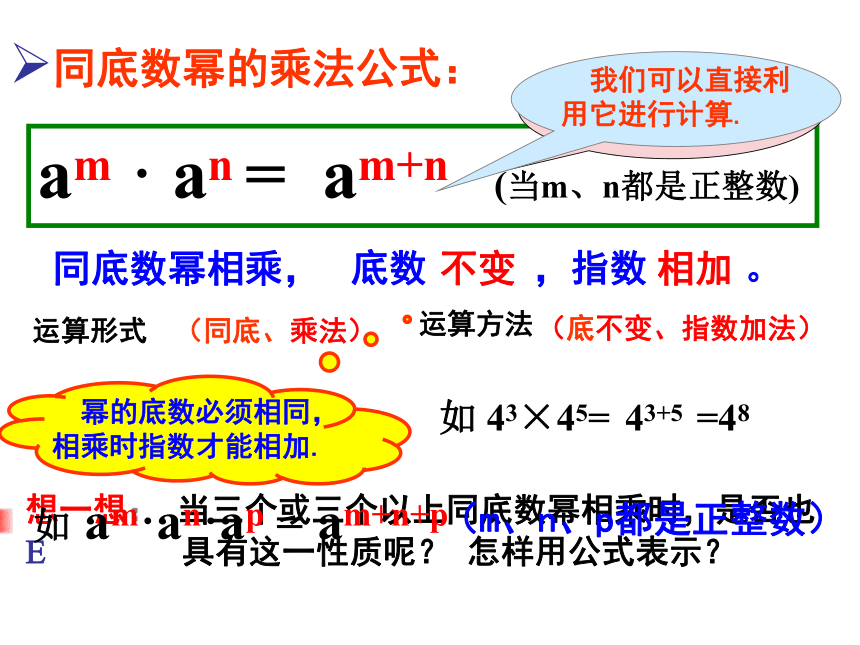
猜想: am · an = (m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a(aa…a)(aa…a)am+n(乘方的意义)(乘法结合律)(乘方的意义)?=am · an = am+n (当m、n都是正整数)同底数幂相乘,想一想: 当三个或三个以上同底数幂相乘时,是否也 ? 具有这一性质呢? 怎样用公式表示?底数 ,指数 。不变相加 同底数幂的乘法公式: 请你尝试用文字概括这个结论。 我们可以直接利用它进行计算.如 43×45=43+5=48 如 am·an·ap = am+n+p (m、n、p都是正整数)运算形式运算方法(同底、乘法) (底不变、指数加法) 幂的底数必须相同,相乘时指数才能相加. “神州六号”宇宙飞船载人航天飞行是我国航天事业的伟大壮举。它飞行的速度约为104米/秒,每天飞行时间约为105秒。它每天约飞行了多少米?解:104×105=109(米)答:它每天约飞行了109米。
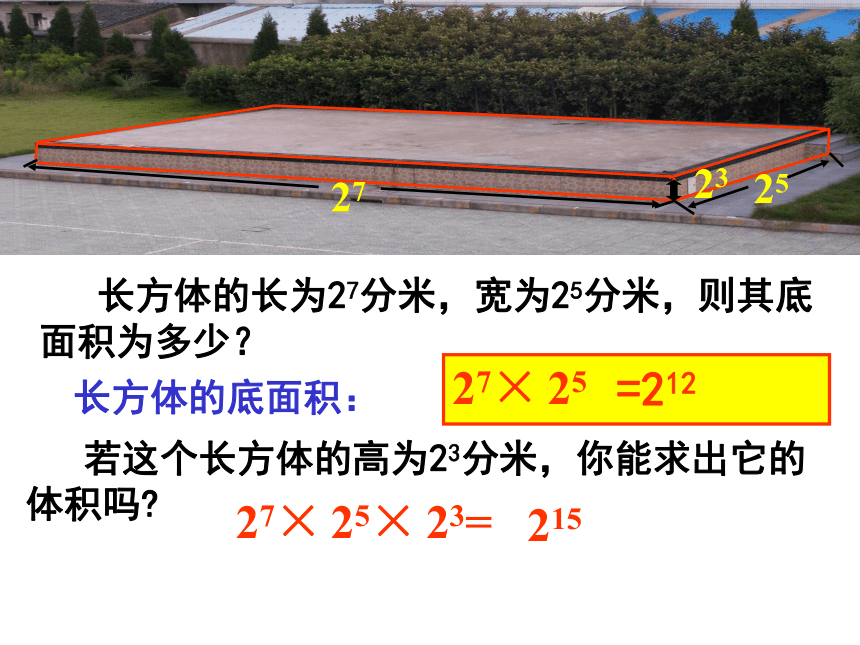
长方体的长为27分米,宽为25分米,则其底面积为多少?长方体的底面积: 27× 25=212 长方体的长为27分米,宽为25分米,则其底面积为多少?长方体的底面积: 27× 25 若这个长方体的高为23分米,你能求出它的体积吗?27× 25× 23=
215=2121.计算: (1)107 ×104 ; (2)x2 · x5 . 解:(1)107 ×104 =107 + 4= 1011
(2)x2 · x5 = x2 + 5 = x72.计算:(1)23×24×25 (2)y · y2 · y3 解:(1)23×24×25=23+4+5=212
(2)y · y2 · y3 = y1+2+3=y6 尝试练习am · an = am+n (当m、n都是正整数) am·an·ap = am+n+p (m、n、p都是正整数) 学以致用
(-5)1+7=(-5)8103+4 =107a3+4=58x · x7=
x1+7(a+b)3 · (a+b)2=(a+b)3+2am · an=am+n
(m、n都是正整数)例1 计算:=a7=x8=(a+b)5
练习一
1.???计算:(抢答)(1011 )( a10 )( x10 )( b6 )(2) a7 ·a3(3) -x5 ·(-x)5 (4) b5 · b (1) 105×106Good!(-x8)(5)-x2 · x62.??计算:
(1)x10 · x (2)10×102×104
(3) x5 ·x ·x3 (4)y4·y3·y2·y
解:(1)x10 ·x = x10+1= x11
(2)10×102×104 =101+2+4 =107
(3)x5 ·x ·x3 = x5+1+3 = x9
(4)y4 ·y3 ·y2 ·y= y4+3+2+1= y10 3.中国奥委会为了把2008年北京奥运会办成一个环保的奥运会,做了一个统计:一平方千米的土地上,一年内从太阳得到的能量相当于燃烧108千克煤所产生的能量。那么105平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤?108 ×105=1013 (千克)(1) (-2)3×24(2) (x+y)3 (y+x) 2(3) (a-b)4(b-a) 3例2.计算:火眼金睛
1.下面的计算对不对?如果不对,怎样改正?
(1) a · a2= a2 ( ) (2 ) x2 ·y5 = xy7 ( )
(3) a +a2 = a3 ( ) (4)a3 · a3 = a9 ( )
(5)a3+a3 = a6 ( ) (6) a3 · a3 =a6 ( )
a · a2= a3 x2 · y5 = x2y5 a +a2 = a +a2 a3 · a3 =a6 a3+a3 = 2a3× × × ×√×你认为,用法则时应该注意些什么?2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .35623 23 3253622 × = 33 32 × ×=填空:
(1)xm+n= x( )·x ( ) (2) x3 ·x4( )=x10
(3)27 × 37= 3( ) ×37
(4)xm ·( )=x3m
(5) 如果8=2x,那么 x= ( )
(6)若am=5,an=6,则am+n= ( )能力挑战mx3 3x2mn3 30 认真思考,我也行!你的思维真灵活!例3.已知:am=2,an=3.
求 am+n 的值.解: am+n=am·an=2×3=6思考:am+1,am+n+3呢?拓展提高23 + 23=2 × 23= 2434 × 27=34 × 33=37 b2· b3+b · b4 =b5 + b5=2b5 计算:(结果用幂的形式表示)15.2.1 同底数幂的乘法49 ×77+6 ×74 ×75=72 ×77+6 ×79=79 +6 ×79=7 ×79=710=1011 =a5=x4m+1= b6 (2)a2 ·a3(3) xm x3m+1 (1)b5 · b (1) 105×1061y · y2 · y4
=y1+2+41(2)计算(5)练习(-3)3×(-3)2(3)y2n . yn+1(4) - a2 ·a3=(-3)5=y3n+1= -a5 am · an · ap = am+n+p (m、n、p都是正整数)=105+6 =a2+3=xm+3m+1=y7= b5+1 =-35(4)(-3)2 . (-3)2=(-3)2+2=(-3)4=34下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2) x5 ·x5 = x25 ( )
(3) b5 + b5 = b10 ( ) (4)y5 +2y5 = 3y10 ( )
﹒
(5) c · c3 = c3 ( ) (6) ﹙-2﹚3 · 24 = 27 ( )
b5 · b5= b10 b5 + b5 = 2b5 x5 · x5 = x10 y5 +2y5 =3y5 c · c3 = c4× × × ×××数学医院注意 am · an 与 am + an的区别﹙-2﹚3﹒24 =-27
注意 同底数幂相乘,底数不变,指数相加.注意 底数相同 注意 指数1不能忘 (-a)2 · (-a)3a2 · (-a)3变式:(-a)2 · a3-a2 · a3变式训练计算:a2· a3(-a2)· a3(n为正整数)=a2· a3=(-a)5=-a5=-a5=a5=-a5=-a2 · a3=-a5公式中的a可以表示数、字母、也可以表示式子
变式:变式训练计算:a2 · a3(n都为正整数)(x+y)2 (x+y)3(x+y)2(y+x)3(x-y)2(x-y)3(y-x)2(x-y)3(a-b)2=(b-a)2(a-b)2n=(b-a)2n=(x+y)5=(x+y)5=(x-y)5=(x-y)2(x-y)3=(x-y)5(y-x)2(x-y)3= — (y-x)2(y-x)3= — (y-x)5(a-b)3= — (b-a)3(a-b)2n-1= — (b-a)2n-1计算下列各式,结果用幂的形式表示.综合运用(1)(-7)3 · 73= - 73 · 73= - 73+3= - 76(2) x2 · (-x)2= x2 . x2= x2+2= x4(3)( a-b)· (b-a)3 = -( a-b)· (a-b)3 = -(a-b)4(4) x2 x4 + x3 x3 = x6 + x6= 2x6 注意: 把不同底数幂(互为相反数)化成同底数幂, 再利用法则计算.闯关游戏第一关: ① b5·b ② xm·x3m+1·x2第二关: ① (-5)2 ·5 3 ② (a-b) (a-b) 2 第三关: ① 10 3 ×10+100 ×10 2 ② x 3 ·xm -xm+3 第四关: ①3×27×9 = 3x,则 x = .
② (a-b) (b-a) 2(b-a ) = .
规则 ①完成上一关,才能进入下一关
②按要求完成第一、二两关就算冲关成功
③完成第三、四关的,将有机会获得本节课的闯关英雄称号。
求助方法:1.看书 2.同学合作探讨 3.请教老师公式中的a可以表示数、字母、也可以表示式子思考方法总结:①(-1)的奇数次幂为-1,(-1)的偶数次幂为1,在计算过程中要判断准确是奇数次幂还是偶数次幂;
②能够化成底数相同的幂尽量化成底数相同的幂进行
运算。课 堂 小 结同底数幂的乘法公式:
1.数学知识:2.数学思想:思维延伸
1已知xa=2,xb=3,求xa+b.
2已知x3·xa·x2a+1=x31,求a的值.综合拓展
已知2x=3,2y=6,2z=12,试写出x,y,z的关系式.
n个a
一种电子计算机每秒可进行1014次运算,它工作103秒可进行多少次运算?创设情境 提出问题(根据乘方的意义)(根据乘方的意义)(根据乘法结合律)解决问题 式子103×102的意义是什么? 思考: 这个式子中的两个因式有何特点?请同学们先根据自己的理解,解答下列各题.
103 ×102 = (10×10×10)×(10×10) =10( ) ;
23 ×22 = = 2( ) ;
5(2×2×2)×(2×2)5 a3×a2 = = a( ) .5(a a a)(a a)=2×2×2×2×2= a a a a a3个a2个a5个a1、你能写出一个同底数幂相乘的式子吗?试一试,议一议 2、你能发现同底数幂相乘的规律吗?
并把你的发现在小组内交流一下。再思考:请同学们观察下面各题左右两边,底数、指数有什么关系?
103 ×102 = 10( )
23 ×22 = 2( )
a3× a2 = a( ) 5 55 猜想:am · an= ? (当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确. 3+2 3+2 3+2 = 10( );
= 2( );
= a( ) 。
猜想: am · an = (m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a(aa…a)(aa…a)am+n(乘方的意义)(乘法结合律)(乘方的意义)?=am · an = am+n (当m、n都是正整数)同底数幂相乘,想一想: 当三个或三个以上同底数幂相乘时,是否也 ? 具有这一性质呢? 怎样用公式表示?底数 ,指数 。不变相加 同底数幂的乘法公式: 请你尝试用文字概括这个结论。 我们可以直接利用它进行计算.如 43×45=43+5=48 如 am·an·ap = am+n+p (m、n、p都是正整数)运算形式运算方法(同底、乘法) (底不变、指数加法) 幂的底数必须相同,相乘时指数才能相加. “神州六号”宇宙飞船载人航天飞行是我国航天事业的伟大壮举。它飞行的速度约为104米/秒,每天飞行时间约为105秒。它每天约飞行了多少米?解:104×105=109(米)答:它每天约飞行了109米。
长方体的长为27分米,宽为25分米,则其底面积为多少?长方体的底面积: 27× 25=212 长方体的长为27分米,宽为25分米,则其底面积为多少?长方体的底面积: 27× 25 若这个长方体的高为23分米,你能求出它的体积吗?27× 25× 23=
215=2121.计算: (1)107 ×104 ; (2)x2 · x5 . 解:(1)107 ×104 =107 + 4= 1011
(2)x2 · x5 = x2 + 5 = x72.计算:(1)23×24×25 (2)y · y2 · y3 解:(1)23×24×25=23+4+5=212
(2)y · y2 · y3 = y1+2+3=y6 尝试练习am · an = am+n (当m、n都是正整数) am·an·ap = am+n+p (m、n、p都是正整数) 学以致用
(-5)1+7=(-5)8103+4 =107a3+4=58x · x7=
x1+7(a+b)3 · (a+b)2=(a+b)3+2am · an=am+n
(m、n都是正整数)例1 计算:=a7=x8=(a+b)5
练习一
1.???计算:(抢答)(1011 )( a10 )( x10 )( b6 )(2) a7 ·a3(3) -x5 ·(-x)5 (4) b5 · b (1) 105×106Good!(-x8)(5)-x2 · x62.??计算:
(1)x10 · x (2)10×102×104
(3) x5 ·x ·x3 (4)y4·y3·y2·y
解:(1)x10 ·x = x10+1= x11
(2)10×102×104 =101+2+4 =107
(3)x5 ·x ·x3 = x5+1+3 = x9
(4)y4 ·y3 ·y2 ·y= y4+3+2+1= y10 3.中国奥委会为了把2008年北京奥运会办成一个环保的奥运会,做了一个统计:一平方千米的土地上,一年内从太阳得到的能量相当于燃烧108千克煤所产生的能量。那么105平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤?108 ×105=1013 (千克)(1) (-2)3×24(2) (x+y)3 (y+x) 2(3) (a-b)4(b-a) 3例2.计算:火眼金睛
1.下面的计算对不对?如果不对,怎样改正?
(1) a · a2= a2 ( ) (2 ) x2 ·y5 = xy7 ( )
(3) a +a2 = a3 ( ) (4)a3 · a3 = a9 ( )
(5)a3+a3 = a6 ( ) (6) a3 · a3 =a6 ( )
a · a2= a3 x2 · y5 = x2y5 a +a2 = a +a2 a3 · a3 =a6 a3+a3 = 2a3× × × ×√×你认为,用法则时应该注意些什么?2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .35623 23 3253622 × = 33 32 × ×=填空:
(1)xm+n= x( )·x ( ) (2) x3 ·x4( )=x10
(3)27 × 37= 3( ) ×37
(4)xm ·( )=x3m
(5) 如果8=2x,那么 x= ( )
(6)若am=5,an=6,则am+n= ( )能力挑战mx3 3x2mn3 30 认真思考,我也行!你的思维真灵活!例3.已知:am=2,an=3.
求 am+n 的值.解: am+n=am·an=2×3=6思考:am+1,am+n+3呢?拓展提高23 + 23=2 × 23= 2434 × 27=34 × 33=37 b2· b3+b · b4 =b5 + b5=2b5 计算:(结果用幂的形式表示)15.2.1 同底数幂的乘法49 ×77+6 ×74 ×75=72 ×77+6 ×79=79 +6 ×79=7 ×79=710=1011 =a5=x4m+1= b6 (2)a2 ·a3(3) xm x3m+1 (1)b5 · b (1) 105×1061y · y2 · y4
=y1+2+41(2)计算(5)练习(-3)3×(-3)2(3)y2n . yn+1(4) - a2 ·a3=(-3)5=y3n+1= -a5 am · an · ap = am+n+p (m、n、p都是正整数)=105+6 =a2+3=xm+3m+1=y7= b5+1 =-35(4)(-3)2 . (-3)2=(-3)2+2=(-3)4=34下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2) x5 ·x5 = x25 ( )
(3) b5 + b5 = b10 ( ) (4)y5 +2y5 = 3y10 ( )
﹒
(5) c · c3 = c3 ( ) (6) ﹙-2﹚3 · 24 = 27 ( )
b5 · b5= b10 b5 + b5 = 2b5 x5 · x5 = x10 y5 +2y5 =3y5 c · c3 = c4× × × ×××数学医院注意 am · an 与 am + an的区别﹙-2﹚3﹒24 =-27
注意 同底数幂相乘,底数不变,指数相加.注意 底数相同 注意 指数1不能忘 (-a)2 · (-a)3a2 · (-a)3变式:(-a)2 · a3-a2 · a3变式训练计算:a2· a3(-a2)· a3(n为正整数)=a2· a3=(-a)5=-a5=-a5=a5=-a5=-a2 · a3=-a5公式中的a可以表示数、字母、也可以表示式子
变式:变式训练计算:a2 · a3(n都为正整数)(x+y)2 (x+y)3(x+y)2(y+x)3(x-y)2(x-y)3(y-x)2(x-y)3(a-b)2=(b-a)2(a-b)2n=(b-a)2n=(x+y)5=(x+y)5=(x-y)5=(x-y)2(x-y)3=(x-y)5(y-x)2(x-y)3= — (y-x)2(y-x)3= — (y-x)5(a-b)3= — (b-a)3(a-b)2n-1= — (b-a)2n-1计算下列各式,结果用幂的形式表示.综合运用(1)(-7)3 · 73= - 73 · 73= - 73+3= - 76(2) x2 · (-x)2= x2 . x2= x2+2= x4(3)( a-b)· (b-a)3 = -( a-b)· (a-b)3 = -(a-b)4(4) x2 x4 + x3 x3 = x6 + x6= 2x6 注意: 把不同底数幂(互为相反数)化成同底数幂, 再利用法则计算.闯关游戏第一关: ① b5·b ② xm·x3m+1·x2第二关: ① (-5)2 ·5 3 ② (a-b) (a-b) 2 第三关: ① 10 3 ×10+100 ×10 2 ② x 3 ·xm -xm+3 第四关: ①3×27×9 = 3x,则 x = .
② (a-b) (b-a) 2(b-a ) = .
规则 ①完成上一关,才能进入下一关
②按要求完成第一、二两关就算冲关成功
③完成第三、四关的,将有机会获得本节课的闯关英雄称号。
求助方法:1.看书 2.同学合作探讨 3.请教老师公式中的a可以表示数、字母、也可以表示式子思考方法总结:①(-1)的奇数次幂为-1,(-1)的偶数次幂为1,在计算过程中要判断准确是奇数次幂还是偶数次幂;
②能够化成底数相同的幂尽量化成底数相同的幂进行
运算。课 堂 小 结同底数幂的乘法公式:
1.数学知识:2.数学思想:思维延伸
1已知xa=2,xb=3,求xa+b.
2已知x3·xa·x2a+1=x31,求a的值.综合拓展
已知2x=3,2y=6,2z=12,试写出x,y,z的关系式.
