15.1.3 积的乘方
图片预览







文档简介
课件24张PPT。15.1.3 积的乘方 1、叙述同底数幂乘法法则并用字母表示。2、叙述幂的乘方法则 并用字母表示。 语言叙述:同底数幂相乘,底数不变,指数相加。 字母表示:am·an=am+n ( m、n都为正整数)语言叙述:幂的乘方,底数不变,指数相乘。
字母表示:(am)n=amn (m,n都是正整数)
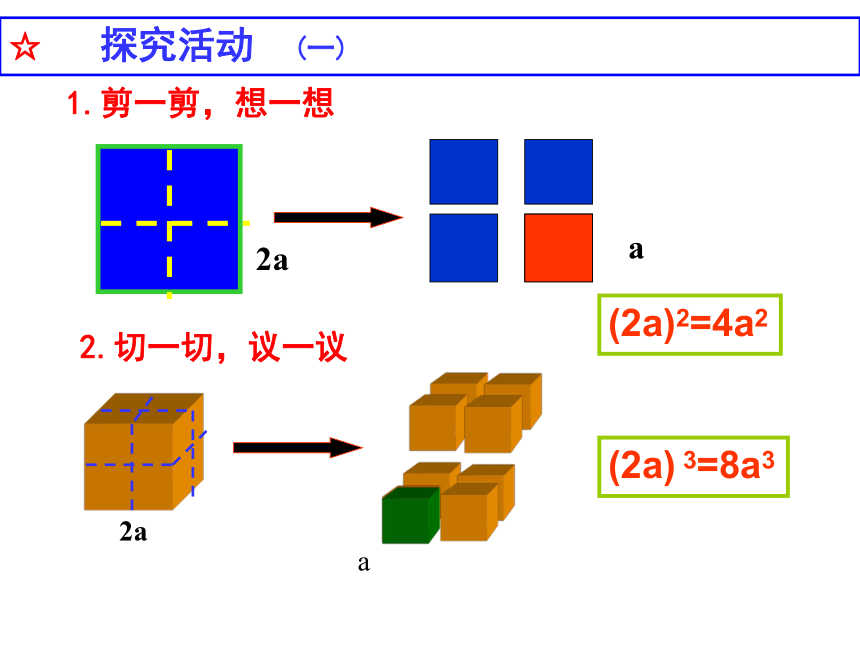
1.2.-1.剪一剪,想一想a2aa2.切一切,议一议☆ 探究活动 (一)(2a)2=4a2(2a) 3=8a3 2、比较下列各组算式的计算结果:
[2 ×(-3)]2 与 22 ×(-3)2 ;
[(-2)×(-3)]3与(-2)3 ×(-3)3
1、计算: (2×3)2与22 × 32,我们发现了什么? ∵ (2×3)2=62=36 ; 22 ×32=4×9=36
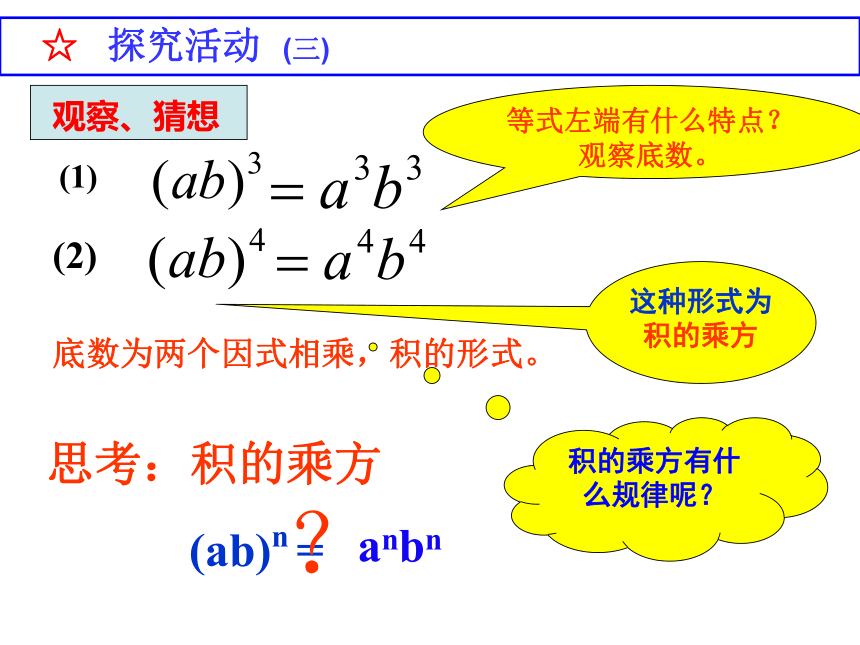
∴ (2×3)2 =22 × 32 都 相 等 ☆ 探究活动 (二) (1)(2) ☆ 探究活动 (三) (乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)同理:(1)(2)等式左端有什么特点?观察底数。底数为两个因式相乘,积的形式。这种形式为积的乘方 ☆ 探究活动 (三) 思考:积的乘方
(ab)n =anbn积的乘方有什么规律呢??探究=anbn(ab)n=anbn (n为正整数) 积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.(ab)n =?(ab)n=anbn (n为正整数) (1)(2a)3 (2)(-5b)3 (3)(xy2)2
(4)(-2x3)4(abc)n=?(5)(- ab2)3当三个或三个以上因式的积乘方时, 也具有这一性质.拓展积的乘方例如 (abc)n=anbncn例1.计算例2.计算下列各题:分析:以上各题底数都含有两个或两个以上的因式,我们运用积的乘方的运算性质。思考: (-a)n= -an(n为正整数)对吗?当n为奇数时, (-a)n= -an(n为正整数)
当n为偶数时, (-a)n=an(n为正整数)
(体现了分类的思想)例3. 地球可以近似地看做是球体,如果用V, r 分别代表球的体积和半径,那么 。 地球的半径约为6×103 千米,它的体积大约是多少立方千米?解:=×(6×103)363×109≈9.05×1011(千米11)注意
运算顺序 !让我们一起来例题解析计算:
(1)(3x)2 ; (2)(-2b)5 ; (3)(-2xy)4 ; (4)(3a2)n . =32x2 = 9x2 ;(1) (3x)2解:(2) (-2b)5= (-2)5b5= -32b25 ;(3) (-2xy)4 = (-2)4 x4 y4(4) (3a2)n = 3n (a2)n = 3n a2n 。=16x4 y4 ;试一试例题解析计算:
(1)(3xy)2 ; (2)(-2ab3 c2)5 ; (3)(-2×10 3)4 ; 试一试 最近我国发射主报奥运天气的气象卫星—风云2号D卫星,该气象卫星的形状为正方体。如果它的棱长是 4×103 mm,你能计算出它的体积吗?解: (4×103 )3=64×109=6.4×1010(mm3)
mm3答:卫星的体积为6.4×1010=43×109试一试1、口答
(1)(ab)6; (2)(-a)3; (3)(-2x)4 ;
(4)( ab)3 (5)(-xy)7; (6)(-3abc)2;
(7)[(-5)3]2 ; (8)[(-t)5]32、计算:
(1)(2×103)3 (2)(- xy2z3)2
(3)[-4(x-y)2]3 (4)(t-s)3(s-t)4练一练a6b6-a316x4-x7y79a2b2c256-t158×109错错错错错a2y±9x2y54618×105例2:
(1) a3 ·a4· a+(a2)4+(-2a4)2
(2) 2(x3)2 · x3-(3x3)3+(5x)2 ·x7
注意:运算顺序是先乘方,再乘除,
最后算加减。(3)(a2b6)n + 3(-ab3)2n + 2(-anb3n)2例3:用简便方法计算拓展训练 逆用公式
即
(1)212×(-0.5)10拓展训练
(5)若n是正整数,且 ,求 的值。(6)已知3x+1● 2x+1=62x-3,求x的值。-2a2b3369 数论被誉为“数学皇后”。而整除又是数论中的
重要内容。下面的一道关于整除问题,你会解决吗?
问题:数 (-0.125)16× 817 被哪一个整数整除?问题探究 用简便方法计算-8-1 ☆ 理一理今天学习的知识同底数幂乘法幂的乘方(m,n都是正整数)1.幂的三个运算性质积的乘方2.学习了一种常见的数学方法把某个式子看作一个数或字母。 (整体思路) 下面的计算对不对?如果不对,应当怎样改正?
①a3·a2=a6 ( ) ②b4·b4=2b4( )
③x5+x5=x10( ) ④y7·y=y8 ( )
⑤(a3)5=a8 ( ) ⑥a3·a5=a15( )
⑦(a2)3·a4=a9( ) ⑧(xy3)2=xy6( )
⑨(-2x)3=-2x3( )××=a5=b8×√×××××=2x5=a15=a8=a10=x2y6=-8x3数学医院
字母表示:(am)n=amn (m,n都是正整数)
1.2.-1.剪一剪,想一想a2aa2.切一切,议一议☆ 探究活动 (一)(2a)2=4a2(2a) 3=8a3 2、比较下列各组算式的计算结果:
[2 ×(-3)]2 与 22 ×(-3)2 ;
[(-2)×(-3)]3与(-2)3 ×(-3)3
1、计算: (2×3)2与22 × 32,我们发现了什么? ∵ (2×3)2=62=36 ; 22 ×32=4×9=36
∴ (2×3)2 =22 × 32 都 相 等 ☆ 探究活动 (二) (1)(2) ☆ 探究活动 (三) (乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)同理:(1)(2)等式左端有什么特点?观察底数。底数为两个因式相乘,积的形式。这种形式为积的乘方 ☆ 探究活动 (三) 思考:积的乘方
(ab)n =anbn积的乘方有什么规律呢??探究=anbn(ab)n=anbn (n为正整数) 积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.(ab)n =?(ab)n=anbn (n为正整数) (1)(2a)3 (2)(-5b)3 (3)(xy2)2
(4)(-2x3)4(abc)n=?(5)(- ab2)3当三个或三个以上因式的积乘方时, 也具有这一性质.拓展积的乘方例如 (abc)n=anbncn例1.计算例2.计算下列各题:分析:以上各题底数都含有两个或两个以上的因式,我们运用积的乘方的运算性质。思考: (-a)n= -an(n为正整数)对吗?当n为奇数时, (-a)n= -an(n为正整数)
当n为偶数时, (-a)n=an(n为正整数)
(体现了分类的思想)例3. 地球可以近似地看做是球体,如果用V, r 分别代表球的体积和半径,那么 。 地球的半径约为6×103 千米,它的体积大约是多少立方千米?解:=×(6×103)363×109≈9.05×1011(千米11)注意
运算顺序 !让我们一起来例题解析计算:
(1)(3x)2 ; (2)(-2b)5 ; (3)(-2xy)4 ; (4)(3a2)n . =32x2 = 9x2 ;(1) (3x)2解:(2) (-2b)5= (-2)5b5= -32b25 ;(3) (-2xy)4 = (-2)4 x4 y4(4) (3a2)n = 3n (a2)n = 3n a2n 。=16x4 y4 ;试一试例题解析计算:
(1)(3xy)2 ; (2)(-2ab3 c2)5 ; (3)(-2×10 3)4 ; 试一试 最近我国发射主报奥运天气的气象卫星—风云2号D卫星,该气象卫星的形状为正方体。如果它的棱长是 4×103 mm,你能计算出它的体积吗?解: (4×103 )3=64×109=6.4×1010(mm3)
mm3答:卫星的体积为6.4×1010=43×109试一试1、口答
(1)(ab)6; (2)(-a)3; (3)(-2x)4 ;
(4)( ab)3 (5)(-xy)7; (6)(-3abc)2;
(7)[(-5)3]2 ; (8)[(-t)5]32、计算:
(1)(2×103)3 (2)(- xy2z3)2
(3)[-4(x-y)2]3 (4)(t-s)3(s-t)4练一练a6b6-a316x4-x7y79a2b2c256-t158×109错错错错错a2y±9x2y54618×105例2:
(1) a3 ·a4· a+(a2)4+(-2a4)2
(2) 2(x3)2 · x3-(3x3)3+(5x)2 ·x7
注意:运算顺序是先乘方,再乘除,
最后算加减。(3)(a2b6)n + 3(-ab3)2n + 2(-anb3n)2例3:用简便方法计算拓展训练 逆用公式
即
(1)212×(-0.5)10拓展训练
(5)若n是正整数,且 ,求 的值。(6)已知3x+1● 2x+1=62x-3,求x的值。-2a2b3369 数论被誉为“数学皇后”。而整除又是数论中的
重要内容。下面的一道关于整除问题,你会解决吗?
问题:数 (-0.125)16× 817 被哪一个整数整除?问题探究 用简便方法计算-8-1 ☆ 理一理今天学习的知识同底数幂乘法幂的乘方(m,n都是正整数)1.幂的三个运算性质积的乘方2.学习了一种常见的数学方法把某个式子看作一个数或字母。 (整体思路) 下面的计算对不对?如果不对,应当怎样改正?
①a3·a2=a6 ( ) ②b4·b4=2b4( )
③x5+x5=x10( ) ④y7·y=y8 ( )
⑤(a3)5=a8 ( ) ⑥a3·a5=a15( )
⑦(a2)3·a4=a9( ) ⑧(xy3)2=xy6( )
⑨(-2x)3=-2x3( )××=a5=b8×√×××××=2x5=a15=a8=a10=x2y6=-8x3数学医院
