15.1.2幂的乘方
图片预览






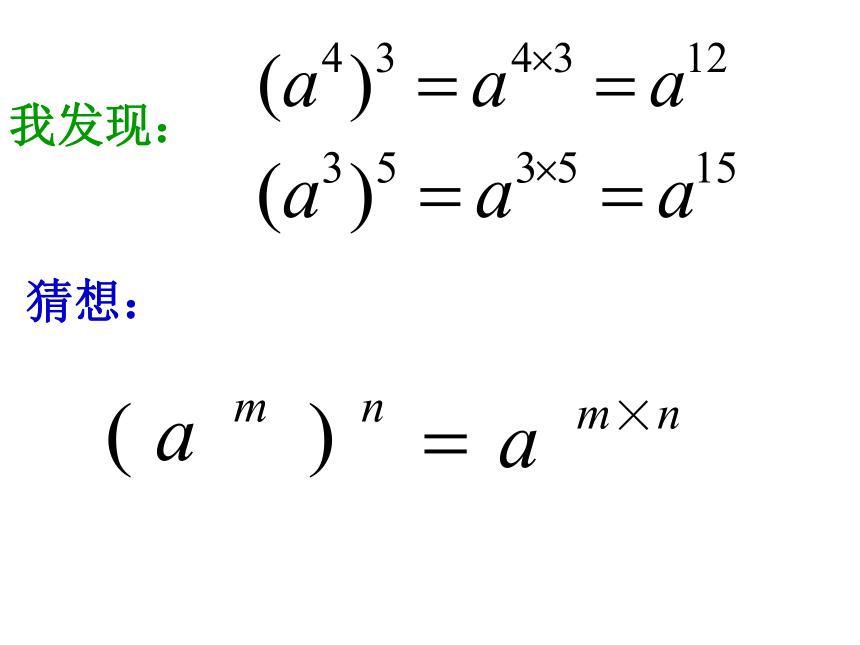


文档简介
课件24张PPT。15.2.2幂的乘方其中m , n都是正整数同底数幂的乘法am · an = am+n (m、n都是正整数)同底数幂相乘,底数不变,指数相加(1)(6)(3)(5)(2)(4)1.计算:25×5m·5n=5 2+m+n(7) x n · xn+1 (8) (x+y)3 · (x+y)4 解:x n · xn+1 =解:(x+y)3 · (x+y)4 =xn+(n+1)= x2n+1(x+y)3+4 =(x+y)7(9)(a-b)2n·(b-a)2n+1·(a-b)=-(a-b)4n+2或=-(b-a)4n+22.若7x=3,7y=5,求
(1) 7y+1 (2)和7x+y+1的值=.mmaa探 究=..333aaa思考:怎样计算
与==你有什么发现吗?
我发现:=猜想:猜想: (m、n都是正整数)(乘方的意义)(同底数幂乘法的法则)这种乘方的底数有什么特点?你能给这种乘方起个名称吗?证明:幂的乘方的运算公式幂的乘方,底数不变,指数相乘 。(m、n都是正整数)你能用文字语言叙述这个结论吗?想一想:
幂的乘方,底数变不变,指数应怎样计算?解:解:原式=例3.计算:
(1)[(-a)3]3+(a4)2(-a)解原式=(-a)9+a8(-a)
=-a9-a9
=-2a9(2)(-x3)2(-y)2+(-x2)3(-y2)解原式=x6y2+(-x6)(-y2)
=x6y2+x6y2
=2x6y2
你会吗?化成的形式.解:想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?乘法乘方不变不变指数
相加指数
相乘看谁说的好!下列各式对吗?请说出你的观点和理由:
(1) (a4)3=a7 ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( ) × × × ×1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x·(x5)m (D) x·x5·xmc变一变2.x14不可以写成( )
(A)x5· (x3)3 (B) (-x) ·(-x2) ·(-x3) ·(-x8)
(C)(x7)7 (D) x3·x4·x5·x2
C仔细想,你肯定会的!计算:(1)(2)(3)(4)(5)幂的乘方的逆运算:
(1)x13·x7=x( )=( )5=( )4=( )10
(2)a2m =( )2 =( )m (m为正整数)
20x4x5 x2ama2幂的乘方法则的逆用:其中m ,n都是正整数例4:求下列式子中的正整数x 4x=2x+1
1、已知3·9n=37,求:n的值.2、已知a3n=5,b2n=3,求:a6nb4n的值.3、设n为正整数,且x2n=2,求9(x3n)2 的值。
考 考 你想一想比较 355,444,533 的大小。解: ∵ 355 =(35)11 = 24311
444 =(44)11 = 25611
533 =(53)11 = 12511
∴ 444 >355 > 533请同学们小结这节课(1)本节课学习了幂的乘方(2)学习了一种常见的数学方法把某个式子看作一个 数或字母。 (整体思路) (3)今后学习中要注意灵活运用幂的乘方,注意符号的确定和逆向运用。幂的乘方,底数不变,指数相乘。 再见!
(1) 7y+1 (2)和7x+y+1的值=.mmaa探 究=..333aaa思考:怎样计算
与==你有什么发现吗?
我发现:=猜想:猜想: (m、n都是正整数)(乘方的意义)(同底数幂乘法的法则)这种乘方的底数有什么特点?你能给这种乘方起个名称吗?证明:幂的乘方的运算公式幂的乘方,底数不变,指数相乘 。(m、n都是正整数)你能用文字语言叙述这个结论吗?想一想:
幂的乘方,底数变不变,指数应怎样计算?解:解:原式=例3.计算:
(1)[(-a)3]3+(a4)2(-a)解原式=(-a)9+a8(-a)
=-a9-a9
=-2a9(2)(-x3)2(-y)2+(-x2)3(-y2)解原式=x6y2+(-x6)(-y2)
=x6y2+x6y2
=2x6y2
你会吗?化成的形式.解:想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?乘法乘方不变不变指数
相加指数
相乘看谁说的好!下列各式对吗?请说出你的观点和理由:
(1) (a4)3=a7 ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( ) × × × ×1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x·(x5)m (D) x·x5·xmc变一变2.x14不可以写成( )
(A)x5· (x3)3 (B) (-x) ·(-x2) ·(-x3) ·(-x8)
(C)(x7)7 (D) x3·x4·x5·x2
C仔细想,你肯定会的!计算:(1)(2)(3)(4)(5)幂的乘方的逆运算:
(1)x13·x7=x( )=( )5=( )4=( )10
(2)a2m =( )2 =( )m (m为正整数)
20x4x5 x2ama2幂的乘方法则的逆用:其中m ,n都是正整数例4:求下列式子中的正整数x 4x=2x+1
1、已知3·9n=37,求:n的值.2、已知a3n=5,b2n=3,求:a6nb4n的值.3、设n为正整数,且x2n=2,求9(x3n)2 的值。
考 考 你想一想比较 355,444,533 的大小。解: ∵ 355 =(35)11 = 24311
444 =(44)11 = 25611
533 =(53)11 = 12511
∴ 444 >355 > 533请同学们小结这节课(1)本节课学习了幂的乘方(2)学习了一种常见的数学方法把某个式子看作一个 数或字母。 (整体思路) (3)今后学习中要注意灵活运用幂的乘方,注意符号的确定和逆向运用。幂的乘方,底数不变,指数相乘。 再见!
