第七章 相交线与平行线 复习课件(共27张PPT)
文档属性
| 名称 | 第七章 相交线与平行线 复习课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
2025七年级数学下册期末复习
第七章
——相交线与平行线
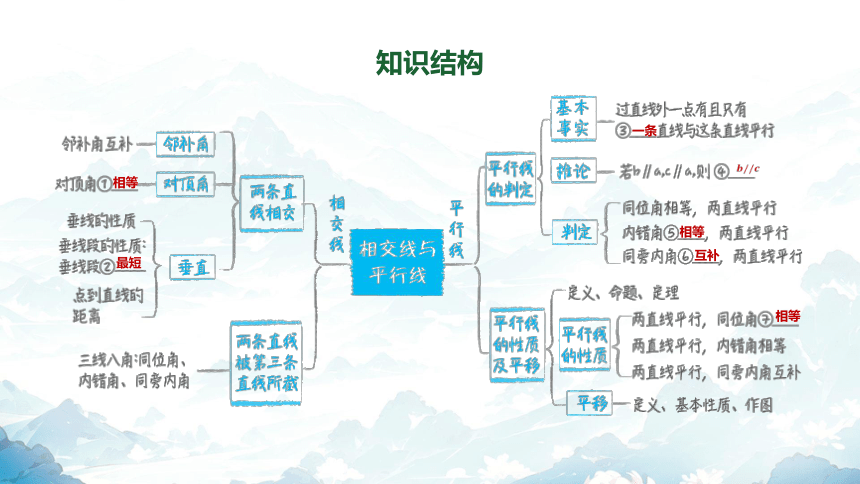
知识结构
相等
最短
一条
相等
互补
相等
达标训练
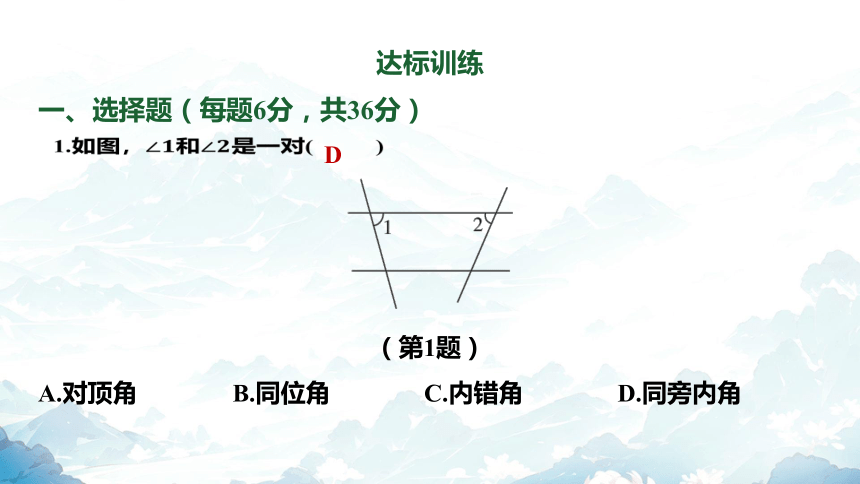
一、选择题(每题6分,共36分)
1.如图,和 是一对( )
D
(第1题)
A.对顶角 B.同位角 C.内错角 D.同旁内角
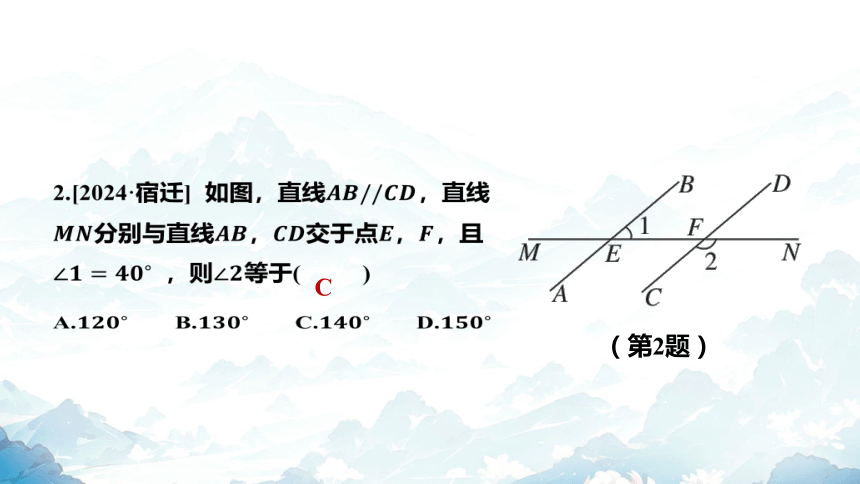
(第2题)
2.[2024·宿迁] 如图,直线 ,直线
分别与直线,交于点, ,且
,则 等于( )
C
A. B. C. D.
3.[2024· 福建] 在同一平面内,将直尺、含 角
的三角尺和木工角尺 按如图方式摆放,
若,则 的大小为( )
A
A. B. C. D.
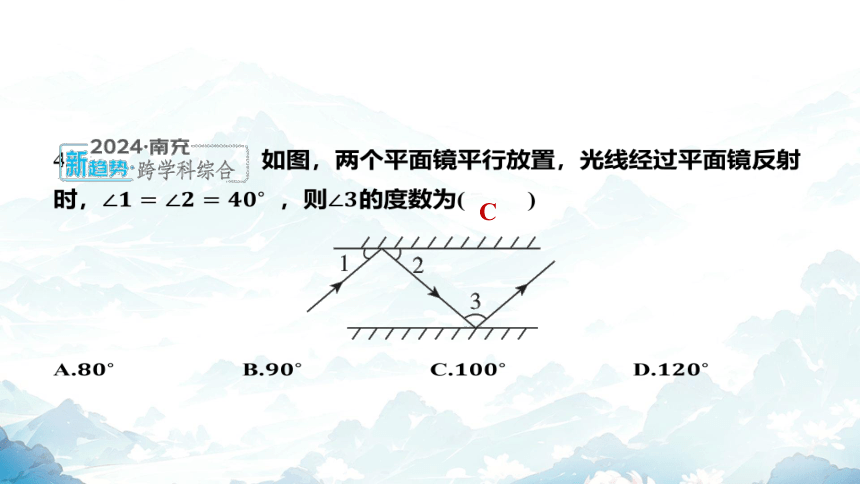
4. 如图,两个平面镜平行放置,光线经过平面镜反射
时, ,则 的度数为( )
C
A. B. C. D.
5. 学行线的判定后,小敏想出了过已知直线
外一点画这条直线的平行线的新方法,她是通过折一张纸得到的,如图,
从图中可知小敏画平行线的依据是( )
C
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.两直线平行,同旁内角互补
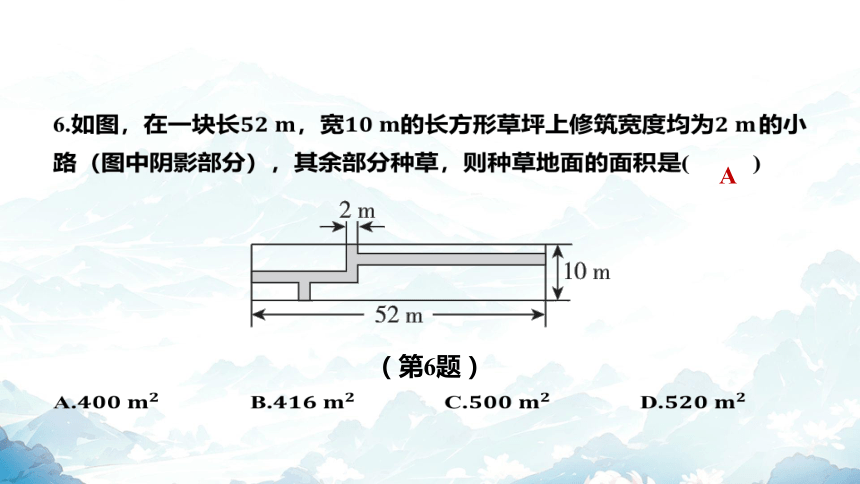
6.如图,在一块长,宽的长方形草坪上修筑宽度均为 的小
路(图中阴影部分),其余部分种草,则种草地面的面积是( )
A
(第6题)
A. B. C. D.
二、填空题(每题6分,共24分)
7.下列命题:
①对顶角相等;②若,,则 ;
③同位角相等;④互补的两个角是邻补角.
其中是真命题的个数为___.
2
8.如图,在三角形中,,,边上的高 ,若
点在边上(不含端点)移动,当 ___时长度最短.
(第8题)
(第9题)
9.[2024· 济宁] 任城区期末 如图,点 在
的延长线上,给出下列条件:
; ;
;④ ;
⑤ ;
⑥ ,
能判定 的条件有________.(填序号)
②④⑤
10.[2024· 无锡锡山区期中] 如图,, , ,
则____ .
27
(第10题)
[解析] 点拨:如图,作, ,
, .
, ,
.
, ,
,
.
三、解答题(共40分)
11.(10分)如图,直线,相交于点 ,过
点作射线,且 .
(1)若平分,求 的度数;
解: ,平分 ,
,
.
(2)若,求 的度数.
解: , .
, .
.
12.(14分)如图,方格纸中每个小正方形的边长都为1,在方格纸中将
三角形经过一次平移后得到三角形,图中标出了点 的对应
点 .
(1)请画出平移后的三角形 ;
解:如图,三角形 即为所求.
(2)连接, ,这两条线段之间的位置关系和数量关系是_______
______;
平行且相等
(3)求三角形 的面积.
解: .
13.(16分)如图是一种躺椅及其简
化结构示意图,扶手与底座
都平行于地面,前支架 与后
支架分别与交于点和点 ,
与交于点 ,
.
(1)试说明: ;
解:, ,
, .
(2)若平分, ,求扶手与靠背 的夹角
的度数.
解:与底座都平行于地面 ,
, .
, .
平分, ,
.
, .
素养发展
1. 【阅读探究】
(1)如图①,,,分别是,上的点,点在,
两平行线之间, , ,求 的度数.
解:如图①,过点作 ,
______.
, .
______.
, ,
.
(2)从上面的推理过程中,我们发现平行线可将和 “凑”在
一起,得出角之间的关系,使问题得以解决.进一步研究,我们可以发
现图①中,和 之间存在一定的数量关系,它们之间
的数量关系为________________________.
【方法应用】
(3)如图②,,,分别是,上的点,点在,
两平行线之间, , ,求 的度数.
解:如图,过点作 ,
,
.
, ,
,
.
【应用拓展】
(4)如图③,,,分别是,上的点,点在,
两平行线之间,作和的平分线,,交于点
(交点在两平行线,之间),若 ,则 的度数
为__________ (用含 的式子表示).
[解析] 点拨:根据(3)得 ,
,分别平分和 ,
,
.根据(1)得
,
.
2025七年级数学下册期末复习
第七章
——相交线与平行线
知识结构
相等
最短
一条
相等
互补
相等
达标训练
一、选择题(每题6分,共36分)
1.如图,和 是一对( )
D
(第1题)
A.对顶角 B.同位角 C.内错角 D.同旁内角
(第2题)
2.[2024·宿迁] 如图,直线 ,直线
分别与直线,交于点, ,且
,则 等于( )
C
A. B. C. D.
3.[2024· 福建] 在同一平面内,将直尺、含 角
的三角尺和木工角尺 按如图方式摆放,
若,则 的大小为( )
A
A. B. C. D.
4. 如图,两个平面镜平行放置,光线经过平面镜反射
时, ,则 的度数为( )
C
A. B. C. D.
5. 学行线的判定后,小敏想出了过已知直线
外一点画这条直线的平行线的新方法,她是通过折一张纸得到的,如图,
从图中可知小敏画平行线的依据是( )
C
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.两直线平行,同旁内角互补
6.如图,在一块长,宽的长方形草坪上修筑宽度均为 的小
路(图中阴影部分),其余部分种草,则种草地面的面积是( )
A
(第6题)
A. B. C. D.
二、填空题(每题6分,共24分)
7.下列命题:
①对顶角相等;②若,,则 ;
③同位角相等;④互补的两个角是邻补角.
其中是真命题的个数为___.
2
8.如图,在三角形中,,,边上的高 ,若
点在边上(不含端点)移动,当 ___时长度最短.
(第8题)
(第9题)
9.[2024· 济宁] 任城区期末 如图,点 在
的延长线上,给出下列条件:
; ;
;④ ;
⑤ ;
⑥ ,
能判定 的条件有________.(填序号)
②④⑤
10.[2024· 无锡锡山区期中] 如图,, , ,
则____ .
27
(第10题)
[解析] 点拨:如图,作, ,
, .
, ,
.
, ,
,
.
三、解答题(共40分)
11.(10分)如图,直线,相交于点 ,过
点作射线,且 .
(1)若平分,求 的度数;
解: ,平分 ,
,
.
(2)若,求 的度数.
解: , .
, .
.
12.(14分)如图,方格纸中每个小正方形的边长都为1,在方格纸中将
三角形经过一次平移后得到三角形,图中标出了点 的对应
点 .
(1)请画出平移后的三角形 ;
解:如图,三角形 即为所求.
(2)连接, ,这两条线段之间的位置关系和数量关系是_______
______;
平行且相等
(3)求三角形 的面积.
解: .
13.(16分)如图是一种躺椅及其简
化结构示意图,扶手与底座
都平行于地面,前支架 与后
支架分别与交于点和点 ,
与交于点 ,
.
(1)试说明: ;
解:, ,
, .
(2)若平分, ,求扶手与靠背 的夹角
的度数.
解:与底座都平行于地面 ,
, .
, .
平分, ,
.
, .
素养发展
1. 【阅读探究】
(1)如图①,,,分别是,上的点,点在,
两平行线之间, , ,求 的度数.
解:如图①,过点作 ,
______.
, .
______.
, ,
.
(2)从上面的推理过程中,我们发现平行线可将和 “凑”在
一起,得出角之间的关系,使问题得以解决.进一步研究,我们可以发
现图①中,和 之间存在一定的数量关系,它们之间
的数量关系为________________________.
【方法应用】
(3)如图②,,,分别是,上的点,点在,
两平行线之间, , ,求 的度数.
解:如图,过点作 ,
,
.
, ,
,
.
【应用拓展】
(4)如图③,,,分别是,上的点,点在,
两平行线之间,作和的平分线,,交于点
(交点在两平行线,之间),若 ,则 的度数
为__________ (用含 的式子表示).
[解析] 点拨:根据(3)得 ,
,分别平分和 ,
,
.根据(1)得
,
.
同课章节目录
