第八单元数学广角——搭配(二)(单元测试)(含解析)-2024-2025学年三年级下册数学(人教版)
文档属性
| 名称 | 第八单元数学广角——搭配(二)(单元测试)(含解析)-2024-2025学年三年级下册数学(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 248.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 14:49:32 | ||
图片预览




文档简介
第8单元复习
一、选择题
1.由2、5、9组成的没有重复数字的三位数共有( )个.
A.5 B.6 C.7
2.书架上有4本不同的科技书和5本不同的文艺书,张梦想借两本不同类的书,共有( )种不同的借法.
A.20 B.15 C.9
3.0时也叫( )。
A.中午12时 B.夜里12时 C.凌晨1时
4.3个好朋友见面,每两个人握1次手,一共要握( )次手.
A.6 B.4 C.3
5.用3、0、6这三个数字,能组成( )个不同的三位数。
A.2 B.4 C.6
6.用数字2、0、5、9可以组成( )个三位数.
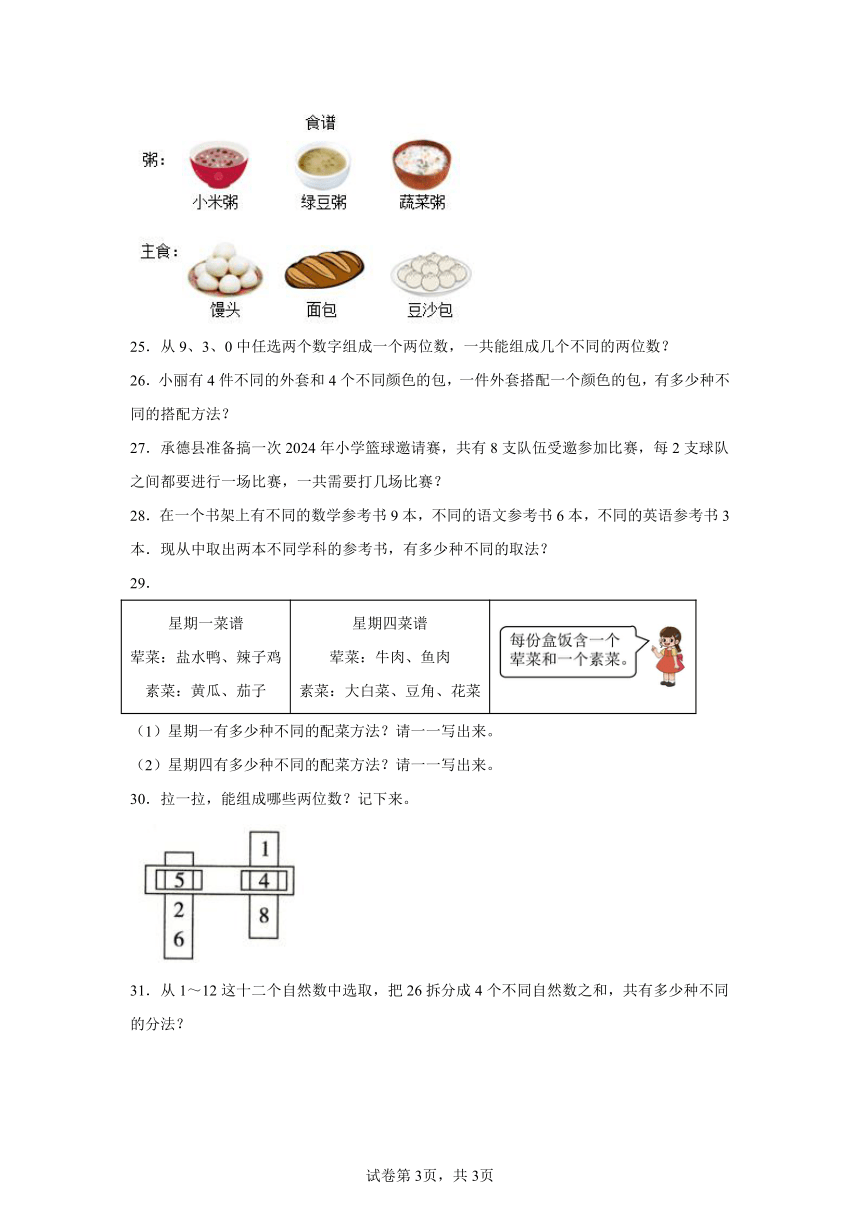
A.24 B.12 C.18
7.张阿姨有3件毛衣,3条牛仔裤,秋游时张阿姨可以有( )种着装方式。
A.3 B.6 C.9
8.两个0和两个7能组成( )个只读一个“零”的四位数。
A.1 B.2 C.3
二、填空题
9.芳有3件衬衫和4条裙子,她共有( )种不同的穿法。
10.小红、小明、小青每两人打一次电话,一共打( )次。
11.某公司准备给办公室购买一台电脑,共有3种显示器和2种主机可供选择,共有( )种搭配方案。
12.由5、6、7、8这四个数组成的能被2整除的四位数共有( )个.
13.王丽有4件上衣,3条裤子,一共有( )种不同的搭配方法。
14.用6、5、8三个数字可以组成( )个不同的三位数,其中最大的三位数是( ),最小的三位数是( ).
15.有1克、2克、5克的砝码各一个,选择其中的一个或者几个放在天平的一边,最多可以称出6种不同的质量。( )
16.志愿者要从学校到少年宫进行服务,如果只允许向东或向北走,一共有( )种不同的线路。
三、判断题
17.3个好朋友聚会,每两个人握一次手,一共要握6次。( )
18.从2、5、0、9中任选2个数字组成没有重复数字的两位数,有9种不同的组法。( )
19.从4、7、6里任选两个数字,可组成3个两位数。( )
20.妈妈向贝贝推荐了《少年智力开发报》、《中国少年报》、《小学生数学报》三种报纸。如果贝贝至少订阅一种,最多订阅三种,贝贝一共有7种不同的订阅方法( )。
21.体育课上,老师要从2名男生和4名女生中任意选出1名男生和1名女生为同学们做广播体操的示范动作,一共有6种不同的选法。( )
22.有5个小朋友,每两个小朋友握一次手,不能重复,那么她们一共握10次手。( )
四、作图题
23.用一顶帽子配一条围巾,一共有(种)搭配方法。请你在下图中表示出“4”的意义。
五、解答题
24.早餐时,粥和主食各取一种,共有( )种不同的搭配方法?连一连。
25.从9、3、0中任选两个数字组成一个两位数,一共能组成几个不同的两位数?
26.小丽有4件不同的外套和4个不同颜色的包,一件外套搭配一个颜色的包,有多少种不同的搭配方法?
27.承德县准备搞一次2024年小学篮球邀请赛,共有8支队伍受邀参加比赛,每2支球队之间都要进行一场比赛,一共需要打几场比赛?
28.在一个书架上有不同的数学参考书9本,不同的语文参考书6本,不同的英语参考书3本.现从中取出两本不同学科的参考书,有多少种不同的取法?
29.
星期一菜谱 荤菜:盐水鸭、辣子鸡 素菜:黄瓜、茄子 星期四菜谱 荤菜:牛肉、鱼肉 素菜:大白菜、豆角、花菜
(1)星期一有多少种不同的配菜方法?请一一写出来。
(2)星期四有多少种不同的配菜方法?请一一写出来。
30.拉一拉,能组成哪些两位数?记下来。
31.从1~12这十二个自然数中选取,把26拆分成4个不同自然数之和,共有多少种不同的分法?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【详解】先确定最前面的一个数,然后再确定后面两个数.
2.A
【详解】任选一本科技书,文艺书有五种选法,四本科技书就有4×5=20种借法.
3.B
4.C
【详解】(3﹣1)×3÷2
=6÷2
=3(次)
答:一共握3次手.
故选:C.
5.B
【分析】根据百位上数字的不同,我们可以将它们分成两类:(1)百位上是3时,能组成哪些三位数;(2)百位上是6时,能组成哪些三位数。
【详解】百位上是3时,组成的数有:306;360;
百位上是6时,组成的数有:603;630;
用3、0、6这三个数字,能组成4个不同的三位数。
故答案为:B
【点睛】此题考查了有关搭配的知识,对于这类问题,注意分类思想的运用,做到不重复不遗漏。
6.C
【详解】试题分析:先将能组成的三位数列举出来,再计算出一共有几个.
解:用2、0、5、9可以组成的三位数有:
205,209,250,259,290,295;
502,509,520,529,590,592;
902,905,920,925,950,952;
一共有18个.
故选C.
点评:解决本题时要注意0不能写在最高数位上.
7.C
【分析】由题意得,当张阿姨随便选其中一件毛衣时,她都可以选择3条牛仔裤中的任意一件进行搭配,有3种搭配方法。所以,3件毛衣和3条牛仔裤一共就有3×3=9(种)搭配方法。
【详解】3×3=9(种)
秋游时张阿姨可以有9种着装方式。
故答案为:C
8.B
【详解】两个0和两个7能组成的四位数有:7007、 7070、 7700;
其中7007读作“七千零七”,7070读作“七千零七十”。
9.12
【分析】1件衬衫可分别搭配4条裙子,小芳有3件衬衫,使用乘法计算即可。
【详解】根据分析可列式得:
3×4=12(种)
则小芳共有12种不同的穿法。
10.3
【分析】一共是3人,由于每个都要和另外的2个人通一次电话,一共要通:3×2=6(次);又因为两个人通一次电话,去掉重复计算的情况,实际只通:6÷2=3(次);由此求解。
【详解】3×(3-1)÷2
=3×2÷2
=6÷2
=3(次)
所以一共打了3次电话。
【点睛】本题是典型的握手问题,如果人数比较少,可以用枚举法解答;如果人数比较多,可以用公式:n(n-1)÷2解答。
11.6
【分析】当选择其中1种显示器时,主机有2种选法;而显示器有3种选法,因此共有(3×2)种搭配方案。
【详解】3×2=6(种),所以3种显示器和2种主机搭配,共有6种方案。
【点睛】熟练掌握搭配问题的计算是解答此题的关键。
12.12
【详解】试题分析:能被2整除的数都是偶数,那么这个四位数的个位上只能是6或8两个数中选择一个,有2种可能,十位上是剩下的3个中选择一个,有3种可能,百位上是剩下的2个数中选择1个是2种可能,千位上只有一种选择的方法;根据乘法原理,它们的积就是全部的选择方法.
解:2×3×2×1=12(个);
答:组成的能被2整除的四位数共有 12个.
故答案为12.
点评:本题抓住2的倍数的特点,找出根据数字的排列规律合理利用乘法原理进行计算求解.
13.12
【分析】根据题意可知:每件上衣都可以与三条裤子搭配,所以有3种穿法;同理,4件上衣搭配三条裤子一共就有4×3种不同的穿法。然后解答即可。
【详解】4×3=12(种),
一共有12种不同的搭配方法。
【点睛】本题考查了排列组合中的乘法原理,需要明确4件上衣和三条裤子各有几种选择,然后相乘即可求出问题。
14.6,865,568
【详解】试题分析:将组成的三位数写出即可得解.
解:用6、5、8三个数字可以组成有:658、685、568、586、865、856;共有6个.
最大的三位数有:865;最小的三位数有568.
故答案为6,865,568.
点评:在列举时要按顺序写,不要重复或漏写.
15.×
【分析】天平的一边可以放一个砝码、两个砝码、三个砝码,据此找到所有组合即可。
【详解】用一个砝码可以称出3种质量,两个砝码可以称出3种质量,三个砝码可以称出1种质量,共3+3+1=7(种)不同的质量,所以原题说法错误。
【点睛】本题考查了搭配问题,要按顺序找到所有组合的情况。
16.6
【分析】把每条路线用数字标出来,并且根据图来看总共有几条路线,列出来即可。注意只许向东或向北走,否则会有重复的情况。
【详解】
第一条路线:从学校出发走1→2→3→4→少年宫
第二条路线:从学校出发走1→8→11→4→少年宫
第三条路线:从学校出发走1→8→9→7→少年宫
第四条路线:从学校出发走5→10→11→4→少年宫
第五条路线:从学校出发走5→10→9→7→少年宫
第六条路线:从学校出发走5→6→12→7→少年宫
一共有6种不同的路线可走。
【点睛】解决本题要有顺序地写出路线,把走的路线列出来并且一定要注意不要走回头路。
17.×
【分析】每个人都要和另外的2个人握一次手,3个人共握3×2=6次,由于每两人握手,应算作一次手,去掉重复的情况,实际只握了6÷2=3次,据此解答。
【详解】(3-1)×3÷2
=6÷2
=3(次)
故答案为:×
【点睛】本题是典型的握手问题,如果人数比较少,可以用枚举法解答;如果人数比较多,可以用公式:n(n-1)÷2解答。
18.√
【分析】应用搭配的方法,将这些数字两两搭配组成一个两位数,注意按顺序搭配,以免遗漏,将搭配的两位数一一写出来即可。据此解答。
【详解】当2为十位上的数时,此时的两位数可以是:20;25;29;
当5为十位上的数时,此时的两位数可以是:50;52;59;
当9为十位上的数时,此时的两位数可以是:90;92;95;
因此用2、0、5、9可以组成9个没有重复数字的两位数。题目说法正确。
故答案为:√
【点睛】本题考查学生对搭配问题的掌握。解决此题时要注意0不能在首位。
19.×
【详解】从4、7、6里任选两个数字组成的两位数有:47、74、46、64、76、67;组成的两位数共有6个.故题干说法错误.
故答案为×
20.√
【分析】分订阅1种,订阅2种,订阅3种进行讨论,求出每种的各有几种订法,再相加。
【详解】(1)订阅1种时:
是从3种报纸中任选1种,有3种选法;
(2)订阅2种时:
是从3种报纸中选2种订阅,即选出1种不订阅的,也有3种选法;
(3)订阅3种时:
3本全选,有1种选法;
3+3+1=7(种)。
故答案为正确。
【点睛】本题分情况讨论后,每一种情况都可以看成简单的组合问题。
21.×
【分析】男生是2选1,所以有2种选法;女生是4选1,所以有4种选法;根据乘法原理,一共有2×4=8(种)不同的选法;据此判断。
【详解】2×4=8(种)
所以体育课上,老师要从2名男生和4名女生中任意选出1名男生和1名女生为同学们做广播体操的示范动作,一共有8种不同的选法;故原题说法错误。
故答案为:×
【点睛】本题考查了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×……×mn种不同的方法。
22.√
【分析】由于每个小朋友都要和另外的4个小朋友握一次手,一共要握了(5×4)次,即20次;又因为两个小朋友只握一次手,去掉重复计算的情况,实际只握了(20÷2)次,即10次;据此解答。
【详解】(5-1)×5÷2
=4×5÷2
=20÷2
=10(次)
所以,有5个小朋友,每两个小朋友握一次手,不能重复,那么她们一共握10次手。
故答案为:√
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况。
23.见详解
【分析】根据题意可知,每顶帽子都可以与2条裙子搭配,所以有2种搭配方法;每条围巾都可以与4顶帽子搭配,所以有4种搭配方法。则4顶帽子搭配2条围巾一共就有4×2种不同的穿法。
【详解】或
【点睛】本题考查了排列组合中的乘法原理,做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法,…,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×…×Mn种不同的方法。
24.9;见详解
【分析】每种主食都可以和每种粥搭配在一起,则小米粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。绿豆粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。蔬菜粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。则一共能3+3+3=9种不同的搭配方法。
【详解】早餐时,粥和主食各取一种,共有9种不同的搭配方法。
【点睛】本题考查搭配问题,采用枚举法解答。
25.4个
【分析】一个两位数,从右往左依次为个位,十位。要组成两位数时,十位不能是0,则分别将9和3放在十位,由此写出组成的数字,数出数量即可。
【详解】由分析可知:组成的两位数有93,90,30,39。
答:一共能组成4个不同的两位数。
26.16种
【分析】因为一个外套配一个颜色的包,有4个不同颜色的包,所以一件外套有4种不同的搭配,又因为有4个不同的外套,根据乘法原理可得:4×4=16(种),因此一共有16种不同的搭配。
【详解】由分析可得:
4×4=16(种)
答:有16种不同的搭配方法。
【点睛】熟练掌握搭配问题是解决此题的关键。
27.28场
【分析】由于每队都要和另外的7个队比赛一场,一共要比(8×7)场;又因为两队之间只比一场,去掉重复计算的情况,实际只比(8×7÷2)场。
【详解】8×(8-1)÷2
=8×7÷2
=56÷2
=28(场)
答:一共需要打28场比赛。
28.99种
【详解】试题分析:分情况讨论:
(1)选择拿语文书和数学书:
数学书有9种不同的拿法,语文书有6种不同的拿法,它们的积就是全部的拿法;
(2)选择语文书和英语书:
语文书有6种不同的拿法,英语书有3种不同的拿法,它们的积就是全部的拿法;
(3)选择数学书和英语书:
数学书有9种不同的拿法,英语书有3种不同的拿法,它们的积就是全部的拿法;
然后把这三种情况的数量加在一起即可.
解:9×6+9×3+6×3,
=54+27+18,
=81+18,
=99(种);
答:有99种不同的取法.
点评:本题先确定拿哪两种类型的书,再看这两种类型的书可以有多少种可能,进而求解.
29.(1)①盐水鸭、黄瓜;②盐水鸭、茄子;③辣子鸡、黄瓜;④辣子鸡、茄子;共4种。
(2)①牛肉、大白菜;②牛肉、豆角;③牛肉、花菜;④鱼肉、大白菜;⑤鱼肉、豆角;⑥鱼肉、花菜;共6种。
【分析】(1)星期一荤菜有2种,素菜有2种,当选择1种荤菜时,对应可以选择2种素菜,所以有2个2种选择方法,可以通过连线来搭配.,如下图;(2)星期四荤菜有2种,素菜有3种,当选择1种荤菜时,对应可以选择3种素菜,所以有2个3种选择方法,可以通过连线来搭配,如下图;
【详解】(1)根据分析可知,星期一有4种不同的配菜方法,分别是①盐水鸭、黄瓜;②盐水鸭、茄子;③辣子鸡、黄瓜;④辣子鸡、茄子;
(2)根据分析可知,星期四有6种不同的配菜方法,分别是①牛肉、大白菜;②牛肉、豆角;③牛肉、花菜;④鱼肉、大白菜;⑤鱼肉、豆角;⑥鱼肉、花菜。
30.51;54;58;21;24;28;61;64;68
【分析】根据有序搭配的思路,先确定十位是5,可以依次组成51、54、58;再确定十位是2,可以依次组成21、24、28;最后确定十位是6,可以依次组成61、64、68。据此解答。
【详解】根据分析可知:
能组成的两位数有:51;54;58;21;24;28;61;64;68
31.11种
【分析】不大于12的整数有1、2、3、4、5、6、7、8、9、10、11、12,从1~12中每次选出4个数,使这4个数的和是12,列举出各种可能的分法。
【详解】26=1+2+11+12
26=1+3+10+12
26=1+4+10+11
26=1+5+8+12
26=1+6+9+10
26=1+6+7+12
26=1+7+8+10
26=3+4+9+10
26=3+5+6+12
26=2+4+9+12
26=5+6+7+8
答:共有11种不同的分法。
【点睛】有序列举才能做到不重复、不遗漏。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.由2、5、9组成的没有重复数字的三位数共有( )个.
A.5 B.6 C.7
2.书架上有4本不同的科技书和5本不同的文艺书,张梦想借两本不同类的书,共有( )种不同的借法.
A.20 B.15 C.9
3.0时也叫( )。
A.中午12时 B.夜里12时 C.凌晨1时
4.3个好朋友见面,每两个人握1次手,一共要握( )次手.
A.6 B.4 C.3
5.用3、0、6这三个数字,能组成( )个不同的三位数。
A.2 B.4 C.6
6.用数字2、0、5、9可以组成( )个三位数.
A.24 B.12 C.18
7.张阿姨有3件毛衣,3条牛仔裤,秋游时张阿姨可以有( )种着装方式。
A.3 B.6 C.9
8.两个0和两个7能组成( )个只读一个“零”的四位数。
A.1 B.2 C.3
二、填空题
9.芳有3件衬衫和4条裙子,她共有( )种不同的穿法。
10.小红、小明、小青每两人打一次电话,一共打( )次。
11.某公司准备给办公室购买一台电脑,共有3种显示器和2种主机可供选择,共有( )种搭配方案。
12.由5、6、7、8这四个数组成的能被2整除的四位数共有( )个.
13.王丽有4件上衣,3条裤子,一共有( )种不同的搭配方法。
14.用6、5、8三个数字可以组成( )个不同的三位数,其中最大的三位数是( ),最小的三位数是( ).
15.有1克、2克、5克的砝码各一个,选择其中的一个或者几个放在天平的一边,最多可以称出6种不同的质量。( )
16.志愿者要从学校到少年宫进行服务,如果只允许向东或向北走,一共有( )种不同的线路。
三、判断题
17.3个好朋友聚会,每两个人握一次手,一共要握6次。( )
18.从2、5、0、9中任选2个数字组成没有重复数字的两位数,有9种不同的组法。( )
19.从4、7、6里任选两个数字,可组成3个两位数。( )
20.妈妈向贝贝推荐了《少年智力开发报》、《中国少年报》、《小学生数学报》三种报纸。如果贝贝至少订阅一种,最多订阅三种,贝贝一共有7种不同的订阅方法( )。
21.体育课上,老师要从2名男生和4名女生中任意选出1名男生和1名女生为同学们做广播体操的示范动作,一共有6种不同的选法。( )
22.有5个小朋友,每两个小朋友握一次手,不能重复,那么她们一共握10次手。( )
四、作图题
23.用一顶帽子配一条围巾,一共有(种)搭配方法。请你在下图中表示出“4”的意义。
五、解答题
24.早餐时,粥和主食各取一种,共有( )种不同的搭配方法?连一连。
25.从9、3、0中任选两个数字组成一个两位数,一共能组成几个不同的两位数?
26.小丽有4件不同的外套和4个不同颜色的包,一件外套搭配一个颜色的包,有多少种不同的搭配方法?
27.承德县准备搞一次2024年小学篮球邀请赛,共有8支队伍受邀参加比赛,每2支球队之间都要进行一场比赛,一共需要打几场比赛?
28.在一个书架上有不同的数学参考书9本,不同的语文参考书6本,不同的英语参考书3本.现从中取出两本不同学科的参考书,有多少种不同的取法?
29.
星期一菜谱 荤菜:盐水鸭、辣子鸡 素菜:黄瓜、茄子 星期四菜谱 荤菜:牛肉、鱼肉 素菜:大白菜、豆角、花菜
(1)星期一有多少种不同的配菜方法?请一一写出来。
(2)星期四有多少种不同的配菜方法?请一一写出来。
30.拉一拉,能组成哪些两位数?记下来。
31.从1~12这十二个自然数中选取,把26拆分成4个不同自然数之和,共有多少种不同的分法?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【详解】先确定最前面的一个数,然后再确定后面两个数.
2.A
【详解】任选一本科技书,文艺书有五种选法,四本科技书就有4×5=20种借法.
3.B
4.C
【详解】(3﹣1)×3÷2
=6÷2
=3(次)
答:一共握3次手.
故选:C.
5.B
【分析】根据百位上数字的不同,我们可以将它们分成两类:(1)百位上是3时,能组成哪些三位数;(2)百位上是6时,能组成哪些三位数。
【详解】百位上是3时,组成的数有:306;360;
百位上是6时,组成的数有:603;630;
用3、0、6这三个数字,能组成4个不同的三位数。
故答案为:B
【点睛】此题考查了有关搭配的知识,对于这类问题,注意分类思想的运用,做到不重复不遗漏。
6.C
【详解】试题分析:先将能组成的三位数列举出来,再计算出一共有几个.
解:用2、0、5、9可以组成的三位数有:
205,209,250,259,290,295;
502,509,520,529,590,592;
902,905,920,925,950,952;
一共有18个.
故选C.
点评:解决本题时要注意0不能写在最高数位上.
7.C
【分析】由题意得,当张阿姨随便选其中一件毛衣时,她都可以选择3条牛仔裤中的任意一件进行搭配,有3种搭配方法。所以,3件毛衣和3条牛仔裤一共就有3×3=9(种)搭配方法。
【详解】3×3=9(种)
秋游时张阿姨可以有9种着装方式。
故答案为:C
8.B
【详解】两个0和两个7能组成的四位数有:7007、 7070、 7700;
其中7007读作“七千零七”,7070读作“七千零七十”。
9.12
【分析】1件衬衫可分别搭配4条裙子,小芳有3件衬衫,使用乘法计算即可。
【详解】根据分析可列式得:
3×4=12(种)
则小芳共有12种不同的穿法。
10.3
【分析】一共是3人,由于每个都要和另外的2个人通一次电话,一共要通:3×2=6(次);又因为两个人通一次电话,去掉重复计算的情况,实际只通:6÷2=3(次);由此求解。
【详解】3×(3-1)÷2
=3×2÷2
=6÷2
=3(次)
所以一共打了3次电话。
【点睛】本题是典型的握手问题,如果人数比较少,可以用枚举法解答;如果人数比较多,可以用公式:n(n-1)÷2解答。
11.6
【分析】当选择其中1种显示器时,主机有2种选法;而显示器有3种选法,因此共有(3×2)种搭配方案。
【详解】3×2=6(种),所以3种显示器和2种主机搭配,共有6种方案。
【点睛】熟练掌握搭配问题的计算是解答此题的关键。
12.12
【详解】试题分析:能被2整除的数都是偶数,那么这个四位数的个位上只能是6或8两个数中选择一个,有2种可能,十位上是剩下的3个中选择一个,有3种可能,百位上是剩下的2个数中选择1个是2种可能,千位上只有一种选择的方法;根据乘法原理,它们的积就是全部的选择方法.
解:2×3×2×1=12(个);
答:组成的能被2整除的四位数共有 12个.
故答案为12.
点评:本题抓住2的倍数的特点,找出根据数字的排列规律合理利用乘法原理进行计算求解.
13.12
【分析】根据题意可知:每件上衣都可以与三条裤子搭配,所以有3种穿法;同理,4件上衣搭配三条裤子一共就有4×3种不同的穿法。然后解答即可。
【详解】4×3=12(种),
一共有12种不同的搭配方法。
【点睛】本题考查了排列组合中的乘法原理,需要明确4件上衣和三条裤子各有几种选择,然后相乘即可求出问题。
14.6,865,568
【详解】试题分析:将组成的三位数写出即可得解.
解:用6、5、8三个数字可以组成有:658、685、568、586、865、856;共有6个.
最大的三位数有:865;最小的三位数有568.
故答案为6,865,568.
点评:在列举时要按顺序写,不要重复或漏写.
15.×
【分析】天平的一边可以放一个砝码、两个砝码、三个砝码,据此找到所有组合即可。
【详解】用一个砝码可以称出3种质量,两个砝码可以称出3种质量,三个砝码可以称出1种质量,共3+3+1=7(种)不同的质量,所以原题说法错误。
【点睛】本题考查了搭配问题,要按顺序找到所有组合的情况。
16.6
【分析】把每条路线用数字标出来,并且根据图来看总共有几条路线,列出来即可。注意只许向东或向北走,否则会有重复的情况。
【详解】
第一条路线:从学校出发走1→2→3→4→少年宫
第二条路线:从学校出发走1→8→11→4→少年宫
第三条路线:从学校出发走1→8→9→7→少年宫
第四条路线:从学校出发走5→10→11→4→少年宫
第五条路线:从学校出发走5→10→9→7→少年宫
第六条路线:从学校出发走5→6→12→7→少年宫
一共有6种不同的路线可走。
【点睛】解决本题要有顺序地写出路线,把走的路线列出来并且一定要注意不要走回头路。
17.×
【分析】每个人都要和另外的2个人握一次手,3个人共握3×2=6次,由于每两人握手,应算作一次手,去掉重复的情况,实际只握了6÷2=3次,据此解答。
【详解】(3-1)×3÷2
=6÷2
=3(次)
故答案为:×
【点睛】本题是典型的握手问题,如果人数比较少,可以用枚举法解答;如果人数比较多,可以用公式:n(n-1)÷2解答。
18.√
【分析】应用搭配的方法,将这些数字两两搭配组成一个两位数,注意按顺序搭配,以免遗漏,将搭配的两位数一一写出来即可。据此解答。
【详解】当2为十位上的数时,此时的两位数可以是:20;25;29;
当5为十位上的数时,此时的两位数可以是:50;52;59;
当9为十位上的数时,此时的两位数可以是:90;92;95;
因此用2、0、5、9可以组成9个没有重复数字的两位数。题目说法正确。
故答案为:√
【点睛】本题考查学生对搭配问题的掌握。解决此题时要注意0不能在首位。
19.×
【详解】从4、7、6里任选两个数字组成的两位数有:47、74、46、64、76、67;组成的两位数共有6个.故题干说法错误.
故答案为×
20.√
【分析】分订阅1种,订阅2种,订阅3种进行讨论,求出每种的各有几种订法,再相加。
【详解】(1)订阅1种时:
是从3种报纸中任选1种,有3种选法;
(2)订阅2种时:
是从3种报纸中选2种订阅,即选出1种不订阅的,也有3种选法;
(3)订阅3种时:
3本全选,有1种选法;
3+3+1=7(种)。
故答案为正确。
【点睛】本题分情况讨论后,每一种情况都可以看成简单的组合问题。
21.×
【分析】男生是2选1,所以有2种选法;女生是4选1,所以有4种选法;根据乘法原理,一共有2×4=8(种)不同的选法;据此判断。
【详解】2×4=8(种)
所以体育课上,老师要从2名男生和4名女生中任意选出1名男生和1名女生为同学们做广播体操的示范动作,一共有8种不同的选法;故原题说法错误。
故答案为:×
【点睛】本题考查了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×……×mn种不同的方法。
22.√
【分析】由于每个小朋友都要和另外的4个小朋友握一次手,一共要握了(5×4)次,即20次;又因为两个小朋友只握一次手,去掉重复计算的情况,实际只握了(20÷2)次,即10次;据此解答。
【详解】(5-1)×5÷2
=4×5÷2
=20÷2
=10(次)
所以,有5个小朋友,每两个小朋友握一次手,不能重复,那么她们一共握10次手。
故答案为:√
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况。
23.见详解
【分析】根据题意可知,每顶帽子都可以与2条裙子搭配,所以有2种搭配方法;每条围巾都可以与4顶帽子搭配,所以有4种搭配方法。则4顶帽子搭配2条围巾一共就有4×2种不同的穿法。
【详解】或
【点睛】本题考查了排列组合中的乘法原理,做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法,…,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×…×Mn种不同的方法。
24.9;见详解
【分析】每种主食都可以和每种粥搭配在一起,则小米粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。绿豆粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。蔬菜粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。则一共能3+3+3=9种不同的搭配方法。
【详解】早餐时,粥和主食各取一种,共有9种不同的搭配方法。
【点睛】本题考查搭配问题,采用枚举法解答。
25.4个
【分析】一个两位数,从右往左依次为个位,十位。要组成两位数时,十位不能是0,则分别将9和3放在十位,由此写出组成的数字,数出数量即可。
【详解】由分析可知:组成的两位数有93,90,30,39。
答:一共能组成4个不同的两位数。
26.16种
【分析】因为一个外套配一个颜色的包,有4个不同颜色的包,所以一件外套有4种不同的搭配,又因为有4个不同的外套,根据乘法原理可得:4×4=16(种),因此一共有16种不同的搭配。
【详解】由分析可得:
4×4=16(种)
答:有16种不同的搭配方法。
【点睛】熟练掌握搭配问题是解决此题的关键。
27.28场
【分析】由于每队都要和另外的7个队比赛一场,一共要比(8×7)场;又因为两队之间只比一场,去掉重复计算的情况,实际只比(8×7÷2)场。
【详解】8×(8-1)÷2
=8×7÷2
=56÷2
=28(场)
答:一共需要打28场比赛。
28.99种
【详解】试题分析:分情况讨论:
(1)选择拿语文书和数学书:
数学书有9种不同的拿法,语文书有6种不同的拿法,它们的积就是全部的拿法;
(2)选择语文书和英语书:
语文书有6种不同的拿法,英语书有3种不同的拿法,它们的积就是全部的拿法;
(3)选择数学书和英语书:
数学书有9种不同的拿法,英语书有3种不同的拿法,它们的积就是全部的拿法;
然后把这三种情况的数量加在一起即可.
解:9×6+9×3+6×3,
=54+27+18,
=81+18,
=99(种);
答:有99种不同的取法.
点评:本题先确定拿哪两种类型的书,再看这两种类型的书可以有多少种可能,进而求解.
29.(1)①盐水鸭、黄瓜;②盐水鸭、茄子;③辣子鸡、黄瓜;④辣子鸡、茄子;共4种。
(2)①牛肉、大白菜;②牛肉、豆角;③牛肉、花菜;④鱼肉、大白菜;⑤鱼肉、豆角;⑥鱼肉、花菜;共6种。
【分析】(1)星期一荤菜有2种,素菜有2种,当选择1种荤菜时,对应可以选择2种素菜,所以有2个2种选择方法,可以通过连线来搭配.,如下图;(2)星期四荤菜有2种,素菜有3种,当选择1种荤菜时,对应可以选择3种素菜,所以有2个3种选择方法,可以通过连线来搭配,如下图;
【详解】(1)根据分析可知,星期一有4种不同的配菜方法,分别是①盐水鸭、黄瓜;②盐水鸭、茄子;③辣子鸡、黄瓜;④辣子鸡、茄子;
(2)根据分析可知,星期四有6种不同的配菜方法,分别是①牛肉、大白菜;②牛肉、豆角;③牛肉、花菜;④鱼肉、大白菜;⑤鱼肉、豆角;⑥鱼肉、花菜。
30.51;54;58;21;24;28;61;64;68
【分析】根据有序搭配的思路,先确定十位是5,可以依次组成51、54、58;再确定十位是2,可以依次组成21、24、28;最后确定十位是6,可以依次组成61、64、68。据此解答。
【详解】根据分析可知:
能组成的两位数有:51;54;58;21;24;28;61;64;68
31.11种
【分析】不大于12的整数有1、2、3、4、5、6、7、8、9、10、11、12,从1~12中每次选出4个数,使这4个数的和是12,列举出各种可能的分法。
【详解】26=1+2+11+12
26=1+3+10+12
26=1+4+10+11
26=1+5+8+12
26=1+6+9+10
26=1+6+7+12
26=1+7+8+10
26=3+4+9+10
26=3+5+6+12
26=2+4+9+12
26=5+6+7+8
答:共有11种不同的分法。
【点睛】有序列举才能做到不重复、不遗漏。
答案第1页,共2页
答案第1页,共2页
