直线与圆的位置关系

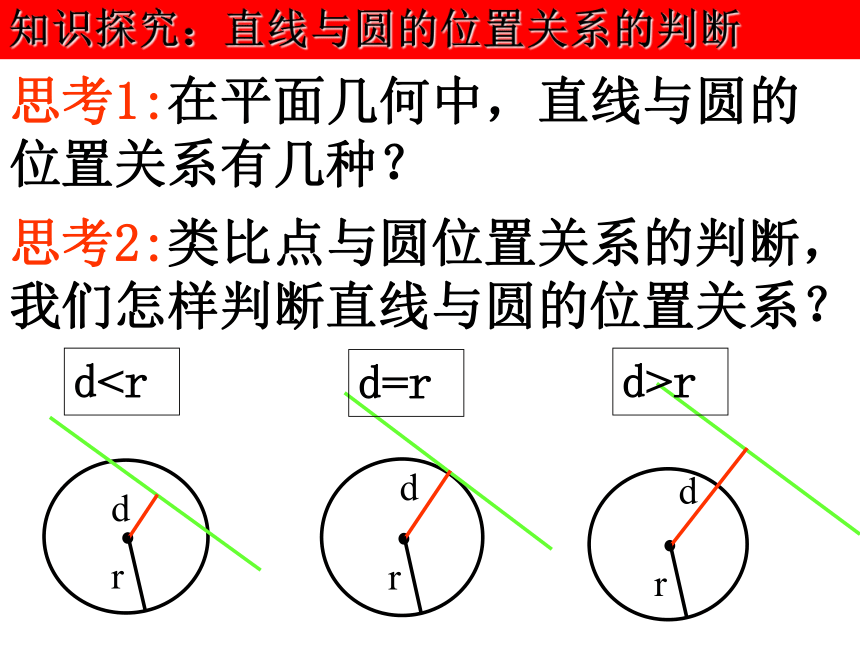
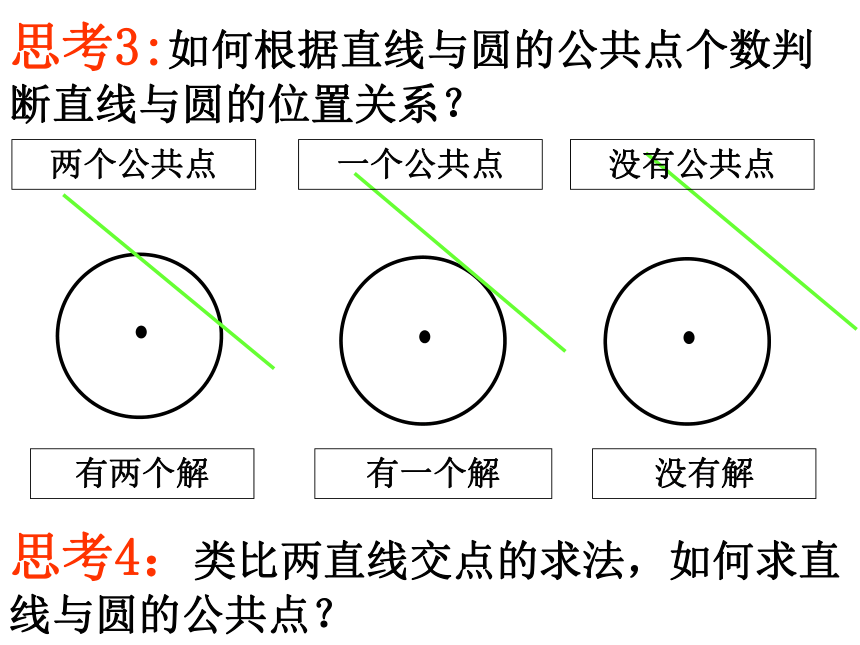
课件20张PPT。直线与圆的位置关系 在2009年08月08日台凤莫拉克袭击宝岛台湾时，一艘轮船在沿直线返回泉州港口的途中，接到气象台的台风预报：台风中心位于轮船正西70km处，受影响的范围是半径长为30km的圆形区域．已知泉州港口位于台风中心正北40km处，如果这艘轮船不改变航线，那么它是否会受到台风莫拉克的影响？ 轮船新情景问题：实例引入知识探究：直线与圆的位置关系的判断 思考1:在平面几何中，直线与圆的位置关系有几种？ 思考2:类比点与圆位置关系的判断，我们怎样判断直线与圆的位置关系？ dr思考3:如何根据直线与圆的公共点个数判断直线与圆的位置关系？ 两个公共点一个公共点没有公共点思考4：类比两直线交点的求法，如何求直线与圆的公共点？有两个解有一个解没有解 方法二:
根据直线与圆的联立方程组的公
共解个数判断； （代数法） 方法一:
根据圆心到直线的距离与圆半径
的大小关系判断.（几何法）判断直线与圆的位置关系的方法：理论迁移：典例精析 例1 已知直线l：3x＋y－6＝0和圆心为C的圆x2＋y2－2y－4＝0，判断直线l与圆的位置关系；如果相交，求两个交点的坐标． 分析：方法一：判断直线l与圆C的位置关系，就是看由它们的方程组成的方程有无实数解；方法二：可以依据圆心C到直线l的距离与半径长的关系，判断直线与圆的位置关系。
所以，直线 l 与圆有两个交点，它们的坐把 代入方程①，得 ；把 代入方程① ，得 ． 标分别是： A（2，0），B（1，3）例题解析：解法一：由直线L与圆的方程，得解得：消去y ，得两种解法都运用了数形结合思想、坐标法运算思想 例2 过点M(－3，－3)的直线l被圆x2＋y2＋4y－21=0所截得的弦长为 ，求直线l的方程. 已知直线过定点，如何求直线方程？解：将圆的方程写成标准形式，得：即圆心到所求直线的距离为 ．如图，因为直线l 被圆所截得的弦长是 ，所以弦心距为例题解析：因为直线l 过点 ，所以可设所求直线l 的方程为：即：根据点到直线的距离公式，得到圆心到直线l
的距离：因此：即：两边平方，并整理得到：解得： 所以，所求直线l有两条，它们的方程分别为：或即:你还有其他的思路吗？本题也运用了数形结合思想、坐标法运算思想规律总结：直线与圆的位置关系判断方法及步骤一、几何法。主要步骤：利用点到直线的距离公式求圆心到直线的距离。作判断: （1）当d>r时，直线与圆相离；
（2）当d=r时，直线与圆相切;
（3）当d（1）当Δ<0时,直线与圆相离；
（2）当Δ=0时, 直线与圆相切 ;
（3）当Δ>0时,直线与圆相交。二、代数方法。主要步骤：利用消元法，得到关于另一个元的一元二次方程由直线l与圆的方程联立；得：问题回顾：用X代入法消去Y，得：因为所以，直线l与圆没有交点，故轮船不会受到台风莫拉克的影响解法1：代数方法 为解决这个问题，我们以台风中心为原点 O，东西方向为 x 轴，建立如图所示的直角坐标系，其中取 10km 为单位长度．受台风影响的圆区域所对应的圆心为O的圆轮船航线所在直线 l 的方程为：4X+7Y-28=0的方程为:X2+Y2=9解析：解法2：几何方法 过点P（1，-1）的直线l与圆M:(x-3)2+(y-4)2=4
（1）当直线和圆相切时，求切线方程和切线长;
（2）若直线的斜率为2，求直线被圆截得的弦AB的长;
（3）若圆的方程加上条件x≥3，直线与圆有且只有一个交点，求直线的斜率的取值范围.培养学生用数形结合的思想
优化解题程序，用运动变化的观
点分析解决问题的能力。举一反三：课堂小结：直线l与圆C的方程组成的方程组是否有解，有几个解．判断圆C的圆心到直线l的距离d与圆的半径r的关系（大于、小于、等于）．判断直线与圆的位置关系三种关系；两种方法；两种思想。作业布置：必做部分：习题4.2 A组 1、 2。
选做部分：（1）已知圆 与直线
相交于 两点， 为坐标原点，
若 ⊥ ，求 的值。（2）已知圆方程x2+y2=2,直线y=x+b，当b为
何值时，圆与直线相交、相切、相离. 放飞心情，成就梦想！再见巨野县实验中学
制作人：刘士臣