直线的倾斜角与斜率
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
直线的倾斜角和斜率(1)
巨野县实验中学 刘士臣
学习目标:
1.正确理解直线的倾斜角和斜率的概念.2.理解直线的倾斜角的唯一性.
3.理解直线的斜率的存在性. 4.斜率公式的推导过程,掌握过两点的直线的斜率公式.
学习重点:直线的倾斜角、斜率的概念,用代数方法刻画直线斜率的过程。
学习难点: 直线的倾斜角与斜率之间的关系.
学习过程:
一、创设情景
上海浦东新区气势宏伟的斜拉桥
二、新知探究
探究(一)直线的倾斜角
请同学们在右下平面直角坐标系中过原点o任作一直线,并与其他同学所作直线相比较,直线的位置是否相同,若不同请指出不同之处。若相同请说明理由。
倾斜角的定义:
倾斜角的范围:
思考:不同的直线其倾斜角一定不相同吗?
确定直线位置的几何要素:
探究(二)直线的斜率:
思考1:初中学过的“坡度(比)”是什么含义?它与这条直线的倾斜角之间有什么关系?它能否表示直线的倾斜程度?
斜率的定义:
思考2::当倾斜角α=0o,30o,45o,60o时,这条直线的斜率分别等于多少?
思考3::当α是锐角时,有tan(180o-α)=-tanα. 那么当倾斜角α=120o,135o,150o时,这条直线的斜率分别等于多少?
思考4:当倾斜角分别为零角、锐角、直角、钝角的直线的斜率的取值范围分别是什么?
倾斜角
斜率
思考5:斜率相等的直线其倾斜角相等吗?
练习: 判断正误:
①直线的倾斜角为,则直线的斜率为, ( )
②任一条直线都有倾斜角,也都有斜率, ( )③因为平行于轴的直线的斜率不存在,所以平行于轴的直线的倾斜角不存在, ( )
④两直线的斜率相等,它们的倾斜角相等, ( )
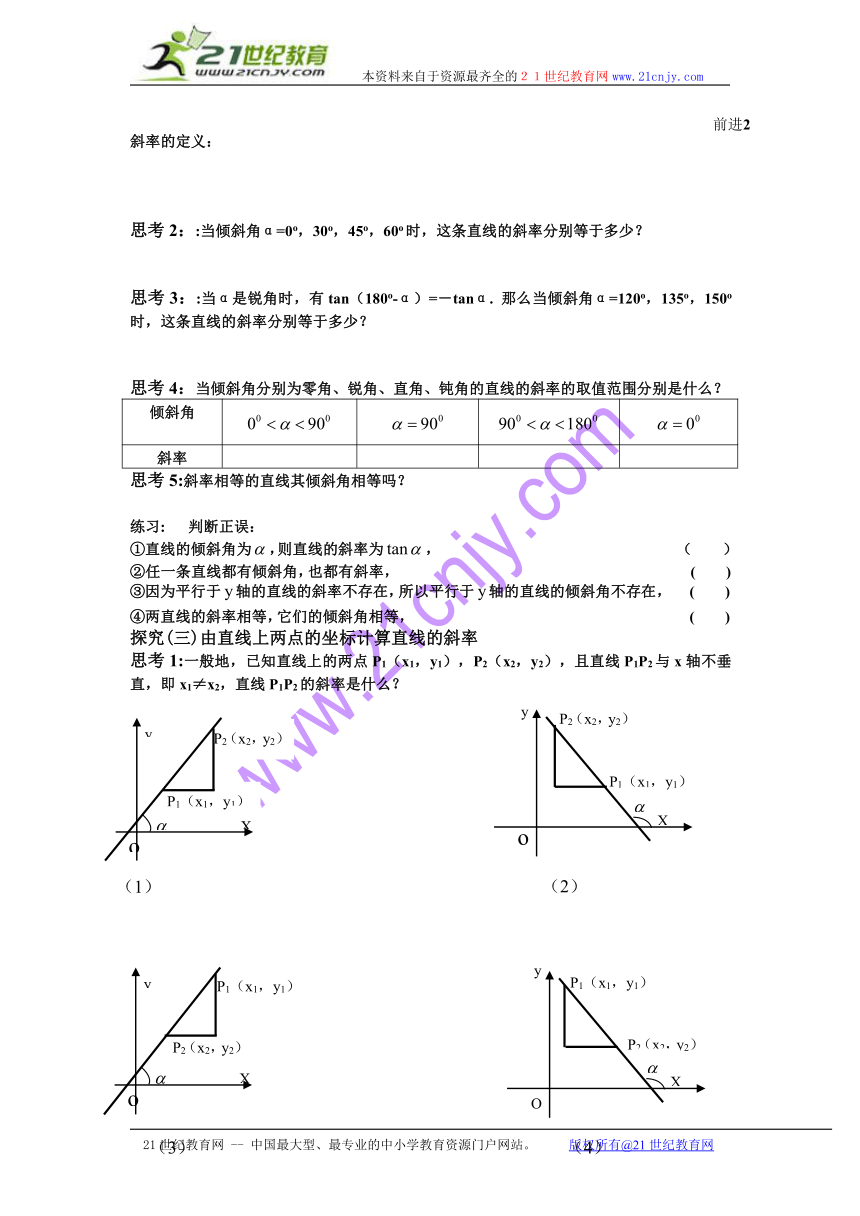
探究(三)由直线上两点的坐标计算直线的斜率
思考1:一般地,已知直线上的两点P1(x1,y1),P2(x2,y2),且直线P1P2与x轴不垂直,即x1≠x2,直线P1P2的斜率是什么?
思考2:当直线平行于x轴,或与x轴重合时,
上述公式还适用吗?为什么?
思考3:当直线平行于y轴,或与y轴重合时,
上述公式还适用吗?为什么?
思考4:已知直线上两点运用上述公式计算直线AB的斜率时,与A、B的顺序有关吗?
练习:
求经过下列两点直线的倾斜角。
1、 A(2,1),B(3,1)
2、 C(2,1),D(2,6)
3、 P(b,b+c),Q(a,c+a)(注:a,b,c是两两不等的实数。)
三、典例精析:
例1 已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB, BC, CA的斜率, 并判断它们的倾斜角是钝角还是锐角.
例2 在平面直角坐标系中, 画出经过原点且斜率分别为1, -1, 2, 及-3的直线l1、l2、l3、l4.
四、课堂小结:
本节课我们学习了那些数学知识、数学方法?用到了那些数学思想?
五、课堂作业:
必做部分:
1、已知直线l经过C(18,8),D(4,-4)两点 , 则l的倾斜角为( )
(A)锐角 (B)钝角 (C)直角 (D)不确定
2.已知点A(- m,2),B(5,3m)
(1)m= 时,过点A、B的直线的斜率为2.
(2)m = 时,过点A、B的直线的倾斜角为135°.
3.P86练习:2,3,4.P89习题3.1A组:3,4,5.
选做部分:P90习题3.1B组:5,6.
o
y
X
升高3
α
α
前进2
α
α
升高2
前进2
(2)
P2(x2,y2)
P1(x1,y1)
y
o
X
(1)
P2(x2,y2)
P1(x1,y1)
o
y
X
(4)
P2(x2,y2)
P1(x1,y1)
y
O
X
(3)
P2(x2,y2)
P1(x1,y1)
o
y
X
o
x
y
o
x
y
y
O
X
y
O
X
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
直线的倾斜角和斜率(1)
巨野县实验中学 刘士臣
学习目标:
1.正确理解直线的倾斜角和斜率的概念.2.理解直线的倾斜角的唯一性.
3.理解直线的斜率的存在性. 4.斜率公式的推导过程,掌握过两点的直线的斜率公式.
学习重点:直线的倾斜角、斜率的概念,用代数方法刻画直线斜率的过程。
学习难点: 直线的倾斜角与斜率之间的关系.
学习过程:
一、创设情景
上海浦东新区气势宏伟的斜拉桥
二、新知探究
探究(一)直线的倾斜角
请同学们在右下平面直角坐标系中过原点o任作一直线,并与其他同学所作直线相比较,直线的位置是否相同,若不同请指出不同之处。若相同请说明理由。
倾斜角的定义:
倾斜角的范围:
思考:不同的直线其倾斜角一定不相同吗?
确定直线位置的几何要素:
探究(二)直线的斜率:
思考1:初中学过的“坡度(比)”是什么含义?它与这条直线的倾斜角之间有什么关系?它能否表示直线的倾斜程度?
斜率的定义:
思考2::当倾斜角α=0o,30o,45o,60o时,这条直线的斜率分别等于多少?
思考3::当α是锐角时,有tan(180o-α)=-tanα. 那么当倾斜角α=120o,135o,150o时,这条直线的斜率分别等于多少?
思考4:当倾斜角分别为零角、锐角、直角、钝角的直线的斜率的取值范围分别是什么?
倾斜角
斜率
思考5:斜率相等的直线其倾斜角相等吗?
练习: 判断正误:
①直线的倾斜角为,则直线的斜率为, ( )
②任一条直线都有倾斜角,也都有斜率, ( )③因为平行于轴的直线的斜率不存在,所以平行于轴的直线的倾斜角不存在, ( )
④两直线的斜率相等,它们的倾斜角相等, ( )
探究(三)由直线上两点的坐标计算直线的斜率
思考1:一般地,已知直线上的两点P1(x1,y1),P2(x2,y2),且直线P1P2与x轴不垂直,即x1≠x2,直线P1P2的斜率是什么?
思考2:当直线平行于x轴,或与x轴重合时,
上述公式还适用吗?为什么?
思考3:当直线平行于y轴,或与y轴重合时,
上述公式还适用吗?为什么?
思考4:已知直线上两点运用上述公式计算直线AB的斜率时,与A、B的顺序有关吗?
练习:
求经过下列两点直线的倾斜角。
1、 A(2,1),B(3,1)
2、 C(2,1),D(2,6)
3、 P(b,b+c),Q(a,c+a)(注:a,b,c是两两不等的实数。)
三、典例精析:
例1 已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB, BC, CA的斜率, 并判断它们的倾斜角是钝角还是锐角.
例2 在平面直角坐标系中, 画出经过原点且斜率分别为1, -1, 2, 及-3的直线l1、l2、l3、l4.
四、课堂小结:
本节课我们学习了那些数学知识、数学方法?用到了那些数学思想?
五、课堂作业:
必做部分:
1、已知直线l经过C(18,8),D(4,-4)两点 , 则l的倾斜角为( )
(A)锐角 (B)钝角 (C)直角 (D)不确定
2.已知点A(- m,2),B(5,3m)
(1)m= 时,过点A、B的直线的斜率为2.
(2)m = 时,过点A、B的直线的倾斜角为135°.
3.P86练习:2,3,4.P89习题3.1A组:3,4,5.
选做部分:P90习题3.1B组:5,6.
o
y
X
升高3
α
α
前进2
α
α
升高2
前进2
(2)
P2(x2,y2)
P1(x1,y1)
y
o
X
(1)
P2(x2,y2)
P1(x1,y1)
o
y
X
(4)
P2(x2,y2)
P1(x1,y1)
y
O
X
(3)
P2(x2,y2)
P1(x1,y1)
o
y
X
o
x
y
o
x
y
y
O
X
y
O
X
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
