山东威海市第三中学高中数学人教B版选修2-1第二章2-2-1《椭圆的标准方程》课件(19张ppt)+教学设计 (3份打包)
文档属性
| 名称 | 山东威海市第三中学高中数学人教B版选修2-1第二章2-2-1《椭圆的标准方程》课件(19张ppt)+教学设计 (3份打包) |

|
|
| 格式 | zip | ||
| 文件大小 | 584.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-06 00:00:00 | ||
图片预览






文档简介
课件19张PPT。2.2.1椭圆的定义以及标准方程天体的运行如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?生活中的椭圆一.课题引入:椭圆的画法注意:椭圆定义中容易遗漏的三处地方:
(1) 必须在平面内;
(2)两个定点---两点间距离确定;
(3)绳长---轨迹上任意点到两定点距离和确定. 1 .椭圆定义:
平面内与两个定点 的距离和等于常数(大于
)的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .二.讲授新课:思考:在同样的绳长下,两定点间距离较长,则所画出的
椭圆较扁( 线段);两定点间距离较短,则所画出的椭圆较圆( 圆).由此可知,椭圆的形状与两定点间距离、绳长有关.? 求动点轨迹方程的一般步骤:(1)建立适当的坐标系,用有序实数对(x,y)
表示曲线上任意一点M的坐标;
(2)写出适合条件 P(M) ;
(3)用坐标表示条件P(M),列出方程 ;
(4)化方程为最简形式;
(5)证明以化简后的方程为所求方程(可以省略
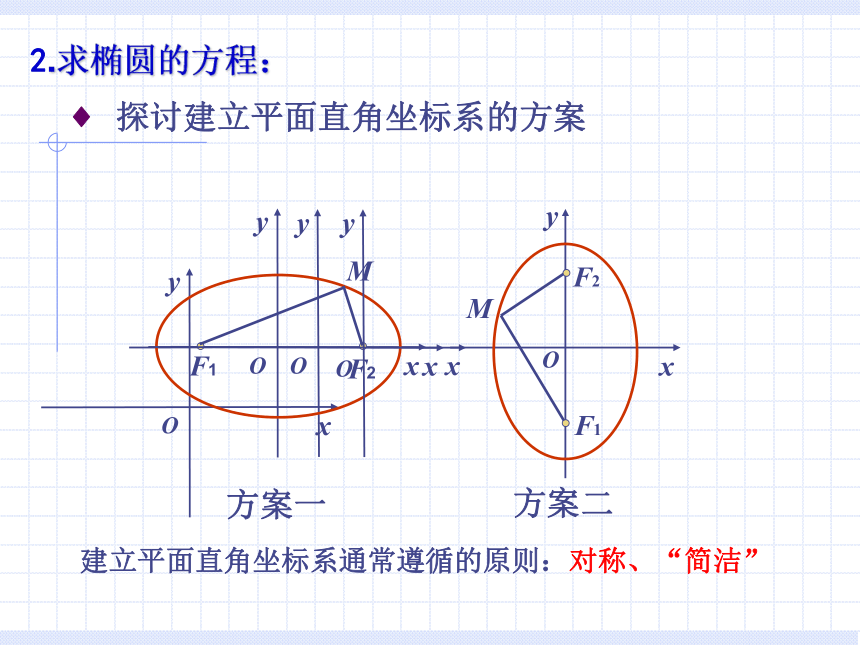
不写,如有特殊情况,可以适当予以说明)坐标法? 探讨建立平面直角坐标系的方案建立平面直角坐标系通常遵循的原则:对称、“简洁”方案一2.求椭圆的方程:解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(问题:下面怎样化简?)由椭圆的定义得,限制条件:代入坐标两边除以 得由椭圆定义可知总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:3.椭圆的标准方程: 图 形方 程焦 点F(±c,0)F(0,±c)a,b,c之间的关系c2=a2-b2|MF1|+|MF2|=2a (2a>2c>0)定 义注:共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.例1 、已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.练习1.下列方程哪些表示椭圆? 若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.?练习2.求适合下列条件的椭圆的标准方程:(2)焦点为F1(0,-3),F2(0,3),且a=5;(1)a= ,b=1,焦点在x轴上;(3)两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点; (4)经过点P(-2,0)和Q(0,-3).小结:求椭圆标准方程的步骤:①定位:确定焦点所在的坐标轴;②定量:求a, b的值.练习3. 已知椭圆的方程为: ,请填空:
(1) a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且CF1=2,则CF2=___. 变式: 若椭圆的方程为 ,试口答完成(1).5436(-3,0)、(3,0)8练习4.已知方程 表示焦点在x轴 上的椭圆,则m的取值范围是 .(0,4) 变1:已知方程 表示焦点在y轴上的椭圆,则m的取值范围是 .(1,2)变2:方程 ,分别求方程满足下列条件的m的取值范围:
①表示一个圆;
②表示一个椭圆;
③表示焦点在x轴上的椭圆。例2、将圆 上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,并说明
它是什么曲线?1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆;
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法。
例3. 已知圆A:(x+3)2+y2=100,圆A内一
定点B(3,0),动圆P过B点且与圆A内切,求
动圆心P的轨迹方程.三、回顾小结:椭圆定义求美意识, 求简意识,前瞻意识已知椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点。今有一个水平放置的台球盘,点A、B是它的两个焦点,焦距是2c,椭圆上的点到A、B的距离的和为2a,当静放在A的小球(半径不计)沿直线出发,经椭圆壁反弹后再回到点A时,求小球经过的路程。探索
(1) 必须在平面内;
(2)两个定点---两点间距离确定;
(3)绳长---轨迹上任意点到两定点距离和确定. 1 .椭圆定义:
平面内与两个定点 的距离和等于常数(大于
)的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .二.讲授新课:思考:在同样的绳长下,两定点间距离较长,则所画出的
椭圆较扁( 线段);两定点间距离较短,则所画出的椭圆较圆( 圆).由此可知,椭圆的形状与两定点间距离、绳长有关.? 求动点轨迹方程的一般步骤:(1)建立适当的坐标系,用有序实数对(x,y)
表示曲线上任意一点M的坐标;
(2)写出适合条件 P(M) ;
(3)用坐标表示条件P(M),列出方程 ;
(4)化方程为最简形式;
(5)证明以化简后的方程为所求方程(可以省略
不写,如有特殊情况,可以适当予以说明)坐标法? 探讨建立平面直角坐标系的方案建立平面直角坐标系通常遵循的原则:对称、“简洁”方案一2.求椭圆的方程:解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(问题:下面怎样化简?)由椭圆的定义得,限制条件:代入坐标两边除以 得由椭圆定义可知总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:3.椭圆的标准方程: 图 形方 程焦 点F(±c,0)F(0,±c)a,b,c之间的关系c2=a2-b2|MF1|+|MF2|=2a (2a>2c>0)定 义注:共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.例1 、已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.练习1.下列方程哪些表示椭圆? 若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.?练习2.求适合下列条件的椭圆的标准方程:(2)焦点为F1(0,-3),F2(0,3),且a=5;(1)a= ,b=1,焦点在x轴上;(3)两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点; (4)经过点P(-2,0)和Q(0,-3).小结:求椭圆标准方程的步骤:①定位:确定焦点所在的坐标轴;②定量:求a, b的值.练习3. 已知椭圆的方程为: ,请填空:
(1) a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且CF1=2,则CF2=___. 变式: 若椭圆的方程为 ,试口答完成(1).5436(-3,0)、(3,0)8练习4.已知方程 表示焦点在x轴 上的椭圆,则m的取值范围是 .(0,4) 变1:已知方程 表示焦点在y轴上的椭圆,则m的取值范围是 .(1,2)变2:方程 ,分别求方程满足下列条件的m的取值范围:
①表示一个圆;
②表示一个椭圆;
③表示焦点在x轴上的椭圆。例2、将圆 上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,并说明
它是什么曲线?1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆;
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法。
例3. 已知圆A:(x+3)2+y2=100,圆A内一
定点B(3,0),动圆P过B点且与圆A内切,求
动圆心P的轨迹方程.三、回顾小结:椭圆定义求美意识, 求简意识,前瞻意识已知椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点。今有一个水平放置的台球盘,点A、B是它的两个焦点,焦距是2c,椭圆上的点到A、B的距离的和为2a,当静放在A的小球(半径不计)沿直线出发,经椭圆壁反弹后再回到点A时,求小球经过的路程。探索
