11.1.1 不等式及其解集 课件(共44张PPT)2024-2025学年人教版数学七年级下册
文档属性
| 名称 | 11.1.1 不等式及其解集 课件(共44张PPT)2024-2025学年人教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 15:08:09 | ||
图片预览










文档简介
(共44张PPT)
第十一章 不等式与不等式组
11.1 不等式
11.1.1 不等式及其解集
目
录
1. 学习目标
3. 知识点1 不等式的概念
7. 课堂小结
8. 当堂小练
CONTENTS
2. 新课导入
4. 知识点2 用不等式表示数量关系
10. 拓展与延伸
5. 知识点3 不等式的解与解集
9. 对接中考
6. 知识点4 不等式的解集的表示方法
1. 了解不等式及其解的概念.
2. 学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
3. 理解不等式的解集及解不等式的意义.
学习目标
新课导入
谁重谁轻
谁快谁慢
新课导入
摩拜单车在2017年3月推出了红包车的运动.用户扫码解锁后有效骑行红包车超过10分钟,锁车后即可获得1个现金红包;骑行红包车次数及领取红包次数不限.红包金额随机,高于1元,且低于100元.你能用关系式表示可获红包金额的大小吗?
x>1 且 x<100
新课讲解
知识点1 不等式的概念
【问题1】如图所示,处于平衡状态的托盘天平的右盘放上一质量为50g的砝码,左盘放上一个圆球后向左倾斜,问圆球的质量x g与质量为50g的砝码之间具有怎样的关系?
我们很容易知道圆球的质量大于砝码的质量,即x > 50.
新课讲解
【问题2】一辆汽车在高速公路上匀速行驶,6:00时汽车距前方的A地210km,汽车要在8:00之前驶过A地,车速应满足什么条件
分析:设车速是x km/h.
汽车要在8:00之前驶过A地,
从时间上看,就是以x km/h的速度行驶210km的时间不到2h,
这个不等关系可以表示为 <2 . ①
从路程上看,就是以x km/h的速度行驶2h的路程要超过210 km,
这个不等关系可以表示为 2x>210. ②
新课讲解
x > 50,<2,2x>210.
它们有什么共同的特点
这样用符号“<”或“>”表示不等关系的式子,叫作不等式.
像a+2≠a-2这样用“≠”表示不等关系的式子也是不等式.
左右不相等
总结
新课讲解
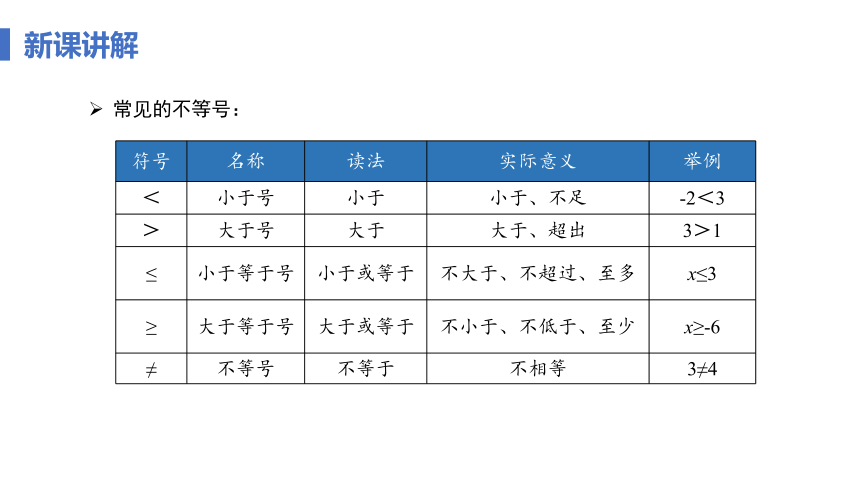
常见的不等号:
符号 名称 读法 实际意义 举例
< 小于号 小于 小于、不足 -2<3
> 大于号 大于 大于、超出 3>1
≤ 小于等于号 小于或等于 不大于、不超过、至多 x≤3
≥ 大于等于号 大于或等于 不小于、不低于、至少 x≥-6
≠ 不等号 不等于 不相等 3≠4
新课讲解
(1) 有些不等式不含字母,如3<4,
有些不等式含有字母如2x<1.
(2) 判断一个式子是不是不等式,关键是看该式子是否含有不等符号.
(3) 不等号具有方向性,不等号两边的数(或式子)不能随意交换.
注意
新课讲解
例
1. 下列式子中是不等式的有_________.(填序号)
① 3<2; ② 2x2-3>0;
③ 5y2-8; ④ 2x+3=7;
⑤ 3x+1≤7; ⑥ x≠5.
①②⑤⑥
不含不等号
含等号
新课讲解
练一练
1. 下列式子:
① -3<0;② 4x+3y>0; ③ 3x=5;④ x2-xy+y2; ⑤ x+2>-7.
其中不等式的个数是( )
A. 5 B. 4 C. 3 D. 2
C
新课讲解
练一练
2. 判断下列式子是不是不等式:
(1)-3>0; (2)4x+3y<0;
(3)x=3; (4)x2+xy+y2;
(5)x≠5; (6)x+2>y+5.
解 : (1)(2)(5)(6)是不等式;
(3)(4)不是不等式.
新课讲解
知识点2 用不等式表示数量关系
2. 用不等式表示下列不等关系:
(1)a与15的和大于27;
(2)b的一半与3的差是负数;
(3)某县在乡村振兴项目的援助下,共种植1333 hm2猕猴桃,种植面积超过全县原有猕猴桃种植面积的18倍.
解:(1)a+15>27;
(2)-3<0;
<0
例
(3)设这个县原有猕猴桃种植面积为x hm2,
那么1 333>18x,也可以表示为18x<1 333.
新课讲解
常见的不等式基本语言及其符号表示:
不等式基本语言 符号表示
a 是正数 a > 0
a 是负数 a < 0
a 是非正数 a ≤ 0
a 是非负数 a ≥ 0
a,b 同号 ab > 0
a,b 异号 ab < 0
新课讲解
练一练
1. 用不等式表示:
(1) a 的一半与3 的和大于5;
(2) x 的3 倍与1 的差小于2;
(3) a 的与1 的差是正数;
(4) m 与2 的差是负数;
(5) 今年植树节,小青和小贤栽种了一棵树,此树的树围(树干一圈的长度)为 15 cm.已知此树树围平均每年增长 3 cm,生长 x 年后,此树树围超过 60 cm.
a+3>5.
3x-1<2.
a-1>0.
m-2<0.
3x+15 > 60.
新课讲解
练一练
2. 已知一支圆珠笔x元,签字笔与圆珠笔相比每支贵y元. 小华想要买3支圆珠笔和10支签字笔,若付50元仍找回若干元,则如何用含x,y的不等式来表示小华所需支付的金额与50元之间的关系?
解: 3x+10(x+y)<50
新课讲解
用不等式表示数量关系关键是找出关键词:例如
“大于”“超过”“多于”等用“>”表示;
“小于”“不足”“少于”等用“<”表示;
“不小于”“至少”用“≥”表示;
“不大于”“至多”用“≤”表示;
“不等于”用“≠”表示。
归纳
新课讲解
知识点3 不等式的解与解集
【探究1】下面给出的数中,能使不等式x>50成立吗?你还能找出其他的数吗?
20, 40, 50, 100.
解:当x=20,20<50,不成立;
当x=40,40<50,不成立;
当x=50,50=50,不成立;
当x=100,100>50,成立.
当x=108,108>50,成立.
新课讲解
例如,110是不等式x>100的解,而90不是不等式x>100的解.
与方程的解类似,我们把使不等式成立的未知数的值叫作不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
注意:一般情况下,不等式的解有无数个,但不等式的特殊解可以是有限个.
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
总结
新课讲解
【探究2】判断下列数中哪些是不等式 的解:
60,73,74.9,75.1,76,79,80,90.
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
比 75 小的数都不是不等式的解,比 75 大的数都是不等式的解.
你从表格中发现了什么规律?
新课讲解
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
例如:x>75是不等式的解集.
求不等式的解集的过程叫作解不等式.
不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
总结
新课讲解
例
3. 下列四个说法:
① x= 是不等式4x-5>0 的一个解;
② x= 是不等式4x-5>0 的一个解;
③ x> 是不等式4x-5>0的解集;
④ x>2 中的任何一个数都可以使不等式4x-5>0 成立,所以x>2 是不等式4x-5>0 的解集.
其中正确的有( )
A.1 个 B.2 个 C.3 个 D.4 个
B
新课讲解
练一练
1. 下列说法中,错误的是( )
A. x=1 是不等式x<2的一个解
B. x=-2 是不等式2x<1的一个解
C. 不等式3x>9 的解集是x=4
D. 不等式x<10 有无数个解
C
新课讲解
练一练
2. 在 4,3,2,1,0,- ,- 中,能使不等式 3x - 2 >2x 成立的数有_______个.
2
新课讲解
归纳
不等式的解 不等式的解集
区 别 定义
特点
形式
联系
能使不等式成立的某个未知数的值.
能使不等式成立的所有未知数的值.
个体
全体
如:是的一个解
如:是的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
新课讲解
知识点4 不等式的解集的表示方法
怎样表示不等式的解集呢?
用式子:用最简形式的不等式(如 x>a 或 x用数轴:一般标出数轴上某一范围,其中的点对应的数值都是不等式的解.
新课讲解
【问题】如何在数轴上表示出不等式x>2的解集呢?
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2.
因此可以像图那样表示不等式的解集x>2.
0
1
2
3
4
5
6
-1
A
把表示2的点A画成空心圆圈,表示解集不包括2.
新课讲解
用数轴表示不等式的解集的步骤:
1. 定边界点:在数轴上要标出原点和边界点,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点).
2. 定方向:大于向右,小于向左.
归纳
不等式的解集 x > a x < a x ≥ a x ≤ a
数轴表示
0
a
0
a
0
a
0
a
常见不等式的解集在数轴上的表示:
新课讲解
例
4. 利用数轴来表示下列不等式的解集.
(1) x>-1 ; (2) x< .
0
-1
0
1
【变式】已知x的解集在数轴上表示如图,你能写出x的解集吗
0
-2
表示-1的点
表示 的点
方向向右
方向向左
空心圆圈表示不含此点
x<-2
新课讲解
练一练
解:(1)x<-4;
(2)x>4.
0
-4
0
4
(1)
(2)
1. 已知x的解集如图所示,你能写出x的解集吗
新课讲解
练一练
2. 直接写出不等式2x>8的解集,并在数轴上表示出来.
解:x>4.
这个解集在数轴上表示为:
0
4
新课讲解
填空:(1) 写出不等式 x<3 的所有正整数解:_______ ;
(2) 写出不等式 x>-4 的所有负整数解: __________ ;
(3) 写出不等式 x<2 的所有非负整数解: _______ ;
(4) 写出不等式 x>-3 的最小整数解: _______ .
1,2
-3, -2, -1
0, 1
-2
【变式】不等式的特殊解
解: 如表所示 .
题号 在数轴上表示解集 找出特殊解
(1) 正整数解:1,2
(2) 负整数解:-3,-2,-1
(3) 非负整数解:0,1
(4) 最小整数解:-2
方法点拨: 将解集表示在数轴上→找出符合要求的解 .
一般情况下,不等式的解有无数个,但不等式的特殊解可以是有限个,比如:不等式 x < 3 的解有无 数 个, 但 是 它 的正整数解只有 1 和 2两个 .
注意
课堂小结
不等式
解集:不等式的所有的解组成解集
解:使不等式成立的未知数的值
用不等号表示不等关系的式子
解及解集
定义
包含
组成
用不等式表示数量关系
在数轴上表示不等式的解集
当堂小练
1. 给出下列式子:①-2<0,②2y-5>1,③m=1,④x2-x,⑤x≠-2,⑥x+1<2x-1.其中是不等式的有 ( )
A.2个 B.3个 C.4个 D.5个
C
2. 下列各项中,蕴含不等关系的是( )
A. 老师的年龄是你年龄的 2 倍
B. 小军和小红一样高
C. 小明比爸爸小 26 岁
D. x2 是非负数
D
当堂小练
4. 下列说法中,正确的是( )
A. -3 是不等式 x+4<1 的解
B. x>1 是不等式 x+1>0 的解集
C. 不等式 x≥-3 的负整数解有无数个
D. 不等式 x<5 的非正整数解有无数个
3. 在 -2,-2.5,0,1 中,是不等式 2x>1 的解的是____.
2×(-2)=-4<1
2×0=0<1
2×(-2.5)=-5<1
1
D
-3+4=1
0+1>0,但0<1
-3,-2,-1
当堂小练
5. 在数轴上表示不等式3x>5的解集,正确的是( )
A
A
0
1
2
B
0
1
2
1
2
D
0
1
2
0
C
当堂小练
6. 直接写出下列不等式的所有整数解:
(1) |x|<4;
(2) |x|<3.
解:|x|<4的所有整数解:-3,-2,-1,0,1,2,3.
解:|x|<3的所有整数解:-2,-1,0,1,2.
当堂小练
7. 【新考法 数形结合法】 已知实数 a, b, c 在数轴上对应的点的位置如图所示,则下列式子中正确的是 ( )
A.cbab
C.cb>ab D.c+b>a+b
C
当堂小练
8. 限高标志牌是指禁止装载高度超过标志所示数值的车辆通行 . 如图所示是某桥洞的限高标志牌,则下列装载高度的车辆不能通过此桥洞的是( )
A.5.5 m B.4.5 m
C.3.5 m D.2.5 m
A
当堂小练
9. 某弹簧测力计的测量范围是 0 至 50 N(含 50 N),佳佳未注意到弹簧测力计的测量范围,用这个弹簧测力计测量一个物体,取下物体后,发现弹簧没有恢复原状.设这个物体的重力为 G,则这个物体的重力范围用不等式表示为_________ .
G > 50 N
方法点拨:
1. 根据测量完成后弹簧没有恢复原状,说明超过了测量范围.
2. 对于实际问题,读懂题意,分析好数量关系,才能正确表示出范围 .
对接中考
1. 下列数中,能使不等式 5x-1 < 6 成立的 x 的值为( )
A.1 B.2 C.3 D.4
方法点拨:本题考查不等式的解,正确理解不等式解的定义是解题的关键 .
A
解:当 x=1 时,5× 1-1=4<6,因 此x=1是不等式5x-1< 6的解.
同理可知,B, C, D 选项不是该不等式的解 .
故能使不等式 5x-1 < 6 成立的 x 的值为 1.
对接中考
2. 据某天气网站预测,某市最高气温是 6℃,最低气温是 -1 ℃,则当天该市气温 t (单位℃)的变化范围是( )
A. t ≤ 6 B. t ≥ -1
C. t ≥ -1 或 t ≤ 6 D. t ≥ -1且 t≤ 6
D
t ≥ -1
t ≤ 6
拓展与延伸
已知关于 x 的不等式 x>a-1 的解集如图,则a 的值为________ .
0
解:因为数轴上表示的不等式的解 集 为 x>-1,
所以 a-1=-1,
解得a=0.
方法点拨:利用数轴上表示解集的“边界点”,将不等式转化为有关字母的方程求解 .
第十一章 不等式与不等式组
11.1 不等式
11.1.1 不等式及其解集
目
录
1. 学习目标
3. 知识点1 不等式的概念
7. 课堂小结
8. 当堂小练
CONTENTS
2. 新课导入
4. 知识点2 用不等式表示数量关系
10. 拓展与延伸
5. 知识点3 不等式的解与解集
9. 对接中考
6. 知识点4 不等式的解集的表示方法
1. 了解不等式及其解的概念.
2. 学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
3. 理解不等式的解集及解不等式的意义.
学习目标
新课导入
谁重谁轻
谁快谁慢
新课导入
摩拜单车在2017年3月推出了红包车的运动.用户扫码解锁后有效骑行红包车超过10分钟,锁车后即可获得1个现金红包;骑行红包车次数及领取红包次数不限.红包金额随机,高于1元,且低于100元.你能用关系式表示可获红包金额的大小吗?
x>1 且 x<100
新课讲解
知识点1 不等式的概念
【问题1】如图所示,处于平衡状态的托盘天平的右盘放上一质量为50g的砝码,左盘放上一个圆球后向左倾斜,问圆球的质量x g与质量为50g的砝码之间具有怎样的关系?
我们很容易知道圆球的质量大于砝码的质量,即x > 50.
新课讲解
【问题2】一辆汽车在高速公路上匀速行驶,6:00时汽车距前方的A地210km,汽车要在8:00之前驶过A地,车速应满足什么条件
分析:设车速是x km/h.
汽车要在8:00之前驶过A地,
从时间上看,就是以x km/h的速度行驶210km的时间不到2h,
这个不等关系可以表示为 <2 . ①
从路程上看,就是以x km/h的速度行驶2h的路程要超过210 km,
这个不等关系可以表示为 2x>210. ②
新课讲解
x > 50,<2,2x>210.
它们有什么共同的特点
这样用符号“<”或“>”表示不等关系的式子,叫作不等式.
像a+2≠a-2这样用“≠”表示不等关系的式子也是不等式.
左右不相等
总结
新课讲解
常见的不等号:
符号 名称 读法 实际意义 举例
< 小于号 小于 小于、不足 -2<3
> 大于号 大于 大于、超出 3>1
≤ 小于等于号 小于或等于 不大于、不超过、至多 x≤3
≥ 大于等于号 大于或等于 不小于、不低于、至少 x≥-6
≠ 不等号 不等于 不相等 3≠4
新课讲解
(1) 有些不等式不含字母,如3<4,
有些不等式含有字母如2x<1.
(2) 判断一个式子是不是不等式,关键是看该式子是否含有不等符号.
(3) 不等号具有方向性,不等号两边的数(或式子)不能随意交换.
注意
新课讲解
例
1. 下列式子中是不等式的有_________.(填序号)
① 3<2; ② 2x2-3>0;
③ 5y2-8; ④ 2x+3=7;
⑤ 3x+1≤7; ⑥ x≠5.
①②⑤⑥
不含不等号
含等号
新课讲解
练一练
1. 下列式子:
① -3<0;② 4x+3y>0; ③ 3x=5;④ x2-xy+y2; ⑤ x+2>-7.
其中不等式的个数是( )
A. 5 B. 4 C. 3 D. 2
C
新课讲解
练一练
2. 判断下列式子是不是不等式:
(1)-3>0; (2)4x+3y<0;
(3)x=3; (4)x2+xy+y2;
(5)x≠5; (6)x+2>y+5.
解 : (1)(2)(5)(6)是不等式;
(3)(4)不是不等式.
新课讲解
知识点2 用不等式表示数量关系
2. 用不等式表示下列不等关系:
(1)a与15的和大于27;
(2)b的一半与3的差是负数;
(3)某县在乡村振兴项目的援助下,共种植1333 hm2猕猴桃,种植面积超过全县原有猕猴桃种植面积的18倍.
解:(1)a+15>27;
(2)-3<0;
<0
例
(3)设这个县原有猕猴桃种植面积为x hm2,
那么1 333>18x,也可以表示为18x<1 333.
新课讲解
常见的不等式基本语言及其符号表示:
不等式基本语言 符号表示
a 是正数 a > 0
a 是负数 a < 0
a 是非正数 a ≤ 0
a 是非负数 a ≥ 0
a,b 同号 ab > 0
a,b 异号 ab < 0
新课讲解
练一练
1. 用不等式表示:
(1) a 的一半与3 的和大于5;
(2) x 的3 倍与1 的差小于2;
(3) a 的与1 的差是正数;
(4) m 与2 的差是负数;
(5) 今年植树节,小青和小贤栽种了一棵树,此树的树围(树干一圈的长度)为 15 cm.已知此树树围平均每年增长 3 cm,生长 x 年后,此树树围超过 60 cm.
a+3>5.
3x-1<2.
a-1>0.
m-2<0.
3x+15 > 60.
新课讲解
练一练
2. 已知一支圆珠笔x元,签字笔与圆珠笔相比每支贵y元. 小华想要买3支圆珠笔和10支签字笔,若付50元仍找回若干元,则如何用含x,y的不等式来表示小华所需支付的金额与50元之间的关系?
解: 3x+10(x+y)<50
新课讲解
用不等式表示数量关系关键是找出关键词:例如
“大于”“超过”“多于”等用“>”表示;
“小于”“不足”“少于”等用“<”表示;
“不小于”“至少”用“≥”表示;
“不大于”“至多”用“≤”表示;
“不等于”用“≠”表示。
归纳
新课讲解
知识点3 不等式的解与解集
【探究1】下面给出的数中,能使不等式x>50成立吗?你还能找出其他的数吗?
20, 40, 50, 100.
解:当x=20,20<50,不成立;
当x=40,40<50,不成立;
当x=50,50=50,不成立;
当x=100,100>50,成立.
当x=108,108>50,成立.
新课讲解
例如,110是不等式x>100的解,而90不是不等式x>100的解.
与方程的解类似,我们把使不等式成立的未知数的值叫作不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
注意:一般情况下,不等式的解有无数个,但不等式的特殊解可以是有限个.
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
总结
新课讲解
【探究2】判断下列数中哪些是不等式 的解:
60,73,74.9,75.1,76,79,80,90.
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
比 75 小的数都不是不等式的解,比 75 大的数都是不等式的解.
你从表格中发现了什么规律?
新课讲解
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
例如:x>75是不等式的解集.
求不等式的解集的过程叫作解不等式.
不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
总结
新课讲解
例
3. 下列四个说法:
① x= 是不等式4x-5>0 的一个解;
② x= 是不等式4x-5>0 的一个解;
③ x> 是不等式4x-5>0的解集;
④ x>2 中的任何一个数都可以使不等式4x-5>0 成立,所以x>2 是不等式4x-5>0 的解集.
其中正确的有( )
A.1 个 B.2 个 C.3 个 D.4 个
B
新课讲解
练一练
1. 下列说法中,错误的是( )
A. x=1 是不等式x<2的一个解
B. x=-2 是不等式2x<1的一个解
C. 不等式3x>9 的解集是x=4
D. 不等式x<10 有无数个解
C
新课讲解
练一练
2. 在 4,3,2,1,0,- ,- 中,能使不等式 3x - 2 >2x 成立的数有_______个.
2
新课讲解
归纳
不等式的解 不等式的解集
区 别 定义
特点
形式
联系
能使不等式成立的某个未知数的值.
能使不等式成立的所有未知数的值.
个体
全体
如:是的一个解
如:是的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
新课讲解
知识点4 不等式的解集的表示方法
怎样表示不等式的解集呢?
用式子:用最简形式的不等式(如 x>a 或 x
新课讲解
【问题】如何在数轴上表示出不等式x>2的解集呢?
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2.
因此可以像图那样表示不等式的解集x>2.
0
1
2
3
4
5
6
-1
A
把表示2的点A画成空心圆圈,表示解集不包括2.
新课讲解
用数轴表示不等式的解集的步骤:
1. 定边界点:在数轴上要标出原点和边界点,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点).
2. 定方向:大于向右,小于向左.
归纳
不等式的解集 x > a x < a x ≥ a x ≤ a
数轴表示
0
a
0
a
0
a
0
a
常见不等式的解集在数轴上的表示:
新课讲解
例
4. 利用数轴来表示下列不等式的解集.
(1) x>-1 ; (2) x< .
0
-1
0
1
【变式】已知x的解集在数轴上表示如图,你能写出x的解集吗
0
-2
表示-1的点
表示 的点
方向向右
方向向左
空心圆圈表示不含此点
x<-2
新课讲解
练一练
解:(1)x<-4;
(2)x>4.
0
-4
0
4
(1)
(2)
1. 已知x的解集如图所示,你能写出x的解集吗
新课讲解
练一练
2. 直接写出不等式2x>8的解集,并在数轴上表示出来.
解:x>4.
这个解集在数轴上表示为:
0
4
新课讲解
填空:(1) 写出不等式 x<3 的所有正整数解:_______ ;
(2) 写出不等式 x>-4 的所有负整数解: __________ ;
(3) 写出不等式 x<2 的所有非负整数解: _______ ;
(4) 写出不等式 x>-3 的最小整数解: _______ .
1,2
-3, -2, -1
0, 1
-2
【变式】不等式的特殊解
解: 如表所示 .
题号 在数轴上表示解集 找出特殊解
(1) 正整数解:1,2
(2) 负整数解:-3,-2,-1
(3) 非负整数解:0,1
(4) 最小整数解:-2
方法点拨: 将解集表示在数轴上→找出符合要求的解 .
一般情况下,不等式的解有无数个,但不等式的特殊解可以是有限个,比如:不等式 x < 3 的解有无 数 个, 但 是 它 的正整数解只有 1 和 2两个 .
注意
课堂小结
不等式
解集:不等式的所有的解组成解集
解:使不等式成立的未知数的值
用不等号表示不等关系的式子
解及解集
定义
包含
组成
用不等式表示数量关系
在数轴上表示不等式的解集
当堂小练
1. 给出下列式子:①-2<0,②2y-5>1,③m=1,④x2-x,⑤x≠-2,⑥x+1<2x-1.其中是不等式的有 ( )
A.2个 B.3个 C.4个 D.5个
C
2. 下列各项中,蕴含不等关系的是( )
A. 老师的年龄是你年龄的 2 倍
B. 小军和小红一样高
C. 小明比爸爸小 26 岁
D. x2 是非负数
D
当堂小练
4. 下列说法中,正确的是( )
A. -3 是不等式 x+4<1 的解
B. x>1 是不等式 x+1>0 的解集
C. 不等式 x≥-3 的负整数解有无数个
D. 不等式 x<5 的非正整数解有无数个
3. 在 -2,-2.5,0,1 中,是不等式 2x>1 的解的是____.
2×(-2)=-4<1
2×0=0<1
2×(-2.5)=-5<1
1
D
-3+4=1
0+1>0,但0<1
-3,-2,-1
当堂小练
5. 在数轴上表示不等式3x>5的解集,正确的是( )
A
A
0
1
2
B
0
1
2
1
2
D
0
1
2
0
C
当堂小练
6. 直接写出下列不等式的所有整数解:
(1) |x|<4;
(2) |x|<3.
解:|x|<4的所有整数解:-3,-2,-1,0,1,2,3.
解:|x|<3的所有整数解:-2,-1,0,1,2.
当堂小练
7. 【新考法 数形结合法】 已知实数 a, b, c 在数轴上对应的点的位置如图所示,则下列式子中正确的是 ( )
A.cb
C.cb>ab D.c+b>a+b
C
当堂小练
8. 限高标志牌是指禁止装载高度超过标志所示数值的车辆通行 . 如图所示是某桥洞的限高标志牌,则下列装载高度的车辆不能通过此桥洞的是( )
A.5.5 m B.4.5 m
C.3.5 m D.2.5 m
A
当堂小练
9. 某弹簧测力计的测量范围是 0 至 50 N(含 50 N),佳佳未注意到弹簧测力计的测量范围,用这个弹簧测力计测量一个物体,取下物体后,发现弹簧没有恢复原状.设这个物体的重力为 G,则这个物体的重力范围用不等式表示为_________ .
G > 50 N
方法点拨:
1. 根据测量完成后弹簧没有恢复原状,说明超过了测量范围.
2. 对于实际问题,读懂题意,分析好数量关系,才能正确表示出范围 .
对接中考
1. 下列数中,能使不等式 5x-1 < 6 成立的 x 的值为( )
A.1 B.2 C.3 D.4
方法点拨:本题考查不等式的解,正确理解不等式解的定义是解题的关键 .
A
解:当 x=1 时,5× 1-1=4<6,因 此x=1是不等式5x-1< 6的解.
同理可知,B, C, D 选项不是该不等式的解 .
故能使不等式 5x-1 < 6 成立的 x 的值为 1.
对接中考
2. 据某天气网站预测,某市最高气温是 6℃,最低气温是 -1 ℃,则当天该市气温 t (单位℃)的变化范围是( )
A. t ≤ 6 B. t ≥ -1
C. t ≥ -1 或 t ≤ 6 D. t ≥ -1且 t≤ 6
D
t ≥ -1
t ≤ 6
拓展与延伸
已知关于 x 的不等式 x>a-1 的解集如图,则a 的值为________ .
0
解:因为数轴上表示的不等式的解 集 为 x>-1,
所以 a-1=-1,
解得a=0.
方法点拨:利用数轴上表示解集的“边界点”,将不等式转化为有关字母的方程求解 .
同课章节目录
