江苏省宜兴市外国语学校苏科版九年级数学下册7.2《正弦、余弦》导学案(无答案)
文档属性
| 名称 | 江苏省宜兴市外国语学校苏科版九年级数学下册7.2《正弦、余弦》导学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 94.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-04 21:47:34 | ||
图片预览

文档简介
宜兴外国语学校初三年级数学导学提纲
课题:7.2正弦、余弦 设计人:吴静飞 审核人:初三数学组
姓名: 班级: 评价
课前参与
一、探索新知:
1、问题1:如图,小明沿着某斜坡向上行走了13m后,他
的相对位置升高了5m,如果他沿着该斜坡行走了20m,
那么他的相对位置升高了多少?行走了a m呢?
2、问题2:在上述问题中,他在水平方向又分别前进了多远?
3、探索活动
(1)思考:从上面的两个问题可以看出:当 ( http: / / www.21cnjy.com )直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值__________;它的邻边与斜边的比值___________。
(2)正弦的定义
如图,在Rt△ABC中,∠C=90°,我们 ( http: / / www.21cnjy.com )把锐角∠A的对边a与斜边c的比叫做∠A的______,记作________,即:sinA=________=________.
(3)余弦的定义
如图,在Rt△ABC中,∠C=90°,我们 ( http: / / www.21cnjy.com )把锐角∠A的邻边b与斜边c的比叫做∠A的______,记作=_________,即:cosA=______=_____。
(你能写出∠B的正弦、余弦的表达式吗?)试试看. ____________________________.
4、利用计算器我们可以更快、更精确地求得各个锐角的正弦值和余弦值。
从sin15°= ,sin30°= ,sin75°= 的值,你们得到什么结论?
从cos15°= ,cos30°= ,cos75°= 的值,你们得到什么结论?
当锐角α越来越大时,它的正弦值是怎样变化的?余弦值又是怎样变化的?
5、锐角A的正弦、余弦和正切都是∠A的__________。
二、牛刀小试
根据如图中条件,分别求出下列直角三角形中锐角的正弦、余弦值。
课中参与
例1 如图,在Rt⊿ABC中,∠C=90°,AC=24,BC=7.
求 sinA、cosA、sinB 、cosB,的值。
例2、在Rt△ABC中,∠C=90°,已知cosA=,请你求出sinA、cosB、tanA、tanB的值
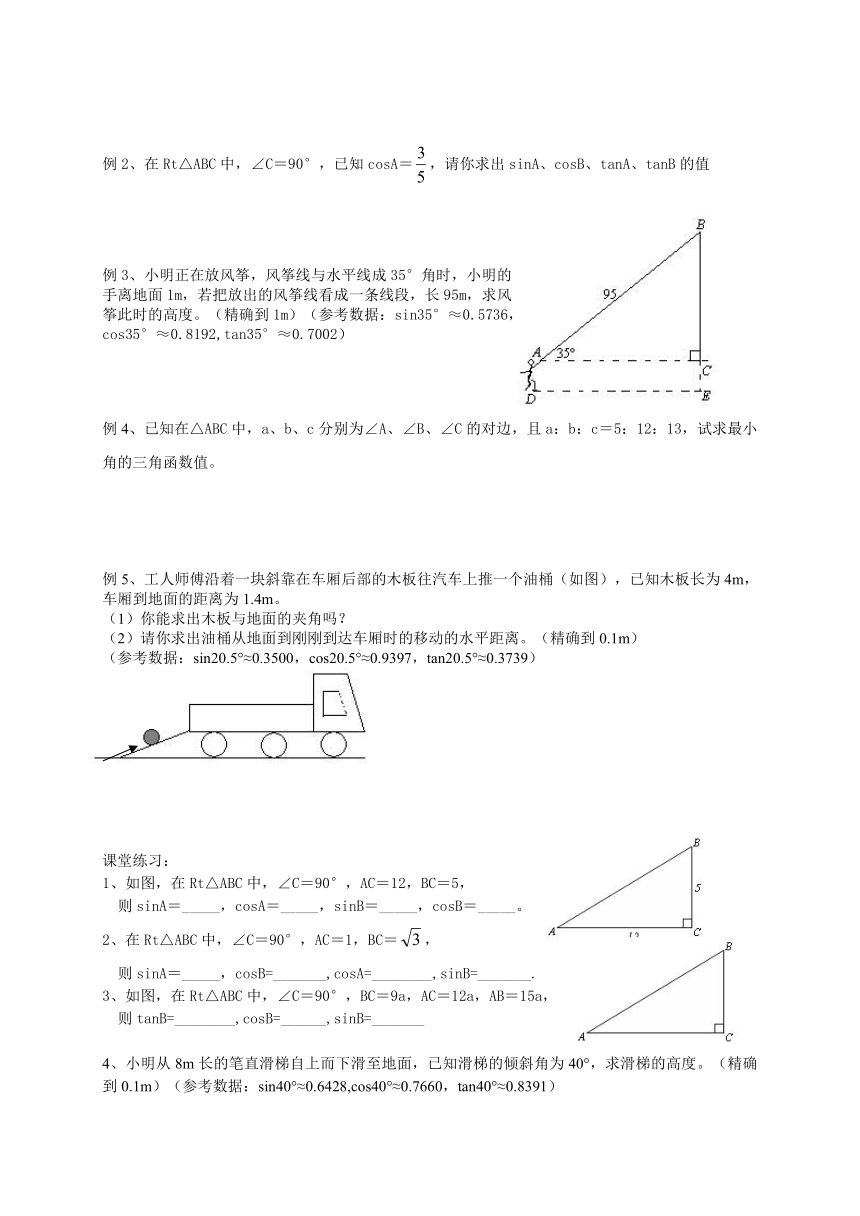
例3、小明正在放风筝,风筝线与水平线成35°角时,小明的
手离地面1m,若把放出的风筝线看成一条线段,长95m,求风
筝此时的高度。(精确到1m)(参考数据:sin35°≈0.5736,
cos35°≈0.8192,tan35°≈0.7002)
例4、已知在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,且a:b:c=5:12:13,试求最小角的三角函数值。
例5、工人师傅沿着一块斜靠在车厢后部的木板往汽车上推一个油桶(如图),已知木板长为4m,车厢到地面的距离为1.4m。
(1)你能求出木板与地面的夹角吗?
(2)请你求出油桶从地面到刚刚到达车厢时的移动的水平距离。(精确到0.1m)
(参考数据:sin20.5°≈0.3500,cos20.5°≈0.9397,tan20.5°≈0.3739)
课堂练习:
1、如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,
则sinA=_____,cosA=_____,sinB=_____,cosB=_____。
2、在Rt△ABC中,∠C=90°,AC=1,BC=,
则sinA=_____,cosB=_______,cosA=________,sinB=_______.
3、如图,在Rt△ABC中,∠C=90°,BC=9a,AC=12a,AB=15a,
则tanB=________,cosB=______,sinB=_______
4、小明从8m长的笔直滑梯 ( http: / / www.21cnjy.com )自上而下滑至地面,已知滑梯的倾斜角为40°,求滑梯的高度。(精确到0.1m)(参考数据:sin40°≈0.6428,cos40°≈0.7660,tan40°≈0.8391)
5、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CD=8,AC=10
(1)求锐角A、B的正弦、余弦:
(2)求AB、BD的长
课后参与
1、①如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,则sinA=_____,cosA=_____,tanA=_____。
②如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,则sinB=_____,cosB=_____,tanB=_____。
③在Rt△ABC中,∠B=90°,AC=2BC,则sinC=_____。
④如图,在Rt△ABC中,∠C=90°,AB=10,sinA=,则BC=_____。
⑤在Rt△ABC中,∠C=90°,AB=10,sinB=,则AC=_____。
⑥如图,在Rt△ABC中,∠B=90°,AC=15,sinC=,则AB=_____。
⑦在Rt△ABC中,∠C=90°,cosA=,AC=12,则AB=_____,BC=_____。
( http: / / www.21cnjy.com )
2、在Rt△ABC中,AC=BC,∠C=90°,
求(1)cosA; (2)当AB=4时,求BC的长。
3、在Rt△ABC中,∠C=90°,tanA=,AB=10,求BC和cosB。
4、等腰三角形周长为16,一边长为6,求底角的余弦值。
5、在Rt△ABC中,∠C=90°,已知cosA=,请你求出sinA、cosB、tanA、tanB的值。
6、在△ABC中,∠C=90°,D是B ( http: / / www.21cnjy.com )C的中点,且∠ADC=50°,AD=2,求tanB的值。(精确到0.01m)(参考数据:sin50°≈0.7660,cos50°≈0.6428,tan50°≈1.1918)
7、如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上。
(1)求证:△ABF∽△DFE; (2)若sin∠DFE=,求tan∠EBC的值.
A
B
C
7
24
课题:7.2正弦、余弦 设计人:吴静飞 审核人:初三数学组
姓名: 班级: 评价
课前参与
一、探索新知:
1、问题1:如图,小明沿着某斜坡向上行走了13m后,他
的相对位置升高了5m,如果他沿着该斜坡行走了20m,
那么他的相对位置升高了多少?行走了a m呢?
2、问题2:在上述问题中,他在水平方向又分别前进了多远?
3、探索活动
(1)思考:从上面的两个问题可以看出:当 ( http: / / www.21cnjy.com )直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值__________;它的邻边与斜边的比值___________。
(2)正弦的定义
如图,在Rt△ABC中,∠C=90°,我们 ( http: / / www.21cnjy.com )把锐角∠A的对边a与斜边c的比叫做∠A的______,记作________,即:sinA=________=________.
(3)余弦的定义
如图,在Rt△ABC中,∠C=90°,我们 ( http: / / www.21cnjy.com )把锐角∠A的邻边b与斜边c的比叫做∠A的______,记作=_________,即:cosA=______=_____。
(你能写出∠B的正弦、余弦的表达式吗?)试试看. ____________________________.
4、利用计算器我们可以更快、更精确地求得各个锐角的正弦值和余弦值。
从sin15°= ,sin30°= ,sin75°= 的值,你们得到什么结论?
从cos15°= ,cos30°= ,cos75°= 的值,你们得到什么结论?
当锐角α越来越大时,它的正弦值是怎样变化的?余弦值又是怎样变化的?
5、锐角A的正弦、余弦和正切都是∠A的__________。
二、牛刀小试
根据如图中条件,分别求出下列直角三角形中锐角的正弦、余弦值。
课中参与
例1 如图,在Rt⊿ABC中,∠C=90°,AC=24,BC=7.
求 sinA、cosA、sinB 、cosB,的值。
例2、在Rt△ABC中,∠C=90°,已知cosA=,请你求出sinA、cosB、tanA、tanB的值
例3、小明正在放风筝,风筝线与水平线成35°角时,小明的
手离地面1m,若把放出的风筝线看成一条线段,长95m,求风
筝此时的高度。(精确到1m)(参考数据:sin35°≈0.5736,
cos35°≈0.8192,tan35°≈0.7002)
例4、已知在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,且a:b:c=5:12:13,试求最小角的三角函数值。
例5、工人师傅沿着一块斜靠在车厢后部的木板往汽车上推一个油桶(如图),已知木板长为4m,车厢到地面的距离为1.4m。
(1)你能求出木板与地面的夹角吗?
(2)请你求出油桶从地面到刚刚到达车厢时的移动的水平距离。(精确到0.1m)
(参考数据:sin20.5°≈0.3500,cos20.5°≈0.9397,tan20.5°≈0.3739)
课堂练习:
1、如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,
则sinA=_____,cosA=_____,sinB=_____,cosB=_____。
2、在Rt△ABC中,∠C=90°,AC=1,BC=,
则sinA=_____,cosB=_______,cosA=________,sinB=_______.
3、如图,在Rt△ABC中,∠C=90°,BC=9a,AC=12a,AB=15a,
则tanB=________,cosB=______,sinB=_______
4、小明从8m长的笔直滑梯 ( http: / / www.21cnjy.com )自上而下滑至地面,已知滑梯的倾斜角为40°,求滑梯的高度。(精确到0.1m)(参考数据:sin40°≈0.6428,cos40°≈0.7660,tan40°≈0.8391)
5、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CD=8,AC=10
(1)求锐角A、B的正弦、余弦:
(2)求AB、BD的长
课后参与
1、①如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,则sinA=_____,cosA=_____,tanA=_____。
②如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,则sinB=_____,cosB=_____,tanB=_____。
③在Rt△ABC中,∠B=90°,AC=2BC,则sinC=_____。
④如图,在Rt△ABC中,∠C=90°,AB=10,sinA=,则BC=_____。
⑤在Rt△ABC中,∠C=90°,AB=10,sinB=,则AC=_____。
⑥如图,在Rt△ABC中,∠B=90°,AC=15,sinC=,则AB=_____。
⑦在Rt△ABC中,∠C=90°,cosA=,AC=12,则AB=_____,BC=_____。
( http: / / www.21cnjy.com )
2、在Rt△ABC中,AC=BC,∠C=90°,
求(1)cosA; (2)当AB=4时,求BC的长。
3、在Rt△ABC中,∠C=90°,tanA=,AB=10,求BC和cosB。
4、等腰三角形周长为16,一边长为6,求底角的余弦值。
5、在Rt△ABC中,∠C=90°,已知cosA=,请你求出sinA、cosB、tanA、tanB的值。
6、在△ABC中,∠C=90°,D是B ( http: / / www.21cnjy.com )C的中点,且∠ADC=50°,AD=2,求tanB的值。(精确到0.01m)(参考数据:sin50°≈0.7660,cos50°≈0.6428,tan50°≈1.1918)
7、如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上。
(1)求证:△ABF∽△DFE; (2)若sin∠DFE=,求tan∠EBC的值.
A
B
C
7
24
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
