江苏省宜兴市外国语学校苏科版九年级数学下册第7章《锐角三角函数》单元复习导学案(无答案)
文档属性
| 名称 | 江苏省宜兴市外国语学校苏科版九年级数学下册第7章《锐角三角函数》单元复习导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 158.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-05 09:54:31 | ||
图片预览


文档简介
《锐角三角函数》单元复习
姓名:
知识要点:锐角三角函数的定义,特殊角的三角函数值,锐角三角函数的应用。
二、例题选讲:
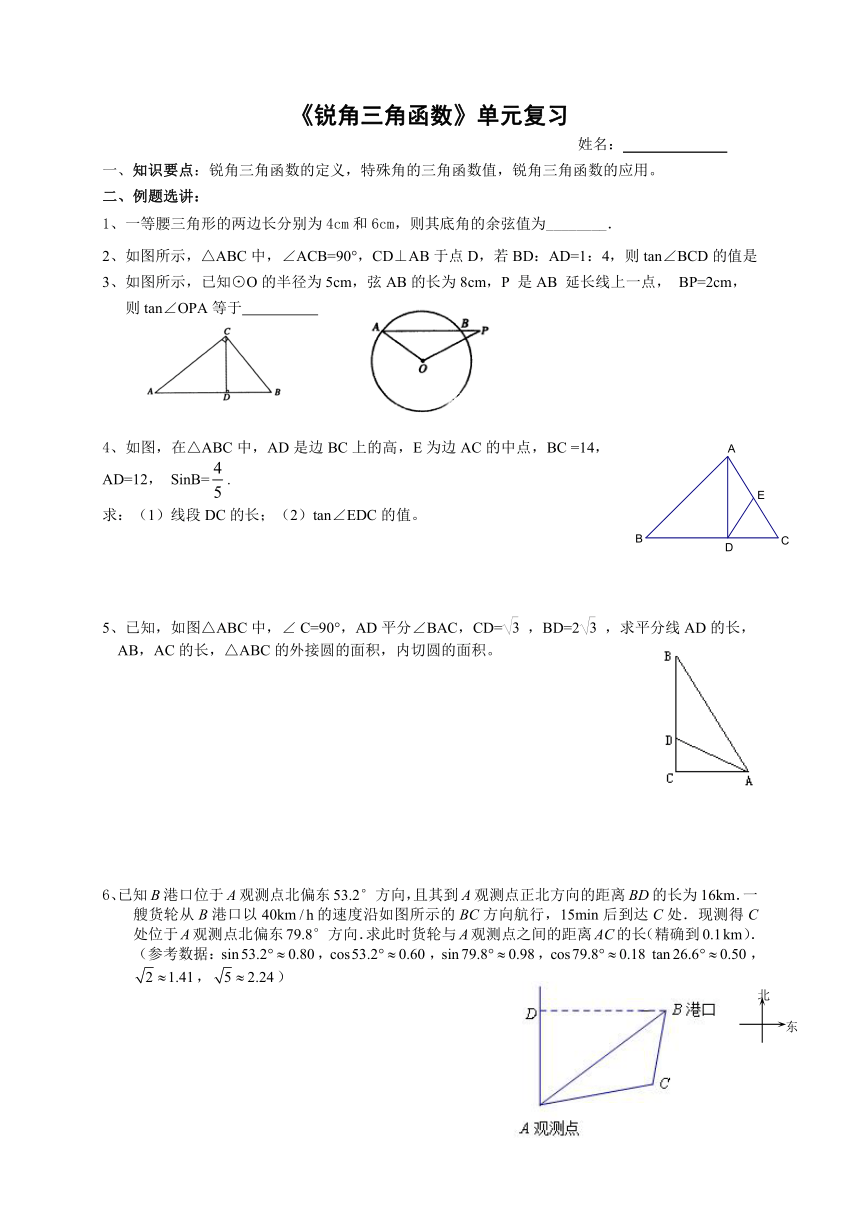
1、一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为________.
2、如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD的值是
3、如图所示,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,
则tan∠OPA等于
4、如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC =14,AD=12, SinB=.
求:(1)线段DC的长;(2)tan∠EDC的值。
5、已知,如图△ABC中,∠ C=90°,AD平分∠BAC,CD=,BD=2,求平分线AD的长,
AB,AC的长,△ABC的外接圆的面积,内切圆的面积。
6、已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km.一艘货轮从B港口以40km的速度沿如图所示的BC方向航行,15min后到达C处.现测得C处位于A观测点北偏东79.8°方向.求此时货轮与A观测点之间的距离AC的长(精确到km).
(参考数据:,,,,,)
课后练习:
1. 如图,铁路MN和公路PQ在点O处交 ( http: / / www.21cnjy.com )汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( ) A.12秒. B.16秒. C.20秒. D.24秒.
2.如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长度是( )
A.10m B.10m C.15m D.5m
(1) (2)
(3) (4) (5)
3.如图,某航天飞船在地球表面P点的正上方 ( http: / / www.21cnjy.com )A处,从A处观测到地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞船距离地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
A. , B. ,C. , D. ,
4.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长l为( )
A. B. C. D. h·sina
5.图(十六)表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,
分针垂直于桌面,A点距桌面 ( http: / / www.21cnjy.com )的高度为10公分。如图(十七),若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分( )
A. B. C.18 D.19
6.如图,是一张宽的矩形台球桌,一球从点(点在长边上)出发沿虚线射向边,然后反弹到边上的点. 如果,.那么点与点的距离为 .
(6) (7) (8) (9)
7.在一次夏令营活动中,小明同学从营地出发,要到地的北偏东60°方向的处,他先沿正东方向走了200m到达地,再沿北偏东30°方向走,恰能到达目的地(如图),那么,由此可知,两地相距 m.
8.某水库大坝的横断面是梯形,坝内斜坡的坡度i=1∶,坝外斜坡的坡度i=1∶1,则两个坡角的和为 。
9.如图,孔明同学背着一桶水,从山脚A出发,沿与地面成30°角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
10.右图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是m,则乘电梯从点B到点C上升的高度h是 m.
11.计算:(1)cos245°+tan30°·sin60°(2)(3)。
12.已知方程x2-5x·sina+1=0的一个根为2+,且a为锐角,求tana的值。
13.如图,AB是江北岸滨江路一段,长 ( http: / / www.21cnjy.com )为3千米,C为南岸一渡口,为了解决两岸交通困难,拟在渡口C处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸的最短的桥长多少?
14.如图,防洪大堤的横断面是梯形,背水坡AB的坡比(指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30 m,求高压电线杆CD的高度(结果保留三个有效数字,1.732).
15.△ABC中,AB=AC,∠B ( http: / / www.21cnjy.com )AC=36°,AD是BC边上的高,BE是∠ABC的平分线,BC=1,试利用这个三角形求出sin18°的值。(结果保留根号)
16(2015 连云港)如图,在△ ( http: / / www.21cnjy.com )ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
(1)求BD cos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
( http: / / www.21cnjy.com )
17(2013.淮安)如图,AB是⊙O的直经,C是上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.
(1)、猜想直线MN与⊙O的位置关系,并说明理由,
(2)若CD=6,cos∠ACD=,求⊙O的半经。
18.若a、b、c是△ABC的三边, a+c=2b,且方程a(1- x2)+2bx+c(1+ x2)=0有两个相等的实数根,
求sinA+sinB的值
19.台风是一种自然灾害,它以台风中心为圆心 ( http: / / www.21cnjy.com )在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测,距沿海某城市A的正南方向220千米的B处有一台风中心,其中心最大风力
为12级,每远离台风中心2 ( http: / / www.21cnjy.com )0千米,风力就会减弱一级,该台风中心现在以15千米/时的速度沿北偏东300方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
20.某河道上有一个半圆形的拱桥,河两岸筑有拦水堤坝,其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME、NF与半圆相切,上、下桥斜面的坡度i=1:3.7,桥下水深OP=5米,水面宽度CD=24米.设半圆的圆心为O,直径AB在直角顶点M、N的连线上,求从M点上坡、过桥、下坡到N点的最短路径长.(参考数据:,,)
( http: / / www.21cnjy.com )
北
东
姓名:
知识要点:锐角三角函数的定义,特殊角的三角函数值,锐角三角函数的应用。
二、例题选讲:
1、一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为________.
2、如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD的值是
3、如图所示,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,
则tan∠OPA等于
4、如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC =14,AD=12, SinB=.
求:(1)线段DC的长;(2)tan∠EDC的值。
5、已知,如图△ABC中,∠ C=90°,AD平分∠BAC,CD=,BD=2,求平分线AD的长,
AB,AC的长,△ABC的外接圆的面积,内切圆的面积。
6、已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km.一艘货轮从B港口以40km的速度沿如图所示的BC方向航行,15min后到达C处.现测得C处位于A观测点北偏东79.8°方向.求此时货轮与A观测点之间的距离AC的长(精确到km).
(参考数据:,,,,,)
课后练习:
1. 如图,铁路MN和公路PQ在点O处交 ( http: / / www.21cnjy.com )汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( ) A.12秒. B.16秒. C.20秒. D.24秒.
2.如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长度是( )
A.10m B.10m C.15m D.5m
(1) (2)
(3) (4) (5)
3.如图,某航天飞船在地球表面P点的正上方 ( http: / / www.21cnjy.com )A处,从A处观测到地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞船距离地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
A. , B. ,C. , D. ,
4.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长l为( )
A. B. C. D. h·sina
5.图(十六)表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,
分针垂直于桌面,A点距桌面 ( http: / / www.21cnjy.com )的高度为10公分。如图(十七),若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分( )
A. B. C.18 D.19
6.如图,是一张宽的矩形台球桌,一球从点(点在长边上)出发沿虚线射向边,然后反弹到边上的点. 如果,.那么点与点的距离为 .
(6) (7) (8) (9)
7.在一次夏令营活动中,小明同学从营地出发,要到地的北偏东60°方向的处,他先沿正东方向走了200m到达地,再沿北偏东30°方向走,恰能到达目的地(如图),那么,由此可知,两地相距 m.
8.某水库大坝的横断面是梯形,坝内斜坡的坡度i=1∶,坝外斜坡的坡度i=1∶1,则两个坡角的和为 。
9.如图,孔明同学背着一桶水,从山脚A出发,沿与地面成30°角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
10.右图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是m,则乘电梯从点B到点C上升的高度h是 m.
11.计算:(1)cos245°+tan30°·sin60°(2)(3)。
12.已知方程x2-5x·sina+1=0的一个根为2+,且a为锐角,求tana的值。
13.如图,AB是江北岸滨江路一段,长 ( http: / / www.21cnjy.com )为3千米,C为南岸一渡口,为了解决两岸交通困难,拟在渡口C处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸的最短的桥长多少?
14.如图,防洪大堤的横断面是梯形,背水坡AB的坡比(指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30 m,求高压电线杆CD的高度(结果保留三个有效数字,1.732).
15.△ABC中,AB=AC,∠B ( http: / / www.21cnjy.com )AC=36°,AD是BC边上的高,BE是∠ABC的平分线,BC=1,试利用这个三角形求出sin18°的值。(结果保留根号)
16(2015 连云港)如图,在△ ( http: / / www.21cnjy.com )ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
(1)求BD cos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
( http: / / www.21cnjy.com )
17(2013.淮安)如图,AB是⊙O的直经,C是上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.
(1)、猜想直线MN与⊙O的位置关系,并说明理由,
(2)若CD=6,cos∠ACD=,求⊙O的半经。
18.若a、b、c是△ABC的三边, a+c=2b,且方程a(1- x2)+2bx+c(1+ x2)=0有两个相等的实数根,
求sinA+sinB的值
19.台风是一种自然灾害,它以台风中心为圆心 ( http: / / www.21cnjy.com )在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测,距沿海某城市A的正南方向220千米的B处有一台风中心,其中心最大风力
为12级,每远离台风中心2 ( http: / / www.21cnjy.com )0千米,风力就会减弱一级,该台风中心现在以15千米/时的速度沿北偏东300方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
20.某河道上有一个半圆形的拱桥,河两岸筑有拦水堤坝,其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME、NF与半圆相切,上、下桥斜面的坡度i=1:3.7,桥下水深OP=5米,水面宽度CD=24米.设半圆的圆心为O,直径AB在直角顶点M、N的连线上,求从M点上坡、过桥、下坡到N点的最短路径长.(参考数据:,,)
( http: / / www.21cnjy.com )
北
东
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
