第27章相似单元测试卷(含答案)人教版九年级数学下册
文档属性
| 名称 | 第27章相似单元测试卷(含答案)人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 954.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 23:10:03 | ||
图片预览

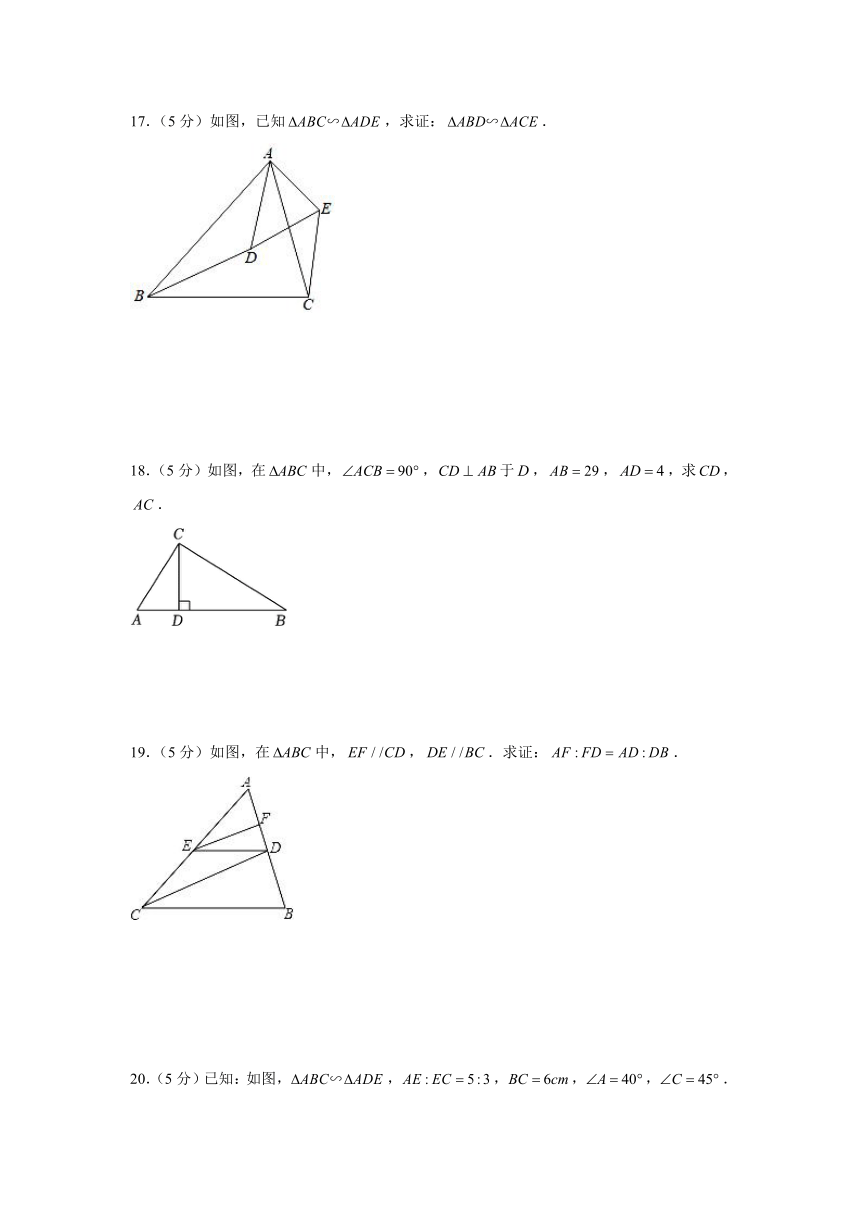

文档简介
人教新版九年级下册第27章 相似 单元测试卷(1)
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)已知,分别为,上的两点,且,,若,则的长为
A.6 B.7 C.8 D.9
2.(2分)两个相似三角形的面积比是,则这两个三角形的相似比是
A. B. C. D.
3.(2分)如图,在大小为的正方形网格中,是相似三角形的是
A.①和② B.②和③ C.①和③ D.②和④
4.(2分)已知,若与的相似比为,则与的周长比为
A. B. C. D.
5.(2分)如图,在中,,若,,则的值为
A. B. C. D.
6.(2分)如图,不能判定和相似的条件是
A. B. C. D.
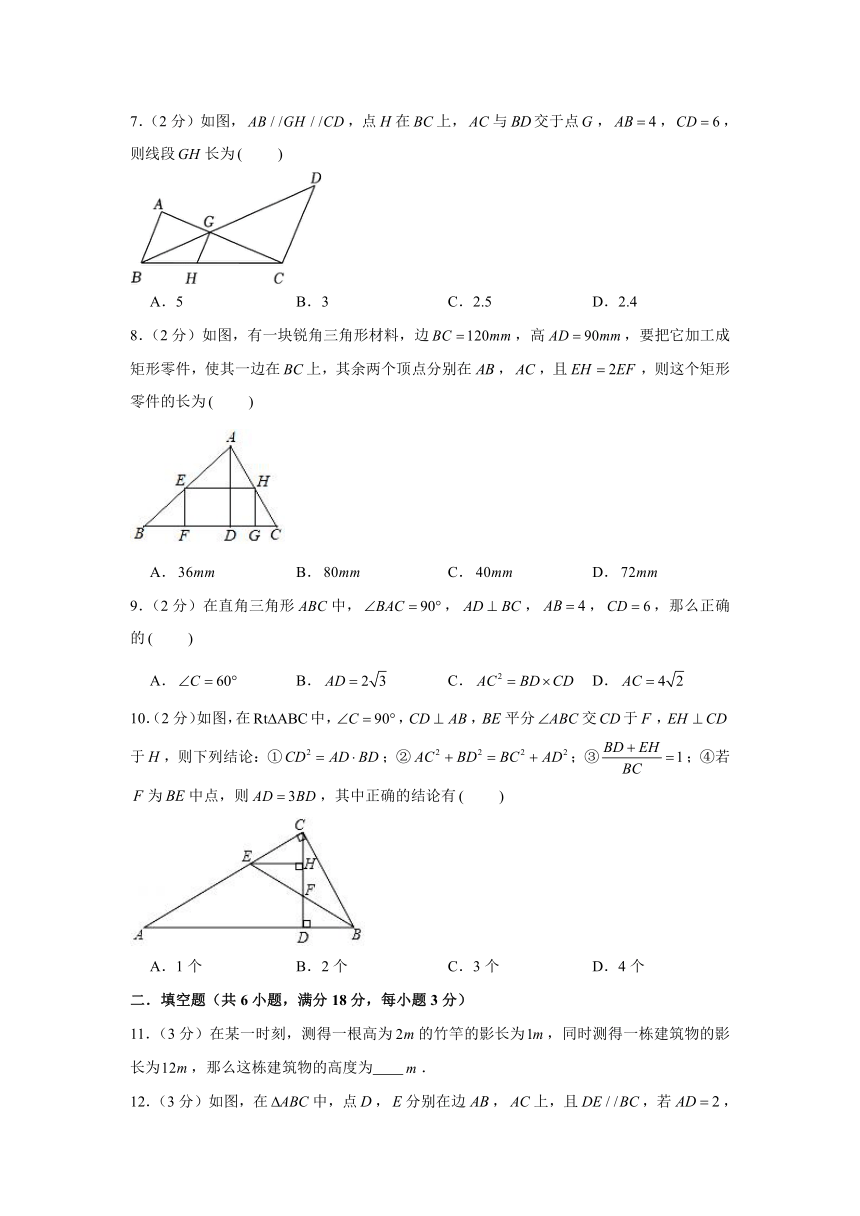
7.(2分)如图,,点在上,与交于点,,,则线段长为
A.5 B.3 C.2.5 D.2.4
8.(2分)如图,有一块锐角三角形材料,边,高,要把它加工成矩形零件,使其一边在上,其余两个顶点分别在,,且,则这个矩形零件的长为
A. B. C. D.
9.(2分)在直角三角形中,,,,,那么正确的
A. B. C. D.
10.(2分)如图,在中,,,平分交于,于,则下列结论:①;②;③;④若为中点,则,其中正确的结论有
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)在某一时刻,测得一根高为的竹竿的影长为,同时测得一栋建筑物的影长为,那么这栋建筑物的高度为 .
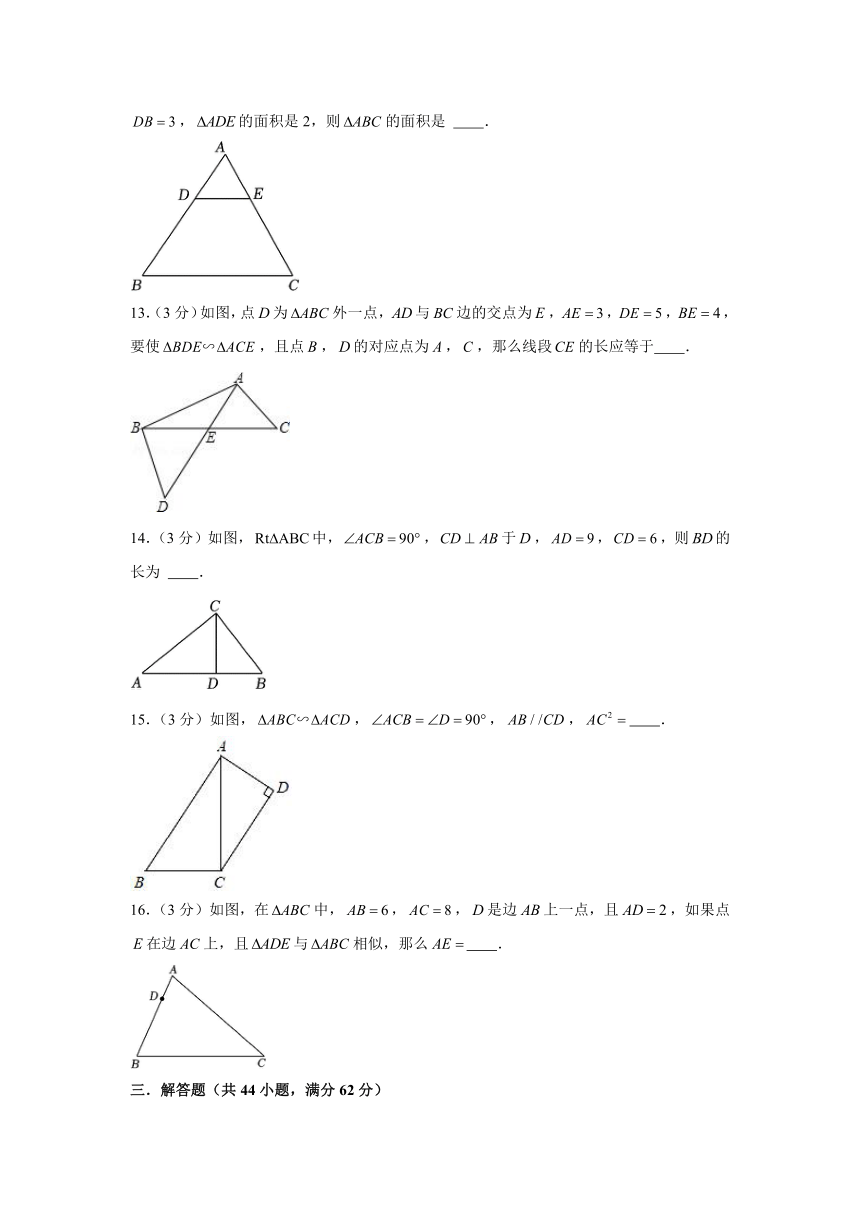
12.(3分)如图,在中,点,分别在边,上,且,若,,的面积是2,则的面积是 .
13.(3分)如图,点为外一点,与边的交点为,,,,要使,且点,的对应点为,,那么线段的长应等于 .
14.(3分)如图,中,,于,,,则的长为 .
15.(3分)如图,,,, .
16.(3分)如图,在中,,,是边上一点,且,如果点在边上,且与相似,那么 .
三.解答题(共44小题,满分62分)
17.(5分)如图,已知,求证:.
18.(5分)如图,在中,,于,,,求,.
19.(5分)如图,在中,,.求证:.
20.(5分)已知:如图,,,,,.
(1)求的大小;
(2)求的长.
21.(5分)我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开门,出北门三十步有
木,出西门七百五十步见木,问:邑方几何?”其大意是:如图,一座正方形城池在各边的中点开门.为北门的中点,出北门往正北方向30步 “步”为古代的长度单位),有一棵树木(点.为西门的中点,出西门往正西方向走750步到处正好看到处的树木,问:正方形城池的边长为多少步?请你用所学知识解决这个问题.
22.(5分)如图,已知、为的边上的两点,且满足,一条平行于的直线分别交、和的延长线于点、和,求的值.
23.(6分)已知:如图,,与交于点.
(1)若,点为的中点,且,,.试求的值;
(2)求证:.
24.(6分)如图,在矩形中,是的中点,,垂足为.
(1)求证:;
(2)若,,求的长.
25.(6分)如图,已知:在正方形中,是边的中点,连接.
(1)请用尺规作图法,在上求作一点,使得;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,求的长.
26.(6分)如图,中的平分线为,为的中点,过点作交的延长线于,交于.
(1)求证:.
(2)若,.,求的长.
27.(8分)如图,在中,,,,为边上的动点(与、不重合),,交于点,连接,设,的面积为.
(1)用含的代数式表示的长;
(2)求与的函数表达式,并求当随增大而减小时的取值范围.
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C B C B D D B D
二.填空题(共6小题,满分18分,每小题3分)
11. 24.
12. 12.5.
13. .
14. 4.
15. .
16. 或.
三.解答题(共44小题,满分62分)
17.
【解答】证明:,
,,
,
,
,
.
18.
【解答】解:,
,
,
,
,
,
,
,
,
,
.
19.
【解答】解:,,
,,
,
即.
20.
【解答】解:(1)在中,,,
;
又,
(相似三角形的对应角相等),
;
(2),
;
又,,
,
.
21.
【解答】解:由题意知:
,
,
,
,
,
设正方形城池的边长为步,
则.
解得:,(舍去),
所以正方形城池的边长为300步.
22.
【解答】解:过、分别作的平行线交于、,交于,如图,
,
,
,
,,
,
,
,
,,
,
.
23.
【解答】(1)解:,
,
,
,,
,
,
,,
,
为的中点,
,
;
(2)证明:,
,,
,,
.
24.
【解答】解:(1)四边形是矩形,
,,
,
,
,
;
(2)是的中点,,
,
,
,
四边形是矩形,
,
,
,
.
25.
【解答】解:(1)如图,即为所求.
(2)四边形是正方形,
,,
,
,
,
,
,
.
26.
【解答】解:(1)如图,过点作,交的延长线于点;
;而平分,,
,,,
,,
;而,,
,
.
(2),.,
,;
平分,
;解得:;
为的中点,
;
,
,
解得:.
27.
【解答】解:(1),
,
,,,
,
,
,
即;
(2)根据题意得,,
当时,随的增大而减小,
,
当随增大而减小时的取值范围为.
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)已知,分别为,上的两点,且,,若,则的长为
A.6 B.7 C.8 D.9
2.(2分)两个相似三角形的面积比是,则这两个三角形的相似比是
A. B. C. D.
3.(2分)如图,在大小为的正方形网格中,是相似三角形的是
A.①和② B.②和③ C.①和③ D.②和④
4.(2分)已知,若与的相似比为,则与的周长比为
A. B. C. D.
5.(2分)如图,在中,,若,,则的值为
A. B. C. D.
6.(2分)如图,不能判定和相似的条件是
A. B. C. D.
7.(2分)如图,,点在上,与交于点,,,则线段长为
A.5 B.3 C.2.5 D.2.4
8.(2分)如图,有一块锐角三角形材料,边,高,要把它加工成矩形零件,使其一边在上,其余两个顶点分别在,,且,则这个矩形零件的长为
A. B. C. D.
9.(2分)在直角三角形中,,,,,那么正确的
A. B. C. D.
10.(2分)如图,在中,,,平分交于,于,则下列结论:①;②;③;④若为中点,则,其中正确的结论有
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)在某一时刻,测得一根高为的竹竿的影长为,同时测得一栋建筑物的影长为,那么这栋建筑物的高度为 .
12.(3分)如图,在中,点,分别在边,上,且,若,,的面积是2,则的面积是 .
13.(3分)如图,点为外一点,与边的交点为,,,,要使,且点,的对应点为,,那么线段的长应等于 .
14.(3分)如图,中,,于,,,则的长为 .
15.(3分)如图,,,, .
16.(3分)如图,在中,,,是边上一点,且,如果点在边上,且与相似,那么 .
三.解答题(共44小题,满分62分)
17.(5分)如图,已知,求证:.
18.(5分)如图,在中,,于,,,求,.
19.(5分)如图,在中,,.求证:.
20.(5分)已知:如图,,,,,.
(1)求的大小;
(2)求的长.
21.(5分)我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开门,出北门三十步有
木,出西门七百五十步见木,问:邑方几何?”其大意是:如图,一座正方形城池在各边的中点开门.为北门的中点,出北门往正北方向30步 “步”为古代的长度单位),有一棵树木(点.为西门的中点,出西门往正西方向走750步到处正好看到处的树木,问:正方形城池的边长为多少步?请你用所学知识解决这个问题.
22.(5分)如图,已知、为的边上的两点,且满足,一条平行于的直线分别交、和的延长线于点、和,求的值.
23.(6分)已知:如图,,与交于点.
(1)若,点为的中点,且,,.试求的值;
(2)求证:.
24.(6分)如图,在矩形中,是的中点,,垂足为.
(1)求证:;
(2)若,,求的长.
25.(6分)如图,已知:在正方形中,是边的中点,连接.
(1)请用尺规作图法,在上求作一点,使得;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,求的长.
26.(6分)如图,中的平分线为,为的中点,过点作交的延长线于,交于.
(1)求证:.
(2)若,.,求的长.
27.(8分)如图,在中,,,,为边上的动点(与、不重合),,交于点,连接,设,的面积为.
(1)用含的代数式表示的长;
(2)求与的函数表达式,并求当随增大而减小时的取值范围.
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C B C B D D B D
二.填空题(共6小题,满分18分,每小题3分)
11. 24.
12. 12.5.
13. .
14. 4.
15. .
16. 或.
三.解答题(共44小题,满分62分)
17.
【解答】证明:,
,,
,
,
,
.
18.
【解答】解:,
,
,
,
,
,
,
,
,
,
.
19.
【解答】解:,,
,,
,
即.
20.
【解答】解:(1)在中,,,
;
又,
(相似三角形的对应角相等),
;
(2),
;
又,,
,
.
21.
【解答】解:由题意知:
,
,
,
,
,
设正方形城池的边长为步,
则.
解得:,(舍去),
所以正方形城池的边长为300步.
22.
【解答】解:过、分别作的平行线交于、,交于,如图,
,
,
,
,,
,
,
,
,,
,
.
23.
【解答】(1)解:,
,
,
,,
,
,
,,
,
为的中点,
,
;
(2)证明:,
,,
,,
.
24.
【解答】解:(1)四边形是矩形,
,,
,
,
,
;
(2)是的中点,,
,
,
,
四边形是矩形,
,
,
,
.
25.
【解答】解:(1)如图,即为所求.
(2)四边形是正方形,
,,
,
,
,
,
,
.
26.
【解答】解:(1)如图,过点作,交的延长线于点;
;而平分,,
,,,
,,
;而,,
,
.
(2),.,
,;
平分,
;解得:;
为的中点,
;
,
,
解得:.
27.
【解答】解:(1),
,
,,,
,
,
,
即;
(2)根据题意得,,
当时,随的增大而减小,
,
当随增大而减小时的取值范围为.
