第五单元 总复习立体图形的表面积和体积课件(共20张PPT)西师大版六年级下册数学
文档属性
| 名称 | 第五单元 总复习立体图形的表面积和体积课件(共20张PPT)西师大版六年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 49.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 20:07:20 | ||
图片预览




文档简介
(共20张PPT)
立体图形的表面积和体积
复习
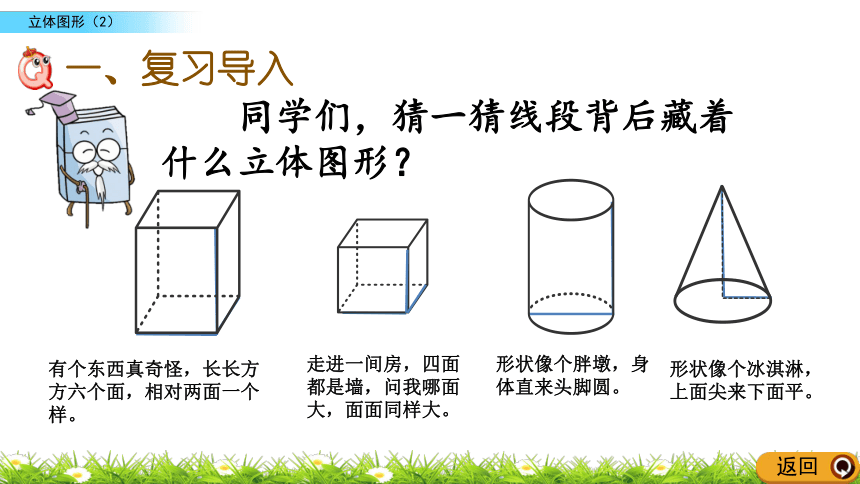
同学们,猜一猜线段背后藏着什么立体图形?
一、复习导入
有个东西真奇怪,长长方方六个面,相对两面一个样。
走进一间房,四面都是墙,问我哪面大,面面同样大。
形状像个胖墩,身体直来头脚圆。
形状像个冰淇淋,上面尖来下面平。
表面积:
一个立体图形所有面的面积总和,叫做它的表面积。
体积:
一个立体图形所占空间的大小叫做它的体积。
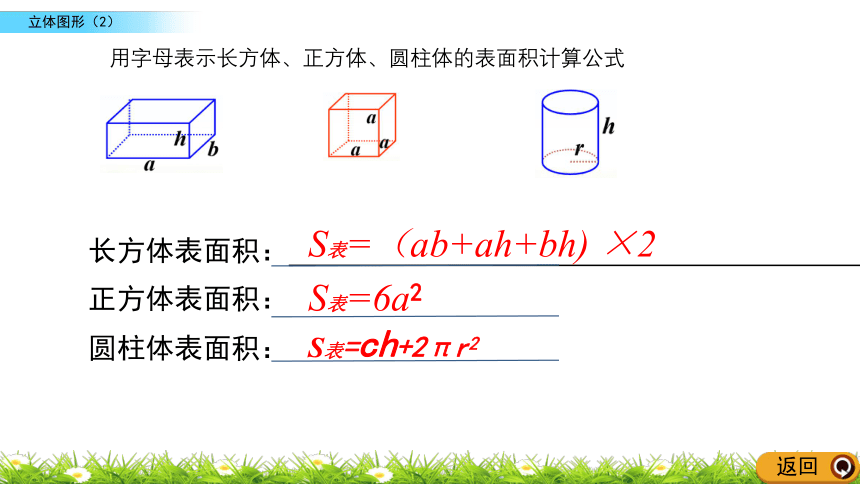
回忆长方体、正方体和圆柱体的表面积计算公式,同桌相互交流并记录下来(不会用字母表示的同学用文字记录)。
二、知识回忆与整理
长方体表面积:
正方体表面积:
圆柱体表面积:
S表=(ab+ah+bh) ×2
S表=6a2
S表=ch+2πr2
用字母表示长方体、正方体、圆柱体的表面积计算公式
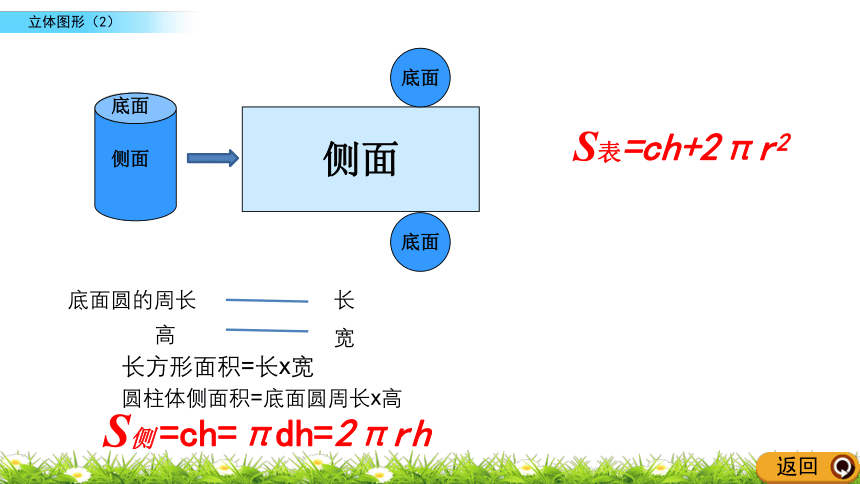
侧面
底面
长方形面积=长x宽
圆柱体侧面积=底面圆周长x高
S侧 =ch=πdh=2πrh
S表=ch+2πr2
长
底面圆的周长
宽
高
底面
底面
侧面
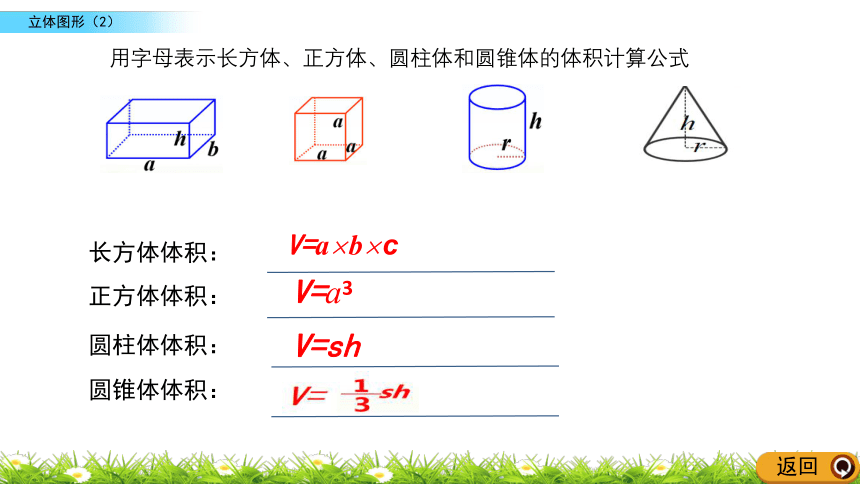
回忆长方体、正方体、圆柱体和圆锥体的体积计算公式,同桌相互交流并记录下来(不会用字母表示的同学用文字记录)。
二、知识回忆与整理
长方体体积:
正方体体积:
圆柱体体积:
V=a×b×c
V=a3
V=sh
圆锥体体积:
用字母表示长方体、正方体、圆柱体和圆锥体的体积计算公式
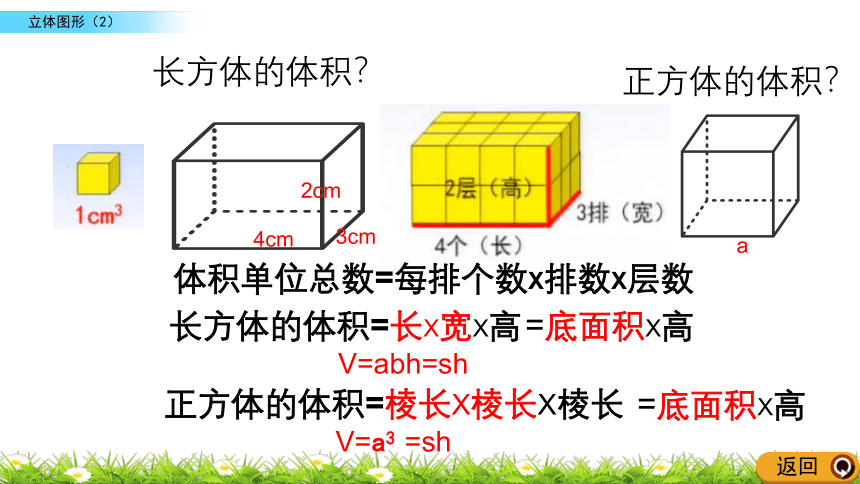
长方体的体积=长X宽X高
正方体的体积=棱长X棱长X棱长
=底面积X高
长方体的体积?
V=abh=sh
V=a3 =sh
4cm
3cm
2cm
a
正方体的体积?
=底面积X高
体积单位总数=每排个数X排数X层数
底面积 = 底面积
高 = 高
因为:长方体的体积=底面积×高
所以:圆柱体的体积=底面积×高
V长=sh
V长=sh
圆柱体的体积?
圆柱的体积是与它等底等高圆锥体积的3倍。圆锥体积等于与它等底等高圆柱体积的三分之一。
圆锥体的体积?
等底等高
思考:哪些立体图形的体积的计算可以用同一种方法计算?理由是什么?
V = sh
1、计算下列立体图形的表面积和体积?
5cm
3cm
2cm
S=(5x2+5x3+2x3)x 2 =31x2 =62c㎡
V=5X2X3 =30cm3
基础过关
S表=3x3x6=54c㎡
V=3x3x3x3=27c
3cm
2、计算圆柱的体积表面积和圆锥体的体积
d=4cm
r=4÷2=2cm
S底=3.14x2x2=12.56c㎡
h=6cm
v=12.56x6÷3=25.12c
r=6.28÷3.14÷2=1cm
S底=3.14x1x1=3.14c㎡
S侧=6.28x5=31.4c㎡
S表=31.4+3.14x2=37.68c㎡
V=3.14X5=15.7c
(1)如果要在水池的底面和内壁贴上瓷砖,贴瓷砖的面积是多少平方米?
(2)每平方米瓷砖50元,购买瓷砖需要多少元?
(3)每立方米水重1吨,这个水池最多能装多少吨水?
解决这些问题要用到哪些知识?请独立解决后再交流。
时代广场有一个圆柱形水池,底面直径4m,深1m。
挑战自我
(1)如果要在水池的底部和内壁贴上瓷砖,贴瓷砖的面积是多少平方米?
时代广场有一个圆柱形水池,底面直径4m,深1m。
12.56+12.56=25.12(m2)
答:贴瓷砖的面积是25.12平方米。
3.14x4x1=12.56(m2)
底面积:3.14×(4÷2)2=12.56m2
侧面积:
(2)每平方米瓷砖50元,购买瓷砖需要多少元?
50×25.12=1256(元)
答:购买贴瓷砖需要1256元。
时代广场有一个圆柱形水池,底面直径4m,深1m。
(3)每立方米水重1吨,这个水池最多能装多少吨水?
时代广场有一个圆柱形水池,底面直径4m,深1m。
3.14×(4÷2)2×1×1
=12.56×1
=12.56(吨)
答:这个水池最多能装12.56吨水。
四、通过这节课的复习你有什么收获
2、会计算这些立体图形的表面积或体积。
1、回忆并整理了长方体、正方体、圆柱体的表面积计算公式和圆锥体的体积计算公式。
3、能用学过的立体图形的知识解决简单的实际问题。
五、课后拓展
?
根据圆柱体的侧面积=底面周长x高
思考:长方体的侧面积=底面周长x高
底面
侧
面
侧
面
立体图形的表面积和体积
复习
同学们,猜一猜线段背后藏着什么立体图形?
一、复习导入
有个东西真奇怪,长长方方六个面,相对两面一个样。
走进一间房,四面都是墙,问我哪面大,面面同样大。
形状像个胖墩,身体直来头脚圆。
形状像个冰淇淋,上面尖来下面平。
表面积:
一个立体图形所有面的面积总和,叫做它的表面积。
体积:
一个立体图形所占空间的大小叫做它的体积。
回忆长方体、正方体和圆柱体的表面积计算公式,同桌相互交流并记录下来(不会用字母表示的同学用文字记录)。
二、知识回忆与整理
长方体表面积:
正方体表面积:
圆柱体表面积:
S表=(ab+ah+bh) ×2
S表=6a2
S表=ch+2πr2
用字母表示长方体、正方体、圆柱体的表面积计算公式
侧面
底面
长方形面积=长x宽
圆柱体侧面积=底面圆周长x高
S侧 =ch=πdh=2πrh
S表=ch+2πr2
长
底面圆的周长
宽
高
底面
底面
侧面
回忆长方体、正方体、圆柱体和圆锥体的体积计算公式,同桌相互交流并记录下来(不会用字母表示的同学用文字记录)。
二、知识回忆与整理
长方体体积:
正方体体积:
圆柱体体积:
V=a×b×c
V=a3
V=sh
圆锥体体积:
用字母表示长方体、正方体、圆柱体和圆锥体的体积计算公式
长方体的体积=长X宽X高
正方体的体积=棱长X棱长X棱长
=底面积X高
长方体的体积?
V=abh=sh
V=a3 =sh
4cm
3cm
2cm
a
正方体的体积?
=底面积X高
体积单位总数=每排个数X排数X层数
底面积 = 底面积
高 = 高
因为:长方体的体积=底面积×高
所以:圆柱体的体积=底面积×高
V长=sh
V长=sh
圆柱体的体积?
圆柱的体积是与它等底等高圆锥体积的3倍。圆锥体积等于与它等底等高圆柱体积的三分之一。
圆锥体的体积?
等底等高
思考:哪些立体图形的体积的计算可以用同一种方法计算?理由是什么?
V = sh
1、计算下列立体图形的表面积和体积?
5cm
3cm
2cm
S=(5x2+5x3+2x3)x 2 =31x2 =62c㎡
V=5X2X3 =30cm3
基础过关
S表=3x3x6=54c㎡
V=3x3x3x3=27c
3cm
2、计算圆柱的体积表面积和圆锥体的体积
d=4cm
r=4÷2=2cm
S底=3.14x2x2=12.56c㎡
h=6cm
v=12.56x6÷3=25.12c
r=6.28÷3.14÷2=1cm
S底=3.14x1x1=3.14c㎡
S侧=6.28x5=31.4c㎡
S表=31.4+3.14x2=37.68c㎡
V=3.14X5=15.7c
(1)如果要在水池的底面和内壁贴上瓷砖,贴瓷砖的面积是多少平方米?
(2)每平方米瓷砖50元,购买瓷砖需要多少元?
(3)每立方米水重1吨,这个水池最多能装多少吨水?
解决这些问题要用到哪些知识?请独立解决后再交流。
时代广场有一个圆柱形水池,底面直径4m,深1m。
挑战自我
(1)如果要在水池的底部和内壁贴上瓷砖,贴瓷砖的面积是多少平方米?
时代广场有一个圆柱形水池,底面直径4m,深1m。
12.56+12.56=25.12(m2)
答:贴瓷砖的面积是25.12平方米。
3.14x4x1=12.56(m2)
底面积:3.14×(4÷2)2=12.56m2
侧面积:
(2)每平方米瓷砖50元,购买瓷砖需要多少元?
50×25.12=1256(元)
答:购买贴瓷砖需要1256元。
时代广场有一个圆柱形水池,底面直径4m,深1m。
(3)每立方米水重1吨,这个水池最多能装多少吨水?
时代广场有一个圆柱形水池,底面直径4m,深1m。
3.14×(4÷2)2×1×1
=12.56×1
=12.56(吨)
答:这个水池最多能装12.56吨水。
四、通过这节课的复习你有什么收获
2、会计算这些立体图形的表面积或体积。
1、回忆并整理了长方体、正方体、圆柱体的表面积计算公式和圆锥体的体积计算公式。
3、能用学过的立体图形的知识解决简单的实际问题。
五、课后拓展
?
根据圆柱体的侧面积=底面周长x高
思考:长方体的侧面积=底面周长x高
底面
侧
面
侧
面
