第5章二次函数的综合应用导学案(无答案)
文档属性
| 名称 | 第5章二次函数的综合应用导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 158.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-05 00:00:00 | ||
图片预览

文档简介
宜兴外国语学校初三年级数学导学提纲
课题:二次函数综合运用 班级 姓名
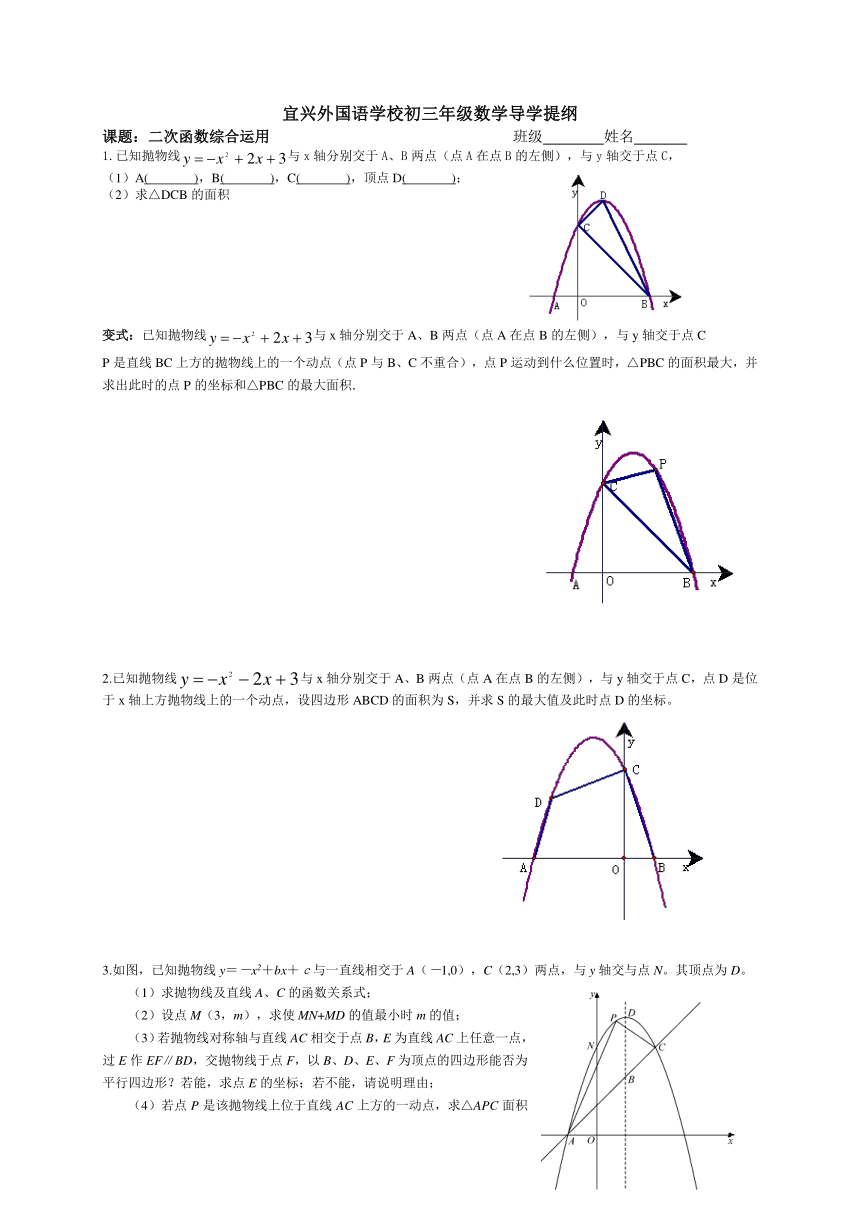
1.已知抛物线与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于点C,
(1)A( ),B( ),C( ),顶点D( );
(2)求△DCB的面积
变式:已知抛物线与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于点C
P是直线BC上方的抛物线上的一个动点(点 ( http: / / www.21cnjy.com )P与B、C不重合),点P运动到什么位置时,△PBC的面积最大,并求出此时的点P的坐标和△PBC的最大面积.
2.已知抛物线与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是位于x轴上方抛物线上的一个动点,设四边形ABCD的面积为S,并求S的最大值及此时点D的坐标。
3.如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交与点N。其顶点为D。
(1)求抛物线及直线A、C的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线对称轴与直线AC相交于点B, ( http: / / www.21cnjy.com )E为直线AC上任意一点,过E作EF∥BD,交抛物线于点F,以B、D、E、F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若点P是该抛物线上位于直线AC上方的一动点,求△APC面积的最大值.
4.如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求及;
(3)是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
5.在平面直角坐标系中,二次函数的图像与轴交于点A,B(点B在点A的左侧),与轴交于点C.过动点H(0, )作平行于轴的直线,直线与二次函数的图像相交于点D,E.
(1)写出点A,点B的坐标;
(2)若,以DE为直径作⊙Q,当⊙Q与轴相切时,求的值;
(3)直线上是否存在一点F,使得△ACF是等腰直角三角形 若存在,求的值;若不存在,请说明理由.
6.如图,已知直线交坐标轴于两点,以线段AB为边向上作正方形,过点的抛物线与直线另一个交点为.
(1)请直接写出点的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒个单位长度的速度沿射线AB下滑,直至顶点D落在轴上时停止.设正方形落在轴下方部分的面积为,求关于滑行时间的函数关系式,并写出相应自变量的取值范围;
(4)在(3)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上两点间的抛物线弧所扫过的面积.
7.如图①,在平面直角坐标系中,一块等腰直角三角板ABC的直角顶点A在y轴上,坐标为(0,﹣1),另一顶点B坐标为(﹣2,0),已知二次函数y=x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式;
(2)若运动过程中直尺的边A′D′交边BC于点M,交抛物线于点N,求线段MN长度的最大值;
(3)如图②,设点P为直尺的边A′D′上的任一点,连接PA、PB、PC,Q为BC的中点,试探究:在直尺平移的过程中,当PQ=时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A在抛物线内,点C在抛物线上,点D′在抛物线外.)
课题:二次函数综合运用 班级 姓名
1.已知抛物线与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于点C,
(1)A( ),B( ),C( ),顶点D( );
(2)求△DCB的面积
变式:已知抛物线与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于点C
P是直线BC上方的抛物线上的一个动点(点 ( http: / / www.21cnjy.com )P与B、C不重合),点P运动到什么位置时,△PBC的面积最大,并求出此时的点P的坐标和△PBC的最大面积.
2.已知抛物线与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是位于x轴上方抛物线上的一个动点,设四边形ABCD的面积为S,并求S的最大值及此时点D的坐标。
3.如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交与点N。其顶点为D。
(1)求抛物线及直线A、C的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线对称轴与直线AC相交于点B, ( http: / / www.21cnjy.com )E为直线AC上任意一点,过E作EF∥BD,交抛物线于点F,以B、D、E、F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若点P是该抛物线上位于直线AC上方的一动点,求△APC面积的最大值.
4.如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求及;
(3)是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
5.在平面直角坐标系中,二次函数的图像与轴交于点A,B(点B在点A的左侧),与轴交于点C.过动点H(0, )作平行于轴的直线,直线与二次函数的图像相交于点D,E.
(1)写出点A,点B的坐标;
(2)若,以DE为直径作⊙Q,当⊙Q与轴相切时,求的值;
(3)直线上是否存在一点F,使得△ACF是等腰直角三角形 若存在,求的值;若不存在,请说明理由.
6.如图,已知直线交坐标轴于两点,以线段AB为边向上作正方形,过点的抛物线与直线另一个交点为.
(1)请直接写出点的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒个单位长度的速度沿射线AB下滑,直至顶点D落在轴上时停止.设正方形落在轴下方部分的面积为,求关于滑行时间的函数关系式,并写出相应自变量的取值范围;
(4)在(3)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上两点间的抛物线弧所扫过的面积.
7.如图①,在平面直角坐标系中,一块等腰直角三角板ABC的直角顶点A在y轴上,坐标为(0,﹣1),另一顶点B坐标为(﹣2,0),已知二次函数y=x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式;
(2)若运动过程中直尺的边A′D′交边BC于点M,交抛物线于点N,求线段MN长度的最大值;
(3)如图②,设点P为直尺的边A′D′上的任一点,连接PA、PB、PC,Q为BC的中点,试探究:在直尺平移的过程中,当PQ=时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A在抛物线内,点C在抛物线上,点D′在抛物线外.)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
