江苏省宜兴市外国语学校苏科版八年级数学上册3.1《勾股定理》导学案(无答案)
文档属性
| 名称 | 江苏省宜兴市外国语学校苏科版八年级数学上册3.1《勾股定理》导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 33.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-05 15:38:37 | ||
图片预览

文档简介
宜兴外国语学校初二数学学科导学提纲 姓名: 班级:
课题:3.1勾股定理 设计人:沈大军 审核人:初二数学备课组
一.预习内容:认真阅读课本
二.尝试探索:
【做一做】
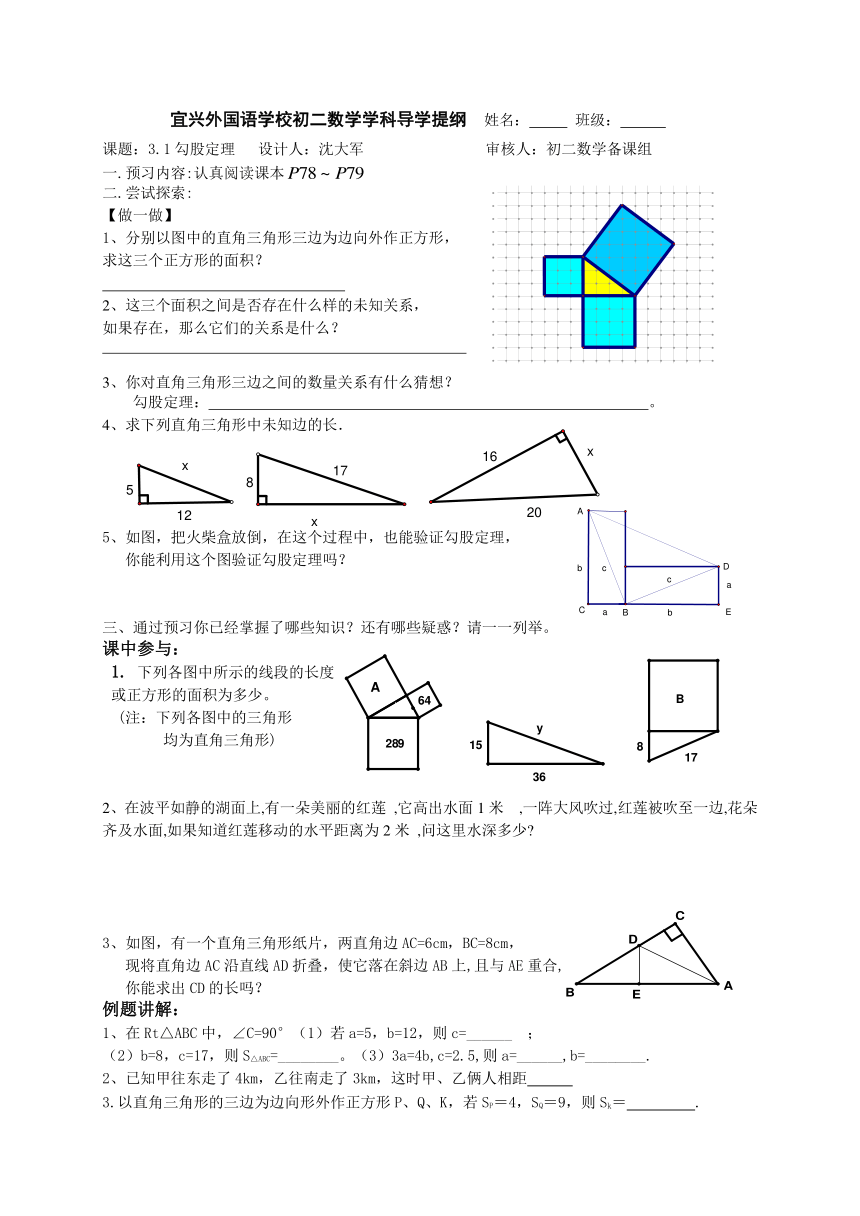
1、分别以图中的直角三角形三边为边向外作正方形,
求这三个正方形的面积?
2、这三个面积之间是否存在什么样的未知关系,
如果存在,那么它们的关系是什么?
3、你对直角三角形三边之间的数量关系有什么猜想?
勾股定理: 。
4、求下列直角三角形中未知边的长.
5、如图,把火柴盒放倒,在这个过程中,也能验证勾股定理,
你能利用这个图验证勾股定理吗?
三、通过预习你已经掌握了哪些知识?还有哪些疑惑?请一一列举。
课中参与:
下列各图中所示的线段的长度
或正方形的面积为多少。
(注:下列各图中的三角形
均为直角三角形)
2、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?
3、如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,
现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,
你能求出CD的长吗?
例题讲解:
1、在Rt△ABC中,∠C=90°(1)若a=5,b=12,则c=______ ;
(2)b=8,c=17,则S△ABC=________。(3)3a=4b,c=2.5,则a=______,b=________.
2、已知甲往东走了4km,乙往南走了3km,这时甲、乙俩人相距
3.以直角三角形的三边为边向形外作正方形P、Q、K,若SP=4,SQ=9,则Sk= .
4、在Rt△ABC中,∠C=90,周长为60,斜边与一条直角边之比为13∶5,则这个三角形三边长分别是( )A、5、4、3、; B、13、12、5; C、10、8、6; D、26、24、10
5、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,
要爬行的最短路程( )(取3)
A.20cm; B.10cm; C.14cm; D.无法确定.
6、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,
那么第三边上的高为 ( ) A. 12 cm B. 10 cm C. 8 cm D. 6 cm
7、一等腰三角形底边长为10cm,腰长为13cm,则腰上的高为 ( )
A. 12cm B. C. D.
三、你能用所学知识解决下列问题
8、如图,在⊿ABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB与D,
求:(1),AC的长; (2)⊿ABC的面积; (3)CD的长。
9、受台风影响,一棵9米高的树断裂,树的顶部落在离树跟底部3米处,这棵树折断后离地面有多高? (画出示意图)
10、假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走了3千米,再折向北走了6千米处往东一拐,仅走了1千米就找到宝藏,问登陆点A到宝藏埋藏点B的距离是多少千米?
11、已知:如图,△ABC中,AB=10,BC=9,AC=17. 求BC边上的高.
课题:3.1勾股定理 设计人:沈大军 审核人:初二数学备课组
一.预习内容:认真阅读课本
二.尝试探索:
【做一做】
1、分别以图中的直角三角形三边为边向外作正方形,
求这三个正方形的面积?
2、这三个面积之间是否存在什么样的未知关系,
如果存在,那么它们的关系是什么?
3、你对直角三角形三边之间的数量关系有什么猜想?
勾股定理: 。
4、求下列直角三角形中未知边的长.
5、如图,把火柴盒放倒,在这个过程中,也能验证勾股定理,
你能利用这个图验证勾股定理吗?
三、通过预习你已经掌握了哪些知识?还有哪些疑惑?请一一列举。
课中参与:
下列各图中所示的线段的长度
或正方形的面积为多少。
(注:下列各图中的三角形
均为直角三角形)
2、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?
3、如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,
现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,
你能求出CD的长吗?
例题讲解:
1、在Rt△ABC中,∠C=90°(1)若a=5,b=12,则c=______ ;
(2)b=8,c=17,则S△ABC=________。(3)3a=4b,c=2.5,则a=______,b=________.
2、已知甲往东走了4km,乙往南走了3km,这时甲、乙俩人相距
3.以直角三角形的三边为边向形外作正方形P、Q、K,若SP=4,SQ=9,则Sk= .
4、在Rt△ABC中,∠C=90,周长为60,斜边与一条直角边之比为13∶5,则这个三角形三边长分别是( )A、5、4、3、; B、13、12、5; C、10、8、6; D、26、24、10
5、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,
要爬行的最短路程( )(取3)
A.20cm; B.10cm; C.14cm; D.无法确定.
6、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,
那么第三边上的高为 ( ) A. 12 cm B. 10 cm C. 8 cm D. 6 cm
7、一等腰三角形底边长为10cm,腰长为13cm,则腰上的高为 ( )
A. 12cm B. C. D.
三、你能用所学知识解决下列问题
8、如图,在⊿ABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB与D,
求:(1),AC的长; (2)⊿ABC的面积; (3)CD的长。
9、受台风影响,一棵9米高的树断裂,树的顶部落在离树跟底部3米处,这棵树折断后离地面有多高? (画出示意图)
10、假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走了3千米,再折向北走了6千米处往东一拐,仅走了1千米就找到宝藏,问登陆点A到宝藏埋藏点B的距离是多少千米?
11、已知:如图,△ABC中,AB=10,BC=9,AC=17. 求BC边上的高.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
