【期末高频易错考点】第1单元分数加减法高频易错押题卷(单元测试)-2024-2025学年五年级下册数学北师大版(含解析)
文档属性
| 名称 | 【期末高频易错考点】第1单元分数加减法高频易错押题卷(单元测试)-2024-2025学年五年级下册数学北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 639.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 22:13:31 | ||
图片预览




文档简介
第1章练习卷
一.选择题(共5小题)
1.(2023春 高淳区期末)下面三个算式中的“8”和“3”可以直接相加减的是( )
A.0.08 B.5.89﹣2.3 C.
2.(2023春 启东市期末)计算时,需要先通分,这是因为通分后,会使( ),从而可以直接相加。
A.相同数位对齐 B.分子相同
C.分数单位相同 D.无法确定
3.(2023春 靖安县期末)两个数的和比其中一个数大,比另一个大,这两个数的和是( )
A. B.1 C. D.
4.(2023春 永嘉县期末)下列说法中,正确的有( )题。
①两个质数的和一定是合数。
②在,,,,中,能化成有限小数的有4个。
③因为42÷7=6所以42是7的倍数,7是42的因数。
④由图可见,阴影部分的长度是米。
A.1 B.2 C.3 D.4
5.(2023春 祥符区期末)转化思想是数学中的一种重要思想,下面体现转化思想的有( )个。
①
A.1 B.2 C.3
二.填空题(共5小题)
6.(2022秋 沂源县期中)一本书,小红已经看了这本书的,还剩 没看;千克比 千克重千克。
7.(2022春 岷县期末)比多的数是 ,比多 。
8.(2022春 揭阳期末)比m少m是 m
比 kg轻kg是kg
9.(2022春 华安县期末)将算式改写成小数加法为 + ,计算结果为 。
10.(2022春 永城市期末)
+ =
三.判断题(共7小题)
11.(2013春 奉化市校级期末)可以化成有限小数. .
12.(2012秋 沧州期末)再加上29个这样的分数单位就是最小的合数. .
13.(2013春 当涂县期末)、和都能化成有限小数.
14.(2013春 双峰县期末)能化成有限小数,不能化成有限小数.
15.(2012 团风县校级模拟)因为的分母含有2、5以外的质因数,所以不能化为有限小数. .
16.(2013春 鄂城区月考)不能化成有限小数. .
17.(2012 台州校级自主招生)因为12=2×2×3,所以用12做分母的分数不能化成有限小数. .
四.计算题(共1小题)
18.(2024春 东坡区期末)直接写出下面各题的得数。
①2.3+3.67= ②11﹣9.5= ③65.8÷10= ④2.5×4=
⑤ ⑥ ⑦ ⑧
⑨ ⑩
五.连线题(共1小题)
19.(2023春 金乡县期中)把相等的两个数用线连起来。
5
2 3 0.5
六.操作题(共1小题)
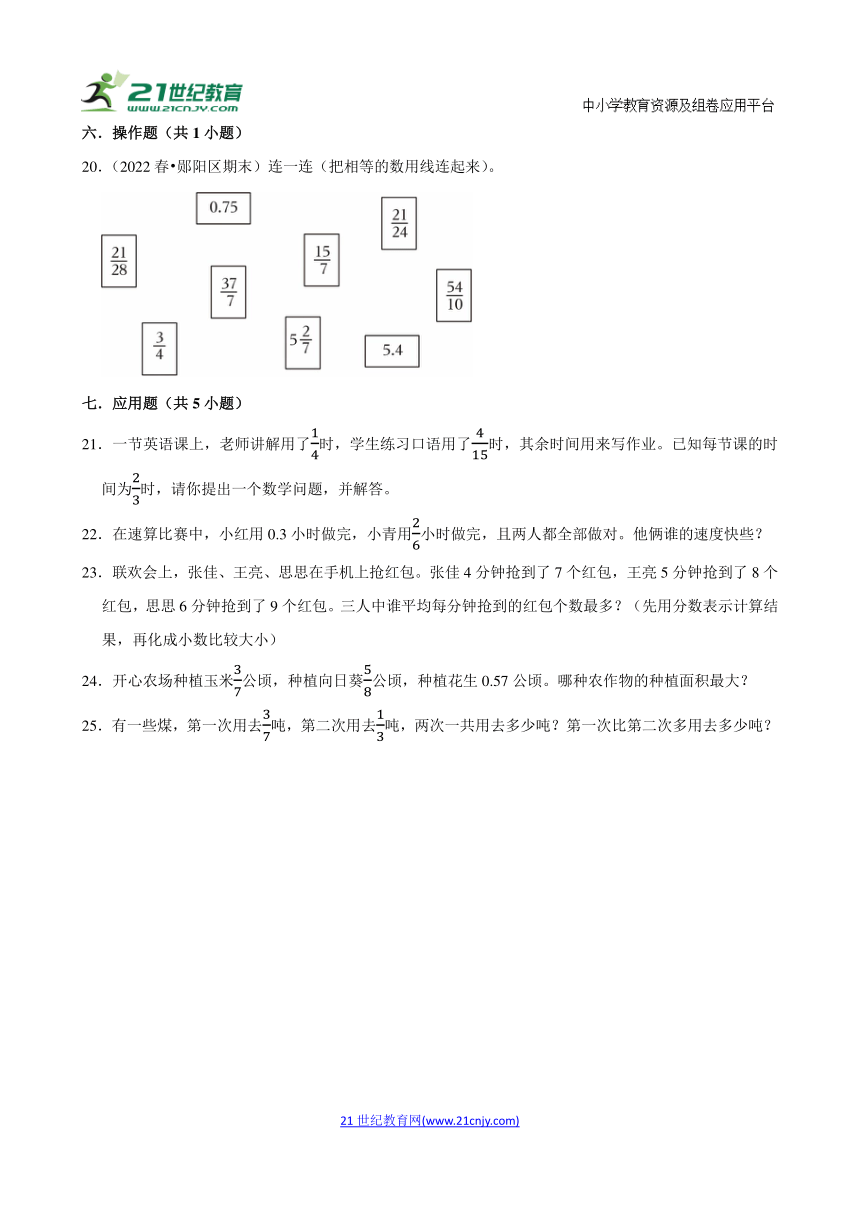
20.(2022春 郧阳区期末)连一连(把相等的数用线连起来)。
七.应用题(共5小题)
21.一节英语课上,老师讲解用了时,学生练习口语用了时,其余时间用来写作业。已知每节课的时间为时,请你提出一个数学问题,并解答。
22.在速算比赛中,小红用0.3小时做完,小青用小时做完,且两人都全部做对。他俩谁的速度快些?
23.联欢会上,张佳、王亮、思思在手机上抢红包。张佳4分钟抢到了7个红包,王亮5分钟抢到了8个红包,思思6分钟抢到了9个红包。三人中谁平均每分钟抢到的红包个数最多?(先用分数表示计算结果,再化成小数比较大小)
24.开心农场种植玉米公顷,种植向日葵公顷,种植花生0.57公顷。哪种农作物的种植面积最大?
25.有一些煤,第一次用去吨,第二次用去吨,两次一共用去多少吨?第一次比第二次多用去多少吨?
第1章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.(2023春 高淳区期末)下面三个算式中的“8”和“3”可以直接相加减的是( )
A.0.08 B.5.89﹣2.3 C.
【考点】分数的加法和减法;小数的加法和减法.
【专题】运算能力.
【答案】B
【分析】只有相同计数单位或分数单位上的数字才能直接相加减,据此解答。
【解答】解:A选项,0.080.08+0.3,8”和“3”不在相同的计数单位,所以不能直接相加。
B选项,5.89﹣2.3,“8”和“3”在相同的计数单位,所以能直接相减。
C选项,,两个分数的计数单位不同,8”和“3”不能直接相减。
所以“8”和“3”可以直接相加减的是5.89﹣2.3。
故选:B。
【点评】本题解题的关键是熟练掌握分数,小数加减法的算理。
2.(2023春 启东市期末)计算时,需要先通分,这是因为通分后,会使( ),从而可以直接相加。
A.相同数位对齐 B.分子相同
C.分数单位相同 D.无法确定
【考点】分数的加法和减法.
【专题】运算能力.
【答案】C
【分析】根据异分母分数加减法的计算方法,计算时,需要先通分,这是因为通分后,会使分数单位相同,从而可以直接相加。
【解答】解:计算时,需要先通分,这是因为通分后,会使分数单位相同,从而可以直接相加。
故选:C。
【点评】本题解题的关键是熟练后掌握异分母分数加减法的计算方法的算理。
3.(2023春 靖安县期末)两个数的和比其中一个数大,比另一个大,这两个数的和是( )
A. B.1 C. D.
【考点】分数的加法和减法.
【专题】文字叙述题;运算能力.
【答案】C
【分析】根据题意:两个数的和比其中一个数大,因为和=加数+加数,和比其中的一个加数多的数就是另一个加数,即另一个加数是;比另一个大,即其中的一个加数是,知道两个加数是多少,求和用加法.
【解答】解:
答:这两个数的和是.
故选:C.
【点评】解答此题关键是根据题意找出两个加数分别是多少,再列式计算.
4.(2023春 永嘉县期末)下列说法中,正确的有( )题。
①两个质数的和一定是合数。
②在,,,,中,能化成有限小数的有4个。
③因为42÷7=6所以42是7的倍数,7是42的因数。
④由图可见,阴影部分的长度是米。
A.1 B.2 C.3 D.4
【考点】小数与分数的互化;因数和倍数的意义;合数与质数的初步认识;分数的意义和读写.
【专题】分数和百分数;数感.
【答案】C
【分析】①一个数只有1和它本身两个因数,这个数叫做质数。一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数。两个质数的和可能是质数,也可能是合数;
②分数化成小数:用分子除以分母,按照除数是整数的小数除法进行计算,能除尽的就化成有限小数,不能除尽的就不能化为有限小数;
③根据因数和倍数的意义,如果数a能被数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;
④观察图可知,把1米看作单位“1”,平均分成5份,阴影部分占其中的2份,根据分数的意义,用分数表示为米。据此解答。
【解答】解:①两个质数的和可能是质数,也可能是合数,
例如:2+3=5
3+5=8
5是质数,8是合数,原题干说法错误;
②0.2
0.83
1.8
0.3
0.6875
、、、可以化为有限小数,共4个,原题干说法正确。
③因为42÷7=6所以42是7的倍数,7是42的因数。原题干说法正确。
④根据分数的意义,可知阴影部分的长度是米。原题干说法正确。
所以正确的有3题。
故选:C。
【点评】本题主要考查了质数和合数的认识、分数和小数的互化、因数和倍数的定义、分数的意义,关键是要掌握相关的知识点。
5.(2023春 祥符区期末)转化思想是数学中的一种重要思想,下面体现转化思想的有( )个。
①
A.1 B.2 C.3
【考点】异分母分数加减法.
【专题】模型思想.
【答案】C
【分析】“转化思想”是数学学习过程中常用的思想方法,是把未学习过的知识转化成已经学习过的知识进行研究,观察给出的3个题目,看是否运用了转化的思想,从而解决问题。
【解答】解:①,这是通过通分,把异分母分数的减法转化成同分母分数的减法进行计算,这是运用了转化的思想;
,这是把平行四边形的面积转化成长方形的面积,运用了转化的思想;
,这是把不规则物体的体积转化成水的体积,运用了转化的思想。
体现转化思想的有3个。
故选:C。
【点评】本题考查了转化思想的运用,把转化的思想运用到数学问题中。
二.填空题(共5小题)
6.(2022秋 沂源县期中)一本书,小红已经看了这本书的,还剩 没看;千克比 千克重千克。
【考点】分数的加法和减法.
【专题】应用意识.
【答案】,。
【分析】把这本书的页数看作单位“1”,用1减;根据减法算式中各部分间的关系即可解答。(千克)。
【解答】解:1
答:还剩没看。
(千克)
答:千克比千克重千克。
故答案为:,。
【点评】此题是考查分数加、减法的意义及应用、分数加法的意义与整数加减法的意义相同。
7.(2022春 岷县期末)比多的数是 ,比多 。
【考点】分数的加法和减法.
【专题】运算能力.
【答案】,。
【分析】比多的数是(),比多的数是(),计算时先通分,再按同分母加、减法法则计算。
【解答】解:,
答:比多的数是,比多。
故答案为:,。
【点评】本题考查异分母分数加法、减法知识点,先通分,再按同分母加法、减法法则计算。
8.(2022春 揭阳期末)比m少m是 m
比 kg轻kg是kg
【考点】分数的加法和减法.
【专题】运算能力.
【答案】;。
【分析】(1)求比m少m是多少m,题干中的两个分数都有单位,都表示具体的长度,所以直接相减即可解答。
(2)比多少kg轻kg是kg,题干中的两个数都有单位,都表示具体的质量,因为要求的数是比kg多kg的数,所以直接相加即可解答。
【解答】解:(1)(m)
(2)(kg)
答:比m少m是m;比kg轻kg是kg。
故答案为:;。
【点评】本题考查了异分母分数的加减法的计算方法。
9.(2022春 华安县期末)将算式改写成小数加法为 0.25 + 0.025 ,计算结果为 0.275 。
【考点】小数与分数的互化;小数的加法和减法.
【专题】运算能力.
【答案】0.25;0.025;0.275。
【分析】根据小数的意义,先把和化成小数后,再计算结果。
【解答】解:
=0.25+0.025
=0.275
答:将算式改写成小数加法为0.25+0.025,计算结果为0.275。
故答案为:0.25;0.025;0.275。
【点评】本题解题关键是理解小数的意义,熟练掌握小数加法的计算方法。
10.(2022春 永城市期末)
+ =
【考点】分数的加法和减法.
【专题】分数和百分数;运算能力.
【答案】,,。
【分析】首先通分,然后按照同分母分数相加(减)的法则进行运算即可。
【解答】解:
故答案为:,,。
【点评】此题主要考查了分数加减法的运算方法,要熟练掌握,解答此题的关键是要明确:(1)同分母分数相加(减),分子进行相加(减)得数作分子,分母不变;(2)异分母分数相加(减),首先通分,然后按照同分母分数相加(减)的法则进行运算即可。
三.判断题(共7小题)
11.(2013春 奉化市校级期末)可以化成有限小数. √ .
【考点】小数与分数的互化.
【专题】运算顺序及法则.
【答案】见试题解答内容
【分析】首先把化简成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.
【解答】解:,的分母中只含有质因数2,所以能化成有限小数.
故题干的说法是正确的.
故答案为:√.
【点评】此题主要考查判断一个分数能否化成有限小数的方法,根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.就能很快判断出什么样的分数能化成有限小数,什么样的分数不能化成有限小数.
12.(2012秋 沧州期末)再加上29个这样的分数单位就是最小的合数. √ .
【考点】分数的加法和减法;合数与质数的初步认识.
【专题】综合判断题;运算顺序及法则.
【答案】见试题解答内容
【分析】根据分数的意义可得,的分数单位是;最小的合数是4,用4得出结果即可判断本题.
【解答】解:根据分数的意义可知,的分数单位是;
4;
里面有29个;
所以,再加上29个这样的分数单位就是最小的合数4.
故答案为:√.
【点评】一个分数的分母是几,其分数单位就是几分之一,分子是几,就含有几个分数单位(带分数除外);注意最小的合数是4.
13.(2013春 当涂县期末)、和都能化成有限小数. √
【考点】小数与分数的互化.
【专题】运算顺序及法则.
【答案】见试题解答内容
【分析】根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.不是最简分数,先把它化成最简分数,再根据分母的情况作出判断.
【解答】解:不是最简分数,化简为,分母中只含有质因数5,能化成有限小数;
是最简分数,分母中只含有质因数2,能化成有限小数;
都是最简分数,分母中只含有质因数2,能化成有限小数;
所以、、都能化成有限小数;
故答案为:√.
【点评】此题主要考查什么样的分数可以化成有限小数,一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数.
14.(2013春 双峰县期末)能化成有限小数,不能化成有限小数. ×
【考点】小数与分数的互化.
【专题】分数和百分数.
【答案】见试题解答内容
【分析】首先,要看分数是否是最简分数,不是的,先把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数;不是最简分数,先把它化成最简分数,再根据分母的情况作出判断.
【解答】解:能化成有限小数,不是最简分数,不能直接看分母的情况,化简后是,分母中只含有质因数2,能化成有限小数;
故答案为:×.
【点评】此题主要考查什么样的分数可以化成有限小数,根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.
15.(2012 团风县校级模拟)因为的分母含有2、5以外的质因数,所以不能化为有限小数. × .
【考点】小数与分数的互化.
【答案】见试题解答内容
【分析】根据一个最简分数,如果分母中只含有质因数2或5,不能含有其它的质因数,这个分数就能化成有限小数;因为不是最简分数,所以先把约分后再进行判断;
【解答】解:约分后是,的分母中只含有质因数5,能化成有限小数;
故答案为:×.
【点评】此题主要考查判断一个最简分数能否化成有限小数的方法,如果分母中只含有质因数2或5,这个分数就能化成有限小数;否则不能;如果这个分数不是最简分数,约分后再按照此方法进行判断.
16.(2013春 鄂城区月考)不能化成有限小数. × .
【考点】小数与分数的互化.
【专题】计算题.
【答案】见试题解答内容
【分析】首先,要看分数是否是最简分数,不是的,先把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数;据此进行分析后再判断.
【解答】解:因为不是最简分数,所以不能直接看分母的情况,
化简后是,的分母中只含有质因数5,所以能化成有限小数;
故答案为:×.
【点评】此题主要考查什么样的分数可以化成有限小数:必须是最简分数,分母中只含有质因数2或5.
17.(2012 台州校级自主招生)因为12=2×2×3,所以用12做分母的分数不能化成有限小数. × .
【考点】小数与分数的互化.
【专题】综合判断题.
【答案】见试题解答内容
【分析】判断一个分数能否化成有限小数,首先要看这个分数是不是最简分数,如果不是最简分数,要先化成最简分数,再根据一个最简分数,如果分母中只含有质因数2或5,这个分数就能化成有限小数,否则就不能化成有限小数.据此判断即可.
【解答】解:如果分母是12,要考分子是多少,如:化简后是,分母中只有质因数2,所以能化成最简分数.
因此,因为12=2×2×3,所以用12做分母的分数不能化成有限小数.此说法错误.
故答案为:×.
【点评】此题考查的目的是掌握判断一个分数能否化成有限小数的方法,根据一个最简分数,如果分母中只含有质因数2或5,这个分数就能化成有限小数,否则就不能化成有限小数.
四.计算题(共1小题)
18.(2024春 东坡区期末)直接写出下面各题的得数。
①2.3+3.67= ②11﹣9.5= ③65.8÷10= ④2.5×4=
⑤ ⑥ ⑦ ⑧
⑨ ⑩
【考点】分数的加法和减法;小数的加法和减法;小数乘法;小数除法.
【专题】运算能力.
【答案】①5.97; ②1.5;③6.58; ④10;⑤1;⑥;⑦;⑧ ⑨1; ⑩; ; 1。
【分析】根据小数、分数加、减、乘、除的计算方法,依次口算结果。
【解答】解:
①2.3+3.67=5.97 ②11﹣9.5=1.5 ③65.8÷10=6.58 ④2.5×4=10
⑤1 ⑥ ⑦ ⑧
⑨1 ⑩ 1
【点评】本题解题的关键是熟练掌握小数、分数加、减、乘、除的计算方法。
五.连线题(共1小题)
19.(2023春 金乡县期中)把相等的两个数用线连起来。
5
2 3 0.5
【考点】小数与分数的互化.
【专题】数感.
【答案】
【分析】把假分数化成整数或带分数、小数化成分数,然后即可连线。假分数化成整数或带分数,用假分数的分子除以分母,如果分子是分母的倍数,所得的商就是整数;如果分子不是分母的倍数,所得的商就是带分数的整数部分,分母不变,余数作分数部分的分子;带分数化成假分数,分母不变,把整数和分母相乘的积加上原来分子做分子;小数化分数,原来有几位小数就在1的后面加几个0作分母,把原来的小数去掉小数点作分子,化成分数后能约分的要约分。
【解答】解:
【点评】此题考查的知识点:假分数与带分数的互化、小数与分数的互化,都属于基础知识,要掌握。
六.操作题(共1小题)
20.(2022春 郧阳区期末)连一连(把相等的数用线连起来)。
【考点】小数与分数的互化.
【专题】运算能力.
【答案】
【分析】小数化分数,原来有几位小数就在1的后面加几个0作分母,把原来的小数去掉小数点作分子,化成分数后能约分的要约分;把假分数化成带分数,用分子除以分母,得到的整数商作带分数的整数部分,余数作分子,分母不变,能约分的要约分,据此解答。
【解答】解:
【点评】本题考查分数与小数的互化,假分数与带分数的互化。
七.应用题(共5小题)
21.一节英语课上,老师讲解用了时,学生练习口语用了时,其余时间用来写作业。已知每节课的时间为时,请你提出一个数学问题,并解答。
【考点】“提问题”、“填条件”应用题.
【专题】运算能力.
【答案】时。
【分析】由题意可得:问题是“学生练习口语用的时间比老师讲解多用几时?”,运用减法进行解答,运用时减去时,由此解答即可。
【解答】解:学生练习口语用的时间比老师讲解多用几时?
(时)
答:学生练习口语用的时间比老师讲解多用时。
【点评】本题考查了学生灵活解决问题的能力,考查了分数减法的计算法则的应用。
22.在速算比赛中,小红用0.3小时做完,小青用小时做完,且两人都全部做对。他俩谁的速度快些?
【考点】小数与分数的互化.
【专题】应用意识.
【答案】小红的速度快些。
【分析】在二人做题数量相同的情况下,用时少的人做题的速度快,比较大小时,根据分数与除法的关系,先把化成小数,再进行比较。
【解答】解:2÷6
0.3
答:小红的速度快些。
【点评】本题解题关键是理解“在二人做题数量相同的情况下,用时少的人做题的速度快”,熟练掌握分数化小数的方法。
23.联欢会上,张佳、王亮、思思在手机上抢红包。张佳4分钟抢到了7个红包,王亮5分钟抢到了8个红包,思思6分钟抢到了9个红包。三人中谁平均每分钟抢到的红包个数最多?(先用分数表示计算结果,再化成小数比较大小)
【考点】小数与分数的互化;小数的读写、意义及分类.
【专题】应用意识.
【答案】张佳平均每分钟抢到的红包个数最多。
【分析】用每个人抢到红包的总数除以抢的时间,可以计算出三个人平均每分钟各抢多少个红包,结果用分数表示,再根据分数与除法的关系,把分数化成小数后,再比较这几个分数的大小。
【解答】解:7÷4
8
9
1.75>1.6>1.5
答:张佳平均每分钟抢到的红包个数最多。
【点评】本题解题关键是根据每个人抢到红包的总数÷抢的时间=平均每分钟抢的个数,列式计算,熟练掌握分数化小数的方法和小数的大小比较方法。
24.开心农场种植玉米公顷,种植向日葵公顷,种植花生0.57公顷。哪种农作物的种植面积最大?
【考点】小数与分数的互化.
【专题】运算能力.
【答案】向日葵种植面积最大。
【分析】根据分数化小数的方法,先把题中的分数都化成小数,再进行比较。
【解答】解:3÷7≈0.429
5÷8=0.625
因为:0.625>0.57>0.429;
所以:0.57。
答:向日葵种植面积最大。
【点评】本题考查分数化小数的方法,解题关键是根据分数与除法的关系,用分子除以分母,就可以得到小数结果。
25.有一些煤,第一次用去吨,第二次用去吨,两次一共用去多少吨?第一次比第二次多用去多少吨?
【考点】异分母分数加减法.
【专题】应用意识.
【答案】吨;吨。
【分析】求两次一共用去多少吨,用加法计算;求第一次比第二次多用去多少吨,用减法计算。
【解答】解:(吨)
(吨)
答:两次一共用去吨。第一次比第二次多用去吨。
【点评】本题考查分数加减法应用题的解题方法,解题关键是理解求两个数的和,用加法计算;求一个数比另一个数多多少,用减法计算。
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2023春 高淳区期末)下面三个算式中的“8”和“3”可以直接相加减的是( )
A.0.08 B.5.89﹣2.3 C.
2.(2023春 启东市期末)计算时,需要先通分,这是因为通分后,会使( ),从而可以直接相加。
A.相同数位对齐 B.分子相同
C.分数单位相同 D.无法确定
3.(2023春 靖安县期末)两个数的和比其中一个数大,比另一个大,这两个数的和是( )
A. B.1 C. D.
4.(2023春 永嘉县期末)下列说法中,正确的有( )题。
①两个质数的和一定是合数。
②在,,,,中,能化成有限小数的有4个。
③因为42÷7=6所以42是7的倍数,7是42的因数。
④由图可见,阴影部分的长度是米。
A.1 B.2 C.3 D.4
5.(2023春 祥符区期末)转化思想是数学中的一种重要思想,下面体现转化思想的有( )个。
①
A.1 B.2 C.3
二.填空题(共5小题)
6.(2022秋 沂源县期中)一本书,小红已经看了这本书的,还剩 没看;千克比 千克重千克。
7.(2022春 岷县期末)比多的数是 ,比多 。
8.(2022春 揭阳期末)比m少m是 m
比 kg轻kg是kg
9.(2022春 华安县期末)将算式改写成小数加法为 + ,计算结果为 。
10.(2022春 永城市期末)
+ =
三.判断题(共7小题)
11.(2013春 奉化市校级期末)可以化成有限小数. .
12.(2012秋 沧州期末)再加上29个这样的分数单位就是最小的合数. .
13.(2013春 当涂县期末)、和都能化成有限小数.
14.(2013春 双峰县期末)能化成有限小数,不能化成有限小数.
15.(2012 团风县校级模拟)因为的分母含有2、5以外的质因数,所以不能化为有限小数. .
16.(2013春 鄂城区月考)不能化成有限小数. .
17.(2012 台州校级自主招生)因为12=2×2×3,所以用12做分母的分数不能化成有限小数. .
四.计算题(共1小题)
18.(2024春 东坡区期末)直接写出下面各题的得数。
①2.3+3.67= ②11﹣9.5= ③65.8÷10= ④2.5×4=
⑤ ⑥ ⑦ ⑧
⑨ ⑩
五.连线题(共1小题)
19.(2023春 金乡县期中)把相等的两个数用线连起来。
5
2 3 0.5
六.操作题(共1小题)
20.(2022春 郧阳区期末)连一连(把相等的数用线连起来)。
七.应用题(共5小题)
21.一节英语课上,老师讲解用了时,学生练习口语用了时,其余时间用来写作业。已知每节课的时间为时,请你提出一个数学问题,并解答。
22.在速算比赛中,小红用0.3小时做完,小青用小时做完,且两人都全部做对。他俩谁的速度快些?
23.联欢会上,张佳、王亮、思思在手机上抢红包。张佳4分钟抢到了7个红包,王亮5分钟抢到了8个红包,思思6分钟抢到了9个红包。三人中谁平均每分钟抢到的红包个数最多?(先用分数表示计算结果,再化成小数比较大小)
24.开心农场种植玉米公顷,种植向日葵公顷,种植花生0.57公顷。哪种农作物的种植面积最大?
25.有一些煤,第一次用去吨,第二次用去吨,两次一共用去多少吨?第一次比第二次多用去多少吨?
第1章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.(2023春 高淳区期末)下面三个算式中的“8”和“3”可以直接相加减的是( )
A.0.08 B.5.89﹣2.3 C.
【考点】分数的加法和减法;小数的加法和减法.
【专题】运算能力.
【答案】B
【分析】只有相同计数单位或分数单位上的数字才能直接相加减,据此解答。
【解答】解:A选项,0.080.08+0.3,8”和“3”不在相同的计数单位,所以不能直接相加。
B选项,5.89﹣2.3,“8”和“3”在相同的计数单位,所以能直接相减。
C选项,,两个分数的计数单位不同,8”和“3”不能直接相减。
所以“8”和“3”可以直接相加减的是5.89﹣2.3。
故选:B。
【点评】本题解题的关键是熟练掌握分数,小数加减法的算理。
2.(2023春 启东市期末)计算时,需要先通分,这是因为通分后,会使( ),从而可以直接相加。
A.相同数位对齐 B.分子相同
C.分数单位相同 D.无法确定
【考点】分数的加法和减法.
【专题】运算能力.
【答案】C
【分析】根据异分母分数加减法的计算方法,计算时,需要先通分,这是因为通分后,会使分数单位相同,从而可以直接相加。
【解答】解:计算时,需要先通分,这是因为通分后,会使分数单位相同,从而可以直接相加。
故选:C。
【点评】本题解题的关键是熟练后掌握异分母分数加减法的计算方法的算理。
3.(2023春 靖安县期末)两个数的和比其中一个数大,比另一个大,这两个数的和是( )
A. B.1 C. D.
【考点】分数的加法和减法.
【专题】文字叙述题;运算能力.
【答案】C
【分析】根据题意:两个数的和比其中一个数大,因为和=加数+加数,和比其中的一个加数多的数就是另一个加数,即另一个加数是;比另一个大,即其中的一个加数是,知道两个加数是多少,求和用加法.
【解答】解:
答:这两个数的和是.
故选:C.
【点评】解答此题关键是根据题意找出两个加数分别是多少,再列式计算.
4.(2023春 永嘉县期末)下列说法中,正确的有( )题。
①两个质数的和一定是合数。
②在,,,,中,能化成有限小数的有4个。
③因为42÷7=6所以42是7的倍数,7是42的因数。
④由图可见,阴影部分的长度是米。
A.1 B.2 C.3 D.4
【考点】小数与分数的互化;因数和倍数的意义;合数与质数的初步认识;分数的意义和读写.
【专题】分数和百分数;数感.
【答案】C
【分析】①一个数只有1和它本身两个因数,这个数叫做质数。一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数。两个质数的和可能是质数,也可能是合数;
②分数化成小数:用分子除以分母,按照除数是整数的小数除法进行计算,能除尽的就化成有限小数,不能除尽的就不能化为有限小数;
③根据因数和倍数的意义,如果数a能被数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;
④观察图可知,把1米看作单位“1”,平均分成5份,阴影部分占其中的2份,根据分数的意义,用分数表示为米。据此解答。
【解答】解:①两个质数的和可能是质数,也可能是合数,
例如:2+3=5
3+5=8
5是质数,8是合数,原题干说法错误;
②0.2
0.83
1.8
0.3
0.6875
、、、可以化为有限小数,共4个,原题干说法正确。
③因为42÷7=6所以42是7的倍数,7是42的因数。原题干说法正确。
④根据分数的意义,可知阴影部分的长度是米。原题干说法正确。
所以正确的有3题。
故选:C。
【点评】本题主要考查了质数和合数的认识、分数和小数的互化、因数和倍数的定义、分数的意义,关键是要掌握相关的知识点。
5.(2023春 祥符区期末)转化思想是数学中的一种重要思想,下面体现转化思想的有( )个。
①
A.1 B.2 C.3
【考点】异分母分数加减法.
【专题】模型思想.
【答案】C
【分析】“转化思想”是数学学习过程中常用的思想方法,是把未学习过的知识转化成已经学习过的知识进行研究,观察给出的3个题目,看是否运用了转化的思想,从而解决问题。
【解答】解:①,这是通过通分,把异分母分数的减法转化成同分母分数的减法进行计算,这是运用了转化的思想;
,这是把平行四边形的面积转化成长方形的面积,运用了转化的思想;
,这是把不规则物体的体积转化成水的体积,运用了转化的思想。
体现转化思想的有3个。
故选:C。
【点评】本题考查了转化思想的运用,把转化的思想运用到数学问题中。
二.填空题(共5小题)
6.(2022秋 沂源县期中)一本书,小红已经看了这本书的,还剩 没看;千克比 千克重千克。
【考点】分数的加法和减法.
【专题】应用意识.
【答案】,。
【分析】把这本书的页数看作单位“1”,用1减;根据减法算式中各部分间的关系即可解答。(千克)。
【解答】解:1
答:还剩没看。
(千克)
答:千克比千克重千克。
故答案为:,。
【点评】此题是考查分数加、减法的意义及应用、分数加法的意义与整数加减法的意义相同。
7.(2022春 岷县期末)比多的数是 ,比多 。
【考点】分数的加法和减法.
【专题】运算能力.
【答案】,。
【分析】比多的数是(),比多的数是(),计算时先通分,再按同分母加、减法法则计算。
【解答】解:,
答:比多的数是,比多。
故答案为:,。
【点评】本题考查异分母分数加法、减法知识点,先通分,再按同分母加法、减法法则计算。
8.(2022春 揭阳期末)比m少m是 m
比 kg轻kg是kg
【考点】分数的加法和减法.
【专题】运算能力.
【答案】;。
【分析】(1)求比m少m是多少m,题干中的两个分数都有单位,都表示具体的长度,所以直接相减即可解答。
(2)比多少kg轻kg是kg,题干中的两个数都有单位,都表示具体的质量,因为要求的数是比kg多kg的数,所以直接相加即可解答。
【解答】解:(1)(m)
(2)(kg)
答:比m少m是m;比kg轻kg是kg。
故答案为:;。
【点评】本题考查了异分母分数的加减法的计算方法。
9.(2022春 华安县期末)将算式改写成小数加法为 0.25 + 0.025 ,计算结果为 0.275 。
【考点】小数与分数的互化;小数的加法和减法.
【专题】运算能力.
【答案】0.25;0.025;0.275。
【分析】根据小数的意义,先把和化成小数后,再计算结果。
【解答】解:
=0.25+0.025
=0.275
答:将算式改写成小数加法为0.25+0.025,计算结果为0.275。
故答案为:0.25;0.025;0.275。
【点评】本题解题关键是理解小数的意义,熟练掌握小数加法的计算方法。
10.(2022春 永城市期末)
+ =
【考点】分数的加法和减法.
【专题】分数和百分数;运算能力.
【答案】,,。
【分析】首先通分,然后按照同分母分数相加(减)的法则进行运算即可。
【解答】解:
故答案为:,,。
【点评】此题主要考查了分数加减法的运算方法,要熟练掌握,解答此题的关键是要明确:(1)同分母分数相加(减),分子进行相加(减)得数作分子,分母不变;(2)异分母分数相加(减),首先通分,然后按照同分母分数相加(减)的法则进行运算即可。
三.判断题(共7小题)
11.(2013春 奉化市校级期末)可以化成有限小数. √ .
【考点】小数与分数的互化.
【专题】运算顺序及法则.
【答案】见试题解答内容
【分析】首先把化简成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.
【解答】解:,的分母中只含有质因数2,所以能化成有限小数.
故题干的说法是正确的.
故答案为:√.
【点评】此题主要考查判断一个分数能否化成有限小数的方法,根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.就能很快判断出什么样的分数能化成有限小数,什么样的分数不能化成有限小数.
12.(2012秋 沧州期末)再加上29个这样的分数单位就是最小的合数. √ .
【考点】分数的加法和减法;合数与质数的初步认识.
【专题】综合判断题;运算顺序及法则.
【答案】见试题解答内容
【分析】根据分数的意义可得,的分数单位是;最小的合数是4,用4得出结果即可判断本题.
【解答】解:根据分数的意义可知,的分数单位是;
4;
里面有29个;
所以,再加上29个这样的分数单位就是最小的合数4.
故答案为:√.
【点评】一个分数的分母是几,其分数单位就是几分之一,分子是几,就含有几个分数单位(带分数除外);注意最小的合数是4.
13.(2013春 当涂县期末)、和都能化成有限小数. √
【考点】小数与分数的互化.
【专题】运算顺序及法则.
【答案】见试题解答内容
【分析】根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.不是最简分数,先把它化成最简分数,再根据分母的情况作出判断.
【解答】解:不是最简分数,化简为,分母中只含有质因数5,能化成有限小数;
是最简分数,分母中只含有质因数2,能化成有限小数;
都是最简分数,分母中只含有质因数2,能化成有限小数;
所以、、都能化成有限小数;
故答案为:√.
【点评】此题主要考查什么样的分数可以化成有限小数,一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数.
14.(2013春 双峰县期末)能化成有限小数,不能化成有限小数. ×
【考点】小数与分数的互化.
【专题】分数和百分数.
【答案】见试题解答内容
【分析】首先,要看分数是否是最简分数,不是的,先把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数;不是最简分数,先把它化成最简分数,再根据分母的情况作出判断.
【解答】解:能化成有限小数,不是最简分数,不能直接看分母的情况,化简后是,分母中只含有质因数2,能化成有限小数;
故答案为:×.
【点评】此题主要考查什么样的分数可以化成有限小数,根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.
15.(2012 团风县校级模拟)因为的分母含有2、5以外的质因数,所以不能化为有限小数. × .
【考点】小数与分数的互化.
【答案】见试题解答内容
【分析】根据一个最简分数,如果分母中只含有质因数2或5,不能含有其它的质因数,这个分数就能化成有限小数;因为不是最简分数,所以先把约分后再进行判断;
【解答】解:约分后是,的分母中只含有质因数5,能化成有限小数;
故答案为:×.
【点评】此题主要考查判断一个最简分数能否化成有限小数的方法,如果分母中只含有质因数2或5,这个分数就能化成有限小数;否则不能;如果这个分数不是最简分数,约分后再按照此方法进行判断.
16.(2013春 鄂城区月考)不能化成有限小数. × .
【考点】小数与分数的互化.
【专题】计算题.
【答案】见试题解答内容
【分析】首先,要看分数是否是最简分数,不是的,先把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不再含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数;据此进行分析后再判断.
【解答】解:因为不是最简分数,所以不能直接看分母的情况,
化简后是,的分母中只含有质因数5,所以能化成有限小数;
故答案为:×.
【点评】此题主要考查什么样的分数可以化成有限小数:必须是最简分数,分母中只含有质因数2或5.
17.(2012 台州校级自主招生)因为12=2×2×3,所以用12做分母的分数不能化成有限小数. × .
【考点】小数与分数的互化.
【专题】综合判断题.
【答案】见试题解答内容
【分析】判断一个分数能否化成有限小数,首先要看这个分数是不是最简分数,如果不是最简分数,要先化成最简分数,再根据一个最简分数,如果分母中只含有质因数2或5,这个分数就能化成有限小数,否则就不能化成有限小数.据此判断即可.
【解答】解:如果分母是12,要考分子是多少,如:化简后是,分母中只有质因数2,所以能化成最简分数.
因此,因为12=2×2×3,所以用12做分母的分数不能化成有限小数.此说法错误.
故答案为:×.
【点评】此题考查的目的是掌握判断一个分数能否化成有限小数的方法,根据一个最简分数,如果分母中只含有质因数2或5,这个分数就能化成有限小数,否则就不能化成有限小数.
四.计算题(共1小题)
18.(2024春 东坡区期末)直接写出下面各题的得数。
①2.3+3.67= ②11﹣9.5= ③65.8÷10= ④2.5×4=
⑤ ⑥ ⑦ ⑧
⑨ ⑩
【考点】分数的加法和减法;小数的加法和减法;小数乘法;小数除法.
【专题】运算能力.
【答案】①5.97; ②1.5;③6.58; ④10;⑤1;⑥;⑦;⑧ ⑨1; ⑩; ; 1。
【分析】根据小数、分数加、减、乘、除的计算方法,依次口算结果。
【解答】解:
①2.3+3.67=5.97 ②11﹣9.5=1.5 ③65.8÷10=6.58 ④2.5×4=10
⑤1 ⑥ ⑦ ⑧
⑨1 ⑩ 1
【点评】本题解题的关键是熟练掌握小数、分数加、减、乘、除的计算方法。
五.连线题(共1小题)
19.(2023春 金乡县期中)把相等的两个数用线连起来。
5
2 3 0.5
【考点】小数与分数的互化.
【专题】数感.
【答案】
【分析】把假分数化成整数或带分数、小数化成分数,然后即可连线。假分数化成整数或带分数,用假分数的分子除以分母,如果分子是分母的倍数,所得的商就是整数;如果分子不是分母的倍数,所得的商就是带分数的整数部分,分母不变,余数作分数部分的分子;带分数化成假分数,分母不变,把整数和分母相乘的积加上原来分子做分子;小数化分数,原来有几位小数就在1的后面加几个0作分母,把原来的小数去掉小数点作分子,化成分数后能约分的要约分。
【解答】解:
【点评】此题考查的知识点:假分数与带分数的互化、小数与分数的互化,都属于基础知识,要掌握。
六.操作题(共1小题)
20.(2022春 郧阳区期末)连一连(把相等的数用线连起来)。
【考点】小数与分数的互化.
【专题】运算能力.
【答案】
【分析】小数化分数,原来有几位小数就在1的后面加几个0作分母,把原来的小数去掉小数点作分子,化成分数后能约分的要约分;把假分数化成带分数,用分子除以分母,得到的整数商作带分数的整数部分,余数作分子,分母不变,能约分的要约分,据此解答。
【解答】解:
【点评】本题考查分数与小数的互化,假分数与带分数的互化。
七.应用题(共5小题)
21.一节英语课上,老师讲解用了时,学生练习口语用了时,其余时间用来写作业。已知每节课的时间为时,请你提出一个数学问题,并解答。
【考点】“提问题”、“填条件”应用题.
【专题】运算能力.
【答案】时。
【分析】由题意可得:问题是“学生练习口语用的时间比老师讲解多用几时?”,运用减法进行解答,运用时减去时,由此解答即可。
【解答】解:学生练习口语用的时间比老师讲解多用几时?
(时)
答:学生练习口语用的时间比老师讲解多用时。
【点评】本题考查了学生灵活解决问题的能力,考查了分数减法的计算法则的应用。
22.在速算比赛中,小红用0.3小时做完,小青用小时做完,且两人都全部做对。他俩谁的速度快些?
【考点】小数与分数的互化.
【专题】应用意识.
【答案】小红的速度快些。
【分析】在二人做题数量相同的情况下,用时少的人做题的速度快,比较大小时,根据分数与除法的关系,先把化成小数,再进行比较。
【解答】解:2÷6
0.3
答:小红的速度快些。
【点评】本题解题关键是理解“在二人做题数量相同的情况下,用时少的人做题的速度快”,熟练掌握分数化小数的方法。
23.联欢会上,张佳、王亮、思思在手机上抢红包。张佳4分钟抢到了7个红包,王亮5分钟抢到了8个红包,思思6分钟抢到了9个红包。三人中谁平均每分钟抢到的红包个数最多?(先用分数表示计算结果,再化成小数比较大小)
【考点】小数与分数的互化;小数的读写、意义及分类.
【专题】应用意识.
【答案】张佳平均每分钟抢到的红包个数最多。
【分析】用每个人抢到红包的总数除以抢的时间,可以计算出三个人平均每分钟各抢多少个红包,结果用分数表示,再根据分数与除法的关系,把分数化成小数后,再比较这几个分数的大小。
【解答】解:7÷4
8
9
1.75>1.6>1.5
答:张佳平均每分钟抢到的红包个数最多。
【点评】本题解题关键是根据每个人抢到红包的总数÷抢的时间=平均每分钟抢的个数,列式计算,熟练掌握分数化小数的方法和小数的大小比较方法。
24.开心农场种植玉米公顷,种植向日葵公顷,种植花生0.57公顷。哪种农作物的种植面积最大?
【考点】小数与分数的互化.
【专题】运算能力.
【答案】向日葵种植面积最大。
【分析】根据分数化小数的方法,先把题中的分数都化成小数,再进行比较。
【解答】解:3÷7≈0.429
5÷8=0.625
因为:0.625>0.57>0.429;
所以:0.57。
答:向日葵种植面积最大。
【点评】本题考查分数化小数的方法,解题关键是根据分数与除法的关系,用分子除以分母,就可以得到小数结果。
25.有一些煤,第一次用去吨,第二次用去吨,两次一共用去多少吨?第一次比第二次多用去多少吨?
【考点】异分母分数加减法.
【专题】应用意识.
【答案】吨;吨。
【分析】求两次一共用去多少吨,用加法计算;求第一次比第二次多用去多少吨,用减法计算。
【解答】解:(吨)
(吨)
答:两次一共用去吨。第一次比第二次多用去吨。
【点评】本题考查分数加减法应用题的解题方法,解题关键是理解求两个数的和,用加法计算;求一个数比另一个数多多少,用减法计算。
21世纪教育网(www.21cnjy.com)
