22.3《二次函数与图形面积问题》专项练习(含答案)人教版数学九年级上册
文档属性
| 名称 | 22.3《二次函数与图形面积问题》专项练习(含答案)人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 331.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览




文档简介
人教版九年级上册
《二次函数与图形面积问题》专项练习
1.如图,在平面角坐标系中,抛物线y=x2+bx+c经过点(﹣1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
(1)求抛物线的解析式;
(2)若抛物线与y轴交于点C,顶点为点P,求△BCP的面积.
2.如图,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点(,0),在第一象限内与直线y=x交于点B(2,t).
(1)求抛物线的解析式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标.
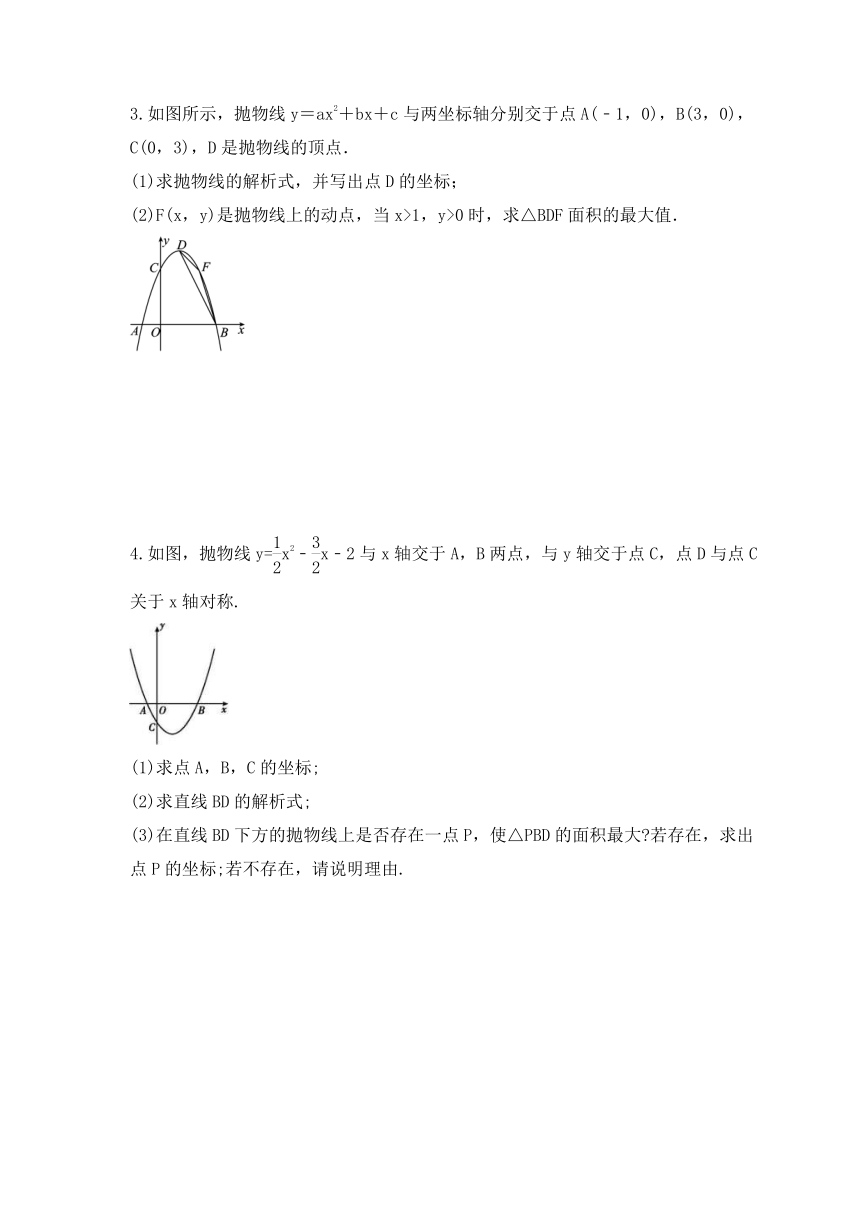
3.如图所示,抛物线y=ax2+bx+c与两坐标轴分别交于点A(﹣1,0),B(3,0),C(0,3),D是抛物线的顶点.
(1)求抛物线的解析式,并写出点D的坐标;
(2)F(x,y)是抛物线上的动点,当x>1,y>0时,求△BDF面积的最大值.
4.如图,抛物线y=x2﹣x﹣2与x轴交于A,B两点,与y轴交于点C,点D与点C关于x轴对称.
(1)求点A,B,C的坐标;
(2)求直线BD的解析式;
(3)在直线BD下方的抛物线上是否存在一点P,使△PBD的面积最大 若存在,求出点P的坐标;若不存在,请说明理由.
5.如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.
(1)求此抛物线的解析式
(2)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.
6.如图,抛物线过轴上两点A(9,0),C(﹣3,0),且与y轴交于点B(0,﹣12).
(1)求抛物线的解析式;
(2)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBNA面积的最大值.
7.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足2S△PCD=S△BCD,求点P的坐标.
8.如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式;
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.
9.如图,已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
10.如图,在平面直角坐标系中,二次函数的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求b,c的值.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形, 那么是否存在点P,使四边形为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
11.如图,抛物线y=ax2+bx(a≠0)交x轴正半轴于点A,直线y=2x经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.
(1)求a,b的值.
(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m,
△OBP的面积为S,记K=.求K关于m的函数表达式及K的范围.
12.如图,已知抛物线y=﹣x2﹣2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=x﹣a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.
(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示点M,A的坐标.
(2)将△NAC沿着y轴翻折,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及△PCD的面积.
(3)在抛物线y=﹣x2﹣2x+a(a>0)上是否存在点Q,使得以Q,A,C,N为顶点的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.
答案
1.解:(1)抛物线经过点与点,
解得:
抛物线的解析式为:
(2),
过点作轴于点,过点作轴交直线于点,过点作轴叫直线于点,如图所示:
2.解:(1)因为B(2,t)在直线y=x上,所以t=2.所以点B的坐标为(2,2).
因为抛物线经过A(,0),B(2,2)两点,
所以解得
所以抛物线的解析式是y=2x2﹣3x.
(2)如图,过点C作CD∥y轴,交x轴于点E,交OB于点D,
过点B作BF⊥CD于点F,
因为点C是抛物线上第四象限的点,所以设C(m,2m2﹣3m),
则E(m,0),D(m,m),
所以OE=m,BF=2﹣m,CD=m﹣(2m2﹣3m)=﹣2m2+4m.
所以S△OBC=S△CDO+S△CDB=CD·OE+CD·BF=CD·(OE+BF)
=(﹣2m2+4m)(m+2﹣m)=﹣2m2+4m.
因为△OBC的面积为2,
所以﹣2m2+4m=2,解得m1=m2=1.
所以点C的坐标为(1,﹣1).
3.解:(1)将A(﹣1,0),B(3,0),C(0,3)分别代入y=ax2+bx+c,
得解得
∴抛物线的解析式为y=﹣x2+2x+3.
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4).
(2)过点F作FF1∥y轴,交BD于点F1,如图所示.
设直线BD的解析式为y=mx+n(m≠0),将(3,0),(1,4)分别代入y=mx+n,
得解得
∴直线BD的解析式为y=﹣2x+6.
∵点F的坐标为(x,﹣x2+2x+3),
∴点F1的坐标为(x,﹣2x+6),
∴FF1=﹣x2+2x+3﹣(﹣2x+6)=﹣x2+4x﹣3,
∴S△BDF=FF1·(xB﹣xD)=﹣x2+4x﹣3=﹣(x﹣2)2+1.
∵﹣1<0,
∴当x=2时,S△BDF取得最大值,最大值为1.
4.解:(1)解方程x2﹣x﹣2=0,得x1=﹣1,x2=4.
所以点A的坐标为(﹣1,0),点B的坐标为(4,0).
当x=0时,y=﹣2,
所以点C的坐标为(0,﹣2).
(2)因为点D与点C关于x轴对称,所以点D的坐标为(0,2).
设直线BD的解析式为y=kx+b,
则解得
所以直线BD的解析式为y=﹣x+2.
(3)存在.理由如下:
如图,作PE∥y轴交BD于E,
设P(m,m2﹣m﹣2),则E(m,﹣m+2),
所以PE=﹣m+2﹣(m2﹣m﹣2)=﹣m2+m+4.
所以S△PBD=PE·(xB﹣xD)=×(﹣m2+m+4)×4=﹣m2+2m+8=﹣(m﹣1)2+9.
因为﹣1<0,所以m=1时,△PBD的面积最大,面积的最大值为9.
所以点P的坐标为(1,﹣3).
5.解.(1)∵该抛物线过点C(0,﹣2),
设该抛物线的解析式为y=ax2+bx﹣2.将A(4,0),B(1,0)代入,
得解得
∴此抛物线的解析式为y=﹣x2+x﹣2.
(2)设D点的横坐标为t(0过D作y轴的平行线交AC于E.
由题意可求得直线AC的解析式为y=x﹣2.
∴E点的坐标为(t,t﹣2).
∴DE=﹣t2+t﹣2﹣(t﹣2)=﹣t2+2t.
∴S△DCA=×(﹣t2+2t)×4=﹣t2+4t=﹣(t﹣2)2+4.
∴当t=2时,△DCA面积最大.
∴D(2,1).
6.解:(1)因抛物线过轴上两点,
故设抛物线解析式为:.
又
;
(2)如图2,设直线的解析式为.
,,,解得,,
则直线的函数关系式为.
设点的横坐标为,则,.
①若四边形为平行四边形,则
即
△,此方程无实数根,
不存在这样的点,使得四边形恰为平行四边形.
②
,,
当时, 最大值此时,,.
7.解:(1)∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得,a+4=3,解得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4;
(2)由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4;
令y=0,则0=﹣(x﹣1)2+4,
∴x=﹣1或x=3,
∴C(﹣1,0),D(3,0);
∴CD=4,
∴S△BCD=CD×|yB|=×4×3=6;
(3)由(2)知,S△BCD=CD×|yB|=×4×3=6;CD=4,
∵S△PCD=S△BCD,∴S△PCD=CD×|yP|=×4×|yP|=3,∴|yP|=,
∵点P在x轴上方的抛物线上,
∴yP>0,∴yP=,
∵抛物线的解析式为y=﹣(x﹣1)2+4;
∴=﹣(x﹣1)2+4,∴x=1±,
∴P(1+,),或P(1﹣,).
8.解:(1)抛物线的函数表达式为y=-x2+x;
(2)由抛物线的对称性得BE=OA=t,
∴AB=10-2t,当x=t时,AD=-t2+t,
∴矩形ABCD的周长=2(AB+AD)
=2[(10-2t)+(-t2+t)]
=-t2+t+20=-(t-1)2+,
∵-<0,
∴当t=1时,矩形ABCD的周长有最大值,最大值为;
(3)如图,当t=2时,点A,B,C,D的坐标分别为(2,0),(8,0),(8,4),(2,4),
∴矩形ABCD对角线的交点P的坐标为(5,2),
∵直线GH平分矩形的面积,
∴点P是GH和BD的中点,
∴DP=PB,由平移知,PQ∥OB,
∴PQ是△ODB的中位线,
∴PQ=OB=4,
所以抛物线向右平移的距离是4个单位.
9.解:(1)y=﹣x2+2x+3
(2)易求直线BC的解析式为y=﹣x+3,
∴M(m,﹣m+3),
又∵MN⊥x轴,
∴N(m,﹣m2+2m+3),
∴MN=(﹣m2+2m+3)﹣(﹣m+3)=﹣m2+3m(0<m<3)
(3)S△BNC=S△CMN+S△MNB=|MN|·|OB|,
∴当|MN|最大时,△BNC的面积最大,
MN=﹣m2+3m=﹣(m﹣)2+,
所以当m=时,△BNC的面积最大为.
10.解:(1)将B、C两点的坐标代入得 解得:
所以二次函数的表达式为:
(2)存在点P,使四边形为菱形.设P点坐标为(x,),交CO于E
若四边形是菱形,则有PC=PO.连结, 则PE⊥CO于E,∴OE=EC=∴=.
∴= 解得=,=(不合题意,舍去)
∴P点的坐标为(,)
(3)过点P作轴的平行线与BC交于点Q,与OB交于点F,设P(x,),
易得,直线BC的解析式为则Q点的坐标为(x,x-3).
=
当时,四边形ABPC的面积最大
此时P点的坐标为,四边形ABPC的面积.
11.解:(1)将x=2代入y=2x,得:y=4,
∴点M(2,4),
由题意,得:,∴;
(2)如图,过点P作PH⊥x轴于点H,
∵点P的横坐标为m,抛物线的解析式为y=﹣x2+4x,
∴PH=﹣m2+4m,
∵B(2,0),
∴OB=2,
∴S=OB PH=×2×(﹣m2+4m)=﹣m2+4m,
∴K==﹣m+4,
由题意得A(4,0),
∵M(2,4),
∴2<m<4,
∵K随着m的增大而减小,
∴0<K<2.
12.解:(1)由题意联立整理得2x2+5x﹣4a=0,
由Δ=25+32a>0,解得a>﹣.
∵a≠0,
∴a>﹣且a≠0.令x=0, 得y=a,
∴A(0,a).
由y=﹣(x+1)2+1+a,得M(﹣1,1+a).
(2)设直线MA为y=kx+b,代入A(0,a)、M(﹣1,1+a),
得解得故直线MA为y=﹣x+a.
联立解得
∴N(a,﹣).由于P点是N点关于y轴的对称点,
因此P(﹣a,﹣),代入y=﹣x2﹣2x+a,得﹣=﹣a2+a+a,解得a=或a=0(舍去).
∴A(0,),C(0,﹣),M(﹣1,),∴AC=.
∴S△PCD=S△PAC﹣S△DAC=AC.|xP|﹣AC.|xD|=××(3﹣1)=.
(3)①当点Q1在y轴左侧时,由四边形AQ1CN为平行四边形,得AC与Q1N相互平分,则点Q1与N关于原点(0,0)中心对称,而N(a,﹣),
故Q1(﹣a,﹣)代入y=﹣x2﹣2x+a,
得=﹣a2+a+a,解得a=或a=0(舍去),∴Q1(﹣,).
②当点Q2在y轴右侧时,由四边形ACQ2N为平行四边形,得NQ2∥AC且NQ2=AC,
而N(a,﹣),A(0,a),C(0,﹣a),故Q2(a,﹣).
代入y=﹣x2﹣2x+a,得﹣=﹣a2﹣a+a,解得a=或a=0(舍去),
∴Q2(,﹣).
∴当点Q的坐标为(﹣,)或(,﹣)时,Q,A,C,N四点能构成平行四边形.
《二次函数与图形面积问题》专项练习
1.如图,在平面角坐标系中,抛物线y=x2+bx+c经过点(﹣1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
(1)求抛物线的解析式;
(2)若抛物线与y轴交于点C,顶点为点P,求△BCP的面积.
2.如图,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点(,0),在第一象限内与直线y=x交于点B(2,t).
(1)求抛物线的解析式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标.
3.如图所示,抛物线y=ax2+bx+c与两坐标轴分别交于点A(﹣1,0),B(3,0),C(0,3),D是抛物线的顶点.
(1)求抛物线的解析式,并写出点D的坐标;
(2)F(x,y)是抛物线上的动点,当x>1,y>0时,求△BDF面积的最大值.
4.如图,抛物线y=x2﹣x﹣2与x轴交于A,B两点,与y轴交于点C,点D与点C关于x轴对称.
(1)求点A,B,C的坐标;
(2)求直线BD的解析式;
(3)在直线BD下方的抛物线上是否存在一点P,使△PBD的面积最大 若存在,求出点P的坐标;若不存在,请说明理由.
5.如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.
(1)求此抛物线的解析式
(2)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.
6.如图,抛物线过轴上两点A(9,0),C(﹣3,0),且与y轴交于点B(0,﹣12).
(1)求抛物线的解析式;
(2)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBNA面积的最大值.
7.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足2S△PCD=S△BCD,求点P的坐标.
8.如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式;
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.
9.如图,已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
10.如图,在平面直角坐标系中,二次函数的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求b,c的值.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形, 那么是否存在点P,使四边形为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
11.如图,抛物线y=ax2+bx(a≠0)交x轴正半轴于点A,直线y=2x经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.
(1)求a,b的值.
(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m,
△OBP的面积为S,记K=.求K关于m的函数表达式及K的范围.
12.如图,已知抛物线y=﹣x2﹣2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=x﹣a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.
(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示点M,A的坐标.
(2)将△NAC沿着y轴翻折,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及△PCD的面积.
(3)在抛物线y=﹣x2﹣2x+a(a>0)上是否存在点Q,使得以Q,A,C,N为顶点的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.
答案
1.解:(1)抛物线经过点与点,
解得:
抛物线的解析式为:
(2),
过点作轴于点,过点作轴交直线于点,过点作轴叫直线于点,如图所示:
2.解:(1)因为B(2,t)在直线y=x上,所以t=2.所以点B的坐标为(2,2).
因为抛物线经过A(,0),B(2,2)两点,
所以解得
所以抛物线的解析式是y=2x2﹣3x.
(2)如图,过点C作CD∥y轴,交x轴于点E,交OB于点D,
过点B作BF⊥CD于点F,
因为点C是抛物线上第四象限的点,所以设C(m,2m2﹣3m),
则E(m,0),D(m,m),
所以OE=m,BF=2﹣m,CD=m﹣(2m2﹣3m)=﹣2m2+4m.
所以S△OBC=S△CDO+S△CDB=CD·OE+CD·BF=CD·(OE+BF)
=(﹣2m2+4m)(m+2﹣m)=﹣2m2+4m.
因为△OBC的面积为2,
所以﹣2m2+4m=2,解得m1=m2=1.
所以点C的坐标为(1,﹣1).
3.解:(1)将A(﹣1,0),B(3,0),C(0,3)分别代入y=ax2+bx+c,
得解得
∴抛物线的解析式为y=﹣x2+2x+3.
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4).
(2)过点F作FF1∥y轴,交BD于点F1,如图所示.
设直线BD的解析式为y=mx+n(m≠0),将(3,0),(1,4)分别代入y=mx+n,
得解得
∴直线BD的解析式为y=﹣2x+6.
∵点F的坐标为(x,﹣x2+2x+3),
∴点F1的坐标为(x,﹣2x+6),
∴FF1=﹣x2+2x+3﹣(﹣2x+6)=﹣x2+4x﹣3,
∴S△BDF=FF1·(xB﹣xD)=﹣x2+4x﹣3=﹣(x﹣2)2+1.
∵﹣1<0,
∴当x=2时,S△BDF取得最大值,最大值为1.
4.解:(1)解方程x2﹣x﹣2=0,得x1=﹣1,x2=4.
所以点A的坐标为(﹣1,0),点B的坐标为(4,0).
当x=0时,y=﹣2,
所以点C的坐标为(0,﹣2).
(2)因为点D与点C关于x轴对称,所以点D的坐标为(0,2).
设直线BD的解析式为y=kx+b,
则解得
所以直线BD的解析式为y=﹣x+2.
(3)存在.理由如下:
如图,作PE∥y轴交BD于E,
设P(m,m2﹣m﹣2),则E(m,﹣m+2),
所以PE=﹣m+2﹣(m2﹣m﹣2)=﹣m2+m+4.
所以S△PBD=PE·(xB﹣xD)=×(﹣m2+m+4)×4=﹣m2+2m+8=﹣(m﹣1)2+9.
因为﹣1<0,所以m=1时,△PBD的面积最大,面积的最大值为9.
所以点P的坐标为(1,﹣3).
5.解.(1)∵该抛物线过点C(0,﹣2),
设该抛物线的解析式为y=ax2+bx﹣2.将A(4,0),B(1,0)代入,
得解得
∴此抛物线的解析式为y=﹣x2+x﹣2.
(2)设D点的横坐标为t(0
由题意可求得直线AC的解析式为y=x﹣2.
∴E点的坐标为(t,t﹣2).
∴DE=﹣t2+t﹣2﹣(t﹣2)=﹣t2+2t.
∴S△DCA=×(﹣t2+2t)×4=﹣t2+4t=﹣(t﹣2)2+4.
∴当t=2时,△DCA面积最大.
∴D(2,1).
6.解:(1)因抛物线过轴上两点,
故设抛物线解析式为:.
又
;
(2)如图2,设直线的解析式为.
,,,解得,,
则直线的函数关系式为.
设点的横坐标为,则,.
①若四边形为平行四边形,则
即
△,此方程无实数根,
不存在这样的点,使得四边形恰为平行四边形.
②
,,
当时, 最大值此时,,.
7.解:(1)∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得,a+4=3,解得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4;
(2)由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4;
令y=0,则0=﹣(x﹣1)2+4,
∴x=﹣1或x=3,
∴C(﹣1,0),D(3,0);
∴CD=4,
∴S△BCD=CD×|yB|=×4×3=6;
(3)由(2)知,S△BCD=CD×|yB|=×4×3=6;CD=4,
∵S△PCD=S△BCD,∴S△PCD=CD×|yP|=×4×|yP|=3,∴|yP|=,
∵点P在x轴上方的抛物线上,
∴yP>0,∴yP=,
∵抛物线的解析式为y=﹣(x﹣1)2+4;
∴=﹣(x﹣1)2+4,∴x=1±,
∴P(1+,),或P(1﹣,).
8.解:(1)抛物线的函数表达式为y=-x2+x;
(2)由抛物线的对称性得BE=OA=t,
∴AB=10-2t,当x=t时,AD=-t2+t,
∴矩形ABCD的周长=2(AB+AD)
=2[(10-2t)+(-t2+t)]
=-t2+t+20=-(t-1)2+,
∵-<0,
∴当t=1时,矩形ABCD的周长有最大值,最大值为;
(3)如图,当t=2时,点A,B,C,D的坐标分别为(2,0),(8,0),(8,4),(2,4),
∴矩形ABCD对角线的交点P的坐标为(5,2),
∵直线GH平分矩形的面积,
∴点P是GH和BD的中点,
∴DP=PB,由平移知,PQ∥OB,
∴PQ是△ODB的中位线,
∴PQ=OB=4,
所以抛物线向右平移的距离是4个单位.
9.解:(1)y=﹣x2+2x+3
(2)易求直线BC的解析式为y=﹣x+3,
∴M(m,﹣m+3),
又∵MN⊥x轴,
∴N(m,﹣m2+2m+3),
∴MN=(﹣m2+2m+3)﹣(﹣m+3)=﹣m2+3m(0<m<3)
(3)S△BNC=S△CMN+S△MNB=|MN|·|OB|,
∴当|MN|最大时,△BNC的面积最大,
MN=﹣m2+3m=﹣(m﹣)2+,
所以当m=时,△BNC的面积最大为.
10.解:(1)将B、C两点的坐标代入得 解得:
所以二次函数的表达式为:
(2)存在点P,使四边形为菱形.设P点坐标为(x,),交CO于E
若四边形是菱形,则有PC=PO.连结, 则PE⊥CO于E,∴OE=EC=∴=.
∴= 解得=,=(不合题意,舍去)
∴P点的坐标为(,)
(3)过点P作轴的平行线与BC交于点Q,与OB交于点F,设P(x,),
易得,直线BC的解析式为则Q点的坐标为(x,x-3).
=
当时,四边形ABPC的面积最大
此时P点的坐标为,四边形ABPC的面积.
11.解:(1)将x=2代入y=2x,得:y=4,
∴点M(2,4),
由题意,得:,∴;
(2)如图,过点P作PH⊥x轴于点H,
∵点P的横坐标为m,抛物线的解析式为y=﹣x2+4x,
∴PH=﹣m2+4m,
∵B(2,0),
∴OB=2,
∴S=OB PH=×2×(﹣m2+4m)=﹣m2+4m,
∴K==﹣m+4,
由题意得A(4,0),
∵M(2,4),
∴2<m<4,
∵K随着m的增大而减小,
∴0<K<2.
12.解:(1)由题意联立整理得2x2+5x﹣4a=0,
由Δ=25+32a>0,解得a>﹣.
∵a≠0,
∴a>﹣且a≠0.令x=0, 得y=a,
∴A(0,a).
由y=﹣(x+1)2+1+a,得M(﹣1,1+a).
(2)设直线MA为y=kx+b,代入A(0,a)、M(﹣1,1+a),
得解得故直线MA为y=﹣x+a.
联立解得
∴N(a,﹣).由于P点是N点关于y轴的对称点,
因此P(﹣a,﹣),代入y=﹣x2﹣2x+a,得﹣=﹣a2+a+a,解得a=或a=0(舍去).
∴A(0,),C(0,﹣),M(﹣1,),∴AC=.
∴S△PCD=S△PAC﹣S△DAC=AC.|xP|﹣AC.|xD|=××(3﹣1)=.
(3)①当点Q1在y轴左侧时,由四边形AQ1CN为平行四边形,得AC与Q1N相互平分,则点Q1与N关于原点(0,0)中心对称,而N(a,﹣),
故Q1(﹣a,﹣)代入y=﹣x2﹣2x+a,
得=﹣a2+a+a,解得a=或a=0(舍去),∴Q1(﹣,).
②当点Q2在y轴右侧时,由四边形ACQ2N为平行四边形,得NQ2∥AC且NQ2=AC,
而N(a,﹣),A(0,a),C(0,﹣a),故Q2(a,﹣).
代入y=﹣x2﹣2x+a,得﹣=﹣a2﹣a+a,解得a=或a=0(舍去),
∴Q2(,﹣).
∴当点Q的坐标为(﹣,)或(,﹣)时,Q,A,C,N四点能构成平行四边形.
同课章节目录
