【期末高频易错考点】第8单元高频易错押题卷(单元测试)-2024-2025学年五年级下册数学北师大版(含解析)
文档属性
| 名称 | 【期末高频易错考点】第8单元高频易错押题卷(单元测试)-2024-2025学年五年级下册数学北师大版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览




文档简介
第8章练习卷
一.选择题(共5小题)
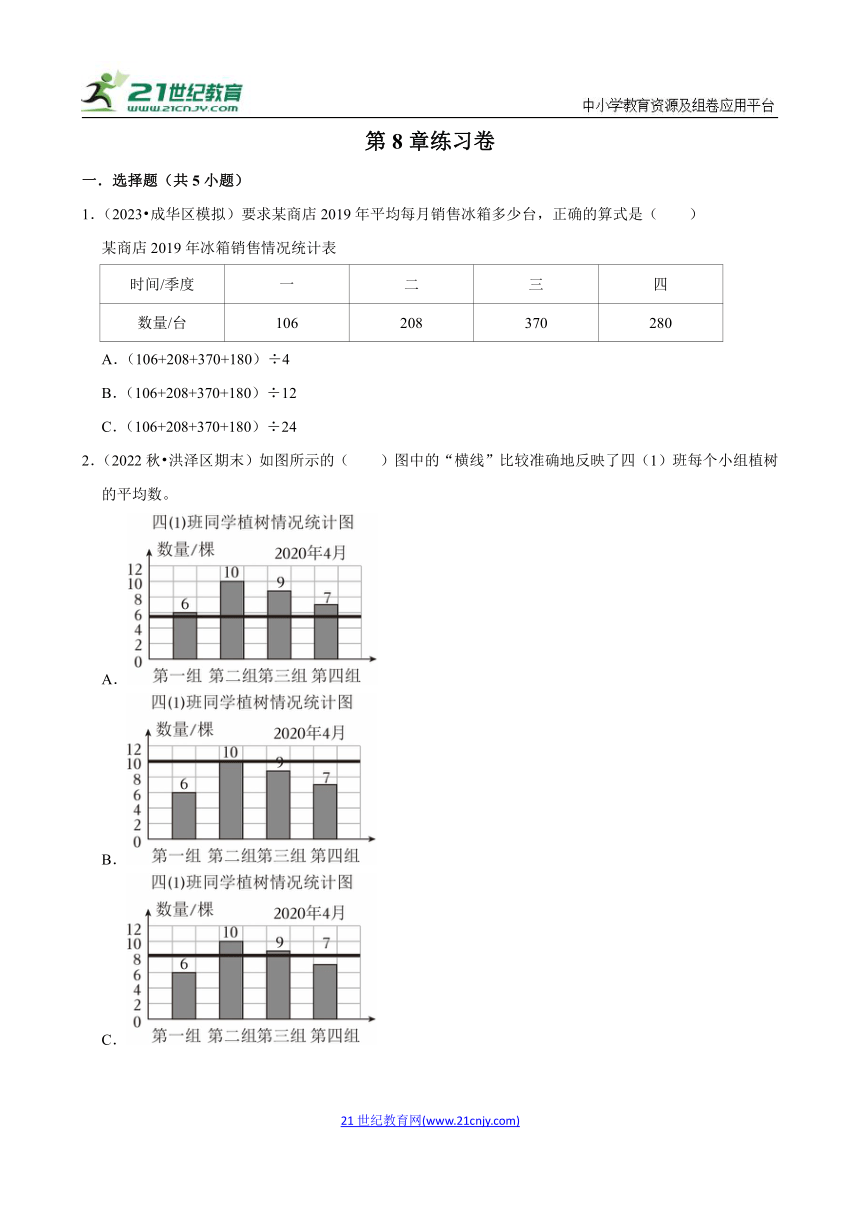
1.(2023 成华区模拟)要求某商店2019年平均每月销售冰箱多少台,正确的算式是( )
某商店2019年冰箱销售情况统计表
时间/季度 一 二 三 四
数量/台 106 208 370 280
A.(106+208+370+180)÷4
B.(106+208+370+180)÷12
C.(106+208+370+180)÷24
2.(2022秋 洪泽区期末)如图所示的( )图中的“横线”比较准确地反映了四(1)班每个小组植树的平均数。
A.
B.
C.
D.
3.(2022秋 顺义区期末)幸福小学统计五年级学生体重情况:五(1)班有30人,平均体重32.7千克;五(2)班有34人,平均体重32.7千克。求五年级全体学生的平均体重是多少千克?列式正确的是( )
A.(32.7+32.7)÷2
B.(30+34)÷2
C.(32.7+32.7)÷(30+34)
D.(32.7×30+32.7×34)÷(30+34)
4.(2022秋 延庆区期末)求全班同学平均身高时,下面算式( )是正确的。
性别 人数 平均身高/厘米
合计
女生 20 145.2
男生 24 143.2
A.(145.2+143.2)÷2
B.(145.2+143.2)÷(20+24)
C.145.2+143.2
D.(145.2×20+143.2×24)÷(20+24)
5.(2014春 延庆区期末)如表是某组学生的身高情况统计表(单位:厘米),小明身高是156厘米,加入这个小组后,平均身高会( )
姓名 马明 范阳 张佳佳 李磊 周小军
身高 145 149 141 154 146
A.增高 B.降低 C.不变 D.不能确定
二.填空题(共5小题)
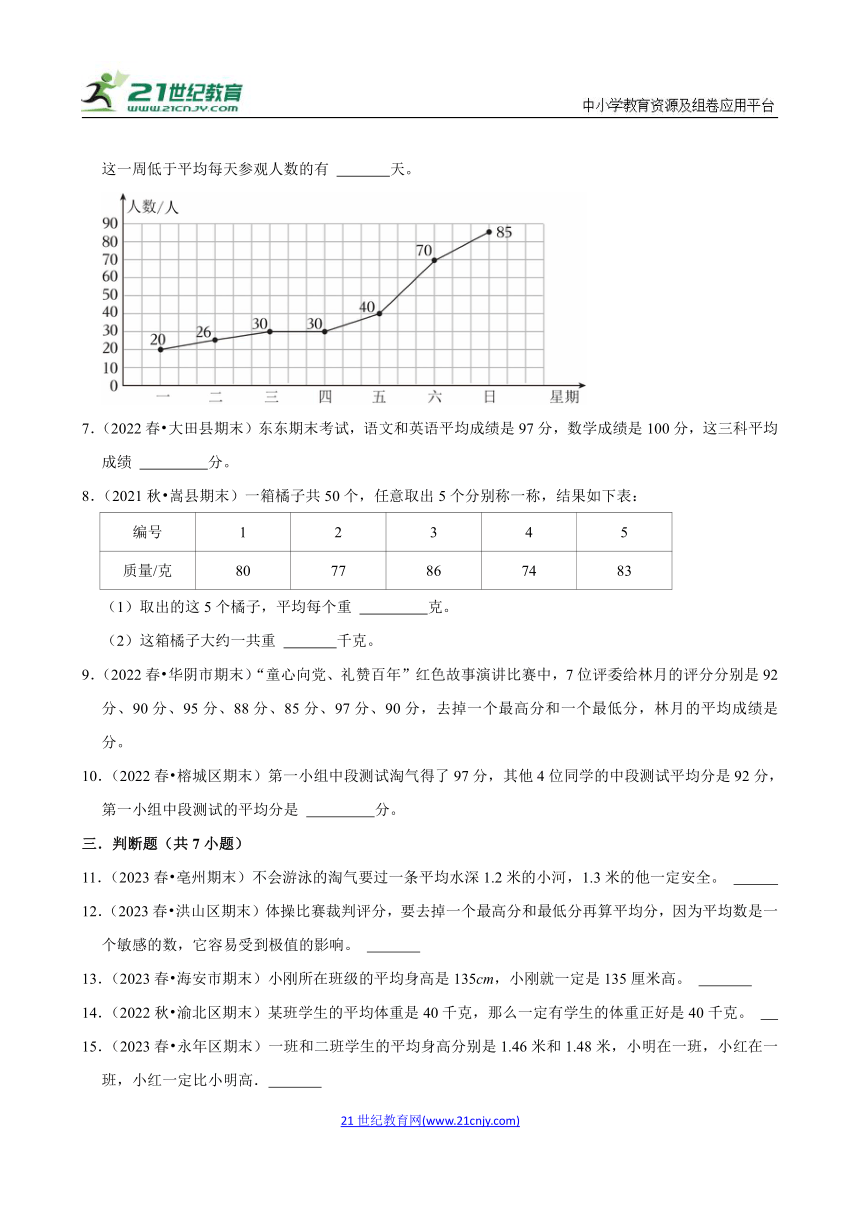
6.(2022春 神木市期末)如图是书法展览室一周参观人数情况统计图。
这一周低于平均每天参观人数的有 天。
7.(2022春 大田县期末)东东期末考试,语文和英语平均成绩是97分,数学成绩是100分,这三科平均成绩 分。
8.(2021秋 嵩县期末)一箱橘子共50个,任意取出5个分别称一称,结果如下表:
编号 1 2 3 4 5
质量/克 80 77 86 74 83
(1)取出的这5个橘子,平均每个重 克。
(2)这箱橘子大约一共重 千克。
9.(2022春 华阴市期末)“童心向党、礼赞百年”红色故事演讲比赛中,7位评委给林月的评分分别是92分、90分、95分、88分、85分、97分、90分,去掉一个最高分和一个最低分,林月的平均成绩是 分。
10.(2022春 榕城区期末)第一小组中段测试淘气得了97分,其他4位同学的中段测试平均分是92分,第一小组中段测试的平均分是 分。
三.判断题(共7小题)
11.(2023春 亳州期末)不会游泳的淘气要过一条平均水深1.2米的小河,1.3米的他一定安全。
12.(2023春 洪山区期末)体操比赛裁判评分,要去掉一个最高分和最低分再算平均分,因为平均数是一个敏感的数,它容易受到极值的影响。
13.(2023春 海安市期末)小刚所在班级的平均身高是135cm,小刚就一定是135厘米高。
14.(2022秋 渝北区期末)某班学生的平均体重是40千克,那么一定有学生的体重正好是40千克。
15.(2023春 永年区期末)一班和二班学生的平均身高分别是1.46米和1.48米,小明在一班,小红在一班,小红一定比小明高.
16.(2023春 江岸区期末)小林的身高是1.56m,他赤脚蹚过平均水深1.2m的小河,肯定不会有危险。
17.(2023 铜梁区)小军所在的篮球队队员的平均身高是160cm,小军的身高一定是160cm。
四.应用题(共3小题)
18.(2022秋 滨城区期末)一本《少年读史记》有320页,丽丽前10天看了200页。如果剩下的6天看完,那么她平均每天看多少页?
19.(2022秋 安泽县期末)五年级两个班参加植树活动,2.5小时共植树60棵。五(2)班平均每小时植10棵树,五(1)班平均每小时植树多少棵?
20.(2022秋 钦南区期中)四年级五个班参加植树活动。第一天植树33棵,第二天植树38棵,第三天植树34棵。
(1)平均每天植树多少棵?
(2)这三天平均每班植树多少棵?
第8章练习卷
参考答案与试题解析
题号 1 2 3 4 5
答案 B C D D A
一.选择题(共5小题)
1.(2023 成华区模拟)要求某商店2019年平均每月销售冰箱多少台,正确的算式是( )
某商店2019年冰箱销售情况统计表
时间/季度 一 二 三 四
数量/台 106 208 370 280
A.(106+208+370+180)÷4
B.(106+208+370+180)÷12
C.(106+208+370+180)÷24
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】B
【分析】将每个季节销售的数量相加,再除以12个月,即可求出2019年平均每月销售冰箱多少台。
【解答】解:106+208+370+180=864(台)
864÷12=72(台)
答:该商店2019年平均每月销售冰箱72台。
故选:B。
【点评】本题考查平均数的计算及应用。理解题意,找出数量关系,列式计算即可。
2.(2022秋 洪泽区期末)如图所示的( )图中的“横线”比较准确地反映了四(1)班每个小组植树的平均数。
A.
B.
C.
D.
【考点】平均数的含义及求平均数的方法.
【专题】数据分析观念.
【答案】C
【分析】根据平均数的意义,平均数是指在一组数据中所有数据之和再除以数据的个数。平均数要比最大的数据小,比最小的数据大,据此解答即可。
【解答】解:(6+10+9+7)÷4
=32÷4
=8
分析可知,
中的“横线”比较准确地反映了四(1)班每个小组植树的平均数。
故选:C。
【点评】本题考查了平均数知识,结合题意分析解答即可。
3.(2022秋 顺义区期末)幸福小学统计五年级学生体重情况:五(1)班有30人,平均体重32.7千克;五(2)班有34人,平均体重32.7千克。求五年级全体学生的平均体重是多少千克?列式正确的是( )
A.(32.7+32.7)÷2
B.(30+34)÷2
C.(32.7+32.7)÷(30+34)
D.(32.7×30+32.7×34)÷(30+34)
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】D
【分析】根据平均数的意义及求法,用两个班学生的总体重除以总人数,就是五年级全体学生的平均体重。
【解答】解:(32.7×30+32.7×34)÷(30+34)
=32.7×(30+34)÷(30+34)
=32.7×64÷64
=32.7(千克)
答:五年级全体学生的平均体重是32.7千克。
故选:D。
【点评】一组数据的和除以这组数据的个数所得的商叫平均数。
4.(2022秋 延庆区期末)求全班同学平均身高时,下面算式( )是正确的。
性别 人数 平均身高/厘米
合计
女生 20 145.2
男生 24 143.2
A.(145.2+143.2)÷2
B.(145.2+143.2)÷(20+24)
C.145.2+143.2
D.(145.2×20+143.2×24)÷(20+24)
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】D
【分析】分别用男、女生人数乘男、女生人数的平均身高,求出全班人数总身高,再除以总人数。
【解答】解:(145.2×20+143.2×24)÷(20+24)
=(2904+3436.8)÷44
=6340.8÷44
≈144.1(cm)
答:全班同学平均身高约144.1cm。
故选:D。
【点评】此题考查了平均数的意义及求法。一组数据的和除以这组数据的个数所得的商叫平均数
5.(2014春 延庆区期末)如表是某组学生的身高情况统计表(单位:厘米),小明身高是156厘米,加入这个小组后,平均身高会( )
姓名 马明 范阳 张佳佳 李磊 周小军
身高 145 149 141 154 146
A.增高 B.降低 C.不变 D.不能确定
【考点】平均数的含义及求平均数的方法.
【专题】应用题;平均数问题.
【答案】A
【分析】先算出这5个人的平均身高,然后再算出加上小明后的平均身高,比较解答即可.
【解答】解:(145+149+141+154+146)÷5
=735÷5
=147(厘米)
(145+149+141+154+146+156)÷6
=891÷6
=148.5(厘米)
148.5>147
所以平均身高会增高.
故选:A。
【点评】本题考查了平均数的含义以及求平均数的方法.平均数:是指在一组数据中所有数据之和再除以数据的个数.
二.填空题(共5小题)
6.(2022春 神木市期末)如图是书法展览室一周参观人数情况统计图。
这一周低于平均每天参观人数的有 5 天。
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】5。
【分析】先根据加法的意义,用加法求出这一周共有多少人参观,再根据求平均数的意义,用这一周参观的总人数除以7,就是平均每天参观的人数,然后再把每天参观的人数与平均数进行比较即可。
【解答】解:(20+26+30+30+40+70+85)÷7
=301÷7
=43(人)
20<26<30=30<40<43,小于43的有5个数。
答:这一周低于平均每天参观人数的有5天。
故答案为:5。
【点评】此题考查的目的是理解掌握统计表的特点及作用,并且能够根据统计表提供的信息,解决有关的实际问题。
7.(2022春 大田县期末)东东期末考试,语文和英语平均成绩是97分,数学成绩是100分,这三科平均成绩 98 分。
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】98。
【分析】用语文和英语平均成绩乘2,求出语文和英语的总成绩,再加上数学的成绩,求出三科的总成绩,再除以3,即可求出这三科平均成绩。
【解答】解:(97×2+100)÷3
=(194+100)÷3
=294÷3
=98(分)
答:这三科平均成绩98分。
故答案为:98。
【点评】本题考查平均数的计算及应用。理解题意,找出数量关系,列式计算即可。
8.(2021秋 嵩县期末)一箱橘子共50个,任意取出5个分别称一称,结果如下表:
编号 1 2 3 4 5
质量/克 80 77 86 74 83
(1)取出的这5个橘子,平均每个重 80 克。
(2)这箱橘子大约一共重 4 千克。
【考点】平均数的含义及求平均数的方法.
【专题】数据分析观念.
【答案】(1)80;(2)4。
【分析】用这5个橘子的总克数除以5就是这5个橘子平均每个的克数;再用平均每个的克数乘50后换算单位即可求得这箱橘子大约一共重多少千克。
【解答】解:(80+77+86+74+83)÷5
=400÷5
=80(克)
80×50=4000(克)
4000克=4千克
答:平均每个重80克,这箱橘子大约一共重4千克。
故答案为:(1)80;(2)4。
【点评】本题是考查平均数的意义及求法,要记住总数、个数及平均数三者之间的关系。
9.(2022春 华阴市期末)“童心向党、礼赞百年”红色故事演讲比赛中,7位评委给林月的评分分别是92分、90分、95分、88分、85分、97分、90分,去掉一个最高分和一个最低分,林月的平均成绩是 91 分。
【考点】平均数的含义及求平均数的方法.
【专题】解题思想方法;数据分析观念.
【答案】91。
【分析】一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数。先去掉最高和最低分,再把剩下5个评委打的分数相加求解总分,最后5个评委的总分除以5即可求解平均分。据此解答。
【解答】解:去掉一个最高分97分,去掉一个最低分85分,林月的平均成绩是:
(92+90+95+88+90)÷5
=455÷5
=91(分)
答:林月的平均成绩是91分。
故答案为:91分。
【点评】本题考查平均数的求法和除数是整数的小数除法的计算,注意去掉最高分和最低分。
10.(2022春 榕城区期末)第一小组中段测试淘气得了97分,其他4位同学的中段测试平均分是92分,第一小组中段测试的平均分是 93 分。
【考点】平均数的含义及求平均数的方法.
【专题】数据分析观念.
【答案】93。
【分析】根据题意,先求出其他4位同学的中段测试的总成绩,加上淘气的成绩,然后除以5即可。
【解答】解:(92×4+97)÷5
=465÷5
=93(分)
答:第一小组中段测试的平均分是93分。
【点评】本题考查了平均数的意义和计算方法,结合题意分析解答即可。
三.判断题(共7小题)
11.(2023春 亳州期末)不会游泳的淘气要过一条平均水深1.2米的小河,1.3米的他一定安全。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】平均水深为1.2米的小河,并不代表河中所有地方的水深都是1.2米,有的地方可能比1.2米要深的多;有的地方可能比1.2米浅的多。据此解答。
【解答】解:平均水深为1.2米的小河,并不代表河中所有地方的水深都是1.2米,有的地方可能比1.2米要深的多,有的地方可能比1.2米浅的多,所以淘气身高1.3米,过河也可能会有危险。
原题说法错误。
故答案为:×。
【点评】解答本题需明确:平均数反映的是一组数据的集中趋势。
12.(2023春 洪山区期末)体操比赛裁判评分,要去掉一个最高分和最低分再算平均分,因为平均数是一个敏感的数,它容易受到极值的影响。 √
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】√
【分析】根据平均数的意义和特征直接判断。
【解答】解:平均数反映的是一组数据的集中趋势,极易受极端数据的影响,所以体操比赛裁判评分,要去掉一个最高分和最低分再算平均分。
原题说法正确。
故答案为:√。
【点评】解答本题需熟练掌握平均数的意义和特征。
13.(2023春 海安市期末)小刚所在班级的平均身高是135cm,小刚就一定是135厘米高。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】平均数反映的是一组数据的集中趋势,不能说明每个数据的大小。据此解答。
【解答】解:小刚所在班级的平均身高是135cm,小刚可能是135厘米高,也可能比135厘米高,还可能比135厘米低。原题说法错误。
故答案为:×。
【点评】解答本题需准确理解平均数的意义和特点。
14.(2022秋 渝北区期末)某班学生的平均体重是40千克,那么一定有学生的体重正好是40千克。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】平均数反映一组数据的集中趋势,某班学生的平均体重是40千克,那么这个班的学生的体重一定有高于40千克的,也有低于40千克的,也可能有正好40千克的,据此解答。
【解答】解:某班学生的平均体重是40千克,那么可能有学生的体重正好是40千克,原题说法错误。
故答案为:×。
【点评】解决本题的关键是掌握平均数的运用。
15.(2023春 永年区期末)一班和二班学生的平均身高分别是1.46米和1.48米,小明在一班,小红在一班,小红一定比小明高. ×
【考点】平均数的含义及求平均数的方法.
【专题】平均数问题;数据分析观念;应用意识.
【答案】×
【分析】平均数是表示一组数据集中趋势的量数,它是反映一组数据的平均水平,平均数会受偏大偏小数据的影响。一班学生的平均身高分别是1.46米,不能说明小明的身高就是1.46米,二班学生的平均身高是1.48米,也不能说明小红的身高就是1.48米。据此判断。
【解答】解:一班学生的平均身高分别是1.46米,不能说明小明的身高就是1.46米,小明的身高可能比1.46米低、也可能比1.46米高;二班学生的平均身高是1.48米,也不能说明小红的身高就是1.48米,小红的身高可能比1.48米低,也可能比1.48米高。由此可知,小红不一定比小明高。
因此,一班和二班学生的平均身高分别是1.46米和1.48米,小明在一班,小红在一班,小红一定比小明高。这种说法是错误的。
故答案为:×。
【点评】平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标,并不说明平均数大的那组数中的每一个数都大,平均数小的那组数中的每一个数都小,据此判断即可。
16.(2023春 江岸区期末)小林的身高是1.56m,他赤脚蹚过平均水深1.2m的小河,肯定不会有危险。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】小河平均水深1.2米,并不是说小河每处都深1.2米,有的地方可能比1.2米深得多,有的地方可能比1.2米浅得多;据此判断。
【解答】解:小河平均水深1.2米,并不是说小河每处都深1.2米,有的地方可能比1.2米深得多,有的地方可能比1.2米浅得多;小林的身高是1.56米,但可能有的地方比1.56米深,所以他过河也存在危险。
原题说法错误。
故答案为:×。
【点评】平均数反映的是一组数据的集中趋势,但不能确定每个数据的大小。
17.(2023 铜梁区)小军所在的篮球队队员的平均身高是160cm,小军的身高一定是160cm。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】平均数反映的是一组数据集中趋势,不是反映每一个数据的大小;所以每个篮球队员的身高可能是比162厘米高,可能等于162厘米,也可能比162厘米矮,据此解答即可。
【解答】解:根据分析可知:160厘米反映的是小军所在的篮球队队员的平均身高的集中趋势,不能反映某个队员的身高;小军的身高可能是比160厘米高,也可能等于160厘米,还可能比160厘米矮。
原题说法错误。
故答案为:×。
【点评】解答本题需熟练掌握平均数的意义。
四.应用题(共3小题)
18.(2022秋 滨城区期末)一本《少年读史记》有320页,丽丽前10天看了200页。如果剩下的6天看完,那么她平均每天看多少页?
【考点】平均数的含义及求平均数的方法.
【专题】数的运算.
【答案】20页。
【分析】先算出剩下的页数,再除以6即可。
【解答】解:(320﹣200)÷6
=120÷6
=20(页)
答:她平均每天看20页。
【点评】根据平均数的含义和求法,解答此题即可。
19.(2022秋 安泽县期末)五年级两个班参加植树活动,2.5小时共植树60棵。五(2)班平均每小时植10棵树,五(1)班平均每小时植树多少棵?
【考点】平均数的含义及求平均数的方法.
【专题】应用题.
【答案】14棵。
【分析】根据题意可知:(五年级(1)班平均每小时植的树+五年级(2)班平均每小时植的树)×2.5=两个班共同植的树,设五年级(1)班平均每小时植x棵,据此列方程解答。
【解答】解:设五年级(1)班平均每小时植x棵。
(10+x)×2.5=60
10+x=24
x=14
答:五年级(1)班平均每小时植14棵。
【点评】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,即:(五年级(1)班平均每小时植的树+五年级(2)班平均每小时植的树)×2.5=两个班共同植的树,进而列出方程是解答此类问题的关键。
20.(2022秋 钦南区期中)四年级五个班参加植树活动。第一天植树33棵,第二天植树38棵,第三天植树34棵。
(1)平均每天植树多少棵?
(2)这三天平均每班植树多少棵?
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】(1)35棵;
(2)21棵。
【分析】(1)把这三天植树的棵数加起来再除以3即可;
(2)用三天植树总棵数除以5即可。
【解答】解:(1)(33+38+34)÷3
=105÷3
=35(棵)
答:平均每天植树35棵。
(2)105÷5=21(棵)
答:这三天平均每班植树21棵。
【点评】本题考查了平均数的求法,要熟练掌握并运用。
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2023 成华区模拟)要求某商店2019年平均每月销售冰箱多少台,正确的算式是( )
某商店2019年冰箱销售情况统计表
时间/季度 一 二 三 四
数量/台 106 208 370 280
A.(106+208+370+180)÷4
B.(106+208+370+180)÷12
C.(106+208+370+180)÷24
2.(2022秋 洪泽区期末)如图所示的( )图中的“横线”比较准确地反映了四(1)班每个小组植树的平均数。
A.
B.
C.
D.
3.(2022秋 顺义区期末)幸福小学统计五年级学生体重情况:五(1)班有30人,平均体重32.7千克;五(2)班有34人,平均体重32.7千克。求五年级全体学生的平均体重是多少千克?列式正确的是( )
A.(32.7+32.7)÷2
B.(30+34)÷2
C.(32.7+32.7)÷(30+34)
D.(32.7×30+32.7×34)÷(30+34)
4.(2022秋 延庆区期末)求全班同学平均身高时,下面算式( )是正确的。
性别 人数 平均身高/厘米
合计
女生 20 145.2
男生 24 143.2
A.(145.2+143.2)÷2
B.(145.2+143.2)÷(20+24)
C.145.2+143.2
D.(145.2×20+143.2×24)÷(20+24)
5.(2014春 延庆区期末)如表是某组学生的身高情况统计表(单位:厘米),小明身高是156厘米,加入这个小组后,平均身高会( )
姓名 马明 范阳 张佳佳 李磊 周小军
身高 145 149 141 154 146
A.增高 B.降低 C.不变 D.不能确定
二.填空题(共5小题)
6.(2022春 神木市期末)如图是书法展览室一周参观人数情况统计图。
这一周低于平均每天参观人数的有 天。
7.(2022春 大田县期末)东东期末考试,语文和英语平均成绩是97分,数学成绩是100分,这三科平均成绩 分。
8.(2021秋 嵩县期末)一箱橘子共50个,任意取出5个分别称一称,结果如下表:
编号 1 2 3 4 5
质量/克 80 77 86 74 83
(1)取出的这5个橘子,平均每个重 克。
(2)这箱橘子大约一共重 千克。
9.(2022春 华阴市期末)“童心向党、礼赞百年”红色故事演讲比赛中,7位评委给林月的评分分别是92分、90分、95分、88分、85分、97分、90分,去掉一个最高分和一个最低分,林月的平均成绩是 分。
10.(2022春 榕城区期末)第一小组中段测试淘气得了97分,其他4位同学的中段测试平均分是92分,第一小组中段测试的平均分是 分。
三.判断题(共7小题)
11.(2023春 亳州期末)不会游泳的淘气要过一条平均水深1.2米的小河,1.3米的他一定安全。
12.(2023春 洪山区期末)体操比赛裁判评分,要去掉一个最高分和最低分再算平均分,因为平均数是一个敏感的数,它容易受到极值的影响。
13.(2023春 海安市期末)小刚所在班级的平均身高是135cm,小刚就一定是135厘米高。
14.(2022秋 渝北区期末)某班学生的平均体重是40千克,那么一定有学生的体重正好是40千克。
15.(2023春 永年区期末)一班和二班学生的平均身高分别是1.46米和1.48米,小明在一班,小红在一班,小红一定比小明高.
16.(2023春 江岸区期末)小林的身高是1.56m,他赤脚蹚过平均水深1.2m的小河,肯定不会有危险。
17.(2023 铜梁区)小军所在的篮球队队员的平均身高是160cm,小军的身高一定是160cm。
四.应用题(共3小题)
18.(2022秋 滨城区期末)一本《少年读史记》有320页,丽丽前10天看了200页。如果剩下的6天看完,那么她平均每天看多少页?
19.(2022秋 安泽县期末)五年级两个班参加植树活动,2.5小时共植树60棵。五(2)班平均每小时植10棵树,五(1)班平均每小时植树多少棵?
20.(2022秋 钦南区期中)四年级五个班参加植树活动。第一天植树33棵,第二天植树38棵,第三天植树34棵。
(1)平均每天植树多少棵?
(2)这三天平均每班植树多少棵?
第8章练习卷
参考答案与试题解析
题号 1 2 3 4 5
答案 B C D D A
一.选择题(共5小题)
1.(2023 成华区模拟)要求某商店2019年平均每月销售冰箱多少台,正确的算式是( )
某商店2019年冰箱销售情况统计表
时间/季度 一 二 三 四
数量/台 106 208 370 280
A.(106+208+370+180)÷4
B.(106+208+370+180)÷12
C.(106+208+370+180)÷24
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】B
【分析】将每个季节销售的数量相加,再除以12个月,即可求出2019年平均每月销售冰箱多少台。
【解答】解:106+208+370+180=864(台)
864÷12=72(台)
答:该商店2019年平均每月销售冰箱72台。
故选:B。
【点评】本题考查平均数的计算及应用。理解题意,找出数量关系,列式计算即可。
2.(2022秋 洪泽区期末)如图所示的( )图中的“横线”比较准确地反映了四(1)班每个小组植树的平均数。
A.
B.
C.
D.
【考点】平均数的含义及求平均数的方法.
【专题】数据分析观念.
【答案】C
【分析】根据平均数的意义,平均数是指在一组数据中所有数据之和再除以数据的个数。平均数要比最大的数据小,比最小的数据大,据此解答即可。
【解答】解:(6+10+9+7)÷4
=32÷4
=8
分析可知,
中的“横线”比较准确地反映了四(1)班每个小组植树的平均数。
故选:C。
【点评】本题考查了平均数知识,结合题意分析解答即可。
3.(2022秋 顺义区期末)幸福小学统计五年级学生体重情况:五(1)班有30人,平均体重32.7千克;五(2)班有34人,平均体重32.7千克。求五年级全体学生的平均体重是多少千克?列式正确的是( )
A.(32.7+32.7)÷2
B.(30+34)÷2
C.(32.7+32.7)÷(30+34)
D.(32.7×30+32.7×34)÷(30+34)
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】D
【分析】根据平均数的意义及求法,用两个班学生的总体重除以总人数,就是五年级全体学生的平均体重。
【解答】解:(32.7×30+32.7×34)÷(30+34)
=32.7×(30+34)÷(30+34)
=32.7×64÷64
=32.7(千克)
答:五年级全体学生的平均体重是32.7千克。
故选:D。
【点评】一组数据的和除以这组数据的个数所得的商叫平均数。
4.(2022秋 延庆区期末)求全班同学平均身高时,下面算式( )是正确的。
性别 人数 平均身高/厘米
合计
女生 20 145.2
男生 24 143.2
A.(145.2+143.2)÷2
B.(145.2+143.2)÷(20+24)
C.145.2+143.2
D.(145.2×20+143.2×24)÷(20+24)
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】D
【分析】分别用男、女生人数乘男、女生人数的平均身高,求出全班人数总身高,再除以总人数。
【解答】解:(145.2×20+143.2×24)÷(20+24)
=(2904+3436.8)÷44
=6340.8÷44
≈144.1(cm)
答:全班同学平均身高约144.1cm。
故选:D。
【点评】此题考查了平均数的意义及求法。一组数据的和除以这组数据的个数所得的商叫平均数
5.(2014春 延庆区期末)如表是某组学生的身高情况统计表(单位:厘米),小明身高是156厘米,加入这个小组后,平均身高会( )
姓名 马明 范阳 张佳佳 李磊 周小军
身高 145 149 141 154 146
A.增高 B.降低 C.不变 D.不能确定
【考点】平均数的含义及求平均数的方法.
【专题】应用题;平均数问题.
【答案】A
【分析】先算出这5个人的平均身高,然后再算出加上小明后的平均身高,比较解答即可.
【解答】解:(145+149+141+154+146)÷5
=735÷5
=147(厘米)
(145+149+141+154+146+156)÷6
=891÷6
=148.5(厘米)
148.5>147
所以平均身高会增高.
故选:A。
【点评】本题考查了平均数的含义以及求平均数的方法.平均数:是指在一组数据中所有数据之和再除以数据的个数.
二.填空题(共5小题)
6.(2022春 神木市期末)如图是书法展览室一周参观人数情况统计图。
这一周低于平均每天参观人数的有 5 天。
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】5。
【分析】先根据加法的意义,用加法求出这一周共有多少人参观,再根据求平均数的意义,用这一周参观的总人数除以7,就是平均每天参观的人数,然后再把每天参观的人数与平均数进行比较即可。
【解答】解:(20+26+30+30+40+70+85)÷7
=301÷7
=43(人)
20<26<30=30<40<43,小于43的有5个数。
答:这一周低于平均每天参观人数的有5天。
故答案为:5。
【点评】此题考查的目的是理解掌握统计表的特点及作用,并且能够根据统计表提供的信息,解决有关的实际问题。
7.(2022春 大田县期末)东东期末考试,语文和英语平均成绩是97分,数学成绩是100分,这三科平均成绩 98 分。
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】98。
【分析】用语文和英语平均成绩乘2,求出语文和英语的总成绩,再加上数学的成绩,求出三科的总成绩,再除以3,即可求出这三科平均成绩。
【解答】解:(97×2+100)÷3
=(194+100)÷3
=294÷3
=98(分)
答:这三科平均成绩98分。
故答案为:98。
【点评】本题考查平均数的计算及应用。理解题意,找出数量关系,列式计算即可。
8.(2021秋 嵩县期末)一箱橘子共50个,任意取出5个分别称一称,结果如下表:
编号 1 2 3 4 5
质量/克 80 77 86 74 83
(1)取出的这5个橘子,平均每个重 80 克。
(2)这箱橘子大约一共重 4 千克。
【考点】平均数的含义及求平均数的方法.
【专题】数据分析观念.
【答案】(1)80;(2)4。
【分析】用这5个橘子的总克数除以5就是这5个橘子平均每个的克数;再用平均每个的克数乘50后换算单位即可求得这箱橘子大约一共重多少千克。
【解答】解:(80+77+86+74+83)÷5
=400÷5
=80(克)
80×50=4000(克)
4000克=4千克
答:平均每个重80克,这箱橘子大约一共重4千克。
故答案为:(1)80;(2)4。
【点评】本题是考查平均数的意义及求法,要记住总数、个数及平均数三者之间的关系。
9.(2022春 华阴市期末)“童心向党、礼赞百年”红色故事演讲比赛中,7位评委给林月的评分分别是92分、90分、95分、88分、85分、97分、90分,去掉一个最高分和一个最低分,林月的平均成绩是 91 分。
【考点】平均数的含义及求平均数的方法.
【专题】解题思想方法;数据分析观念.
【答案】91。
【分析】一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数。先去掉最高和最低分,再把剩下5个评委打的分数相加求解总分,最后5个评委的总分除以5即可求解平均分。据此解答。
【解答】解:去掉一个最高分97分,去掉一个最低分85分,林月的平均成绩是:
(92+90+95+88+90)÷5
=455÷5
=91(分)
答:林月的平均成绩是91分。
故答案为:91分。
【点评】本题考查平均数的求法和除数是整数的小数除法的计算,注意去掉最高分和最低分。
10.(2022春 榕城区期末)第一小组中段测试淘气得了97分,其他4位同学的中段测试平均分是92分,第一小组中段测试的平均分是 93 分。
【考点】平均数的含义及求平均数的方法.
【专题】数据分析观念.
【答案】93。
【分析】根据题意,先求出其他4位同学的中段测试的总成绩,加上淘气的成绩,然后除以5即可。
【解答】解:(92×4+97)÷5
=465÷5
=93(分)
答:第一小组中段测试的平均分是93分。
【点评】本题考查了平均数的意义和计算方法,结合题意分析解答即可。
三.判断题(共7小题)
11.(2023春 亳州期末)不会游泳的淘气要过一条平均水深1.2米的小河,1.3米的他一定安全。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】平均水深为1.2米的小河,并不代表河中所有地方的水深都是1.2米,有的地方可能比1.2米要深的多;有的地方可能比1.2米浅的多。据此解答。
【解答】解:平均水深为1.2米的小河,并不代表河中所有地方的水深都是1.2米,有的地方可能比1.2米要深的多,有的地方可能比1.2米浅的多,所以淘气身高1.3米,过河也可能会有危险。
原题说法错误。
故答案为:×。
【点评】解答本题需明确:平均数反映的是一组数据的集中趋势。
12.(2023春 洪山区期末)体操比赛裁判评分,要去掉一个最高分和最低分再算平均分,因为平均数是一个敏感的数,它容易受到极值的影响。 √
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】√
【分析】根据平均数的意义和特征直接判断。
【解答】解:平均数反映的是一组数据的集中趋势,极易受极端数据的影响,所以体操比赛裁判评分,要去掉一个最高分和最低分再算平均分。
原题说法正确。
故答案为:√。
【点评】解答本题需熟练掌握平均数的意义和特征。
13.(2023春 海安市期末)小刚所在班级的平均身高是135cm,小刚就一定是135厘米高。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】平均数反映的是一组数据的集中趋势,不能说明每个数据的大小。据此解答。
【解答】解:小刚所在班级的平均身高是135cm,小刚可能是135厘米高,也可能比135厘米高,还可能比135厘米低。原题说法错误。
故答案为:×。
【点评】解答本题需准确理解平均数的意义和特点。
14.(2022秋 渝北区期末)某班学生的平均体重是40千克,那么一定有学生的体重正好是40千克。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】平均数反映一组数据的集中趋势,某班学生的平均体重是40千克,那么这个班的学生的体重一定有高于40千克的,也有低于40千克的,也可能有正好40千克的,据此解答。
【解答】解:某班学生的平均体重是40千克,那么可能有学生的体重正好是40千克,原题说法错误。
故答案为:×。
【点评】解决本题的关键是掌握平均数的运用。
15.(2023春 永年区期末)一班和二班学生的平均身高分别是1.46米和1.48米,小明在一班,小红在一班,小红一定比小明高. ×
【考点】平均数的含义及求平均数的方法.
【专题】平均数问题;数据分析观念;应用意识.
【答案】×
【分析】平均数是表示一组数据集中趋势的量数,它是反映一组数据的平均水平,平均数会受偏大偏小数据的影响。一班学生的平均身高分别是1.46米,不能说明小明的身高就是1.46米,二班学生的平均身高是1.48米,也不能说明小红的身高就是1.48米。据此判断。
【解答】解:一班学生的平均身高分别是1.46米,不能说明小明的身高就是1.46米,小明的身高可能比1.46米低、也可能比1.46米高;二班学生的平均身高是1.48米,也不能说明小红的身高就是1.48米,小红的身高可能比1.48米低,也可能比1.48米高。由此可知,小红不一定比小明高。
因此,一班和二班学生的平均身高分别是1.46米和1.48米,小明在一班,小红在一班,小红一定比小明高。这种说法是错误的。
故答案为:×。
【点评】平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标,并不说明平均数大的那组数中的每一个数都大,平均数小的那组数中的每一个数都小,据此判断即可。
16.(2023春 江岸区期末)小林的身高是1.56m,他赤脚蹚过平均水深1.2m的小河,肯定不会有危险。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】小河平均水深1.2米,并不是说小河每处都深1.2米,有的地方可能比1.2米深得多,有的地方可能比1.2米浅得多;据此判断。
【解答】解:小河平均水深1.2米,并不是说小河每处都深1.2米,有的地方可能比1.2米深得多,有的地方可能比1.2米浅得多;小林的身高是1.56米,但可能有的地方比1.56米深,所以他过河也存在危险。
原题说法错误。
故答案为:×。
【点评】平均数反映的是一组数据的集中趋势,但不能确定每个数据的大小。
17.(2023 铜梁区)小军所在的篮球队队员的平均身高是160cm,小军的身高一定是160cm。 ×
【考点】平均数的含义及求平均数的方法.
【专题】推理能力.
【答案】×
【分析】平均数反映的是一组数据集中趋势,不是反映每一个数据的大小;所以每个篮球队员的身高可能是比162厘米高,可能等于162厘米,也可能比162厘米矮,据此解答即可。
【解答】解:根据分析可知:160厘米反映的是小军所在的篮球队队员的平均身高的集中趋势,不能反映某个队员的身高;小军的身高可能是比160厘米高,也可能等于160厘米,还可能比160厘米矮。
原题说法错误。
故答案为:×。
【点评】解答本题需熟练掌握平均数的意义。
四.应用题(共3小题)
18.(2022秋 滨城区期末)一本《少年读史记》有320页,丽丽前10天看了200页。如果剩下的6天看完,那么她平均每天看多少页?
【考点】平均数的含义及求平均数的方法.
【专题】数的运算.
【答案】20页。
【分析】先算出剩下的页数,再除以6即可。
【解答】解:(320﹣200)÷6
=120÷6
=20(页)
答:她平均每天看20页。
【点评】根据平均数的含义和求法,解答此题即可。
19.(2022秋 安泽县期末)五年级两个班参加植树活动,2.5小时共植树60棵。五(2)班平均每小时植10棵树,五(1)班平均每小时植树多少棵?
【考点】平均数的含义及求平均数的方法.
【专题】应用题.
【答案】14棵。
【分析】根据题意可知:(五年级(1)班平均每小时植的树+五年级(2)班平均每小时植的树)×2.5=两个班共同植的树,设五年级(1)班平均每小时植x棵,据此列方程解答。
【解答】解:设五年级(1)班平均每小时植x棵。
(10+x)×2.5=60
10+x=24
x=14
答:五年级(1)班平均每小时植14棵。
【点评】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,即:(五年级(1)班平均每小时植的树+五年级(2)班平均每小时植的树)×2.5=两个班共同植的树,进而列出方程是解答此类问题的关键。
20.(2022秋 钦南区期中)四年级五个班参加植树活动。第一天植树33棵,第二天植树38棵,第三天植树34棵。
(1)平均每天植树多少棵?
(2)这三天平均每班植树多少棵?
【考点】平均数的含义及求平均数的方法.
【专题】应用意识.
【答案】(1)35棵;
(2)21棵。
【分析】(1)把这三天植树的棵数加起来再除以3即可;
(2)用三天植树总棵数除以5即可。
【解答】解:(1)(33+38+34)÷3
=105÷3
=35(棵)
答:平均每天植树35棵。
(2)105÷5=21(棵)
答:这三天平均每班植树21棵。
【点评】本题考查了平均数的求法,要熟练掌握并运用。
21世纪教育网(www.21cnjy.com)
