22.3三角形的中位线 课后练习(含详解)冀教版数学八年级下册
文档属性
| 名称 | 22.3三角形的中位线 课后练习(含详解)冀教版数学八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 07:57:52 | ||
图片预览


文档简介
三角形的中位线
一、单选题
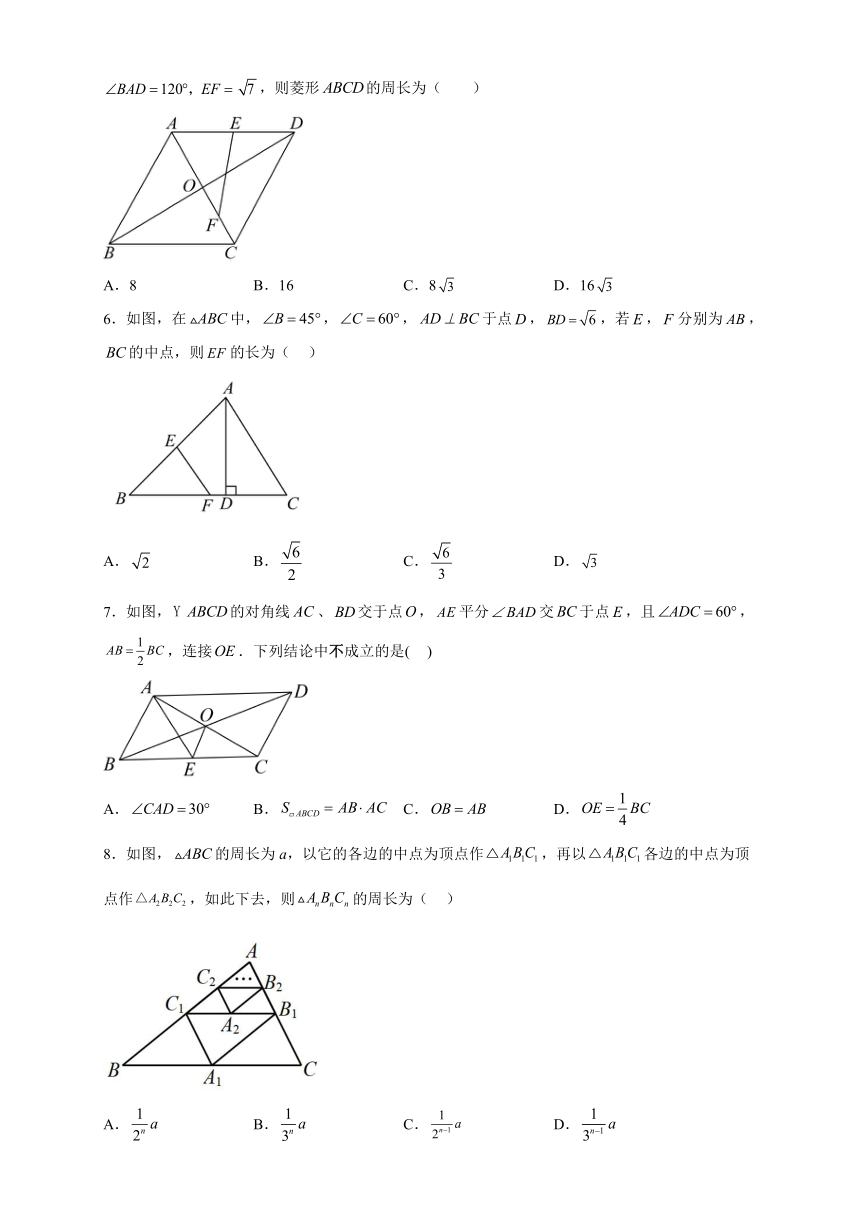
1.如图,在中,,,分别是,,的中点.若,,则四边形的周长是( )
A.17 B.20 C.24 D.28
2.如图,在四边形中,点M是上动点,点N是上一定点,点E、F分别是、的中点,当点M从点A向点D移动时,下列结论一定正确的是( )
A.线段EF的长度逐渐减小 B.线段EF的长度逐渐增大
C.线段EF的长度不改变 D.线段EF的长度不能确定
3.如图,为中的外角平分线,于,为中点,,,则长为( )
A. B. C. D.
4.已知,中,,,平分,,垂足为D,E为中点,连结,,则的值为( )
A. B. C. D.
5.如图,菱形的对角线相交于点O.E,F分别是的中点,若,则菱形的周长为( )
A.8 B.16 C.8 D.16
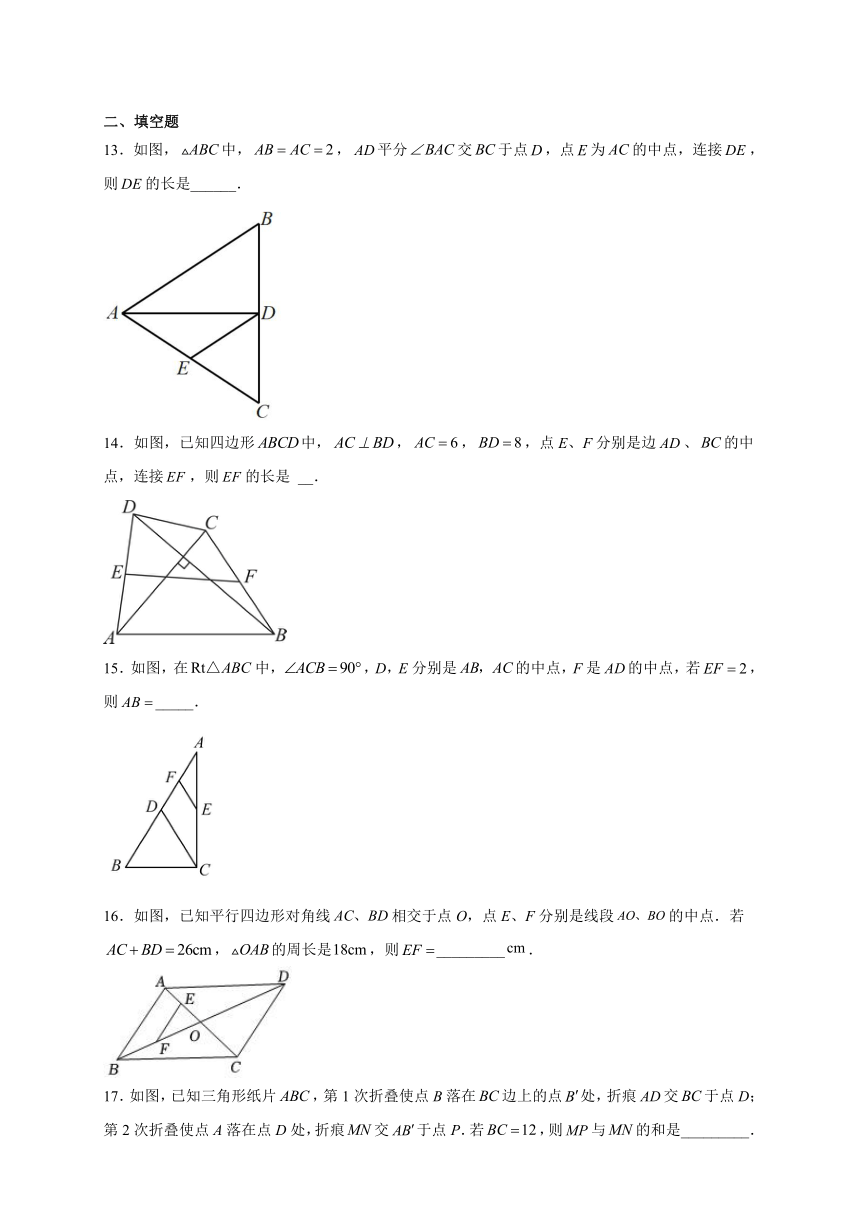
6.如图,在中,,,于点,,若,分别为,的中点,则的长为( )
A. B. C. D.
7.如图,的对角线、交于点,平分交于点,且,,连接.下列结论中不成立的是( )
A. B. C. D.
8.如图,的周长为a,以它的各边的中点为顶点作,再以各边的中点为顶点作,如此下去,则的周长为( )
A. B. C. D.
9.如图,在中,平分,于点E,点F是的中点,若,,则的长为( )
A.2 B.3 C.4 D.5
10.数学综合与实践活动课上,某兴趣小组要测定被池塘隔开的A、B两点间的距离,他们在外选一点C,连接、,并分别找出它们的中点D、E,连接.现测得,,,则A、B两点间的距离为( )
A. B. C. D.不能确定
11.如图,平行四边形中,为对角线交点,平分,平分,,,则的长为( )
A.1.5 B.2 C.2.5 D.3
12.如图,平行四边形的对角线、相交于点O,交于点E.若,的周长为10,则平行四边形的周长为( )
A.16 B.32 C.36 D.40
二、填空题
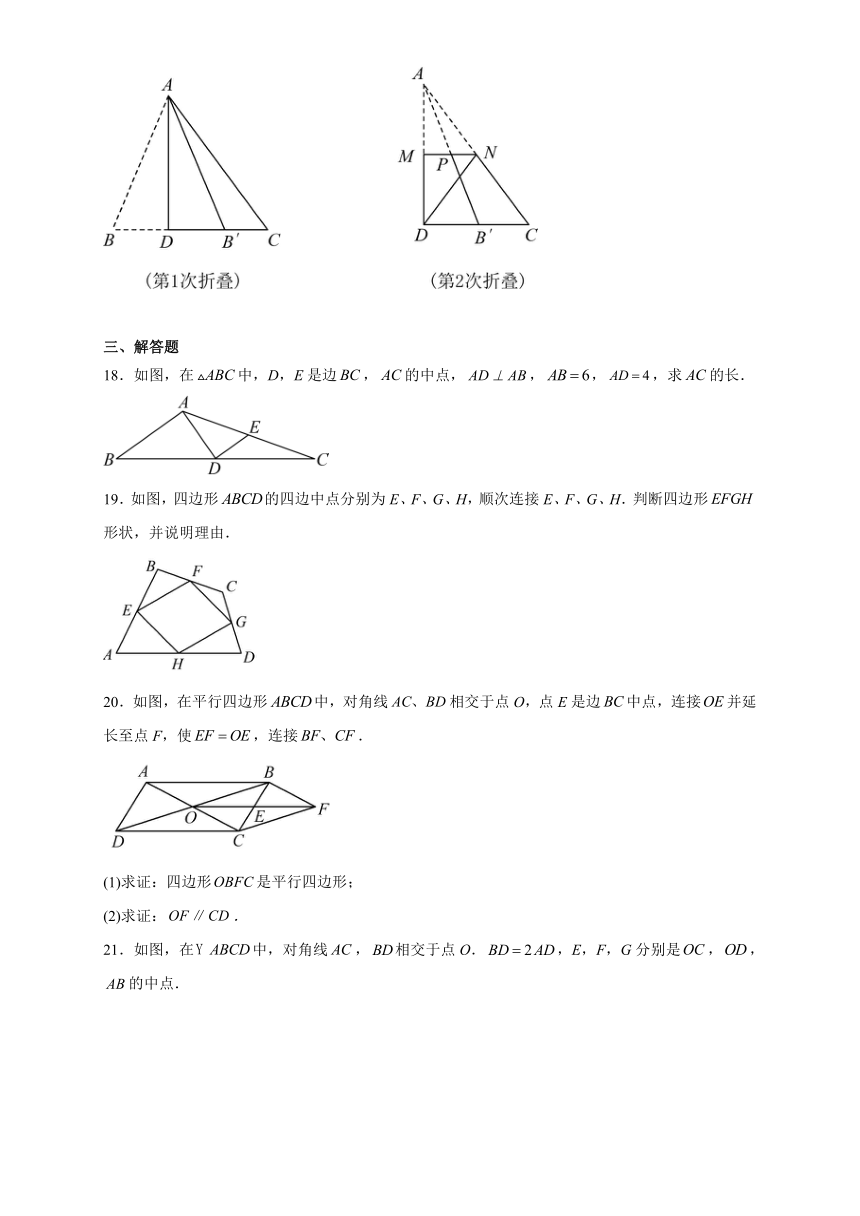
13.如图,中,,平分交于点,点为的中点,连接,则的长是______.
14.如图,已知四边形中,,,,点E、F分别是边、的中点,连接,则的长是 __.
15.如图,在中,,D,E分别是的中点,F是的中点,若,则_____.
16.如图,已知平行四边形对角线相交于点O,点E、F分别是线段的中点.若,的周长是,则_________.
17.如图,已知三角形纸片,第1次折叠使点B落在边上的点处,折痕交于点D;第2次折叠使点A落在点D处,折痕交于点P.若,则与的和是_________.
三、解答题
18.如图,在中,D,E是边,的中点,,,,求的长.
19.如图,四边形的四边中点分别为E、F、G、H,顺次连接E、F、G、H.判断四边形形状,并说明理由.
20.如图,在平行四边形中,对角线相交于点O,点E是边中点,连接并延长至点F,使,连接.
(1)求证:四边形是平行四边形;
(2)求证:.
21.如图,在中,对角线,相交于点O.,E,F,G分别是,,的中点.
(1)求证:;
(2)若,求的长.
22.如图,等边的边长是2,分别为的中点,延长至点,使,连接和.
(1)求证:四边形是平行四边形
(2)求的长.
23.如图,在中,,点D是上一点,连接,,平分交于点E.
(1)求证:垂直平分;
(2)若,,点F为的中点,连接,求的长.
参考答案
1.C
解:,,分别是,,的中点,
、分别是的中位线,
,且,,
四边形是平行四边形,
,,
四边形的周长为:
,
故选:C.
2.C
解:连接,
是定点,
是定值,
点E、F分别是、的中点,
,
是定值.
故选:C.
3.D
解:延长,交于点F,
,
∵为中的外角平分线,
∴,
∵,
∴,
在和中,
,
∴,
∴,,
又为中点,,
∴,
又,
∴.
故选:D.
4.D
解:如图,延长与相交于点F,过点B作于M,
∵,
∴,
∵平分,
∴,
∴,
∴,
∴,
∵E为中点,
∴是的中位线,
∴,
∴,
由勾股定理得:,
∵
∴,
∴,
由勾股定理得:,
∴,
由勾股定理得:,
∵,即,
∴.
故选D.
5.B
解:取的中点,连接,,
点为的中点,点为的中点,
,,,,
四边形是菱形,,
,,,
,,
设,则,,
,
,
解得,
,
菱形的周长为:,
故选:B.
6.A
解:,,
是等腰直角三角形,
,
,
,
,
,
即,
,
,分别为,的中点,
,
故选:A.
7.C
解:四边形是平行四边形,
,,
平分,
,
是等边三角形,
,
,
,
,
,故A正确;
,
,故B正确,
,,
,
,故C错误;
,,
,
,故D正确.
故选:C.
8.A
解:点、、分别为、、的中点,
,,,
的周长,
同理,的周长,
则的周长,
故选:A.
9.A
解:延长,交于点M,
∵平分,,
∴,,
∵,
∴,
∴,,
∵,
∴,
∵点F是的中点,,
∴为中位线,
∴.
故选:A.
10.C
解:、分别是、的中点,
是的中位线,
故选C.
11.A
解:如图,延长交于点,
四边形是平行四边形,
,,,,
,,
平分,平分,
,,
,,
,,
是的中位线,
,
故选:A.
12.B
解:∵四边形是平行四边形,
∴,,,,
∵,
∴,
∴是的中位线,
∴,,
∵的周长等于10,
∴,
∴,
∴,
∴;
故选:B.
13.1
解:∵中,,平分交于点D,
∴点D是的中点,
∵点E为的中点,
∴是的中位线,
∴,
故答案为:1.
14.5
解:如图,取的中点G,连接、,
∵E、F分别是边、的中点,
∴且,
且,
∵,
∴,
∴.
故答案为:5.
15.8
解:∵E、F分别是的中点,
∴是的中位线,
∴,
∵在中,,D是的中点,
∴,
故答案为:8.
16.
解:∵四边形是平行四边形,
∴,
∵,
∴,
∵的周长是,
∴,
∴,
∵点E、F分别是线段的中点,
∴,
故答案为:.
17.6
解:如图2,由折叠得:,,,连接,
∴, 是的垂直平分线,
∴,
∴,
∵,
∴,
∴
∴,
同理可得:,
∴是的中位线, 而,
∴,
∵,
∴.
故答案为:6.
18.10
解:、分别是、的中点,,,
根据中位线定理可知:,,
∴,
又,
在中,,
.
19.四边形EFGH为平行四边形,理由见解析
解:四边形为平行四边形,理由如下:
连接,如图,
在和中,
∵、分别为其中位线,
∴,且;且,
∴,,
∴四边形为平行四边形.
20.(1)证明见解析
(2)证明见解析
(1)证明:∵点E是边中点,
∴,
又∵,
∴四边形是平行四边形;
(2)证明:∵四边形是平行四边形,对角线相交于点O,
∴点O是的中点,
又∵点E是边中点,
∴是的中位线,
∴,即.
21.(1)见解析
(2)
(1)解:四边形是平行四边形,
,.
由已知,
.
又是中点,
.
(2)由(1),又是中点,
是斜边上的中线.
又是的中位线,
.
又,
.
22.(1)见解析
(2)
(1)证明:分别为的中点,
为的中位线,
,,
,
,
,
四边形是平行四边形;
(2)解:四边形是平行四边形,
为的中点,等边三角形的边长为2,
,
.
23.(1)见解析
(2)2
(1)证明:∵,
∴,
∵,
∴,
∴,即为等腰三角形,
∵平分,
∴,,
∴垂直平分;
(2)解:在中,,,
∴,,
∴,
∵点E为中点,点F为中点,
∴为的中位线,
∴.
一、单选题
1.如图,在中,,,分别是,,的中点.若,,则四边形的周长是( )
A.17 B.20 C.24 D.28
2.如图,在四边形中,点M是上动点,点N是上一定点,点E、F分别是、的中点,当点M从点A向点D移动时,下列结论一定正确的是( )
A.线段EF的长度逐渐减小 B.线段EF的长度逐渐增大
C.线段EF的长度不改变 D.线段EF的长度不能确定
3.如图,为中的外角平分线,于,为中点,,,则长为( )
A. B. C. D.
4.已知,中,,,平分,,垂足为D,E为中点,连结,,则的值为( )
A. B. C. D.
5.如图,菱形的对角线相交于点O.E,F分别是的中点,若,则菱形的周长为( )
A.8 B.16 C.8 D.16
6.如图,在中,,,于点,,若,分别为,的中点,则的长为( )
A. B. C. D.
7.如图,的对角线、交于点,平分交于点,且,,连接.下列结论中不成立的是( )
A. B. C. D.
8.如图,的周长为a,以它的各边的中点为顶点作,再以各边的中点为顶点作,如此下去,则的周长为( )
A. B. C. D.
9.如图,在中,平分,于点E,点F是的中点,若,,则的长为( )
A.2 B.3 C.4 D.5
10.数学综合与实践活动课上,某兴趣小组要测定被池塘隔开的A、B两点间的距离,他们在外选一点C,连接、,并分别找出它们的中点D、E,连接.现测得,,,则A、B两点间的距离为( )
A. B. C. D.不能确定
11.如图,平行四边形中,为对角线交点,平分,平分,,,则的长为( )
A.1.5 B.2 C.2.5 D.3
12.如图,平行四边形的对角线、相交于点O,交于点E.若,的周长为10,则平行四边形的周长为( )
A.16 B.32 C.36 D.40
二、填空题
13.如图,中,,平分交于点,点为的中点,连接,则的长是______.
14.如图,已知四边形中,,,,点E、F分别是边、的中点,连接,则的长是 __.
15.如图,在中,,D,E分别是的中点,F是的中点,若,则_____.
16.如图,已知平行四边形对角线相交于点O,点E、F分别是线段的中点.若,的周长是,则_________.
17.如图,已知三角形纸片,第1次折叠使点B落在边上的点处,折痕交于点D;第2次折叠使点A落在点D处,折痕交于点P.若,则与的和是_________.
三、解答题
18.如图,在中,D,E是边,的中点,,,,求的长.
19.如图,四边形的四边中点分别为E、F、G、H,顺次连接E、F、G、H.判断四边形形状,并说明理由.
20.如图,在平行四边形中,对角线相交于点O,点E是边中点,连接并延长至点F,使,连接.
(1)求证:四边形是平行四边形;
(2)求证:.
21.如图,在中,对角线,相交于点O.,E,F,G分别是,,的中点.
(1)求证:;
(2)若,求的长.
22.如图,等边的边长是2,分别为的中点,延长至点,使,连接和.
(1)求证:四边形是平行四边形
(2)求的长.
23.如图,在中,,点D是上一点,连接,,平分交于点E.
(1)求证:垂直平分;
(2)若,,点F为的中点,连接,求的长.
参考答案
1.C
解:,,分别是,,的中点,
、分别是的中位线,
,且,,
四边形是平行四边形,
,,
四边形的周长为:
,
故选:C.
2.C
解:连接,
是定点,
是定值,
点E、F分别是、的中点,
,
是定值.
故选:C.
3.D
解:延长,交于点F,
,
∵为中的外角平分线,
∴,
∵,
∴,
在和中,
,
∴,
∴,,
又为中点,,
∴,
又,
∴.
故选:D.
4.D
解:如图,延长与相交于点F,过点B作于M,
∵,
∴,
∵平分,
∴,
∴,
∴,
∴,
∵E为中点,
∴是的中位线,
∴,
∴,
由勾股定理得:,
∵
∴,
∴,
由勾股定理得:,
∴,
由勾股定理得:,
∵,即,
∴.
故选D.
5.B
解:取的中点,连接,,
点为的中点,点为的中点,
,,,,
四边形是菱形,,
,,,
,,
设,则,,
,
,
解得,
,
菱形的周长为:,
故选:B.
6.A
解:,,
是等腰直角三角形,
,
,
,
,
,
即,
,
,分别为,的中点,
,
故选:A.
7.C
解:四边形是平行四边形,
,,
平分,
,
是等边三角形,
,
,
,
,
,故A正确;
,
,故B正确,
,,
,
,故C错误;
,,
,
,故D正确.
故选:C.
8.A
解:点、、分别为、、的中点,
,,,
的周长,
同理,的周长,
则的周长,
故选:A.
9.A
解:延长,交于点M,
∵平分,,
∴,,
∵,
∴,
∴,,
∵,
∴,
∵点F是的中点,,
∴为中位线,
∴.
故选:A.
10.C
解:、分别是、的中点,
是的中位线,
故选C.
11.A
解:如图,延长交于点,
四边形是平行四边形,
,,,,
,,
平分,平分,
,,
,,
,,
是的中位线,
,
故选:A.
12.B
解:∵四边形是平行四边形,
∴,,,,
∵,
∴,
∴是的中位线,
∴,,
∵的周长等于10,
∴,
∴,
∴,
∴;
故选:B.
13.1
解:∵中,,平分交于点D,
∴点D是的中点,
∵点E为的中点,
∴是的中位线,
∴,
故答案为:1.
14.5
解:如图,取的中点G,连接、,
∵E、F分别是边、的中点,
∴且,
且,
∵,
∴,
∴.
故答案为:5.
15.8
解:∵E、F分别是的中点,
∴是的中位线,
∴,
∵在中,,D是的中点,
∴,
故答案为:8.
16.
解:∵四边形是平行四边形,
∴,
∵,
∴,
∵的周长是,
∴,
∴,
∵点E、F分别是线段的中点,
∴,
故答案为:.
17.6
解:如图2,由折叠得:,,,连接,
∴, 是的垂直平分线,
∴,
∴,
∵,
∴,
∴
∴,
同理可得:,
∴是的中位线, 而,
∴,
∵,
∴.
故答案为:6.
18.10
解:、分别是、的中点,,,
根据中位线定理可知:,,
∴,
又,
在中,,
.
19.四边形EFGH为平行四边形,理由见解析
解:四边形为平行四边形,理由如下:
连接,如图,
在和中,
∵、分别为其中位线,
∴,且;且,
∴,,
∴四边形为平行四边形.
20.(1)证明见解析
(2)证明见解析
(1)证明:∵点E是边中点,
∴,
又∵,
∴四边形是平行四边形;
(2)证明:∵四边形是平行四边形,对角线相交于点O,
∴点O是的中点,
又∵点E是边中点,
∴是的中位线,
∴,即.
21.(1)见解析
(2)
(1)解:四边形是平行四边形,
,.
由已知,
.
又是中点,
.
(2)由(1),又是中点,
是斜边上的中线.
又是的中位线,
.
又,
.
22.(1)见解析
(2)
(1)证明:分别为的中点,
为的中位线,
,,
,
,
,
四边形是平行四边形;
(2)解:四边形是平行四边形,
为的中点,等边三角形的边长为2,
,
.
23.(1)见解析
(2)2
(1)证明:∵,
∴,
∵,
∴,
∴,即为等腰三角形,
∵平分,
∴,,
∴垂直平分;
(2)解:在中,,,
∴,,
∴,
∵点E为中点,点F为中点,
∴为的中位线,
∴.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
