【期末高频易错考点】第2单元高频易错提高卷(含解析)-2024-2025学年五年级下册数学北师大版
文档属性
| 名称 | 【期末高频易错考点】第2单元高频易错提高卷(含解析)-2024-2025学年五年级下册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 458.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 08:11:34 | ||
图片预览



文档简介
第2章练习卷
一.选择题(共5小题)
1.(2024春 怀安县期末)一根钢丝恰好可以焊接成一个长8厘米、宽5厘米、高5厘米的长方体框架,如果把这根钢丝焊接成一个正方体框架,则正方体框架的棱长是____厘米。( )
A.18 B.72 C.6
2.(2024春 霍州市期中)如图小男孩用手中的长方体最多可以画出( )不同的长方形.
A.6个 B.3个 C.5个
3.(2022秋 陵水县期末)下面的图形中,折叠后能围成正方体的是( )
A. B. C. D.
4.(2023春 思明区期末)某产品说明书上标注包装尺寸为712×667×1888(mm),它们分别表示这个长方体的长、宽、高,根据这组数据,联系生活想象一下它可能是( )
A.一台电视机 B.一台微波炉
C.一部手机 D.一台冰箱
5.(2023 秦都区开学)一个正方体的棱长之和为36cm,这个正方体一个面的面积是( )cm2。
A.9 B.12 C.24
二.填空题(共5小题)
6.(2024 龙岗区)笑笑在剪一个正方体纸盒时,不小心把一个正方形S断开了,如图。现在她把正方形S粘回到左边的图上,变成一个完整的正方体展开图,共有 种不同的放置方法。
7.(2024春 盘山县期末)一个长方体的长是1.5分米,宽是1.2分米,高是1分米,它的棱长和是 分米.
8.(2024春 前郭县期末)用铁丝做一个长5dm,宽4dm,高3dm的长方体框架,至少需要铁丝 dm.(不计接口)
9.(2024春 开封期末)用一根80厘米长的铁丝刚好焊接成一个正方体框架,这个正方体框架的每条棱长是这根铁丝的,每条棱的长度是 厘米。(损耗和接口处忽略不计)
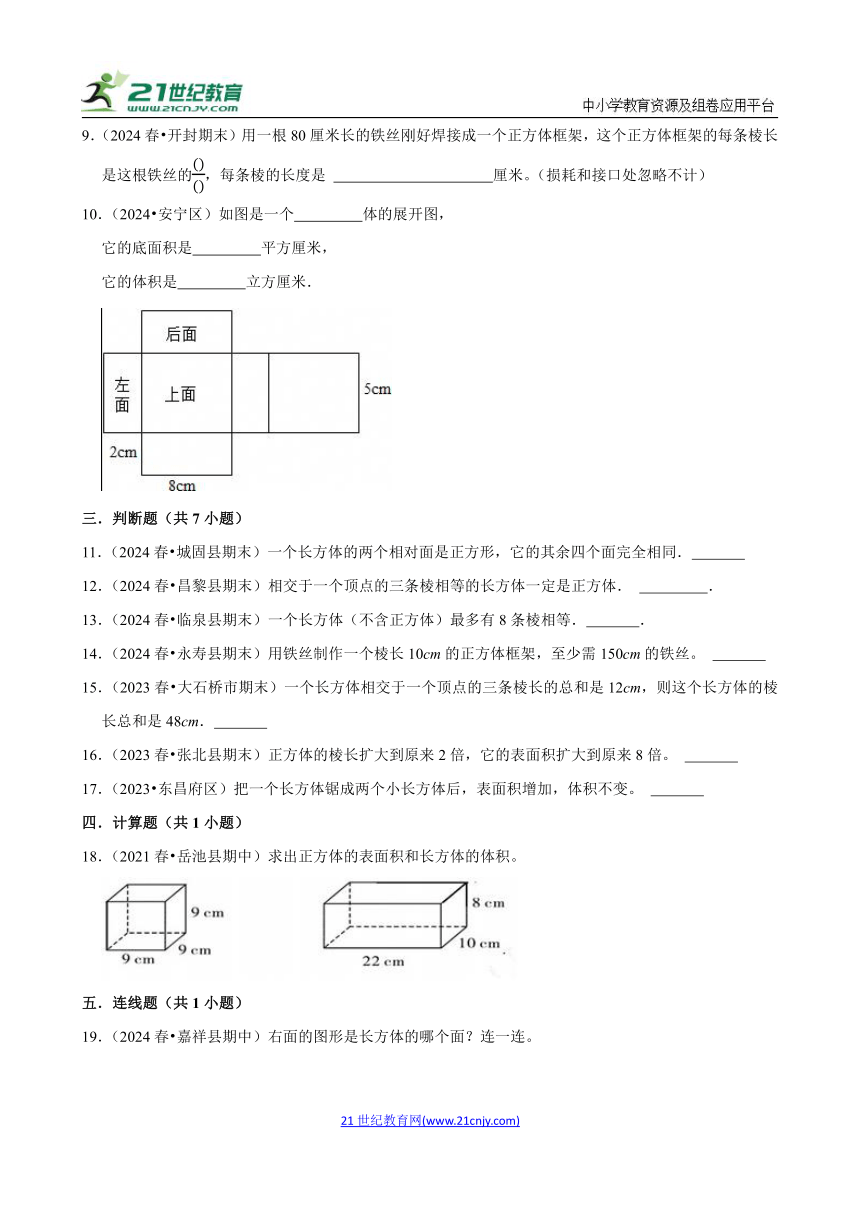
10.(2024 安宁区)如图是一个 体的展开图,
它的底面积是 平方厘米,
它的体积是 立方厘米.
三.判断题(共7小题)
11.(2024春 城固县期末)一个长方体的两个相对面是正方形,它的其余四个面完全相同.
12.(2024春 昌黎县期末)相交于一个顶点的三条棱相等的长方体一定是正方体. .
13.(2024春 临泉县期末)一个长方体(不含正方体)最多有8条棱相等. .
14.(2024春 永寿县期末)用铁丝制作一个棱长10cm的正方体框架,至少需150cm的铁丝。
15.(2023春 大石桥市期末)一个长方体相交于一个顶点的三条棱长的总和是12cm,则这个长方体的棱长总和是48cm.
16.(2023春 张北县期末)正方体的棱长扩大到原来2倍,它的表面积扩大到原来8倍。
17.(2023 东昌府区)把一个长方体锯成两个小长方体后,表面积增加,体积不变。
四.计算题(共1小题)
18.(2021春 岳池县期中)求出正方体的表面积和长方体的体积。
五.连线题(共1小题)
19.(2024春 嘉祥县期中)右面的图形是长方体的哪个面?连一连。
六.操作题(共1小题)
20.(2022秋 涟水县期末)在方格纸上画出长方体表面展开图的另外三个面,并标上相应名称。
七.应用题(共5小题)
21.(2024春 永寿县期末)明明的爸爸利用废旧的木板做了一个一面无门的小鞋柜(如图),制作这样一个小鞋柜,至少需要多少平方分米的木板?
22.(2024春 北票市期中)学校餐厅长10m,宽8m,高5m。除去门窗面积18.4m2,餐厅的墙壁和房顶都贴上壁纸。平均每平方米壁纸的价钱为5元,购买壁纸至少需要多少元?
23.(2023春 大庆期末)做一个正方体的玻璃鱼缸(无盖),棱长6分米.制作这个鱼缸时至少需要玻璃多少平方分米?
24.(2023春 赣县区期末)一个长方体形状的儿童一次性口罩包装盒,长13cm,宽11cm,高10cm。如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有多少平方厘米?
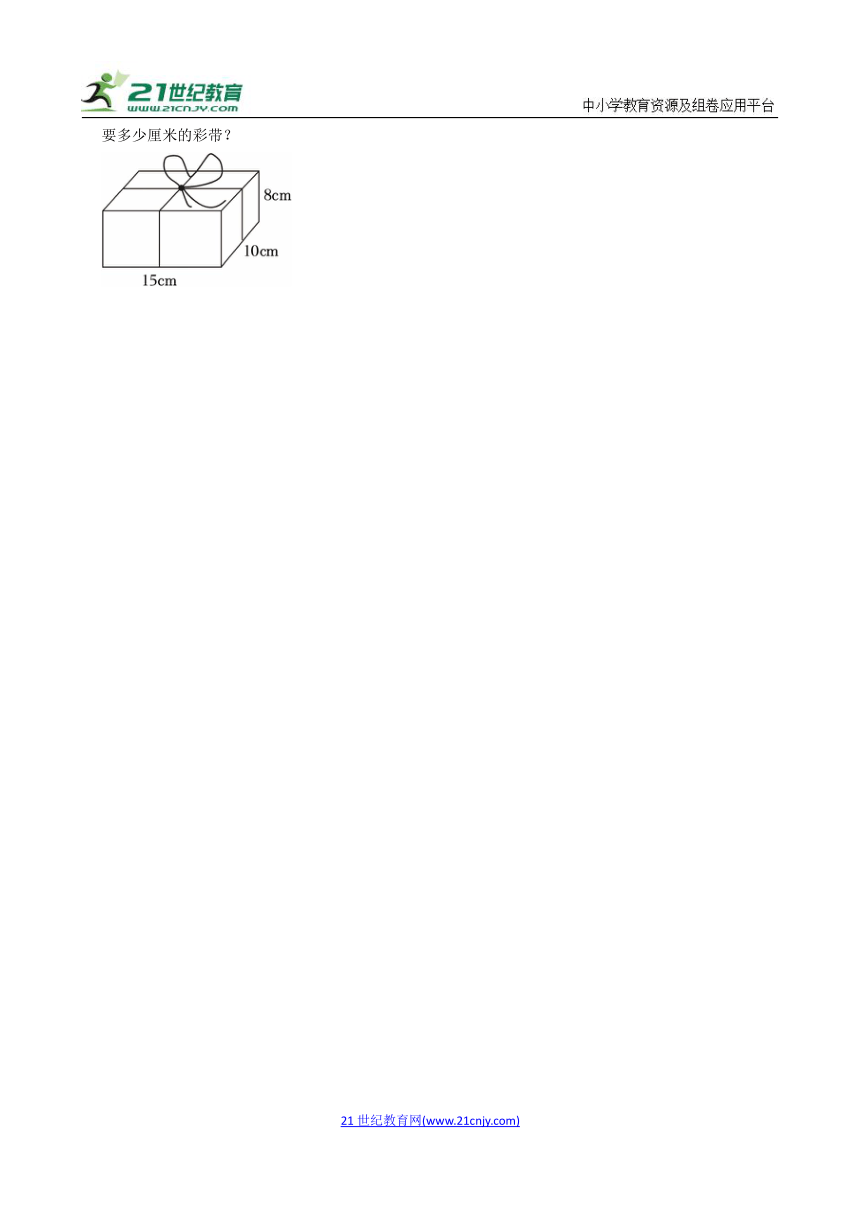
25.(2022秋 盱眙县期末)妈妈为小明准备了六一儿童节礼物,如图是这个节日礼物的包装盒,它的长、宽、高分别是15厘米、10厘米、8厘米,用彩带把这个包装盒捆上,捆扎处用去彩带16厘米,一共需要多少厘米的彩带?
第2章练习卷
参考答案与试题解析
题号 1 2 3 4 5
答案 C B A D A
一.选择题(共5小题)
1.(2024春 怀安县期末)一根钢丝恰好可以焊接成一个长8厘米、宽5厘米、高5厘米的长方体框架,如果把这根钢丝焊接成一个正方体框架,则正方体框架的棱长是____厘米。( )
A.18 B.72 C.6
【考点】正方体的特征;长方体的特征.
【专题】几何直观.
【答案】C
【分析】先计算出长方体框架的棱长和:(5+5+8)×4=48(厘米),再根据题意可知:长方体框架的棱长和也就是正方体的棱长和,用正方体的棱长和除以12就可以计算出正方体框架的棱长了。
【解答】解:(5+5+8)×4=72(厘米)
72÷12=6(厘米)
答:这个正方体框架的棱长是6厘米。
故选:C。
【点评】这道题解题的关键是熟练掌握长方体和正方体的棱长和公式。
2.(2024春 霍州市期中)如图小男孩用手中的长方体最多可以画出( )不同的长方形.
A.6个 B.3个 C.5个
【考点】长方体的特征.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】B
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等.据此解答.
【解答】解:通过观察图形可知,这个长方体的6个面都是长方形,所以用长方体最多可以画出3个不同的长方形.
故选:B.
【点评】此题考查的目的是理解掌握长方体的特征及应用.
3.(2022秋 陵水县期末)下面的图形中,折叠后能围成正方体的是( )
A. B. C. D.
【考点】正方体的展开图.
【答案】A
【分析】由平面图形的折叠及正方体的展开图解题.注意只要有“田”字格的展开图都不是正方体的表面展开图.
【解答】解:A可以折叠成一个正方体,符合题意,
B只要有“田”字格的展开图都不是正方体的表面展开图所以它折叠不成正方体,不符合题意,
C围成几何体时,多了一个底面,少了一个侧面,所以不能围成正方体,不符合题意,
D围成几何体时,有两个面重合,故不能围成正方体,不符合题意.
故选:A.
【点评】此题主要考查了展开图折叠成几何体,考查同学们的空间想象能力.
4.(2023春 思明区期末)某产品说明书上标注包装尺寸为712×667×1888(mm),它们分别表示这个长方体的长、宽、高,根据这组数据,联系生活想象一下它可能是( )
A.一台电视机 B.一台微波炉
C.一部手机 D.一台冰箱
【考点】长方体的特征.
【专题】常规题型;推理能力.
【答案】D
【分析】这个长方体的高是1888毫米=1.888米,长712毫米=0.712米,宽667毫米=0.667米,所以它可能是一台冰箱,据此解答即可。
【解答】解:这个长方体的高是1888毫米=1.888米,长712毫米=0.712米,宽667毫米=0.667米,所以它可能是一台冰箱。
故选:D。
【点评】先把毫米化为米,然后联系生活实际,想象一下就可以得出结论。
5.(2023 秦都区开学)一个正方体的棱长之和为36cm,这个正方体一个面的面积是( )cm2。
A.9 B.12 C.24
【考点】正方体的特征.
【专题】应用意识.
【答案】A
【分析】由正方体的特征可知:正方体有12条棱长,且每条棱长都相等,再据“一个正方体的棱长总和是60厘米”即可求出这个正方体的棱长,进而求出面一个面的面积。
【解答】解:正方体的棱长:36÷12=3(厘米),正方体的一个面的面积:3×3=9(平方厘米)
答:这个正方体一个面的面积是9cm2。
故选:A。
【点评】此题主要考查正方形面积的计算方法,关键是先依据正方体的特征先求出正方体的棱长,进而逐步求解。
二.填空题(共5小题)
6.(2024 龙岗区)笑笑在剪一个正方体纸盒时,不小心把一个正方形S断开了,如图。现在她把正方形S粘回到左边的图上,变成一个完整的正方体展开图,共有 4 种不同的放置方法。
【考点】正方体的展开图.
【专题】立体图形的认识与计算;空间观念.
【答案】4。
【分析】不论如何放置,中间一行的第一个和第三个面相对,上下两个面相对,所以正方形S有4个位置可以放(如下图),据此解答即可。
【解答】解:如下图所示:
共有4种不同的放置方法。
故答案为:4。
【点评】此题考查了正方体展开图的灵活运用。
7.(2024春 盘山县期末)一个长方体的长是1.5分米,宽是1.2分米,高是1分米,它的棱长和是 14.8 分米.
【考点】长方体的特征.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答即可.
【解答】解:棱长总和:
(1.2+1.5+1)×4
=3.7×4
=14.8(分米);
答:这个长方体的棱长总和是14.8分米.
故答案为:14.8.
【点评】此题主要考查长方体的特征,以及棱长总和的计算.
8.(2024春 前郭县期末)用铁丝做一个长5dm,宽4dm,高3dm的长方体框架,至少需要铁丝 48 dm.(不计接口)
【考点】长方体的特征.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】长方体有12条棱,相对的四条棱长度相等.求至少需要多少厘米的铁丝就是求长方体的棱长和是多少,用(长+宽+高)×4列式计算.
【解答】解:(5+4+3)×4
=12×4
=48(分米)
答:至少需要48分米的铁丝.
故答案为:48.
【点评】此题主要考查长方体的特征及棱长总和的计算方法.
9.(2024春 开封期末)用一根80厘米长的铁丝刚好焊接成一个正方体框架,这个正方体框架的每条棱长是这根铁丝的,每条棱的长度是 厘米。(损耗和接口处忽略不计)
【考点】正方体的特征.
【专题】几何直观.
【答案】,。
【分析】用80厘米的铁丝焊接成一个正方体框架,也就是这个正方体的棱长总和是80厘米,正方体的12条棱长都相等,则这个正方体框架的每条棱长是这根铁丝的,根据棱长=正方体的棱长总和÷12即可求得棱长。
【解答】解:1÷12
棱长:80÷12(厘米)
答:这个正方体框架的每条棱长是这根铁丝的,每条棱的长度是厘米。
故答案为:,。
【点评】此题考查的目的是理解掌握正方体的特征以及正方体的棱长总和公式,注意基础知识的灵活运用。
10.(2024 安宁区)如图是一个 长方 体的展开图,
它的底面积是 40 平方厘米,
它的体积是 80 立方厘米.
【考点】长方体的特征.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等.根据它的展开图可知,底面的长是8厘米,宽是5厘米,根据长方形的面积公式:
s=ab,体积公式:v=abh,把数据代入公式解答.
【解答】解:底面积是:8×5=40(平方厘米),
体积是:8×5×2=80(立方厘米);
故答案为:长方,40,80.
【点评】此题主要考查长方体的特征和它的底面积、体积的计算.首先根据展开图确定长、宽、高,把数据代入公式解答.
三.判断题(共7小题)
11.(2024春 城固县期末)一个长方体的两个相对面是正方形,它的其余四个面完全相同. √
【考点】长方体的特征.
【专题】立体图形的认识与计算;空间观念.
【答案】见试题解答内容
【分析】假设是上、下两个面都是正方形的长方体,即长方体的长和宽相等,其它四个面的面积都等于正方形的边长×高,因为正方形的边长都相等,长方体的高不变,所以它的其余四个面完全相同,面积相等.
【解答】解:由分析知:有两个相对面是正方形的长方体,它的其余四个面完全相同,面积相等;
所以原题说法正确.
故答案为:√.
【点评】解答此题的关键:应明确长方体的特征,可画图进行分析.
12.(2024春 昌黎县期末)相交于一个顶点的三条棱相等的长方体一定是正方体. √ .
【考点】正方体的特征.
【答案】√
【分析】根据正方体的意义,长、宽、高都相等的长方体叫做正方体,也叫立方体.由此解答.
【解答】解:如果相交于一个顶点的三条棱相等也就是长、宽、高相等,长、宽、高都相等的长方体叫做正方体.
所以,相交于一个顶点的三条棱相等的长方体一定是正方体.此说法正确.
故答案为:√.
【点评】此题主要根据正方体的特征和长方体与正方体的之间的关系解决问题.
13.(2024春 临泉县期末)一个长方体(不含正方体)最多有8条棱相等. √ .
【考点】长方体的特征.
【答案】见试题解答内容
【分析】根据长方体的特征,12条棱分为互相平行的3组,每组4条棱的长度相等,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等;如果长方体有两个相对的面是正方形,这时最多有8条棱相等;由此解答.
【解答】解:如果长方体有两个相对的面是正方形,这时最多有8条棱相等;因此,一个长方体(不含正方体)最多有8条棱相等.此说法正确.
故答案为:√.
【点评】此题主要考查长方体的特征,长、宽、高各不相等时,12条棱分为互相平行的3组,每组4条棱的长度相等,如果长方体有两个相对的面是正方形,这时最多有8条棱相等;据此解决问题.
14.(2024春 永寿县期末)用铁丝制作一个棱长10cm的正方体框架,至少需150cm的铁丝。 ×
【考点】正方体的特征.
【专题】应用题;几何直观.
【答案】×
【分析】根据正方体的特征,12条棱的长度都相等,正方体的棱长总和=棱长×12,把数据代入棱长总和公式解答即可判断。
【解答】解:10×12=120(cm)
所以用铁丝制作一个棱长10cm的正方体框架,至少需120cm的铁丝,原题说法错误。
故答案为:×。
【点评】本题考查了正方体的特征。
15.(2023春 大石桥市期末)一个长方体相交于一个顶点的三条棱长的总和是12cm,则这个长方体的棱长总和是48cm. √
【考点】长方体的特征.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】√
【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式求出这个长方体的棱长总和与48厘米进行比较即可.
【解答】解:12×4=48(厘米)
所以这个长方体的棱长总和是48厘米.
故答案为:√.
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和公式的灵活运用,关键是熟记公式.
16.(2023春 张北县期末)正方体的棱长扩大到原来2倍,它的表面积扩大到原来8倍。 ×
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】见试题解答内容
【分析】根据正方体表面积扩大的倍数是棱长扩大倍数的平方,列式计算后再判断即可。
【解答】解:一个正方体棱长扩大到原来的2倍,则表面积扩大到原来的2×2=4倍,所以原题说法错误。
故答案为:×。
【点评】考查了正方体的表面积和正方体棱长的之间关系,是基础题型。
17.(2023 东昌府区)把一个长方体锯成两个小长方体后,表面积增加,体积不变。 √
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】√
【分析】长方体切开的时候表面积增加了,因为由于切开,增加了新的面,所以表面积增加;物体所占空间的大小不变,即体积不变;据此即可解答。
【解答】解:因为将长方体切成两个长方体后,表面积将增加2个新的面,所以表面积变大了;而把一个长方体分成两个长方体,它的形状变了,但体积没有变。题干说法正确。
故答案为:√。
【点评】根据长方体切割的特点,即可判断表面积与体积的变化情况。
四.计算题(共1小题)
18.(2021春 岳池县期中)求出正方体的表面积和长方体的体积。
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】486平方厘米,300立方厘米。
【分析】根据正方体的表面积公式:S=6a2,再根据长方体的体积公式:V=abh,把数据分别代入公式解答。
【解答】解:9×9×6
=81×6
=486(平方厘米)
答:这个正方体的表面积是486平方厘米。
22×10×8=1760(立方厘米)
答:长方体的体积是300立方厘米。
【点评】此题主要考查正方体的表面积公式、长方体的体积公式的灵活运用,关键是熟记公式。
五.连线题(共1小题)
19.(2024春 嘉祥县期中)右面的图形是长方体的哪个面?连一连。
【考点】长方体的特征.
【专题】应用意识.
【答案】
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的形状和大小完全相同。据此解答。
【解答】解:
【点评】此题考查的目的是理解掌握长方体的特征及应用。
六.操作题(共1小题)
20.(2022秋 涟水县期末)在方格纸上画出长方体表面展开图的另外三个面,并标上相应名称。
【考点】长方体的展开图.
【专题】几何直观.
【答案】(画法不唯一)
【分析】根据长方体的特征,6个面的长方形(特殊情况有两个相对的面是正方形),上面对下面,前面对后面,左面对右面,对面相等。
【解答】解:
(画法不唯一)
【点评】此题主要考查长方体的特征。
七.应用题(共5小题)
21.(2024春 永寿县期末)明明的爸爸利用废旧的木板做了一个一面无门的小鞋柜(如图),制作这样一个小鞋柜,至少需要多少平方分米的木板?
【考点】长方体和正方体的表面积.
【专题】立体图形的认识与计算;空间观念.
【答案】142.5平方分米。
【分析】通过观察图形可知,需要木板的面积等于这个长方体的后面、上下、左右5个面的总面积,根据长方体的表面积公式解答。
【解答】解:45×60+55×45×2+60×55×2
=2700+4950+6600
=14250(平方厘米)
14250平方厘米=142.5平方分米
答:至少需要142.5平方分米的木板。
【点评】此题主要考查长方体表面积公式的灵活应用,关键是熟记公式。
22.(2024春 北票市期中)学校餐厅长10m,宽8m,高5m。除去门窗面积18.4m2,餐厅的墙壁和房顶都贴上壁纸。平均每平方米壁纸的价钱为5元,购买壁纸至少需要多少元?
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】1208元。
【分析】“要在餐厅的墙壁和房顶都贴上壁纸”,就是贴壁纸的面积是5个面,求出5个面的面积,再减去门窗的面积,就是需要壁纸的面积,求出面积再乘上5,就是需要花的钱数。据此解答。
【解答】解:10×8+10×5×2+8×5×2﹣18.4
=80+100+80﹣18.4
=260﹣18.4
=241.6(平方米)
5×241.6=1208(元)
答:购买壁纸至少需要1208元。
【点评】本题的关键是求出要贴壁纸的面积,再根据乘法的意义求出需要的钱数。
23.(2023春 大庆期末)做一个正方体的玻璃鱼缸(无盖),棱长6分米.制作这个鱼缸时至少需要玻璃多少平方分米?
【考点】长方体和正方体的表面积.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】见试题解答内容
【分析】根据正方体的表面积公式:S=6a2,由于鱼缸无盖,所以只它的5个面的总面积即可.
【解答】解:6×6×5=180(平方分米)
答:制作这个鱼缸时至少需要玻璃180平方分米.
【点评】此题主要考查正方体表面积公式的灵活运用,关键是熟记公式.
24.(2023春 赣县区期末)一个长方体形状的儿童一次性口罩包装盒,长13cm,宽11cm,高10cm。如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有多少平方厘米?
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】480平方厘米。
【分析】根据题意可知:“围着它贴一圈商标纸(上下面不贴)”,也就是求这个长方体的4个侧面的总面积,即(长×高+宽×高)×2,代入数字即可求解。
【解答】解:(13×10+11×10)×2
=(130+110)×2
=240×2
=480(平方厘米)
答:这张商标纸的面积至少有480平方厘米。
【点评】此题解答关键是搞清商标纸所贴的位置只在4个侧面上,然后根据长方体表面积公式求解。
25.(2022秋 盱眙县期末)妈妈为小明准备了六一儿童节礼物,如图是这个节日礼物的包装盒,它的长、宽、高分别是15厘米、10厘米、8厘米,用彩带把这个包装盒捆上,捆扎处用去彩带16厘米,一共需要多少厘米的彩带?
【考点】长方体的特征.
【专题】数据分析观念.
【答案】98厘米。
【分析】根据长方体的特征即可解答。
【解答】解:15×2+10×2+8×4
=30+20+32
=82(厘米)
82+16=98(厘米)
答:一共需要98厘米的彩带。
【点评】本题主要考查长方体的特征。
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024春 怀安县期末)一根钢丝恰好可以焊接成一个长8厘米、宽5厘米、高5厘米的长方体框架,如果把这根钢丝焊接成一个正方体框架,则正方体框架的棱长是____厘米。( )
A.18 B.72 C.6
2.(2024春 霍州市期中)如图小男孩用手中的长方体最多可以画出( )不同的长方形.
A.6个 B.3个 C.5个
3.(2022秋 陵水县期末)下面的图形中,折叠后能围成正方体的是( )
A. B. C. D.
4.(2023春 思明区期末)某产品说明书上标注包装尺寸为712×667×1888(mm),它们分别表示这个长方体的长、宽、高,根据这组数据,联系生活想象一下它可能是( )
A.一台电视机 B.一台微波炉
C.一部手机 D.一台冰箱
5.(2023 秦都区开学)一个正方体的棱长之和为36cm,这个正方体一个面的面积是( )cm2。
A.9 B.12 C.24
二.填空题(共5小题)
6.(2024 龙岗区)笑笑在剪一个正方体纸盒时,不小心把一个正方形S断开了,如图。现在她把正方形S粘回到左边的图上,变成一个完整的正方体展开图,共有 种不同的放置方法。
7.(2024春 盘山县期末)一个长方体的长是1.5分米,宽是1.2分米,高是1分米,它的棱长和是 分米.
8.(2024春 前郭县期末)用铁丝做一个长5dm,宽4dm,高3dm的长方体框架,至少需要铁丝 dm.(不计接口)
9.(2024春 开封期末)用一根80厘米长的铁丝刚好焊接成一个正方体框架,这个正方体框架的每条棱长是这根铁丝的,每条棱的长度是 厘米。(损耗和接口处忽略不计)
10.(2024 安宁区)如图是一个 体的展开图,
它的底面积是 平方厘米,
它的体积是 立方厘米.
三.判断题(共7小题)
11.(2024春 城固县期末)一个长方体的两个相对面是正方形,它的其余四个面完全相同.
12.(2024春 昌黎县期末)相交于一个顶点的三条棱相等的长方体一定是正方体. .
13.(2024春 临泉县期末)一个长方体(不含正方体)最多有8条棱相等. .
14.(2024春 永寿县期末)用铁丝制作一个棱长10cm的正方体框架,至少需150cm的铁丝。
15.(2023春 大石桥市期末)一个长方体相交于一个顶点的三条棱长的总和是12cm,则这个长方体的棱长总和是48cm.
16.(2023春 张北县期末)正方体的棱长扩大到原来2倍,它的表面积扩大到原来8倍。
17.(2023 东昌府区)把一个长方体锯成两个小长方体后,表面积增加,体积不变。
四.计算题(共1小题)
18.(2021春 岳池县期中)求出正方体的表面积和长方体的体积。
五.连线题(共1小题)
19.(2024春 嘉祥县期中)右面的图形是长方体的哪个面?连一连。
六.操作题(共1小题)
20.(2022秋 涟水县期末)在方格纸上画出长方体表面展开图的另外三个面,并标上相应名称。
七.应用题(共5小题)
21.(2024春 永寿县期末)明明的爸爸利用废旧的木板做了一个一面无门的小鞋柜(如图),制作这样一个小鞋柜,至少需要多少平方分米的木板?
22.(2024春 北票市期中)学校餐厅长10m,宽8m,高5m。除去门窗面积18.4m2,餐厅的墙壁和房顶都贴上壁纸。平均每平方米壁纸的价钱为5元,购买壁纸至少需要多少元?
23.(2023春 大庆期末)做一个正方体的玻璃鱼缸(无盖),棱长6分米.制作这个鱼缸时至少需要玻璃多少平方分米?
24.(2023春 赣县区期末)一个长方体形状的儿童一次性口罩包装盒,长13cm,宽11cm,高10cm。如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有多少平方厘米?
25.(2022秋 盱眙县期末)妈妈为小明准备了六一儿童节礼物,如图是这个节日礼物的包装盒,它的长、宽、高分别是15厘米、10厘米、8厘米,用彩带把这个包装盒捆上,捆扎处用去彩带16厘米,一共需要多少厘米的彩带?
第2章练习卷
参考答案与试题解析
题号 1 2 3 4 5
答案 C B A D A
一.选择题(共5小题)
1.(2024春 怀安县期末)一根钢丝恰好可以焊接成一个长8厘米、宽5厘米、高5厘米的长方体框架,如果把这根钢丝焊接成一个正方体框架,则正方体框架的棱长是____厘米。( )
A.18 B.72 C.6
【考点】正方体的特征;长方体的特征.
【专题】几何直观.
【答案】C
【分析】先计算出长方体框架的棱长和:(5+5+8)×4=48(厘米),再根据题意可知:长方体框架的棱长和也就是正方体的棱长和,用正方体的棱长和除以12就可以计算出正方体框架的棱长了。
【解答】解:(5+5+8)×4=72(厘米)
72÷12=6(厘米)
答:这个正方体框架的棱长是6厘米。
故选:C。
【点评】这道题解题的关键是熟练掌握长方体和正方体的棱长和公式。
2.(2024春 霍州市期中)如图小男孩用手中的长方体最多可以画出( )不同的长方形.
A.6个 B.3个 C.5个
【考点】长方体的特征.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】B
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等.据此解答.
【解答】解:通过观察图形可知,这个长方体的6个面都是长方形,所以用长方体最多可以画出3个不同的长方形.
故选:B.
【点评】此题考查的目的是理解掌握长方体的特征及应用.
3.(2022秋 陵水县期末)下面的图形中,折叠后能围成正方体的是( )
A. B. C. D.
【考点】正方体的展开图.
【答案】A
【分析】由平面图形的折叠及正方体的展开图解题.注意只要有“田”字格的展开图都不是正方体的表面展开图.
【解答】解:A可以折叠成一个正方体,符合题意,
B只要有“田”字格的展开图都不是正方体的表面展开图所以它折叠不成正方体,不符合题意,
C围成几何体时,多了一个底面,少了一个侧面,所以不能围成正方体,不符合题意,
D围成几何体时,有两个面重合,故不能围成正方体,不符合题意.
故选:A.
【点评】此题主要考查了展开图折叠成几何体,考查同学们的空间想象能力.
4.(2023春 思明区期末)某产品说明书上标注包装尺寸为712×667×1888(mm),它们分别表示这个长方体的长、宽、高,根据这组数据,联系生活想象一下它可能是( )
A.一台电视机 B.一台微波炉
C.一部手机 D.一台冰箱
【考点】长方体的特征.
【专题】常规题型;推理能力.
【答案】D
【分析】这个长方体的高是1888毫米=1.888米,长712毫米=0.712米,宽667毫米=0.667米,所以它可能是一台冰箱,据此解答即可。
【解答】解:这个长方体的高是1888毫米=1.888米,长712毫米=0.712米,宽667毫米=0.667米,所以它可能是一台冰箱。
故选:D。
【点评】先把毫米化为米,然后联系生活实际,想象一下就可以得出结论。
5.(2023 秦都区开学)一个正方体的棱长之和为36cm,这个正方体一个面的面积是( )cm2。
A.9 B.12 C.24
【考点】正方体的特征.
【专题】应用意识.
【答案】A
【分析】由正方体的特征可知:正方体有12条棱长,且每条棱长都相等,再据“一个正方体的棱长总和是60厘米”即可求出这个正方体的棱长,进而求出面一个面的面积。
【解答】解:正方体的棱长:36÷12=3(厘米),正方体的一个面的面积:3×3=9(平方厘米)
答:这个正方体一个面的面积是9cm2。
故选:A。
【点评】此题主要考查正方形面积的计算方法,关键是先依据正方体的特征先求出正方体的棱长,进而逐步求解。
二.填空题(共5小题)
6.(2024 龙岗区)笑笑在剪一个正方体纸盒时,不小心把一个正方形S断开了,如图。现在她把正方形S粘回到左边的图上,变成一个完整的正方体展开图,共有 4 种不同的放置方法。
【考点】正方体的展开图.
【专题】立体图形的认识与计算;空间观念.
【答案】4。
【分析】不论如何放置,中间一行的第一个和第三个面相对,上下两个面相对,所以正方形S有4个位置可以放(如下图),据此解答即可。
【解答】解:如下图所示:
共有4种不同的放置方法。
故答案为:4。
【点评】此题考查了正方体展开图的灵活运用。
7.(2024春 盘山县期末)一个长方体的长是1.5分米,宽是1.2分米,高是1分米,它的棱长和是 14.8 分米.
【考点】长方体的特征.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答即可.
【解答】解:棱长总和:
(1.2+1.5+1)×4
=3.7×4
=14.8(分米);
答:这个长方体的棱长总和是14.8分米.
故答案为:14.8.
【点评】此题主要考查长方体的特征,以及棱长总和的计算.
8.(2024春 前郭县期末)用铁丝做一个长5dm,宽4dm,高3dm的长方体框架,至少需要铁丝 48 dm.(不计接口)
【考点】长方体的特征.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】长方体有12条棱,相对的四条棱长度相等.求至少需要多少厘米的铁丝就是求长方体的棱长和是多少,用(长+宽+高)×4列式计算.
【解答】解:(5+4+3)×4
=12×4
=48(分米)
答:至少需要48分米的铁丝.
故答案为:48.
【点评】此题主要考查长方体的特征及棱长总和的计算方法.
9.(2024春 开封期末)用一根80厘米长的铁丝刚好焊接成一个正方体框架,这个正方体框架的每条棱长是这根铁丝的,每条棱的长度是 厘米。(损耗和接口处忽略不计)
【考点】正方体的特征.
【专题】几何直观.
【答案】,。
【分析】用80厘米的铁丝焊接成一个正方体框架,也就是这个正方体的棱长总和是80厘米,正方体的12条棱长都相等,则这个正方体框架的每条棱长是这根铁丝的,根据棱长=正方体的棱长总和÷12即可求得棱长。
【解答】解:1÷12
棱长:80÷12(厘米)
答:这个正方体框架的每条棱长是这根铁丝的,每条棱的长度是厘米。
故答案为:,。
【点评】此题考查的目的是理解掌握正方体的特征以及正方体的棱长总和公式,注意基础知识的灵活运用。
10.(2024 安宁区)如图是一个 长方 体的展开图,
它的底面积是 40 平方厘米,
它的体积是 80 立方厘米.
【考点】长方体的特征.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等.根据它的展开图可知,底面的长是8厘米,宽是5厘米,根据长方形的面积公式:
s=ab,体积公式:v=abh,把数据代入公式解答.
【解答】解:底面积是:8×5=40(平方厘米),
体积是:8×5×2=80(立方厘米);
故答案为:长方,40,80.
【点评】此题主要考查长方体的特征和它的底面积、体积的计算.首先根据展开图确定长、宽、高,把数据代入公式解答.
三.判断题(共7小题)
11.(2024春 城固县期末)一个长方体的两个相对面是正方形,它的其余四个面完全相同. √
【考点】长方体的特征.
【专题】立体图形的认识与计算;空间观念.
【答案】见试题解答内容
【分析】假设是上、下两个面都是正方形的长方体,即长方体的长和宽相等,其它四个面的面积都等于正方形的边长×高,因为正方形的边长都相等,长方体的高不变,所以它的其余四个面完全相同,面积相等.
【解答】解:由分析知:有两个相对面是正方形的长方体,它的其余四个面完全相同,面积相等;
所以原题说法正确.
故答案为:√.
【点评】解答此题的关键:应明确长方体的特征,可画图进行分析.
12.(2024春 昌黎县期末)相交于一个顶点的三条棱相等的长方体一定是正方体. √ .
【考点】正方体的特征.
【答案】√
【分析】根据正方体的意义,长、宽、高都相等的长方体叫做正方体,也叫立方体.由此解答.
【解答】解:如果相交于一个顶点的三条棱相等也就是长、宽、高相等,长、宽、高都相等的长方体叫做正方体.
所以,相交于一个顶点的三条棱相等的长方体一定是正方体.此说法正确.
故答案为:√.
【点评】此题主要根据正方体的特征和长方体与正方体的之间的关系解决问题.
13.(2024春 临泉县期末)一个长方体(不含正方体)最多有8条棱相等. √ .
【考点】长方体的特征.
【答案】见试题解答内容
【分析】根据长方体的特征,12条棱分为互相平行的3组,每组4条棱的长度相等,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等;如果长方体有两个相对的面是正方形,这时最多有8条棱相等;由此解答.
【解答】解:如果长方体有两个相对的面是正方形,这时最多有8条棱相等;因此,一个长方体(不含正方体)最多有8条棱相等.此说法正确.
故答案为:√.
【点评】此题主要考查长方体的特征,长、宽、高各不相等时,12条棱分为互相平行的3组,每组4条棱的长度相等,如果长方体有两个相对的面是正方形,这时最多有8条棱相等;据此解决问题.
14.(2024春 永寿县期末)用铁丝制作一个棱长10cm的正方体框架,至少需150cm的铁丝。 ×
【考点】正方体的特征.
【专题】应用题;几何直观.
【答案】×
【分析】根据正方体的特征,12条棱的长度都相等,正方体的棱长总和=棱长×12,把数据代入棱长总和公式解答即可判断。
【解答】解:10×12=120(cm)
所以用铁丝制作一个棱长10cm的正方体框架,至少需120cm的铁丝,原题说法错误。
故答案为:×。
【点评】本题考查了正方体的特征。
15.(2023春 大石桥市期末)一个长方体相交于一个顶点的三条棱长的总和是12cm,则这个长方体的棱长总和是48cm. √
【考点】长方体的特征.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】√
【分析】根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式求出这个长方体的棱长总和与48厘米进行比较即可.
【解答】解:12×4=48(厘米)
所以这个长方体的棱长总和是48厘米.
故答案为:√.
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和公式的灵活运用,关键是熟记公式.
16.(2023春 张北县期末)正方体的棱长扩大到原来2倍,它的表面积扩大到原来8倍。 ×
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】见试题解答内容
【分析】根据正方体表面积扩大的倍数是棱长扩大倍数的平方,列式计算后再判断即可。
【解答】解:一个正方体棱长扩大到原来的2倍,则表面积扩大到原来的2×2=4倍,所以原题说法错误。
故答案为:×。
【点评】考查了正方体的表面积和正方体棱长的之间关系,是基础题型。
17.(2023 东昌府区)把一个长方体锯成两个小长方体后,表面积增加,体积不变。 √
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】√
【分析】长方体切开的时候表面积增加了,因为由于切开,增加了新的面,所以表面积增加;物体所占空间的大小不变,即体积不变;据此即可解答。
【解答】解:因为将长方体切成两个长方体后,表面积将增加2个新的面,所以表面积变大了;而把一个长方体分成两个长方体,它的形状变了,但体积没有变。题干说法正确。
故答案为:√。
【点评】根据长方体切割的特点,即可判断表面积与体积的变化情况。
四.计算题(共1小题)
18.(2021春 岳池县期中)求出正方体的表面积和长方体的体积。
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】486平方厘米,300立方厘米。
【分析】根据正方体的表面积公式:S=6a2,再根据长方体的体积公式:V=abh,把数据分别代入公式解答。
【解答】解:9×9×6
=81×6
=486(平方厘米)
答:这个正方体的表面积是486平方厘米。
22×10×8=1760(立方厘米)
答:长方体的体积是300立方厘米。
【点评】此题主要考查正方体的表面积公式、长方体的体积公式的灵活运用,关键是熟记公式。
五.连线题(共1小题)
19.(2024春 嘉祥县期中)右面的图形是长方体的哪个面?连一连。
【考点】长方体的特征.
【专题】应用意识.
【答案】
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的形状和大小完全相同。据此解答。
【解答】解:
【点评】此题考查的目的是理解掌握长方体的特征及应用。
六.操作题(共1小题)
20.(2022秋 涟水县期末)在方格纸上画出长方体表面展开图的另外三个面,并标上相应名称。
【考点】长方体的展开图.
【专题】几何直观.
【答案】(画法不唯一)
【分析】根据长方体的特征,6个面的长方形(特殊情况有两个相对的面是正方形),上面对下面,前面对后面,左面对右面,对面相等。
【解答】解:
(画法不唯一)
【点评】此题主要考查长方体的特征。
七.应用题(共5小题)
21.(2024春 永寿县期末)明明的爸爸利用废旧的木板做了一个一面无门的小鞋柜(如图),制作这样一个小鞋柜,至少需要多少平方分米的木板?
【考点】长方体和正方体的表面积.
【专题】立体图形的认识与计算;空间观念.
【答案】142.5平方分米。
【分析】通过观察图形可知,需要木板的面积等于这个长方体的后面、上下、左右5个面的总面积,根据长方体的表面积公式解答。
【解答】解:45×60+55×45×2+60×55×2
=2700+4950+6600
=14250(平方厘米)
14250平方厘米=142.5平方分米
答:至少需要142.5平方分米的木板。
【点评】此题主要考查长方体表面积公式的灵活应用,关键是熟记公式。
22.(2024春 北票市期中)学校餐厅长10m,宽8m,高5m。除去门窗面积18.4m2,餐厅的墙壁和房顶都贴上壁纸。平均每平方米壁纸的价钱为5元,购买壁纸至少需要多少元?
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】1208元。
【分析】“要在餐厅的墙壁和房顶都贴上壁纸”,就是贴壁纸的面积是5个面,求出5个面的面积,再减去门窗的面积,就是需要壁纸的面积,求出面积再乘上5,就是需要花的钱数。据此解答。
【解答】解:10×8+10×5×2+8×5×2﹣18.4
=80+100+80﹣18.4
=260﹣18.4
=241.6(平方米)
5×241.6=1208(元)
答:购买壁纸至少需要1208元。
【点评】本题的关键是求出要贴壁纸的面积,再根据乘法的意义求出需要的钱数。
23.(2023春 大庆期末)做一个正方体的玻璃鱼缸(无盖),棱长6分米.制作这个鱼缸时至少需要玻璃多少平方分米?
【考点】长方体和正方体的表面积.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】见试题解答内容
【分析】根据正方体的表面积公式:S=6a2,由于鱼缸无盖,所以只它的5个面的总面积即可.
【解答】解:6×6×5=180(平方分米)
答:制作这个鱼缸时至少需要玻璃180平方分米.
【点评】此题主要考查正方体表面积公式的灵活运用,关键是熟记公式.
24.(2023春 赣县区期末)一个长方体形状的儿童一次性口罩包装盒,长13cm,宽11cm,高10cm。如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有多少平方厘米?
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】480平方厘米。
【分析】根据题意可知:“围着它贴一圈商标纸(上下面不贴)”,也就是求这个长方体的4个侧面的总面积,即(长×高+宽×高)×2,代入数字即可求解。
【解答】解:(13×10+11×10)×2
=(130+110)×2
=240×2
=480(平方厘米)
答:这张商标纸的面积至少有480平方厘米。
【点评】此题解答关键是搞清商标纸所贴的位置只在4个侧面上,然后根据长方体表面积公式求解。
25.(2022秋 盱眙县期末)妈妈为小明准备了六一儿童节礼物,如图是这个节日礼物的包装盒,它的长、宽、高分别是15厘米、10厘米、8厘米,用彩带把这个包装盒捆上,捆扎处用去彩带16厘米,一共需要多少厘米的彩带?
【考点】长方体的特征.
【专题】数据分析观念.
【答案】98厘米。
【分析】根据长方体的特征即可解答。
【解答】解:15×2+10×2+8×4
=30+20+32
=82(厘米)
82+16=98(厘米)
答:一共需要98厘米的彩带。
【点评】本题主要考查长方体的特征。
21世纪教育网(www.21cnjy.com)
