第十章 二元一次方程组 复习课件(共24张PPT)
文档属性
| 名称 | 第十章 二元一次方程组 复习课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 21:22:20 | ||
图片预览







文档简介
(共24张PPT)
2025七年级数学下册期末复习
第十章
——二元一次方程组
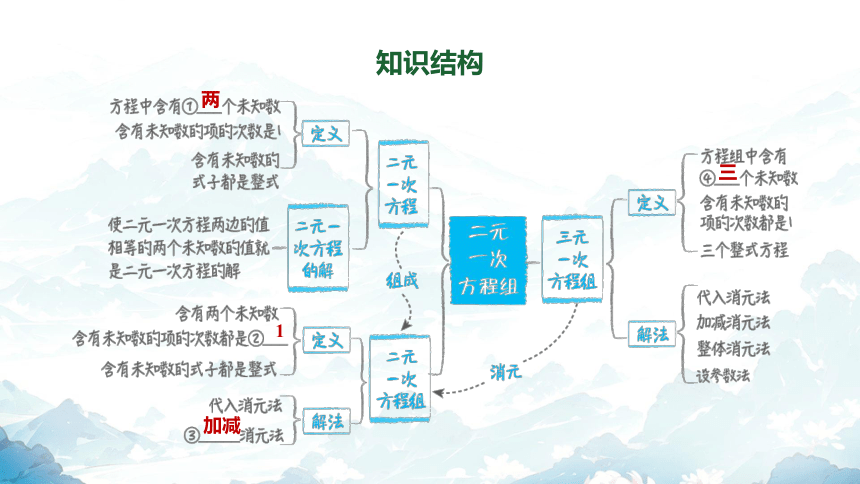
知识结构
两
1
加减
三
达标训练
一、选择题(每题6分,共36分)
1.下列方程组中是二元一次方程组的是( )
C
A. B.
C. D.
2.若是关于,的二元一次方程的解,则 的值
为( )
B
A. B.1 C.7 D.2
3.用加减消元法解方程组 时,下列方法中能消元的是
( )
D
A. B. C. D.
4. 《九章算术》是我国古老的数学经典著作,书中提到
这样一道题目:以绳测井.若将绳三折测之,绳多四尺;若将绳四折测
之,绳多一尺.绳长、井深各几何?题目大意是:用绳子测量水井的深
度.如果将绳子折成三等份,一份绳长比井深多4尺;如果将绳子折成四
等份,一份绳长比井深多1尺.绳长、井深各是多少尺?若设绳长 尺,
井深 尺,则符合题意的方程组是( )
C
A. B.
C. D.
5.解方程组时,一学生把看错而得到 而正确的
解是那么 的值为( )
D
A.4 B.5 C.6 D.7
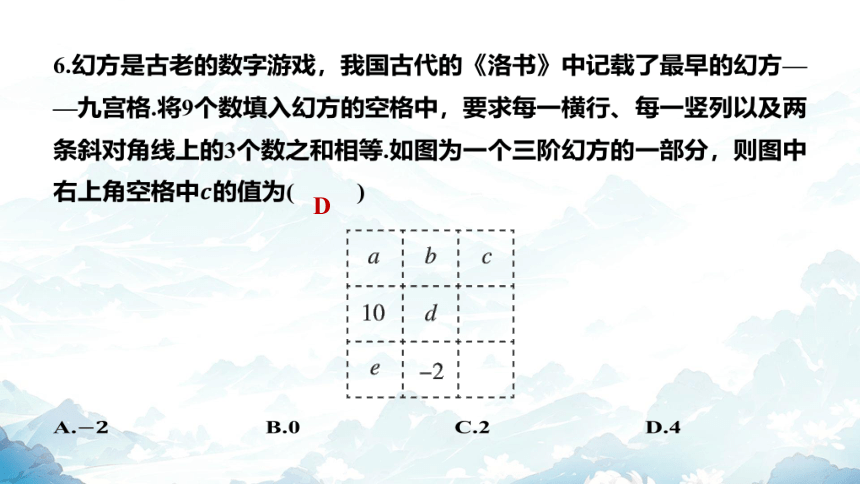
6.幻方是古老的数字游戏,我国古代的《洛书》中记载了最早的幻方—
—九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两
条斜对角线上的3个数之和相等.如图为一个三阶幻方的一部分,则图中
右上角空格中 的值为( )
D
A. B.0 C.2 D.4
二、填空题(每题6分,共18分)
7.如果把方程写成用含的代数式表示的形式,那么
________.
8. 若关于,的二元一次方程组 的解是
则含字母和的一次多项式 可以是______________________
(写出一个即可).
(答案不唯一)
9. 某班为奖励在数学竞赛中成绩优异的同学,花费48元
钱购买了甲、乙两种奖品,每种奖品至少购买1件,其中甲种奖品每件4
元,乙种奖品每件3元,则购买方案有___种.
3
[解析] 点拨:设购买甲种奖品件,乙种奖品 件,
由题意可得, .
,且,都是正整数, 是4的整数倍,
当时,;当时, ;当
时,;当时, ,不符
合题意,故有3种购买方案.
三、解答题(共46分)
10.(12分)解方程组:
(1)
解:把②代入①,得,解得 ,
把代入②,得 ,
方程组的解是
(2)
解:②去分母,得 ,
整理,得 ,③
将①与③联立,得,得 ,
.把代入①得,, ,
原方程组的解为
11.(16分)定义:关于, 的二元一次方程
与互为“共轭二元一次方程”,例如:
与 互为“共轭二元一次方程”.
(1)二元一次方程 的“共轭二元一次方程”为____________;
(2)二元一次方程 与它的“共轭二元一次方程”有一个相同
的解求, 的值.
解:二元一次方程的“共轭二元一次方程”是 ,
二元一次方程 与它的“共轭二元一次方程”有一个相同的解
解得
12.(18分)为拓展学生视野,某中学组织八年级师生开展研学活动,
原计划租用45座(不含司机座位)客车若干辆,但有15人没有座位;若
租用同样数量的60座(不含司机座位)客车,则多出三辆车,且其余客
车恰好坐满.现有甲、乙两种客车,它们的载客量(不含司机)和租金
如下表所示:
甲种客车 乙种客车
载客量/(人/辆) 45 60
租金/(元/辆) 200 300
(1)参加此次研学活动的师生人数是多少?原计划租用多少辆45座客车?
解:设参加此次研学活动的师生人数是,原计划租用 辆45座客车.
根据题意,得解得
答:参加此次研学活动的师生人数是600,原计划租用13辆45座客车.
(2)若租用同一种客车,要使每位师生都有座位,应该怎样租用才合算?
解:租用45座客车:(辆) (人),
(辆),所以需租用14辆,租金为
(元),
租用60座客车: (辆),所以需租用10辆,租金为
(元),
, 租用14辆45座客车才合算.
素养发展
1.阅读下列材料并填空:
对于二元一次方程组我们可以将, 的系数和相应的常
数项排成一个数表,求得的一次方程组的解 用数表
可表示为 .
(1)用数表简化解一次方程组的过程如下,请补全其中的空白:
从而得到该方程组的解为
=___,
=____;
下行-上行
6
10
(2)仿照(1)中数表的书写格式写出解方程组 的过程.
解:
方程组的解为
2.
【探究】 在平面直角坐标系中,把方程的解中的和 值分别
作为点的横、纵坐标,请完成表格信息,并在坐标系中描出对应点.
… 0 1 ①___ …
… ②___ 4 3 2 …
2
5
解:如图.
【发现】 过这些点中的任意两点画直线,你有什么发现?
解:过这些点中的任意两点画直线,所有的点都在同一条直线上.
【归纳】以方程 的解为坐标的点的全体叫作方程的“图象”.一般
地,在平面直角坐标系中,任何一个二元一次方程的“图象”都是一条直线.
【应用】 二元一次方程 的“图象”上有两个点分别为点
,点 ,请求出这个二元一次方程.
解: 二元一次方程 的“图象”上有两个点分别为点
,点 ,
解得
这个二元一次方程为 .
2025七年级数学下册期末复习
第十章
——二元一次方程组
知识结构
两
1
加减
三
达标训练
一、选择题(每题6分,共36分)
1.下列方程组中是二元一次方程组的是( )
C
A. B.
C. D.
2.若是关于,的二元一次方程的解,则 的值
为( )
B
A. B.1 C.7 D.2
3.用加减消元法解方程组 时,下列方法中能消元的是
( )
D
A. B. C. D.
4. 《九章算术》是我国古老的数学经典著作,书中提到
这样一道题目:以绳测井.若将绳三折测之,绳多四尺;若将绳四折测
之,绳多一尺.绳长、井深各几何?题目大意是:用绳子测量水井的深
度.如果将绳子折成三等份,一份绳长比井深多4尺;如果将绳子折成四
等份,一份绳长比井深多1尺.绳长、井深各是多少尺?若设绳长 尺,
井深 尺,则符合题意的方程组是( )
C
A. B.
C. D.
5.解方程组时,一学生把看错而得到 而正确的
解是那么 的值为( )
D
A.4 B.5 C.6 D.7
6.幻方是古老的数字游戏,我国古代的《洛书》中记载了最早的幻方—
—九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两
条斜对角线上的3个数之和相等.如图为一个三阶幻方的一部分,则图中
右上角空格中 的值为( )
D
A. B.0 C.2 D.4
二、填空题(每题6分,共18分)
7.如果把方程写成用含的代数式表示的形式,那么
________.
8. 若关于,的二元一次方程组 的解是
则含字母和的一次多项式 可以是______________________
(写出一个即可).
(答案不唯一)
9. 某班为奖励在数学竞赛中成绩优异的同学,花费48元
钱购买了甲、乙两种奖品,每种奖品至少购买1件,其中甲种奖品每件4
元,乙种奖品每件3元,则购买方案有___种.
3
[解析] 点拨:设购买甲种奖品件,乙种奖品 件,
由题意可得, .
,且,都是正整数, 是4的整数倍,
当时,;当时, ;当
时,;当时, ,不符
合题意,故有3种购买方案.
三、解答题(共46分)
10.(12分)解方程组:
(1)
解:把②代入①,得,解得 ,
把代入②,得 ,
方程组的解是
(2)
解:②去分母,得 ,
整理,得 ,③
将①与③联立,得,得 ,
.把代入①得,, ,
原方程组的解为
11.(16分)定义:关于, 的二元一次方程
与互为“共轭二元一次方程”,例如:
与 互为“共轭二元一次方程”.
(1)二元一次方程 的“共轭二元一次方程”为____________;
(2)二元一次方程 与它的“共轭二元一次方程”有一个相同
的解求, 的值.
解:二元一次方程的“共轭二元一次方程”是 ,
二元一次方程 与它的“共轭二元一次方程”有一个相同的解
解得
12.(18分)为拓展学生视野,某中学组织八年级师生开展研学活动,
原计划租用45座(不含司机座位)客车若干辆,但有15人没有座位;若
租用同样数量的60座(不含司机座位)客车,则多出三辆车,且其余客
车恰好坐满.现有甲、乙两种客车,它们的载客量(不含司机)和租金
如下表所示:
甲种客车 乙种客车
载客量/(人/辆) 45 60
租金/(元/辆) 200 300
(1)参加此次研学活动的师生人数是多少?原计划租用多少辆45座客车?
解:设参加此次研学活动的师生人数是,原计划租用 辆45座客车.
根据题意,得解得
答:参加此次研学活动的师生人数是600,原计划租用13辆45座客车.
(2)若租用同一种客车,要使每位师生都有座位,应该怎样租用才合算?
解:租用45座客车:(辆) (人),
(辆),所以需租用14辆,租金为
(元),
租用60座客车: (辆),所以需租用10辆,租金为
(元),
, 租用14辆45座客车才合算.
素养发展
1.阅读下列材料并填空:
对于二元一次方程组我们可以将, 的系数和相应的常
数项排成一个数表,求得的一次方程组的解 用数表
可表示为 .
(1)用数表简化解一次方程组的过程如下,请补全其中的空白:
从而得到该方程组的解为
=___,
=____;
下行-上行
6
10
(2)仿照(1)中数表的书写格式写出解方程组 的过程.
解:
方程组的解为
2.
【探究】 在平面直角坐标系中,把方程的解中的和 值分别
作为点的横、纵坐标,请完成表格信息,并在坐标系中描出对应点.
… 0 1 ①___ …
… ②___ 4 3 2 …
2
5
解:如图.
【发现】 过这些点中的任意两点画直线,你有什么发现?
解:过这些点中的任意两点画直线,所有的点都在同一条直线上.
【归纳】以方程 的解为坐标的点的全体叫作方程的“图象”.一般
地,在平面直角坐标系中,任何一个二元一次方程的“图象”都是一条直线.
【应用】 二元一次方程 的“图象”上有两个点分别为点
,点 ,请求出这个二元一次方程.
解: 二元一次方程 的“图象”上有两个点分别为点
,点 ,
解得
这个二元一次方程为 .
同课章节目录
