整理与复习:图形与几何14大考点全汇总+针对性训练(学案)-2024-2025学年数学六年级下册人教版
文档属性
| 名称 | 整理与复习:图形与几何14大考点全汇总+针对性训练(学案)-2024-2025学年数学六年级下册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 09:45:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
整理与复习:图形与几何14大考点全汇总+针对性训练-2024-2025学年数学六年级下册人教版
14大考点全汇总
考点一:圆柱的认识与展开图
考点二:表面积-压路机问题
考点三:表面积-通风管道问题
考点四:表面积-包装纸问题
考点五:表面积-圆柱切割问题
考点六:圆柱表面积计算题
考点七:圆柱与圆锥的体积计算题
考点八:圆柱体积的简单应用
考点九:圆柱水中浸物问题
考点十:求水瓶容积
考点十一:圆柱与长方体正方体综合
考点十二:圆锥体积的简单应用
考点十三:圆锥水中浸物问题
考点十四:圆柱与圆锥综合
针对性训练
考点一:圆柱的认识与展开图
1.(2024春 安阳期末)人民币一元硬币的正反两个面都是( )
A.长方形 B.圆 C.正方形 D.三角形
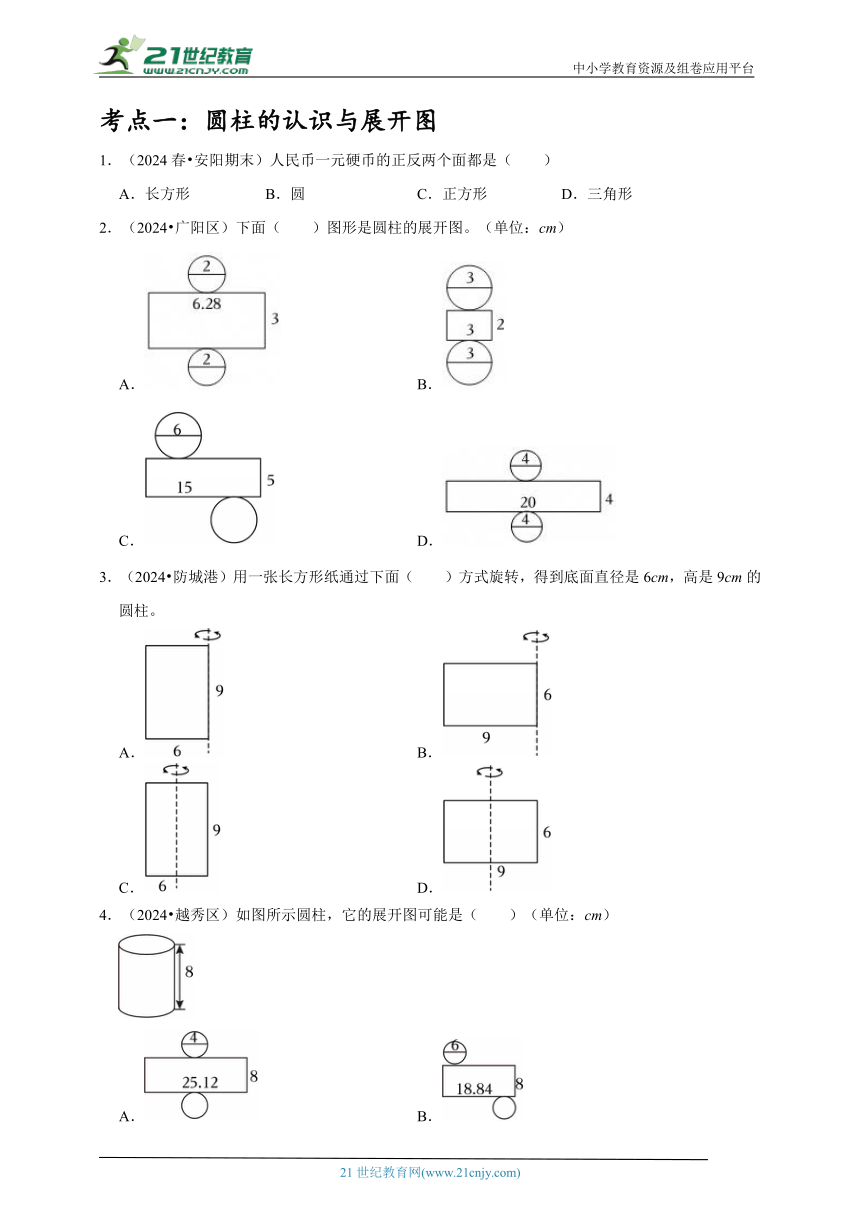
2.(2024 广阳区)下面( )图形是圆柱的展开图。(单位:cm)
A. B.
C. D.
3.(2024 防城港)用一张长方形纸通过下面( )方式旋转,得到底面直径是6cm,高是9cm的圆柱。
A. B.
C. D.
4.(2024 越秀区)如图所示圆柱,它的展开图可能是( )(单位:cm)
A. B.
C. D.
考点二:表面积-压路机问题
5.(2024春 肇源县期末)压路机的前轮是圆柱形,轮宽3m,直径1.6m,前轮转动一周,压路的面积是
m2。
6.(2024 滨海新区)一台压路机的前轮是圆柱形,轮宽2米,直径1.5米,前轮转动一周,压路的面积是
平方米。
7.(2023春 通榆县月考)一台压路机的前轮是圆柱形,轮宽2m,直径1.5m。前轮转动一周,压路的面积是 m2。
8.(2022春 泾阳县期中)压路机的前轮是圆柱形,轮宽2米,直径1.8米,前轮每分钟转动10周,则这个压路机每分钟压路 平方米。
考点三:表面积-通风管道问题
9.(2023春 霸州市期中)一个圆柱形烟囱的底面直径是8厘米,高是8分米,它的侧面积是
平方分米。
10.(2023 武进区)做一根长3米、管口直径2米的圆柱形白铁皮通风管,至少需要白铁皮 平方米。
11.(2023 邵阳)做5节长2米,底面直径4分米的圆柱形通风管,至少需要 平方米的铁皮。
12.(2022春 莘县期中)做一个底面直径为2分米,长为90厘米的烟囱,至少需要 平方分米的铁皮。
考点四:表面积-包装纸问题
13.(2022春 青岛期末)把一个圆柱形点心盒侧面贴满一圈商标纸,把商标纸展开,得到一个正方形,这个点心盒的高是15.7厘米,点心盒的底面半径是 厘米。
14.(2022 米脂县)一种固体胶棒,它的底面周长是3.14cm,高是6cm,只包装它的侧面,包装一个需要
cm2的包装纸。如果有1m2的包装纸,最多能包装 个固体胶棒。
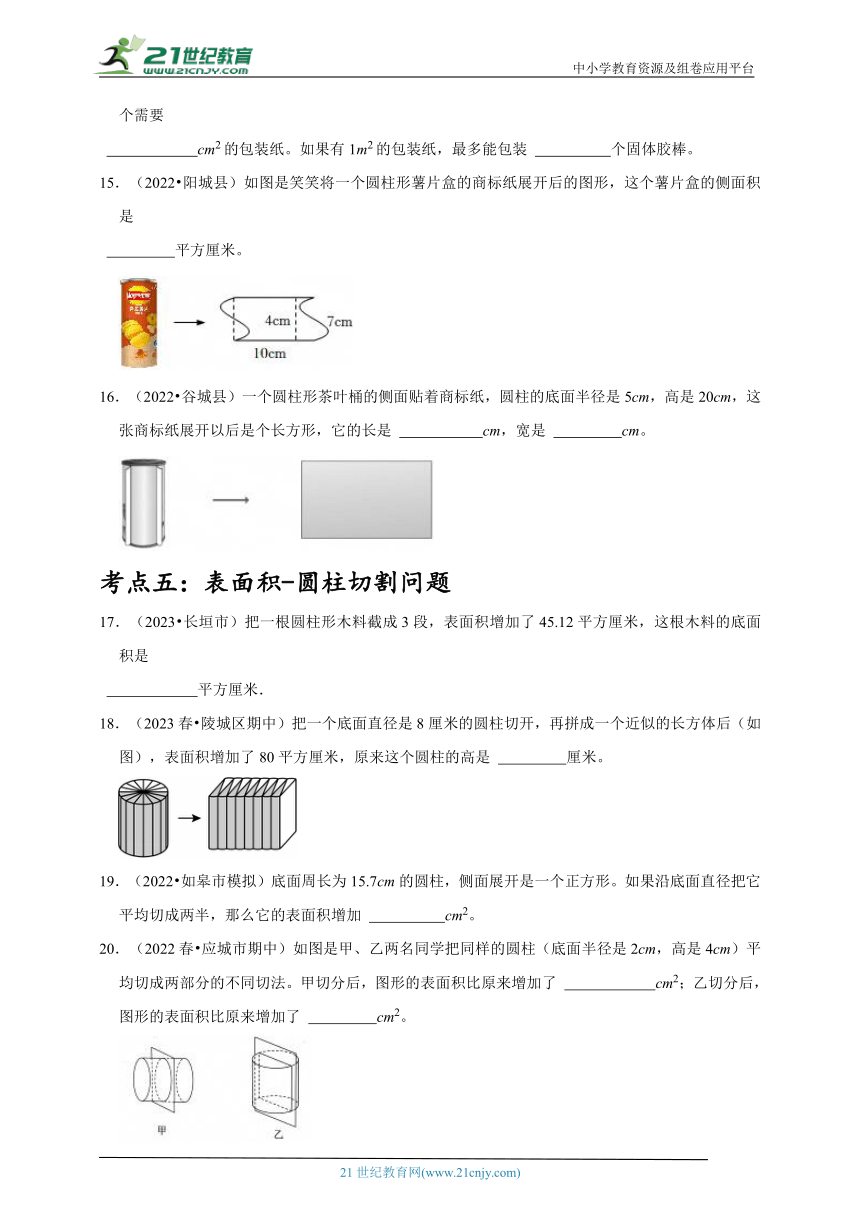
15.(2022 阳城县)如图是笑笑将一个圆柱形薯片盒的商标纸展开后的图形,这个薯片盒的侧面积是
平方厘米。
16.(2022 谷城县)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,这张商标纸展开以后是个长方形,它的长是 cm,宽是 cm。
考点五:表面积-圆柱切割问题
17.(2023 长垣市)把一根圆柱形木料截成3段,表面积增加了45.12平方厘米,这根木料的底面积是
平方厘米.
18.(2023春 陵城区期中)把一个底面直径是8厘米的圆柱切开,再拼成一个近似的长方体后(如图),表面积增加了80平方厘米,原来这个圆柱的高是 厘米。
19.(2022 如皋市模拟)底面周长为15.7cm的圆柱,侧面展开是一个正方形。如果沿底面直径把它平均切成两半,那么它的表面积增加 cm2。
20.(2022春 应城市期中)如图是甲、乙两名同学把同样的圆柱(底面半径是2cm,高是4cm)平均切成两部分的不同切法。甲切分后,图形的表面积比原来增加了 cm2;乙切分后,图形的表面积比原来增加了 cm2。
考点六:圆柱表面积计算题
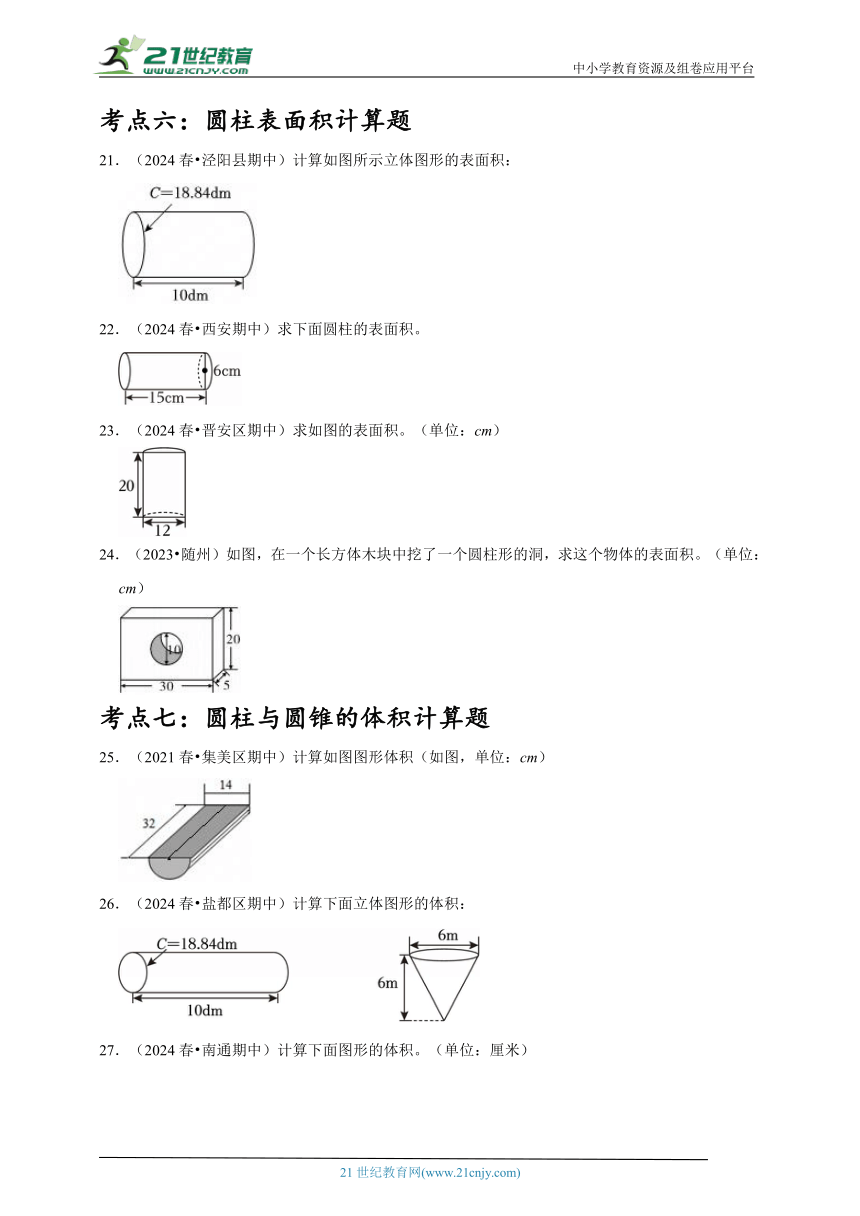
21.(2024春 泾阳县期中)计算如图所示立体图形的表面积:
22.(2024春 西安期中)求下面圆柱的表面积。
23.(2024春 晋安区期中)求如图的表面积。(单位:cm)
24.(2023 随州)如图,在一个长方体木块中挖了一个圆柱形的洞,求这个物体的表面积。(单位:cm)
考点七:圆柱与圆锥的体积计算题
25.(2021春 集美区期中)计算如图图形体积(如图,单位:cm)
26.(2024春 盐都区期中)计算下面立体图形的体积:
27.(2024春 南通期中)计算下面图形的体积。(单位:厘米)
28.(2024 连云港模拟)计算如图的体积。
考点八:圆柱体积的简单应用
29.(2024 沈丘县)北京时间2023年10月26日,“神十七”发射成功。当它升空后,会与“天和核心舱”端口进行对接,形成一条长约10dm,直径约8dm的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道”的容积约是多少?
30.(2024春 肇源县期末)一个圆柱形钢管长100厘米,外半径是4厘米,内半径是3厘米。这根钢管的体积是多少?
31.(2024 伊川县)在洛阳博物馆,帕孜勒看到一种古代的圆形铜钱币(如图),直径约为8厘米,厚度为4毫米,正中间的正方形缺口边长为2厘米。如果把20个这样的钱币对齐正方形缺口垒起来,垒起来的钱币的体积大约有多少立方厘米?
32.(2024 丰台区)王亮家即将喜迁新居,选择购买这款空调(如图)。请你算一算这款空调占据的空间大约是多少立方米?(精确到百分位)
考点九:圆柱水中浸物问题
33.(2024 榕城区模拟)有一块长9.42厘米,宽8厘米,高7.5厘米的长方体木块漂浮在一个底面半径为10厘米的圆柱形水缸里,其中露出水面,现把木块从水缸里取出,水缸里的水位下降多少厘米?(附着在木块上的水忽略不计)
34.(2024 兴化市)一个长方体储水桶里完全浸没着一段底面直径是4厘米的圆柱形钢材。把这段钢材竖着拉出水面6厘米,水面下降了2厘米。继续把这段钢材全部拉出水面,这时水面又下降了6厘米。这段钢材的体积是多少立方厘米?
35.(2024 邻水县)一个底面直径是8分米,高是7.5分米的圆柱形水桶里装有4分米高的水,现放入一个石块,石块全部没入水中,水面上升了2分米,这个石块的体积是多少立方分米?(水桶厚度忽略不计)
36.(2024春 嘉祥县期中)一个圆柱形水杯,底面半径为8厘米。杯里装有水,水深10厘米,在杯中浸没一块马铃薯后,杯中水面上升到12厘米(水没有溢出)。马铃薯的体积是多少?
考点十:求水瓶容积
37.(2024 寻乌县)一个内直径是6cm的瓶子里,水的高度是8cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是10cm。这个瓶子的容积是多少?
38.(2024 宣州区)华华在学完圆柱的体积后做了下面的实验:
实验器材:一把刻度尺,一个内直径是6cm的瓶子(瓶子带盖,没装满水),10个大小相同的小球 实验步骤: ①先测量出瓶中水的高度为10cm; ②再将瓶子倒放,测量出瓶中无水部分的高度为6cm; ③将10个小球放入瓶中,此时瓶中水面的高度是12cm。
根据实验过程,提取数学信息。
(1)请你帮华华计算出瓶子的容积是多少?
(2)请你帮华华计算出每个小球的体积是多少?
39.(2024 怀安县)把一个装有351.68mL水的瓶子倒置、放平,无水部分是圆柱形,高度是18cm。已知这个瓶子的容积是1256mL,现在把这个瓶子正放过来,水的高度是多少cm?
40.(2024春 云浮期中)一个瓶子装满3L的果汁。如图,喝掉一部分后,瓶内果汁高20cm,把瓶盖拧紧,把瓶子倒置、放平,无果汁的部分高5cm。求喝掉了多少升果汁。
考点十一:圆柱与长方体正方体综合
41.(2023 江阳区)如图所示,甲是底面半径为4cm的圆柱体空容器,乙是长方体容器,水深6.28cm。如果将乙容器中的水全部倒入甲容器,甲容器内水深多少厘米?(图中单位:cm)
42.(2024春 西安期中)小军家来了3位客人,他用一种长方体盒子包装的果汁招待(如图),如果给每位客人都倒满一杯,够吗?(数据是从容器里面测量得到的)
43.(2023 玉田县模拟)如图,把一块圆柱形钢锭铸造成一个长方体钢锭。长方体钢锭的宽是多少厘米?
44.(2023 遵化市)有块正方体的木料,它的棱长是4分米。把这块木料加工成一个最大的圆柱。这个圆柱的体积是多少?
考点十二:圆锥体积的简单应用
45.(2024春 市北区校级期中)在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.5吨,这堆沙约重多少吨?
46.(2024 寻乌县)一个圆锥形沙堆的底面积是28.26m2,高是2m。用这堆沙在10米宽的公路上铺2cm厚的路面,能铺多少米?
47.(2024 襄城县)长征二号运载火箭顶部是逃逸塔的发动机部分。为了方便研究,学校科学小组的同学制作了一个模型(实线部分为模型)。这个模型的体积是多少立方分米?(π取3)
48.(2024 曹县)一个圆柱形玻璃缸,底面直径是6dm,高4dm,水深25cm,把一个底面半径是4dm的圆锥完全浸没在水中,水面上升到27cm,这个圆锥的高是多少厘米?
考点十三:圆锥水中浸物问题
49.(2024 卧龙区)“攀登数学的山峰,享受挑战的趣味。”某学校数学社团的聪聪想到了一个测量圆锥高的方法:把一个底面直径是20cm的圆锥形铁块放入一个底面半径是2dm,高是7dm的圆柱形容器里,铁块完全浸没水中,水面上升了5cm且水未溢出。这个铁块的高是多少厘米?
50.(2024 江安县)一个圆柱形玻璃水杯,从里面量底面直径8cm,高10cm,杯里装了一些水,把一个底面直径是4cm的圆锥形铁块放入(完全淹没),水面上升了0.5cm,圆锥的高是多少?
51.(2024 冷水滩区)一个装水的圆柱形容器的底面内直径是12厘米,一个底面周长是18.84厘米的圆锥形铁锤完全浸没在这个容器的水中,将铁锤取出后,水面下降了2厘米,这个铁锤的高是多少厘米?
52.(2024 郏县)在一个底面半径5厘米,高18厘米的圆柱形水桶内装满了水,另有一个圆锥形空水桶,它的上口周长为37.68厘米,现在把圆柱形水桶里的水往圆锥形水桶里倒,当圆锥形水桶装满时,圆柱形水桶还剩12厘米高的水,求圆锥形水桶的高。
考点十四:圆柱与圆锥综合
53.(2024 无棣县)张师傅想用一个底面直径为20厘米、高为30厘米的圆柱体木桩加工工艺品。有以下几道工序:
工序一:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是1570立方厘米;
工序二:把圆锥和剩下的圆柱拼接起来,在圆锥部分雕刻上花纹,圆柱部分涂上颜料;
工序三:把做好的工艺品用长方体纸盒进行包装。
请你帮张师傅算一算。
(1)截取的木桩有多高?
(2)拼接后,涂颜料的面积是多少平方厘米?
(3)这个长方体纸盒的体积至少是多少立方厘米?
54.(2024 田家庵区)李红用橡皮泥做玩具小丑帽,造型如图1。
图1 图2
(1)这个帽子的体积是多少立方厘米?
(2)如果用纸板给这个帽子制作一个长方体的包装盒(如图2),至少需要多少平方厘米的纸板?(接头处忽略不计)
55.(2024 官渡区)整流罩是运载火箭的重要组成部分,它可以保护飞船免受高速气流和极端温度的伤害,某型号的整流罩是右图以红线为轴旋转一周后形成的立体图形,请求出这个整流罩的体积。
56.(2024 凤县模拟)零件A和零件B可以组合成零件C。现在有一块长方体钢坯,长25.12分米,宽10分米,高12分米。如果用这块钢坯单铸A零件,可以铸120个;如果单铸B零件,可以做40个。如果铸C零件,可以铸多少个?
整理与复习:图形与几何14大考点全汇总+针对性训练-2024-2025学年数学六年级下册人教版
参考答案与试题解析
题号 1 2 3 4
答案 B A C B
一.选择题(共4小题)
1.(2024春 安阳期末)人民币一元硬币的正反两个面都是( )
A.长方形 B.圆 C.正方形 D.三角形
【解答】解:因为硬币的形状是一个圆柱,圆柱的正反两个面都是圆形,所以人民币一元硬币的正反两个面都是圆。
故选:B。
2.(2024 广阳区)下面( )图形是圆柱的展开图。(单位:cm)
A. B.
C. D.
【解答】解:选项A:圆柱的底面直径是2厘米,侧面展开图的长是6.28厘米,因为3.14×2=6.28(厘米),所以图A是圆柱的展开图。其它选项长方形的长都不是宽的3.14倍,所以不符合要求。
故选:A。
3.(2024 防城港)用一张长方形纸通过下面( )方式旋转,得到底面直径是6cm,高是9cm的圆柱。
A. B.
C. D.
【解答】解:通过旋转,得到底面直径是6cm,高是9cm的圆柱。
故选:C。
4.(2024 越秀区)如图所示圆柱,它的展开图可能是( )(单位:cm)
A. B.
C. D.
【解答】解:已知圆柱的高是8厘米
图A.底面直径是4厘米,那么底面周长是:3.14×4=12.56(厘米),所以图A不符合题意;
图B.底面直径是6厘米,底面周长是:3.14×6=18.84(厘米),符合题意;
图C.底面直径是2厘米,底面周长是:3.14×2=6.28(厘米),不符合题意;
图D.底面直径是8厘米,底面周长是:3.14×8=25.12(厘米),不符合题意。
故选:B。
二.填空题(共16小题)
5.(2024春 肇源县期末)压路机的前轮是圆柱形,轮宽3m,直径1.6m,前轮转动一周,压路的面积是 15.072 m2。
【解答】解:3.14×1.6×3
=3.14×4.8
=15.072(平方米)
答:压路的面积是15.072m2。
故答案为:15.072。
6.(2024 滨海新区)一台压路机的前轮是圆柱形,轮宽2米,直径1.5米,前轮转动一周,压路的面积是 9.42 平方米。
【解答】解:3.14×1.5×2
=3.14×3
=9.42(平方米)
答:压路的面积是9.42平方米。
7.(2023春 通榆县月考)一台压路机的前轮是圆柱形,轮宽2m,直径1.5m。前轮转动一周,压路的面积是 9.42 m2。
【解答】解:3.14×2×1.5
=6.28×1.5
=9.42(平方米)
答:压路的面积是9.42平方米。
故答案为:9.42。
8.(2022春 泾阳县期中)压路机的前轮是圆柱形,轮宽2米,直径1.8米,前轮每分钟转动10周,则这个压路机每分钟压路 113.04 平方米。
【解答】解:3.14×1.8×2×10
=3.14×36
=113.04(平方米)
答:每分钟压路113.04平方米。
9.(2023春 霸州市期中)一个圆柱形烟囱的底面直径是8厘米,高是8分米,它的侧面积是 20.096 平方分米。
【解答】解:8厘米=0.8分米
3.14×0.8×8
=2.512×8
=20.096(平方分米)
答:它的侧面积是20.096平方分米。
故答案为:20.096。
10.(2023 武进区)做一根长3米、管口直径2米的圆柱形白铁皮通风管,至少需要白铁皮 18.84 平方米。
【解答】解:3.14×2×3
=6.28×3
=18.84(平方米)
答:至少需要白铁皮18.84平方米。
故答案为:18.84。
11.(2023 邵阳)做5节长2米,底面直径4分米的圆柱形通风管,至少需要 12.56 平方米的铁皮。
【解答】解:4分米=0.4米
3.14×0.4×2×5
=3.14×4
=12.56(平方米)
答:至少需要 12.56平方米的铁皮。
故答案为:12.56。
12.(2022春 莘县期中)做一个底面直径为2分米,长为90厘米的烟囱,至少需要 56.52 平方分米的铁皮。
【解答】解:90厘米=9分米
3.14×2×9
=6.28×9
=56.52(平方分米)
答:至少需要56.52平方分米的铁皮。
故答案为:56.52。
13.(2022春 青岛期末)把一个圆柱形点心盒侧面贴满一圈商标纸,把商标纸展开,得到一个正方形,这个点心盒的高是15.7厘米,点心盒的底面半径是 2.5 厘米。
【解答】解:15.7÷3.14÷2
=5÷2
=2.5(厘米)
答:点心盒的底面半径是2.5厘米。
故答案为:2.5。
14.(2022 米脂县)一种固体胶棒,它的底面周长是3.14cm,高是6cm,只包装它的侧面,包装一个需要 18.84 cm2的包装纸。如果有1m2的包装纸,最多能包装 530 个固体胶棒。
【解答】解:3.14×6=18.84(平方厘米)
1平方米=10000平方厘米
10000÷18.84≈530(个)
答:包装一个需要18.84cm2的包装纸。如果有1m2的包装纸,最多能包装530个固体胶棒。
故答案为:18.84,530。
15.(2022 阳城县)如图是笑笑将一个圆柱形薯片盒的商标纸展开后的图形,这个薯片盒的侧面积是 40 平方厘米。
【解答】解:10×4=40(平方厘米)
答:这个薯片盒的侧面积是40平方厘米。
故答案为:40。
16.(2022 谷城县)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,这张商标纸展开以后是个长方形,它的长是 31.4 cm,宽是 20 cm。
【解答】解:3.14×5×2
=3.14×10
=31.4(厘米)
答:它的长是31.4cm,宽是20cm。
故答案为:31.4,20。
17.(2023 长垣市)把一根圆柱形木料截成3段,表面积增加了45.12平方厘米,这根木料的底面积是 11.28 平方厘米.
【解答】解:45.12÷4=11.28(平方厘米);
答:这根木料的底面积是11.28平方厘米.
故答案为:11.28.
18.(2023春 陵城区期中)把一个底面直径是8厘米的圆柱切开,再拼成一个近似的长方体后(如图),表面积增加了80平方厘米,原来这个圆柱的高是 10 厘米。
【解答】解:圆柱的高:
80÷2÷(8÷2)
=40÷4
=10(厘米)
答:原来这个圆柱的高是10厘米。
故答案为:10。
19.(2022 如皋市模拟)底面周长为15.7cm的圆柱,侧面展开是一个正方形。如果沿底面直径把它平均切成两半,那么它的表面积增加 157 cm2。
【解答】解:15.7÷3.14=5(厘米)
15.7×5×2=157(平方厘米)
答:它的表面积增加157平方厘米。
故答案为:157。
20.(2022春 应城市期中)如图是甲、乙两名同学把同样的圆柱(底面半径是2cm,高是4cm)平均切成两部分的不同切法。甲切分后,图形的表面积比原来增加了 25.12 cm2;乙切分后,图形的表面积比原来增加了 32 cm2。
【解答】解:3.14×22×2
=3.14×4×2
=25.12(平方厘米)
4×(2×2)×2
=4×4×2
=32(平方厘米)
答:甲切开后表面积增加25.12平方厘米,乙切开后表面积增加32平方厘米。
故答案为:25.12,32。
三.计算题(共8小题)
21.(2024春 泾阳县期中)计算如图所示立体图形的表面积:
【解答】解:18.84÷3.14÷2
=6÷2
=3(分米)
3.14×32×2+18.84×10
=3.14×9×2+188.4
=28.26×2+188.4
=56.52+188.4
=244.92(平方分米)
答:这个圆柱的表面积是244.92平方分米。
22.(2024春 西安期中)求下面圆柱的表面积。
【解答】解:3.14×6×15+3.14×(6÷2)2×2
=3.14×90+3.14×18
=3.14×108
=339.12(平方厘米)
答:圆柱的表面积是339.12平方厘米。
23.(2024春 晋安区期中)求如图的表面积。(单位:cm)
【解答】解:3.14×(12÷2)2+3.14×12×20÷2+12×20
=3.14×36+3.14×120+240
=113.04+376.8+240
=729.84(平方厘米)
24.(2023 随州)如图,在一个长方体木块中挖了一个圆柱形的洞,求这个物体的表面积。(单位:cm)
【解答】解:(30×5+30×20+5×20)×2
=850×2
=1700(平方厘米)
1700﹣3.14×(10÷2)2×2+3.14×10×5
=1700﹣157+157
=1700(平方厘米)
答:这个物体的表面积是1700平方厘米。
25.(2021春 集美区期中)计算如图图形体积(如图,单位:cm)
【解答】解:14÷2=7(厘米)
3.14×7×7×32÷2
=3.14×49×16
=153.86×16
=2461.76(立方厘米)
答:该立体的体积是2461.76立方厘米。
26.(2024春 盐都区期中)计算下面立体图形的体积:
【解答】解:①18.84÷3.14÷2=3(分米)
3.14×3×3×10=282.6(立方分米)
②6÷2=3(米)
3.14×3×3×6÷3=56.52(立方米)
27.(2024春 南通期中)计算下面图形的体积。(单位:厘米)
【解答】解:4÷2=2(厘米)
π×22×5π×22×3
=π×4×5π×4×3
=20π+4π
=24π
=24×3.14
=75.36(立方厘米)
这个图形的体积是75.36立方厘米。
28.(2024 连云港模拟)计算如图的体积。
【解答】解:10÷2=5(分米)
4÷2=2(分米)
3.14×(52﹣22)×20
=3.14×(25﹣4)×20
=3.14×21×20
=65.94×20
=1318.8(立方分米)
答:这个空心圆柱的体积是1318.8立方分米。
四.应用题(共28小题)
29.(2024 沈丘县)北京时间2023年10月26日,“神十七”发射成功。当它升空后,会与“天和核心舱”端口进行对接,形成一条长约10dm,直径约8dm的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道”的容积约是多少?
【解答】解:3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方分米)
答:这个“生命通道”的容积约是502.4立方分米。
30.(2024春 肇源县期末)一个圆柱形钢管长100厘米,外半径是4厘米,内半径是3厘米。这根钢管的体积是多少?
【解答】解:(3.14×4×4﹣3.14×3×3)×100
=21.98×100
=2198(立方厘米)
答:这根钢管的体积是2198立方厘米。
31.(2024 伊川县)在洛阳博物馆,帕孜勒看到一种古代的圆形铜钱币(如图),直径约为8厘米,厚度为4毫米,正中间的正方形缺口边长为2厘米。如果把20个这样的钱币对齐正方形缺口垒起来,垒起来的钱币的体积大约有多少立方厘米?
【解答】解:4毫米=0.4厘米
3.14×(8÷2)2×0.4×20﹣2×2×0.4×20
=3.14×16×0.4×20﹣1.6×20
=401.92﹣32
=369.92(立方厘米)
答:垒起来的钱币的体积大约是369.92立方厘米。
32.(2024 丰台区)王亮家即将喜迁新居,选择购买这款空调(如图)。请你算一算这款空调占据的空间大约是多少立方米?(精确到百分位)
【解答】解:3.14×(40÷2)2×180
=3.14×400×180
=1256×180
=226080(立方厘米)
226080立方厘米=0.22608立方米≈0.23立方米
答:这款空调占据的空间大约是0.23立方米。
33.(2024 榕城区模拟)有一块长9.42厘米,宽8厘米,高7.5厘米的长方体木块漂浮在一个底面半径为10厘米的圆柱形水缸里,其中露出水面,现把木块从水缸里取出,水缸里的水位下降多少厘米?(附着在木块上的水忽略不计)
【解答】解:9.42×8×7.5
=75.36×7.5
=565.2
=188.4(立方厘米)
188.4÷(3.14×102)
=188.4÷314
=0.6(厘米)
答:水缸里的水位下降0.6厘米。
34.(2024 兴化市)一个长方体储水桶里完全浸没着一段底面直径是4厘米的圆柱形钢材。把这段钢材竖着拉出水面6厘米,水面下降了2厘米。继续把这段钢材全部拉出水面,这时水面又下降了6厘米。这段钢材的体积是多少立方厘米?
【解答】解:钢材的长度:(2+6)÷2×6
=8÷2×6
=24(厘米)
钢材的体积:3.14×(4÷2)2×24
=3.14×4×24
=301.44(立方厘米)
答:这段钢材的体积是301.44立方厘米。
35.(2024 邻水县)一个底面直径是8分米,高是7.5分米的圆柱形水桶里装有4分米高的水,现放入一个石块,石块全部没入水中,水面上升了2分米,这个石块的体积是多少立方分米?(水桶厚度忽略不计)
【解答】解:3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方分米)
50.24×2=100.48(立方分米)
答:这个石块的体积是100.48立方分米。
36.(2024春 嘉祥县期中)一个圆柱形水杯,底面半径为8厘米。杯里装有水,水深10厘米,在杯中浸没一块马铃薯后,杯中水面上升到12厘米(水没有溢出)。马铃薯的体积是多少?
【解答】解:3.14×82×(12﹣10)
=3.14×64×2
=200.96×2
=401.92(立方厘米)
答:马铃薯的体积是401.92立方厘米。
37.(2024 寻乌县)一个内直径是6cm的瓶子里,水的高度是8cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是10cm。这个瓶子的容积是多少?
【解答】解:3.14×(6÷2)2×(8+10)
=3.14×9×18
=28.26×18
=508.68(立方厘米)
508.68立方厘米=508.68毫升
答:这个瓶子的容积是508.68毫升。
38.(2024 宣州区)华华在学完圆柱的体积后做了下面的实验:
实验器材:一把刻度尺,一个内直径是6cm的瓶子(瓶子带盖,没装满水),10个大小相同的小球 实验步骤: ①先测量出瓶中水的高度为10cm; ②再将瓶子倒放,测量出瓶中无水部分的高度为6cm; ③将10个小球放入瓶中,此时瓶中水面的高度是12cm。
根据实验过程,提取数学信息。
(1)请你帮华华计算出瓶子的容积是多少?
(2)请你帮华华计算出每个小球的体积是多少?
【解答】(1)3.14×(6÷2)2×(10+6)
=3.14×9×16
=452.16(ml)
答:瓶子的容积是452.16毫升。
(2)3.14×(6÷2)2×(12﹣10)÷10
=3.14×9×2÷10
=5.652(立方厘米)
答:每个小球的体积是5.652立方厘米。
39.(2024 怀安县)把一个装有351.68mL水的瓶子倒置、放平,无水部分是圆柱形,高度是18cm。已知这个瓶子的容积是1256mL,现在把这个瓶子正放过来,水的高度是多少cm?
【解答】解:1256毫升=1256立方厘米
351.68毫升=351.68立方厘米
351.68÷[(1256﹣351.68)÷18]
=351.68÷[904.32÷18]
=351.68÷50.24
=7(厘米)
答:水的高度是7厘米。
40.(2024春 云浮期中)一个瓶子装满3L的果汁。如图,喝掉一部分后,瓶内果汁高20cm,把瓶盖拧紧,把瓶子倒置、放平,无果汁的部分高5cm。求喝掉了多少升果汁。
【解答】解:设圆柱的底面积x为平方厘米。
20x+5x=3×1000
25x=3000
x=120
120×5=600(立方厘米)
600立方厘米=0.6立方分米=0.6升
答:喝掉了0.6升果汁。
41.(2023 江阳区)如图所示,甲是底面半径为4cm的圆柱体空容器,乙是长方体容器,水深6.28cm。如果将乙容器中的水全部倒入甲容器,甲容器内水深多少厘米?(图中单位:cm)
【解答】解:8×8×6.28÷(3.14×42)
=64×6.28÷(3.14×16)
=401.92÷50.24
=8(厘米)
答:甲容器内水深8厘米。
42.(2024春 西安期中)小军家来了3位客人,他用一种长方体盒子包装的果汁招待(如图),如果给每位客人都倒满一杯,够吗?(数据是从容器里面测量得到的)
【解答】解:10×12×6
=120×6
=720(立方厘米)
26×8×3
=26×24
=624(立方厘米)
624<720
答:如果给每位客人都倒满一杯,果汁够。
43.(2023 玉田县模拟)如图,把一块圆柱形钢锭铸造成一个长方体钢锭。长方体钢锭的宽是多少厘米?
【解答】解:(3.14×52×60)÷(20×15.7)
=4710÷314
=15(厘米)
答:长方体钢锭的宽是15厘米。
44.(2023 遵化市)有块正方体的木料,它的棱长是4分米。把这块木料加工成一个最大的圆柱。这个圆柱的体积是多少?
【解答】解:3.14×(4÷2)2×4
=3.14×4×4
=12.56×4
=50.24(立方分米)
答:这个圆柱的体积是50.24立方分米。
45.(2024春 市北区校级期中)在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.5吨,这堆沙约重多少吨?
【解答】解:3.14×(4÷2)2×1.5×1.5
3.14×4×1.5×1.5
=6.28×1.5
=9.42(吨)
答:这堆沙约重9.42吨。
46.(2024 寻乌县)一个圆锥形沙堆的底面积是28.26m2,高是2m。用这堆沙在10米宽的公路上铺2cm厚的路面,能铺多少米?
【解答】解:28.26×2
=56.52
=18.84(立方米)
2cm=0.02m
18.84÷(10×0.02)
=18.84÷0.2
=94.2(米)
答:能铺94.2米。
47.(2024 襄城县)长征二号运载火箭顶部是逃逸塔的发动机部分。为了方便研究,学校科学小组的同学制作了一个模型(实线部分为模型)。这个模型的体积是多少立方分米?(π取3)
【解答】解:3×(6÷2)2×(8+8)3×(3÷2)2×8
3×9×163×2.25×8
=144﹣18
=126(立方分米)
答:这个模型的体积是126立方分米。
48.(2024 曹县)一个圆柱形玻璃缸,底面直径是6dm,高4dm,水深25cm,把一个底面半径是4dm的圆锥完全浸没在水中,水面上升到27cm,这个圆锥的高是多少厘米?
【解答】解:27厘米=2.7分米
25厘米=2.5分米
3.14×(6÷2)2×(2.7﹣2.5)
=3.14×9×0.2
=5.652(立方分米)
5.652÷3.1442
=5.652÷3.14×3÷16
=0.3375(分米)
0.3375分米=3.375厘米
答:这个圆锥的高是3.375厘米。
49.(2024 卧龙区)“攀登数学的山峰,享受挑战的趣味。”某学校数学社团的聪聪想到了一个测量圆锥高的方法:把一个底面直径是20cm的圆锥形铁块放入一个底面半径是2dm,高是7dm的圆柱形容器里,铁块完全浸没水中,水面上升了5cm且水未溢出。这个铁块的高是多少厘米?
【解答】解:2分米=20厘米
3.14×202×5[3.14×(20÷2)]2
=3.14×400×5×3÷[3.14×100]
=6280×3÷314
=18840÷314
=60(厘米)
答:这个铁块的高是60厘米。
50.(2024 江安县)一个圆柱形玻璃水杯,从里面量底面直径8cm,高10cm,杯里装了一些水,把一个底面直径是4cm的圆锥形铁块放入(完全淹没),水面上升了0.5cm,圆锥的高是多少?
【解答】解:3.14×(8÷2)2×0.5[3.14×(4÷2)2]
=3.14×16×0.5×3÷[3.14×4]
=25.12×3÷12.56
=75.36÷12.56
=6(厘米)
答:圆锥的高是6厘米。
51.(2024 冷水滩区)一个装水的圆柱形容器的底面内直径是12厘米,一个底面周长是18.84厘米的圆锥形铁锤完全浸没在这个容器的水中,将铁锤取出后,水面下降了2厘米,这个铁锤的高是多少厘米?
【解答】解:圆柱底面半径为12÷2=6(厘米)
圆柱底面积为πr2=π×62=36π(平方厘米)
铁锤的体积为36π×2=72π(立方厘米)
铁锤的底面半径为18.84÷3.14÷2=3(厘米)
铁锤的底面积为π×32=9π(平方厘米)
铁锤的高为
72π×3÷9π
=216π÷9π
=24(厘米)
答:这个铁锤的高是24厘米。
52.(2024 郏县)在一个底面半径5厘米,高18厘米的圆柱形水桶内装满了水,另有一个圆锥形空水桶,它的上口周长为37.68厘米,现在把圆柱形水桶里的水往圆锥形水桶里倒,当圆锥形水桶装满时,圆柱形水桶还剩12厘米高的水,求圆锥形水桶的高。
【解答】解:3.14×52×(18﹣12)
=3.14×25×6
=78.5×6
=471(立方厘米)
471×3÷[3.14×(37.68÷3.14÷2)2]
=1413÷[3.14×36]
=1413÷113.04
=12.5(厘米)
答:圆锥形水桶的高是12.5厘米。
53.(2024 无棣县)张师傅想用一个底面直径为20厘米、高为30厘米的圆柱体木桩加工工艺品。有以下几道工序:
工序一:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是1570立方厘米;
工序二:把圆锥和剩下的圆柱拼接起来,在圆锥部分雕刻上花纹,圆柱部分涂上颜料;
工序三:把做好的工艺品用长方体纸盒进行包装。
请你帮张师傅算一算。
(1)截取的木桩有多高?
(2)拼接后,涂颜料的面积是多少平方厘米?
(3)这个长方体纸盒的体积至少是多少立方厘米?
【解答】解:(1)1570×3÷[3.14×(20÷2)2]
=4710÷314
=15(厘米)
答:截取的木桩的高是15厘米。
(2)3.14×20×(30﹣15)
=3.14×20×15
=942(平方厘米)
答:涂颜料的面积是942平方厘米。
(3)20×20×30
=400×30
=12000(立方厘米)
答:这个长方体纸盒的体积至少是12000立方厘米。
54.(2024 田家庵区)李红用橡皮泥做玩具小丑帽,造型如图1。
图1 图2
(1)这个帽子的体积是多少立方厘米?
(2)如果用纸板给这个帽子制作一个长方体的包装盒(如图2),至少需要多少平方厘米的纸板?(接头处忽略不计)
【解答】解:(1)圆柱底面半径为:8÷2=4(厘米)
圆锥底面半径为:(8﹣2×2)÷2
=(8﹣4)÷2
=4÷2
=2(厘米)
3.14×42×1+3.14×22×9
=3.14×16×1+3.14×4×9
=50.24+37.68
=87.92(立方厘米)
答:这个帽子的体积是87.92立方厘米。
(2)包装盒的高为:9+1=10(厘米)
8×8×2+8×10×4
=128+320
=448(平方厘米)
答:至少需要448平方厘米的纸板。
55.(2024 官渡区)整流罩是运载火箭的重要组成部分,它可以保护飞船免受高速气流和极端温度的伤害,某型号的整流罩是右图以红线为轴旋转一周后形成的立体图形,请求出这个整流罩的体积。
【解答】解:3.14×22×103.14×22×6
=3.14×4×10+3.14×4×2
=125.6+25.12
=150.72(m3)
答:这个整流罩的体积是150.72m3。
56.(2024 凤县模拟)零件A和零件B可以组合成零件C。现在有一块长方体钢坯,长25.12分米,宽10分米,高12分米。如果用这块钢坯单铸A零件,可以铸120个;如果单铸B零件,可以做40个。如果铸C零件,可以铸多少个?
【解答】解:120÷40=3
120÷(3+1)
=120÷54
=30(个)
答:如果铸C零件,可以铸成30个。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
整理与复习:图形与几何14大考点全汇总+针对性训练-2024-2025学年数学六年级下册人教版
14大考点全汇总
考点一:圆柱的认识与展开图
考点二:表面积-压路机问题
考点三:表面积-通风管道问题
考点四:表面积-包装纸问题
考点五:表面积-圆柱切割问题
考点六:圆柱表面积计算题
考点七:圆柱与圆锥的体积计算题
考点八:圆柱体积的简单应用
考点九:圆柱水中浸物问题
考点十:求水瓶容积
考点十一:圆柱与长方体正方体综合
考点十二:圆锥体积的简单应用
考点十三:圆锥水中浸物问题
考点十四:圆柱与圆锥综合
针对性训练
考点一:圆柱的认识与展开图
1.(2024春 安阳期末)人民币一元硬币的正反两个面都是( )
A.长方形 B.圆 C.正方形 D.三角形
2.(2024 广阳区)下面( )图形是圆柱的展开图。(单位:cm)
A. B.
C. D.
3.(2024 防城港)用一张长方形纸通过下面( )方式旋转,得到底面直径是6cm,高是9cm的圆柱。
A. B.
C. D.
4.(2024 越秀区)如图所示圆柱,它的展开图可能是( )(单位:cm)
A. B.
C. D.
考点二:表面积-压路机问题
5.(2024春 肇源县期末)压路机的前轮是圆柱形,轮宽3m,直径1.6m,前轮转动一周,压路的面积是
m2。
6.(2024 滨海新区)一台压路机的前轮是圆柱形,轮宽2米,直径1.5米,前轮转动一周,压路的面积是
平方米。
7.(2023春 通榆县月考)一台压路机的前轮是圆柱形,轮宽2m,直径1.5m。前轮转动一周,压路的面积是 m2。
8.(2022春 泾阳县期中)压路机的前轮是圆柱形,轮宽2米,直径1.8米,前轮每分钟转动10周,则这个压路机每分钟压路 平方米。
考点三:表面积-通风管道问题
9.(2023春 霸州市期中)一个圆柱形烟囱的底面直径是8厘米,高是8分米,它的侧面积是
平方分米。
10.(2023 武进区)做一根长3米、管口直径2米的圆柱形白铁皮通风管,至少需要白铁皮 平方米。
11.(2023 邵阳)做5节长2米,底面直径4分米的圆柱形通风管,至少需要 平方米的铁皮。
12.(2022春 莘县期中)做一个底面直径为2分米,长为90厘米的烟囱,至少需要 平方分米的铁皮。
考点四:表面积-包装纸问题
13.(2022春 青岛期末)把一个圆柱形点心盒侧面贴满一圈商标纸,把商标纸展开,得到一个正方形,这个点心盒的高是15.7厘米,点心盒的底面半径是 厘米。
14.(2022 米脂县)一种固体胶棒,它的底面周长是3.14cm,高是6cm,只包装它的侧面,包装一个需要
cm2的包装纸。如果有1m2的包装纸,最多能包装 个固体胶棒。
15.(2022 阳城县)如图是笑笑将一个圆柱形薯片盒的商标纸展开后的图形,这个薯片盒的侧面积是
平方厘米。
16.(2022 谷城县)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,这张商标纸展开以后是个长方形,它的长是 cm,宽是 cm。
考点五:表面积-圆柱切割问题
17.(2023 长垣市)把一根圆柱形木料截成3段,表面积增加了45.12平方厘米,这根木料的底面积是
平方厘米.
18.(2023春 陵城区期中)把一个底面直径是8厘米的圆柱切开,再拼成一个近似的长方体后(如图),表面积增加了80平方厘米,原来这个圆柱的高是 厘米。
19.(2022 如皋市模拟)底面周长为15.7cm的圆柱,侧面展开是一个正方形。如果沿底面直径把它平均切成两半,那么它的表面积增加 cm2。
20.(2022春 应城市期中)如图是甲、乙两名同学把同样的圆柱(底面半径是2cm,高是4cm)平均切成两部分的不同切法。甲切分后,图形的表面积比原来增加了 cm2;乙切分后,图形的表面积比原来增加了 cm2。
考点六:圆柱表面积计算题
21.(2024春 泾阳县期中)计算如图所示立体图形的表面积:
22.(2024春 西安期中)求下面圆柱的表面积。
23.(2024春 晋安区期中)求如图的表面积。(单位:cm)
24.(2023 随州)如图,在一个长方体木块中挖了一个圆柱形的洞,求这个物体的表面积。(单位:cm)
考点七:圆柱与圆锥的体积计算题
25.(2021春 集美区期中)计算如图图形体积(如图,单位:cm)
26.(2024春 盐都区期中)计算下面立体图形的体积:
27.(2024春 南通期中)计算下面图形的体积。(单位:厘米)
28.(2024 连云港模拟)计算如图的体积。
考点八:圆柱体积的简单应用
29.(2024 沈丘县)北京时间2023年10月26日,“神十七”发射成功。当它升空后,会与“天和核心舱”端口进行对接,形成一条长约10dm,直径约8dm的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道”的容积约是多少?
30.(2024春 肇源县期末)一个圆柱形钢管长100厘米,外半径是4厘米,内半径是3厘米。这根钢管的体积是多少?
31.(2024 伊川县)在洛阳博物馆,帕孜勒看到一种古代的圆形铜钱币(如图),直径约为8厘米,厚度为4毫米,正中间的正方形缺口边长为2厘米。如果把20个这样的钱币对齐正方形缺口垒起来,垒起来的钱币的体积大约有多少立方厘米?
32.(2024 丰台区)王亮家即将喜迁新居,选择购买这款空调(如图)。请你算一算这款空调占据的空间大约是多少立方米?(精确到百分位)
考点九:圆柱水中浸物问题
33.(2024 榕城区模拟)有一块长9.42厘米,宽8厘米,高7.5厘米的长方体木块漂浮在一个底面半径为10厘米的圆柱形水缸里,其中露出水面,现把木块从水缸里取出,水缸里的水位下降多少厘米?(附着在木块上的水忽略不计)
34.(2024 兴化市)一个长方体储水桶里完全浸没着一段底面直径是4厘米的圆柱形钢材。把这段钢材竖着拉出水面6厘米,水面下降了2厘米。继续把这段钢材全部拉出水面,这时水面又下降了6厘米。这段钢材的体积是多少立方厘米?
35.(2024 邻水县)一个底面直径是8分米,高是7.5分米的圆柱形水桶里装有4分米高的水,现放入一个石块,石块全部没入水中,水面上升了2分米,这个石块的体积是多少立方分米?(水桶厚度忽略不计)
36.(2024春 嘉祥县期中)一个圆柱形水杯,底面半径为8厘米。杯里装有水,水深10厘米,在杯中浸没一块马铃薯后,杯中水面上升到12厘米(水没有溢出)。马铃薯的体积是多少?
考点十:求水瓶容积
37.(2024 寻乌县)一个内直径是6cm的瓶子里,水的高度是8cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是10cm。这个瓶子的容积是多少?
38.(2024 宣州区)华华在学完圆柱的体积后做了下面的实验:
实验器材:一把刻度尺,一个内直径是6cm的瓶子(瓶子带盖,没装满水),10个大小相同的小球 实验步骤: ①先测量出瓶中水的高度为10cm; ②再将瓶子倒放,测量出瓶中无水部分的高度为6cm; ③将10个小球放入瓶中,此时瓶中水面的高度是12cm。
根据实验过程,提取数学信息。
(1)请你帮华华计算出瓶子的容积是多少?
(2)请你帮华华计算出每个小球的体积是多少?
39.(2024 怀安县)把一个装有351.68mL水的瓶子倒置、放平,无水部分是圆柱形,高度是18cm。已知这个瓶子的容积是1256mL,现在把这个瓶子正放过来,水的高度是多少cm?
40.(2024春 云浮期中)一个瓶子装满3L的果汁。如图,喝掉一部分后,瓶内果汁高20cm,把瓶盖拧紧,把瓶子倒置、放平,无果汁的部分高5cm。求喝掉了多少升果汁。
考点十一:圆柱与长方体正方体综合
41.(2023 江阳区)如图所示,甲是底面半径为4cm的圆柱体空容器,乙是长方体容器,水深6.28cm。如果将乙容器中的水全部倒入甲容器,甲容器内水深多少厘米?(图中单位:cm)
42.(2024春 西安期中)小军家来了3位客人,他用一种长方体盒子包装的果汁招待(如图),如果给每位客人都倒满一杯,够吗?(数据是从容器里面测量得到的)
43.(2023 玉田县模拟)如图,把一块圆柱形钢锭铸造成一个长方体钢锭。长方体钢锭的宽是多少厘米?
44.(2023 遵化市)有块正方体的木料,它的棱长是4分米。把这块木料加工成一个最大的圆柱。这个圆柱的体积是多少?
考点十二:圆锥体积的简单应用
45.(2024春 市北区校级期中)在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.5吨,这堆沙约重多少吨?
46.(2024 寻乌县)一个圆锥形沙堆的底面积是28.26m2,高是2m。用这堆沙在10米宽的公路上铺2cm厚的路面,能铺多少米?
47.(2024 襄城县)长征二号运载火箭顶部是逃逸塔的发动机部分。为了方便研究,学校科学小组的同学制作了一个模型(实线部分为模型)。这个模型的体积是多少立方分米?(π取3)
48.(2024 曹县)一个圆柱形玻璃缸,底面直径是6dm,高4dm,水深25cm,把一个底面半径是4dm的圆锥完全浸没在水中,水面上升到27cm,这个圆锥的高是多少厘米?
考点十三:圆锥水中浸物问题
49.(2024 卧龙区)“攀登数学的山峰,享受挑战的趣味。”某学校数学社团的聪聪想到了一个测量圆锥高的方法:把一个底面直径是20cm的圆锥形铁块放入一个底面半径是2dm,高是7dm的圆柱形容器里,铁块完全浸没水中,水面上升了5cm且水未溢出。这个铁块的高是多少厘米?
50.(2024 江安县)一个圆柱形玻璃水杯,从里面量底面直径8cm,高10cm,杯里装了一些水,把一个底面直径是4cm的圆锥形铁块放入(完全淹没),水面上升了0.5cm,圆锥的高是多少?
51.(2024 冷水滩区)一个装水的圆柱形容器的底面内直径是12厘米,一个底面周长是18.84厘米的圆锥形铁锤完全浸没在这个容器的水中,将铁锤取出后,水面下降了2厘米,这个铁锤的高是多少厘米?
52.(2024 郏县)在一个底面半径5厘米,高18厘米的圆柱形水桶内装满了水,另有一个圆锥形空水桶,它的上口周长为37.68厘米,现在把圆柱形水桶里的水往圆锥形水桶里倒,当圆锥形水桶装满时,圆柱形水桶还剩12厘米高的水,求圆锥形水桶的高。
考点十四:圆柱与圆锥综合
53.(2024 无棣县)张师傅想用一个底面直径为20厘米、高为30厘米的圆柱体木桩加工工艺品。有以下几道工序:
工序一:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是1570立方厘米;
工序二:把圆锥和剩下的圆柱拼接起来,在圆锥部分雕刻上花纹,圆柱部分涂上颜料;
工序三:把做好的工艺品用长方体纸盒进行包装。
请你帮张师傅算一算。
(1)截取的木桩有多高?
(2)拼接后,涂颜料的面积是多少平方厘米?
(3)这个长方体纸盒的体积至少是多少立方厘米?
54.(2024 田家庵区)李红用橡皮泥做玩具小丑帽,造型如图1。
图1 图2
(1)这个帽子的体积是多少立方厘米?
(2)如果用纸板给这个帽子制作一个长方体的包装盒(如图2),至少需要多少平方厘米的纸板?(接头处忽略不计)
55.(2024 官渡区)整流罩是运载火箭的重要组成部分,它可以保护飞船免受高速气流和极端温度的伤害,某型号的整流罩是右图以红线为轴旋转一周后形成的立体图形,请求出这个整流罩的体积。
56.(2024 凤县模拟)零件A和零件B可以组合成零件C。现在有一块长方体钢坯,长25.12分米,宽10分米,高12分米。如果用这块钢坯单铸A零件,可以铸120个;如果单铸B零件,可以做40个。如果铸C零件,可以铸多少个?
整理与复习:图形与几何14大考点全汇总+针对性训练-2024-2025学年数学六年级下册人教版
参考答案与试题解析
题号 1 2 3 4
答案 B A C B
一.选择题(共4小题)
1.(2024春 安阳期末)人民币一元硬币的正反两个面都是( )
A.长方形 B.圆 C.正方形 D.三角形
【解答】解:因为硬币的形状是一个圆柱,圆柱的正反两个面都是圆形,所以人民币一元硬币的正反两个面都是圆。
故选:B。
2.(2024 广阳区)下面( )图形是圆柱的展开图。(单位:cm)
A. B.
C. D.
【解答】解:选项A:圆柱的底面直径是2厘米,侧面展开图的长是6.28厘米,因为3.14×2=6.28(厘米),所以图A是圆柱的展开图。其它选项长方形的长都不是宽的3.14倍,所以不符合要求。
故选:A。
3.(2024 防城港)用一张长方形纸通过下面( )方式旋转,得到底面直径是6cm,高是9cm的圆柱。
A. B.
C. D.
【解答】解:通过旋转,得到底面直径是6cm,高是9cm的圆柱。
故选:C。
4.(2024 越秀区)如图所示圆柱,它的展开图可能是( )(单位:cm)
A. B.
C. D.
【解答】解:已知圆柱的高是8厘米
图A.底面直径是4厘米,那么底面周长是:3.14×4=12.56(厘米),所以图A不符合题意;
图B.底面直径是6厘米,底面周长是:3.14×6=18.84(厘米),符合题意;
图C.底面直径是2厘米,底面周长是:3.14×2=6.28(厘米),不符合题意;
图D.底面直径是8厘米,底面周长是:3.14×8=25.12(厘米),不符合题意。
故选:B。
二.填空题(共16小题)
5.(2024春 肇源县期末)压路机的前轮是圆柱形,轮宽3m,直径1.6m,前轮转动一周,压路的面积是 15.072 m2。
【解答】解:3.14×1.6×3
=3.14×4.8
=15.072(平方米)
答:压路的面积是15.072m2。
故答案为:15.072。
6.(2024 滨海新区)一台压路机的前轮是圆柱形,轮宽2米,直径1.5米,前轮转动一周,压路的面积是 9.42 平方米。
【解答】解:3.14×1.5×2
=3.14×3
=9.42(平方米)
答:压路的面积是9.42平方米。
7.(2023春 通榆县月考)一台压路机的前轮是圆柱形,轮宽2m,直径1.5m。前轮转动一周,压路的面积是 9.42 m2。
【解答】解:3.14×2×1.5
=6.28×1.5
=9.42(平方米)
答:压路的面积是9.42平方米。
故答案为:9.42。
8.(2022春 泾阳县期中)压路机的前轮是圆柱形,轮宽2米,直径1.8米,前轮每分钟转动10周,则这个压路机每分钟压路 113.04 平方米。
【解答】解:3.14×1.8×2×10
=3.14×36
=113.04(平方米)
答:每分钟压路113.04平方米。
9.(2023春 霸州市期中)一个圆柱形烟囱的底面直径是8厘米,高是8分米,它的侧面积是 20.096 平方分米。
【解答】解:8厘米=0.8分米
3.14×0.8×8
=2.512×8
=20.096(平方分米)
答:它的侧面积是20.096平方分米。
故答案为:20.096。
10.(2023 武进区)做一根长3米、管口直径2米的圆柱形白铁皮通风管,至少需要白铁皮 18.84 平方米。
【解答】解:3.14×2×3
=6.28×3
=18.84(平方米)
答:至少需要白铁皮18.84平方米。
故答案为:18.84。
11.(2023 邵阳)做5节长2米,底面直径4分米的圆柱形通风管,至少需要 12.56 平方米的铁皮。
【解答】解:4分米=0.4米
3.14×0.4×2×5
=3.14×4
=12.56(平方米)
答:至少需要 12.56平方米的铁皮。
故答案为:12.56。
12.(2022春 莘县期中)做一个底面直径为2分米,长为90厘米的烟囱,至少需要 56.52 平方分米的铁皮。
【解答】解:90厘米=9分米
3.14×2×9
=6.28×9
=56.52(平方分米)
答:至少需要56.52平方分米的铁皮。
故答案为:56.52。
13.(2022春 青岛期末)把一个圆柱形点心盒侧面贴满一圈商标纸,把商标纸展开,得到一个正方形,这个点心盒的高是15.7厘米,点心盒的底面半径是 2.5 厘米。
【解答】解:15.7÷3.14÷2
=5÷2
=2.5(厘米)
答:点心盒的底面半径是2.5厘米。
故答案为:2.5。
14.(2022 米脂县)一种固体胶棒,它的底面周长是3.14cm,高是6cm,只包装它的侧面,包装一个需要 18.84 cm2的包装纸。如果有1m2的包装纸,最多能包装 530 个固体胶棒。
【解答】解:3.14×6=18.84(平方厘米)
1平方米=10000平方厘米
10000÷18.84≈530(个)
答:包装一个需要18.84cm2的包装纸。如果有1m2的包装纸,最多能包装530个固体胶棒。
故答案为:18.84,530。
15.(2022 阳城县)如图是笑笑将一个圆柱形薯片盒的商标纸展开后的图形,这个薯片盒的侧面积是 40 平方厘米。
【解答】解:10×4=40(平方厘米)
答:这个薯片盒的侧面积是40平方厘米。
故答案为:40。
16.(2022 谷城县)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,这张商标纸展开以后是个长方形,它的长是 31.4 cm,宽是 20 cm。
【解答】解:3.14×5×2
=3.14×10
=31.4(厘米)
答:它的长是31.4cm,宽是20cm。
故答案为:31.4,20。
17.(2023 长垣市)把一根圆柱形木料截成3段,表面积增加了45.12平方厘米,这根木料的底面积是 11.28 平方厘米.
【解答】解:45.12÷4=11.28(平方厘米);
答:这根木料的底面积是11.28平方厘米.
故答案为:11.28.
18.(2023春 陵城区期中)把一个底面直径是8厘米的圆柱切开,再拼成一个近似的长方体后(如图),表面积增加了80平方厘米,原来这个圆柱的高是 10 厘米。
【解答】解:圆柱的高:
80÷2÷(8÷2)
=40÷4
=10(厘米)
答:原来这个圆柱的高是10厘米。
故答案为:10。
19.(2022 如皋市模拟)底面周长为15.7cm的圆柱,侧面展开是一个正方形。如果沿底面直径把它平均切成两半,那么它的表面积增加 157 cm2。
【解答】解:15.7÷3.14=5(厘米)
15.7×5×2=157(平方厘米)
答:它的表面积增加157平方厘米。
故答案为:157。
20.(2022春 应城市期中)如图是甲、乙两名同学把同样的圆柱(底面半径是2cm,高是4cm)平均切成两部分的不同切法。甲切分后,图形的表面积比原来增加了 25.12 cm2;乙切分后,图形的表面积比原来增加了 32 cm2。
【解答】解:3.14×22×2
=3.14×4×2
=25.12(平方厘米)
4×(2×2)×2
=4×4×2
=32(平方厘米)
答:甲切开后表面积增加25.12平方厘米,乙切开后表面积增加32平方厘米。
故答案为:25.12,32。
三.计算题(共8小题)
21.(2024春 泾阳县期中)计算如图所示立体图形的表面积:
【解答】解:18.84÷3.14÷2
=6÷2
=3(分米)
3.14×32×2+18.84×10
=3.14×9×2+188.4
=28.26×2+188.4
=56.52+188.4
=244.92(平方分米)
答:这个圆柱的表面积是244.92平方分米。
22.(2024春 西安期中)求下面圆柱的表面积。
【解答】解:3.14×6×15+3.14×(6÷2)2×2
=3.14×90+3.14×18
=3.14×108
=339.12(平方厘米)
答:圆柱的表面积是339.12平方厘米。
23.(2024春 晋安区期中)求如图的表面积。(单位:cm)
【解答】解:3.14×(12÷2)2+3.14×12×20÷2+12×20
=3.14×36+3.14×120+240
=113.04+376.8+240
=729.84(平方厘米)
24.(2023 随州)如图,在一个长方体木块中挖了一个圆柱形的洞,求这个物体的表面积。(单位:cm)
【解答】解:(30×5+30×20+5×20)×2
=850×2
=1700(平方厘米)
1700﹣3.14×(10÷2)2×2+3.14×10×5
=1700﹣157+157
=1700(平方厘米)
答:这个物体的表面积是1700平方厘米。
25.(2021春 集美区期中)计算如图图形体积(如图,单位:cm)
【解答】解:14÷2=7(厘米)
3.14×7×7×32÷2
=3.14×49×16
=153.86×16
=2461.76(立方厘米)
答:该立体的体积是2461.76立方厘米。
26.(2024春 盐都区期中)计算下面立体图形的体积:
【解答】解:①18.84÷3.14÷2=3(分米)
3.14×3×3×10=282.6(立方分米)
②6÷2=3(米)
3.14×3×3×6÷3=56.52(立方米)
27.(2024春 南通期中)计算下面图形的体积。(单位:厘米)
【解答】解:4÷2=2(厘米)
π×22×5π×22×3
=π×4×5π×4×3
=20π+4π
=24π
=24×3.14
=75.36(立方厘米)
这个图形的体积是75.36立方厘米。
28.(2024 连云港模拟)计算如图的体积。
【解答】解:10÷2=5(分米)
4÷2=2(分米)
3.14×(52﹣22)×20
=3.14×(25﹣4)×20
=3.14×21×20
=65.94×20
=1318.8(立方分米)
答:这个空心圆柱的体积是1318.8立方分米。
四.应用题(共28小题)
29.(2024 沈丘县)北京时间2023年10月26日,“神十七”发射成功。当它升空后,会与“天和核心舱”端口进行对接,形成一条长约10dm,直径约8dm的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道”的容积约是多少?
【解答】解:3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方分米)
答:这个“生命通道”的容积约是502.4立方分米。
30.(2024春 肇源县期末)一个圆柱形钢管长100厘米,外半径是4厘米,内半径是3厘米。这根钢管的体积是多少?
【解答】解:(3.14×4×4﹣3.14×3×3)×100
=21.98×100
=2198(立方厘米)
答:这根钢管的体积是2198立方厘米。
31.(2024 伊川县)在洛阳博物馆,帕孜勒看到一种古代的圆形铜钱币(如图),直径约为8厘米,厚度为4毫米,正中间的正方形缺口边长为2厘米。如果把20个这样的钱币对齐正方形缺口垒起来,垒起来的钱币的体积大约有多少立方厘米?
【解答】解:4毫米=0.4厘米
3.14×(8÷2)2×0.4×20﹣2×2×0.4×20
=3.14×16×0.4×20﹣1.6×20
=401.92﹣32
=369.92(立方厘米)
答:垒起来的钱币的体积大约是369.92立方厘米。
32.(2024 丰台区)王亮家即将喜迁新居,选择购买这款空调(如图)。请你算一算这款空调占据的空间大约是多少立方米?(精确到百分位)
【解答】解:3.14×(40÷2)2×180
=3.14×400×180
=1256×180
=226080(立方厘米)
226080立方厘米=0.22608立方米≈0.23立方米
答:这款空调占据的空间大约是0.23立方米。
33.(2024 榕城区模拟)有一块长9.42厘米,宽8厘米,高7.5厘米的长方体木块漂浮在一个底面半径为10厘米的圆柱形水缸里,其中露出水面,现把木块从水缸里取出,水缸里的水位下降多少厘米?(附着在木块上的水忽略不计)
【解答】解:9.42×8×7.5
=75.36×7.5
=565.2
=188.4(立方厘米)
188.4÷(3.14×102)
=188.4÷314
=0.6(厘米)
答:水缸里的水位下降0.6厘米。
34.(2024 兴化市)一个长方体储水桶里完全浸没着一段底面直径是4厘米的圆柱形钢材。把这段钢材竖着拉出水面6厘米,水面下降了2厘米。继续把这段钢材全部拉出水面,这时水面又下降了6厘米。这段钢材的体积是多少立方厘米?
【解答】解:钢材的长度:(2+6)÷2×6
=8÷2×6
=24(厘米)
钢材的体积:3.14×(4÷2)2×24
=3.14×4×24
=301.44(立方厘米)
答:这段钢材的体积是301.44立方厘米。
35.(2024 邻水县)一个底面直径是8分米,高是7.5分米的圆柱形水桶里装有4分米高的水,现放入一个石块,石块全部没入水中,水面上升了2分米,这个石块的体积是多少立方分米?(水桶厚度忽略不计)
【解答】解:3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方分米)
50.24×2=100.48(立方分米)
答:这个石块的体积是100.48立方分米。
36.(2024春 嘉祥县期中)一个圆柱形水杯,底面半径为8厘米。杯里装有水,水深10厘米,在杯中浸没一块马铃薯后,杯中水面上升到12厘米(水没有溢出)。马铃薯的体积是多少?
【解答】解:3.14×82×(12﹣10)
=3.14×64×2
=200.96×2
=401.92(立方厘米)
答:马铃薯的体积是401.92立方厘米。
37.(2024 寻乌县)一个内直径是6cm的瓶子里,水的高度是8cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是10cm。这个瓶子的容积是多少?
【解答】解:3.14×(6÷2)2×(8+10)
=3.14×9×18
=28.26×18
=508.68(立方厘米)
508.68立方厘米=508.68毫升
答:这个瓶子的容积是508.68毫升。
38.(2024 宣州区)华华在学完圆柱的体积后做了下面的实验:
实验器材:一把刻度尺,一个内直径是6cm的瓶子(瓶子带盖,没装满水),10个大小相同的小球 实验步骤: ①先测量出瓶中水的高度为10cm; ②再将瓶子倒放,测量出瓶中无水部分的高度为6cm; ③将10个小球放入瓶中,此时瓶中水面的高度是12cm。
根据实验过程,提取数学信息。
(1)请你帮华华计算出瓶子的容积是多少?
(2)请你帮华华计算出每个小球的体积是多少?
【解答】(1)3.14×(6÷2)2×(10+6)
=3.14×9×16
=452.16(ml)
答:瓶子的容积是452.16毫升。
(2)3.14×(6÷2)2×(12﹣10)÷10
=3.14×9×2÷10
=5.652(立方厘米)
答:每个小球的体积是5.652立方厘米。
39.(2024 怀安县)把一个装有351.68mL水的瓶子倒置、放平,无水部分是圆柱形,高度是18cm。已知这个瓶子的容积是1256mL,现在把这个瓶子正放过来,水的高度是多少cm?
【解答】解:1256毫升=1256立方厘米
351.68毫升=351.68立方厘米
351.68÷[(1256﹣351.68)÷18]
=351.68÷[904.32÷18]
=351.68÷50.24
=7(厘米)
答:水的高度是7厘米。
40.(2024春 云浮期中)一个瓶子装满3L的果汁。如图,喝掉一部分后,瓶内果汁高20cm,把瓶盖拧紧,把瓶子倒置、放平,无果汁的部分高5cm。求喝掉了多少升果汁。
【解答】解:设圆柱的底面积x为平方厘米。
20x+5x=3×1000
25x=3000
x=120
120×5=600(立方厘米)
600立方厘米=0.6立方分米=0.6升
答:喝掉了0.6升果汁。
41.(2023 江阳区)如图所示,甲是底面半径为4cm的圆柱体空容器,乙是长方体容器,水深6.28cm。如果将乙容器中的水全部倒入甲容器,甲容器内水深多少厘米?(图中单位:cm)
【解答】解:8×8×6.28÷(3.14×42)
=64×6.28÷(3.14×16)
=401.92÷50.24
=8(厘米)
答:甲容器内水深8厘米。
42.(2024春 西安期中)小军家来了3位客人,他用一种长方体盒子包装的果汁招待(如图),如果给每位客人都倒满一杯,够吗?(数据是从容器里面测量得到的)
【解答】解:10×12×6
=120×6
=720(立方厘米)
26×8×3
=26×24
=624(立方厘米)
624<720
答:如果给每位客人都倒满一杯,果汁够。
43.(2023 玉田县模拟)如图,把一块圆柱形钢锭铸造成一个长方体钢锭。长方体钢锭的宽是多少厘米?
【解答】解:(3.14×52×60)÷(20×15.7)
=4710÷314
=15(厘米)
答:长方体钢锭的宽是15厘米。
44.(2023 遵化市)有块正方体的木料,它的棱长是4分米。把这块木料加工成一个最大的圆柱。这个圆柱的体积是多少?
【解答】解:3.14×(4÷2)2×4
=3.14×4×4
=12.56×4
=50.24(立方分米)
答:这个圆柱的体积是50.24立方分米。
45.(2024春 市北区校级期中)在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.5吨,这堆沙约重多少吨?
【解答】解:3.14×(4÷2)2×1.5×1.5
3.14×4×1.5×1.5
=6.28×1.5
=9.42(吨)
答:这堆沙约重9.42吨。
46.(2024 寻乌县)一个圆锥形沙堆的底面积是28.26m2,高是2m。用这堆沙在10米宽的公路上铺2cm厚的路面,能铺多少米?
【解答】解:28.26×2
=56.52
=18.84(立方米)
2cm=0.02m
18.84÷(10×0.02)
=18.84÷0.2
=94.2(米)
答:能铺94.2米。
47.(2024 襄城县)长征二号运载火箭顶部是逃逸塔的发动机部分。为了方便研究,学校科学小组的同学制作了一个模型(实线部分为模型)。这个模型的体积是多少立方分米?(π取3)
【解答】解:3×(6÷2)2×(8+8)3×(3÷2)2×8
3×9×163×2.25×8
=144﹣18
=126(立方分米)
答:这个模型的体积是126立方分米。
48.(2024 曹县)一个圆柱形玻璃缸,底面直径是6dm,高4dm,水深25cm,把一个底面半径是4dm的圆锥完全浸没在水中,水面上升到27cm,这个圆锥的高是多少厘米?
【解答】解:27厘米=2.7分米
25厘米=2.5分米
3.14×(6÷2)2×(2.7﹣2.5)
=3.14×9×0.2
=5.652(立方分米)
5.652÷3.1442
=5.652÷3.14×3÷16
=0.3375(分米)
0.3375分米=3.375厘米
答:这个圆锥的高是3.375厘米。
49.(2024 卧龙区)“攀登数学的山峰,享受挑战的趣味。”某学校数学社团的聪聪想到了一个测量圆锥高的方法:把一个底面直径是20cm的圆锥形铁块放入一个底面半径是2dm,高是7dm的圆柱形容器里,铁块完全浸没水中,水面上升了5cm且水未溢出。这个铁块的高是多少厘米?
【解答】解:2分米=20厘米
3.14×202×5[3.14×(20÷2)]2
=3.14×400×5×3÷[3.14×100]
=6280×3÷314
=18840÷314
=60(厘米)
答:这个铁块的高是60厘米。
50.(2024 江安县)一个圆柱形玻璃水杯,从里面量底面直径8cm,高10cm,杯里装了一些水,把一个底面直径是4cm的圆锥形铁块放入(完全淹没),水面上升了0.5cm,圆锥的高是多少?
【解答】解:3.14×(8÷2)2×0.5[3.14×(4÷2)2]
=3.14×16×0.5×3÷[3.14×4]
=25.12×3÷12.56
=75.36÷12.56
=6(厘米)
答:圆锥的高是6厘米。
51.(2024 冷水滩区)一个装水的圆柱形容器的底面内直径是12厘米,一个底面周长是18.84厘米的圆锥形铁锤完全浸没在这个容器的水中,将铁锤取出后,水面下降了2厘米,这个铁锤的高是多少厘米?
【解答】解:圆柱底面半径为12÷2=6(厘米)
圆柱底面积为πr2=π×62=36π(平方厘米)
铁锤的体积为36π×2=72π(立方厘米)
铁锤的底面半径为18.84÷3.14÷2=3(厘米)
铁锤的底面积为π×32=9π(平方厘米)
铁锤的高为
72π×3÷9π
=216π÷9π
=24(厘米)
答:这个铁锤的高是24厘米。
52.(2024 郏县)在一个底面半径5厘米,高18厘米的圆柱形水桶内装满了水,另有一个圆锥形空水桶,它的上口周长为37.68厘米,现在把圆柱形水桶里的水往圆锥形水桶里倒,当圆锥形水桶装满时,圆柱形水桶还剩12厘米高的水,求圆锥形水桶的高。
【解答】解:3.14×52×(18﹣12)
=3.14×25×6
=78.5×6
=471(立方厘米)
471×3÷[3.14×(37.68÷3.14÷2)2]
=1413÷[3.14×36]
=1413÷113.04
=12.5(厘米)
答:圆锥形水桶的高是12.5厘米。
53.(2024 无棣县)张师傅想用一个底面直径为20厘米、高为30厘米的圆柱体木桩加工工艺品。有以下几道工序:
工序一:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是1570立方厘米;
工序二:把圆锥和剩下的圆柱拼接起来,在圆锥部分雕刻上花纹,圆柱部分涂上颜料;
工序三:把做好的工艺品用长方体纸盒进行包装。
请你帮张师傅算一算。
(1)截取的木桩有多高?
(2)拼接后,涂颜料的面积是多少平方厘米?
(3)这个长方体纸盒的体积至少是多少立方厘米?
【解答】解:(1)1570×3÷[3.14×(20÷2)2]
=4710÷314
=15(厘米)
答:截取的木桩的高是15厘米。
(2)3.14×20×(30﹣15)
=3.14×20×15
=942(平方厘米)
答:涂颜料的面积是942平方厘米。
(3)20×20×30
=400×30
=12000(立方厘米)
答:这个长方体纸盒的体积至少是12000立方厘米。
54.(2024 田家庵区)李红用橡皮泥做玩具小丑帽,造型如图1。
图1 图2
(1)这个帽子的体积是多少立方厘米?
(2)如果用纸板给这个帽子制作一个长方体的包装盒(如图2),至少需要多少平方厘米的纸板?(接头处忽略不计)
【解答】解:(1)圆柱底面半径为:8÷2=4(厘米)
圆锥底面半径为:(8﹣2×2)÷2
=(8﹣4)÷2
=4÷2
=2(厘米)
3.14×42×1+3.14×22×9
=3.14×16×1+3.14×4×9
=50.24+37.68
=87.92(立方厘米)
答:这个帽子的体积是87.92立方厘米。
(2)包装盒的高为:9+1=10(厘米)
8×8×2+8×10×4
=128+320
=448(平方厘米)
答:至少需要448平方厘米的纸板。
55.(2024 官渡区)整流罩是运载火箭的重要组成部分,它可以保护飞船免受高速气流和极端温度的伤害,某型号的整流罩是右图以红线为轴旋转一周后形成的立体图形,请求出这个整流罩的体积。
【解答】解:3.14×22×103.14×22×6
=3.14×4×10+3.14×4×2
=125.6+25.12
=150.72(m3)
答:这个整流罩的体积是150.72m3。
56.(2024 凤县模拟)零件A和零件B可以组合成零件C。现在有一块长方体钢坯,长25.12分米,宽10分米,高12分米。如果用这块钢坯单铸A零件,可以铸120个;如果单铸B零件,可以做40个。如果铸C零件,可以铸多少个?
【解答】解:120÷40=3
120÷(3+1)
=120÷54
=30(个)
答:如果铸C零件,可以铸成30个。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
