【期末押题卷】整理与复习高频易错提高卷(含解析)-2024-2025学年五年级下册数学北师大版
文档属性
| 名称 | 【期末押题卷】整理与复习高频易错提高卷(含解析)-2024-2025学年五年级下册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 12:09:21 | ||
图片预览



文档简介
整理与复习单元高频易错提高卷
一.选择题(共5小题)
1.(2024 青秀区)一个物体包装盒长、宽、高分别是25厘米、12厘米、5厘米,这个物体可能是( )
A.一个文具盒 B.一把羽毛球拍
C.一块橡皮 D.一个行李箱
2.(2024 渝北区)算式的结果,一定( )
A.大于2 B.大于
C.大于且小于 D.大于0且小于
3.(2024秋 东莞市月考)小明在计算时,采用了不同的计算方法,计算方法错误的是( )
A.
B.
C.
D.以上全是
4.(2024秋 东莞市月考)下面各图中,有( )幅图能正确表示“”的意义。
A.1 B.2 C.3 D.4
5.(2024 西安)如图是测量一颗玻璃球体积的过程:(1)将300mL水倒进一个容量为500mL的杯子中;(2)将四颗相同的玻璃球放入水中,结果杯子没有满;(3)再将一颗同样的玻璃球放入水中,结果水满溢出。根据以上过程,推测这样一颗玻璃球的体积范围是( )
A.50cm3以上,60cm3以下
B.30cm3以上,40cm3以下
C.40cm3以上,50cm3以下
D.无法确定
二.填空题(共5小题)
6.(2024秋 淮安月考)如图,一个完全封闭的容器,从里面测量,长20厘米,宽16厘米,高10厘米。装了一些水,水深7厘米,如果将它向右侧面翻转90度,这时水面的高度是 厘米。
7.(2024秋 岳西县月考)
2.8m2= dm2 30cm3= dm3 时= 分
0.09L= cm3 2.01m3= L 公顷= 平方米
8.(2024秋 岳西县月考)一张长方形卡纸,在它的四角各剪掉一个边长为3cm的正方形后,粘成一个无盖的长方体纸盒,这个纸盒的容积是 cm3(可以在图中画一画)。
9.(2024秋 沭阳县校级月考)在横线里填“>”“<”或“=”。
420÷60 560÷70 6000毫升 6升
360÷90 360÷60 900毫升 10升
8700毫升 7800毫升 326÷45 426÷45
10.(2024秋 沭阳县校级月考)妈妈把4升花生油平均装在5个油壶里,每个油壶装 毫升。
三.判断题(共7小题)
11.(2024 甘孜州)一个棱长是6分米的正方体,表面积和体积一样大。
12.(2024春 巴中期末)将一块正方体橡皮泥捏成长方体,正方体和长方体相比,体积相等,表面积不一定相等。
13.(2024春 禅城区期末)一个正方体的表面积是24m2,则它的棱长是2m。
14.(2024春 惠来县期末)一个正方体的棱长扩大到原来的3倍,它的表面积也扩大到原来的3倍。
15.(2024 郸城县)3千克的与1千克的同样重。
16.(2024春 湛江期末)一般来说,长方体和正方体容器的体积比容积小。
17.(2024春 沈河区期末)两个长方体的底面周长相等,高相等,则体积也相等。
四.计算题(共1小题)
18.(2023秋 天桥区期末)直接写得数。
40×8= 42+18= 60×3= 32×3=
700×2= 520+300= 24÷6= 42×2=
350+70= 0+45= 250×4= 52×0=
300×4= 2000×4= 750﹣530= 32﹣4=
1
五.连线题(共1小题)
19.(2024春 亳州期中)连一连。
学校主席台的体积 24立方厘米
书包的体积 24立方米
碳素墨水盒的体积 24立方分米
六.操作题(共1小题)
20.(2023秋 扬州期末)如图,左面画斜线的6个相连的小正方形可以拼成一个正方体,且相对面点数的和都是7。在右面16个小正方形中找出6个相连的小正方形,使其能拼成相对面点数的和都是7的正方体。请你找到2种不同的方法,并画斜线表示。
七.应用题(共5小题)
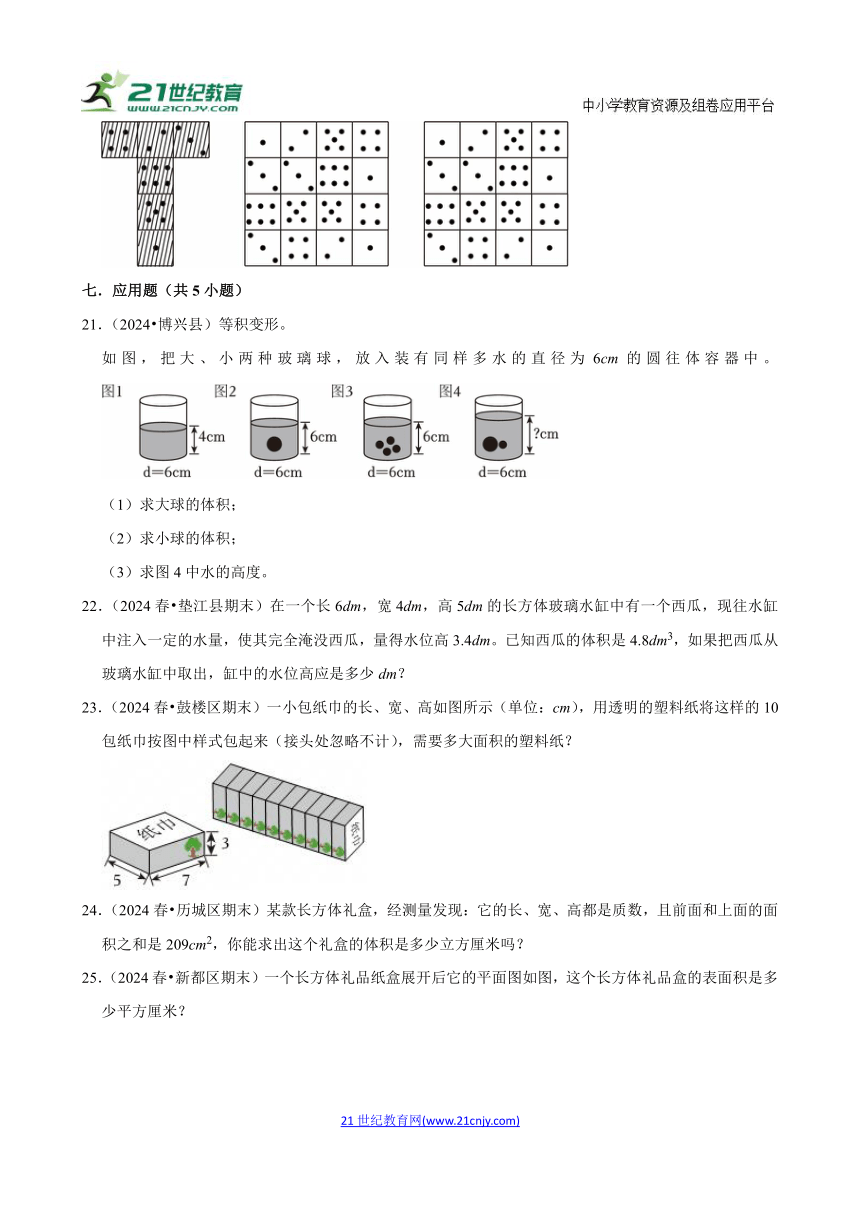
21.(2024 博兴县)等积变形。
如图,把大、小两种玻璃球,放入装有同样多水的直径为6cm的圆往体容器中。
(1)求大球的体积;
(2)求小球的体积;
(3)求图4中水的高度。
22.(2024春 垫江县期末)在一个长6dm,宽4dm,高5dm的长方体玻璃水缸中有一个西瓜,现往水缸中注入一定的水量,使其完全淹没西瓜,量得水位高3.4dm。已知西瓜的体积是4.8dm3,如果把西瓜从玻璃水缸中取出,缸中的水位高应是多少dm?
23.(2024春 鼓楼区期末)一小包纸巾的长、宽、高如图所示(单位:cm),用透明的塑料纸将这样的10包纸巾按图中样式包起来(接头处忽略不计),需要多大面积的塑料纸?
24.(2024春 历城区期末)某款长方体礼盒,经测量发现:它的长、宽、高都是质数,且前面和上面的面积之和是209cm2,你能求出这个礼盒的体积是多少立方厘米吗?
25.(2024春 新都区期末)一个长方体礼品纸盒展开后它的平面图如图,这个长方体礼品盒的表面积是多少平方厘米?
整理与复习单元高频易错提高卷
参考答案与试题解析
一.选择题(共5小题)
1.(2024 青秀区)一个物体包装盒长、宽、高分别是25厘米、12厘米、5厘米,这个物体可能是( )
A.一个文具盒 B.一把羽毛球拍
C.一块橡皮 D.一个行李箱
【考点】长方体的特征.
【专题】几何直观.
【答案】A
【分析】根据长方体的特征以及生活常识进行解答即可。
【解答】解:一个物体包装盒长、宽、高分别是25厘米、12厘米、5厘米,这个物体可能是 一个文具盒。
故选:A。
【点评】本题考查长方体的特征,注重生活常识的积累是解决本题的关键。
2.(2024 渝北区)算式的结果,一定( )
A.大于2 B.大于
C.大于且小于 D.大于0且小于
【考点】分数乘法;分数大小的比较.
【专题】数据分析观念.
【答案】D
【分析】一个数乘以一个比1小的数,积一定比原数小。
【解答】解:因为一个数乘以一个比1小的数,积一定比原数小,所以乘积一定小于所有的因数。
故选:D。
【点评】掌握一个数乘以一个比1小的数,积一定比原数小这一规律。
3.(2024秋 东莞市月考)小明在计算时,采用了不同的计算方法,计算方法错误的是( )
A.
B.
C.
D.以上全是
【考点】分数乘法.
【专题】运算顺序及法则;运算能力.
【答案】C
【分析】可以把4.2分成(4+0.2)利用乘法分配律进行简便计算;还可以把小数化成分数,利用分数乘分数进行计算。
【解答】解:A.(4+0.2)40.21+0.05=1.05
B.1.05
C.1.05,因此不能化成带分数进行计算。
故选:C。
【点评】本题考查了小数乘分数的计算方法。
4.(2024秋 东莞市月考)下面各图中,有( )幅图能正确表示“”的意义。
A.1 B.2 C.3 D.4
【考点】分数乘法.
【专题】运算能力.
【答案】B
【分析】算式表示先将单位“1”平均分成4份,取其中的3份,再将这3份平均分成2份,取其中的1份,据此解答。
【解答】解:左起第1个图:先将大长方形平均分成4份,取其中的3份,再将这3份平均分成2份,取其中的1份,可以用算式表示;
左起第2个图:先将大长方形平均分成2份,取其中的1份,再将这2份平均分成4份,取其中的1份,可以用算式表示;
左起第3个图:先将直条平均分成2份,取其中的1份,再将这2份平均分成4份,取其中的1份,可以用算式表示;
左起第4个图:先将整条线段平均分成4份,取其中的3份,再将这3份平均分成2份,取其中的1份,可以用算式表示。
有2幅图能正确表示的意义。
故选:B。
【点评】本题考查了分数乘分数,突出了对算理的理解。
5.(2024 西安)如图是测量一颗玻璃球体积的过程:(1)将300mL水倒进一个容量为500mL的杯子中;(2)将四颗相同的玻璃球放入水中,结果杯子没有满;(3)再将一颗同样的玻璃球放入水中,结果水满溢出。根据以上过程,推测这样一颗玻璃球的体积范围是( )
A.50cm3以上,60cm3以下
B.30cm3以上,40cm3以下
C.40cm3以上,50cm3以下
D.无法确定
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】C
【分析】要求每颗玻璃球的体积在哪一个范围内,根据题意,先求出5颗玻璃球的体积最少是多少,5颗玻璃球的体积最少是(500﹣300)立方厘米,进而推测这样一颗玻璃球的体积的范围即可。
【解答】解:因为把5颗玻璃球放入水中,结果水满溢出,所以5颗玻璃球的体积最少是:500﹣300=200(立方厘米)
一颗玻璃球的体积最少是:200÷5=40(立方厘米)
一颗玻璃球的体积最多是:200÷4=50(立方厘米)
答:这样一颗玻璃球的体积在40立方厘米以上,50立方厘米以下。
故选:C。
【点评】此题考查了探索某些实物体积的测量方法,结合题意分析解答即可。
二.填空题(共5小题)
6.(2024秋 淮安月考)如图,一个完全封闭的容器,从里面测量,长20厘米,宽16厘米,高10厘米。装了一些水,水深7厘米,如果将它向右侧面翻转90度,这时水面的高度是 14 厘米。
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】14。
【分析】根据体积的意义可知,这个密封的容器无论横放还是竖放,容器内水的体积不变,根据长方体的体积公式:V=abh,把数据代入公式求出水的体积,然后用水的体积除以容器右侧面的面积即可。
【解答】解:20×16×7÷(16×10)
=320×7÷160
=2240÷160
=14(厘米)
答:这时水面的高度是14厘米。
故答案为:14。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
7.(2024秋 岳西县月考)
2.8m2= 280 dm2 30cm3= 0.03 dm3 时= 45 分
0.09L= 90 cm3 2.01m3= 2010 L 公顷= 2000 平方米
【考点】体积、容积进率及单位换算;时、分、秒及其关系、单位换算与计算;小面积单位间的进率及单位换算.
【专题】长度、面积、体积单位;数据分析观念.
【答案】280,0.03,45,90,2010,2000。
【分析】单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
【解答】解:
2.8m2= 280dm2 30cm3= 0.03dm3 时= 45分
0.09L= 90cm3 2.01m3= 2010L 公顷= 2000平方米
故答案为:280,0.03,45,90,2010,2000。
【点评】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率;把低级单位的名数换算成高级单位的名数,就除以单位间的进率。
8.(2024秋 岳西县月考)一张长方形卡纸,在它的四角各剪掉一个边长为3cm的正方形后,粘成一个无盖的长方体纸盒,这个纸盒的容积是 224 cm3(可以在图中画一画)。
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】224。
【分析】根据题意可知,这个纸盒的长是(18﹣2﹣2)厘米,宽是(12﹣2﹣2)厘米,高是2厘米,根据长方体的容积公式:V=abh,把数据代入公式解答。
【解答】解:如图:
(18﹣2﹣2)×(12﹣2﹣2)×2
=14×8×2
=112×2
=224(立方厘米)
答:这个纸盒的容积是224立方厘米。
故答案为:224。
【点评】此题主要考查长方体容积公式的灵活运用,关键是熟记公式。
9.(2024秋 沭阳县校级月考)在横线里填“>”“<”或“=”。
420÷60 < 560÷70 6000毫升 = 6升
360÷90 < 360÷60 900毫升 < 10升
8700毫升 > 7800毫升 326÷45 < 426÷45
【考点】体积、容积进率及单位换算;两位数除两、三位数.
【专题】运算顺序及法则;长度、面积、体积单位;运算能力.
【答案】<;=;<;<;>;<。
【分析】单位大小的比较,先把单位化成统一的单位再比较大小;大单位换小单位乘以它们之间的进制,小单位换大单位除以它们之间的进制;算式大小的比较要先计算出得数,再比较得数的大小。
【解答】解:
420÷60<560÷70 6000毫升=6升
360÷90<360÷60 900毫升<10升
8700毫升>7800毫升 326÷45<426÷45
故答案为:<;=;<;<;>;<。
【点评】本题考查了容积单位的换算,除数是两位数的除法计算,数的大小比较。
10.(2024秋 沭阳县校级月考)妈妈把4升花生油平均装在5个油壶里,每个油壶装 800 毫升。
【考点】体积、容积进率及单位换算;一位数除多位数.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】800。
【分析】4升=4000毫升,再根据除法的意义列式即可解答。
【解答】解:4升=4000毫升
4000÷5=800(毫升)
答:每个油壶装800毫升。
故答案为:800。
【点评】本题考查了容积单位的换算及除法的意义。
三.判断题(共7小题)
11.(2024 甘孜州)一个棱长是6分米的正方体,表面积和体积一样大。 ×
【考点】长方体和正方体的表面积.
【专题】空间观念.
【答案】×
【分析】正方体的表面积是指它的6个面的总面积,正方体的体积是指它所占空间的大小,因为表面积和体积不是同类量,所以不能进行比较。据此判断。
【解答】解:因为表面积和体积不是同类量,所以不能进行比较。
因此题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解正方体的表面积、体积的意义,明确:只有同类量才能进行比较。
12.(2024春 巴中期末)将一块正方体橡皮泥捏成长方体,正方体和长方体相比,体积相等,表面积不一定相等。 √
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】√
【分析】根据体积、表面积的意义,将一块正方体橡皮泥无论捏成什么形状体积都不变,表面积变了,据此判断。
【解答】解:将一块正方体橡皮泥捏成长方体,正方体和长方体相比,体积相等,表面积不一定相等。这种说法是正确的。
故答案为:√。
【点评】此题考查的目的是理解掌握长方体、正方体的体积的意义、表面积的意义及应用。
13.(2024春 禅城区期末)一个正方体的表面积是24m2,则它的棱长是2m。 √
【考点】长方体和正方体的表面积.
【专题】运算能力.
【答案】√
【分析】根据正方体的表面积公式:S=6a2,首先用表面积除以6求出一个面的面积,进而求出棱长即可。
【解答】解:24÷6=4(平方米)
因为2×2=4,
所以棱长是2米。
所以题干说法正确。
故答案为:√。
【点评】此题主要考查正方体的表面积公式的灵活运用。
14.(2024春 惠来县期末)一个正方体的棱长扩大到原来的3倍,它的表面积也扩大到原来的3倍。 ×
【考点】长方体和正方体的表面积.
【专题】空间观念;应用意识.
【答案】×
【分析】根据正方体的表面积公式:S=6a2,再根据积的变化规律,如果正方体的棱长扩大到原来的3倍,它的表面积也扩大到原来的9倍。据此判断。
【解答】解:3×3=9
一个正方体的棱长扩大到原来的3倍,它的表面积也扩大到原来的9倍。
因此,题干中的结论是错误的。
故答案为:×。
【点评】此题主要考查正方体表面积公式的灵活运用,积的变化规律及应用。
15.(2024 郸城县)3千克的与1千克的同样重。 √
【考点】分数乘法;分数的意义和读写.
【专题】综合判断题;应用意识.
【答案】√
【分析】根据分数乘法的意义,3千克的是3(千克),1千克的是1(千克),即3千克的和1千克的一样重。
【解答】解:3(千克)
1(千克)
即千克的和1千克的一样重。
故答案为:√。
【点评】求一个数的几分之几是多少,用乘法。
16.(2024春 湛江期末)一般来说,长方体和正方体容器的体积比容积小。 ×
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】×
【分析】根据体积、容积的意义,物体所占空间的大小叫作物体的体积,某容器所能容纳别的物体的体积叫作容器的容积,因为任何容器壁有一定的厚度,所以某容器的容积一定比它的体积小。据此判断。
【解答】解:因为任何容器壁有一定的厚度,所以某容器的容积一定比它的体积小。故原题说法错误。
故答案为:×。
【点评】此题考查的目的是理解掌握体积、容积的意义及应用。
17.(2024春 沈河区期末)两个长方体的底面周长相等,高相等,则体积也相等。 ×
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】×
【分析】两个长方体的底面周长相等,这两个长方体的长和宽不一定相等,高相等,它们的体积不一定相等,可以通过举例证明。
【解答】解:假设两个长方形的底面周长都是24厘米,高都是5厘米。
第一个长方体的长、宽可能是:
24÷2=12(厘米)
12=11+1=10+2=9+3=8+4=7+5
体积可能是:
12×1×5=60(立方厘米)
10×2×5=100(立方厘米)
9×3×5=135(立方厘米)
8×4×5=160(立方厘米)
7×5×5=175(立方厘米)
另一个长方体的底边边长:
24÷4=6(厘米)
体积:
6×6×5=180(立方厘米)
所以,两个长方体的底面周长相等,高相等,体积不一定相等。
因此题干中的结论是错误的。
故答案为:×。
【点评】此题主要考查长方形、正方形的周长公式、长方体的体积公式的灵活运用,关键是熟记公式。
四.计算题(共1小题)
18.(2023秋 天桥区期末)直接写得数。
40×8= 42+18= 60×3= 32×3=
700×2= 520+300= 24÷6= 42×2=
350+70= 0+45= 250×4= 52×0=
300×4= 2000×4= 750﹣530= 32﹣4=
1
【考点】分数的加法和减法;千以内加减法;一位数乘三位数.
【专题】运算能力.
【答案】320;60;180;96;1400;820;4;84;420;45;1000;0;1200;8000;220;28;;;1;。
【分析】根据整数加减乘除法、分数加减法的计算方法进行计算。
【解答】解:
40×8=320 42+18=60 60×3=180 32×3=96
700×2=1400 520+300=820 24÷6=4 42×2=84
350+70=420 0+45=45 250×4=1000 52×0=0
300×4=1200 2000×4=8000 750﹣530=220 32﹣4=28
1 1
【点评】口算时,注意运算符号和数据,然后再进一步计算。
五.连线题(共1小题)
19.(2024春 亳州期中)连一连。
学校主席台的体积 24立方厘米
书包的体积 24立方米
碳素墨水盒的体积 24立方分米
【考点】体积、容积及其单位.
【专题】整数的认识;数据分析观念.
【答案】
【分析】体积和容积是两个不同的概念,意义不同:容积是指容器所能容纳物体的体积,箱子、油桶、仓库等所能容纳物体的体积,叫作它们的容积或容量;物体所占的空间的大小叫作体积。
【解答】解:如图:
【点评】正确区分体积和容积的意义,是解决此题的关键。
六.操作题(共1小题)
20.(2023秋 扬州期末)如图,左面画斜线的6个相连的小正方形可以拼成一个正方体,且相对面点数的和都是7。在右面16个小正方形中找出6个相连的小正方形,使其能拼成相对面点数的和都是7的正方体。请你找到2种不同的方法,并画斜线表示。
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】(答案不唯一)。
【分析】左图属于正方体展开图的“1﹣4﹣1”型,折成正方体后,4点与3点相对,2点与5点相对,1点与6点相对,即对面点数的和都是7。1+6=2+5=3+4=7,要使正方体相对面点数的和都是7,则相对的面的点数应分别1和6、2和5或3和4。结合正方体展开图的四种类型:“1﹣4﹣1”型、“1﹣3﹣2”型、“2﹣2﹣2”型、“3﹣3”型,即可找出相对面点数的和都是7的正方体展开图。
【解答】解:
(答案不唯一)。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,掌握规律是解答本题的关键。
七.应用题(共5小题)
21.(2024 博兴县)等积变形。
如图,把大、小两种玻璃球,放入装有同样多水的直径为6cm的圆往体容器中。
(1)求大球的体积;
(2)求小球的体积;
(3)求图4中水的高度。
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】(1)56.52立方厘米;(2)14.13立方厘米;(3)6.5厘米。
【分析】(1)根据用排水法测量实物体积的方法,大球的体积等于圆柱内水上升的体积,根据圆柱的体积公式V=πr2h,解答即可。
(2)根据用排水法测量实物体积的方法,大球的体积等于圆柱内水上升的体积,根据圆柱的体积公式V=πr2h,求出4个小球的体积,除以4,解答即可。
(3)根据用排水法测量实物体积的方法,用1个大球和1个小球的体积和除以圆柱的底面积,求出水的高度,解答即可。
【解答】解:圆柱的半径是6÷2=3(厘米)
(1)3.14×32×(6﹣4)
=28.26×2
=56.52(立方厘米)
答:大球的体积是56.52立方厘米。
(2)3.14×32×(6﹣4)÷4
=28.26×2÷4
=14.13(立方厘米)
答:小球的体积是14.13立方厘米。
(3)(56.52+14.13)÷(3.14×32)+4
=70.65÷28.26+4
=2.5+4
=6.5(厘米)
答:图4中水的高度是6.5厘米。
【点评】本题考查了用排水法测量实物体积的方法,结合圆柱的体积公式解答即可。
22.(2024春 垫江县期末)在一个长6dm,宽4dm,高5dm的长方体玻璃水缸中有一个西瓜,现往水缸中注入一定的水量,使其完全淹没西瓜,量得水位高3.4dm。已知西瓜的体积是4.8dm3,如果把西瓜从玻璃水缸中取出,缸中的水位高应是多少dm?
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】3.2分米。
【分析】根据用排水法测量实物体积的方法,西瓜的体积等于长方体玻璃水缸中水下降的体积,结合长方体的体积公式:V=abh,先求出把西瓜从玻璃水缸中取出后下降的高度,然后用3.4分米减去下降的高度,解答即可。
【解答】解:4.8÷(6×4)
=4.8÷24
=0.2(分米)
3.4﹣0.2=3.2(分米)
答:缸中的水位高应是3.2分米。
【点评】本题考查了用排水法测量实物体积的方法,结合题意分析解答即可。
23.(2024春 鼓楼区期末)一小包纸巾的长、宽、高如图所示(单位:cm),用透明的塑料纸将这样的10包纸巾按图中样式包起来(接头处忽略不计),需要多大面积的塑料纸?
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】见试题解答内容
【分析】题干观察图形可知,把这样10包纸巾拼成的大长方体的长是(3×10)厘米,宽是5厘米,高是7厘米,根据长方体的表面积公式:S(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:3×10=30(厘米)
(30×5+30×7+5×7)×2
=(150+210+35)×2
=395×2
=790(平方厘米)
答:需要790平方厘米的塑料纸。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
24.(2024春 历城区期末)某款长方体礼盒,经测量发现:它的长、宽、高都是质数,且前面和上面的面积之和是209cm2,你能求出这个礼盒的体积是多少立方厘米吗?
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】374立方厘米。
【分析】前面和上面的面积之和是209平方厘米,即长×宽+长×高=209,且长、宽、高都是质数,据此可以求出长、宽、高,然后根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:长×宽+长×高=209
长×(宽+高)=209
209=11×19
要么宽+高=11,要么宽+高=19
11=2+9=3+8=4+7=5+6,这样都有一个数是合数,不符合题意;
19=2+17=3+16=5+14=7+12=11+8=13+6,只有2和17都是质数。
所以这个长方体的长、宽、高分别11厘米,2厘米,17厘米。
11×2×17
=22×17
=374(立方厘米)
答:这个长方体的体积是374立方厘米。
【点评】此题考查的目的是理解掌握质数的意义及应用,长方体的体积公式及应用,关键是求出长方体的长、宽、高。
25.(2024春 新都区期末)一个长方体礼品纸盒展开后它的平面图如图,这个长方体礼品盒的表面积是多少平方厘米?
【考点】长方体和正方体的表面积.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】由展开图得出:长方体的长是30﹣6﹣6=18(厘米),宽是26﹣18=8(厘米),高是6厘米,根据长方体表面积=(长×宽+长×高+宽×高)×2,代数计算即可。
【解答】解:长是30﹣6﹣6=18(厘米)
宽是26﹣18=8(厘米)
高是6厘米
(18×8+8×6+18×6)×2
=(144+48+108)×2
=300×2
=600(平方厘米)
答:这个长方体礼品盒的表面积是600平方厘米。
【点评】解决本题的关键是根据长方体展开图得出长方体的长、宽、高,再根据长方体表面积公式计算。
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024 青秀区)一个物体包装盒长、宽、高分别是25厘米、12厘米、5厘米,这个物体可能是( )
A.一个文具盒 B.一把羽毛球拍
C.一块橡皮 D.一个行李箱
2.(2024 渝北区)算式的结果,一定( )
A.大于2 B.大于
C.大于且小于 D.大于0且小于
3.(2024秋 东莞市月考)小明在计算时,采用了不同的计算方法,计算方法错误的是( )
A.
B.
C.
D.以上全是
4.(2024秋 东莞市月考)下面各图中,有( )幅图能正确表示“”的意义。
A.1 B.2 C.3 D.4
5.(2024 西安)如图是测量一颗玻璃球体积的过程:(1)将300mL水倒进一个容量为500mL的杯子中;(2)将四颗相同的玻璃球放入水中,结果杯子没有满;(3)再将一颗同样的玻璃球放入水中,结果水满溢出。根据以上过程,推测这样一颗玻璃球的体积范围是( )
A.50cm3以上,60cm3以下
B.30cm3以上,40cm3以下
C.40cm3以上,50cm3以下
D.无法确定
二.填空题(共5小题)
6.(2024秋 淮安月考)如图,一个完全封闭的容器,从里面测量,长20厘米,宽16厘米,高10厘米。装了一些水,水深7厘米,如果将它向右侧面翻转90度,这时水面的高度是 厘米。
7.(2024秋 岳西县月考)
2.8m2= dm2 30cm3= dm3 时= 分
0.09L= cm3 2.01m3= L 公顷= 平方米
8.(2024秋 岳西县月考)一张长方形卡纸,在它的四角各剪掉一个边长为3cm的正方形后,粘成一个无盖的长方体纸盒,这个纸盒的容积是 cm3(可以在图中画一画)。
9.(2024秋 沭阳县校级月考)在横线里填“>”“<”或“=”。
420÷60 560÷70 6000毫升 6升
360÷90 360÷60 900毫升 10升
8700毫升 7800毫升 326÷45 426÷45
10.(2024秋 沭阳县校级月考)妈妈把4升花生油平均装在5个油壶里,每个油壶装 毫升。
三.判断题(共7小题)
11.(2024 甘孜州)一个棱长是6分米的正方体,表面积和体积一样大。
12.(2024春 巴中期末)将一块正方体橡皮泥捏成长方体,正方体和长方体相比,体积相等,表面积不一定相等。
13.(2024春 禅城区期末)一个正方体的表面积是24m2,则它的棱长是2m。
14.(2024春 惠来县期末)一个正方体的棱长扩大到原来的3倍,它的表面积也扩大到原来的3倍。
15.(2024 郸城县)3千克的与1千克的同样重。
16.(2024春 湛江期末)一般来说,长方体和正方体容器的体积比容积小。
17.(2024春 沈河区期末)两个长方体的底面周长相等,高相等,则体积也相等。
四.计算题(共1小题)
18.(2023秋 天桥区期末)直接写得数。
40×8= 42+18= 60×3= 32×3=
700×2= 520+300= 24÷6= 42×2=
350+70= 0+45= 250×4= 52×0=
300×4= 2000×4= 750﹣530= 32﹣4=
1
五.连线题(共1小题)
19.(2024春 亳州期中)连一连。
学校主席台的体积 24立方厘米
书包的体积 24立方米
碳素墨水盒的体积 24立方分米
六.操作题(共1小题)
20.(2023秋 扬州期末)如图,左面画斜线的6个相连的小正方形可以拼成一个正方体,且相对面点数的和都是7。在右面16个小正方形中找出6个相连的小正方形,使其能拼成相对面点数的和都是7的正方体。请你找到2种不同的方法,并画斜线表示。
七.应用题(共5小题)
21.(2024 博兴县)等积变形。
如图,把大、小两种玻璃球,放入装有同样多水的直径为6cm的圆往体容器中。
(1)求大球的体积;
(2)求小球的体积;
(3)求图4中水的高度。
22.(2024春 垫江县期末)在一个长6dm,宽4dm,高5dm的长方体玻璃水缸中有一个西瓜,现往水缸中注入一定的水量,使其完全淹没西瓜,量得水位高3.4dm。已知西瓜的体积是4.8dm3,如果把西瓜从玻璃水缸中取出,缸中的水位高应是多少dm?
23.(2024春 鼓楼区期末)一小包纸巾的长、宽、高如图所示(单位:cm),用透明的塑料纸将这样的10包纸巾按图中样式包起来(接头处忽略不计),需要多大面积的塑料纸?
24.(2024春 历城区期末)某款长方体礼盒,经测量发现:它的长、宽、高都是质数,且前面和上面的面积之和是209cm2,你能求出这个礼盒的体积是多少立方厘米吗?
25.(2024春 新都区期末)一个长方体礼品纸盒展开后它的平面图如图,这个长方体礼品盒的表面积是多少平方厘米?
整理与复习单元高频易错提高卷
参考答案与试题解析
一.选择题(共5小题)
1.(2024 青秀区)一个物体包装盒长、宽、高分别是25厘米、12厘米、5厘米,这个物体可能是( )
A.一个文具盒 B.一把羽毛球拍
C.一块橡皮 D.一个行李箱
【考点】长方体的特征.
【专题】几何直观.
【答案】A
【分析】根据长方体的特征以及生活常识进行解答即可。
【解答】解:一个物体包装盒长、宽、高分别是25厘米、12厘米、5厘米,这个物体可能是 一个文具盒。
故选:A。
【点评】本题考查长方体的特征,注重生活常识的积累是解决本题的关键。
2.(2024 渝北区)算式的结果,一定( )
A.大于2 B.大于
C.大于且小于 D.大于0且小于
【考点】分数乘法;分数大小的比较.
【专题】数据分析观念.
【答案】D
【分析】一个数乘以一个比1小的数,积一定比原数小。
【解答】解:因为一个数乘以一个比1小的数,积一定比原数小,所以乘积一定小于所有的因数。
故选:D。
【点评】掌握一个数乘以一个比1小的数,积一定比原数小这一规律。
3.(2024秋 东莞市月考)小明在计算时,采用了不同的计算方法,计算方法错误的是( )
A.
B.
C.
D.以上全是
【考点】分数乘法.
【专题】运算顺序及法则;运算能力.
【答案】C
【分析】可以把4.2分成(4+0.2)利用乘法分配律进行简便计算;还可以把小数化成分数,利用分数乘分数进行计算。
【解答】解:A.(4+0.2)40.21+0.05=1.05
B.1.05
C.1.05,因此不能化成带分数进行计算。
故选:C。
【点评】本题考查了小数乘分数的计算方法。
4.(2024秋 东莞市月考)下面各图中,有( )幅图能正确表示“”的意义。
A.1 B.2 C.3 D.4
【考点】分数乘法.
【专题】运算能力.
【答案】B
【分析】算式表示先将单位“1”平均分成4份,取其中的3份,再将这3份平均分成2份,取其中的1份,据此解答。
【解答】解:左起第1个图:先将大长方形平均分成4份,取其中的3份,再将这3份平均分成2份,取其中的1份,可以用算式表示;
左起第2个图:先将大长方形平均分成2份,取其中的1份,再将这2份平均分成4份,取其中的1份,可以用算式表示;
左起第3个图:先将直条平均分成2份,取其中的1份,再将这2份平均分成4份,取其中的1份,可以用算式表示;
左起第4个图:先将整条线段平均分成4份,取其中的3份,再将这3份平均分成2份,取其中的1份,可以用算式表示。
有2幅图能正确表示的意义。
故选:B。
【点评】本题考查了分数乘分数,突出了对算理的理解。
5.(2024 西安)如图是测量一颗玻璃球体积的过程:(1)将300mL水倒进一个容量为500mL的杯子中;(2)将四颗相同的玻璃球放入水中,结果杯子没有满;(3)再将一颗同样的玻璃球放入水中,结果水满溢出。根据以上过程,推测这样一颗玻璃球的体积范围是( )
A.50cm3以上,60cm3以下
B.30cm3以上,40cm3以下
C.40cm3以上,50cm3以下
D.无法确定
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】C
【分析】要求每颗玻璃球的体积在哪一个范围内,根据题意,先求出5颗玻璃球的体积最少是多少,5颗玻璃球的体积最少是(500﹣300)立方厘米,进而推测这样一颗玻璃球的体积的范围即可。
【解答】解:因为把5颗玻璃球放入水中,结果水满溢出,所以5颗玻璃球的体积最少是:500﹣300=200(立方厘米)
一颗玻璃球的体积最少是:200÷5=40(立方厘米)
一颗玻璃球的体积最多是:200÷4=50(立方厘米)
答:这样一颗玻璃球的体积在40立方厘米以上,50立方厘米以下。
故选:C。
【点评】此题考查了探索某些实物体积的测量方法,结合题意分析解答即可。
二.填空题(共5小题)
6.(2024秋 淮安月考)如图,一个完全封闭的容器,从里面测量,长20厘米,宽16厘米,高10厘米。装了一些水,水深7厘米,如果将它向右侧面翻转90度,这时水面的高度是 14 厘米。
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】14。
【分析】根据体积的意义可知,这个密封的容器无论横放还是竖放,容器内水的体积不变,根据长方体的体积公式:V=abh,把数据代入公式求出水的体积,然后用水的体积除以容器右侧面的面积即可。
【解答】解:20×16×7÷(16×10)
=320×7÷160
=2240÷160
=14(厘米)
答:这时水面的高度是14厘米。
故答案为:14。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
7.(2024秋 岳西县月考)
2.8m2= 280 dm2 30cm3= 0.03 dm3 时= 45 分
0.09L= 90 cm3 2.01m3= 2010 L 公顷= 2000 平方米
【考点】体积、容积进率及单位换算;时、分、秒及其关系、单位换算与计算;小面积单位间的进率及单位换算.
【专题】长度、面积、体积单位;数据分析观念.
【答案】280,0.03,45,90,2010,2000。
【分析】单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
【解答】解:
2.8m2= 280dm2 30cm3= 0.03dm3 时= 45分
0.09L= 90cm3 2.01m3= 2010L 公顷= 2000平方米
故答案为:280,0.03,45,90,2010,2000。
【点评】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率;把低级单位的名数换算成高级单位的名数,就除以单位间的进率。
8.(2024秋 岳西县月考)一张长方形卡纸,在它的四角各剪掉一个边长为3cm的正方形后,粘成一个无盖的长方体纸盒,这个纸盒的容积是 224 cm3(可以在图中画一画)。
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】224。
【分析】根据题意可知,这个纸盒的长是(18﹣2﹣2)厘米,宽是(12﹣2﹣2)厘米,高是2厘米,根据长方体的容积公式:V=abh,把数据代入公式解答。
【解答】解:如图:
(18﹣2﹣2)×(12﹣2﹣2)×2
=14×8×2
=112×2
=224(立方厘米)
答:这个纸盒的容积是224立方厘米。
故答案为:224。
【点评】此题主要考查长方体容积公式的灵活运用,关键是熟记公式。
9.(2024秋 沭阳县校级月考)在横线里填“>”“<”或“=”。
420÷60 < 560÷70 6000毫升 = 6升
360÷90 < 360÷60 900毫升 < 10升
8700毫升 > 7800毫升 326÷45 < 426÷45
【考点】体积、容积进率及单位换算;两位数除两、三位数.
【专题】运算顺序及法则;长度、面积、体积单位;运算能力.
【答案】<;=;<;<;>;<。
【分析】单位大小的比较,先把单位化成统一的单位再比较大小;大单位换小单位乘以它们之间的进制,小单位换大单位除以它们之间的进制;算式大小的比较要先计算出得数,再比较得数的大小。
【解答】解:
420÷60<560÷70 6000毫升=6升
360÷90<360÷60 900毫升<10升
8700毫升>7800毫升 326÷45<426÷45
故答案为:<;=;<;<;>;<。
【点评】本题考查了容积单位的换算,除数是两位数的除法计算,数的大小比较。
10.(2024秋 沭阳县校级月考)妈妈把4升花生油平均装在5个油壶里,每个油壶装 800 毫升。
【考点】体积、容积进率及单位换算;一位数除多位数.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】800。
【分析】4升=4000毫升,再根据除法的意义列式即可解答。
【解答】解:4升=4000毫升
4000÷5=800(毫升)
答:每个油壶装800毫升。
故答案为:800。
【点评】本题考查了容积单位的换算及除法的意义。
三.判断题(共7小题)
11.(2024 甘孜州)一个棱长是6分米的正方体,表面积和体积一样大。 ×
【考点】长方体和正方体的表面积.
【专题】空间观念.
【答案】×
【分析】正方体的表面积是指它的6个面的总面积,正方体的体积是指它所占空间的大小,因为表面积和体积不是同类量,所以不能进行比较。据此判断。
【解答】解:因为表面积和体积不是同类量,所以不能进行比较。
因此题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解正方体的表面积、体积的意义,明确:只有同类量才能进行比较。
12.(2024春 巴中期末)将一块正方体橡皮泥捏成长方体,正方体和长方体相比,体积相等,表面积不一定相等。 √
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】√
【分析】根据体积、表面积的意义,将一块正方体橡皮泥无论捏成什么形状体积都不变,表面积变了,据此判断。
【解答】解:将一块正方体橡皮泥捏成长方体,正方体和长方体相比,体积相等,表面积不一定相等。这种说法是正确的。
故答案为:√。
【点评】此题考查的目的是理解掌握长方体、正方体的体积的意义、表面积的意义及应用。
13.(2024春 禅城区期末)一个正方体的表面积是24m2,则它的棱长是2m。 √
【考点】长方体和正方体的表面积.
【专题】运算能力.
【答案】√
【分析】根据正方体的表面积公式:S=6a2,首先用表面积除以6求出一个面的面积,进而求出棱长即可。
【解答】解:24÷6=4(平方米)
因为2×2=4,
所以棱长是2米。
所以题干说法正确。
故答案为:√。
【点评】此题主要考查正方体的表面积公式的灵活运用。
14.(2024春 惠来县期末)一个正方体的棱长扩大到原来的3倍,它的表面积也扩大到原来的3倍。 ×
【考点】长方体和正方体的表面积.
【专题】空间观念;应用意识.
【答案】×
【分析】根据正方体的表面积公式:S=6a2,再根据积的变化规律,如果正方体的棱长扩大到原来的3倍,它的表面积也扩大到原来的9倍。据此判断。
【解答】解:3×3=9
一个正方体的棱长扩大到原来的3倍,它的表面积也扩大到原来的9倍。
因此,题干中的结论是错误的。
故答案为:×。
【点评】此题主要考查正方体表面积公式的灵活运用,积的变化规律及应用。
15.(2024 郸城县)3千克的与1千克的同样重。 √
【考点】分数乘法;分数的意义和读写.
【专题】综合判断题;应用意识.
【答案】√
【分析】根据分数乘法的意义,3千克的是3(千克),1千克的是1(千克),即3千克的和1千克的一样重。
【解答】解:3(千克)
1(千克)
即千克的和1千克的一样重。
故答案为:√。
【点评】求一个数的几分之几是多少,用乘法。
16.(2024春 湛江期末)一般来说,长方体和正方体容器的体积比容积小。 ×
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】×
【分析】根据体积、容积的意义,物体所占空间的大小叫作物体的体积,某容器所能容纳别的物体的体积叫作容器的容积,因为任何容器壁有一定的厚度,所以某容器的容积一定比它的体积小。据此判断。
【解答】解:因为任何容器壁有一定的厚度,所以某容器的容积一定比它的体积小。故原题说法错误。
故答案为:×。
【点评】此题考查的目的是理解掌握体积、容积的意义及应用。
17.(2024春 沈河区期末)两个长方体的底面周长相等,高相等,则体积也相等。 ×
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】×
【分析】两个长方体的底面周长相等,这两个长方体的长和宽不一定相等,高相等,它们的体积不一定相等,可以通过举例证明。
【解答】解:假设两个长方形的底面周长都是24厘米,高都是5厘米。
第一个长方体的长、宽可能是:
24÷2=12(厘米)
12=11+1=10+2=9+3=8+4=7+5
体积可能是:
12×1×5=60(立方厘米)
10×2×5=100(立方厘米)
9×3×5=135(立方厘米)
8×4×5=160(立方厘米)
7×5×5=175(立方厘米)
另一个长方体的底边边长:
24÷4=6(厘米)
体积:
6×6×5=180(立方厘米)
所以,两个长方体的底面周长相等,高相等,体积不一定相等。
因此题干中的结论是错误的。
故答案为:×。
【点评】此题主要考查长方形、正方形的周长公式、长方体的体积公式的灵活运用,关键是熟记公式。
四.计算题(共1小题)
18.(2023秋 天桥区期末)直接写得数。
40×8= 42+18= 60×3= 32×3=
700×2= 520+300= 24÷6= 42×2=
350+70= 0+45= 250×4= 52×0=
300×4= 2000×4= 750﹣530= 32﹣4=
1
【考点】分数的加法和减法;千以内加减法;一位数乘三位数.
【专题】运算能力.
【答案】320;60;180;96;1400;820;4;84;420;45;1000;0;1200;8000;220;28;;;1;。
【分析】根据整数加减乘除法、分数加减法的计算方法进行计算。
【解答】解:
40×8=320 42+18=60 60×3=180 32×3=96
700×2=1400 520+300=820 24÷6=4 42×2=84
350+70=420 0+45=45 250×4=1000 52×0=0
300×4=1200 2000×4=8000 750﹣530=220 32﹣4=28
1 1
【点评】口算时,注意运算符号和数据,然后再进一步计算。
五.连线题(共1小题)
19.(2024春 亳州期中)连一连。
学校主席台的体积 24立方厘米
书包的体积 24立方米
碳素墨水盒的体积 24立方分米
【考点】体积、容积及其单位.
【专题】整数的认识;数据分析观念.
【答案】
【分析】体积和容积是两个不同的概念,意义不同:容积是指容器所能容纳物体的体积,箱子、油桶、仓库等所能容纳物体的体积,叫作它们的容积或容量;物体所占的空间的大小叫作体积。
【解答】解:如图:
【点评】正确区分体积和容积的意义,是解决此题的关键。
六.操作题(共1小题)
20.(2023秋 扬州期末)如图,左面画斜线的6个相连的小正方形可以拼成一个正方体,且相对面点数的和都是7。在右面16个小正方形中找出6个相连的小正方形,使其能拼成相对面点数的和都是7的正方体。请你找到2种不同的方法,并画斜线表示。
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】(答案不唯一)。
【分析】左图属于正方体展开图的“1﹣4﹣1”型,折成正方体后,4点与3点相对,2点与5点相对,1点与6点相对,即对面点数的和都是7。1+6=2+5=3+4=7,要使正方体相对面点数的和都是7,则相对的面的点数应分别1和6、2和5或3和4。结合正方体展开图的四种类型:“1﹣4﹣1”型、“1﹣3﹣2”型、“2﹣2﹣2”型、“3﹣3”型,即可找出相对面点数的和都是7的正方体展开图。
【解答】解:
(答案不唯一)。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,掌握规律是解答本题的关键。
七.应用题(共5小题)
21.(2024 博兴县)等积变形。
如图,把大、小两种玻璃球,放入装有同样多水的直径为6cm的圆往体容器中。
(1)求大球的体积;
(2)求小球的体积;
(3)求图4中水的高度。
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】(1)56.52立方厘米;(2)14.13立方厘米;(3)6.5厘米。
【分析】(1)根据用排水法测量实物体积的方法,大球的体积等于圆柱内水上升的体积,根据圆柱的体积公式V=πr2h,解答即可。
(2)根据用排水法测量实物体积的方法,大球的体积等于圆柱内水上升的体积,根据圆柱的体积公式V=πr2h,求出4个小球的体积,除以4,解答即可。
(3)根据用排水法测量实物体积的方法,用1个大球和1个小球的体积和除以圆柱的底面积,求出水的高度,解答即可。
【解答】解:圆柱的半径是6÷2=3(厘米)
(1)3.14×32×(6﹣4)
=28.26×2
=56.52(立方厘米)
答:大球的体积是56.52立方厘米。
(2)3.14×32×(6﹣4)÷4
=28.26×2÷4
=14.13(立方厘米)
答:小球的体积是14.13立方厘米。
(3)(56.52+14.13)÷(3.14×32)+4
=70.65÷28.26+4
=2.5+4
=6.5(厘米)
答:图4中水的高度是6.5厘米。
【点评】本题考查了用排水法测量实物体积的方法,结合圆柱的体积公式解答即可。
22.(2024春 垫江县期末)在一个长6dm,宽4dm,高5dm的长方体玻璃水缸中有一个西瓜,现往水缸中注入一定的水量,使其完全淹没西瓜,量得水位高3.4dm。已知西瓜的体积是4.8dm3,如果把西瓜从玻璃水缸中取出,缸中的水位高应是多少dm?
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】3.2分米。
【分析】根据用排水法测量实物体积的方法,西瓜的体积等于长方体玻璃水缸中水下降的体积,结合长方体的体积公式:V=abh,先求出把西瓜从玻璃水缸中取出后下降的高度,然后用3.4分米减去下降的高度,解答即可。
【解答】解:4.8÷(6×4)
=4.8÷24
=0.2(分米)
3.4﹣0.2=3.2(分米)
答:缸中的水位高应是3.2分米。
【点评】本题考查了用排水法测量实物体积的方法,结合题意分析解答即可。
23.(2024春 鼓楼区期末)一小包纸巾的长、宽、高如图所示(单位:cm),用透明的塑料纸将这样的10包纸巾按图中样式包起来(接头处忽略不计),需要多大面积的塑料纸?
【考点】长方体和正方体的表面积.
【专题】应用意识.
【答案】见试题解答内容
【分析】题干观察图形可知,把这样10包纸巾拼成的大长方体的长是(3×10)厘米,宽是5厘米,高是7厘米,根据长方体的表面积公式:S(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:3×10=30(厘米)
(30×5+30×7+5×7)×2
=(150+210+35)×2
=395×2
=790(平方厘米)
答:需要790平方厘米的塑料纸。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
24.(2024春 历城区期末)某款长方体礼盒,经测量发现:它的长、宽、高都是质数,且前面和上面的面积之和是209cm2,你能求出这个礼盒的体积是多少立方厘米吗?
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】374立方厘米。
【分析】前面和上面的面积之和是209平方厘米,即长×宽+长×高=209,且长、宽、高都是质数,据此可以求出长、宽、高,然后根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:长×宽+长×高=209
长×(宽+高)=209
209=11×19
要么宽+高=11,要么宽+高=19
11=2+9=3+8=4+7=5+6,这样都有一个数是合数,不符合题意;
19=2+17=3+16=5+14=7+12=11+8=13+6,只有2和17都是质数。
所以这个长方体的长、宽、高分别11厘米,2厘米,17厘米。
11×2×17
=22×17
=374(立方厘米)
答:这个长方体的体积是374立方厘米。
【点评】此题考查的目的是理解掌握质数的意义及应用,长方体的体积公式及应用,关键是求出长方体的长、宽、高。
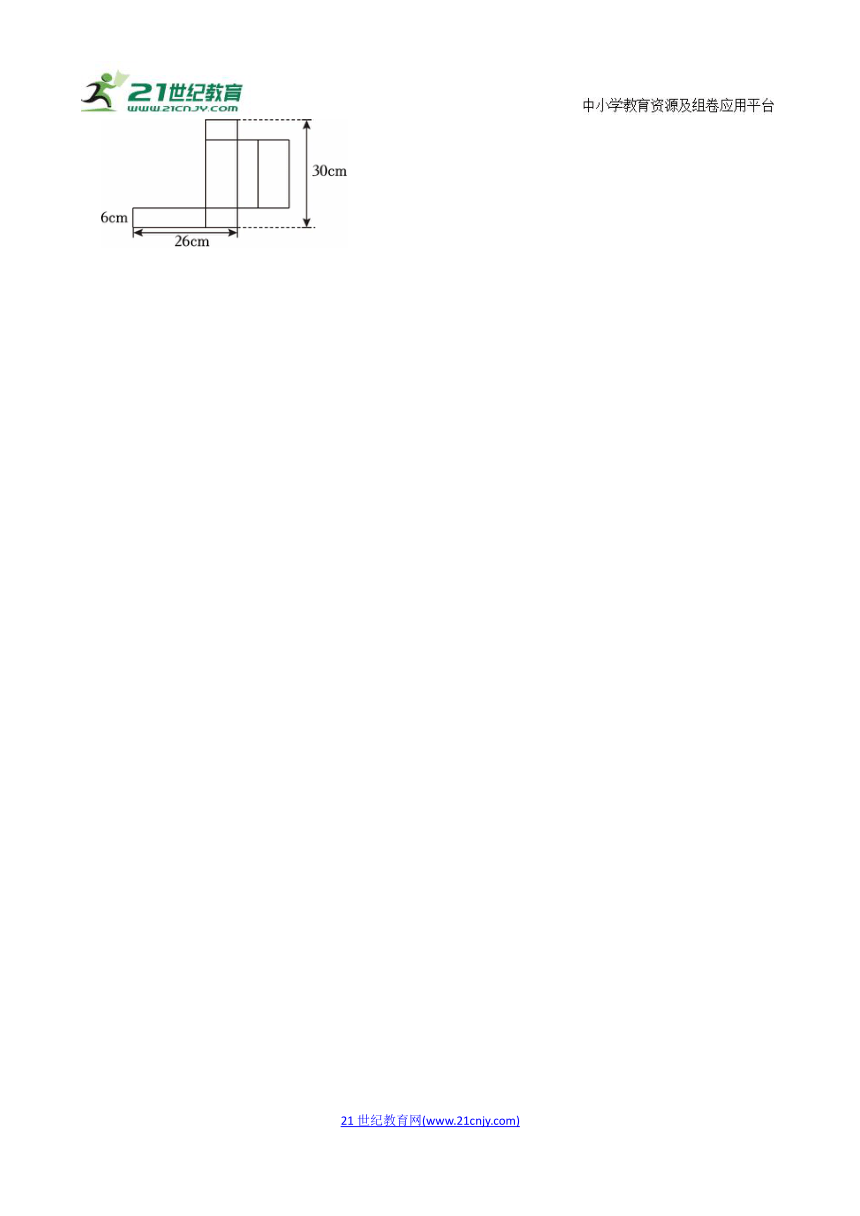
25.(2024春 新都区期末)一个长方体礼品纸盒展开后它的平面图如图,这个长方体礼品盒的表面积是多少平方厘米?
【考点】长方体和正方体的表面积.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】由展开图得出:长方体的长是30﹣6﹣6=18(厘米),宽是26﹣18=8(厘米),高是6厘米,根据长方体表面积=(长×宽+长×高+宽×高)×2,代数计算即可。
【解答】解:长是30﹣6﹣6=18(厘米)
宽是26﹣18=8(厘米)
高是6厘米
(18×8+8×6+18×6)×2
=(144+48+108)×2
=300×2
=600(平方厘米)
答:这个长方体礼品盒的表面积是600平方厘米。
【点评】解决本题的关键是根据长方体展开图得出长方体的长、宽、高,再根据长方体表面积公式计算。
21世纪教育网(www.21cnjy.com)
