24.2.4 圆的确定 教学设计 (表格式)沪科版数学九年级下册
文档属性
| 名称 | 24.2.4 圆的确定 教学设计 (表格式)沪科版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 255.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 14:43:02 | ||
图片预览

文档简介
沪科版九年级下册数 24.2.4圆的确定 教学设计
课题 24.2.4圆的确定 单元 第24单元 学科 数学 年级 九
教材分析 前面学习了圆的弦、弧、弦心距等概念,以及垂径定理,在圆的基本概念基础上,本节内容主要探究不在一条直线的三个点,可以确定一个圆,另外,学习了反证法证明命题的步骤。
核心素养分析 本节探究不在一条直线的三个点,可以确定一个圆,另外,学习了反证法证明命题的步骤,培养了学生几何直观的素养,以及推理的能力。
学习 目标 1.掌握经过一个点、2个点可以画圆,经过不共线的三点可以确定唯一的圆; 2.理解外接圆、外心的概念,会作出三角形的外接圆; 3.理解反证法证明的步骤。
重点 掌握经过一个点、2个点可以画圆,经过不共线的三点可以确定唯一的圆。
难点 理解外接圆、外心的概念,会作出三角形的外接圆。 理解反证法证明的步骤。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 圆心角、弦、弧、弦心距之间的关系是什么? 在同圆或等圆中,两个圆心角、弦、弧、弦心距之间,有一组量相等,其余各组量都相等。 回顾上节的内容,以培养学生温顾知识,大胆发言的良好习惯。 回顾上节知识,导入本节新课,不过三点确定一个圆。
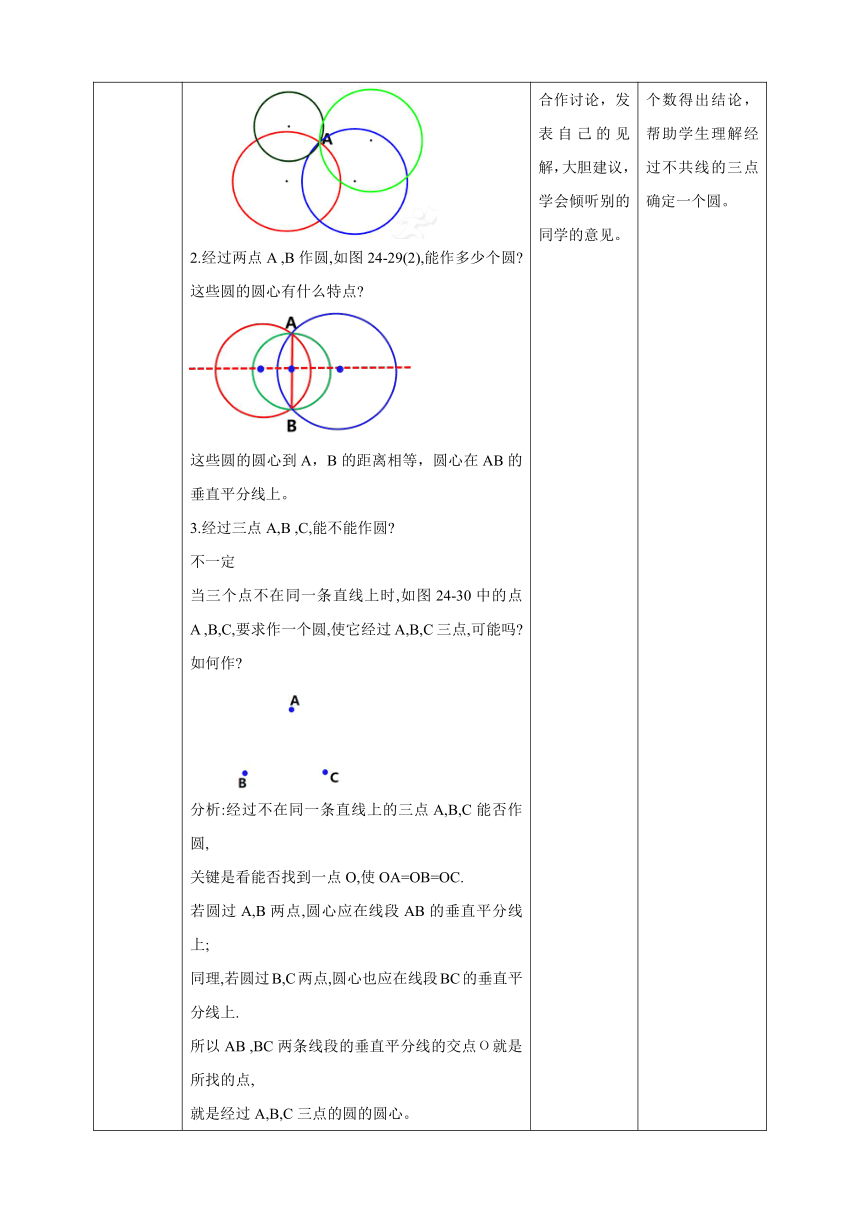
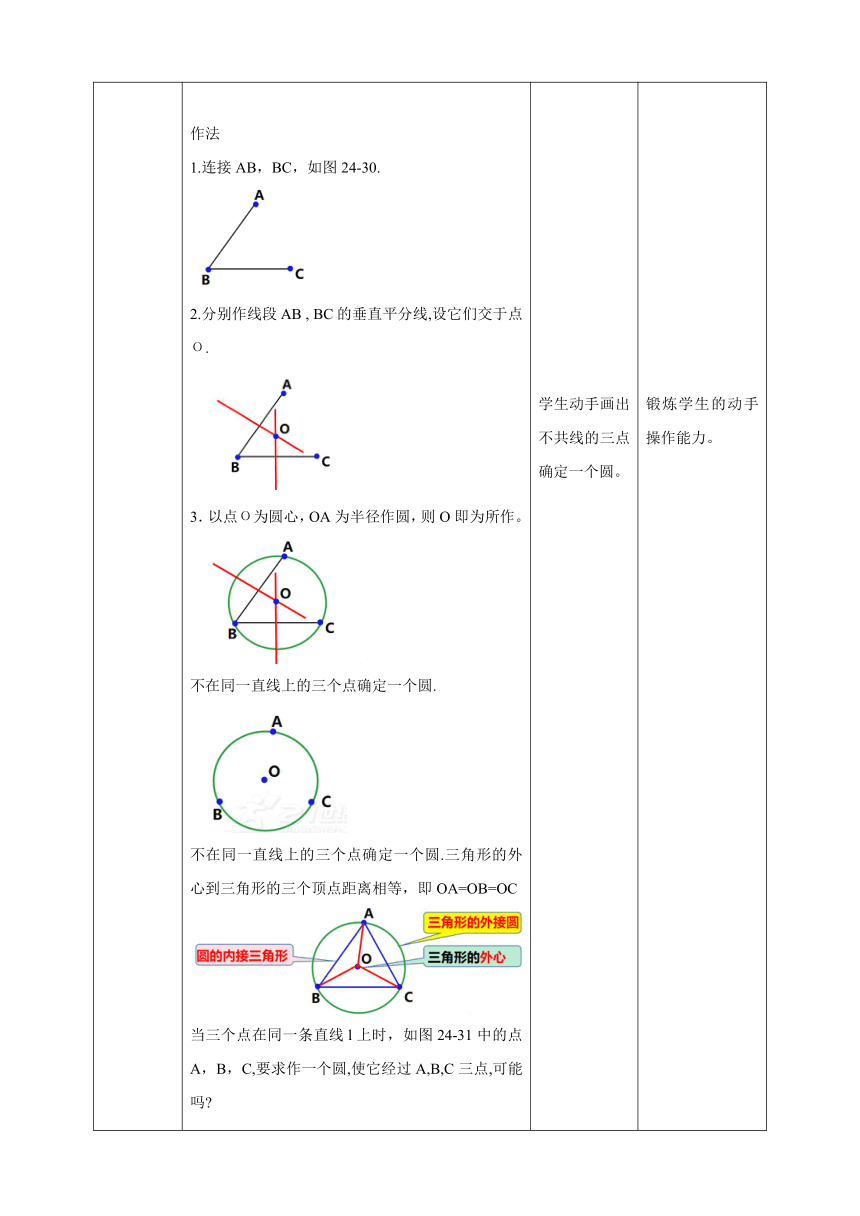
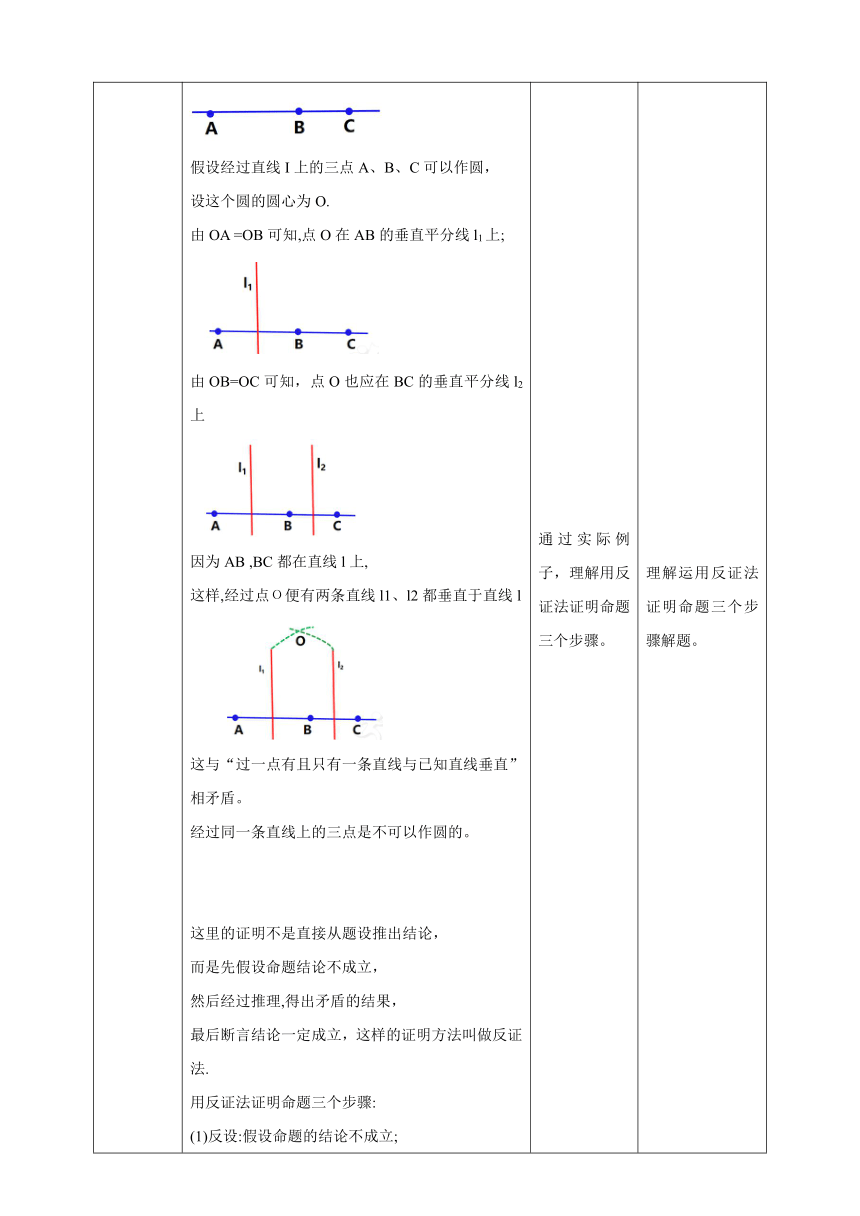
讲授新课 经过一点可以作无数条直线。 经过两点有且仅有1条直线。 那么确定一个圆需要几个已知点呢 思考 1、经过一点A作圆,如图24-29(1),能作多少个圆 2.经过两点A ,B作圆,如图24-29(2),能作多少个圆 这些圆的圆心有什么特点 这些圆的圆心到A,B的距离相等,圆心在AB的垂直平分线上。 3.经过三点A,B ,C,能不能作圆 不一定 当三个点不在同一条直线上时,如图24-30中的点A ,B,C,要求作一个圆,使它经过A,B,C三点,可能吗 如何作 分析:经过不在同一条直线上的三点A,B,C能否作圆, 关键是看能否找到一点O,使OA=OB=OC. 若圆过A,B两点,圆心应在线段AB的垂直平分线上; 同理,若圆过B,C两点,圆心也应在线段BC的垂直平分线上. 所以AB ,BC两条线段的垂直平分线的交点О就是所找的点, 就是经过A,B,C三点的圆的圆心。 作法 1.连接AB,BC,如图24-30. 2.分别作线段AB , BC的垂直平分线,设它们交于点О. 3.以点О为圆心,OA为半径作圆,则O即为所作。 不在同一直线上的三个点确定一个圆. 不在同一直线上的三个点确定一个圆.三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC 当三个点在同一条直线l上时,如图24-31中的点A,B,C,要求作一个圆,使它经过A,B,C三点,可能吗 假设经过直线I上的三点A、B、C可以作圆, 设这个圆的圆心为O. 由OA =OB可知,点O在AB的垂直平分线l1上; 由OB=OC可知,点O也应在BC的垂直平分线l2上 因为AB ,BC都在直线l上, 这样,经过点О便有两条直线l1、l2都垂直于直线l 这与“过一点有且只有一条直线与已知直线垂直”相矛盾。 经过同一条直线上的三点是不可以作圆的。 这里的证明不是直接从题设推出结论, 而是先假设命题结论不成立, 然后经过推理,得出矛盾的结果, 最后断言结论一定成立,这样的证明方法叫做反证法. 用反证法证明命题三个步骤: (1)反设:假设命题的结论不成立; (2)推理:从(1)中的“反设”出发,逐步推理直至出现与已知条件、定义、基本事实、定理等中任一个相矛盾的结果; (3)结论:由矛盾的结果判定(1)中的“反设”不成立,从而肯定命题的结论成立. 已知:如图24-32,直线AB//直线CD,直线EF分别交AB,CD于点O1,O2. 求证:∠EO1B=∠EO2D. 解:证明假设∠EO1B≠∠EO2D, 过点O1作直线A'B', 使∠EO1B'=∠EO2D. 根据”同位角相等,两直线平行”, 得A'B'// CD. 这样,过点O1就有两条直线AB, A'B'平行于直线CD, 这与“过直线外一点有且只有一条直线 与这条直线平行”相矛盾, 即∠EO1B≠∠EO2D的假设不成立, 所以∠EO1B=∠EO2D. 从一个和2个点确定直线个数,引入到一个点确定圆的个数,学生独立思考、小组合作讨论,发表自己的见解,大胆建议,学会倾听别的同学的意见。 学生动手画出不共线的三点确定一个圆。 通过实际例子,理解用反证法证明命题三个步骤。 学生思考。 通过一个点或者2个点确定圆的个数得出结论,帮助学生理解经过不共线的三点确定一个圆。 锻炼学生的动手操作能力。 理解运用反证法证明命题三个步骤解题。 通过实例,掌握理解反证法,会运用反证法解决问题。
课堂练习 1、三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形外接圆的半径为_____ 解:方程x2-12x+35=0, 分解因式得:(x-5)(x-7)=0, 可得x-5=0或x-7=0, 解得:x=5或x=7, ∵三角形第三边的长是方程x2-12x+35=0的根, ∴第三边的长为5或7, 当第三边长为5时, ∵3+4>5; 当第三边长为7时,3+4=7,不能构成三角形,舍去, ∴第三边为5, ∵32+42=52, ∴三角形是直角三角形,此三角形的外接圆的直径为最大边5,则此三角形的外接圆半径为2.5, 故答案为:2.5。 2.如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,点O为坐标原点(网格纸中每个小正方形的边长为1). (1)该图中弧所在圆的圆心D的坐标为___(2,-1) __. (2)根据(1)中的条件填空; ①⊙D的半径=_____(结果保留根号); ②点(-3,0)在⊙D_外___.(填“上”、“内”或“外”); ③求出∠ADC的度数. 连接AD,CD,AC, 由平面直角坐标系得A(0,3),C(6,1), ∴ ∵圆D的半径为 , ∴AD=CD= , ∴AD2+CD2=AC2, ∴△ACD是直角三角形, ∠ADC=90°. 3.如图,已知⊙O是△ABC的外接圆,圆心O在△ABC的外部,AB=AC=4,BC=,求⊙O的半径. 解:如图,连接AO,交BC于点D,连接BO ∵AB=AC, ∴AB=AC 又AO是半径, ∴AO⊥BC,BD=CD ∵BC= , ∴BD= ∴在Rt△ABD中, ∠ADB=90°, ∴BD2+AD2=AB2 又∵AB=4, ∴AD=2 设半径为r. 在Rt△BDO中, ∵BD2+DO2=BO2 ∴()2+(r-2)2=r2 ∴r=4 ∴⊙O的半径为4. 学生做本节练习,互相补充,教师订正答案,做最后总结。 练习是为了巩固学生所学的新知,教会学生用外接圆的知识解决问题,同时培养学生建模的能力。
课堂小结 不在同一直线上的三个点确定一个圆. 三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC 用反证法证明命题三个步骤: (1)反设:假设命题的结论不成立; (2)推理:从(1)中的“反设”出发,逐步推理直至出现与已知条件、定义、基本事实、定理等中任一个相矛盾的结果; (3)结论:由矛盾的结果判定(1)中的“反设”不成立,从而肯定命题的结论成立. 学生先发言总结本节圆的确定,用反证法证明命题三个步骤,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:24.2.4 圆的确定 1.不共线的三点确定一个圆 2.反证法
课题 24.2.4圆的确定 单元 第24单元 学科 数学 年级 九
教材分析 前面学习了圆的弦、弧、弦心距等概念,以及垂径定理,在圆的基本概念基础上,本节内容主要探究不在一条直线的三个点,可以确定一个圆,另外,学习了反证法证明命题的步骤。
核心素养分析 本节探究不在一条直线的三个点,可以确定一个圆,另外,学习了反证法证明命题的步骤,培养了学生几何直观的素养,以及推理的能力。
学习 目标 1.掌握经过一个点、2个点可以画圆,经过不共线的三点可以确定唯一的圆; 2.理解外接圆、外心的概念,会作出三角形的外接圆; 3.理解反证法证明的步骤。
重点 掌握经过一个点、2个点可以画圆,经过不共线的三点可以确定唯一的圆。
难点 理解外接圆、外心的概念,会作出三角形的外接圆。 理解反证法证明的步骤。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 圆心角、弦、弧、弦心距之间的关系是什么? 在同圆或等圆中,两个圆心角、弦、弧、弦心距之间,有一组量相等,其余各组量都相等。 回顾上节的内容,以培养学生温顾知识,大胆发言的良好习惯。 回顾上节知识,导入本节新课,不过三点确定一个圆。
讲授新课 经过一点可以作无数条直线。 经过两点有且仅有1条直线。 那么确定一个圆需要几个已知点呢 思考 1、经过一点A作圆,如图24-29(1),能作多少个圆 2.经过两点A ,B作圆,如图24-29(2),能作多少个圆 这些圆的圆心有什么特点 这些圆的圆心到A,B的距离相等,圆心在AB的垂直平分线上。 3.经过三点A,B ,C,能不能作圆 不一定 当三个点不在同一条直线上时,如图24-30中的点A ,B,C,要求作一个圆,使它经过A,B,C三点,可能吗 如何作 分析:经过不在同一条直线上的三点A,B,C能否作圆, 关键是看能否找到一点O,使OA=OB=OC. 若圆过A,B两点,圆心应在线段AB的垂直平分线上; 同理,若圆过B,C两点,圆心也应在线段BC的垂直平分线上. 所以AB ,BC两条线段的垂直平分线的交点О就是所找的点, 就是经过A,B,C三点的圆的圆心。 作法 1.连接AB,BC,如图24-30. 2.分别作线段AB , BC的垂直平分线,设它们交于点О. 3.以点О为圆心,OA为半径作圆,则O即为所作。 不在同一直线上的三个点确定一个圆. 不在同一直线上的三个点确定一个圆.三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC 当三个点在同一条直线l上时,如图24-31中的点A,B,C,要求作一个圆,使它经过A,B,C三点,可能吗 假设经过直线I上的三点A、B、C可以作圆, 设这个圆的圆心为O. 由OA =OB可知,点O在AB的垂直平分线l1上; 由OB=OC可知,点O也应在BC的垂直平分线l2上 因为AB ,BC都在直线l上, 这样,经过点О便有两条直线l1、l2都垂直于直线l 这与“过一点有且只有一条直线与已知直线垂直”相矛盾。 经过同一条直线上的三点是不可以作圆的。 这里的证明不是直接从题设推出结论, 而是先假设命题结论不成立, 然后经过推理,得出矛盾的结果, 最后断言结论一定成立,这样的证明方法叫做反证法. 用反证法证明命题三个步骤: (1)反设:假设命题的结论不成立; (2)推理:从(1)中的“反设”出发,逐步推理直至出现与已知条件、定义、基本事实、定理等中任一个相矛盾的结果; (3)结论:由矛盾的结果判定(1)中的“反设”不成立,从而肯定命题的结论成立. 已知:如图24-32,直线AB//直线CD,直线EF分别交AB,CD于点O1,O2. 求证:∠EO1B=∠EO2D. 解:证明假设∠EO1B≠∠EO2D, 过点O1作直线A'B', 使∠EO1B'=∠EO2D. 根据”同位角相等,两直线平行”, 得A'B'// CD. 这样,过点O1就有两条直线AB, A'B'平行于直线CD, 这与“过直线外一点有且只有一条直线 与这条直线平行”相矛盾, 即∠EO1B≠∠EO2D的假设不成立, 所以∠EO1B=∠EO2D. 从一个和2个点确定直线个数,引入到一个点确定圆的个数,学生独立思考、小组合作讨论,发表自己的见解,大胆建议,学会倾听别的同学的意见。 学生动手画出不共线的三点确定一个圆。 通过实际例子,理解用反证法证明命题三个步骤。 学生思考。 通过一个点或者2个点确定圆的个数得出结论,帮助学生理解经过不共线的三点确定一个圆。 锻炼学生的动手操作能力。 理解运用反证法证明命题三个步骤解题。 通过实例,掌握理解反证法,会运用反证法解决问题。
课堂练习 1、三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形外接圆的半径为_____ 解:方程x2-12x+35=0, 分解因式得:(x-5)(x-7)=0, 可得x-5=0或x-7=0, 解得:x=5或x=7, ∵三角形第三边的长是方程x2-12x+35=0的根, ∴第三边的长为5或7, 当第三边长为5时, ∵3+4>5; 当第三边长为7时,3+4=7,不能构成三角形,舍去, ∴第三边为5, ∵32+42=52, ∴三角形是直角三角形,此三角形的外接圆的直径为最大边5,则此三角形的外接圆半径为2.5, 故答案为:2.5。 2.如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,点O为坐标原点(网格纸中每个小正方形的边长为1). (1)该图中弧所在圆的圆心D的坐标为___(2,-1) __. (2)根据(1)中的条件填空; ①⊙D的半径=_____(结果保留根号); ②点(-3,0)在⊙D_外___.(填“上”、“内”或“外”); ③求出∠ADC的度数. 连接AD,CD,AC, 由平面直角坐标系得A(0,3),C(6,1), ∴ ∵圆D的半径为 , ∴AD=CD= , ∴AD2+CD2=AC2, ∴△ACD是直角三角形, ∠ADC=90°. 3.如图,已知⊙O是△ABC的外接圆,圆心O在△ABC的外部,AB=AC=4,BC=,求⊙O的半径. 解:如图,连接AO,交BC于点D,连接BO ∵AB=AC, ∴AB=AC 又AO是半径, ∴AO⊥BC,BD=CD ∵BC= , ∴BD= ∴在Rt△ABD中, ∠ADB=90°, ∴BD2+AD2=AB2 又∵AB=4, ∴AD=2 设半径为r. 在Rt△BDO中, ∵BD2+DO2=BO2 ∴()2+(r-2)2=r2 ∴r=4 ∴⊙O的半径为4. 学生做本节练习,互相补充,教师订正答案,做最后总结。 练习是为了巩固学生所学的新知,教会学生用外接圆的知识解决问题,同时培养学生建模的能力。
课堂小结 不在同一直线上的三个点确定一个圆. 三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC 用反证法证明命题三个步骤: (1)反设:假设命题的结论不成立; (2)推理:从(1)中的“反设”出发,逐步推理直至出现与已知条件、定义、基本事实、定理等中任一个相矛盾的结果; (3)结论:由矛盾的结果判定(1)中的“反设”不成立,从而肯定命题的结论成立. 学生先发言总结本节圆的确定,用反证法证明命题三个步骤,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:24.2.4 圆的确定 1.不共线的三点确定一个圆 2.反证法
