19.2.1 菱形的性质(第一课时) 课件(共16张PPT) 2024-2025学年华东师大版八年级数学下册
文档属性
| 名称 | 19.2.1 菱形的性质(第一课时) 课件(共16张PPT) 2024-2025学年华东师大版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 12:09:57 | ||
图片预览





文档简介
(共16张PPT)
19.2.1 菱形的性质
八下 数学
华师版
学习目标
1.通过观察动画演示,经历图形观察到知识归纳的过程,总结菱形的定义及其与平行四边形的关系。
2.通过折纸活动,经历“动手--观察--猜想--证明”的活动过程,探索并验证菱形的性质。
新课引入
是平行四边形吗?
禁止出境文物之越王勾践剑
出土于1965年,历经 两千四百余年,仍然纹饰清晰精美,被誉 为"天下第一剑",是我国的国宝。
几何画板演示
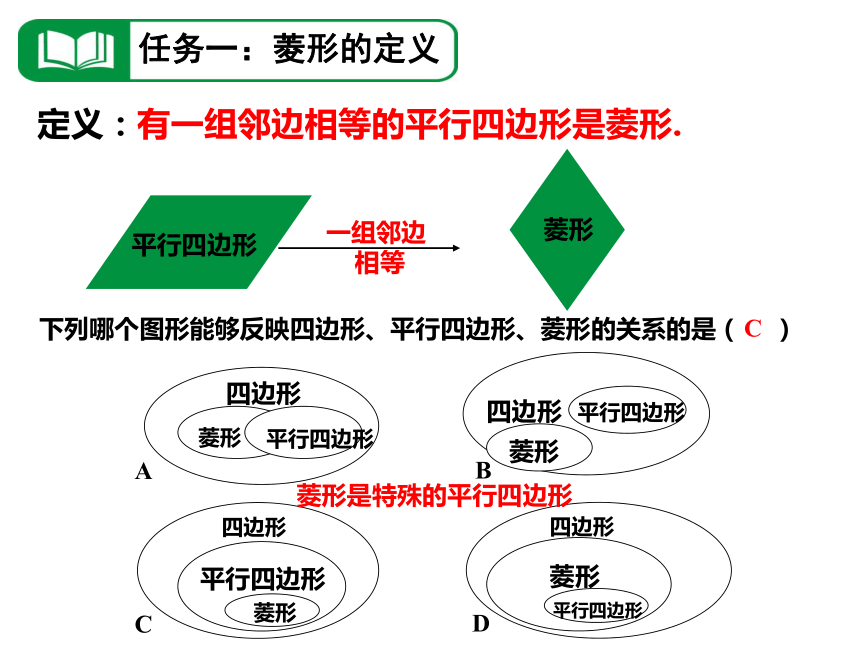
任务一:菱形的定义
平行四边形
菱形
一组邻边
相等
定义:有一组邻边相等的平行四边形是菱形.
下列哪个图形能够反映四边形、平行四边形、菱形的关系的是( )
D
C
四边形
菱形
平行四边形
四边形
菱形
平行四边形
四边形
菱形
平行四边形
平行四边形
菱形
四边形
A
B
C
菱形是特殊的平行四边形
新课引入
任务二:探究菱形的性质
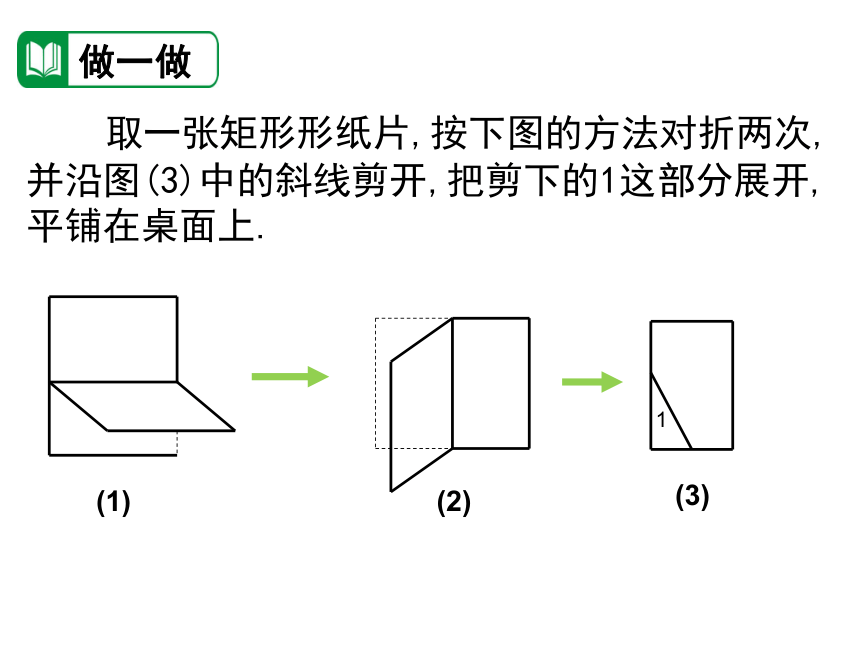
做一做
取一张矩形形纸片,按下图的方法对折两次,并沿图(3)中的斜线剪开,把剪下的1这部分展开,平铺在桌面上.
(1)
(2)
(3)
1
任务二:探究菱形的性质
图形 边 角 对角线 对称性
菱形
特殊的平行四边形
对边平行且相等;
四边都相等
对角相等
邻角互补
对角线垂直
且互相平分
中心对称;
轴对称
证明:由定义,菱形的邻边相等,
设AD=DC,AB=CB
∵四边形ABCD是平行四边形
∴AD=CB,AB=DC
∴AD=CB=AB=DC
即菱形ABCD四条边都相等.
A
B
C
D
求证
菱形的四条边都相等.
已知:
求证:
如图,四边形ABCD是菱形
AB=BC=CD=DA
∵四边形ABCD是菱形
菱形的性质定理1
菱形的四条边都相等.
性质定理
A
B
C
D
几何语言:
∴AB=BC=CD=DA
求证
菱形的对角线互相垂直
已知:
求证:
如图,四边形ABCD是菱形
AC⊥BD
A
B
C
O
D
证明:∵四边形ABCD是菱形,
∴AD=DC,AO=OC,
∴△ADC是等腰三角形,且DO是△ADC底边的中线
根据等腰三角形中“三线合一”,
∴DO也是△ADC底边的高
∴DO⊥AC,即AC⊥BD
∵四边形ABCD是菱形
菱形的性质定理2
菱形的对角线互相垂直
性质定理
几何语言:
∴AC⊥BD
A
B
C
O
D
例1 如图,在菱形ABCD中,∠BAD=2∠B.试求出∠B的大小,并说明△ABC是等边三角形.
解:在菱形ABCD中,
∵∠B+∠BAD=180°,∠BAD=2∠B,
∴∠B=60°.
在菱形ABCD中,
∵AB=BC(菱形的四条边都相等),∠B=60°,
∴△ABC是等边三角形.
针对训练
1.如图,在菱形ABCD中,AB=5,OA=4.求菱形的周长与两条对角线的长度.
解:在菱形ABCD中,
有AB=BC=CD=DA,AC与BD互相垂直且平分.
∴菱形周长为4×5=20
∵OA=4
∴AC=8
Rt△ABO中,由勾股定理可知BO=3,∴BD=6
课堂小结
菱形的性质
菱形的性质定理 1 菱形的四条边都相等.
菱形的性质定理 2 菱形的对角线互相垂直.
今天你学到了哪些知识和方法?
作业布置
完成ST-book课后作业A组
19.2.1 菱形的性质
八下 数学
华师版
学习目标
1.通过观察动画演示,经历图形观察到知识归纳的过程,总结菱形的定义及其与平行四边形的关系。
2.通过折纸活动,经历“动手--观察--猜想--证明”的活动过程,探索并验证菱形的性质。
新课引入
是平行四边形吗?
禁止出境文物之越王勾践剑
出土于1965年,历经 两千四百余年,仍然纹饰清晰精美,被誉 为"天下第一剑",是我国的国宝。
几何画板演示
任务一:菱形的定义
平行四边形
菱形
一组邻边
相等
定义:有一组邻边相等的平行四边形是菱形.
下列哪个图形能够反映四边形、平行四边形、菱形的关系的是( )
D
C
四边形
菱形
平行四边形
四边形
菱形
平行四边形
四边形
菱形
平行四边形
平行四边形
菱形
四边形
A
B
C
菱形是特殊的平行四边形
新课引入
任务二:探究菱形的性质
做一做
取一张矩形形纸片,按下图的方法对折两次,并沿图(3)中的斜线剪开,把剪下的1这部分展开,平铺在桌面上.
(1)
(2)
(3)
1
任务二:探究菱形的性质
图形 边 角 对角线 对称性
菱形
特殊的平行四边形
对边平行且相等;
四边都相等
对角相等
邻角互补
对角线垂直
且互相平分
中心对称;
轴对称
证明:由定义,菱形的邻边相等,
设AD=DC,AB=CB
∵四边形ABCD是平行四边形
∴AD=CB,AB=DC
∴AD=CB=AB=DC
即菱形ABCD四条边都相等.
A
B
C
D
求证
菱形的四条边都相等.
已知:
求证:
如图,四边形ABCD是菱形
AB=BC=CD=DA
∵四边形ABCD是菱形
菱形的性质定理1
菱形的四条边都相等.
性质定理
A
B
C
D
几何语言:
∴AB=BC=CD=DA
求证
菱形的对角线互相垂直
已知:
求证:
如图,四边形ABCD是菱形
AC⊥BD
A
B
C
O
D
证明:∵四边形ABCD是菱形,
∴AD=DC,AO=OC,
∴△ADC是等腰三角形,且DO是△ADC底边的中线
根据等腰三角形中“三线合一”,
∴DO也是△ADC底边的高
∴DO⊥AC,即AC⊥BD
∵四边形ABCD是菱形
菱形的性质定理2
菱形的对角线互相垂直
性质定理
几何语言:
∴AC⊥BD
A
B
C
O
D
例1 如图,在菱形ABCD中,∠BAD=2∠B.试求出∠B的大小,并说明△ABC是等边三角形.
解:在菱形ABCD中,
∵∠B+∠BAD=180°,∠BAD=2∠B,
∴∠B=60°.
在菱形ABCD中,
∵AB=BC(菱形的四条边都相等),∠B=60°,
∴△ABC是等边三角形.
针对训练
1.如图,在菱形ABCD中,AB=5,OA=4.求菱形的周长与两条对角线的长度.
解:在菱形ABCD中,
有AB=BC=CD=DA,AC与BD互相垂直且平分.
∴菱形周长为4×5=20
∵OA=4
∴AC=8
Rt△ABO中,由勾股定理可知BO=3,∴BD=6
课堂小结
菱形的性质
菱形的性质定理 1 菱形的四条边都相等.
菱形的性质定理 2 菱形的对角线互相垂直.
今天你学到了哪些知识和方法?
作业布置
完成ST-book课后作业A组
