苏科版八年级数学下册 11.2反比例函数的图像与性质(含解析)
文档属性
| 名称 | 苏科版八年级数学下册 11.2反比例函数的图像与性质(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 796.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 12:20:22 | ||
图片预览



文档简介
11.2反比例函数的图像与性质
【类型一:反比例函数的概念】
1.下列函数:①y=2x,②,③xy=﹣2,④,⑤.其中反比例函数有( )
A.0个 B.1个 C.2个 D.3个
2.下面几组相关联的量中,不成反比例关系的是( )
A.车间计划加工800个零件,加工时间与每天加工的零件个数
B.社团共有50名学生,按各组人数相等的要求分组,组数与每组人数
C.圆柱体的体积为6m3,圆柱的底面积与高
D.计划用100元购买苹果和香蕉两种水果,购买苹果的金额与购买香蕉的金额
【类型二:用待定系数法求反比例函数解析式】
3.在面积为定值的一组矩形中,当矩形的一边长为7.5cm时,它的另一边长为8cm.
(1)设矩形相邻的两边长分别为x(cm),y(cm),求y关于x的函数表达式.这个函数是反比例函数吗?如果是,指出比例系数.
(2)若其中一个矩形的一条边长为5cm,求这个矩形与之相邻的另一边长.
4.已知函数.
(1)若y是关于x的正比例函数,求m的值;
(2)若y是关于x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
5.已知y是z的反比例函数,z是x的正比例函数.
(1)当时,y=6.当x=6时,z=4.求y与x之间的函数关系式;
(2)证明y是x的反比例函数.
6.已知y=y1+y2,其中y1与x成正比例,y2与x2成反比例,且当x=2和x=3时,y的值都为19,求y与变量x的函数关系式.
【类型三:反比例函数的图像与性质】
7.矩形的面积为6,它的长y与宽x之间的关系用图象大致可表示为( )
A. B.
C. D.
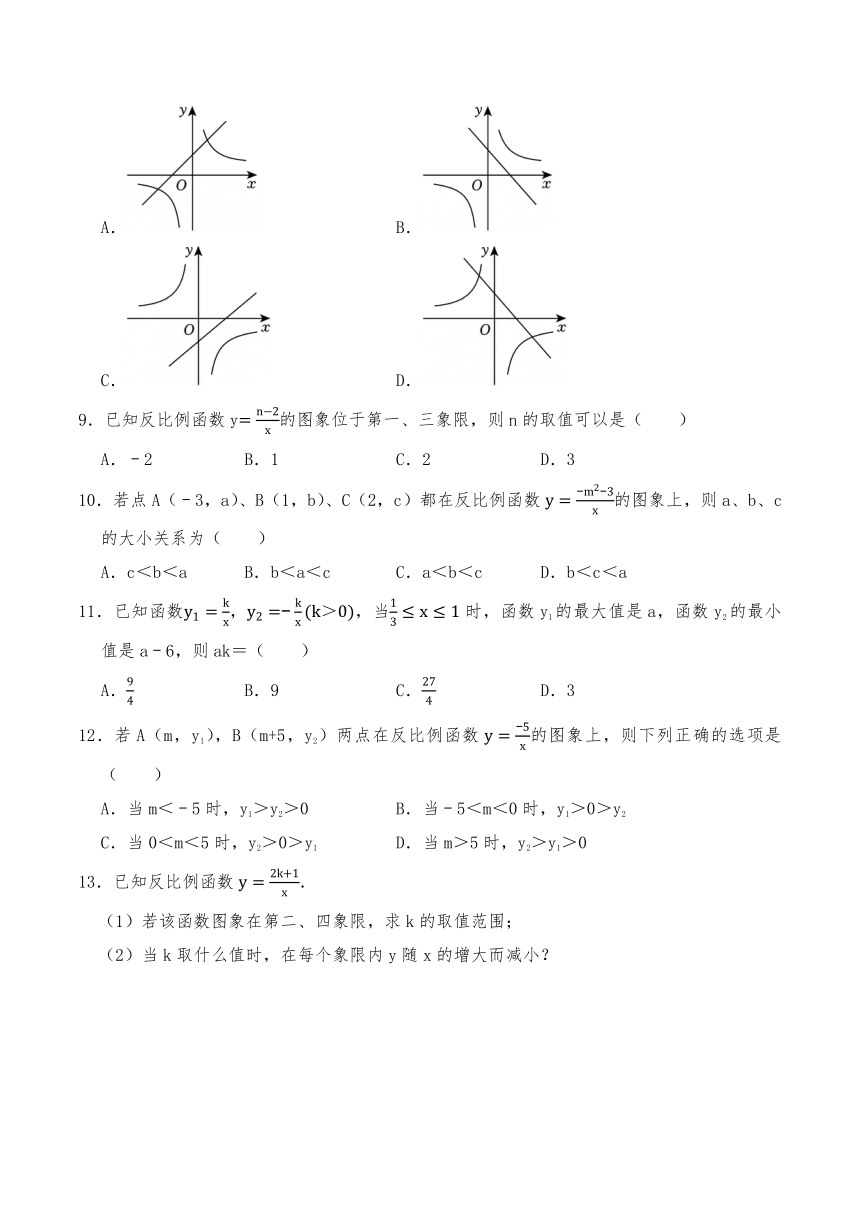
8.函数和y=kx﹣k(k≠0)在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
9.已知反比例函数y的图象位于第一、三象限,则n的取值可以是( )
A.﹣2 B.1 C.2 D.3
10.若点A(﹣3,a)、B(1,b)、C(2,c)都在反比例函数的图象上,则a、b、c的大小关系为( )
A.c<b<a B.b<a<c C.a<b<c D.b<c<a
11.已知函数,,当时,函数y1的最大值是a,函数y2的最小值是a﹣6,则ak=( )
A. B.9 C. D.3
12.若A(m,y1),B(m+5,y2)两点在反比例函数的图象上,则下列正确的选项是( )
A.当m<﹣5时,y1>y2>0 B.当﹣5<m<0时,y1>0>y2
C.当0<m<5时,y2>0>y1 D.当m>5时,y2>y1>0
13.已知反比例函数.
(1)若该函数图象在第二、四象限,求k的取值范围;
(2)当k取什么值时,在每个象限内y随x的增大而减小?
14.已知反比例函数的图象位于第二、四象限.
(1)求k的取值范围;
(2)若点A(﹣4,y1),B(﹣1,y2)是该反比例函数图象上的两点,试比较函数值y1,y2的大小.
【类型四:反比例函数与一次函数】
15.如图,一次函数y=kx+b的图象与反比例函数的图象交于A(﹣2,1),B(n,﹣2)两点.当一次函数的值大于反比例函数的值时,自变量x的取值范围是( )
A.﹣2<x<1 B.0<x<1
C.﹣2<x<0或x>1 D.x<﹣2或0<x<1
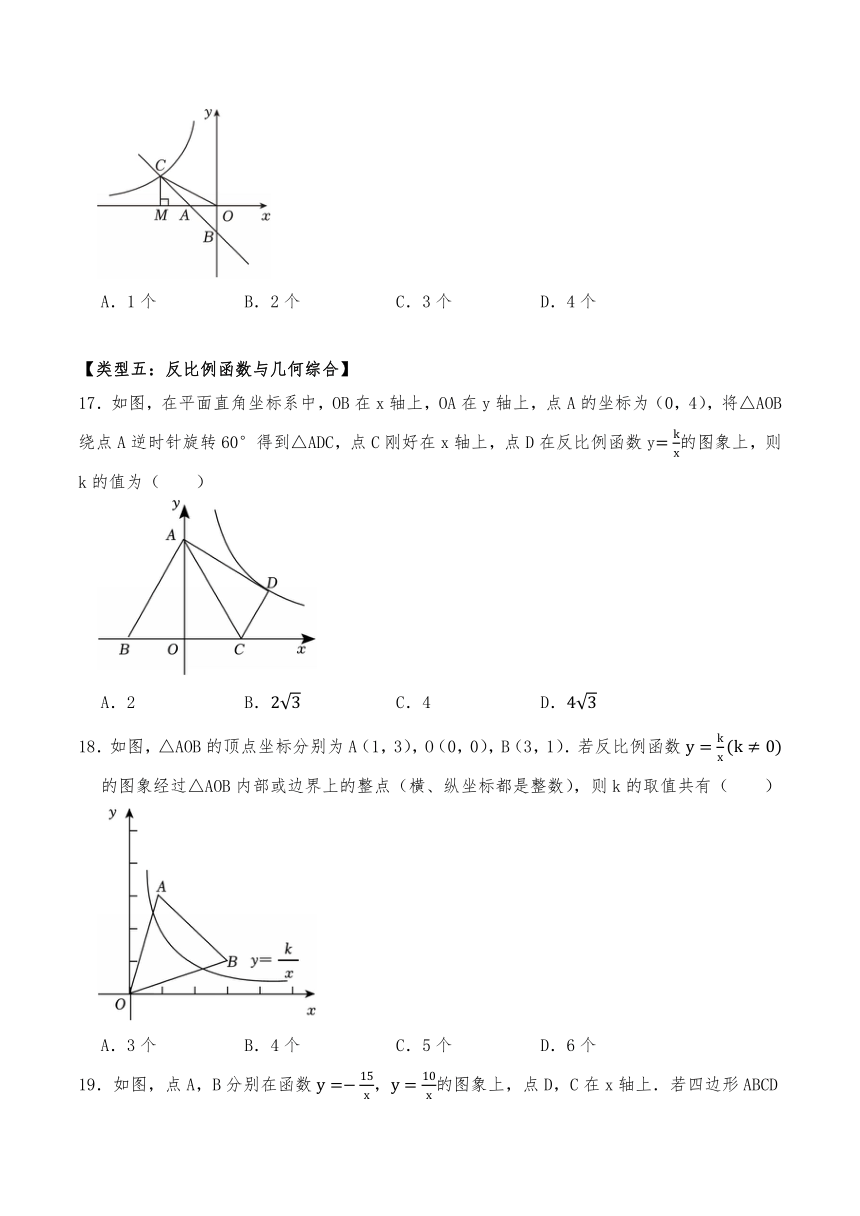
16.如图,在直角坐标系中,直线y1=﹣x﹣1与坐标轴交于A,B两点,与双曲线交于点C,连接OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( )
①S△CMO=1;
②当x<0时,y1随x的增大而减小,y2随x的增大而增大;
③方程只有一个解为x=﹣2;
④当x<﹣2,y1<y2.
A.1个 B.2个 C.3个 D.4个
【类型五:反比例函数与几何综合】
17.如图,在平面直角坐标系中,OB在x轴上,OA在y轴上,点A的坐标为(0,4),将△AOB绕点A逆时针旋转60°得到△ADC,点C刚好在x轴上,点D在反比例函数y的图象上,则k的值为( )
A.2 B. C.4 D.
18.如图,△AOB的顶点坐标分别为A(1,3),O(0,0),B(3,1).若反比例函数的图象经过△AOB内部或边界上的整点(横、纵坐标都是整数),则k的取值共有( )
A.3个 B.4个 C.5个 D.6个
19.如图,点A,B分别在函数,的图象上,点D,C在x轴上.若四边形ABCD为正方形.则点A的坐标是( )
A.(﹣2,5) B.(﹣2,4) C.(﹣3,5) D.(﹣3,4)
20.如图,在平面直角坐标系xOy中,反比例函数的图象和菱形ABCD都在第一象限内,,B∥x轴,且BD=4,点A的坐标为(3,5).
(1)若反比例函数(x>0)的图象经过点C,求此反比例函数的解析式;
(2)若将菱形ABCD向下平移m(m>0)个单位长度,使菱形ABCD的两个顶点的对应点同时落在反比例函数图象上,求m及此时k的值.
21.如图,一次函数y=kx+b与反比例函数的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式的解集 ;
(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
22.如图,一次函数y=mx+n(m≠0)的图象与反比例函数的图象交于点A(﹣2,a),B(b,﹣1),过点A作x轴的垂线,垂足为C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)在y轴上取一点P,使|PB|﹣|PA|取得最大值,求出此时点P的坐标.
23.如图,在平面直角坐标系中,直线l1:yx与反比例函数y的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是﹣4;
(1)求反比例函数的表达式;
(2)根据图象直接写出x的解集;
(3)将直线l1:yx沿y向上平移后的直线l2与反比例函数y在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
24.如图,在平面直角坐标系xOy中,直线y=mx+1与双曲线y(k>0)相交于点A,B,已知点B(a,﹣2),点C在x轴正半轴上,点D(2,﹣3),连接OA,OD,DC,AC,四边形AODC为菱形.
(1)反比例函数的表达式为 ;
(2)不等式mx+1的解集是 ;
(3)设P是y轴上一动点,且△OAP的面积等于菱形OACD的面积,则点P的坐标为 .
25.如图,四边形ABCD为正方形,点A在x轴上,点B在y轴上,且OA=2,OB=4,反比例函数y(k≠0)在第一象限的图象经过正方形的顶点D.
(1)求反比例函数的关系式;
(2)将正方形ABCD沿x轴负方向平移多少个单位长度时,点C恰好落在反比例函数的图形上.
26.如图,在平面直角坐标系xOy中,Rt△ABC的直角边AB在x轴上,∠ABC=90°.点A的坐标为(1,0),点C的坐标为(3,4),M是BC边的中点,函数y(x>0)的图象经过点M.
(1)求k的值;
(2)将△ABC绕某个点旋转180°后得到△DEF(点A,B,C的对应点分别为点D,E,F),且EF在y轴上,点D在函数y(x>0)的图象上,求直线DF的表达式.
参考答案
【类型一:反比例函数的概念】
1.
【分析】根据反比例函数的定义即可作答.
【解答】解:①是正比例函数,不是反比例函数;
②是反比例函数;
③是反比例函数;
④y是x+1反比例函数;
⑤y﹣3是x反比例函数;
所以反比例函数有2个.
故选:C.
2.
【分析】根据反比例函数的定义逐一判断即可.
【解答】解:A、加工时间×每天加工的零件个数=800,则加工时间与每天加工的零件个数的乘积是定值,此选项正确,成反比例关系,不符合题意;
B、组数×每组人数=50,则组数与每组人数的乘积是定值,成反比例关系,此选项正确,不符合题意;
C、底面积×高=6,则底面积与高的乘积是定值,成反比例关系,此选项正确,不符合题意;
D、购买苹果的金额+购买香蕉的金额=100,则购买苹果的金额与购买香蕉的金额的和是定值,不成反比例关系,此选项错误,符合题意,
故选:D.
【类型二:用待定系数法求反比例函数解析式】
3.解:(1)设矩形的面积为S cm2,则S=7.5×8=60,
即xy=60,y,
即y关于x的函数解析式是y,这个函数是反比例函数,系数为60;
(2)当x=5时,y12,
故这个矩形与之相邻的另一边长为12.
4.解:(1)由y=(m2﹣2m)是正比例函数,得
m2﹣m﹣1=1且m2﹣2m≠0,
解得m=﹣1;
(2)由y=(m2﹣2m)是反比例函数,得
m2﹣m﹣1=﹣1且m2﹣2m≠0,
解得m=1.
故y与x的函数关系式y=﹣x﹣1.
5.(1)解:∵y是z的反比例函数,
∴设(a≠0),
∵当时,y=6,
∴a4,
∴①,
∵z是x的正比例函数,
∴设z=bx(b≠0),
又∵当x=6时,z=4,
∴,
∴②,
将②代入①,得:;
(2)证明:由(1)得:(a≠0),z=bx,
∴,
∴y是x的反比例函数.
6.解:∵y1与x成正比例,y2与x2成反比例,
∴设y1=ax(a≠0),y2(k≠0),
∴y=y1+y2=ax,
∵当x=2和x=3时,y的值都为19,
∴,
解得a=5,k=36,
所以y与变量x的函数关系式是.
【类型三:反比例函数的图像与性质】
7.
【分析】由题意y,(x>0),所以y是x的反比例函数,由此即可解决问题.
【解答】解:由题意y,(x>0),
所以y是x的反比例函数,图象在第一象限,
故选:D.
8.
【分析】根据题目中的函数解析式和反比例函数的性质、一次函数的性质,可以判断哪个选项中的图象符合题意.
【解答】解:当k<0时,反比例函数的图象位于第二、四象限,一次函数y=kx﹣k的图象经过一、二、四象限,故选项C不符合题意.选项D符合题意;
当k>0时,反比例函数的图象位于第一、三象限,一次函数y=kx﹣k的图象经过一、三、四象限,故选项A、B均不符合题意;
故选:D.
9.
【分析】直接利用当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小,进而得出n的取值范围,即可得出答案.
【解答】解:∵反比例函数y的图象位于第一、三象限,
∴n﹣2>0,
解得:n>2.
故n的取值可以是:3.
故选:D.
10.
【分析】先根据反比例函数中k<0判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
【解答】解:∵反比例函数常数k=﹣m2﹣3<0,
∴反比例函数图象分布在第二、四象限,在每个象限内,y随x的增大而增大,
∵A(﹣3,a)在第二象限,
∴a>0,
∵B(1,b)、C(2,c)在第四象限,
∴0>c>b,
∴b<c<a.
故选:D.
11.
【分析】根据题意可得函数经过第一、三象限,在每个象限内y1随x增大而减小,经过第二、四象限,在每个象限内y2随x增大而增大,则,解方程组即可得到答案.
【解答】解:由条件可知:函数经过第一、三象限,在每个象限内y1随x增大而减小,经过第二、四象限,在每个象限内y2随x增大而增大,
∵当时,函数y1的最大值是a,函数y2的最小值是a﹣6,
,
∴,
∴ak=3,
故选:D.
12.
【分析】根据反比例函数的解析式得到反比例函数经过第二、四象限,每个象限y随x的增大而增大,由此即可求解.
【解答】解:反比例函数k=﹣5<0,
∴图象经过第二、四象限,每个象限y随x的增大而增大,
当m<﹣5时,0<y1<y2,故A选项错误,不符合题意;
当,﹣5<m<0时,y1>0>y2,故B选项正确,符合题意;
当m>0时,y1<y2<0,故C,D选项错误,不符合题意;
故选:B.
13.解:(1)∵反比例函数的图象在第二、四象限,
∴2k+1<0,
解得:;
(2)∵反比例函数的图象在每个象限内y随x的增大而减小,
∴2k+1>0,
∴.
14.解:(1)∵反比例函数的图象位于第二、四象限,
∴k﹣2<0,
∴k<2;
(2)∵反比例函数的图象位于第二、四象限,
∴当x<0时,y随x的增大而增大,
∵﹣4<﹣1<0,
∴y1<y2.
【类型四:反比例函数与一次函数】
15.
【分析】将A(2,1)代入,求出m的值可得反比例函数的解析式.将B(﹣1,n)代入反比例函数的解析式,求出n的值,结合图象可直接得出答案.
【解答】解:将A(﹣2,1)代入,
得m=﹣2,
∴反比例函数的表达式为y,
将B(n,﹣2)代入y,
得n=1,
∴B(1,﹣2),
∴当一次函数的值大于反比例函数的值时,自变量x的取值范围是x<﹣2或0<x<1,
故选:D.
16.
【分析】根据题意当y=0,可求出x的值,即可得出A点的坐标,即可得出AO的长度,根据题意可知MO的长度,即可得出点M的坐标,由一次函数解析式即可算出点C的坐标,即可得出CM的长度,即可计算出△CMO的面积,即可判定①的结论是否正确;根据图象的增减性即可得出②的结论是否正确;由一次函数与反比例函数的交点坐标即可得出③结论是否正确;由图象可知比较函数的大小即可得出④结论是否正确.
【解答】解:当y=0时,x=﹣1,
∴点A(﹣1,0),
∴AO=1,
∵AO=MA,
∴MO=2AO=2,
∴点M(﹣2,0),
把点x=﹣2代入y=﹣x﹣1中,
得y=1,
∴点C(﹣2,1),CM=1,
∴,
∴①结论正确;
由图象可知,当x<0时,y1随x的增大而减小,y2随x的增大而增大,
∴②结论正确;
解方程可得:x2+x+k=0,Δ=12﹣4k>0,有两个解,
∴③结论错误;
由图象可知,当x<﹣2,y1>y2,
∴④结论错误.
故选:B.
【类型五:反比例函数与几何综合】
17.
【分析】作DE⊥x轴于E,如图,根据旋转的性质得到AB=AC,AD=AO,OB=CD,利用等腰三角形三线合一的性质得出OB=OC,进一步得出OC=CD,即可证得Rt△AOC≌Rt△ADC(HL),得出∠OAC=∠DAC=30°,在Rt△ACO中利用直角三角函数得到CD=OCOA,通过解直角三角形CDE,确定CE、DE,然后根据反比例函数图象上点的坐标特征可计算出k的值.
【解答】解:作DE⊥x轴于E,
∵点A的坐标为(0,4),
∴OA=4,
∵将△AOB绕点A逆时针旋转60°得到△ADC,点C刚好在x轴上,
∴AB=AC,AD=AO,OB=CD,
∵AB=AC,AO⊥BC,
∴OB=OC,
∴OC=CD,
∵∠AOC=∠ADC=90°,
∴Rt△AOC≌Rt△ADC(HL),
∴∠OAC=∠DAC,
∵∠OAD=60°,
∴∠OAC=∠DAC=30°,
∴∠ACO=∠ACD=60°,
∴OCOA,∠DCE=180°﹣60°﹣60°=60°,
∴CD,
∴CE,DECD=2,
∴OE=OC+CE2,
∴D(2,2),
∵点D在反比例函数y的图象上,
∴k=24.
故选:D.
18.
【分析】根据题意,找到符合条件整点即可得到k的个数.
【解答】解:∵△OAB的顶点坐标分别为O(0,0),A(1,3),B(3,1),点P为△OAB内部或边界上的整点,
∴这样的整点有:(1,1),(1,2),(1,3),(2,2),
∵反比例函数的图象经过△AOB内部或边界上的整点(横、纵坐标都是整数),
∴k值有1,2,3,4,共4个.
故选:B.
19.
【分析】设点A的纵坐标为n,则点B的纵坐标为n,根据点A,B分别在函数,的图象上得,,根据四边形ABCD为正方形得,解得n=5,得点A的纵坐标为5,将n=5代入,进行计算即可得.
【解答】解:设点A的纵坐标为n,则点B的纵坐标为n,
∵点A,B分别在两个反比例函数的图象上,
∴,,
∴,
n2=25,
n=5,n=﹣5(舍),
∴点A的纵坐标为5,
将n=5代入得,,
x=﹣3,
∴A(﹣3,5),
故选:C.
20.解:(1)连接AC,
∴四边形ABCD是菱形,
∴AC⊥BD,AE=CE,BE=DE,
∵反比例函数的图象和菱形ABCD都在第一象限内,,BD∥x轴,BD=4,
∴AB=AC,BE=DE=2,
∴CE=AE,
∵点A(3,5),
∴B(1,),D(5,),
∴C(3,2),
若反比例函数(x>0)的图象经过点C,则k=3×2=6,
∴反比例函数的解析式为y;
(2)∵点A(3,5).D(5,),
将菱形ABCD向下平移m(m>0)个单位长度,
∴A′(3,5﹣m),B′(1,m),C′(3,2﹣m),D′(5,m),
当A′,D′两点同时落在反比例函数图象上时,
∴3(5﹣m)=5(m),
∴m,
∴A′(3,),
k=3.
当B′,C′两点同时落在反比例函数图象上时,则B′(1,),
∴k=1.
故m的值为,此时k的值为或.
21.解:(1)把A(2,3)代入反比例解析式得:m=6,
∴反比例解析式为y,
把B(﹣3,n)代入反比例解析式得:n=﹣2,即B(﹣3,﹣2),
把A与B代入一次函数解析式得:,
解得:k=1,b=1,即一次函数解析式为y=x+1;
(2)∵A(2,3),B(﹣3,﹣2),
∴由图象得:kx+b的解集为x<﹣3或0<x<2,
故答案为:x<﹣3或0<x<2;
(3)根据题意得:△ABC的面积S|﹣2|×[2﹣(﹣3)]=5.
22.解:(1)(1)点A(﹣2,a)在第二象限,过点A作x轴的垂线,垂足为点C,△AOC的面积为4,
∴OC=2,AC=a,
∴S△AOC=4OC a,解得a=4,即A(﹣2,4),
∵点A(﹣2,4)在反比例函数y=(k≠0)的图象上,
∴4,解得k=﹣8,
∴反比例函数y,
∵点B(b,﹣1)在反比例函数y的图象上,
∴b=8,
∴a=4,b=8;
(2)如图所示,作点A(﹣2,4)关于y轴的对称点A′,
∴A′(2,4),且点B(8,﹣1),
设A′B所在直线的解析式为y=ex+f(e≠0),
∴,解得,
∴直线A′B的解析式为y=﹣,yx,
当点P,A′,B三点共线时,|PA﹣PB|取得最大值,且点P在y轴上,
∴令x=0时,y,
∴点P的坐标为(0,).
23.解:(1)∵直线l1:yx经过点A,A点的横坐标是﹣4,
∴当x=﹣4时,y=2,
∴A(﹣4,2),
∵反比例函数y的图象经过点A,
∴k=﹣4×2=﹣8,
∴反比例函数的表达式为y;
(2)∵直线l1:yx与反比例函数y的图象交于A,B两点,
∴B(4,﹣2),
∴不等式x的解集为x<﹣4或0<x<4;
(3)如图,设平移后的直线l2与x轴交于点D,连接AD,BD,
∵CD∥AB,
∴△ABC的面积与△ABD的面积相等,
∵△ABC的面积为30,
∴S△ABD=S△AOD+S△BOD=30,即OD(|yA|+|yB|)=30,
∴OD×4=30,
∴OD=15,
∴D(15,0),
设平移后的直线l2的函数表达式为yx+b,
把D(15,0)代入,可得015+b,
解得b,
∴平移后的直线l2的函数表达式为yx.
24.解:(1)连接AD,与x轴交于点E,
∵D(2,﹣3),
∴OE=2,ED=3,
∵菱形AODC,
∴AE=DE=3,EC=OE=2,
∴A(2,3),
将A坐标代入直线y=mx+1得:2m+1=3,即m=1,
将A坐标代入反比例y得:k=6,
∴反比例函数的表达式为y,
故答案为:y;
(2)联立直线与反比例解析式得:,
解得:或,
由图象可知当x<﹣3或0<x<2时,反比例函数值大于一次函数值;
∴不等式mx+1的解集是x<﹣3或0<x<2,
故答案为:x<﹣3或0<x<2;
(3)∵OC=2OE=4,AD=2DE=6,
∴S菱形AODCOC AD=12,
∵S△OAP=S菱形OACD,即OP OE=12,
∴设P(0,p),则|p|×2=12,即|p|=12,
解得:p=12或p=﹣12,
则P的坐标为(0,12)或(0,﹣12).
故答案为:(0,12)或(0,﹣12).
25.解:(1)如图1,过点D作DE⊥x轴于点E.则∠DEA=∠AOB=90°,
∵四边形ABCD为正方形,
∴∠BAD=90°,AB=DA,
∴∠2+∠3=90°,
∵∠1+∠3=90°,
∴∠1=∠2,
∴△AOB≌△DEA,
∴ED=OA=2,EA=OB=4,
∴OE=OA+EA=6,
∴点D的坐标为(6,2),
把D(6,2)代入得:,解得:k=12,
∴所求的反比例函数关系式为;
(2)如图2,过点C作CF⊥y轴于点F,交双曲线于点M,
同(1)可得△AOB≌△BFC,故CF=OB=4,BF=OA=2,
∴C(4,6),
∵在反比例函数y中,当y=6时,x2,
∴M(2,6),
∵CM=CF﹣MF=4﹣2=2,
∴将正方形ABCD沿x轴向左平移2个单位长度时,点C恰好落在反比例函数的图象上.
26.解:(1)∵Rt△ABC的直角边AB在x轴上,∠ABC=90°,点C的坐标为(3,4),
∴点B的坐标为(3,0),CB=4.
∵M是BC边的中点,
∴点M的坐标为(3,2).
∵函数(x>0)的图象经过点M,
∴k=3×2=6.
(2)∵△ABC绕某个点旋转180°后得到△DEF,
∴△DEF≌△ABC.
∴DE=AB,EF=BC,∠DEF=∠ABC=90°.
∵点A的坐标为(1,0),点B的坐标为(3,0),
∴AB=2.
∴DE=2.
∵EF在y轴上,
∴点D的横坐标为2.
∵点D在函数(x>0)的图象上,
当x=2时,y=3.
∴点D的坐标为(2,3).
∴点E的坐标为(0,3).
∵EF=BC=4,
∴点F的坐标为(0,﹣1).
设直线DF的表达式为y=ax+b,将点D,F的坐标代入,
得 解得
∴直线DF的表达式为y=2x﹣1.
【类型一:反比例函数的概念】
1.下列函数:①y=2x,②,③xy=﹣2,④,⑤.其中反比例函数有( )
A.0个 B.1个 C.2个 D.3个
2.下面几组相关联的量中,不成反比例关系的是( )
A.车间计划加工800个零件,加工时间与每天加工的零件个数
B.社团共有50名学生,按各组人数相等的要求分组,组数与每组人数
C.圆柱体的体积为6m3,圆柱的底面积与高
D.计划用100元购买苹果和香蕉两种水果,购买苹果的金额与购买香蕉的金额
【类型二:用待定系数法求反比例函数解析式】
3.在面积为定值的一组矩形中,当矩形的一边长为7.5cm时,它的另一边长为8cm.
(1)设矩形相邻的两边长分别为x(cm),y(cm),求y关于x的函数表达式.这个函数是反比例函数吗?如果是,指出比例系数.
(2)若其中一个矩形的一条边长为5cm,求这个矩形与之相邻的另一边长.
4.已知函数.
(1)若y是关于x的正比例函数,求m的值;
(2)若y是关于x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
5.已知y是z的反比例函数,z是x的正比例函数.
(1)当时,y=6.当x=6时,z=4.求y与x之间的函数关系式;
(2)证明y是x的反比例函数.
6.已知y=y1+y2,其中y1与x成正比例,y2与x2成反比例,且当x=2和x=3时,y的值都为19,求y与变量x的函数关系式.
【类型三:反比例函数的图像与性质】
7.矩形的面积为6,它的长y与宽x之间的关系用图象大致可表示为( )
A. B.
C. D.
8.函数和y=kx﹣k(k≠0)在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
9.已知反比例函数y的图象位于第一、三象限,则n的取值可以是( )
A.﹣2 B.1 C.2 D.3
10.若点A(﹣3,a)、B(1,b)、C(2,c)都在反比例函数的图象上,则a、b、c的大小关系为( )
A.c<b<a B.b<a<c C.a<b<c D.b<c<a
11.已知函数,,当时,函数y1的最大值是a,函数y2的最小值是a﹣6,则ak=( )
A. B.9 C. D.3
12.若A(m,y1),B(m+5,y2)两点在反比例函数的图象上,则下列正确的选项是( )
A.当m<﹣5时,y1>y2>0 B.当﹣5<m<0时,y1>0>y2
C.当0<m<5时,y2>0>y1 D.当m>5时,y2>y1>0
13.已知反比例函数.
(1)若该函数图象在第二、四象限,求k的取值范围;
(2)当k取什么值时,在每个象限内y随x的增大而减小?
14.已知反比例函数的图象位于第二、四象限.
(1)求k的取值范围;
(2)若点A(﹣4,y1),B(﹣1,y2)是该反比例函数图象上的两点,试比较函数值y1,y2的大小.
【类型四:反比例函数与一次函数】
15.如图,一次函数y=kx+b的图象与反比例函数的图象交于A(﹣2,1),B(n,﹣2)两点.当一次函数的值大于反比例函数的值时,自变量x的取值范围是( )
A.﹣2<x<1 B.0<x<1
C.﹣2<x<0或x>1 D.x<﹣2或0<x<1
16.如图,在直角坐标系中,直线y1=﹣x﹣1与坐标轴交于A,B两点,与双曲线交于点C,连接OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( )
①S△CMO=1;
②当x<0时,y1随x的增大而减小,y2随x的增大而增大;
③方程只有一个解为x=﹣2;
④当x<﹣2,y1<y2.
A.1个 B.2个 C.3个 D.4个
【类型五:反比例函数与几何综合】
17.如图,在平面直角坐标系中,OB在x轴上,OA在y轴上,点A的坐标为(0,4),将△AOB绕点A逆时针旋转60°得到△ADC,点C刚好在x轴上,点D在反比例函数y的图象上,则k的值为( )
A.2 B. C.4 D.
18.如图,△AOB的顶点坐标分别为A(1,3),O(0,0),B(3,1).若反比例函数的图象经过△AOB内部或边界上的整点(横、纵坐标都是整数),则k的取值共有( )
A.3个 B.4个 C.5个 D.6个
19.如图,点A,B分别在函数,的图象上,点D,C在x轴上.若四边形ABCD为正方形.则点A的坐标是( )
A.(﹣2,5) B.(﹣2,4) C.(﹣3,5) D.(﹣3,4)
20.如图,在平面直角坐标系xOy中,反比例函数的图象和菱形ABCD都在第一象限内,,B∥x轴,且BD=4,点A的坐标为(3,5).
(1)若反比例函数(x>0)的图象经过点C,求此反比例函数的解析式;
(2)若将菱形ABCD向下平移m(m>0)个单位长度,使菱形ABCD的两个顶点的对应点同时落在反比例函数图象上,求m及此时k的值.
21.如图,一次函数y=kx+b与反比例函数的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式的解集 ;
(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
22.如图,一次函数y=mx+n(m≠0)的图象与反比例函数的图象交于点A(﹣2,a),B(b,﹣1),过点A作x轴的垂线,垂足为C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)在y轴上取一点P,使|PB|﹣|PA|取得最大值,求出此时点P的坐标.
23.如图,在平面直角坐标系中,直线l1:yx与反比例函数y的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是﹣4;
(1)求反比例函数的表达式;
(2)根据图象直接写出x的解集;
(3)将直线l1:yx沿y向上平移后的直线l2与反比例函数y在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
24.如图,在平面直角坐标系xOy中,直线y=mx+1与双曲线y(k>0)相交于点A,B,已知点B(a,﹣2),点C在x轴正半轴上,点D(2,﹣3),连接OA,OD,DC,AC,四边形AODC为菱形.
(1)反比例函数的表达式为 ;
(2)不等式mx+1的解集是 ;
(3)设P是y轴上一动点,且△OAP的面积等于菱形OACD的面积,则点P的坐标为 .
25.如图,四边形ABCD为正方形,点A在x轴上,点B在y轴上,且OA=2,OB=4,反比例函数y(k≠0)在第一象限的图象经过正方形的顶点D.
(1)求反比例函数的关系式;
(2)将正方形ABCD沿x轴负方向平移多少个单位长度时,点C恰好落在反比例函数的图形上.
26.如图,在平面直角坐标系xOy中,Rt△ABC的直角边AB在x轴上,∠ABC=90°.点A的坐标为(1,0),点C的坐标为(3,4),M是BC边的中点,函数y(x>0)的图象经过点M.
(1)求k的值;
(2)将△ABC绕某个点旋转180°后得到△DEF(点A,B,C的对应点分别为点D,E,F),且EF在y轴上,点D在函数y(x>0)的图象上,求直线DF的表达式.
参考答案
【类型一:反比例函数的概念】
1.
【分析】根据反比例函数的定义即可作答.
【解答】解:①是正比例函数,不是反比例函数;
②是反比例函数;
③是反比例函数;
④y是x+1反比例函数;
⑤y﹣3是x反比例函数;
所以反比例函数有2个.
故选:C.
2.
【分析】根据反比例函数的定义逐一判断即可.
【解答】解:A、加工时间×每天加工的零件个数=800,则加工时间与每天加工的零件个数的乘积是定值,此选项正确,成反比例关系,不符合题意;
B、组数×每组人数=50,则组数与每组人数的乘积是定值,成反比例关系,此选项正确,不符合题意;
C、底面积×高=6,则底面积与高的乘积是定值,成反比例关系,此选项正确,不符合题意;
D、购买苹果的金额+购买香蕉的金额=100,则购买苹果的金额与购买香蕉的金额的和是定值,不成反比例关系,此选项错误,符合题意,
故选:D.
【类型二:用待定系数法求反比例函数解析式】
3.解:(1)设矩形的面积为S cm2,则S=7.5×8=60,
即xy=60,y,
即y关于x的函数解析式是y,这个函数是反比例函数,系数为60;
(2)当x=5时,y12,
故这个矩形与之相邻的另一边长为12.
4.解:(1)由y=(m2﹣2m)是正比例函数,得
m2﹣m﹣1=1且m2﹣2m≠0,
解得m=﹣1;
(2)由y=(m2﹣2m)是反比例函数,得
m2﹣m﹣1=﹣1且m2﹣2m≠0,
解得m=1.
故y与x的函数关系式y=﹣x﹣1.
5.(1)解:∵y是z的反比例函数,
∴设(a≠0),
∵当时,y=6,
∴a4,
∴①,
∵z是x的正比例函数,
∴设z=bx(b≠0),
又∵当x=6时,z=4,
∴,
∴②,
将②代入①,得:;
(2)证明:由(1)得:(a≠0),z=bx,
∴,
∴y是x的反比例函数.
6.解:∵y1与x成正比例,y2与x2成反比例,
∴设y1=ax(a≠0),y2(k≠0),
∴y=y1+y2=ax,
∵当x=2和x=3时,y的值都为19,
∴,
解得a=5,k=36,
所以y与变量x的函数关系式是.
【类型三:反比例函数的图像与性质】
7.
【分析】由题意y,(x>0),所以y是x的反比例函数,由此即可解决问题.
【解答】解:由题意y,(x>0),
所以y是x的反比例函数,图象在第一象限,
故选:D.
8.
【分析】根据题目中的函数解析式和反比例函数的性质、一次函数的性质,可以判断哪个选项中的图象符合题意.
【解答】解:当k<0时,反比例函数的图象位于第二、四象限,一次函数y=kx﹣k的图象经过一、二、四象限,故选项C不符合题意.选项D符合题意;
当k>0时,反比例函数的图象位于第一、三象限,一次函数y=kx﹣k的图象经过一、三、四象限,故选项A、B均不符合题意;
故选:D.
9.
【分析】直接利用当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小,进而得出n的取值范围,即可得出答案.
【解答】解:∵反比例函数y的图象位于第一、三象限,
∴n﹣2>0,
解得:n>2.
故n的取值可以是:3.
故选:D.
10.
【分析】先根据反比例函数中k<0判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
【解答】解:∵反比例函数常数k=﹣m2﹣3<0,
∴反比例函数图象分布在第二、四象限,在每个象限内,y随x的增大而增大,
∵A(﹣3,a)在第二象限,
∴a>0,
∵B(1,b)、C(2,c)在第四象限,
∴0>c>b,
∴b<c<a.
故选:D.
11.
【分析】根据题意可得函数经过第一、三象限,在每个象限内y1随x增大而减小,经过第二、四象限,在每个象限内y2随x增大而增大,则,解方程组即可得到答案.
【解答】解:由条件可知:函数经过第一、三象限,在每个象限内y1随x增大而减小,经过第二、四象限,在每个象限内y2随x增大而增大,
∵当时,函数y1的最大值是a,函数y2的最小值是a﹣6,
,
∴,
∴ak=3,
故选:D.
12.
【分析】根据反比例函数的解析式得到反比例函数经过第二、四象限,每个象限y随x的增大而增大,由此即可求解.
【解答】解:反比例函数k=﹣5<0,
∴图象经过第二、四象限,每个象限y随x的增大而增大,
当m<﹣5时,0<y1<y2,故A选项错误,不符合题意;
当,﹣5<m<0时,y1>0>y2,故B选项正确,符合题意;
当m>0时,y1<y2<0,故C,D选项错误,不符合题意;
故选:B.
13.解:(1)∵反比例函数的图象在第二、四象限,
∴2k+1<0,
解得:;
(2)∵反比例函数的图象在每个象限内y随x的增大而减小,
∴2k+1>0,
∴.
14.解:(1)∵反比例函数的图象位于第二、四象限,
∴k﹣2<0,
∴k<2;
(2)∵反比例函数的图象位于第二、四象限,
∴当x<0时,y随x的增大而增大,
∵﹣4<﹣1<0,
∴y1<y2.
【类型四:反比例函数与一次函数】
15.
【分析】将A(2,1)代入,求出m的值可得反比例函数的解析式.将B(﹣1,n)代入反比例函数的解析式,求出n的值,结合图象可直接得出答案.
【解答】解:将A(﹣2,1)代入,
得m=﹣2,
∴反比例函数的表达式为y,
将B(n,﹣2)代入y,
得n=1,
∴B(1,﹣2),
∴当一次函数的值大于反比例函数的值时,自变量x的取值范围是x<﹣2或0<x<1,
故选:D.
16.
【分析】根据题意当y=0,可求出x的值,即可得出A点的坐标,即可得出AO的长度,根据题意可知MO的长度,即可得出点M的坐标,由一次函数解析式即可算出点C的坐标,即可得出CM的长度,即可计算出△CMO的面积,即可判定①的结论是否正确;根据图象的增减性即可得出②的结论是否正确;由一次函数与反比例函数的交点坐标即可得出③结论是否正确;由图象可知比较函数的大小即可得出④结论是否正确.
【解答】解:当y=0时,x=﹣1,
∴点A(﹣1,0),
∴AO=1,
∵AO=MA,
∴MO=2AO=2,
∴点M(﹣2,0),
把点x=﹣2代入y=﹣x﹣1中,
得y=1,
∴点C(﹣2,1),CM=1,
∴,
∴①结论正确;
由图象可知,当x<0时,y1随x的增大而减小,y2随x的增大而增大,
∴②结论正确;
解方程可得:x2+x+k=0,Δ=12﹣4k>0,有两个解,
∴③结论错误;
由图象可知,当x<﹣2,y1>y2,
∴④结论错误.
故选:B.
【类型五:反比例函数与几何综合】
17.
【分析】作DE⊥x轴于E,如图,根据旋转的性质得到AB=AC,AD=AO,OB=CD,利用等腰三角形三线合一的性质得出OB=OC,进一步得出OC=CD,即可证得Rt△AOC≌Rt△ADC(HL),得出∠OAC=∠DAC=30°,在Rt△ACO中利用直角三角函数得到CD=OCOA,通过解直角三角形CDE,确定CE、DE,然后根据反比例函数图象上点的坐标特征可计算出k的值.
【解答】解:作DE⊥x轴于E,
∵点A的坐标为(0,4),
∴OA=4,
∵将△AOB绕点A逆时针旋转60°得到△ADC,点C刚好在x轴上,
∴AB=AC,AD=AO,OB=CD,
∵AB=AC,AO⊥BC,
∴OB=OC,
∴OC=CD,
∵∠AOC=∠ADC=90°,
∴Rt△AOC≌Rt△ADC(HL),
∴∠OAC=∠DAC,
∵∠OAD=60°,
∴∠OAC=∠DAC=30°,
∴∠ACO=∠ACD=60°,
∴OCOA,∠DCE=180°﹣60°﹣60°=60°,
∴CD,
∴CE,DECD=2,
∴OE=OC+CE2,
∴D(2,2),
∵点D在反比例函数y的图象上,
∴k=24.
故选:D.
18.
【分析】根据题意,找到符合条件整点即可得到k的个数.
【解答】解:∵△OAB的顶点坐标分别为O(0,0),A(1,3),B(3,1),点P为△OAB内部或边界上的整点,
∴这样的整点有:(1,1),(1,2),(1,3),(2,2),
∵反比例函数的图象经过△AOB内部或边界上的整点(横、纵坐标都是整数),
∴k值有1,2,3,4,共4个.
故选:B.
19.
【分析】设点A的纵坐标为n,则点B的纵坐标为n,根据点A,B分别在函数,的图象上得,,根据四边形ABCD为正方形得,解得n=5,得点A的纵坐标为5,将n=5代入,进行计算即可得.
【解答】解:设点A的纵坐标为n,则点B的纵坐标为n,
∵点A,B分别在两个反比例函数的图象上,
∴,,
∴,
n2=25,
n=5,n=﹣5(舍),
∴点A的纵坐标为5,
将n=5代入得,,
x=﹣3,
∴A(﹣3,5),
故选:C.
20.解:(1)连接AC,
∴四边形ABCD是菱形,
∴AC⊥BD,AE=CE,BE=DE,
∵反比例函数的图象和菱形ABCD都在第一象限内,,BD∥x轴,BD=4,
∴AB=AC,BE=DE=2,
∴CE=AE,
∵点A(3,5),
∴B(1,),D(5,),
∴C(3,2),
若反比例函数(x>0)的图象经过点C,则k=3×2=6,
∴反比例函数的解析式为y;
(2)∵点A(3,5).D(5,),
将菱形ABCD向下平移m(m>0)个单位长度,
∴A′(3,5﹣m),B′(1,m),C′(3,2﹣m),D′(5,m),
当A′,D′两点同时落在反比例函数图象上时,
∴3(5﹣m)=5(m),
∴m,
∴A′(3,),
k=3.
当B′,C′两点同时落在反比例函数图象上时,则B′(1,),
∴k=1.
故m的值为,此时k的值为或.
21.解:(1)把A(2,3)代入反比例解析式得:m=6,
∴反比例解析式为y,
把B(﹣3,n)代入反比例解析式得:n=﹣2,即B(﹣3,﹣2),
把A与B代入一次函数解析式得:,
解得:k=1,b=1,即一次函数解析式为y=x+1;
(2)∵A(2,3),B(﹣3,﹣2),
∴由图象得:kx+b的解集为x<﹣3或0<x<2,
故答案为:x<﹣3或0<x<2;
(3)根据题意得:△ABC的面积S|﹣2|×[2﹣(﹣3)]=5.
22.解:(1)(1)点A(﹣2,a)在第二象限,过点A作x轴的垂线,垂足为点C,△AOC的面积为4,
∴OC=2,AC=a,
∴S△AOC=4OC a,解得a=4,即A(﹣2,4),
∵点A(﹣2,4)在反比例函数y=(k≠0)的图象上,
∴4,解得k=﹣8,
∴反比例函数y,
∵点B(b,﹣1)在反比例函数y的图象上,
∴b=8,
∴a=4,b=8;
(2)如图所示,作点A(﹣2,4)关于y轴的对称点A′,
∴A′(2,4),且点B(8,﹣1),
设A′B所在直线的解析式为y=ex+f(e≠0),
∴,解得,
∴直线A′B的解析式为y=﹣,yx,
当点P,A′,B三点共线时,|PA﹣PB|取得最大值,且点P在y轴上,
∴令x=0时,y,
∴点P的坐标为(0,).
23.解:(1)∵直线l1:yx经过点A,A点的横坐标是﹣4,
∴当x=﹣4时,y=2,
∴A(﹣4,2),
∵反比例函数y的图象经过点A,
∴k=﹣4×2=﹣8,
∴反比例函数的表达式为y;
(2)∵直线l1:yx与反比例函数y的图象交于A,B两点,
∴B(4,﹣2),
∴不等式x的解集为x<﹣4或0<x<4;
(3)如图,设平移后的直线l2与x轴交于点D,连接AD,BD,
∵CD∥AB,
∴△ABC的面积与△ABD的面积相等,
∵△ABC的面积为30,
∴S△ABD=S△AOD+S△BOD=30,即OD(|yA|+|yB|)=30,
∴OD×4=30,
∴OD=15,
∴D(15,0),
设平移后的直线l2的函数表达式为yx+b,
把D(15,0)代入,可得015+b,
解得b,
∴平移后的直线l2的函数表达式为yx.
24.解:(1)连接AD,与x轴交于点E,
∵D(2,﹣3),
∴OE=2,ED=3,
∵菱形AODC,
∴AE=DE=3,EC=OE=2,
∴A(2,3),
将A坐标代入直线y=mx+1得:2m+1=3,即m=1,
将A坐标代入反比例y得:k=6,
∴反比例函数的表达式为y,
故答案为:y;
(2)联立直线与反比例解析式得:,
解得:或,
由图象可知当x<﹣3或0<x<2时,反比例函数值大于一次函数值;
∴不等式mx+1的解集是x<﹣3或0<x<2,
故答案为:x<﹣3或0<x<2;
(3)∵OC=2OE=4,AD=2DE=6,
∴S菱形AODCOC AD=12,
∵S△OAP=S菱形OACD,即OP OE=12,
∴设P(0,p),则|p|×2=12,即|p|=12,
解得:p=12或p=﹣12,
则P的坐标为(0,12)或(0,﹣12).
故答案为:(0,12)或(0,﹣12).
25.解:(1)如图1,过点D作DE⊥x轴于点E.则∠DEA=∠AOB=90°,
∵四边形ABCD为正方形,
∴∠BAD=90°,AB=DA,
∴∠2+∠3=90°,
∵∠1+∠3=90°,
∴∠1=∠2,
∴△AOB≌△DEA,
∴ED=OA=2,EA=OB=4,
∴OE=OA+EA=6,
∴点D的坐标为(6,2),
把D(6,2)代入得:,解得:k=12,
∴所求的反比例函数关系式为;
(2)如图2,过点C作CF⊥y轴于点F,交双曲线于点M,
同(1)可得△AOB≌△BFC,故CF=OB=4,BF=OA=2,
∴C(4,6),
∵在反比例函数y中,当y=6时,x2,
∴M(2,6),
∵CM=CF﹣MF=4﹣2=2,
∴将正方形ABCD沿x轴向左平移2个单位长度时,点C恰好落在反比例函数的图象上.
26.解:(1)∵Rt△ABC的直角边AB在x轴上,∠ABC=90°,点C的坐标为(3,4),
∴点B的坐标为(3,0),CB=4.
∵M是BC边的中点,
∴点M的坐标为(3,2).
∵函数(x>0)的图象经过点M,
∴k=3×2=6.
(2)∵△ABC绕某个点旋转180°后得到△DEF,
∴△DEF≌△ABC.
∴DE=AB,EF=BC,∠DEF=∠ABC=90°.
∵点A的坐标为(1,0),点B的坐标为(3,0),
∴AB=2.
∴DE=2.
∵EF在y轴上,
∴点D的横坐标为2.
∵点D在函数(x>0)的图象上,
当x=2时,y=3.
∴点D的坐标为(2,3).
∴点E的坐标为(0,3).
∵EF=BC=4,
∴点F的坐标为(0,﹣1).
设直线DF的表达式为y=ax+b,将点D,F的坐标代入,
得 解得
∴直线DF的表达式为y=2x﹣1.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
