初中数学苏科版八年级下册 11.3 用反比例函数解决问题 同步练习(含解析)
文档属性
| 名称 | 初中数学苏科版八年级下册 11.3 用反比例函数解决问题 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 14:47:50 | ||
图片预览




文档简介
11.3用反比例函数解决问题
【类型一:压强问题】
1.根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图象如图所示.当S=0.25m2时,该物体承受的压强p的值为 Pa.
2.力F(N)作用于物体,产生的压强p(kPa)与物体受力面积S(m2)之间满足,在某次实验中,当F一定时,p关于S的函数图象如图所示.若压强p由40kPa增压至60kPa,则物体受力面积S( )
A.减小了25m2 B.增大了25m2
C.减小了20m2 D.增大了20m2
3.如图1,这是一个可改变体积的密闭容器的简易图,在该容器内装有一定质量的氧气,当改变容器的体积时,气体的密度也会随之改变.随着容器体积的改变,该密闭容器内氧气的密度ρ(单位:kg/m3)随容器体积V(单位:m3)变化的关系图象如图2所示,结合图3信息窗中的内容,下列说法不正确的是( )
A.当该容器的体积V为25m3时,氧气的密度ρ为0.32kg/m3
B.该容器内氧气的密度ρ是关于体积V的反比例函数
C.若容器内氧气的密度为1.43kg/m3,则该容器的体积约为4.59m3
D.该容器内氧气的质量为8kg
4.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化.已知密度ρ与体积V是反比例函数关系,它的图象如图所示,当V=2.5m3时,ρ=4kg/m3.
(1)求密度ρ关于体积V的函数表达式;
(2)当V=5m3时,求二氧化碳密度ρ的值.
【类型二:杠杆原理问题】
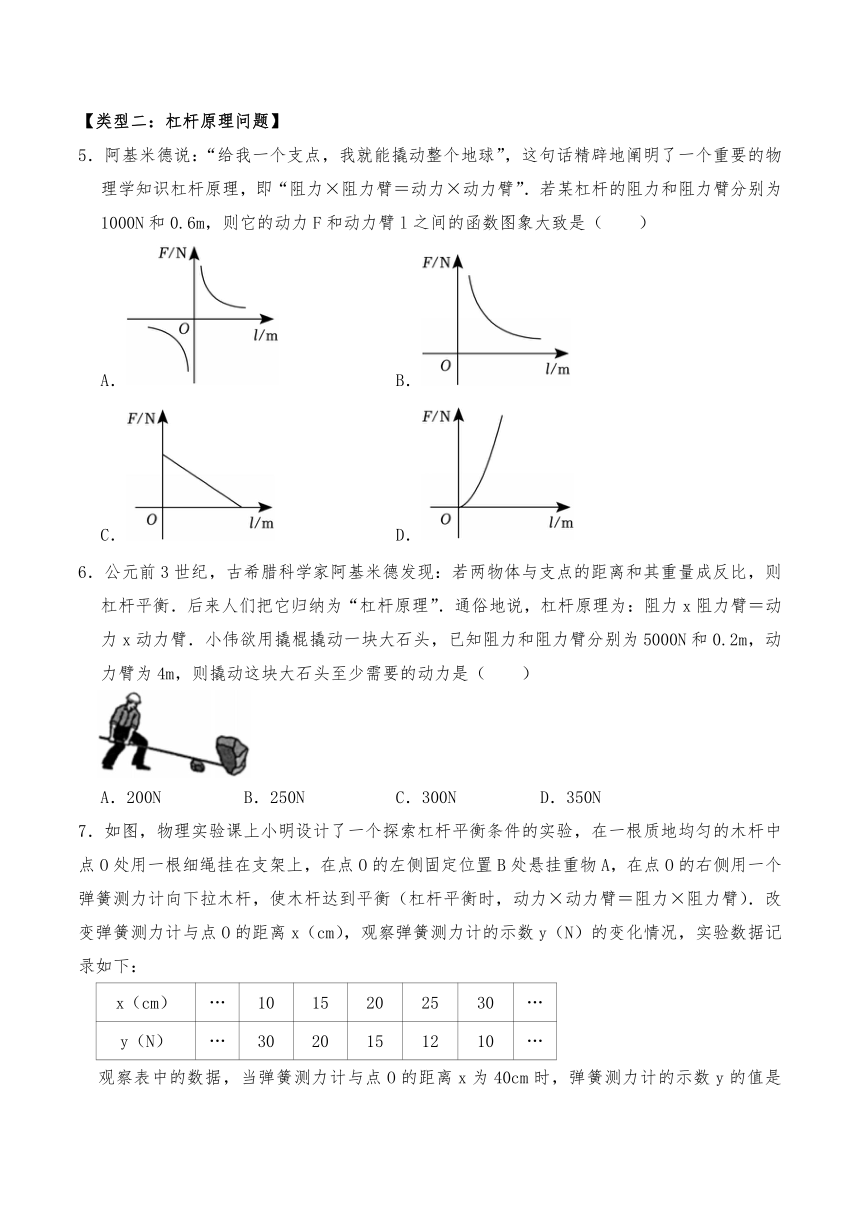
5.阿基米德说:“给我一个支点,我就能撬动整个地球”,这句话精辟地阐明了一个重要的物理学知识杠杆原理,即“阻力×阻力臂=动力×动力臂”.若某杠杆的阻力和阻力臂分别为1000N和0.6m,则它的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
6.公元前3世纪,古希腊科学家阿基米德发现:若两物体与支点的距离和其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力x阻力臂=动力x动力臂.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为5000N和0.2m,动力臂为4m,则撬动这块大石头至少需要的动力是( )
A.200N B.250N C.300N D.350N
7.如图,物理实验课上小明设计了一个探索杠杆平衡条件的实验,在一根质地均匀的木杆中点O处用一根细绳挂在支架上,在点O的左侧固定位置B处悬挂重物A,在点O的右侧用一个弹簧测力计向下拉木杆,使木杆达到平衡(杠杆平衡时,动力×动力臂=阻力×阻力臂).改变弹簧测力计与点O的距离x(cm),观察弹簧测力计的示数y(N)的变化情况,实验数据记录如下:
x(cm) … 10 15 20 25 30 …
y(N) … 30 20 15 12 10 …
观察表中的数据,当弹簧测力计与点O的距离x为40cm时,弹簧测力计的示数y的值是( )
A.5 B.7.5 C.10 D.120
8.杠杆原理在生活中应用广泛,我国早在春秋时期就有使用,杠杆原理为:阻力×阻力臂=动力×动力臂(如图①).某数学兴趣小组利用所学的函数知识对以上原理进行探究:如图②,小明取一根长100cm质地均匀的木杆,用细绳绑在木杆的中点O处将其吊在空中,在中点的左侧距中点25cm处挂一个重10N的物体(即支点为O,阻力为10N,阻力臂为25cm),在中点右侧用一个弹簧测力计(重力忽略不计)竖直向下拉,使木杆处于水平状态,改变弹簧测力计与中点O的距离x(cm),观察弹簧测力计的示数y(N)的变化(即动力臂为x cm,动力为yN),在平面直角坐标系中描出了一系列点(x,y),并用平滑的曲线顺次连接,得到如图③所示的函数图象.
(1)求图③中的函数解析式;
(2)若点O的位置不变,在不改变点O与物体的距离及物体重力的前提下,要想使木杆平衡,弹簧测力计的示数最小可以是多少?
9.如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) 10 15 20 25 30
y(g) 30 20 15 12 10
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
【类型三:温度问题】
10.我校的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至20℃时自动开机加热,重复上述自动程序.若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示.
(1)a= ,b= .
(2)直接写出图中y关于x的函数表达式.
(3)饮水机有多少时间能使水温保持在50℃及以上?
(4)若某天上午7:00饮水机自动接通电源,开机温度正好是20℃,问学生上午第一节下课时(8:40)能喝到50℃以上的水吗?请说明理由.
11.喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分半钟后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是25℃,降温过程中水温不低于25℃.
(1)分别写出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
12.某水果生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启后阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)这个恒温系统设定的恒定温度为多少℃;
(2)求全天的温度y(℃)与时间x(h)之间的函数关系式;
(3)若大棚内的温度低于12℃时,蔬菜会受到伤害,问:这天内恒温系统最多可以关闭多少小时,才能避免水果生长受到影响?
13.小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)有一天,小明在上午7:10(水温20℃),开机通电后去上学,中午放学回到家时间刚好11:15,请问此时饮水机内水的温度约为多少℃?并求:在7:10﹣11:15这段时间里,水温共有几次达到100℃?
【类型四:课堂注意力问题】
14.通过实验研究发现:初中生在数学课上听课注意力指标数随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标数y随时间x(分)变化的函数图象如图所示.当0≤x<10和10≤x<20时,图象是线段:当20≤x≤40时,图象是双曲线的一部分,根据函数图象回答下列问题:
(1)点A的注意力指标数是 ;
(2)当0≤x<10时,求注意力指标数y随时间x(分)的函数解析式;
(3)张老师在一节课上讲解一道数学综合题需要20分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36?请说明理由.
【类型五:浓度问题】
15.某校对教室采用药薰法进行灭蚊.根据药品使用说明,药物燃烧时,室内每立方米空气中含药量y(mg/m3)与药物点燃后的时间x(min)成正比例,药物燃尽后,y与x成反比例(如图).已知药物点燃后8min燃尽,此时室内每立方米空气中含药量为6mg.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)根据灭蚊药品使用说明,当空气中每立方米的含药量低于1.6mg时,对人体是安全的.那么从开始药薰,至少经过多少时间,学生才能进入教室?
(4)根据灭蚊药品使用说明,当每立方米空气中含药量不低于3mg且持续时间不低于10min时,才能有效杀灭室内的蚊虫,那么此次灭蚊是否有效?为什么?
16.新冠疫情下的中国在全世界抗疫战斗中全方位领跑.某制药公司生产3支单针疫苗和2支双针疫苗需要19min;生产2支单针疫苗和1支双针疫苗需要11min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间?
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:min/mL)与时间x(单位:天)的函数关系如图所示:疫苗注射后体内抗体浓度首先y与x成一次函数关系,体内抗体到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50min/mL时,并且不低于23min/mL,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.请问:小明可以在哪个时间段内打第二针疫苗?请通过计算说明.
【类型六:电路问题】
17.如图所示为一测量电路,Ry为待测电阻,Rx为可调电阻,R,R1,R2为已知电阻,E为直流电压源,A为电流表,调节Rx的电阻时会出现一种现象,即当电流表读数为0时,有,这个现象叫做电桥平衡,并且此时的电阻R对电路无影响.由上式便可通过Rx的电阻求得Ry的电阻,现已知R1=2Ω,R2=8Ω.当Rx=4Ω时电流表读数为0,那么此时将Ry减小3Ω,则Rx需要如何变,电流表示数才能为0?( )
A.增大12Ω B.增大8Ω C.减小3Ω D.减小1Ω
18.小宁利用如图(1)所示的电路(电源电压不变,R为定值电阻)进行了如下实验:在开关S闭合的情况下,改变电阻箱R1的阻值,读取电流表示数.根据实验数据,小宁绘制了如图(2)所示的电流表示数I随R1变化的曲线.
信息框 1.欧姆定律:导体中的电流,跟导体两端的电压成正比,跟导体的电阻成反比. 2.电流表的电阻忽略不计.
下列说法正确的是( )
A.电流I随电阻R1的增大而增大
B.电流I与电阻R1成反比例函数关系
C.电阻R两端的电压随R1的增大而减小
D.当电阻R1为0时,电路中的电流最小
19.在一次物理实验中,小冉同学用一固定电压为U=12(V)的蓄电池,通过调节滑动变阻器R(Ω)来改变电流大小,完成控制灯泡L(灯丝的阻值R1=2Ω)亮度的实验(如图1,假设灯泡的电阻不随温度的变化而变化),已知串联电路中,电流I与电阻R、RL之间关系为,通过得出如下数据(表格数据不完整):
R/Ω … 1 a 4 6 …
I/A … 4 3 2 b …
(1)a= ,b= ;
(2)根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质.
①在直角坐标系中画出对应函数的图象:
②随着自变量x的不断增大,函数值y的变化趋势是 .
(3)请结合函数图象分析,当x≥0时,的解集为 .
【类型七:效率问题】
20.装卸机往一艘轮船上装载货物,装完货物所需时间y(分钟)与装载速度x(吨/分钟)之间的函数关系如图所示.若要求在120分钟内(包括120分钟)装完这批货物,则x的取值范围是( )
A.x≥5 B.x≥3 C.0<x≤5 D.0<x≤3
21.快递运载机器人是一种应用于配送领域的智能机器人,它的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数.已知一款快递运载机器人载重后总质量m=60kg时,它的最快移动速度v=6m/s;当其载重后总质量m=100kg时,它的最快移动速度v= m/s.
22.小明家购买一套商品房,首付45万元,剩余部分需贷款并按“等额本金”的形式偿还,即贷款金额按月分期还款,且每月偿还贷款金额数相同.若设每月偿还贷款金额y万元,x个月还清,且y是x的反比例函数,其图象如图所示.
(1)求y与x的函数关系式;
(2)若小明家计划每月偿还贷款金额不超过3000元,求至少需要多少个月还清?
23.码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/天)与装完货物所需时间x(天)之间是反比例函数关系,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)由于紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸货多少吨?
(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
【其他问题】
24.学校举行数学文化竞赛.图中的四个点分别描述了八(1)、八(2)、八(3)、八(4)四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图象上,则成绩优秀人数最多的是( )
A.八(1)班 B.八(2)班 C.八(3)班 D.八(4)班
25.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
A.甲 B.乙 C.丙 D.丁
26.某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图象大致是( )
A. B.
C. D.
27.如图(1)所示的家用扫地机器人,其底部安装有滚刷,内置集尘器.机器人在除尘时先“脱灰”(滚刷将灰尘从地面上脱离附着),后“吸灰”(将脱附的灰尘转移进集尘器).为研究滚刷滚速对“脱灰”效果的影响,小静在保持扫地机器人“吸灰”效果一定的情况下,对“吸灰”过程中滚刷的滚速与除尘能力C(在地面撒灰后,清扫十次所减少的灰占所撒的灰总质量的百分比)进行了试验,得到如图(2)所示的关系图,规定除尘能力C超过36%即为及格.则下列说法正确的是( )
A.除尘能力关于滚刷的滚速的图象是反比例函数图象的一部分
B.除尘能力与滚刷的滚速成正比
C.当滚速为1300转/分时,除尘能力为及格
D.当除尘能力为36.5%时,滚剧的滚速为1400转/分
参考答案
【类型一:压强问题】
1.
【分析】设p,把(0.1,1000)代入得到反比例函数的解析式,再把S=0.25代入解析式即可解决问题.
【解答】解:设p,
∵函数图象经过(0.1,1000),
∴k=100,
∴p,
当S=0.25m2时,物体所受的压强p400(Pa),
故答案为:400.
2.
【分析】结合图象得到,再分别求出当压强p为40kPa和60kPa时的受力面积,并进行比较,即可解题.
【解答】解:∵F一定,
结合图象可知F=100×30=3000(N),即,
当压强p为40kPa时,有,解得S=75(m2),
当压强p为60kPa时,有,解得S=50(m2),
∵75﹣50=25(m2),
故选:A.
3.
【分析】先求出反比例函数解析式,然后对各选项分析即可.
【解答】解:∵,且容器内氧气的质量一定,
∴是反比例函数,故B正确,不符合题意;
当V=2时,ρ=4,
∴m=ρV=8,故D正确,不符合题意;
∴,
当V=25m3时,,故A正确,不符合题意;
当ρ=1.43时,,故C不正确,符合题意.
故选:C.
4.解:(1)设p,
由题意得:k=p V=2.5×4=10,
∴密度ρ关于体积V的函数表达式为:p;
当V=5m3时,p2kg/m3.
【类型二:杠杆原理问题】
5.
【分析】直接利用阻力×阻力臂=动力×动力臂,进而得出动力F关于动力臂l的函数关系式,从而确定其图象即可.
【解答】解:∵阻力×阻力臂=动力×动力臂,且阻力和阻力臂分别为1000N和0.6m,
∴动力F关于动力臂l的函数解析式为:1000×0.6=Fl,
即F,是反比例函数,
又∵动力臂l>0,
反比例函数F的图象是双曲线,且在第一象限.
故选:B.
6.
【分析】根据“阻力×阻力臂=动力×动力臂”,代入数据即可解答.
【解答】解:∵“阻力×阻力臂=动力×动力臂”,
∴5000×0.2=动力×4,
∴动力为250N,
因此,撬动这块大石头至少需要的动力是250N,
故选:B.
7.
【分析】依据题意,根据表格数据求出y与x的函数关系,求出解析式,将x=40代入即可.
【解答】解:观察表格数据可得,y与x成反比例函数关系,设y,
∴k=10×30=300.
∴函数为y.
又当x=400时,y7.5
∴弹簧测力计的示数y的值是7.5.
故选:B.
8.解:(1)已知杠杆原理的公式:阻力×阻力臂=动力×动力臂,阻力为10N,阻力臂为25cm,动力臂为x cm,动力为y N,则有x y=10×25,
∴图③中的函数解析式为.
(2)由反比例函数解析式可知:当x最大时,y最小,
∵由于支点即为细绳悬挂点,
∴x>0.
∴x≤50.
综上,0<x≤50.
∴当x=50cm时,.
9.解:(1)由图象猜测y与x之间的函数关系为反比例函数,
∴设y(k≠0),
把x=10,y=30代入得:k=300,
∴y,
将其余各点代入验证均适合,
∴y与x的函数关系式为:y;
(2)把y=24代入y得:x=12.5,
∴当砝码的质量为24g时,活动托盘B与点O的距离是12.5cm.
(3)根据反比例函数的增减性,即可得出,随着活动托盘B与O点的距离不断减小,砝码的示数会不断增大;
∴应添加砝码.
【类型三:温度问题】
10.解:(1)∵开机加热时每分钟上升10℃,
∴从20℃到100℃需要8分钟,
设一次函数关系式为:y=k1x+b,
将(0,20),(8,100)代入y=k1x+b,得k1=10,b=20.
∴y=10x+20(0≤x≤8),
设反比例函数关系式为:y,
将(8,100)代入,得k=800,
∴y,
当y=20时,代入关系式可得x=40;
故答案为:8;40.
(2)由(1)中计算可得,y.
(3)在y=10x+20(0≤x≤8)中,
令y=50,解得x=3;
反比例函数y中,令y=50,解得:x=16,
∴学生在每次温度升降过程中能喝到50℃以上水的时间有16﹣3=13分钟.
(4)由题意可知,饮水机工作时40分钟为一个循环,
上午七点到上午第一节下课时(8:40)的时间是100分钟,是2个40分钟多20分钟,
∴40(℃),
∴学生上午第一节下课时(8:40)不能喝到超过50℃的水.
11.解:(1)停止加热时,设y与x的函数解析式为y,
由题意得:50,
解得k=750,
y,
当y=25时,x30,
当y=100时,x7.5,
∴B点坐标为(7.5,100),
∴A点坐标为(6,100),
当加热烧水时,设y=ax+25,
由题意得:100=6a+25,
解得:a=12.5,
∴当加热烧水,函数关系式为y=12.5x+25(0≤x≤6);
当停止加热,得y与x的函数关系式为y=100(6<x≤7.5);y(7.5<x≤30);
(2)把y=80代入y得,80,
解得x=9.375,
9.375﹣6=3.375,
因此从烧水开到泡茶需要等待3.375分钟.
12.解:(1)设直线AB的函数解析式为:y=kx+b(k≠0),根据题意,可得,
解得,
∴直线y=2x+10,
当x=5时,y=2×5+10=20,
∴恒定温度为:20℃;
(2)由(1)可知:正比例函数解析式为y=2x+10(0≤x≤5),
根据图象可知:y=20(5<x≤10),
设10<x≤24小时内函数解析式为:,
根据题意,可得方程:,
∴k=200,
∴函数解析式为:,
∴24小时函数解析式为:y;
(3)当0≤x≤5时,12=2x+10,
∴x=1,
∵当10<x≤24时,12,
∴x,
∴(h),
∴这天内恒温系统最多可以关闭小时,才能避免水果生长受到影响.
13.解:(1)由图象可知,当0 x 8时是一次函数,
设y=kx+b将(0,20)、(8,100)代入得:
,解得,
水温y(℃)与开机时间x(分)的函数关系式为:y=10x+20(0≤x≤8);
(2)在水温下降过程中,设水温y(℃)与开机时间x(分)的函数关系式为y,依据题意得:100即m=800,
∴反比例函数解析式为:y,
当y=20时,20,
解得:t=40;
(3)由(2)t=40,结合图象,可知每40分钟图象重复出现一次,
7:10到11:15经历时间为245分钟,
245÷40=6 5,8>5,
∴当x=5时,y=10×5+20=70(℃),
答:饮水机内水温约为70℃,共有6次达到100℃.
【类型四:课堂注意力问题】
14.解:(1)设CD的解析式为:,
由C(20,48)得k=960,
∴D(40,24),
由图可知:点A的注意力指标数是24.
(2)当0≤x<10时,设AB的解析式为y=kx+b,
∴,
∴.
∴.
(3):张老师能经过适当安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36.
理由:当y≥36时,,
解得x≥5;
当20≤x≤40时,反比例函数解析为,
当y≥36时,,
解得.
∴当时,注意力指标数都不低于36.
而,
∴张老师能经过适当安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36.
【类型五:浓度问题】
15.解:(1)由题意,设药物燃烧时y关于x的函数关系式是y=kx(k≠0),将点(8,6)代入,∴8k=6.
∴k.
∴药物燃烧时y关于x的函数关系式是yx,自变量 x的取值范围是0≤x≤8;
(2)由题意,设药物燃烧后y关于x的函数关系式是y,把(8,6)代入,
∴m=48.
∴药物燃烧后y与x的函数关系式为y.
(3)由题意,当y=1.6时,代入y,
∴x=30.
∴从药薰开始,至少需要经过 30 分钟后,学生才能回到教室;
(4)此次灭蚊有效,将y=3分别代入yx,y,
∴x=4和x=16,
∴持续时间是16﹣4=12(min)>10min,
∴能有效杀灭室内的蚊虫.
16.解:(1)设生产1支单针疫苗需要a min,生产1支双针疫苗需要b min.
根据题意得:,
解得:,
答:生产1支单针疫苗需要3min;生产1支双针疫苗需要5min;
(2)当x>0.7时,设函数解析式为,
将(0.7,910)代入,
解得m=637,故,
当y=50时,则,
当y=23时,则,
所以小明应在打第二针疫苗的时间段为打第一针后的第13天到27天内.
【类型六:电路问题】
17.
【分析】根据,R1=2Ω,R2=8Ω,Rx=4Ω,求出Ry=4Ω,因为将Ry减小3Ω,故把Ry=1Ω代入算出调整后的Rx=16Ω,即可作答.
【解答】解:∵,R1=2Ω,R2=8Ω,Rx=4Ω,
∴,
∴Ry=4Ω,
∵将Ry减小3Ω,
∴调整后的Ry=1Ω,
∵电流表示数才能为0,
∴,
则,
解得Rx=16Ω,
∴16Ω﹣4Ω=12Ω,
即Rx增大12Ω,
故选:A.
18.
【分析】根据图象和已知条件利用反比例函数的关系解答即可.
【解答】解:根据图象和已知条件利用反比例函数的关系解答如下:
A.电流I随电阻R1的增大而减小,故该选项不正确,不符合题意;
B.电流I与总电阻成反比例函数关系,故该选项不正确,不符合题意;
C.电阻R两端的电压随R1的增大而减小,故该选项正确,符合题意;
D.当电阻R1为0时,电路中的电流最大,故该选项不正确,不符合题意.
故选:C.
19.解:(1)根据题意,3,b,
∴a=2,b=1.5;
故答案为:2,1.5;
(2)①根据表格数据描点:(1,4),(2,3),(3,2.4),(4,2),(6,1.5),在平面直角坐标系中画出对应函数y(x≥0)的图象如下:
②由图象可知,随着自变量x的不断增大,函数值y的变化趋势是不断减小,
故答案为:不断减小;
(3)如图:
由函数图象知,当x≥2或x=0时,x+6,
即当x≥0时,x+6的解集为 x≥2或x=0,
故答案为:x≥2或x=0.
【类型七:效率问题】
20.
【分析】求出反比例函数的解析式,再根据题意列出x的不等式,即可解得答案.
【解答】解:设y,把(1.5,400)代入得:
400,
解得k=600,
∴y,
当y≤120时,
120,
∴x≥5,
故选:A.
21.
【分析】利用待定系数法求出反比例函数解析式,后再将m=100代入计算即可.
【解答】解:∵智能机器人的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,机器狗载重后总质量m=60kg时,它的最快移动速度v=6m/s,
设反比例函数解析式为,代入得:
k=60×6=360,
∴反比例函数解析式为,
当m=100时,,
故答案为:3.6.
22.解:(1)设反比例函数解析式为y,
∵点(120,0.5)在反比例函数图象上,
∴k=120×0.5=60,
∴反比例函数解析式为:y;
(2)当y≤3000=0.3万元时,
即0.3,解得x≥200.
答:计划每月偿还贷款不超过3000元,则至少需要200个月还清.
23.解:(1)设y与x之间的函数表达式为y,
根据题意得:50,
解得k=400,
∴y与x之间的函数表达式为y;
(2)∵x=5,∴y=400÷5=80,
解得:y=80;
答:平均每天至少要卸80吨货物;
(3)∵每人一天可卸货:50÷10=5(吨),
∴80÷5=16(人),16﹣10=6(人).
答:码头至少需要再增加6名工人才能按时完成任务.
【其他问题】
24.
【分析】设反比例函数表达式为(k>0),过八(1)点,八(3)点作y轴的平行线交反比例函数于A,B,设八(1)点为(x1,y1),八(2)点为(x2,y2),八(3)点为(x3,y3),八(4)点为(x4,y4),点A为(x1,y1'),点B为x3,y3'),然后比较x1y1,x2y2,x3y3,x4y4与k的大小即可得出答案.
【解答】解:设反比例函数的表达式为(k>0),
过八(1)点,八(3)点作y轴的平行线交反比例函数于A,B,
设八(1)点为(x1,y1),八(2)点(x2,y2),八(3)点为(x3,y3),八(4)点(x4,y4),点A为(x1,y1'),点B为(x3,y3'),
由图象可知:y1>y1',y3<y3',
依题意得:x1y1,x2y2,x3y3,x4y4分别为八(1),八(2),八(3),八(4)的优秀人数.
∵八(2)点,A点,B点,八(4)点在反比例函数的图象上,
∴k=x2y2=x1y1'=x3y3'=x4y4,
∵y1>y1',y3<y3',
∴x1y1>x1y1'=k,x3y3<x3y3'=k,
∴x1y1>x2y2=x4y4>x3y3,
即:八(1)班优秀人数>八(2)班优秀人数=八(4)班优秀人数>八(3)班优秀人数,
∴八(1)班的优秀人数为最多.
故选:A.
25.
【分析】根据题意可知xy的值即为该级部的优秀人数,再根据图象即可确定丙学校的优秀人数最多,甲学校的优秀人数最少,乙、丁两学校的优秀人数相同.
【解答】解:根据题意,可知xy的值即为该校的优秀人数,
∵描述乙、丁两学校情况的点恰好在同一个反比例函数的图象上,
∴乙、丁两学校的优秀人数相同,
∵点丙在反比例函数图象上面,点甲在反比例函数图象下面,
∴丙学校的xy的值最大,即优秀人数最多,甲学校的xy的值最小,即优秀人数最少,
故选:C.
26.
【分析】先根据V=Sh得出S关于h的函数解析式,再根据反比例函数的性质解答.
【解答】解:∵V=Sh(V为不等于0的常数),
∴,S是h的反比例函数,
∵V>0,h>0,
∴图象为双曲线在第一象限内的部分,
故选:C.
27.
【分析】根据题意和图象,分别分析判断各选项正误即可.
【解答】解:根据题意和图象,分别分析判断各选项正误如下:
A、反比例函数的走向是越来越靠近坐标轴,故说法错误,不符合题意;
B、随着滚刷滚速的增加,除尘能力增加得越来越慢,但成正比例是一条直线,而图中是一条曲线,故说法错误,不符合题意;
C、当滚速为1300转/分时,除尘能力为35.5不及格,故说法错误,不符合题意;
D.当除尘能力为36.5%时,滚剧的滚速为1400转/分,故说法正确,符合题意.
故选:D.
【类型一:压强问题】
1.根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图象如图所示.当S=0.25m2时,该物体承受的压强p的值为 Pa.
2.力F(N)作用于物体,产生的压强p(kPa)与物体受力面积S(m2)之间满足,在某次实验中,当F一定时,p关于S的函数图象如图所示.若压强p由40kPa增压至60kPa,则物体受力面积S( )
A.减小了25m2 B.增大了25m2
C.减小了20m2 D.增大了20m2
3.如图1,这是一个可改变体积的密闭容器的简易图,在该容器内装有一定质量的氧气,当改变容器的体积时,气体的密度也会随之改变.随着容器体积的改变,该密闭容器内氧气的密度ρ(单位:kg/m3)随容器体积V(单位:m3)变化的关系图象如图2所示,结合图3信息窗中的内容,下列说法不正确的是( )
A.当该容器的体积V为25m3时,氧气的密度ρ为0.32kg/m3
B.该容器内氧气的密度ρ是关于体积V的反比例函数
C.若容器内氧气的密度为1.43kg/m3,则该容器的体积约为4.59m3
D.该容器内氧气的质量为8kg
4.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化.已知密度ρ与体积V是反比例函数关系,它的图象如图所示,当V=2.5m3时,ρ=4kg/m3.
(1)求密度ρ关于体积V的函数表达式;
(2)当V=5m3时,求二氧化碳密度ρ的值.
【类型二:杠杆原理问题】
5.阿基米德说:“给我一个支点,我就能撬动整个地球”,这句话精辟地阐明了一个重要的物理学知识杠杆原理,即“阻力×阻力臂=动力×动力臂”.若某杠杆的阻力和阻力臂分别为1000N和0.6m,则它的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
6.公元前3世纪,古希腊科学家阿基米德发现:若两物体与支点的距离和其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力x阻力臂=动力x动力臂.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为5000N和0.2m,动力臂为4m,则撬动这块大石头至少需要的动力是( )
A.200N B.250N C.300N D.350N
7.如图,物理实验课上小明设计了一个探索杠杆平衡条件的实验,在一根质地均匀的木杆中点O处用一根细绳挂在支架上,在点O的左侧固定位置B处悬挂重物A,在点O的右侧用一个弹簧测力计向下拉木杆,使木杆达到平衡(杠杆平衡时,动力×动力臂=阻力×阻力臂).改变弹簧测力计与点O的距离x(cm),观察弹簧测力计的示数y(N)的变化情况,实验数据记录如下:
x(cm) … 10 15 20 25 30 …
y(N) … 30 20 15 12 10 …
观察表中的数据,当弹簧测力计与点O的距离x为40cm时,弹簧测力计的示数y的值是( )
A.5 B.7.5 C.10 D.120
8.杠杆原理在生活中应用广泛,我国早在春秋时期就有使用,杠杆原理为:阻力×阻力臂=动力×动力臂(如图①).某数学兴趣小组利用所学的函数知识对以上原理进行探究:如图②,小明取一根长100cm质地均匀的木杆,用细绳绑在木杆的中点O处将其吊在空中,在中点的左侧距中点25cm处挂一个重10N的物体(即支点为O,阻力为10N,阻力臂为25cm),在中点右侧用一个弹簧测力计(重力忽略不计)竖直向下拉,使木杆处于水平状态,改变弹簧测力计与中点O的距离x(cm),观察弹簧测力计的示数y(N)的变化(即动力臂为x cm,动力为yN),在平面直角坐标系中描出了一系列点(x,y),并用平滑的曲线顺次连接,得到如图③所示的函数图象.
(1)求图③中的函数解析式;
(2)若点O的位置不变,在不改变点O与物体的距离及物体重力的前提下,要想使木杆平衡,弹簧测力计的示数最小可以是多少?
9.如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) 10 15 20 25 30
y(g) 30 20 15 12 10
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
【类型三:温度问题】
10.我校的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至20℃时自动开机加热,重复上述自动程序.若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示.
(1)a= ,b= .
(2)直接写出图中y关于x的函数表达式.
(3)饮水机有多少时间能使水温保持在50℃及以上?
(4)若某天上午7:00饮水机自动接通电源,开机温度正好是20℃,问学生上午第一节下课时(8:40)能喝到50℃以上的水吗?请说明理由.
11.喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分半钟后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是25℃,降温过程中水温不低于25℃.
(1)分别写出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
12.某水果生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启后阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)这个恒温系统设定的恒定温度为多少℃;
(2)求全天的温度y(℃)与时间x(h)之间的函数关系式;
(3)若大棚内的温度低于12℃时,蔬菜会受到伤害,问:这天内恒温系统最多可以关闭多少小时,才能避免水果生长受到影响?
13.小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)有一天,小明在上午7:10(水温20℃),开机通电后去上学,中午放学回到家时间刚好11:15,请问此时饮水机内水的温度约为多少℃?并求:在7:10﹣11:15这段时间里,水温共有几次达到100℃?
【类型四:课堂注意力问题】
14.通过实验研究发现:初中生在数学课上听课注意力指标数随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标数y随时间x(分)变化的函数图象如图所示.当0≤x<10和10≤x<20时,图象是线段:当20≤x≤40时,图象是双曲线的一部分,根据函数图象回答下列问题:
(1)点A的注意力指标数是 ;
(2)当0≤x<10时,求注意力指标数y随时间x(分)的函数解析式;
(3)张老师在一节课上讲解一道数学综合题需要20分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36?请说明理由.
【类型五:浓度问题】
15.某校对教室采用药薰法进行灭蚊.根据药品使用说明,药物燃烧时,室内每立方米空气中含药量y(mg/m3)与药物点燃后的时间x(min)成正比例,药物燃尽后,y与x成反比例(如图).已知药物点燃后8min燃尽,此时室内每立方米空气中含药量为6mg.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)根据灭蚊药品使用说明,当空气中每立方米的含药量低于1.6mg时,对人体是安全的.那么从开始药薰,至少经过多少时间,学生才能进入教室?
(4)根据灭蚊药品使用说明,当每立方米空气中含药量不低于3mg且持续时间不低于10min时,才能有效杀灭室内的蚊虫,那么此次灭蚊是否有效?为什么?
16.新冠疫情下的中国在全世界抗疫战斗中全方位领跑.某制药公司生产3支单针疫苗和2支双针疫苗需要19min;生产2支单针疫苗和1支双针疫苗需要11min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间?
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:min/mL)与时间x(单位:天)的函数关系如图所示:疫苗注射后体内抗体浓度首先y与x成一次函数关系,体内抗体到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50min/mL时,并且不低于23min/mL,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.请问:小明可以在哪个时间段内打第二针疫苗?请通过计算说明.
【类型六:电路问题】
17.如图所示为一测量电路,Ry为待测电阻,Rx为可调电阻,R,R1,R2为已知电阻,E为直流电压源,A为电流表,调节Rx的电阻时会出现一种现象,即当电流表读数为0时,有,这个现象叫做电桥平衡,并且此时的电阻R对电路无影响.由上式便可通过Rx的电阻求得Ry的电阻,现已知R1=2Ω,R2=8Ω.当Rx=4Ω时电流表读数为0,那么此时将Ry减小3Ω,则Rx需要如何变,电流表示数才能为0?( )
A.增大12Ω B.增大8Ω C.减小3Ω D.减小1Ω
18.小宁利用如图(1)所示的电路(电源电压不变,R为定值电阻)进行了如下实验:在开关S闭合的情况下,改变电阻箱R1的阻值,读取电流表示数.根据实验数据,小宁绘制了如图(2)所示的电流表示数I随R1变化的曲线.
信息框 1.欧姆定律:导体中的电流,跟导体两端的电压成正比,跟导体的电阻成反比. 2.电流表的电阻忽略不计.
下列说法正确的是( )
A.电流I随电阻R1的增大而增大
B.电流I与电阻R1成反比例函数关系
C.电阻R两端的电压随R1的增大而减小
D.当电阻R1为0时,电路中的电流最小
19.在一次物理实验中,小冉同学用一固定电压为U=12(V)的蓄电池,通过调节滑动变阻器R(Ω)来改变电流大小,完成控制灯泡L(灯丝的阻值R1=2Ω)亮度的实验(如图1,假设灯泡的电阻不随温度的变化而变化),已知串联电路中,电流I与电阻R、RL之间关系为,通过得出如下数据(表格数据不完整):
R/Ω … 1 a 4 6 …
I/A … 4 3 2 b …
(1)a= ,b= ;
(2)根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质.
①在直角坐标系中画出对应函数的图象:
②随着自变量x的不断增大,函数值y的变化趋势是 .
(3)请结合函数图象分析,当x≥0时,的解集为 .
【类型七:效率问题】
20.装卸机往一艘轮船上装载货物,装完货物所需时间y(分钟)与装载速度x(吨/分钟)之间的函数关系如图所示.若要求在120分钟内(包括120分钟)装完这批货物,则x的取值范围是( )
A.x≥5 B.x≥3 C.0<x≤5 D.0<x≤3
21.快递运载机器人是一种应用于配送领域的智能机器人,它的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数.已知一款快递运载机器人载重后总质量m=60kg时,它的最快移动速度v=6m/s;当其载重后总质量m=100kg时,它的最快移动速度v= m/s.
22.小明家购买一套商品房,首付45万元,剩余部分需贷款并按“等额本金”的形式偿还,即贷款金额按月分期还款,且每月偿还贷款金额数相同.若设每月偿还贷款金额y万元,x个月还清,且y是x的反比例函数,其图象如图所示.
(1)求y与x的函数关系式;
(2)若小明家计划每月偿还贷款金额不超过3000元,求至少需要多少个月还清?
23.码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/天)与装完货物所需时间x(天)之间是反比例函数关系,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)由于紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸货多少吨?
(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
【其他问题】
24.学校举行数学文化竞赛.图中的四个点分别描述了八(1)、八(2)、八(3)、八(4)四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图象上,则成绩优秀人数最多的是( )
A.八(1)班 B.八(2)班 C.八(3)班 D.八(4)班
25.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
A.甲 B.乙 C.丙 D.丁
26.某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图象大致是( )
A. B.
C. D.
27.如图(1)所示的家用扫地机器人,其底部安装有滚刷,内置集尘器.机器人在除尘时先“脱灰”(滚刷将灰尘从地面上脱离附着),后“吸灰”(将脱附的灰尘转移进集尘器).为研究滚刷滚速对“脱灰”效果的影响,小静在保持扫地机器人“吸灰”效果一定的情况下,对“吸灰”过程中滚刷的滚速与除尘能力C(在地面撒灰后,清扫十次所减少的灰占所撒的灰总质量的百分比)进行了试验,得到如图(2)所示的关系图,规定除尘能力C超过36%即为及格.则下列说法正确的是( )
A.除尘能力关于滚刷的滚速的图象是反比例函数图象的一部分
B.除尘能力与滚刷的滚速成正比
C.当滚速为1300转/分时,除尘能力为及格
D.当除尘能力为36.5%时,滚剧的滚速为1400转/分
参考答案
【类型一:压强问题】
1.
【分析】设p,把(0.1,1000)代入得到反比例函数的解析式,再把S=0.25代入解析式即可解决问题.
【解答】解:设p,
∵函数图象经过(0.1,1000),
∴k=100,
∴p,
当S=0.25m2时,物体所受的压强p400(Pa),
故答案为:400.
2.
【分析】结合图象得到,再分别求出当压强p为40kPa和60kPa时的受力面积,并进行比较,即可解题.
【解答】解:∵F一定,
结合图象可知F=100×30=3000(N),即,
当压强p为40kPa时,有,解得S=75(m2),
当压强p为60kPa时,有,解得S=50(m2),
∵75﹣50=25(m2),
故选:A.
3.
【分析】先求出反比例函数解析式,然后对各选项分析即可.
【解答】解:∵,且容器内氧气的质量一定,
∴是反比例函数,故B正确,不符合题意;
当V=2时,ρ=4,
∴m=ρV=8,故D正确,不符合题意;
∴,
当V=25m3时,,故A正确,不符合题意;
当ρ=1.43时,,故C不正确,符合题意.
故选:C.
4.解:(1)设p,
由题意得:k=p V=2.5×4=10,
∴密度ρ关于体积V的函数表达式为:p;
当V=5m3时,p2kg/m3.
【类型二:杠杆原理问题】
5.
【分析】直接利用阻力×阻力臂=动力×动力臂,进而得出动力F关于动力臂l的函数关系式,从而确定其图象即可.
【解答】解:∵阻力×阻力臂=动力×动力臂,且阻力和阻力臂分别为1000N和0.6m,
∴动力F关于动力臂l的函数解析式为:1000×0.6=Fl,
即F,是反比例函数,
又∵动力臂l>0,
反比例函数F的图象是双曲线,且在第一象限.
故选:B.
6.
【分析】根据“阻力×阻力臂=动力×动力臂”,代入数据即可解答.
【解答】解:∵“阻力×阻力臂=动力×动力臂”,
∴5000×0.2=动力×4,
∴动力为250N,
因此,撬动这块大石头至少需要的动力是250N,
故选:B.
7.
【分析】依据题意,根据表格数据求出y与x的函数关系,求出解析式,将x=40代入即可.
【解答】解:观察表格数据可得,y与x成反比例函数关系,设y,
∴k=10×30=300.
∴函数为y.
又当x=400时,y7.5
∴弹簧测力计的示数y的值是7.5.
故选:B.
8.解:(1)已知杠杆原理的公式:阻力×阻力臂=动力×动力臂,阻力为10N,阻力臂为25cm,动力臂为x cm,动力为y N,则有x y=10×25,
∴图③中的函数解析式为.
(2)由反比例函数解析式可知:当x最大时,y最小,
∵由于支点即为细绳悬挂点,
∴x>0.
∴x≤50.
综上,0<x≤50.
∴当x=50cm时,.
9.解:(1)由图象猜测y与x之间的函数关系为反比例函数,
∴设y(k≠0),
把x=10,y=30代入得:k=300,
∴y,
将其余各点代入验证均适合,
∴y与x的函数关系式为:y;
(2)把y=24代入y得:x=12.5,
∴当砝码的质量为24g时,活动托盘B与点O的距离是12.5cm.
(3)根据反比例函数的增减性,即可得出,随着活动托盘B与O点的距离不断减小,砝码的示数会不断增大;
∴应添加砝码.
【类型三:温度问题】
10.解:(1)∵开机加热时每分钟上升10℃,
∴从20℃到100℃需要8分钟,
设一次函数关系式为:y=k1x+b,
将(0,20),(8,100)代入y=k1x+b,得k1=10,b=20.
∴y=10x+20(0≤x≤8),
设反比例函数关系式为:y,
将(8,100)代入,得k=800,
∴y,
当y=20时,代入关系式可得x=40;
故答案为:8;40.
(2)由(1)中计算可得,y.
(3)在y=10x+20(0≤x≤8)中,
令y=50,解得x=3;
反比例函数y中,令y=50,解得:x=16,
∴学生在每次温度升降过程中能喝到50℃以上水的时间有16﹣3=13分钟.
(4)由题意可知,饮水机工作时40分钟为一个循环,
上午七点到上午第一节下课时(8:40)的时间是100分钟,是2个40分钟多20分钟,
∴40(℃),
∴学生上午第一节下课时(8:40)不能喝到超过50℃的水.
11.解:(1)停止加热时,设y与x的函数解析式为y,
由题意得:50,
解得k=750,
y,
当y=25时,x30,
当y=100时,x7.5,
∴B点坐标为(7.5,100),
∴A点坐标为(6,100),
当加热烧水时,设y=ax+25,
由题意得:100=6a+25,
解得:a=12.5,
∴当加热烧水,函数关系式为y=12.5x+25(0≤x≤6);
当停止加热,得y与x的函数关系式为y=100(6<x≤7.5);y(7.5<x≤30);
(2)把y=80代入y得,80,
解得x=9.375,
9.375﹣6=3.375,
因此从烧水开到泡茶需要等待3.375分钟.
12.解:(1)设直线AB的函数解析式为:y=kx+b(k≠0),根据题意,可得,
解得,
∴直线y=2x+10,
当x=5时,y=2×5+10=20,
∴恒定温度为:20℃;
(2)由(1)可知:正比例函数解析式为y=2x+10(0≤x≤5),
根据图象可知:y=20(5<x≤10),
设10<x≤24小时内函数解析式为:,
根据题意,可得方程:,
∴k=200,
∴函数解析式为:,
∴24小时函数解析式为:y;
(3)当0≤x≤5时,12=2x+10,
∴x=1,
∵当10<x≤24时,12,
∴x,
∴(h),
∴这天内恒温系统最多可以关闭小时,才能避免水果生长受到影响.
13.解:(1)由图象可知,当0 x 8时是一次函数,
设y=kx+b将(0,20)、(8,100)代入得:
,解得,
水温y(℃)与开机时间x(分)的函数关系式为:y=10x+20(0≤x≤8);
(2)在水温下降过程中,设水温y(℃)与开机时间x(分)的函数关系式为y,依据题意得:100即m=800,
∴反比例函数解析式为:y,
当y=20时,20,
解得:t=40;
(3)由(2)t=40,结合图象,可知每40分钟图象重复出现一次,
7:10到11:15经历时间为245分钟,
245÷40=6 5,8>5,
∴当x=5时,y=10×5+20=70(℃),
答:饮水机内水温约为70℃,共有6次达到100℃.
【类型四:课堂注意力问题】
14.解:(1)设CD的解析式为:,
由C(20,48)得k=960,
∴D(40,24),
由图可知:点A的注意力指标数是24.
(2)当0≤x<10时,设AB的解析式为y=kx+b,
∴,
∴.
∴.
(3):张老师能经过适当安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36.
理由:当y≥36时,,
解得x≥5;
当20≤x≤40时,反比例函数解析为,
当y≥36时,,
解得.
∴当时,注意力指标数都不低于36.
而,
∴张老师能经过适当安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36.
【类型五:浓度问题】
15.解:(1)由题意,设药物燃烧时y关于x的函数关系式是y=kx(k≠0),将点(8,6)代入,∴8k=6.
∴k.
∴药物燃烧时y关于x的函数关系式是yx,自变量 x的取值范围是0≤x≤8;
(2)由题意,设药物燃烧后y关于x的函数关系式是y,把(8,6)代入,
∴m=48.
∴药物燃烧后y与x的函数关系式为y.
(3)由题意,当y=1.6时,代入y,
∴x=30.
∴从药薰开始,至少需要经过 30 分钟后,学生才能回到教室;
(4)此次灭蚊有效,将y=3分别代入yx,y,
∴x=4和x=16,
∴持续时间是16﹣4=12(min)>10min,
∴能有效杀灭室内的蚊虫.
16.解:(1)设生产1支单针疫苗需要a min,生产1支双针疫苗需要b min.
根据题意得:,
解得:,
答:生产1支单针疫苗需要3min;生产1支双针疫苗需要5min;
(2)当x>0.7时,设函数解析式为,
将(0.7,910)代入,
解得m=637,故,
当y=50时,则,
当y=23时,则,
所以小明应在打第二针疫苗的时间段为打第一针后的第13天到27天内.
【类型六:电路问题】
17.
【分析】根据,R1=2Ω,R2=8Ω,Rx=4Ω,求出Ry=4Ω,因为将Ry减小3Ω,故把Ry=1Ω代入算出调整后的Rx=16Ω,即可作答.
【解答】解:∵,R1=2Ω,R2=8Ω,Rx=4Ω,
∴,
∴Ry=4Ω,
∵将Ry减小3Ω,
∴调整后的Ry=1Ω,
∵电流表示数才能为0,
∴,
则,
解得Rx=16Ω,
∴16Ω﹣4Ω=12Ω,
即Rx增大12Ω,
故选:A.
18.
【分析】根据图象和已知条件利用反比例函数的关系解答即可.
【解答】解:根据图象和已知条件利用反比例函数的关系解答如下:
A.电流I随电阻R1的增大而减小,故该选项不正确,不符合题意;
B.电流I与总电阻成反比例函数关系,故该选项不正确,不符合题意;
C.电阻R两端的电压随R1的增大而减小,故该选项正确,符合题意;
D.当电阻R1为0时,电路中的电流最大,故该选项不正确,不符合题意.
故选:C.
19.解:(1)根据题意,3,b,
∴a=2,b=1.5;
故答案为:2,1.5;
(2)①根据表格数据描点:(1,4),(2,3),(3,2.4),(4,2),(6,1.5),在平面直角坐标系中画出对应函数y(x≥0)的图象如下:
②由图象可知,随着自变量x的不断增大,函数值y的变化趋势是不断减小,
故答案为:不断减小;
(3)如图:
由函数图象知,当x≥2或x=0时,x+6,
即当x≥0时,x+6的解集为 x≥2或x=0,
故答案为:x≥2或x=0.
【类型七:效率问题】
20.
【分析】求出反比例函数的解析式,再根据题意列出x的不等式,即可解得答案.
【解答】解:设y,把(1.5,400)代入得:
400,
解得k=600,
∴y,
当y≤120时,
120,
∴x≥5,
故选:A.
21.
【分析】利用待定系数法求出反比例函数解析式,后再将m=100代入计算即可.
【解答】解:∵智能机器人的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,机器狗载重后总质量m=60kg时,它的最快移动速度v=6m/s,
设反比例函数解析式为,代入得:
k=60×6=360,
∴反比例函数解析式为,
当m=100时,,
故答案为:3.6.
22.解:(1)设反比例函数解析式为y,
∵点(120,0.5)在反比例函数图象上,
∴k=120×0.5=60,
∴反比例函数解析式为:y;
(2)当y≤3000=0.3万元时,
即0.3,解得x≥200.
答:计划每月偿还贷款不超过3000元,则至少需要200个月还清.
23.解:(1)设y与x之间的函数表达式为y,
根据题意得:50,
解得k=400,
∴y与x之间的函数表达式为y;
(2)∵x=5,∴y=400÷5=80,
解得:y=80;
答:平均每天至少要卸80吨货物;
(3)∵每人一天可卸货:50÷10=5(吨),
∴80÷5=16(人),16﹣10=6(人).
答:码头至少需要再增加6名工人才能按时完成任务.
【其他问题】
24.
【分析】设反比例函数表达式为(k>0),过八(1)点,八(3)点作y轴的平行线交反比例函数于A,B,设八(1)点为(x1,y1),八(2)点为(x2,y2),八(3)点为(x3,y3),八(4)点为(x4,y4),点A为(x1,y1'),点B为x3,y3'),然后比较x1y1,x2y2,x3y3,x4y4与k的大小即可得出答案.
【解答】解:设反比例函数的表达式为(k>0),
过八(1)点,八(3)点作y轴的平行线交反比例函数于A,B,
设八(1)点为(x1,y1),八(2)点(x2,y2),八(3)点为(x3,y3),八(4)点(x4,y4),点A为(x1,y1'),点B为(x3,y3'),
由图象可知:y1>y1',y3<y3',
依题意得:x1y1,x2y2,x3y3,x4y4分别为八(1),八(2),八(3),八(4)的优秀人数.
∵八(2)点,A点,B点,八(4)点在反比例函数的图象上,
∴k=x2y2=x1y1'=x3y3'=x4y4,
∵y1>y1',y3<y3',
∴x1y1>x1y1'=k,x3y3<x3y3'=k,
∴x1y1>x2y2=x4y4>x3y3,
即:八(1)班优秀人数>八(2)班优秀人数=八(4)班优秀人数>八(3)班优秀人数,
∴八(1)班的优秀人数为最多.
故选:A.
25.
【分析】根据题意可知xy的值即为该级部的优秀人数,再根据图象即可确定丙学校的优秀人数最多,甲学校的优秀人数最少,乙、丁两学校的优秀人数相同.
【解答】解:根据题意,可知xy的值即为该校的优秀人数,
∵描述乙、丁两学校情况的点恰好在同一个反比例函数的图象上,
∴乙、丁两学校的优秀人数相同,
∵点丙在反比例函数图象上面,点甲在反比例函数图象下面,
∴丙学校的xy的值最大,即优秀人数最多,甲学校的xy的值最小,即优秀人数最少,
故选:C.
26.
【分析】先根据V=Sh得出S关于h的函数解析式,再根据反比例函数的性质解答.
【解答】解:∵V=Sh(V为不等于0的常数),
∴,S是h的反比例函数,
∵V>0,h>0,
∴图象为双曲线在第一象限内的部分,
故选:C.
27.
【分析】根据题意和图象,分别分析判断各选项正误即可.
【解答】解:根据题意和图象,分别分析判断各选项正误如下:
A、反比例函数的走向是越来越靠近坐标轴,故说法错误,不符合题意;
B、随着滚刷滚速的增加,除尘能力增加得越来越慢,但成正比例是一条直线,而图中是一条曲线,故说法错误,不符合题意;
C、当滚速为1300转/分时,除尘能力为35.5不及格,故说法错误,不符合题意;
D.当除尘能力为36.5%时,滚剧的滚速为1400转/分,故说法正确,符合题意.
故选:D.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
