安徽省2025年普通高等学校招生全国统一考试 数学冲刺卷(一)(含详解)
文档属性
| 名称 | 安徽省2025年普通高等学校招生全国统一考试 数学冲刺卷(一)(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 127.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览



文档简介
2025年安徽省普通高等学校招生全国统一考试
数学冲刺卷(一)
本试卷共150分 考试时间120分钟
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={0,1},N={x|x2+x=0},则M∪N=
A.{-1,0} B.{-1,0,1} C.{1,0} D.{-1,1}
2.已知函数f(x)=5sin(ωx+φ)ω>0,|φ|<的部分图象如图所示,则ω=
A.3 B.4 C. D.2
3.(x+y)6的展开式中x3y3项的系数为
A.120 B.15 C.20 D.45
4.已知数列{an}是公差为2的等差数列,数列{bn}为等比数列,且满足b2024=2b2023,b1=2a1,b4=a9-1,则使得b10>a1+a2+a3+…+an成立的n的最大值为
A.32 B.29 C.30 D.31
5.已知直线y=kx-e与曲线y=xln x相切,则k=
A.0 B.1 C.2 D.3
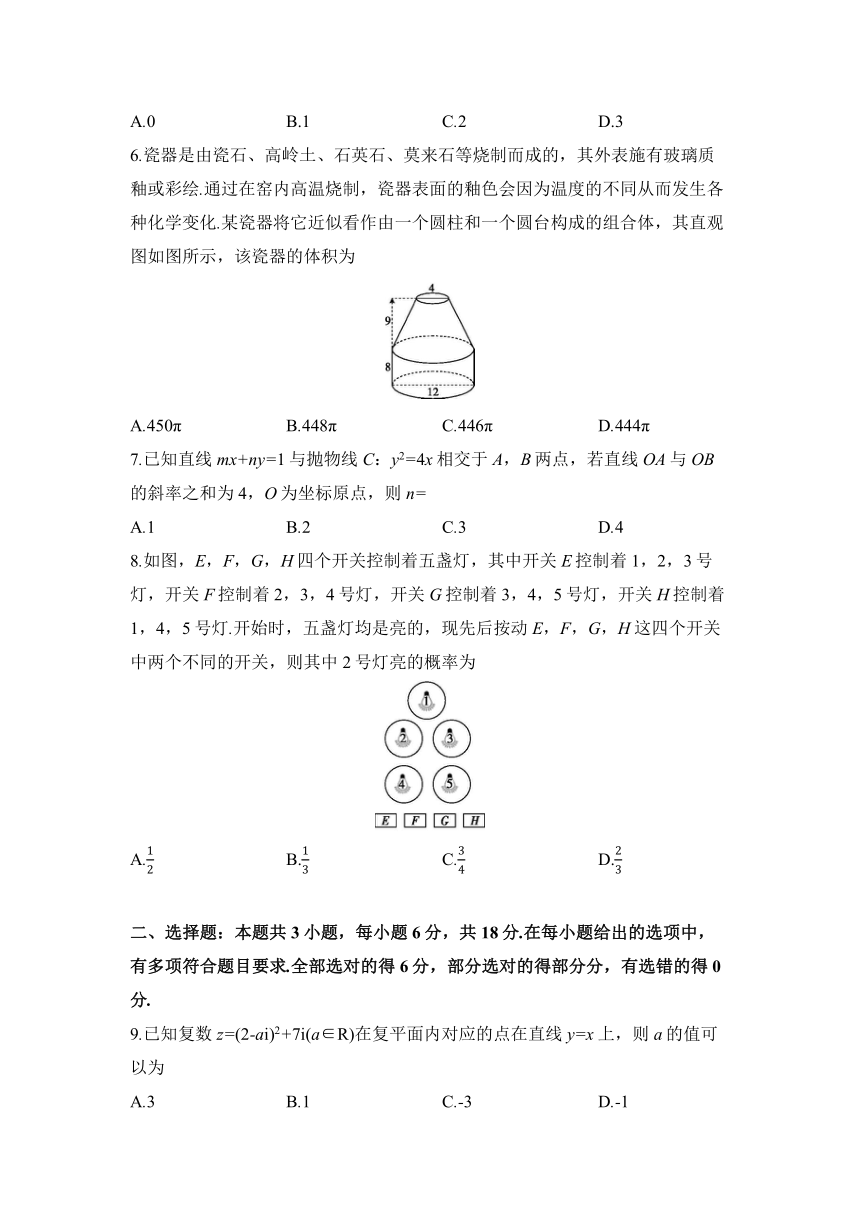
6.瓷器是由瓷石、高岭土、石英石、莫来石等烧制而成的,其外表施有玻璃质釉或彩绘.通过在窑内高温烧制,瓷器表面的釉色会因为温度的不同从而发生各种化学变化.某瓷器将它近似看作由一个圆柱和一个圆台构成的组合体,其直观图如图所示,该瓷器的体积为
A.450π B.448π C.446π D.444π
7.已知直线mx+ny=1与抛物线C:y2=4x相交于A,B两点,若直线OA与OB的斜率之和为4,O为坐标原点,则n=
A.1 B.2 C.3 D.4
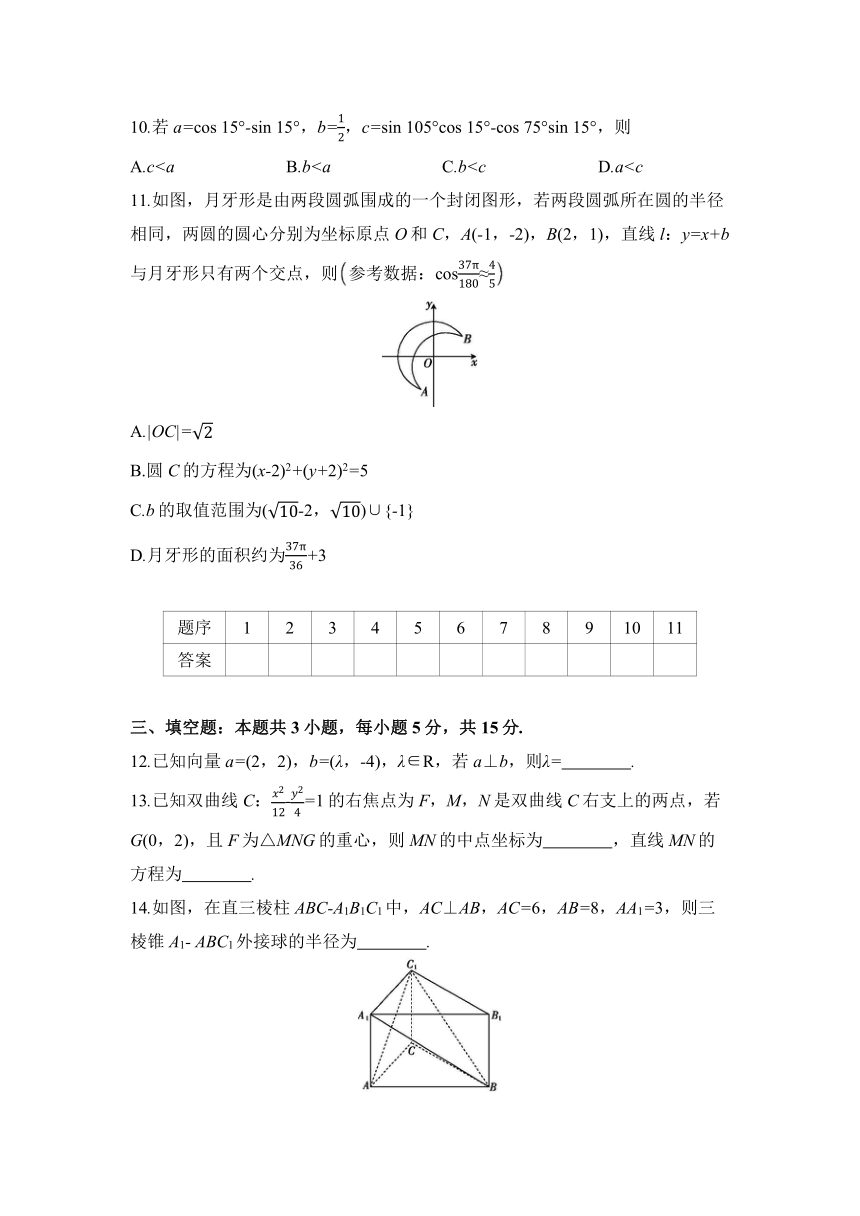
8.如图,E,F,G,H四个开关控制着五盏灯,其中开关E控制着1,2,3号灯,开关F控制着2,3,4号灯,开关G控制着3,4,5号灯,开关H控制着1,4,5号灯.开始时,五盏灯均是亮的,现先后按动E,F,G,H这四个开关中两个不同的开关,则其中2号灯亮的概率为
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数z=(2-ai)2+7i(a∈R)在复平面内对应的点在直线y=x上,则a的值可以为
A.3 B.1 C.-3 D.-1
10.若a=cos 15°-sin 15°,b=,c=sin 105°cos 15°-cos 75°sin 15°,则
A.c11.如图,月牙形是由两段圆弧围成的一个封闭图形,若两段圆弧所在圆的半径相同,两圆的圆心分别为坐标原点O和C,A(-1,-2),B(2,1),直线l:y=x+b与月牙形只有两个交点,则参考数据:cos≈
A.|OC|=
B.圆C的方程为(x-2)2+(y+2)2=5
C.b的取值范围为(-2,)∪{-1}
D.月牙形的面积约为+3
题序 1 2 3 4 5 6 7 8 9 10 11
答案
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量a=(2,2),b=(λ,-4),λ∈R,若a⊥b,则λ= .
13.已知双曲线C:-=1的右焦点为F,M,N是双曲线C右支上的两点,若G(0,2),且F为△MNG的重心,则MN的中点坐标为 ,直线MN的方程为 .
14.如图,在直三棱柱ABC-A1B1C1中,AC⊥AB,AC=6,AB=8,AA1=3,则三棱锥A1- ABC1外接球的半径为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)在△ABC中,内角A,B,C所对的边分别为a,b,c,(a+b-c)(b-a+c)-3ac=0.
(1)求B;
(2)若∠ABC的角平分线交AC于点D,且AD=2DC=,求BD.
16.(15分)如图,在正四棱柱ABCD-A1B1C1D1中,E,F分别为BB1,DD1的中点.
(1)证明:点F在平面AEC1内.
(2)若AA1=2AB,求平面A1EC1与平面AEC1夹角的余弦值.
17.(15分)已知椭圆C:+=1(a>b>0)的离心率为,直线x=ky+1过椭圆C的一个焦点,且与椭圆C相交于A,B两点,D(3,0),直线AD,BD分别与直线x=4相交于E(x1,y1),F(x2,y2)两点.
(1)求椭圆C的方程;
(2)求y1y2的值.
18.(17分)甲、乙两人进行游戏,且都有1个红色弹珠和1个黄色弹珠,每人每次独立地随机取出1个弹珠相互交换.
(1)若只交换1次,求甲的弹珠的颜色相同的概率;
(2)若只交换1次,记甲有红色弹珠的个数为X,求X的分布列及期望;
(3)若一共交换3次,最后甲的2个弹珠颜色相同,则甲获胜,否则乙获胜,试问这个游戏是否公平
19.(17分)已知函数f(x)=x2-axln x(a∈R).
(1)讨论函数f(x)极值点的个数;
(2)若x0是方程f(x)=x在(1,+∞)上的一个根,证明:x0参考答案
1.B 【命题意图】本题考查集合的基本运算,要求考生理解两个集合的并集的含义.
【解题分析】由题意得,N={-1,0},因为M={0,1},所以M∪N={-1,0,1}.
2.A 【命题意图】本题考查三角函数的图象及性质,要求考生掌握三角函数的周期性.
【解题分析】由题图知=-=,所以T==,解得ω=3.
3.C 【命题意图】本题考查二项式定理,要求考生会用二项式定理解决简单的问题.
【解题分析】(x+y)6的展开式中x3y3项的系数为=20.
4.D 【命题意图】本题考查等差及等比数列,要求考生理解等差与等比数列的通项公式及前n项和.
【解题分析】因为b2024=2b2023,所以数列{bn}的公比为2,因为b4=a9-1,所以23b1=a1+16-1,因为b1=2a1,所以15a1=15,解得a1=1,b1=2,所以an=2n-1,bn=2n,所以a1+a2+a3+…+an=n2,b10=210=1024,由1024>n2,且n∈N*,得n的最大值为31.
5.C 【命题意图】本题考查导数的几何意义,要求考生掌握导数的几何意义.
【解题分析】设切点坐标为(x0,x0ln x0),y'=1+ln x,所以y'=1+ln x0,所以切线方程为y-x0ln x0=(1+ln x0)(x-x0),即y=(1+ln x0)x-x0,所以解得k=2.
6.D 【命题意图】本题考查几何体的体积,要求考生知道圆台、圆柱体积的计算公式.
【解题分析】由直观图知,圆柱的底面半径为6,高为8,圆台的上底面半径为2,下底面半径为6,高为9,所以该瓷器的体积为π×62×8+(62+22+)×9=444π.
7.A 【命题意图】本题考查直线与抛物线的位置关系,要求考生了解抛物线的简单几何性质.
【解题分析】(方法一)由得y2=4x(mx+ny),所以-4n·-4m=0,因为直线OA与OB的斜率之和为4,所以4n=4,即n=1.
(方法二)设A点的坐标为,y1,B点的坐标为,y2,因为直线OA与OB的斜率之和为4,所以+=4,即+=1,所以y1+y2=y1y2.由得y2+y-=0,所以y1+y2=-,y1y2=-,所以-=-,解得n=1.
8.B 【命题意图】本题考查古典概型,要求考生理解古典概型.
【解题分析】先后按动E,F,G,H这四个开关中两个不同的开关,有=12种方法.
2号灯亮有两类情形.第一类,按第一个开关时,2号灯灭,按第二个开关时,2号灯亮,此时对应的方法有=2种(E,F两个开关进行全排列);
第二类,按第一个开关和第二个开关均与2号灯无关,此时对应的方法有=2种(G,H两个开关进行全排列).故所求事件的概率为=.
9.AB 【命题意图】本题考查复数的运算及几何意义,要求考生能进行复数代数表示式的四则运算并理解复数的几何意义.
【解题分析】因为z=(2-ai)2+7i=4-a2+(7-4a)i,所以4-a2=7-4a,解得a=3或a=1.
10.BCD 【命题意图】本题考查三角恒等变换,要求考生掌握两角和与差的正、余弦公式.
【解题分析】a=cos 15°-sin 15°=sin(45°-15°)=,c=sin 105°cos 15°-cos 75°sin 15°=sin 75°cos 15°-cos 75°sin 15°=sin(75°-15°)=sin 60°=,所以b11.ACD 【命题意图】本题考查直线与圆的位置关系,要求考生能根据直线、圆的方程判断直线与圆的位置关系.
【解题分析】由题易知,圆O的半径为,设圆心C的坐标为(a,-a),且a≠0,所以(a-2)2+(1+a)2=5,解得a=1,所以圆C的方程为(x-1)2+(y+1)2=5,|OC|=,故选项A正确,选项B错误.
设直线l1:y=x+t,当直线l1过点B(2,1)时,t=-1,
当直线l1与圆O相切时,=,解得t=±,
当直线l1与圆C相切时,=,
解得t=-2或t=--2,
因为直线l:y=x+b与月牙形只有两个交点,所以b的取值范围为(-2,)∪{-1},故选项C正确.
连接AC,BC,AB(图略),易求得△ABC的面积为,
设∠ACB=θ,=(-2,-1),=(1,2),所以cos θ==-,所以θ≈π-=,所以月牙形的面积约为5π-2××()2×-=+3,故选项D正确.
12.4 【命题意图】本题考查向量的运算,要求考生掌握平面向量数量积的坐标运算.
【解题分析】因为a=(2,2),b=(λ,-4),且a⊥b,所以2×λ+2×(-4)=0,解得λ=4.
13.(6,-1) 2x+y-11=0 【命题意图】本题考查直线与双曲线的位置关系,要求考生了解双曲线的简单几何性质.
【解题分析】由题知,F(4,0),设M点的坐标为(x1,y1),N点的坐标为(x2,y2),因为F为△MNG的重心,所以=4,=0,即x1+x2=12,y1+y2=-2,所以MN的中点坐标为(6,-1).因为M,N是双曲线C右支上的两点,所以两式相减并化简得=×=-2,所以直线MN的方程为y+1=-2×(x-6),即2x+y-11=0.
14. 【命题意图】本题考查立体几何的综合应用,要求考生了解几何体的外接球.
【解题分析】设G,H分别为AC1,A1B的中点,过点G,H分别作平面AA1C1,平面AA1B的垂线,交点为O,连接GH,由题知,GH=BC=5,OG2+OH2=GH2,设三棱锥A1- ABC1外接球的半径为R,所以OG2=R2-AG2,OH2=R2-AH2,所以OG2+OH2=2R2-AG2-AH2,即2R2=GH2+AG2+AH2,所以2R2=25++,解得R=.
15.【命题意图】本题考查解三角形,要求考生理解正、余弦定理.
【解题分析】(1)因为(a+b-c)(b-a+c)-3ac=0,所以b2-(a-c)2-3ac=0,
所以-ac=a2+c2-b2,所以cos B==-,因为B∈(0,π),所以B=. 6分
(2)因为AD=2DC=,所以b=,因为BD平分∠ABC,所以=,即c=2a,
由(1)知,-ac=a2+c2-b2,解得a=1,c=2,因为S△ABC=S△ABD+S△DBC,所以acsin B=a·BDsin+c·BDsin,解得BD==. 13分
16.【命题意图】本题考查点面关系及平面与平面的夹角,要求考生能用向量解决平面与平面的夹角问题.
【解题分析】(1)设G为CC1的中点,连接GF,AF,BG(图略).
由题易知GF CD,BA CD,所以GF BA,所以四边形ABGF为平行四边形,所以AF∥BG,易知BG∥EC1,所以AF∥EC1,故点F在平面AEC1内. 6分
(2)不妨设AB=1,则AA1=2,以BC,BA,BB1所在的直线分别为x,y,z轴建立空间直角坐标系,如图所示,则A(0,1,0),A1(0,1,2),E(0,0,1),C1(1,0,2),
所以=(1,0,1),=(0,1,1),=(0,1,-1).
设m=(x1,y1,z1)为平面A1EC1的法向量,
所以即令x1=1,得y1=1,z1=-1,
所以平面A1EC1的一个法向量为m=(1,1,-1).
设n=(x2,y2,z2)为平面AEC1的法向量,
所以即令x2=1,得y2=z2=-1,
所以平面AEC1的一个法向量为n=(1,-1,-1).
因为cos===,
所以平面A1EC1与平面AEC1夹角的余弦值为. 15分
17.【命题意图】本题考查直线与椭圆的位置关系,要求考生掌握椭圆的标准方程及简单几何性质.
【解题分析】(1)设c=,因为椭圆C的离心率为,所以=,因为直线x=ky+1过定点(1,0),且过椭圆C的焦点,所以c=1,所以a=3,解得b2=8,所以椭圆C的方程为+=1. 6分
(2)设A(x3,y3),B(x4,y4),由得(8k2+9)y2+16ky-64=0,
易知Δ>0,所以y3+y4=,y3y4=,
直线AD的方程为y=(x-3),令x=4得y1==,
同理可得y2=, 12分
所以y1y2====-. 15分
18.【命题意图】本题考查离散型随机变量,要求考生理解离散型随机变量的概念及分布列.
【解题分析】(1)由题知,交换1次,甲的弹珠的颜色相同的概率为×+×=. 3分
(2)由题知,若只交换1次,则甲、乙两人取红色弹珠和黄色弹珠的概率均为,X的所有可能取值为0,1,2,
P(X=0)=×=,P(X=1)=×+×=,P(X=2)=×=,
所以X的分布列为
X 0 1 2
P
所以X的期望E(X)=0×+1×+2×=1. 9分
(3)用A1,A2,A3分别表示甲第1次、第2次、第3次交换后,甲的2个弹珠颜色相同,
用B1,B2,B3分别表示甲第1次、第2次、第3次交换后,甲的2个弹珠颜色不相同.
由(1)知,P(A1)=P(B1)=P(B3|B2)=P(B2|B1)=P(A3|B2)=P(A2|B1)=,
易知P(A3|A2)=P(A2|A1)=0,由全概率公式知,
P(A3)=P(A2)P(A3|A2)+P(B2)P(A3|B2)=P(B2)P(A3|B2)=P(B2)=[1-P(A2)],
同理可得P(A2)=[1-P(A1)]=,所以P(A3)=1-=<.
故这个游戏不公平. 17分
19.【命题意图】本题考查函数与导数的综合,要求考生理解用导数讨论函数的单调性及函数的零点.
【解题分析】(1)f'(x)=2x-a(1+ln x)=2x-aln x-a,
令φ(x)=f'(x)=2x-aln x-a,则φ'(x)=2-. 1分
当a<0时,φ'(x)>0,φ(x)在(0,+∞)上单调递增,当x→0时,φ(x)→-∞,且φ(1)=2-a>0,故存在x1∈(0,1),使得φ(x1)=0,且当0x1时,φ(x)>0,所以函数f(x)有一个极值点; 3分
当a=0时,f(x)=x2在(0,+∞)上无极值点; 4分
当a>0时,若0,则φ'(x)>0,所以函数φ(x)在0,上单调递减,在,+∞上单调递增,φ=-aln.
当0当a>2时,φ<0且当x→0时,φ(x)→+∞,当x→+∞时,φ(x)→+∞,此时函数f(x)有两个极值点. 6分
综上所述,当a<0时,函数f(x)有一个极值点;当0≤a≤2时,函数f(x)无极值点;当a>2时,函数f(x)有两个极值点. 7分
(2)f(x)=x,即x2-axln x=x,所以x-1-aln x=0, 8分
令G(x)=x-1-aln x,则G'(x)=1-=. 9分
当a≤1时,G(x)在(1,+∞)上单调递增,G(x)>G(1)=0,方程f(x)=x无解, 10分
当a>1时,易知G(x)在(1,a)上单调递减,在(a,+∞)上单调递增,
所以G(a)令g(x)=x2-2xln x-1(x>1),则g'(x)=2x-2(1+ln x)(x>1),
设h(x)=x-1-ln x(x>1),则h'(x)=1-=>0,
所以h(x)在区间(1,+∞)上单调递增,所以h(x)>h(1)=0,即g'(x)>0, 15分
所以g(x)在区间(1,+∞)上单调递增,所以g(a)>g(1)=0,即G(a2)>0, 16分
因为G(x0)=0,所以x0
数学冲刺卷(一)
本试卷共150分 考试时间120分钟
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={0,1},N={x|x2+x=0},则M∪N=
A.{-1,0} B.{-1,0,1} C.{1,0} D.{-1,1}
2.已知函数f(x)=5sin(ωx+φ)ω>0,|φ|<的部分图象如图所示,则ω=
A.3 B.4 C. D.2
3.(x+y)6的展开式中x3y3项的系数为
A.120 B.15 C.20 D.45
4.已知数列{an}是公差为2的等差数列,数列{bn}为等比数列,且满足b2024=2b2023,b1=2a1,b4=a9-1,则使得b10>a1+a2+a3+…+an成立的n的最大值为
A.32 B.29 C.30 D.31
5.已知直线y=kx-e与曲线y=xln x相切,则k=
A.0 B.1 C.2 D.3
6.瓷器是由瓷石、高岭土、石英石、莫来石等烧制而成的,其外表施有玻璃质釉或彩绘.通过在窑内高温烧制,瓷器表面的釉色会因为温度的不同从而发生各种化学变化.某瓷器将它近似看作由一个圆柱和一个圆台构成的组合体,其直观图如图所示,该瓷器的体积为
A.450π B.448π C.446π D.444π
7.已知直线mx+ny=1与抛物线C:y2=4x相交于A,B两点,若直线OA与OB的斜率之和为4,O为坐标原点,则n=
A.1 B.2 C.3 D.4
8.如图,E,F,G,H四个开关控制着五盏灯,其中开关E控制着1,2,3号灯,开关F控制着2,3,4号灯,开关G控制着3,4,5号灯,开关H控制着1,4,5号灯.开始时,五盏灯均是亮的,现先后按动E,F,G,H这四个开关中两个不同的开关,则其中2号灯亮的概率为
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数z=(2-ai)2+7i(a∈R)在复平面内对应的点在直线y=x上,则a的值可以为
A.3 B.1 C.-3 D.-1
10.若a=cos 15°-sin 15°,b=,c=sin 105°cos 15°-cos 75°sin 15°,则
A.c11.如图,月牙形是由两段圆弧围成的一个封闭图形,若两段圆弧所在圆的半径相同,两圆的圆心分别为坐标原点O和C,A(-1,-2),B(2,1),直线l:y=x+b与月牙形只有两个交点,则参考数据:cos≈
A.|OC|=
B.圆C的方程为(x-2)2+(y+2)2=5
C.b的取值范围为(-2,)∪{-1}
D.月牙形的面积约为+3
题序 1 2 3 4 5 6 7 8 9 10 11
答案
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量a=(2,2),b=(λ,-4),λ∈R,若a⊥b,则λ= .
13.已知双曲线C:-=1的右焦点为F,M,N是双曲线C右支上的两点,若G(0,2),且F为△MNG的重心,则MN的中点坐标为 ,直线MN的方程为 .
14.如图,在直三棱柱ABC-A1B1C1中,AC⊥AB,AC=6,AB=8,AA1=3,则三棱锥A1- ABC1外接球的半径为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)在△ABC中,内角A,B,C所对的边分别为a,b,c,(a+b-c)(b-a+c)-3ac=0.
(1)求B;
(2)若∠ABC的角平分线交AC于点D,且AD=2DC=,求BD.
16.(15分)如图,在正四棱柱ABCD-A1B1C1D1中,E,F分别为BB1,DD1的中点.
(1)证明:点F在平面AEC1内.
(2)若AA1=2AB,求平面A1EC1与平面AEC1夹角的余弦值.
17.(15分)已知椭圆C:+=1(a>b>0)的离心率为,直线x=ky+1过椭圆C的一个焦点,且与椭圆C相交于A,B两点,D(3,0),直线AD,BD分别与直线x=4相交于E(x1,y1),F(x2,y2)两点.
(1)求椭圆C的方程;
(2)求y1y2的值.
18.(17分)甲、乙两人进行游戏,且都有1个红色弹珠和1个黄色弹珠,每人每次独立地随机取出1个弹珠相互交换.
(1)若只交换1次,求甲的弹珠的颜色相同的概率;
(2)若只交换1次,记甲有红色弹珠的个数为X,求X的分布列及期望;
(3)若一共交换3次,最后甲的2个弹珠颜色相同,则甲获胜,否则乙获胜,试问这个游戏是否公平
19.(17分)已知函数f(x)=x2-axln x(a∈R).
(1)讨论函数f(x)极值点的个数;
(2)若x0是方程f(x)=x在(1,+∞)上的一个根,证明:x0
1.B 【命题意图】本题考查集合的基本运算,要求考生理解两个集合的并集的含义.
【解题分析】由题意得,N={-1,0},因为M={0,1},所以M∪N={-1,0,1}.
2.A 【命题意图】本题考查三角函数的图象及性质,要求考生掌握三角函数的周期性.
【解题分析】由题图知=-=,所以T==,解得ω=3.
3.C 【命题意图】本题考查二项式定理,要求考生会用二项式定理解决简单的问题.
【解题分析】(x+y)6的展开式中x3y3项的系数为=20.
4.D 【命题意图】本题考查等差及等比数列,要求考生理解等差与等比数列的通项公式及前n项和.
【解题分析】因为b2024=2b2023,所以数列{bn}的公比为2,因为b4=a9-1,所以23b1=a1+16-1,因为b1=2a1,所以15a1=15,解得a1=1,b1=2,所以an=2n-1,bn=2n,所以a1+a2+a3+…+an=n2,b10=210=1024,由1024>n2,且n∈N*,得n的最大值为31.
5.C 【命题意图】本题考查导数的几何意义,要求考生掌握导数的几何意义.
【解题分析】设切点坐标为(x0,x0ln x0),y'=1+ln x,所以y'=1+ln x0,所以切线方程为y-x0ln x0=(1+ln x0)(x-x0),即y=(1+ln x0)x-x0,所以解得k=2.
6.D 【命题意图】本题考查几何体的体积,要求考生知道圆台、圆柱体积的计算公式.
【解题分析】由直观图知,圆柱的底面半径为6,高为8,圆台的上底面半径为2,下底面半径为6,高为9,所以该瓷器的体积为π×62×8+(62+22+)×9=444π.
7.A 【命题意图】本题考查直线与抛物线的位置关系,要求考生了解抛物线的简单几何性质.
【解题分析】(方法一)由得y2=4x(mx+ny),所以-4n·-4m=0,因为直线OA与OB的斜率之和为4,所以4n=4,即n=1.
(方法二)设A点的坐标为,y1,B点的坐标为,y2,因为直线OA与OB的斜率之和为4,所以+=4,即+=1,所以y1+y2=y1y2.由得y2+y-=0,所以y1+y2=-,y1y2=-,所以-=-,解得n=1.
8.B 【命题意图】本题考查古典概型,要求考生理解古典概型.
【解题分析】先后按动E,F,G,H这四个开关中两个不同的开关,有=12种方法.
2号灯亮有两类情形.第一类,按第一个开关时,2号灯灭,按第二个开关时,2号灯亮,此时对应的方法有=2种(E,F两个开关进行全排列);
第二类,按第一个开关和第二个开关均与2号灯无关,此时对应的方法有=2种(G,H两个开关进行全排列).故所求事件的概率为=.
9.AB 【命题意图】本题考查复数的运算及几何意义,要求考生能进行复数代数表示式的四则运算并理解复数的几何意义.
【解题分析】因为z=(2-ai)2+7i=4-a2+(7-4a)i,所以4-a2=7-4a,解得a=3或a=1.
10.BCD 【命题意图】本题考查三角恒等变换,要求考生掌握两角和与差的正、余弦公式.
【解题分析】a=cos 15°-sin 15°=sin(45°-15°)=,c=sin 105°cos 15°-cos 75°sin 15°=sin 75°cos 15°-cos 75°sin 15°=sin(75°-15°)=sin 60°=,所以b
【解题分析】由题易知,圆O的半径为,设圆心C的坐标为(a,-a),且a≠0,所以(a-2)2+(1+a)2=5,解得a=1,所以圆C的方程为(x-1)2+(y+1)2=5,|OC|=,故选项A正确,选项B错误.
设直线l1:y=x+t,当直线l1过点B(2,1)时,t=-1,
当直线l1与圆O相切时,=,解得t=±,
当直线l1与圆C相切时,=,
解得t=-2或t=--2,
因为直线l:y=x+b与月牙形只有两个交点,所以b的取值范围为(-2,)∪{-1},故选项C正确.
连接AC,BC,AB(图略),易求得△ABC的面积为,
设∠ACB=θ,=(-2,-1),=(1,2),所以cos θ==-,所以θ≈π-=,所以月牙形的面积约为5π-2××()2×-=+3,故选项D正确.
12.4 【命题意图】本题考查向量的运算,要求考生掌握平面向量数量积的坐标运算.
【解题分析】因为a=(2,2),b=(λ,-4),且a⊥b,所以2×λ+2×(-4)=0,解得λ=4.
13.(6,-1) 2x+y-11=0 【命题意图】本题考查直线与双曲线的位置关系,要求考生了解双曲线的简单几何性质.
【解题分析】由题知,F(4,0),设M点的坐标为(x1,y1),N点的坐标为(x2,y2),因为F为△MNG的重心,所以=4,=0,即x1+x2=12,y1+y2=-2,所以MN的中点坐标为(6,-1).因为M,N是双曲线C右支上的两点,所以两式相减并化简得=×=-2,所以直线MN的方程为y+1=-2×(x-6),即2x+y-11=0.
14. 【命题意图】本题考查立体几何的综合应用,要求考生了解几何体的外接球.
【解题分析】设G,H分别为AC1,A1B的中点,过点G,H分别作平面AA1C1,平面AA1B的垂线,交点为O,连接GH,由题知,GH=BC=5,OG2+OH2=GH2,设三棱锥A1- ABC1外接球的半径为R,所以OG2=R2-AG2,OH2=R2-AH2,所以OG2+OH2=2R2-AG2-AH2,即2R2=GH2+AG2+AH2,所以2R2=25++,解得R=.
15.【命题意图】本题考查解三角形,要求考生理解正、余弦定理.
【解题分析】(1)因为(a+b-c)(b-a+c)-3ac=0,所以b2-(a-c)2-3ac=0,
所以-ac=a2+c2-b2,所以cos B==-,因为B∈(0,π),所以B=. 6分
(2)因为AD=2DC=,所以b=,因为BD平分∠ABC,所以=,即c=2a,
由(1)知,-ac=a2+c2-b2,解得a=1,c=2,因为S△ABC=S△ABD+S△DBC,所以acsin B=a·BDsin+c·BDsin,解得BD==. 13分
16.【命题意图】本题考查点面关系及平面与平面的夹角,要求考生能用向量解决平面与平面的夹角问题.
【解题分析】(1)设G为CC1的中点,连接GF,AF,BG(图略).
由题易知GF CD,BA CD,所以GF BA,所以四边形ABGF为平行四边形,所以AF∥BG,易知BG∥EC1,所以AF∥EC1,故点F在平面AEC1内. 6分
(2)不妨设AB=1,则AA1=2,以BC,BA,BB1所在的直线分别为x,y,z轴建立空间直角坐标系,如图所示,则A(0,1,0),A1(0,1,2),E(0,0,1),C1(1,0,2),
所以=(1,0,1),=(0,1,1),=(0,1,-1).
设m=(x1,y1,z1)为平面A1EC1的法向量,
所以即令x1=1,得y1=1,z1=-1,
所以平面A1EC1的一个法向量为m=(1,1,-1).
设n=(x2,y2,z2)为平面AEC1的法向量,
所以即令x2=1,得y2=z2=-1,
所以平面AEC1的一个法向量为n=(1,-1,-1).
因为cos
所以平面A1EC1与平面AEC1夹角的余弦值为. 15分
17.【命题意图】本题考查直线与椭圆的位置关系,要求考生掌握椭圆的标准方程及简单几何性质.
【解题分析】(1)设c=,因为椭圆C的离心率为,所以=,因为直线x=ky+1过定点(1,0),且过椭圆C的焦点,所以c=1,所以a=3,解得b2=8,所以椭圆C的方程为+=1. 6分
(2)设A(x3,y3),B(x4,y4),由得(8k2+9)y2+16ky-64=0,
易知Δ>0,所以y3+y4=,y3y4=,
直线AD的方程为y=(x-3),令x=4得y1==,
同理可得y2=, 12分
所以y1y2====-. 15分
18.【命题意图】本题考查离散型随机变量,要求考生理解离散型随机变量的概念及分布列.
【解题分析】(1)由题知,交换1次,甲的弹珠的颜色相同的概率为×+×=. 3分
(2)由题知,若只交换1次,则甲、乙两人取红色弹珠和黄色弹珠的概率均为,X的所有可能取值为0,1,2,
P(X=0)=×=,P(X=1)=×+×=,P(X=2)=×=,
所以X的分布列为
X 0 1 2
P
所以X的期望E(X)=0×+1×+2×=1. 9分
(3)用A1,A2,A3分别表示甲第1次、第2次、第3次交换后,甲的2个弹珠颜色相同,
用B1,B2,B3分别表示甲第1次、第2次、第3次交换后,甲的2个弹珠颜色不相同.
由(1)知,P(A1)=P(B1)=P(B3|B2)=P(B2|B1)=P(A3|B2)=P(A2|B1)=,
易知P(A3|A2)=P(A2|A1)=0,由全概率公式知,
P(A3)=P(A2)P(A3|A2)+P(B2)P(A3|B2)=P(B2)P(A3|B2)=P(B2)=[1-P(A2)],
同理可得P(A2)=[1-P(A1)]=,所以P(A3)=1-=<.
故这个游戏不公平. 17分
19.【命题意图】本题考查函数与导数的综合,要求考生理解用导数讨论函数的单调性及函数的零点.
【解题分析】(1)f'(x)=2x-a(1+ln x)=2x-aln x-a,
令φ(x)=f'(x)=2x-aln x-a,则φ'(x)=2-. 1分
当a<0时,φ'(x)>0,φ(x)在(0,+∞)上单调递增,当x→0时,φ(x)→-∞,且φ(1)=2-a>0,故存在x1∈(0,1),使得φ(x1)=0,且当0
当a=0时,f(x)=x2在(0,+∞)上无极值点; 4分
当a>0时,若0
当0
综上所述,当a<0时,函数f(x)有一个极值点;当0≤a≤2时,函数f(x)无极值点;当a>2时,函数f(x)有两个极值点. 7分
(2)f(x)=x,即x2-axln x=x,所以x-1-aln x=0, 8分
令G(x)=x-1-aln x,则G'(x)=1-=. 9分
当a≤1时,G(x)在(1,+∞)上单调递增,G(x)>G(1)=0,方程f(x)=x无解, 10分
当a>1时,易知G(x)在(1,a)上单调递减,在(a,+∞)上单调递增,
所以G(a)
设h(x)=x-1-ln x(x>1),则h'(x)=1-=>0,
所以h(x)在区间(1,+∞)上单调递增,所以h(x)>h(1)=0,即g'(x)>0, 15分
所以g(x)在区间(1,+∞)上单调递增,所以g(a)>g(1)=0,即G(a2)>0, 16分
因为G(x0)=0,所以x0
同课章节目录
