【同步分层】整理与复习基础卷(含解析)-2024-2025学年六年级下册数学北师大版
文档属性
| 名称 | 【同步分层】整理与复习基础卷(含解析)-2024-2025学年六年级下册数学北师大版 | 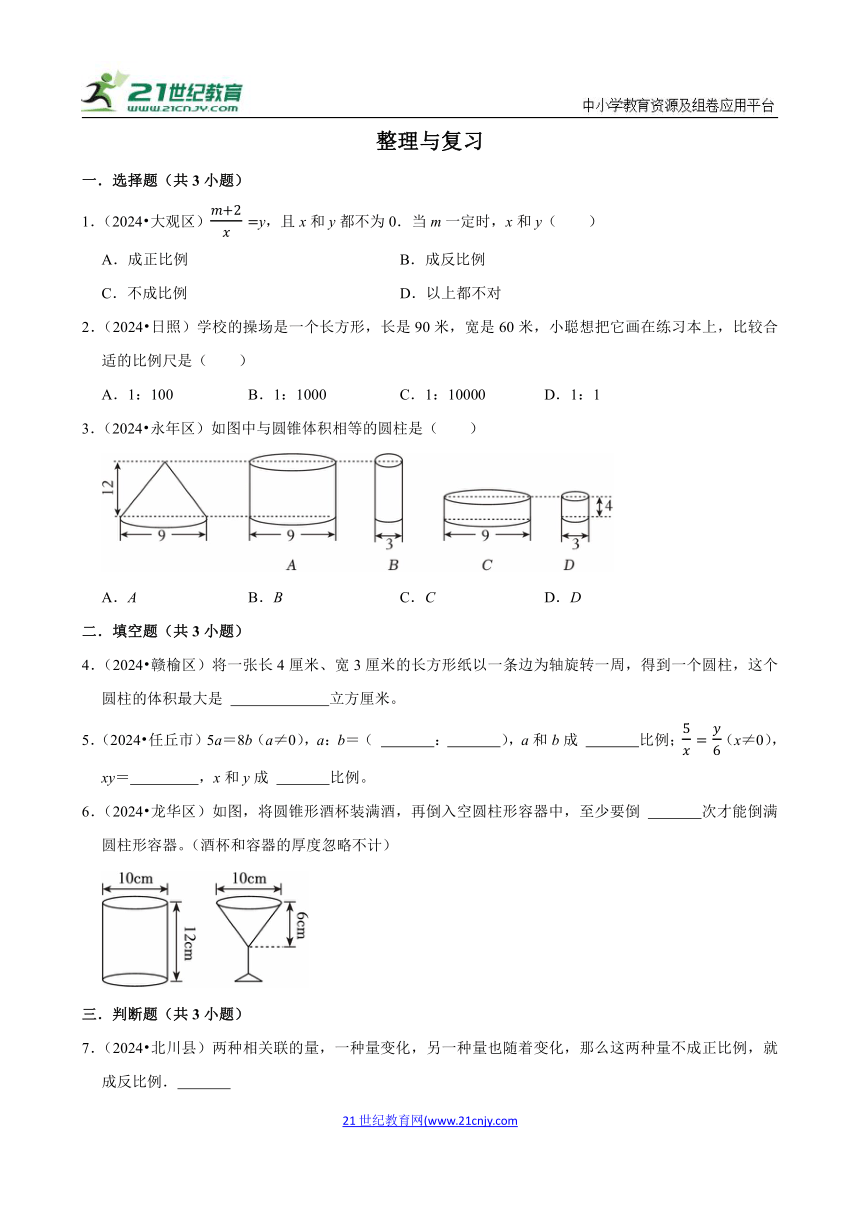 | |
| 格式 | docx | ||
| 文件大小 | 341.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 13:41:54 | ||
图片预览




文档简介
整理与复习
一.选择题(共3小题)
1.(2024 大观区)y,且x和y都不为0.当m一定时,x和y( )
A.成正比例 B.成反比例
C.不成比例 D.以上都不对
2.(2024 日照)学校的操场是一个长方形,长是90米,宽是60米,小聪想把它画在练习本上,比较合适的比例尺是( )
A.1:100 B.1:1000 C.1:10000 D.1:1
3.(2024 永年区)如图中与圆锥体积相等的圆柱是( )
A.A B.B C.C D.D
二.填空题(共3小题)
4.(2024 赣榆区)将一张长4厘米、宽3厘米的长方形纸以一条边为轴旋转一周,得到一个圆柱,这个圆柱的体积最大是 立方厘米。
5.(2024 任丘市)5a=8b(a≠0),a:b=( : ),a和b成 比例;(x≠0),xy= ,x和y成 比例。
6.(2024 龙华区)如图,将圆锥形酒杯装满酒,再倒入空圆柱形容器中,至少要倒 次才能倒满圆柱形容器。(酒杯和容器的厚度忽略不计)
三.判断题(共3小题)
7.(2024 北川县)两种相关联的量,一种量变化,另一种量也随着变化,那么这两种量不成正比例,就成反比例.
8.(2024 德州)等底等高的圆柱和圆锥,圆柱体积比圆锥大30立方分米,则圆柱的体积是30立方分米。
9.(2024 城固县)一个长方形绕其一条边旋转一周后,会得到一个圆锥。
四.应用题(共1小题)
10.(2023秋 渝中区期中)用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:cm),在底面圆心处打结用去了35cm长的绳子,在它的整个侧面贴上一圈商标.
(1)贴商标的面积是多少平方厘米?
(2)这个蛋糕盒的容积是多少?(纸板厚度不计)
(3)捆扎这个盒子至少用去多少厘米的塑料绳?
整理与复习
参考答案与试题解析
一.选择题(共3小题)
1.(2024 大观区)y,且x和y都不为0.当m一定时,x和y( )
A.成正比例 B.成反比例
C.不成比例 D.以上都不对
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】B
【分析】判断x和y成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.据此进行判断并选择.
【解答】解:因为y,则有xy=m+2,m一定,则m+2就一定,是x和y对应的乘积一定,
所以x和y成反比例;
故选:B.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断.
2.(2024 日照)学校的操场是一个长方形,长是90米,宽是60米,小聪想把它画在练习本上,比较合适的比例尺是( )
A.1:100 B.1:1000 C.1:10000 D.1:1
【考点】比例尺.
【专题】应用意识.
【答案】B
【分析】实际距离和比例尺已知,依据“图上距离=实际距离×比例尺”即可求出操场的长和宽的图上距离,再与练习本的实际长度比较即可选出合适的答案。
【解答】解:因为90米=9000厘米,60米=6000厘米,
选项A.900090厘米,6000厘米60(厘米),画在练习本上,尺寸过大,不符合实际情况,故不合适;
选项B.90009(厘米),60006(厘米),画在练习本上比较合适;
选项C.90000.9(厘米),60000.6(厘米),画在练习本上太小,故不合适;
选项D.90009000(厘米),60006000(厘米),画在练习本上,尺寸太大,不符合实际情况,故不合适。
故选:B。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意结合实际情况。
3.(2024 永年区)如图中与圆锥体积相等的圆柱是( )
A.A B.B C.C D.D
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】C
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱和圆锥的体积相等,底面积相等时,圆柱的高是圆锥高的.据此解答即可.
【解答】解:124
所以与圆锥体积相等的圆柱是C.
故选:C.
【点评】此题考查的目的是理解掌握等底等高的圆柱和圆锥体积之间的关系及应用.
二.填空题(共3小题)
4.(2024 赣榆区)将一张长4厘米、宽3厘米的长方形纸以一条边为轴旋转一周,得到一个圆柱,这个圆柱的体积最大是 150.72 立方厘米。
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;应用意识.
【答案】150.72。
【分析】(1)以4厘米的边为轴旋转时,它的底面半径是3厘米,高是4厘米,再根据圆柱的体积公式可求出它的体积;
(2)以3厘米的边为轴旋转时,它的底面半径是4厘米,高是3厘米,再根据圆柱的体积公式可求出它的体积。
再比较大小即可求解。
【解答】解:(1)以4厘米的边为轴旋转时,它的体积是:
3.14×32×4
=3.14×9×4
=113.04(立方厘米)
(2)以3厘米的边为轴旋转时,它的体积是:
3.14×42×3
=3.14×16×3
=150.72(立方厘米)
150.72>113.04
答:这个圆柱的最大体积是150.72立方厘米。
故答案为:150.72。
【点评】本题的关键是分两种情况进行讨论求它的体积。
5.(2024 任丘市)5a=8b(a≠0),a:b=( 8 : 5 ),a和b成 正 比例;(x≠0),xy= 30 ,x和y成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】运算能力.
【答案】见试题解答内容
【分析】逆用比例的基本性质“两个外项的积等于两个内项的积”,可把等式5a=8b改写成比例式为a:b=8:5,根据a:b=8:5(一定),是a和b对应的比值一定,进而确定a和b成正比例关系;
根据两个外项的积等于两个内项的积,把变形,即可得xy的值,再根据如果是比值一定,就成正比例关系;如果是乘积一定,就成反比例关系,判断即可。
【解答】解:(1)因为5a=8b,所以a:b=8:5
(2)a:b=8:5(一定),
是a和b对应的比值一定,符合成正比例关系的意义,
所以a和b成正比例关系;
如果(x≠0),那么xy=30,是乘积一定,那么x和y成反比例。
故答案为:8,5,正;30,反。
【点评】此题主要考查比例基本性质的逆运用,也考查了辨识两个相关联的量成什么比例关系:如果是比值一定,就成正比例关系;如果是乘积一定,就成反比例关系。
6.(2024 龙华区)如图,将圆锥形酒杯装满酒,再倒入空圆柱形容器中,至少要倒 6 次才能倒满圆柱形容器。(酒杯和容器的厚度忽略不计)
【考点】圆锥的体积;圆柱的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】6。
【分析】圆锥的体积:V=πr2h÷3,据此求出圆锥形容器的容积,即水的体积;圆柱的体积:V=πr2h,据此求出圆柱形容器的容积,用圆柱形容器的容积除以圆锥形酒杯的容积,就是需要倒满的次数。
【解答】解:圆柱的容积:π×(10÷2)2×12
=π×52×12
=π×25×12
=300π(立方厘米)
圆锥的容积:π×(10÷2)2×6÷3
=π×52×6÷3
=π×25×6÷3
=150π÷3
=50π(立方厘米)
300π÷50π=6(次)
答:至少要倒6次才能倒满圆柱形容器。
故答案为:6。
【点评】此题考查圆锥和圆柱的体积计算公式的应用。掌握圆锥和圆柱的体积计算公式是解答的关键。
三.判断题(共3小题)
7.(2024 北川县)两种相关联的量,一种量变化,另一种量也随着变化,那么这两种量不成正比例,就成反比例. ×
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:两种相关联的量,一种量变化,另一种量也随着变化,那么这两种量不成正比例,就成反比例.说法错误;
故答案为:×.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
8.(2024 德州)等底等高的圆柱和圆锥,圆柱体积比圆锥大30立方分米,则圆柱的体积是30立方分米。 ×
【考点】圆锥的体积;圆柱的体积.
【专题】立体图形的认识与计算;空间观念.
【答案】×
【分析】等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱的体积比圆锥的体积多2倍,由此求出圆锥的体积,再进一步解答即可。
【解答】解:30÷(3﹣1)
=30÷2
=15(立方分米)
15×3=45(立方分米)
即圆柱的体积是45立方分米,所以原题说法错误。
故答案为:×。
【点评】此题主要考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
9.(2024 城固县)一个长方形绕其一条边旋转一周后,会得到一个圆锥。 ×
【考点】圆锥的特征;圆柱的特征.
【专题】几何直观.
【答案】×
【分析】我们知道,点运动构成线,线运动构成面,而面运动构成体,以长方形或正方形的一边为轴,旋转一周,长方形或正方形的另外两个顶点绕轴旋转构成两个等圆,这两个圆面是圆柱的两个底,与轴平行的一边构成一个曲面,这就是圆柱的侧面,长方形或正方形这个面就构成圆柱,据此判断。
【解答】解:一个长方形绕其一条边旋转一周后,会得到一个圆柱,所以原题说法错误。
故答案为:×。
【点评】此题考查的目的是理解掌握圆柱的特征。
四.应用题(共1小题)
10.(2023秋 渝中区期中)用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:cm),在底面圆心处打结用去了35cm长的绳子,在它的整个侧面贴上一圈商标.
(1)贴商标的面积是多少平方厘米?
(2)这个蛋糕盒的容积是多少?(纸板厚度不计)
(3)捆扎这个盒子至少用去多少厘米的塑料绳?
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】见试题解答内容
【分析】(1)根据圆柱的侧面积公式:S=Ch,把数据代入公式解答.
(2)根据圆柱的容积(体积)公式:V=πr2h,把数据代入公式解答.
(3)根据捆扎的特点可知,需要塑料绳的长度等于这个圆柱的8条直径加上8条高再加上打结用的35厘米即可.
【解答】解:(1)3.14×60×10=1884(平方厘米)
答:贴商标的面积是1884平方厘米.
(2)3.14×(60÷2)2×10
=3.14×900×10
=28260(立方厘米)
答:这个蛋糕盒的容积是28260立方厘米.
(3)60×8+10×8+35
=480+80+35
=595(厘米)
答:捆扎这个盒子至少用去595厘米的塑料绳.
【点评】此题主要考查圆柱的侧面积公式、圆柱的容积(体积)公式在实际生活中的应用,关键是熟记公式.
21世纪教育网(www.21cnjy.com
一.选择题(共3小题)
1.(2024 大观区)y,且x和y都不为0.当m一定时,x和y( )
A.成正比例 B.成反比例
C.不成比例 D.以上都不对
2.(2024 日照)学校的操场是一个长方形,长是90米,宽是60米,小聪想把它画在练习本上,比较合适的比例尺是( )
A.1:100 B.1:1000 C.1:10000 D.1:1
3.(2024 永年区)如图中与圆锥体积相等的圆柱是( )
A.A B.B C.C D.D
二.填空题(共3小题)
4.(2024 赣榆区)将一张长4厘米、宽3厘米的长方形纸以一条边为轴旋转一周,得到一个圆柱,这个圆柱的体积最大是 立方厘米。
5.(2024 任丘市)5a=8b(a≠0),a:b=( : ),a和b成 比例;(x≠0),xy= ,x和y成 比例。
6.(2024 龙华区)如图,将圆锥形酒杯装满酒,再倒入空圆柱形容器中,至少要倒 次才能倒满圆柱形容器。(酒杯和容器的厚度忽略不计)
三.判断题(共3小题)
7.(2024 北川县)两种相关联的量,一种量变化,另一种量也随着变化,那么这两种量不成正比例,就成反比例.
8.(2024 德州)等底等高的圆柱和圆锥,圆柱体积比圆锥大30立方分米,则圆柱的体积是30立方分米。
9.(2024 城固县)一个长方形绕其一条边旋转一周后,会得到一个圆锥。
四.应用题(共1小题)
10.(2023秋 渝中区期中)用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:cm),在底面圆心处打结用去了35cm长的绳子,在它的整个侧面贴上一圈商标.
(1)贴商标的面积是多少平方厘米?
(2)这个蛋糕盒的容积是多少?(纸板厚度不计)
(3)捆扎这个盒子至少用去多少厘米的塑料绳?
整理与复习
参考答案与试题解析
一.选择题(共3小题)
1.(2024 大观区)y,且x和y都不为0.当m一定时,x和y( )
A.成正比例 B.成反比例
C.不成比例 D.以上都不对
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】B
【分析】判断x和y成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.据此进行判断并选择.
【解答】解:因为y,则有xy=m+2,m一定,则m+2就一定,是x和y对应的乘积一定,
所以x和y成反比例;
故选:B.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断.
2.(2024 日照)学校的操场是一个长方形,长是90米,宽是60米,小聪想把它画在练习本上,比较合适的比例尺是( )
A.1:100 B.1:1000 C.1:10000 D.1:1
【考点】比例尺.
【专题】应用意识.
【答案】B
【分析】实际距离和比例尺已知,依据“图上距离=实际距离×比例尺”即可求出操场的长和宽的图上距离,再与练习本的实际长度比较即可选出合适的答案。
【解答】解:因为90米=9000厘米,60米=6000厘米,
选项A.900090厘米,6000厘米60(厘米),画在练习本上,尺寸过大,不符合实际情况,故不合适;
选项B.90009(厘米),60006(厘米),画在练习本上比较合适;
选项C.90000.9(厘米),60000.6(厘米),画在练习本上太小,故不合适;
选项D.90009000(厘米),60006000(厘米),画在练习本上,尺寸太大,不符合实际情况,故不合适。
故选:B。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意结合实际情况。
3.(2024 永年区)如图中与圆锥体积相等的圆柱是( )
A.A B.B C.C D.D
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】C
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱和圆锥的体积相等,底面积相等时,圆柱的高是圆锥高的.据此解答即可.
【解答】解:124
所以与圆锥体积相等的圆柱是C.
故选:C.
【点评】此题考查的目的是理解掌握等底等高的圆柱和圆锥体积之间的关系及应用.
二.填空题(共3小题)
4.(2024 赣榆区)将一张长4厘米、宽3厘米的长方形纸以一条边为轴旋转一周,得到一个圆柱,这个圆柱的体积最大是 150.72 立方厘米。
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;应用意识.
【答案】150.72。
【分析】(1)以4厘米的边为轴旋转时,它的底面半径是3厘米,高是4厘米,再根据圆柱的体积公式可求出它的体积;
(2)以3厘米的边为轴旋转时,它的底面半径是4厘米,高是3厘米,再根据圆柱的体积公式可求出它的体积。
再比较大小即可求解。
【解答】解:(1)以4厘米的边为轴旋转时,它的体积是:
3.14×32×4
=3.14×9×4
=113.04(立方厘米)
(2)以3厘米的边为轴旋转时,它的体积是:
3.14×42×3
=3.14×16×3
=150.72(立方厘米)
150.72>113.04
答:这个圆柱的最大体积是150.72立方厘米。
故答案为:150.72。
【点评】本题的关键是分两种情况进行讨论求它的体积。
5.(2024 任丘市)5a=8b(a≠0),a:b=( 8 : 5 ),a和b成 正 比例;(x≠0),xy= 30 ,x和y成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】运算能力.
【答案】见试题解答内容
【分析】逆用比例的基本性质“两个外项的积等于两个内项的积”,可把等式5a=8b改写成比例式为a:b=8:5,根据a:b=8:5(一定),是a和b对应的比值一定,进而确定a和b成正比例关系;
根据两个外项的积等于两个内项的积,把变形,即可得xy的值,再根据如果是比值一定,就成正比例关系;如果是乘积一定,就成反比例关系,判断即可。
【解答】解:(1)因为5a=8b,所以a:b=8:5
(2)a:b=8:5(一定),
是a和b对应的比值一定,符合成正比例关系的意义,
所以a和b成正比例关系;
如果(x≠0),那么xy=30,是乘积一定,那么x和y成反比例。
故答案为:8,5,正;30,反。
【点评】此题主要考查比例基本性质的逆运用,也考查了辨识两个相关联的量成什么比例关系:如果是比值一定,就成正比例关系;如果是乘积一定,就成反比例关系。
6.(2024 龙华区)如图,将圆锥形酒杯装满酒,再倒入空圆柱形容器中,至少要倒 6 次才能倒满圆柱形容器。(酒杯和容器的厚度忽略不计)
【考点】圆锥的体积;圆柱的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】6。
【分析】圆锥的体积:V=πr2h÷3,据此求出圆锥形容器的容积,即水的体积;圆柱的体积:V=πr2h,据此求出圆柱形容器的容积,用圆柱形容器的容积除以圆锥形酒杯的容积,就是需要倒满的次数。
【解答】解:圆柱的容积:π×(10÷2)2×12
=π×52×12
=π×25×12
=300π(立方厘米)
圆锥的容积:π×(10÷2)2×6÷3
=π×52×6÷3
=π×25×6÷3
=150π÷3
=50π(立方厘米)
300π÷50π=6(次)
答:至少要倒6次才能倒满圆柱形容器。
故答案为:6。
【点评】此题考查圆锥和圆柱的体积计算公式的应用。掌握圆锥和圆柱的体积计算公式是解答的关键。
三.判断题(共3小题)
7.(2024 北川县)两种相关联的量,一种量变化,另一种量也随着变化,那么这两种量不成正比例,就成反比例. ×
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:两种相关联的量,一种量变化,另一种量也随着变化,那么这两种量不成正比例,就成反比例.说法错误;
故答案为:×.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
8.(2024 德州)等底等高的圆柱和圆锥,圆柱体积比圆锥大30立方分米,则圆柱的体积是30立方分米。 ×
【考点】圆锥的体积;圆柱的体积.
【专题】立体图形的认识与计算;空间观念.
【答案】×
【分析】等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱的体积比圆锥的体积多2倍,由此求出圆锥的体积,再进一步解答即可。
【解答】解:30÷(3﹣1)
=30÷2
=15(立方分米)
15×3=45(立方分米)
即圆柱的体积是45立方分米,所以原题说法错误。
故答案为:×。
【点评】此题主要考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
9.(2024 城固县)一个长方形绕其一条边旋转一周后,会得到一个圆锥。 ×
【考点】圆锥的特征;圆柱的特征.
【专题】几何直观.
【答案】×
【分析】我们知道,点运动构成线,线运动构成面,而面运动构成体,以长方形或正方形的一边为轴,旋转一周,长方形或正方形的另外两个顶点绕轴旋转构成两个等圆,这两个圆面是圆柱的两个底,与轴平行的一边构成一个曲面,这就是圆柱的侧面,长方形或正方形这个面就构成圆柱,据此判断。
【解答】解:一个长方形绕其一条边旋转一周后,会得到一个圆柱,所以原题说法错误。
故答案为:×。
【点评】此题考查的目的是理解掌握圆柱的特征。
四.应用题(共1小题)
10.(2023秋 渝中区期中)用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:cm),在底面圆心处打结用去了35cm长的绳子,在它的整个侧面贴上一圈商标.
(1)贴商标的面积是多少平方厘米?
(2)这个蛋糕盒的容积是多少?(纸板厚度不计)
(3)捆扎这个盒子至少用去多少厘米的塑料绳?
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;空间观念;应用意识.
【答案】见试题解答内容
【分析】(1)根据圆柱的侧面积公式:S=Ch,把数据代入公式解答.
(2)根据圆柱的容积(体积)公式:V=πr2h,把数据代入公式解答.
(3)根据捆扎的特点可知,需要塑料绳的长度等于这个圆柱的8条直径加上8条高再加上打结用的35厘米即可.
【解答】解:(1)3.14×60×10=1884(平方厘米)
答:贴商标的面积是1884平方厘米.
(2)3.14×(60÷2)2×10
=3.14×900×10
=28260(立方厘米)
答:这个蛋糕盒的容积是28260立方厘米.
(3)60×8+10×8+35
=480+80+35
=595(厘米)
答:捆扎这个盒子至少用去595厘米的塑料绳.
【点评】此题主要考查圆柱的侧面积公式、圆柱的容积(体积)公式在实际生活中的应用,关键是熟记公式.
21世纪教育网(www.21cnjy.com
