8.1.2认识三角形(三角形中的重要线段) 课件(共32张PPT)
文档属性
| 名称 | 8.1.2认识三角形(三角形中的重要线段) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
华东师大版 七年级 下册
08
认识三角形
第二课时:三角形中的重要线段
复习提问:
1、什么叫三角形?
由不在同一直线上的三条线段首尾顺次连接而成的封闭图形叫三角形。
①位置关系:不在同一直线上;②连结方式:首尾顺次。
三角形应满足以下两个条件:
表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此,△ABC还可记作△BCA、△ CAB、 △ ACB等。
A
B
C
复习提问:
2、三角形基本要素有哪些?
A
B
C
c
a
b
三角形的边:边AB、BC、CA;
三角形的顶点:顶点A、B、C;
三角形的角:∠ A、 ∠ B、 ∠ C。
特别规定:
三角形ABC的三边,一般的:顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c。
邻边和对边
内角和外角
复习提问:
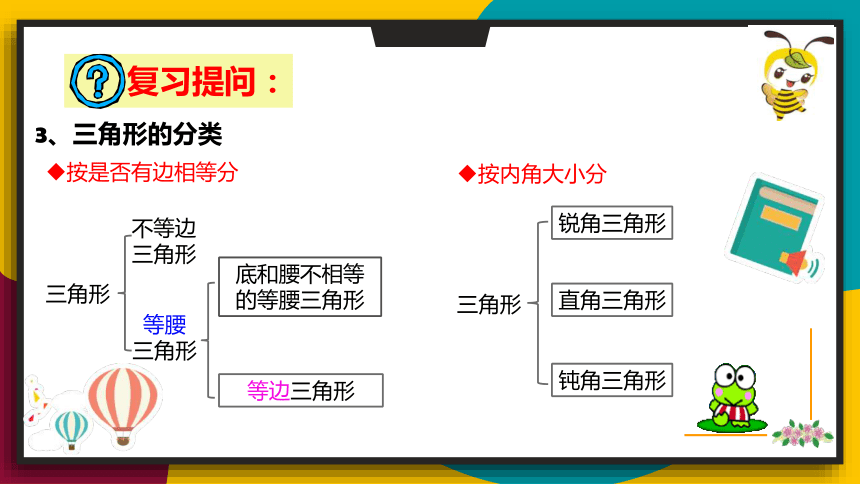
3、三角形的分类
按是否有边相等分
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
按内角大小分
三角形
锐角三角形
直角三角形
钝角三角形
情境导入
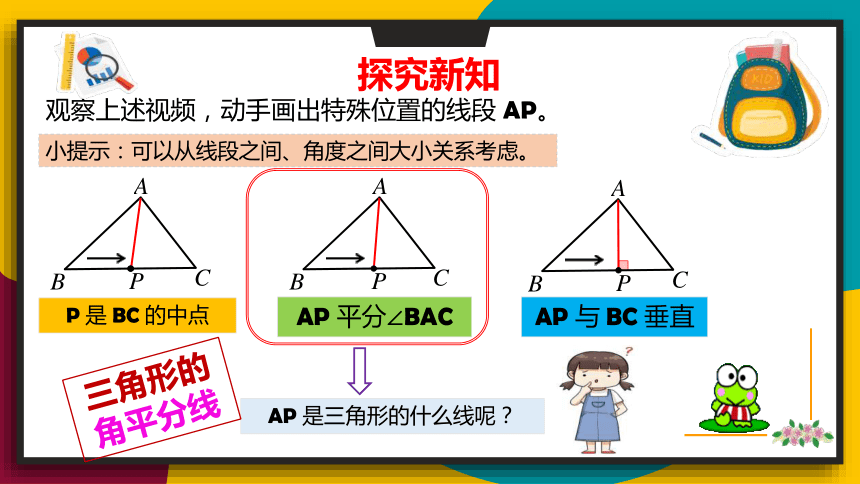
如图,在△ABC 中,点 D 是 BC 边上的一个动点,连接 AD,在点 D 的运动过程中,观察点 D或线段 AD 有没有特殊的位置?你认为有哪些特殊位置?
探究新知
小提示:可以从线段之间、角度之间大小关系考虑。
观察上述视频,动手画出特殊位置的线段 AP。
P 是 BC 的中点
AP 是三角形的什么线呢?
AP 平分∠BAC
AP 与 BC 垂直
三角形的中线
定义:如图∶取△ABC边AB的中点P,连结CP,线段 CP 就是△ABC的一条中线。
知识点1——三角形的中线
几何语言:
∵ CP 是△ABC 的中线
∴ BP=CP=BC或BC=2BP=2CP
问题1:画出锐角三角形、直角三角形和钝角三角形的中线。
你发现了什么?
归纳总结
三角形的三条中线交于内部一点,这点称为三角形的重心。
课堂小练习——
如图:AB边上的中线是______
BC边上的中线是______
AC边上的中线是______
∵ BE是中线
∴ ____=_____= _____
∴ AB=2______=2_______
∵ CF是中线
CF
BE
AD
AE
CE
AC
AF
BF
问题2:三角形的一条中线所分的两个小三角形在面积和周长上有哪些特征?
归纳总结
1、中线所分两个小三角形的面积相等,均等于原三角形的一半。 2、中线所分两个小三角形的周长差,等于另两边边长差。
B
C
D
E
A
发现1:面积相等,因为两个三角形等底同高,且均等于原三角形的一半,所以它们面积相等。
发现2:中线所分两个小三角形的周长差,等于另两边边长差。
即:C△ABD-C△ACD=AB-AC
例1 如图,已知AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90 °,试求:
(1)△ABE的面积;(2)△ACE和△ABE的周长的差。
例题讲解——
A
B
C
D
E
解:(1)∵ S△ABC=AB·AC=AB·AC
∴ 6×8=10AD 即:AD=4.8
∵ AE分别是△ABC的高和中线
∴ BE=BC=5 cm
∴ S△ABE=BE·AD=×5×4.8=12(cm2)
中线分成两个小三角形面积相等
(2)∵ AE是△ABC的中线
∴ BE=CE
∴ C△ACE-C△ABE
=(AC+AE+CE)-(AB+AE+BE)
=AC+AE+CE-AB-AE-BE
=AC-AB
=8-6
=2(cm)
即:C△ACE-C△ABE=AC-AB
中线分成两个小三角形周长差等于另两边边长差
探究新知
小提示:可以从线段之间、角度之间大小关系考虑。
观察上述视频,动手画出特殊位置的线段 AP。
P 是 BC 的中点
AP 是三角形的什么线呢?
AP 平分∠BAC
AP 与 BC 垂直
三角形的角平分线
定义:如图∶作△ABC 的内角∠BAC 的平分线交对边 BC 于点 P,线段 AP就是△ABC 的一条角平分线。
知识点2——三角形的角平分线
几何语言:
∵ AP 是△ABC 的角平分线
∴∠BAP=∠CAP=∠BAC或∠BAC=2∠BAP=2∠CAP
问题1:画出锐角三角形、直角三角形和钝角三角形的角平分线。你发现了什么?
归纳总结
三角形的三条角平分线交于内部一点,这点称为三角形的内心。
问题2:三如图,在ΔABC中,角平分线BD、CE相交于
点O,计算:
(1)当∠A=50°时,求∠BOC。
(2)当∠BOC=130°时,求∠A。
(3)如果设∠A为α,求∠BOC(用α表示)。
归纳总结
两条角平分线相交的夹角等于90度加上第三个角的一半。
(1)在△ABC中:
∵ ∠A=50
∴ ∠ACB+∠ABC=180-∠A=130
∵ BD、CE平分∠ACB、∠ABC
∴ ∠OCB+∠OBC=0.5(∠ACB+∠ABC)=65
在△ABC中:
∠BOC=180-(∠OCB+∠OBC)=115
80°
90°+0.5α
课堂小练习——
如图:
∵ BE是△ABC的角平分线
∴ ______=______= ______
∴ ∠ACB=2_______=2_______
∵ CF是△ABC的角平分线
∠ABE
∠CBE
∠ABC
∠ACF
∠BCF
例2 如图,AD是△ABC的角平分线,DE∥AC,DE交AB于E,DF∥AB,DF交AC于F。图中∠1与∠2有什么关系?为什么?
例题讲解——
解:∠1=∠2 理由如下:
∵ DE∥AC( )
∴ ∠1=∠DAC( )
∵ DF∥AB( )
∴ ∠2=∠BAD( )
∵ AD是△ABC的角平分线( )
∴ ∠BAD=∠DAC( )
∴ ∠1=∠2( )
∵ AD是△ABC的角平分线( )
∴ ∠BAD=∠DAC( )
∵ DE∥AC( )
∴ ∠1=∠DAC( )
∵ DF∥AB( )
∴ ∠2=∠BAD( )
∴ ∠1=∠2( )
区分两种写法
探究新知
小提示:可以从线段之间、角度之间大小关系考虑。
观察上述视频,动手画出特殊位置的线段 AP。
P 是 BC 的中点
AP 是三角形的什么线呢?
AP 平分∠BAC
AP 与 BC 垂直
三角形的角高
定义:如图∶过顶点 A 作△ABC 的边 BC 的垂线,垂足为点 P ,线段 AP 就是△ABC 的一条高。
知识点3——三角形的高
几何语言:∵AP 是△ABC 的高
∴AP⊥BC或∠BPA =∠CPA = 90°
问题1:画出锐角三角形、直角三角形和钝角三角形的高。你发现了什么?
归纳总结
三角形的三条高交于一点。锐角三角形的高交于三角形内一点;直角三角形的高交于直角的顶点;钝角三角形的高交于三角形外一点。
边BC边上的高是 ;边AB边上的高是 ;AC边上的高是 。
D
D
D
E
E
F
F
O
O
三角形高知识点归纳
从三角形中的一个顶点向它的对边所在直线作垂线,
叫做三角形这边的高。
顶点和垂足之间的线段
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1(2直角边上)
相交
相交
不相交
相交
相交
相交
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
1(2三角形外)
三角形的三条高所在直线交于一点,交点位置由三角形形状而定。
课堂小练习——
2、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形
3、三角形的三条高相交于一点,此交点定在( )
A.三角形的内部 B.三角形的外部
C.三角形的边上(直角顶点) D.不能确定
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
B
D
D
例3 如图如图,在△ABC中,请作图:
(1)画出△ABC的∠C的平分线;
(2)画出△ABC的边AC上的中线;
(3)画出△ABC的边BC上的高。
例题讲解——
A
B
C
D
E
F
解:如图:(1)CF即为所求;(2)BE即为所求;(3)AD即为所求。
画高要标明垂直符号,三角形的角平分线、中线及高都要画成线段。
注意:
——巩固训练——
1、如图,在△ABC中有四条线段DE、BE、EF、FG,其中
有一条线段是△ABC的中线,则该线段是( )
A.线段DE B.线段BE C.线段EF D.线段FG
B
2、如图,△的中线、角平分线交于点 ,则下列选项
正确的是( )
A.是 的角平分线
B.是 的角平分线
C.是 的中线
D.是 的角平分线
D
——巩固训练——
3、能将三角形分成面积相等的两个三角形的线是( )
A. 三角形高线 B. 三角形 中线
C. 三角形角平分线 D.以上均有可能
B
4、在△ABC中,若∠A∶ ∠B∶∠C=5∶6∶7,则△ABC的形状是 三角形(选填“钝角”、“直角”、锐角)
锐角
——巩固训练——
5、李大爷有一块三角形的菜地,现在要将它们平均分给四个儿子,在菜地的一角A处有一口池塘,为了使分开后的四块菜地都就近取水,李大爷为此很伤脑筋。你能想出什么办法帮帮李大爷吗?如果不考虑水源,你认为还可以怎样分
A
(思路提示:想到三角形的中线能把三角形分成面积相等的两部分)
——巩固训练——
6、如图:在△ABC中,已知AE平分∠BAC,
∠ADC=90°,∠B=40°,∠C=84°。
求:∠1的度数
7、如图:已知BM是△ABC的中线,AB=6,BC=8。
那么△MBC的周长与△ABM的周长差 。
B
A
M
C
中线分成两个小三角形的周长差等于另两边的边长差:
即:C△MBC-C△ABM=BC-AB
课堂小结
三角形的 重要线段 概念 图形 表示法(几何语言)
三角形 的中线 (共3条)
三角形 的高线 (共3条)
三角形的 角平分线 (共3条)
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
三角形中,连结一个顶点和它对边中点的线段
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵AD是△ABC的BC上的高线
∴AD⊥BC
或∠ADB=∠ADC=90°
∵ AD是△ABC的BC上的中线
∴ BD=CD= BC
∵AD是△ABC∠BAC的平分线
∴ ∠1=∠2= ∠BAC
学会构方程
1、从课后习题中选取;
2、完成练习册本课时的习题。
课后作业
谢谢欣赏
THANK YOU FOR LISTENING
不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
【知识技能类作业】能力提高
如图:在△ABC中(AC>AB),AC=2BC,BC边上的中线AD把△ABC的周长分成60 cm和40cm两部分,则AC的长为 cm,AB的长为 cm。
x
x
4x
y
48
28
学会构造方程
华东师大版 七年级 下册
08
认识三角形
第二课时:三角形中的重要线段
复习提问:
1、什么叫三角形?
由不在同一直线上的三条线段首尾顺次连接而成的封闭图形叫三角形。
①位置关系:不在同一直线上;②连结方式:首尾顺次。
三角形应满足以下两个条件:
表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此,△ABC还可记作△BCA、△ CAB、 △ ACB等。
A
B
C
复习提问:
2、三角形基本要素有哪些?
A
B
C
c
a
b
三角形的边:边AB、BC、CA;
三角形的顶点:顶点A、B、C;
三角形的角:∠ A、 ∠ B、 ∠ C。
特别规定:
三角形ABC的三边,一般的:顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c。
邻边和对边
内角和外角
复习提问:
3、三角形的分类
按是否有边相等分
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
按内角大小分
三角形
锐角三角形
直角三角形
钝角三角形
情境导入
如图,在△ABC 中,点 D 是 BC 边上的一个动点,连接 AD,在点 D 的运动过程中,观察点 D或线段 AD 有没有特殊的位置?你认为有哪些特殊位置?
探究新知
小提示:可以从线段之间、角度之间大小关系考虑。
观察上述视频,动手画出特殊位置的线段 AP。
P 是 BC 的中点
AP 是三角形的什么线呢?
AP 平分∠BAC
AP 与 BC 垂直
三角形的中线
定义:如图∶取△ABC边AB的中点P,连结CP,线段 CP 就是△ABC的一条中线。
知识点1——三角形的中线
几何语言:
∵ CP 是△ABC 的中线
∴ BP=CP=BC或BC=2BP=2CP
问题1:画出锐角三角形、直角三角形和钝角三角形的中线。
你发现了什么?
归纳总结
三角形的三条中线交于内部一点,这点称为三角形的重心。
课堂小练习——
如图:AB边上的中线是______
BC边上的中线是______
AC边上的中线是______
∵ BE是中线
∴ ____=_____= _____
∴ AB=2______=2_______
∵ CF是中线
CF
BE
AD
AE
CE
AC
AF
BF
问题2:三角形的一条中线所分的两个小三角形在面积和周长上有哪些特征?
归纳总结
1、中线所分两个小三角形的面积相等,均等于原三角形的一半。 2、中线所分两个小三角形的周长差,等于另两边边长差。
B
C
D
E
A
发现1:面积相等,因为两个三角形等底同高,且均等于原三角形的一半,所以它们面积相等。
发现2:中线所分两个小三角形的周长差,等于另两边边长差。
即:C△ABD-C△ACD=AB-AC
例1 如图,已知AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90 °,试求:
(1)△ABE的面积;(2)△ACE和△ABE的周长的差。
例题讲解——
A
B
C
D
E
解:(1)∵ S△ABC=AB·AC=AB·AC
∴ 6×8=10AD 即:AD=4.8
∵ AE分别是△ABC的高和中线
∴ BE=BC=5 cm
∴ S△ABE=BE·AD=×5×4.8=12(cm2)
中线分成两个小三角形面积相等
(2)∵ AE是△ABC的中线
∴ BE=CE
∴ C△ACE-C△ABE
=(AC+AE+CE)-(AB+AE+BE)
=AC+AE+CE-AB-AE-BE
=AC-AB
=8-6
=2(cm)
即:C△ACE-C△ABE=AC-AB
中线分成两个小三角形周长差等于另两边边长差
探究新知
小提示:可以从线段之间、角度之间大小关系考虑。
观察上述视频,动手画出特殊位置的线段 AP。
P 是 BC 的中点
AP 是三角形的什么线呢?
AP 平分∠BAC
AP 与 BC 垂直
三角形的角平分线
定义:如图∶作△ABC 的内角∠BAC 的平分线交对边 BC 于点 P,线段 AP就是△ABC 的一条角平分线。
知识点2——三角形的角平分线
几何语言:
∵ AP 是△ABC 的角平分线
∴∠BAP=∠CAP=∠BAC或∠BAC=2∠BAP=2∠CAP
问题1:画出锐角三角形、直角三角形和钝角三角形的角平分线。你发现了什么?
归纳总结
三角形的三条角平分线交于内部一点,这点称为三角形的内心。
问题2:三如图,在ΔABC中,角平分线BD、CE相交于
点O,计算:
(1)当∠A=50°时,求∠BOC。
(2)当∠BOC=130°时,求∠A。
(3)如果设∠A为α,求∠BOC(用α表示)。
归纳总结
两条角平分线相交的夹角等于90度加上第三个角的一半。
(1)在△ABC中:
∵ ∠A=50
∴ ∠ACB+∠ABC=180-∠A=130
∵ BD、CE平分∠ACB、∠ABC
∴ ∠OCB+∠OBC=0.5(∠ACB+∠ABC)=65
在△ABC中:
∠BOC=180-(∠OCB+∠OBC)=115
80°
90°+0.5α
课堂小练习——
如图:
∵ BE是△ABC的角平分线
∴ ______=______= ______
∴ ∠ACB=2_______=2_______
∵ CF是△ABC的角平分线
∠ABE
∠CBE
∠ABC
∠ACF
∠BCF
例2 如图,AD是△ABC的角平分线,DE∥AC,DE交AB于E,DF∥AB,DF交AC于F。图中∠1与∠2有什么关系?为什么?
例题讲解——
解:∠1=∠2 理由如下:
∵ DE∥AC( )
∴ ∠1=∠DAC( )
∵ DF∥AB( )
∴ ∠2=∠BAD( )
∵ AD是△ABC的角平分线( )
∴ ∠BAD=∠DAC( )
∴ ∠1=∠2( )
∵ AD是△ABC的角平分线( )
∴ ∠BAD=∠DAC( )
∵ DE∥AC( )
∴ ∠1=∠DAC( )
∵ DF∥AB( )
∴ ∠2=∠BAD( )
∴ ∠1=∠2( )
区分两种写法
探究新知
小提示:可以从线段之间、角度之间大小关系考虑。
观察上述视频,动手画出特殊位置的线段 AP。
P 是 BC 的中点
AP 是三角形的什么线呢?
AP 平分∠BAC
AP 与 BC 垂直
三角形的角高
定义:如图∶过顶点 A 作△ABC 的边 BC 的垂线,垂足为点 P ,线段 AP 就是△ABC 的一条高。
知识点3——三角形的高
几何语言:∵AP 是△ABC 的高
∴AP⊥BC或∠BPA =∠CPA = 90°
问题1:画出锐角三角形、直角三角形和钝角三角形的高。你发现了什么?
归纳总结
三角形的三条高交于一点。锐角三角形的高交于三角形内一点;直角三角形的高交于直角的顶点;钝角三角形的高交于三角形外一点。
边BC边上的高是 ;边AB边上的高是 ;AC边上的高是 。
D
D
D
E
E
F
F
O
O
三角形高知识点归纳
从三角形中的一个顶点向它的对边所在直线作垂线,
叫做三角形这边的高。
顶点和垂足之间的线段
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1(2直角边上)
相交
相交
不相交
相交
相交
相交
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
1(2三角形外)
三角形的三条高所在直线交于一点,交点位置由三角形形状而定。
课堂小练习——
2、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形
3、三角形的三条高相交于一点,此交点定在( )
A.三角形的内部 B.三角形的外部
C.三角形的边上(直角顶点) D.不能确定
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
B
D
D
例3 如图如图,在△ABC中,请作图:
(1)画出△ABC的∠C的平分线;
(2)画出△ABC的边AC上的中线;
(3)画出△ABC的边BC上的高。
例题讲解——
A
B
C
D
E
F
解:如图:(1)CF即为所求;(2)BE即为所求;(3)AD即为所求。
画高要标明垂直符号,三角形的角平分线、中线及高都要画成线段。
注意:
——巩固训练——
1、如图,在△ABC中有四条线段DE、BE、EF、FG,其中
有一条线段是△ABC的中线,则该线段是( )
A.线段DE B.线段BE C.线段EF D.线段FG
B
2、如图,△的中线、角平分线交于点 ,则下列选项
正确的是( )
A.是 的角平分线
B.是 的角平分线
C.是 的中线
D.是 的角平分线
D
——巩固训练——
3、能将三角形分成面积相等的两个三角形的线是( )
A. 三角形高线 B. 三角形 中线
C. 三角形角平分线 D.以上均有可能
B
4、在△ABC中,若∠A∶ ∠B∶∠C=5∶6∶7,则△ABC的形状是 三角形(选填“钝角”、“直角”、锐角)
锐角
——巩固训练——
5、李大爷有一块三角形的菜地,现在要将它们平均分给四个儿子,在菜地的一角A处有一口池塘,为了使分开后的四块菜地都就近取水,李大爷为此很伤脑筋。你能想出什么办法帮帮李大爷吗?如果不考虑水源,你认为还可以怎样分
A
(思路提示:想到三角形的中线能把三角形分成面积相等的两部分)
——巩固训练——
6、如图:在△ABC中,已知AE平分∠BAC,
∠ADC=90°,∠B=40°,∠C=84°。
求:∠1的度数
7、如图:已知BM是△ABC的中线,AB=6,BC=8。
那么△MBC的周长与△ABM的周长差 。
B
A
M
C
中线分成两个小三角形的周长差等于另两边的边长差:
即:C△MBC-C△ABM=BC-AB
课堂小结
三角形的 重要线段 概念 图形 表示法(几何语言)
三角形 的中线 (共3条)
三角形 的高线 (共3条)
三角形的 角平分线 (共3条)
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
三角形中,连结一个顶点和它对边中点的线段
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵AD是△ABC的BC上的高线
∴AD⊥BC
或∠ADB=∠ADC=90°
∵ AD是△ABC的BC上的中线
∴ BD=CD= BC
∵AD是△ABC∠BAC的平分线
∴ ∠1=∠2= ∠BAC
学会构方程
1、从课后习题中选取;
2、完成练习册本课时的习题。
课后作业
谢谢欣赏
THANK YOU FOR LISTENING
不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
【知识技能类作业】能力提高
如图:在△ABC中(AC>AB),AC=2BC,BC边上的中线AD把△ABC的周长分成60 cm和40cm两部分,则AC的长为 cm,AB的长为 cm。
x
x
4x
y
48
28
学会构造方程
