【同步分层培优】4.5有趣的测量提高卷(含解析)-2024-2025学年五年级下册数学北师大版
文档属性
| 名称 | 【同步分层培优】4.5有趣的测量提高卷(含解析)-2024-2025学年五年级下册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 713.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 16:37:48 | ||
图片预览


文档简介
4.5有趣的测量
一.选择题(共3小题)
1.(2024 安宁市)将图中石块依次放入四个容器中,石块均能完全浸没在水中,且水未溢出容器。容器底面数据如图所示,水位上升最多的是( )(单位:cm)
A. B.
C. D.
2.(2024春 龙海区期末)小丽想知道一块小石头的体积,她把小石头放进一个长、宽都是8cm的长方体容器(完全浸没),水面高度由原来的5cm上升到6cm,小石头的体积是( )cm3。
A.64 B.240 C.320 D.384
3.(2024春 鲤城区期末)把相同的一块石头放到下面四个容器中(完全浸没未溢出),( )水面上升的最高。
A. B.
C. D.
二.填空题(共3小题)
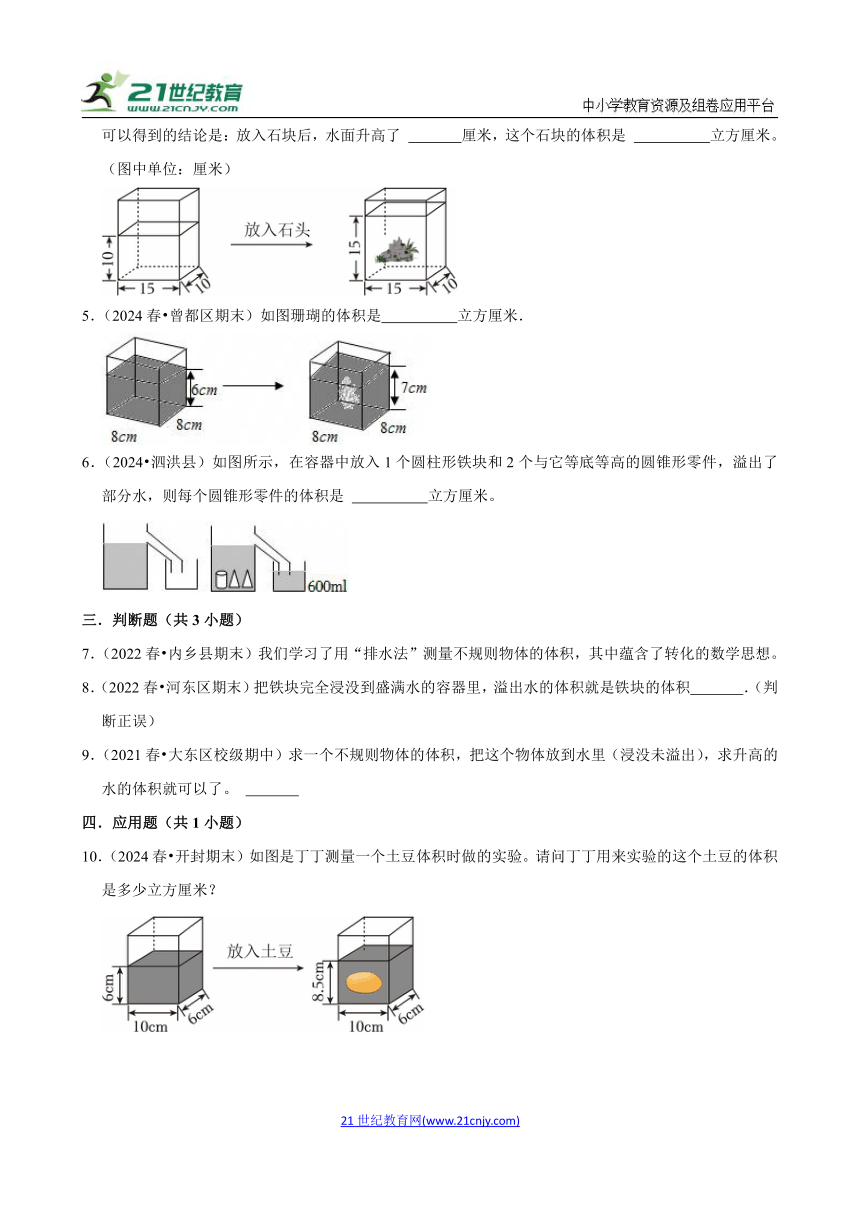
4.(2024 西乡塘区)明明在研究如何得到不规则图形的体积时,做了如下的实验,观察他的实验过程,可以得到的结论是:放入石块后,水面升高了 厘米,这个石块的体积是 立方厘米。
(图中单位:厘米)
5.(2024春 曾都区期末)如图珊瑚的体积是 立方厘米.
6.(2024 泗洪县)如图所示,在容器中放入1个圆柱形铁块和2个与它等底等高的圆锥形零件,溢出了部分水,则每个圆锥形零件的体积是 立方厘米。
三.判断题(共3小题)
7.(2022春 内乡县期末)我们学习了用“排水法”测量不规则物体的体积,其中蕴含了转化的数学思想。
8.(2022春 河东区期末)把铁块完全浸没到盛满水的容器里,溢出水的体积就是铁块的体积 .(判断正误)
9.(2021春 大东区校级期中)求一个不规则物体的体积,把这个物体放到水里(浸没未溢出),求升高的水的体积就可以了。
四.应用题(共1小题)
10.(2024春 开封期末)如图是丁丁测量一个土豆体积时做的实验。请问丁丁用来实验的这个土豆的体积是多少立方厘米?
4.5有趣的测量
参考答案与试题解析
一.选择题(共3小题)
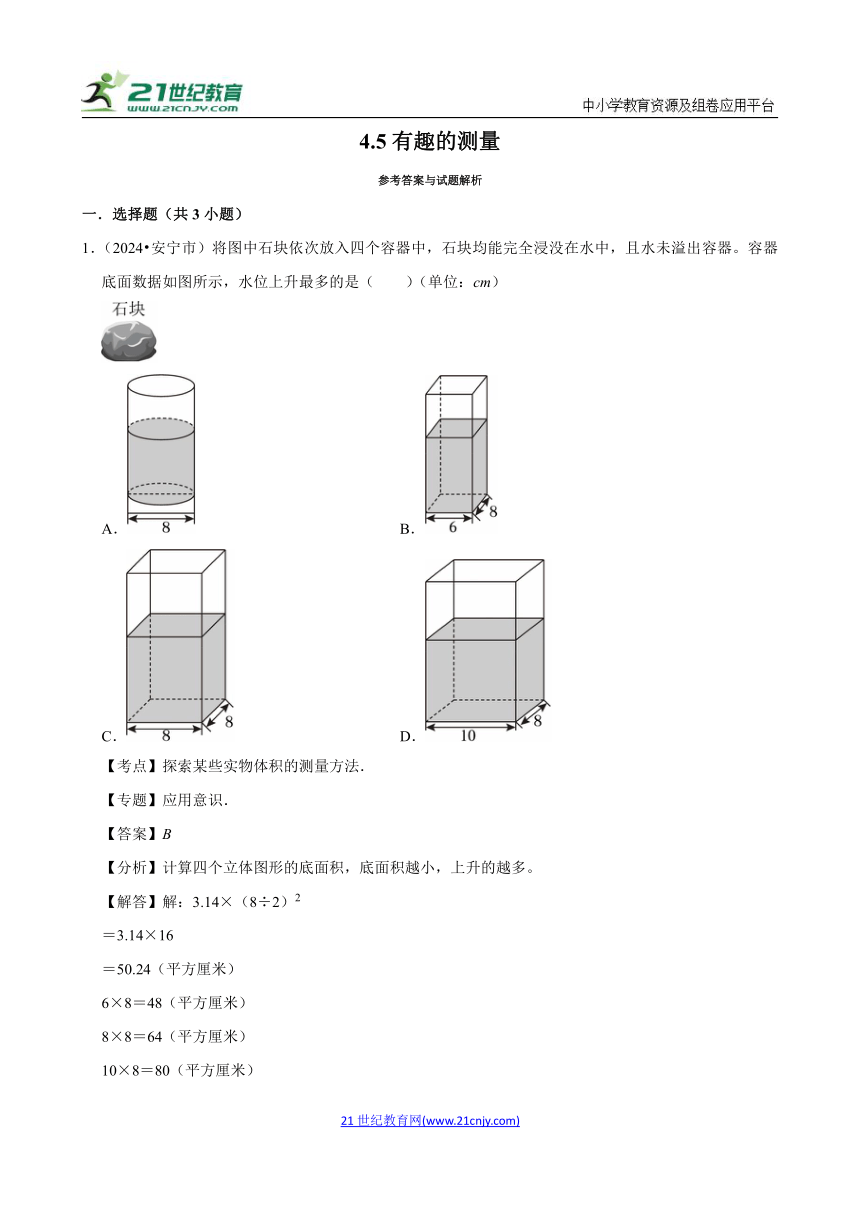
1.(2024 安宁市)将图中石块依次放入四个容器中,石块均能完全浸没在水中,且水未溢出容器。容器底面数据如图所示,水位上升最多的是( )(单位:cm)
A. B.
C. D.
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】B
【分析】计算四个立体图形的底面积,底面积越小,上升的越多。
【解答】解:3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
6×8=48(平方厘米)
8×8=64(平方厘米)
10×8=80(平方厘米)
48<50.24<64<80
答:水位上升最多的是B。
故选:B。
【点评】本题考查圆柱体和长方体底面积的计算。
2.(2024春 龙海区期末)小丽想知道一块小石头的体积,她把小石头放进一个长、宽都是8cm的长方体容器(完全浸没),水面高度由原来的5cm上升到6cm,小石头的体积是( )cm3。
A.64 B.240 C.320 D.384
【考点】探索某些实物体积的测量方法.
【专题】空间观念.
【答案】A
【分析】由题意得:石块的体积等于上升的水的体积,上升水的体积等于高为1厘米的长方体的体积,即根据长方体的体积公式V=abh,即可列式解答。
【解答】解:8×8×(6﹣5)
=64(立方厘米)
答:这块小石头的体积是64立方厘米。
故选:A。
【点评】解答此题的关键是明确:不规则物体的体积等于上升水的体积。
3.(2024春 鲤城区期末)把相同的一块石头放到下面四个容器中(完全浸没未溢出),( )水面上升的最高。
A. B.
C. D.
【考点】探索某些实物体积的测量方法;体积、容积及其单位.
【专题】解题思想方法;空间观念.
【答案】C
【分析】由于石头放入容器中,完全浸没未溢出,所以石头的体积为水面上升的体积,装水的长方体容器体积计算为:底面积×高,体积一定,底面积越小,高越大,因此要选出水面上升最高的容器,即选出底面积最小的即可。
【解答】解:A的底面积为:6×4=24(cm);
B的底面积为:8×4=32(cm);
C的底面积为:4×4=16(cm);
D的底面积为:7×4=28(cm)。
根据计算,C的底面积最小,故水面上升的最高。
故选:C。
【点评】容器的底面积越大,水面上升的就越小,反之就越大。
二.填空题(共3小题)
4.(2024 西乡塘区)明明在研究如何得到不规则图形的体积时,做了如下的实验,观察他的实验过程,可以得到的结论是:放入石块后,水面升高了 5 厘米,这个石块的体积是 750 立方厘米。
(图中单位:厘米)
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】5,750。
【分析】由题意可知:上升的水的体积就是石块的体积,水面上升了15﹣10=5(厘米),因此根据长方体体积公式V=abh,求出上升部分的水的体积,就知道了石块的体积,从而问题得解。
【解答】解:15﹣10=5(厘米)
15×10×(15﹣10)
=150×5
=750(立方厘米)
答:这个石块的体积是750立方厘米。
故答案为:5,750。
【点评】解答此题的关键是明白:上升的水的体积就是石块的体积,结合长方体的体积公式解答即可。
5.(2024春 曾都区期末)如图珊瑚的体积是 128 立方厘米.
【考点】探索某些实物体积的测量方法;长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】将一块珊瑚放入5厘米深的水中后,水面升高了,升高了的水的体积就是这珊瑚的体积,升高的部分是一个底面积是8×8平方厘米,高7﹣5=2厘米的长方体,根据长方体的体积计算公式:长方体的体积=底面积×高列式解答即可.
【解答】解:8×8×(7﹣5)
=64×2
=128(立方厘米)
答:珊瑚的体积是128立方厘米.
故答案为:128.
【点评】此题主要考查特殊物体体积的计算方法,将物体放入或取出水中,水面上升或下降的体积就是物体的体积;也考查了长方体的体积=底面积×高.
6.(2024 泗洪县)如图所示,在容器中放入1个圆柱形铁块和2个与它等底等高的圆锥形零件,溢出了部分水,则每个圆锥形零件的体积是 120 立方厘米。
【考点】探索某些实物体积的测量方法.
【专题】推理能力.
【答案】见试题解答内容
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,在容器中放入1个圆柱形铁块和2个与它等底等高的圆锥形零件,等于放入了5个等底等高的圆锥形零件,用溢出水的体积除以5即可求出每个圆锥形零件的体积。
【解答】解:600毫升=600立方厘米
600÷(3+2)
=600÷5
=120(立方厘米)
答:每个圆锥形零件的体积是120立方厘米。
故答案为:120。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用,注意:体积单位与容积之间的换算。
三.判断题(共3小题)
7.(2022春 内乡县期末)我们学习了用“排水法”测量不规则物体的体积,其中蕴含了转化的数学思想。 √
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】√
【分析】我们在测量不规则物体的体积时,常常把不规则物体转化为规则物体后进行计算。据此解答即可。
【解答】解:用“排水法”测量不规则物体的体积,其中蕴含了转化的数学思想。原题干说法正确。
故答案为:√。
【点评】本题考查求不规则物体的体积,明确我们常常把不规则物体转化为规则物体是解题的关键。
8.(2022春 河东区期末)把铁块完全浸没到盛满水的容器里,溢出水的体积就是铁块的体积 √ .(判断正误)
【考点】探索某些实物体积的测量方法.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】由于此容器里面装满水,放入铁块,使铁块完全浸没在水中.容器里溢出的水即为铁块的体积.
【解答】解:把铁块完全浸没到盛满水的容器里,溢出水的体积就是铁块的体积.
故答案为:√.
【点评】考查了探索某些实物体积的测量方法.本题注意题目中两个条件:装满水的容器,使铁块完全浸没在水中所要表达的意思.
9.(2021春 大东区校级期中)求一个不规则物体的体积,把这个物体放到水里(浸没未溢出),求升高的水的体积就可以了。 √
【考点】探索某些实物体积的测量方法.
【专题】空间观念.
【答案】√
【分析】用排水法来测量不规则物体的体积.在有刻度的量杯里装上水,记下水的体积,把不规则的物体放入杯中,记下此时的体积,求出两次体积的差,就求出了不规则物体的体积,据此判断。
【解答】解:求一个不规则物体的体积,把这个物体放到水里(浸没未溢出),求升高的水的体积就可以了,原题说法正确。
故答案为:√。
【点评】此题主要考查某些实物体积的测量方法。
四.应用题(共1小题)
10.(2024春 开封期末)如图是丁丁测量一个土豆体积时做的实验。请问丁丁用来实验的这个土豆的体积是多少立方厘米?
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】150立方厘米。
【分析】土豆浸没入水中后,土豆体积等于土豆放入后水面上升部分体积;据此解答即可。
【解答】解:10×6×(8.5﹣6)
=60×2.5
=150(立方厘米)
答:这个土豆的体积是150立方厘米。
【点评】本题考查了不规则物体体积测量知识点,浸没入水中物体体积=物体放入后水面上升部分体积。
21世纪教育网(www.21cnjy.com)
一.选择题(共3小题)
1.(2024 安宁市)将图中石块依次放入四个容器中,石块均能完全浸没在水中,且水未溢出容器。容器底面数据如图所示,水位上升最多的是( )(单位:cm)
A. B.
C. D.
2.(2024春 龙海区期末)小丽想知道一块小石头的体积,她把小石头放进一个长、宽都是8cm的长方体容器(完全浸没),水面高度由原来的5cm上升到6cm,小石头的体积是( )cm3。
A.64 B.240 C.320 D.384
3.(2024春 鲤城区期末)把相同的一块石头放到下面四个容器中(完全浸没未溢出),( )水面上升的最高。
A. B.
C. D.
二.填空题(共3小题)
4.(2024 西乡塘区)明明在研究如何得到不规则图形的体积时,做了如下的实验,观察他的实验过程,可以得到的结论是:放入石块后,水面升高了 厘米,这个石块的体积是 立方厘米。
(图中单位:厘米)
5.(2024春 曾都区期末)如图珊瑚的体积是 立方厘米.
6.(2024 泗洪县)如图所示,在容器中放入1个圆柱形铁块和2个与它等底等高的圆锥形零件,溢出了部分水,则每个圆锥形零件的体积是 立方厘米。
三.判断题(共3小题)
7.(2022春 内乡县期末)我们学习了用“排水法”测量不规则物体的体积,其中蕴含了转化的数学思想。
8.(2022春 河东区期末)把铁块完全浸没到盛满水的容器里,溢出水的体积就是铁块的体积 .(判断正误)
9.(2021春 大东区校级期中)求一个不规则物体的体积,把这个物体放到水里(浸没未溢出),求升高的水的体积就可以了。
四.应用题(共1小题)
10.(2024春 开封期末)如图是丁丁测量一个土豆体积时做的实验。请问丁丁用来实验的这个土豆的体积是多少立方厘米?
4.5有趣的测量
参考答案与试题解析
一.选择题(共3小题)
1.(2024 安宁市)将图中石块依次放入四个容器中,石块均能完全浸没在水中,且水未溢出容器。容器底面数据如图所示,水位上升最多的是( )(单位:cm)
A. B.
C. D.
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】B
【分析】计算四个立体图形的底面积,底面积越小,上升的越多。
【解答】解:3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
6×8=48(平方厘米)
8×8=64(平方厘米)
10×8=80(平方厘米)
48<50.24<64<80
答:水位上升最多的是B。
故选:B。
【点评】本题考查圆柱体和长方体底面积的计算。
2.(2024春 龙海区期末)小丽想知道一块小石头的体积,她把小石头放进一个长、宽都是8cm的长方体容器(完全浸没),水面高度由原来的5cm上升到6cm,小石头的体积是( )cm3。
A.64 B.240 C.320 D.384
【考点】探索某些实物体积的测量方法.
【专题】空间观念.
【答案】A
【分析】由题意得:石块的体积等于上升的水的体积,上升水的体积等于高为1厘米的长方体的体积,即根据长方体的体积公式V=abh,即可列式解答。
【解答】解:8×8×(6﹣5)
=64(立方厘米)
答:这块小石头的体积是64立方厘米。
故选:A。
【点评】解答此题的关键是明确:不规则物体的体积等于上升水的体积。
3.(2024春 鲤城区期末)把相同的一块石头放到下面四个容器中(完全浸没未溢出),( )水面上升的最高。
A. B.
C. D.
【考点】探索某些实物体积的测量方法;体积、容积及其单位.
【专题】解题思想方法;空间观念.
【答案】C
【分析】由于石头放入容器中,完全浸没未溢出,所以石头的体积为水面上升的体积,装水的长方体容器体积计算为:底面积×高,体积一定,底面积越小,高越大,因此要选出水面上升最高的容器,即选出底面积最小的即可。
【解答】解:A的底面积为:6×4=24(cm);
B的底面积为:8×4=32(cm);
C的底面积为:4×4=16(cm);
D的底面积为:7×4=28(cm)。
根据计算,C的底面积最小,故水面上升的最高。
故选:C。
【点评】容器的底面积越大,水面上升的就越小,反之就越大。
二.填空题(共3小题)
4.(2024 西乡塘区)明明在研究如何得到不规则图形的体积时,做了如下的实验,观察他的实验过程,可以得到的结论是:放入石块后,水面升高了 5 厘米,这个石块的体积是 750 立方厘米。
(图中单位:厘米)
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】5,750。
【分析】由题意可知:上升的水的体积就是石块的体积,水面上升了15﹣10=5(厘米),因此根据长方体体积公式V=abh,求出上升部分的水的体积,就知道了石块的体积,从而问题得解。
【解答】解:15﹣10=5(厘米)
15×10×(15﹣10)
=150×5
=750(立方厘米)
答:这个石块的体积是750立方厘米。
故答案为:5,750。
【点评】解答此题的关键是明白:上升的水的体积就是石块的体积,结合长方体的体积公式解答即可。
5.(2024春 曾都区期末)如图珊瑚的体积是 128 立方厘米.
【考点】探索某些实物体积的测量方法;长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】将一块珊瑚放入5厘米深的水中后,水面升高了,升高了的水的体积就是这珊瑚的体积,升高的部分是一个底面积是8×8平方厘米,高7﹣5=2厘米的长方体,根据长方体的体积计算公式:长方体的体积=底面积×高列式解答即可.
【解答】解:8×8×(7﹣5)
=64×2
=128(立方厘米)
答:珊瑚的体积是128立方厘米.
故答案为:128.
【点评】此题主要考查特殊物体体积的计算方法,将物体放入或取出水中,水面上升或下降的体积就是物体的体积;也考查了长方体的体积=底面积×高.
6.(2024 泗洪县)如图所示,在容器中放入1个圆柱形铁块和2个与它等底等高的圆锥形零件,溢出了部分水,则每个圆锥形零件的体积是 120 立方厘米。
【考点】探索某些实物体积的测量方法.
【专题】推理能力.
【答案】见试题解答内容
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,在容器中放入1个圆柱形铁块和2个与它等底等高的圆锥形零件,等于放入了5个等底等高的圆锥形零件,用溢出水的体积除以5即可求出每个圆锥形零件的体积。
【解答】解:600毫升=600立方厘米
600÷(3+2)
=600÷5
=120(立方厘米)
答:每个圆锥形零件的体积是120立方厘米。
故答案为:120。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用,注意:体积单位与容积之间的换算。
三.判断题(共3小题)
7.(2022春 内乡县期末)我们学习了用“排水法”测量不规则物体的体积,其中蕴含了转化的数学思想。 √
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】√
【分析】我们在测量不规则物体的体积时,常常把不规则物体转化为规则物体后进行计算。据此解答即可。
【解答】解:用“排水法”测量不规则物体的体积,其中蕴含了转化的数学思想。原题干说法正确。
故答案为:√。
【点评】本题考查求不规则物体的体积,明确我们常常把不规则物体转化为规则物体是解题的关键。
8.(2022春 河东区期末)把铁块完全浸没到盛满水的容器里,溢出水的体积就是铁块的体积 √ .(判断正误)
【考点】探索某些实物体积的测量方法.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】由于此容器里面装满水,放入铁块,使铁块完全浸没在水中.容器里溢出的水即为铁块的体积.
【解答】解:把铁块完全浸没到盛满水的容器里,溢出水的体积就是铁块的体积.
故答案为:√.
【点评】考查了探索某些实物体积的测量方法.本题注意题目中两个条件:装满水的容器,使铁块完全浸没在水中所要表达的意思.
9.(2021春 大东区校级期中)求一个不规则物体的体积,把这个物体放到水里(浸没未溢出),求升高的水的体积就可以了。 √
【考点】探索某些实物体积的测量方法.
【专题】空间观念.
【答案】√
【分析】用排水法来测量不规则物体的体积.在有刻度的量杯里装上水,记下水的体积,把不规则的物体放入杯中,记下此时的体积,求出两次体积的差,就求出了不规则物体的体积,据此判断。
【解答】解:求一个不规则物体的体积,把这个物体放到水里(浸没未溢出),求升高的水的体积就可以了,原题说法正确。
故答案为:√。
【点评】此题主要考查某些实物体积的测量方法。
四.应用题(共1小题)
10.(2024春 开封期末)如图是丁丁测量一个土豆体积时做的实验。请问丁丁用来实验的这个土豆的体积是多少立方厘米?
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】150立方厘米。
【分析】土豆浸没入水中后,土豆体积等于土豆放入后水面上升部分体积;据此解答即可。
【解答】解:10×6×(8.5﹣6)
=60×2.5
=150(立方厘米)
答:这个土豆的体积是150立方厘米。
【点评】本题考查了不规则物体体积测量知识点,浸没入水中物体体积=物体放入后水面上升部分体积。
21世纪教育网(www.21cnjy.com)
