【同步分层培优】8.2复式折线统计图提高卷(含解析)-2024-2025学年五年级下册数学北师大版
文档属性
| 名称 | 【同步分层培优】8.2复式折线统计图提高卷(含解析)-2024-2025学年五年级下册数学北师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 16:47:30 | ||
图片预览

文档简介
8.2复式折线统计图
一.选择题(共3小题)
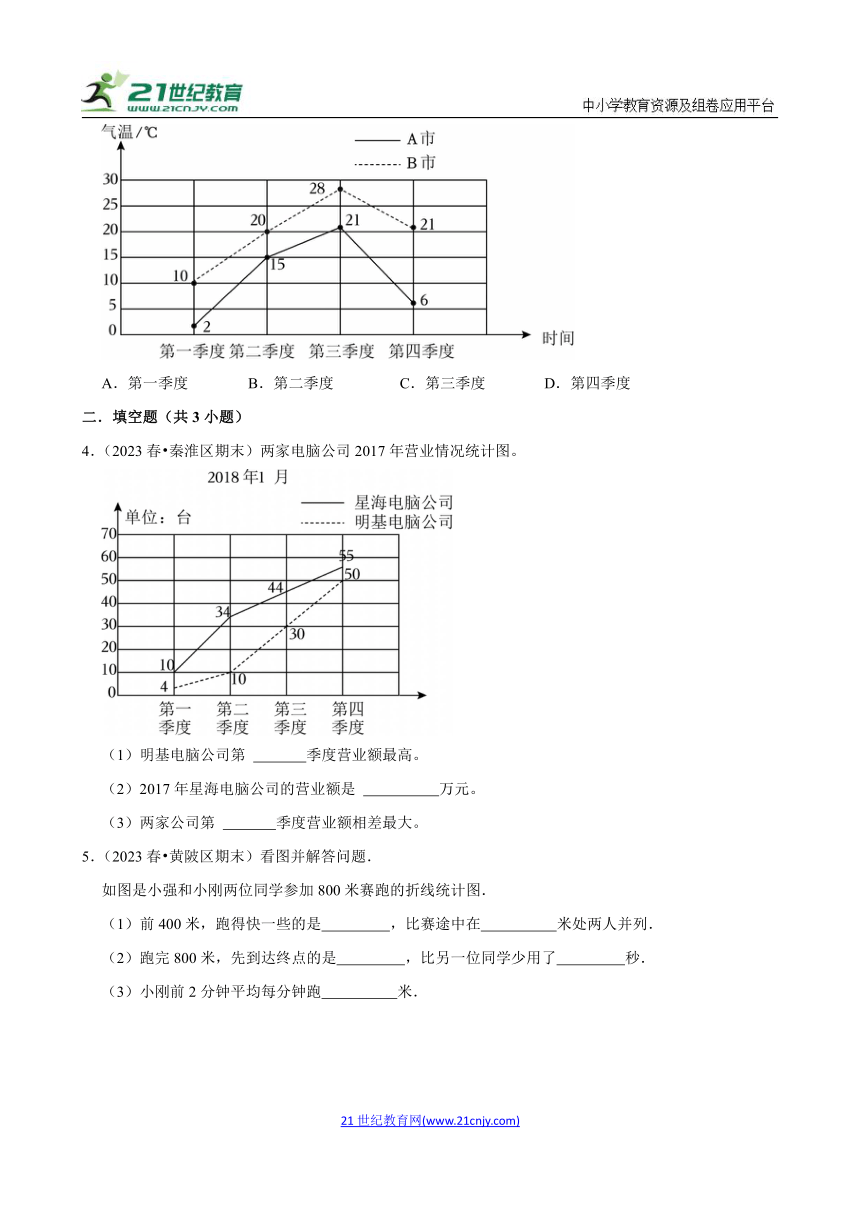
1.(2024春 新都区期末)新都区某校两名运动员平时10天跳绳成绩折线统计图如图所示。如果这2人中只选派一名运动员去参赛,你认为应派( )最合适。
A.乙 B.甲 C.都可以 D.无法确定
2.(2024春 沛县期中)下面是甲、乙两架模型飞机的飞行情况统计图,对图中信息表述不正确的是( )
A.第9秒时,两架模型飞机飞行高度都是27米
B.第15~18秒,甲模型飞机飞行高度保持不变,乙模型飞机飞行高度在急速下降
C.甲模型飞机飞行的时间长,乙模型飞机的最高飞行高度高
D.在同一时刻,两架模型飞机飞行高度最多相差6米
3.(2021春 郾城区期末)如图是A市和B市四个季度的平均气温统计图。( )温度相差最小。
A.第一季度 B.第二季度 C.第三季度 D.第四季度
二.填空题(共3小题)
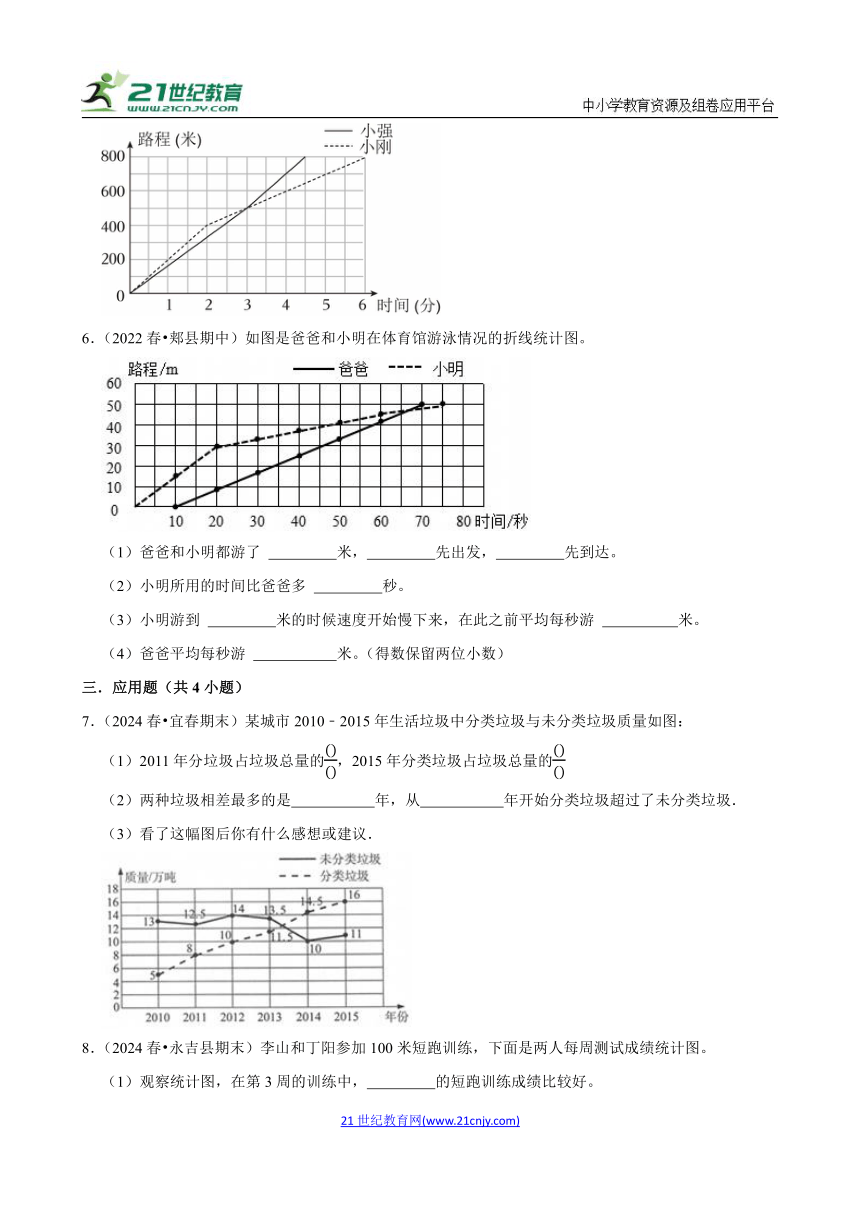
4.(2023春 秦淮区期末)两家电脑公司2017年营业情况统计图。
(1)明基电脑公司第 季度营业额最高。
(2)2017年星海电脑公司的营业额是 万元。
(3)两家公司第 季度营业额相差最大。
5.(2023春 黄陂区期末)看图并解答问题.
如图是小强和小刚两位同学参加800米赛跑的折线统计图.
(1)前400米,跑得快一些的是 ,比赛途中在 米处两人并列.
(2)跑完800米,先到达终点的是 ,比另一位同学少用了 秒.
(3)小刚前2分钟平均每分钟跑 米.
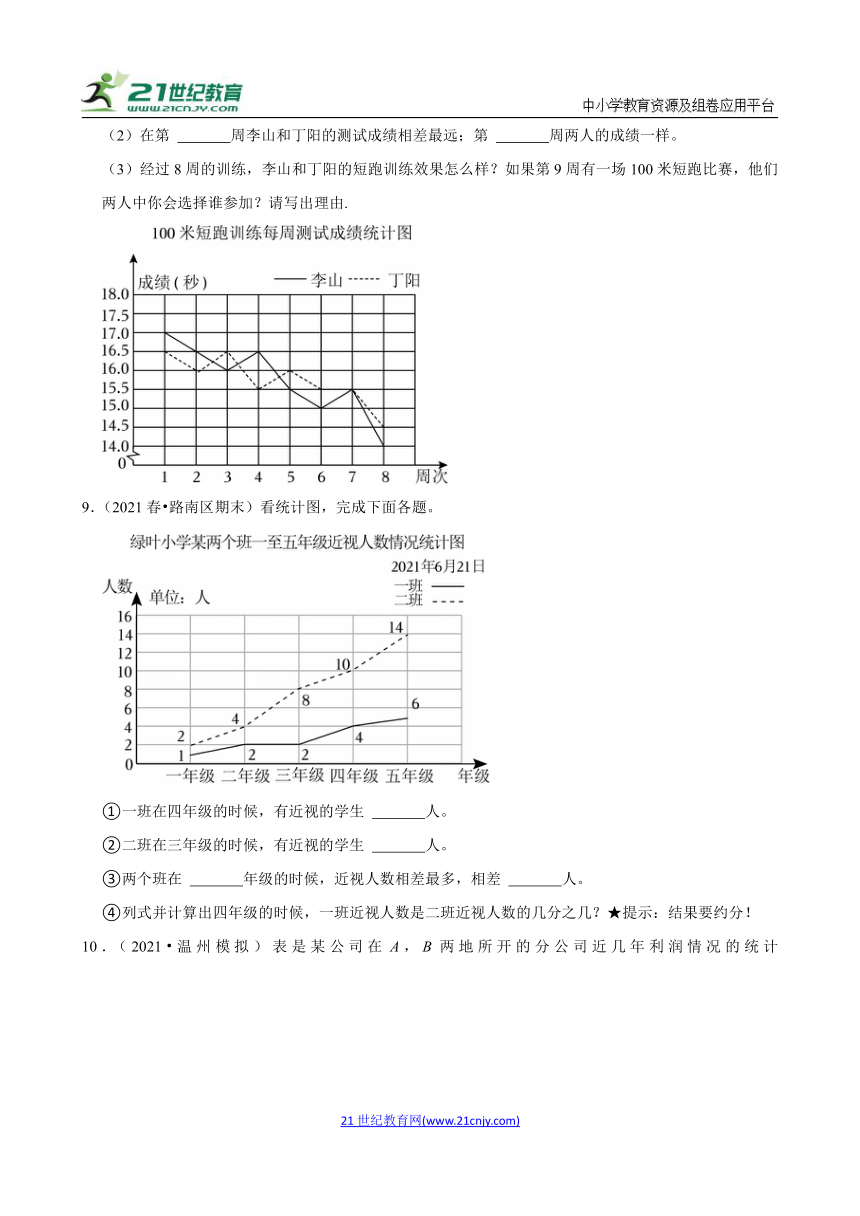
6.(2022春 郏县期中)如图是爸爸和小明在体育馆游泳情况的折线统计图。
(1)爸爸和小明都游了 米, 先出发, 先到达。
(2)小明所用的时间比爸爸多 秒。
(3)小明游到 米的时候速度开始慢下来,在此之前平均每秒游 米。
(4)爸爸平均每秒游 米。(得数保留两位小数)
三.应用题(共4小题)
7.(2024春 宜春期末)某城市2010﹣2015年生活垃圾中分类垃圾与未分类垃圾质量如图:
(1)2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的
(2)两种垃圾相差最多的是 年,从 年开始分类垃圾超过了未分类垃圾.
(3)看了这幅图后你有什么感想或建议.
8.(2024春 永吉县期末)李山和丁阳参加100米短跑训练,下面是两人每周测试成绩统计图。
(1)观察统计图,在第3周的训练中, 的短跑训练成绩比较好。
(2)在第 周李山和丁阳的测试成绩相差最远;第 周两人的成绩一样。
(3)经过8周的训练,李山和丁阳的短跑训练效果怎么样?如果第9周有一场100米短跑比赛,他们两人中你会选择谁参加?请写出理由.
9.(2021春 路南区期末)看统计图,完成下面各题。
①一班在四年级的时候,有近视的学生 人。
②二班在三年级的时候,有近视的学生 人。
③两个班在 年级的时候,近视人数相差最多,相差 人。
④列式并计算出四年级的时候,一班近视人数是二班近视人数的几分之几?★提示:结果要约分!
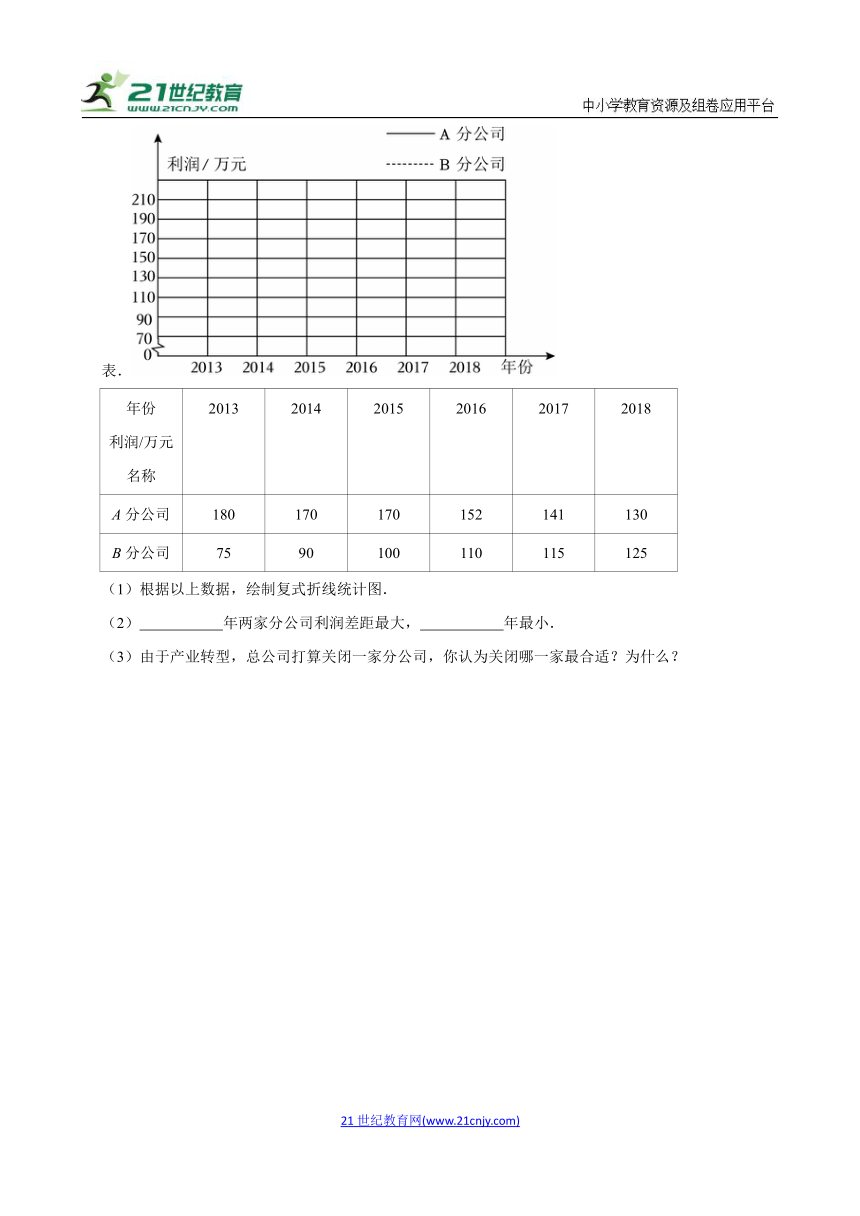
10.(2021 温州模拟)表是某公司在A,B两地所开的分公司近几年利润情况的统计表.
年份 利润/万元 名称 2013 2014 2015 2016 2017 2018
A分公司 180 170 170 152 141 130
B分公司 75 90 100 110 115 125
(1)根据以上数据,绘制复式折线统计图.
(2) 年两家分公司利润差距最大, 年最小.
(3)由于产业转型,总公司打算关闭一家分公司,你认为关闭哪一家最合适?为什么?
8.2复式折线统计图
参考答案与试题解析
一.选择题(共3小题)
1.(2024春 新都区期末)新都区某校两名运动员平时10天跳绳成绩折线统计图如图所示。如果这2人中只选派一名运动员去参赛,你认为应派( )最合适。
A.乙 B.甲 C.都可以 D.无法确定
【考点】复式折线统计图.
【专题】数据分析观念.
【答案】B
【分析】观察复式折线统计图,甲运动员成绩呈稳定上升的趋势,乙运动员的成绩整体呈上升趋势,但后面几天波动比较大,应选派成绩相对稳定的运动员去参赛。
【解答】解:观察图可得,甲运动员成绩呈稳定上升的趋势,应派甲最合适。
故选:B。
【点评】本题考查复式折线统计图,从图中提取所需信息是解题的关键。
2.(2024春 沛县期中)下面是甲、乙两架模型飞机的飞行情况统计图,对图中信息表述不正确的是( )
A.第9秒时,两架模型飞机飞行高度都是27米
B.第15~18秒,甲模型飞机飞行高度保持不变,乙模型飞机飞行高度在急速下降
C.甲模型飞机飞行的时间长,乙模型飞机的最高飞行高度高
D.在同一时刻,两架模型飞机飞行高度最多相差6米
【考点】复式折线统计图.
【专题】综合题;应用意识.
【答案】D
【分析】对于A,据图可知,甲、乙两架模型飞机的飞行高度情况,在第9秒时处于同一点,据此判断;
对于B,据图可知,第15~18秒期间,甲模型飞机飞行高度保持不变,乙模型飞机由30米高度直接降落,据此判断;
对于C,据图可得出,甲模型飞机与乙模型飞机的飞行时长;乙模型飞机与甲模型飞机的最高飞行高度,相互比较即可判断;
对于D,观察统计图即可判断。
【解答】解:A.据图可知,甲、乙两架模型飞机在第9秒时处于同一高度,都是27米。故说法正确;
B.据图可知,第15~18秒期间,甲模型飞机飞行高度保持24米不变,乙模型飞机由30米高度直接降落,呈急速下降。故说法正确;
C.据图可知,甲模型飞机飞行时长24秒,大于乙模型飞机的18秒;乙模型飞机最高高度为36米,大于甲模型飞机的30米。故说法正确;
D.据图可知,在第18秒时,甲模型飞机飞行高度为24米,乙模型飞机为0米。故说法错误。
故选:D。
【点评】本题考查复式折线统计图,从图中提取所需信息是解题的关键。
3.(2021春 郾城区期末)如图是A市和B市四个季度的平均气温统计图。( )温度相差最小。
A.第一季度 B.第二季度 C.第三季度 D.第四季度
【考点】复式折线统计图.
【专题】数据分析观念.
【答案】B
【分析】分别计算出两个城市每个季度的平均气温差,再比较大小后即可确定哪个季节温度差最小。
【解答】解:10﹣2=8(℃)
20﹣15=(℃)
28﹣21=7(℃)
21﹣6=15(℃)
5<7<8<15
答:第二季度温度相差最小。
故选:B。
【点评】此题考查的目的是理解和掌握折线统计图的特点和作用,能够根据它的特点和作用解决有关的实际问题。
二.填空题(共3小题)
4.(2023春 秦淮区期末)两家电脑公司2017年营业情况统计图。
(1)明基电脑公司第 四 季度营业额最高。
(2)2017年星海电脑公司的营业额是 143 万元。
(3)两家公司第 二 季度营业额相差最大。
【考点】复式折线统计图.
【专题】数感;数据分析观念;运算能力.
【答案】(1)四;(2)143;(3)二。
【分析】(1)比较明基电脑公司每个季度的营业额,然后找到最高的即可;
(2)把2017年星海电脑公司每个季度的营业额加起来即可;
(3)把每个季度两家公司的营业额作差,然后找到最大的即可。
【解答】解:(1)4<10<30<50,所以明基电脑公司第四季度营业额最高;
(2)10+34+44+55=143(万元),所以2017年星海电脑公司的营业额是143万元;
(3)10﹣4=6(万元),34﹣10=24(万元),44﹣30=14(万元),55﹣50=5(万元),5<6<14<24,所以两家公司第二季度营业额相差最大。
故答案为:(1)四;(2)143;(3)二。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,再根据整数加减法的意义解决问题。
5.(2023春 黄陂区期末)看图并解答问题.
如图是小强和小刚两位同学参加800米赛跑的折线统计图.
(1)前400米,跑得快一些的是 小刚 ,比赛途中在 500 米处两人并列.
(2)跑完800米,先到达终点的是 小强 ,比另一位同学少用了 90 秒.
(3)小刚前2分钟平均每分钟跑 200 米.
【考点】复式折线统计图.
【专题】统计数据的计算与应用.
【答案】见试题解答内容
【分析】(1)由表示小强、小刚跑的路程与时间的拆线可以看出,前400米小刚的比小强跑得快一些;到500米时小强追上了小刚,二人并列.
(2)跑完800米,小强先到达终点,用时4.5分钟,小刚后到达终点,用时6分钟.小强比小刚少用6﹣4.5=1.5分钟,再乘进率60化秒.
(3)小刚前2分钟跑了400米,根据“速度=路程÷时间”即可求出小刚前2分钟平均每分钟跑的米数.
【解答】解:(1)答:前400米,跑得快一些的是小刚,比赛途中在500米处两人并列.
(2)6﹣4.5=1.5(分)
1.5分=90秒
答:跑完800米,先到达终点的是小强,比另一位同学少用了90秒.
(3)400÷2=200(米)
答:小刚前2分钟平均每分钟跑200米.
故答案为:小刚,500,小强,90,200.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
6.(2022春 郏县期中)如图是爸爸和小明在体育馆游泳情况的折线统计图。
(1)爸爸和小明都游了 50 米, 小明 先出发, 爸爸 先到达。
(2)小明所用的时间比爸爸多 15 秒。
(3)小明游到 30 米的时候速度开始慢下来,在此之前平均每秒游 1.5 米。
(4)爸爸平均每秒游 0.83 米。(得数保留两位小数)
【考点】复式折线统计图.
【专题】应用意识.
【答案】(1)50,小明,爸爸;(2)15;(3)30,1.5;(4)0.83。
【分析】(1)根据统计图可知:折线统计图中虚线代表小明的游泳情况,实线代表爸爸的游泳情况,爸爸和小明都游了50米,小明先出发,爸爸先到达。
(2)爸爸让小明先游10秒,爸爸又比小明提前5秒到达,小明所用的时间比爸爸多15秒。
(3)根据统计图可知:小明游到30米的时候速度开始慢下来,在此之前平均每秒游30÷20=1.5(米)。
(4)爸爸平均每秒游50÷60≈0.83(米)。
【解答】解:(1)爸爸和小明都游了50米,小明先出发,爸爸先到达。
(2)75﹣60=15(秒)
答:小明所用的时间比爸爸多15秒。
(3)30÷20=1.5(米)
答:小明游到30米的时候速度开始慢下来,在此之前平均每秒游1.5米。
(4)50÷60≈0.83(米)
答:爸爸平均每秒游0.83米。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
三.应用题(共4小题)
7.(2024春 宜春期末)某城市2010﹣2015年生活垃圾中分类垃圾与未分类垃圾质量如图:
(1)2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的
(2)两种垃圾相差最多的是 2010 年,从 2015 年开始分类垃圾超过了未分类垃圾.
(3)看了这幅图后你有什么感想或建议.
【考点】复式折线统计图.
【专题】统计数据的计算与应用.
【答案】见试题解答内容
【分析】(1)由复式折线统计图可以看出,2011年未分类的垃圾为12.5万吨,分类的是8万吨,垃圾总量为12.5+8=20.5(万吨),用分类垃圾的吨数除以总吨数;同理,2015年未分类的垃圾为16万吨,分类的是1万吨,垃圾总量为16+11=27(万吨),用分类垃圾的吨数除以总吨数.
(2)由复式折线统计图可以看出,表示未分类垃圾、分类垃圾的点,2010年距离最大,说明该年两种垃圾相差最多;表示分类垃圾的折线从2015年在表示未分类垃圾折线的上方,说明该年开始分类垃圾超过了未分类垃圾.
(3)垃圾分类处理的好处有:减少占地;减少污染;变废为宝;减少危害.看了这幅图感到人们的环保意识在增强,感到欣慰;建议所有垃圾能够完全分类.
【解答】解:(1)8÷(12.5+8)
=8÷20.5
11÷(16+11)
=11÷27
答:2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的.
(2)答:两种垃圾相差最多的是 2010年,从 2015年开始分类垃圾超过了未分类垃圾.
(3)答:的感想和建议:看了这幅图感到人们的环保意识在增强,感到欣慰;建议所有垃圾能够完全分类.
故答案为:2010,2015.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
8.(2024春 永吉县期末)李山和丁阳参加100米短跑训练,下面是两人每周测试成绩统计图。
(1)观察统计图,在第3周的训练中, 李山 的短跑训练成绩比较好。
(2)在第 4 周李山和丁阳的测试成绩相差最远;第 7 周两人的成绩一样。
(3)经过8周的训练,李山和丁阳的短跑训练效果怎么样?如果第9周有一场100米短跑比赛,他们两人中你会选择谁参加?请写出理由.
【考点】复式折线统计图.
【专题】数据分析观念.
【答案】(1)李山;(2)4,7。
(3)根据复式折线统计图可知,根据8周的训练结果可以看出,两个人短跑用时呈下降趋势,所以训练的效果非常明显。如果第9周有一场100米短跑比赛,会选择李山参加,因为李山的用时比较少,获胜的可能性大一些。(答案不唯一)
【分析】(1)观察统计图,在第3周的训练中,李山的短跑训练成绩比较好。
(2)在第4周李山和丁阳的测试成绩相差最远;第7周两人的成绩一样。
(3)根据复式折线统计图可知,根据8周的训练结果可以看出,两个人短跑用时呈下降趋势,所以训练的效果非常明显。如果第9周有一场100米短跑比赛,会选择李山参加,因为李山的用时比较少,获胜的可能性大一些。(答案不唯一)
【解答】解:(1)在第3周的训练中,李山的短跑训练成绩比较好。
(2)在第4周李山和丁阳的测试成绩相差最远;第7周两人的成绩一样。
(3)根据复式折线统计图可知,根据8周的训练结果可以看出,两个人短跑用时呈下降趋势,所以训练的效果非常明显。如果第9周有一场100米短跑比赛,会选择李山参加,因为李山的用时比较少,获胜的可能性大一些。(答案不唯一)
故答案为:李山;4,7。
【点评】本题主要考查复式折线统计图的应用,关键根据统计图找到解决问题的条件,解决问题。
9.(2021春 路南区期末)看统计图,完成下面各题。
①一班在四年级的时候,有近视的学生 4 人。
②二班在三年级的时候,有近视的学生 8 人。
③两个班在 五 年级的时候,近视人数相差最多,相差 9 人。
④列式并计算出四年级的时候,一班近视人数是二班近视人数的几分之几?★提示:结果要约分!
【考点】复式折线统计图.
【专题】综合题;数据分析观念.
【答案】①4;
②8;
③五,9;
④。
【分析】折线统计图横轴表示年级,纵轴表示近视人数,实线表示一班各年级时的近视人数,虚线表示二班各年级时的近视人数;
①实线四年级所对应的近视人数是4人,即一班在四年级时近视人数为4人;
②虚线三年级所对应的近视人数是8人,即二班在三年级时近视人数为8人;
③实线和虚线在五年级时相距最远,表示两个班近视人数相差最多,用两个班在五年级时的近视人数相减,就是相差多少人;
④四年级时一班近视人数4人,二班近视人数10人,求一班近视人数是二班的几分之几,用4除以10。
【解答】解:①一班在四年级的时候,有近视的学生4人;
②二班在三年级的时候,有近视的学生8人;
③14﹣5=9(人)
答:两个班在五年级的时候,近视人数相差最多,相差9人。
④4÷10
答:四年级的时候,一班近视人数是二班近视人数的。
故答案为:4;8;五,9。
【点评】此题重点考查从复式折线统计图中读取信息进行分析的能力及求一个数是另一个数的几分之几的方法。
10.(2021 温州模拟)表是某公司在A,B两地所开的分公司近几年利润情况的统计表.
年份 利润/万元 名称 2013 2014 2015 2016 2017 2018
A分公司 180 170 170 152 141 130
B分公司 75 90 100 110 115 125
(1)根据以上数据,绘制复式折线统计图.
(2) 2013 年两家分公司利润差距最大, 2018 年最小.
(3)由于产业转型,总公司打算关闭一家分公司,你认为关闭哪一家最合适?为什么?
【考点】复式折线统计图.
【专题】统计数据的计算与应用;数据分析观念;应用意识.
【答案】见试题解答内容
【分析】(1)根据折线统计图的绘制方法,先按照统计表中的数据描出各点,然后顺次连接各点完成统计图.
(2)通过观察统计图表可知,2013年两家分公司利润差最大,2018年两家分公司利润差最小.
(3)我认为关闭A分公司,因为到2018年,两家分公司利润差不多,可是A分公司利润呈下降趋势,B分公司利润呈上升趋势.据此解答.
【解答】解:(1)作图如下:
某公司在A,B两地所开的分公司近几年利润情况的统计图
(2)2013年两家分公司利润差最大,2018年两家分公司利润差最小.
(3)我认为关闭A分公司,因为到2018年,两家分公司利润差不多,可是A分公司利润呈下降趋势,B分公司利润呈上升趋势.
故答案为:2013、2018.
【点评】此题考查的目的是理解掌握折线统计图的绘制方法及应用,并且能够根据统计图表提供的信息,解决有关的实际问题.
21世纪教育网(www.21cnjy.com)
一.选择题(共3小题)
1.(2024春 新都区期末)新都区某校两名运动员平时10天跳绳成绩折线统计图如图所示。如果这2人中只选派一名运动员去参赛,你认为应派( )最合适。
A.乙 B.甲 C.都可以 D.无法确定
2.(2024春 沛县期中)下面是甲、乙两架模型飞机的飞行情况统计图,对图中信息表述不正确的是( )
A.第9秒时,两架模型飞机飞行高度都是27米
B.第15~18秒,甲模型飞机飞行高度保持不变,乙模型飞机飞行高度在急速下降
C.甲模型飞机飞行的时间长,乙模型飞机的最高飞行高度高
D.在同一时刻,两架模型飞机飞行高度最多相差6米
3.(2021春 郾城区期末)如图是A市和B市四个季度的平均气温统计图。( )温度相差最小。
A.第一季度 B.第二季度 C.第三季度 D.第四季度
二.填空题(共3小题)
4.(2023春 秦淮区期末)两家电脑公司2017年营业情况统计图。
(1)明基电脑公司第 季度营业额最高。
(2)2017年星海电脑公司的营业额是 万元。
(3)两家公司第 季度营业额相差最大。
5.(2023春 黄陂区期末)看图并解答问题.
如图是小强和小刚两位同学参加800米赛跑的折线统计图.
(1)前400米,跑得快一些的是 ,比赛途中在 米处两人并列.
(2)跑完800米,先到达终点的是 ,比另一位同学少用了 秒.
(3)小刚前2分钟平均每分钟跑 米.
6.(2022春 郏县期中)如图是爸爸和小明在体育馆游泳情况的折线统计图。
(1)爸爸和小明都游了 米, 先出发, 先到达。
(2)小明所用的时间比爸爸多 秒。
(3)小明游到 米的时候速度开始慢下来,在此之前平均每秒游 米。
(4)爸爸平均每秒游 米。(得数保留两位小数)
三.应用题(共4小题)
7.(2024春 宜春期末)某城市2010﹣2015年生活垃圾中分类垃圾与未分类垃圾质量如图:
(1)2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的
(2)两种垃圾相差最多的是 年,从 年开始分类垃圾超过了未分类垃圾.
(3)看了这幅图后你有什么感想或建议.
8.(2024春 永吉县期末)李山和丁阳参加100米短跑训练,下面是两人每周测试成绩统计图。
(1)观察统计图,在第3周的训练中, 的短跑训练成绩比较好。
(2)在第 周李山和丁阳的测试成绩相差最远;第 周两人的成绩一样。
(3)经过8周的训练,李山和丁阳的短跑训练效果怎么样?如果第9周有一场100米短跑比赛,他们两人中你会选择谁参加?请写出理由.
9.(2021春 路南区期末)看统计图,完成下面各题。
①一班在四年级的时候,有近视的学生 人。
②二班在三年级的时候,有近视的学生 人。
③两个班在 年级的时候,近视人数相差最多,相差 人。
④列式并计算出四年级的时候,一班近视人数是二班近视人数的几分之几?★提示:结果要约分!
10.(2021 温州模拟)表是某公司在A,B两地所开的分公司近几年利润情况的统计表.
年份 利润/万元 名称 2013 2014 2015 2016 2017 2018
A分公司 180 170 170 152 141 130
B分公司 75 90 100 110 115 125
(1)根据以上数据,绘制复式折线统计图.
(2) 年两家分公司利润差距最大, 年最小.
(3)由于产业转型,总公司打算关闭一家分公司,你认为关闭哪一家最合适?为什么?
8.2复式折线统计图
参考答案与试题解析
一.选择题(共3小题)
1.(2024春 新都区期末)新都区某校两名运动员平时10天跳绳成绩折线统计图如图所示。如果这2人中只选派一名运动员去参赛,你认为应派( )最合适。
A.乙 B.甲 C.都可以 D.无法确定
【考点】复式折线统计图.
【专题】数据分析观念.
【答案】B
【分析】观察复式折线统计图,甲运动员成绩呈稳定上升的趋势,乙运动员的成绩整体呈上升趋势,但后面几天波动比较大,应选派成绩相对稳定的运动员去参赛。
【解答】解:观察图可得,甲运动员成绩呈稳定上升的趋势,应派甲最合适。
故选:B。
【点评】本题考查复式折线统计图,从图中提取所需信息是解题的关键。
2.(2024春 沛县期中)下面是甲、乙两架模型飞机的飞行情况统计图,对图中信息表述不正确的是( )
A.第9秒时,两架模型飞机飞行高度都是27米
B.第15~18秒,甲模型飞机飞行高度保持不变,乙模型飞机飞行高度在急速下降
C.甲模型飞机飞行的时间长,乙模型飞机的最高飞行高度高
D.在同一时刻,两架模型飞机飞行高度最多相差6米
【考点】复式折线统计图.
【专题】综合题;应用意识.
【答案】D
【分析】对于A,据图可知,甲、乙两架模型飞机的飞行高度情况,在第9秒时处于同一点,据此判断;
对于B,据图可知,第15~18秒期间,甲模型飞机飞行高度保持不变,乙模型飞机由30米高度直接降落,据此判断;
对于C,据图可得出,甲模型飞机与乙模型飞机的飞行时长;乙模型飞机与甲模型飞机的最高飞行高度,相互比较即可判断;
对于D,观察统计图即可判断。
【解答】解:A.据图可知,甲、乙两架模型飞机在第9秒时处于同一高度,都是27米。故说法正确;
B.据图可知,第15~18秒期间,甲模型飞机飞行高度保持24米不变,乙模型飞机由30米高度直接降落,呈急速下降。故说法正确;
C.据图可知,甲模型飞机飞行时长24秒,大于乙模型飞机的18秒;乙模型飞机最高高度为36米,大于甲模型飞机的30米。故说法正确;
D.据图可知,在第18秒时,甲模型飞机飞行高度为24米,乙模型飞机为0米。故说法错误。
故选:D。
【点评】本题考查复式折线统计图,从图中提取所需信息是解题的关键。
3.(2021春 郾城区期末)如图是A市和B市四个季度的平均气温统计图。( )温度相差最小。
A.第一季度 B.第二季度 C.第三季度 D.第四季度
【考点】复式折线统计图.
【专题】数据分析观念.
【答案】B
【分析】分别计算出两个城市每个季度的平均气温差,再比较大小后即可确定哪个季节温度差最小。
【解答】解:10﹣2=8(℃)
20﹣15=(℃)
28﹣21=7(℃)
21﹣6=15(℃)
5<7<8<15
答:第二季度温度相差最小。
故选:B。
【点评】此题考查的目的是理解和掌握折线统计图的特点和作用,能够根据它的特点和作用解决有关的实际问题。
二.填空题(共3小题)
4.(2023春 秦淮区期末)两家电脑公司2017年营业情况统计图。
(1)明基电脑公司第 四 季度营业额最高。
(2)2017年星海电脑公司的营业额是 143 万元。
(3)两家公司第 二 季度营业额相差最大。
【考点】复式折线统计图.
【专题】数感;数据分析观念;运算能力.
【答案】(1)四;(2)143;(3)二。
【分析】(1)比较明基电脑公司每个季度的营业额,然后找到最高的即可;
(2)把2017年星海电脑公司每个季度的营业额加起来即可;
(3)把每个季度两家公司的营业额作差,然后找到最大的即可。
【解答】解:(1)4<10<30<50,所以明基电脑公司第四季度营业额最高;
(2)10+34+44+55=143(万元),所以2017年星海电脑公司的营业额是143万元;
(3)10﹣4=6(万元),34﹣10=24(万元),44﹣30=14(万元),55﹣50=5(万元),5<6<14<24,所以两家公司第二季度营业额相差最大。
故答案为:(1)四;(2)143;(3)二。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,再根据整数加减法的意义解决问题。
5.(2023春 黄陂区期末)看图并解答问题.
如图是小强和小刚两位同学参加800米赛跑的折线统计图.
(1)前400米,跑得快一些的是 小刚 ,比赛途中在 500 米处两人并列.
(2)跑完800米,先到达终点的是 小强 ,比另一位同学少用了 90 秒.
(3)小刚前2分钟平均每分钟跑 200 米.
【考点】复式折线统计图.
【专题】统计数据的计算与应用.
【答案】见试题解答内容
【分析】(1)由表示小强、小刚跑的路程与时间的拆线可以看出,前400米小刚的比小强跑得快一些;到500米时小强追上了小刚,二人并列.
(2)跑完800米,小强先到达终点,用时4.5分钟,小刚后到达终点,用时6分钟.小强比小刚少用6﹣4.5=1.5分钟,再乘进率60化秒.
(3)小刚前2分钟跑了400米,根据“速度=路程÷时间”即可求出小刚前2分钟平均每分钟跑的米数.
【解答】解:(1)答:前400米,跑得快一些的是小刚,比赛途中在500米处两人并列.
(2)6﹣4.5=1.5(分)
1.5分=90秒
答:跑完800米,先到达终点的是小强,比另一位同学少用了90秒.
(3)400÷2=200(米)
答:小刚前2分钟平均每分钟跑200米.
故答案为:小刚,500,小强,90,200.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
6.(2022春 郏县期中)如图是爸爸和小明在体育馆游泳情况的折线统计图。
(1)爸爸和小明都游了 50 米, 小明 先出发, 爸爸 先到达。
(2)小明所用的时间比爸爸多 15 秒。
(3)小明游到 30 米的时候速度开始慢下来,在此之前平均每秒游 1.5 米。
(4)爸爸平均每秒游 0.83 米。(得数保留两位小数)
【考点】复式折线统计图.
【专题】应用意识.
【答案】(1)50,小明,爸爸;(2)15;(3)30,1.5;(4)0.83。
【分析】(1)根据统计图可知:折线统计图中虚线代表小明的游泳情况,实线代表爸爸的游泳情况,爸爸和小明都游了50米,小明先出发,爸爸先到达。
(2)爸爸让小明先游10秒,爸爸又比小明提前5秒到达,小明所用的时间比爸爸多15秒。
(3)根据统计图可知:小明游到30米的时候速度开始慢下来,在此之前平均每秒游30÷20=1.5(米)。
(4)爸爸平均每秒游50÷60≈0.83(米)。
【解答】解:(1)爸爸和小明都游了50米,小明先出发,爸爸先到达。
(2)75﹣60=15(秒)
答:小明所用的时间比爸爸多15秒。
(3)30÷20=1.5(米)
答:小明游到30米的时候速度开始慢下来,在此之前平均每秒游1.5米。
(4)50÷60≈0.83(米)
答:爸爸平均每秒游0.83米。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
三.应用题(共4小题)
7.(2024春 宜春期末)某城市2010﹣2015年生活垃圾中分类垃圾与未分类垃圾质量如图:
(1)2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的
(2)两种垃圾相差最多的是 2010 年,从 2015 年开始分类垃圾超过了未分类垃圾.
(3)看了这幅图后你有什么感想或建议.
【考点】复式折线统计图.
【专题】统计数据的计算与应用.
【答案】见试题解答内容
【分析】(1)由复式折线统计图可以看出,2011年未分类的垃圾为12.5万吨,分类的是8万吨,垃圾总量为12.5+8=20.5(万吨),用分类垃圾的吨数除以总吨数;同理,2015年未分类的垃圾为16万吨,分类的是1万吨,垃圾总量为16+11=27(万吨),用分类垃圾的吨数除以总吨数.
(2)由复式折线统计图可以看出,表示未分类垃圾、分类垃圾的点,2010年距离最大,说明该年两种垃圾相差最多;表示分类垃圾的折线从2015年在表示未分类垃圾折线的上方,说明该年开始分类垃圾超过了未分类垃圾.
(3)垃圾分类处理的好处有:减少占地;减少污染;变废为宝;减少危害.看了这幅图感到人们的环保意识在增强,感到欣慰;建议所有垃圾能够完全分类.
【解答】解:(1)8÷(12.5+8)
=8÷20.5
11÷(16+11)
=11÷27
答:2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的.
(2)答:两种垃圾相差最多的是 2010年,从 2015年开始分类垃圾超过了未分类垃圾.
(3)答:的感想和建议:看了这幅图感到人们的环保意识在增强,感到欣慰;建议所有垃圾能够完全分类.
故答案为:2010,2015.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
8.(2024春 永吉县期末)李山和丁阳参加100米短跑训练,下面是两人每周测试成绩统计图。
(1)观察统计图,在第3周的训练中, 李山 的短跑训练成绩比较好。
(2)在第 4 周李山和丁阳的测试成绩相差最远;第 7 周两人的成绩一样。
(3)经过8周的训练,李山和丁阳的短跑训练效果怎么样?如果第9周有一场100米短跑比赛,他们两人中你会选择谁参加?请写出理由.
【考点】复式折线统计图.
【专题】数据分析观念.
【答案】(1)李山;(2)4,7。
(3)根据复式折线统计图可知,根据8周的训练结果可以看出,两个人短跑用时呈下降趋势,所以训练的效果非常明显。如果第9周有一场100米短跑比赛,会选择李山参加,因为李山的用时比较少,获胜的可能性大一些。(答案不唯一)
【分析】(1)观察统计图,在第3周的训练中,李山的短跑训练成绩比较好。
(2)在第4周李山和丁阳的测试成绩相差最远;第7周两人的成绩一样。
(3)根据复式折线统计图可知,根据8周的训练结果可以看出,两个人短跑用时呈下降趋势,所以训练的效果非常明显。如果第9周有一场100米短跑比赛,会选择李山参加,因为李山的用时比较少,获胜的可能性大一些。(答案不唯一)
【解答】解:(1)在第3周的训练中,李山的短跑训练成绩比较好。
(2)在第4周李山和丁阳的测试成绩相差最远;第7周两人的成绩一样。
(3)根据复式折线统计图可知,根据8周的训练结果可以看出,两个人短跑用时呈下降趋势,所以训练的效果非常明显。如果第9周有一场100米短跑比赛,会选择李山参加,因为李山的用时比较少,获胜的可能性大一些。(答案不唯一)
故答案为:李山;4,7。
【点评】本题主要考查复式折线统计图的应用,关键根据统计图找到解决问题的条件,解决问题。
9.(2021春 路南区期末)看统计图,完成下面各题。
①一班在四年级的时候,有近视的学生 4 人。
②二班在三年级的时候,有近视的学生 8 人。
③两个班在 五 年级的时候,近视人数相差最多,相差 9 人。
④列式并计算出四年级的时候,一班近视人数是二班近视人数的几分之几?★提示:结果要约分!
【考点】复式折线统计图.
【专题】综合题;数据分析观念.
【答案】①4;
②8;
③五,9;
④。
【分析】折线统计图横轴表示年级,纵轴表示近视人数,实线表示一班各年级时的近视人数,虚线表示二班各年级时的近视人数;
①实线四年级所对应的近视人数是4人,即一班在四年级时近视人数为4人;
②虚线三年级所对应的近视人数是8人,即二班在三年级时近视人数为8人;
③实线和虚线在五年级时相距最远,表示两个班近视人数相差最多,用两个班在五年级时的近视人数相减,就是相差多少人;
④四年级时一班近视人数4人,二班近视人数10人,求一班近视人数是二班的几分之几,用4除以10。
【解答】解:①一班在四年级的时候,有近视的学生4人;
②二班在三年级的时候,有近视的学生8人;
③14﹣5=9(人)
答:两个班在五年级的时候,近视人数相差最多,相差9人。
④4÷10
答:四年级的时候,一班近视人数是二班近视人数的。
故答案为:4;8;五,9。
【点评】此题重点考查从复式折线统计图中读取信息进行分析的能力及求一个数是另一个数的几分之几的方法。
10.(2021 温州模拟)表是某公司在A,B两地所开的分公司近几年利润情况的统计表.
年份 利润/万元 名称 2013 2014 2015 2016 2017 2018
A分公司 180 170 170 152 141 130
B分公司 75 90 100 110 115 125
(1)根据以上数据,绘制复式折线统计图.
(2) 2013 年两家分公司利润差距最大, 2018 年最小.
(3)由于产业转型,总公司打算关闭一家分公司,你认为关闭哪一家最合适?为什么?
【考点】复式折线统计图.
【专题】统计数据的计算与应用;数据分析观念;应用意识.
【答案】见试题解答内容
【分析】(1)根据折线统计图的绘制方法,先按照统计表中的数据描出各点,然后顺次连接各点完成统计图.
(2)通过观察统计图表可知,2013年两家分公司利润差最大,2018年两家分公司利润差最小.
(3)我认为关闭A分公司,因为到2018年,两家分公司利润差不多,可是A分公司利润呈下降趋势,B分公司利润呈上升趋势.据此解答.
【解答】解:(1)作图如下:
某公司在A,B两地所开的分公司近几年利润情况的统计图
(2)2013年两家分公司利润差最大,2018年两家分公司利润差最小.
(3)我认为关闭A分公司,因为到2018年,两家分公司利润差不多,可是A分公司利润呈下降趋势,B分公司利润呈上升趋势.
故答案为:2013、2018.
【点评】此题考查的目的是理解掌握折线统计图的绘制方法及应用,并且能够根据统计图表提供的信息,解决有关的实际问题.
21世纪教育网(www.21cnjy.com)
