【同步分层培优】2.2展开与折叠基础卷(含解析)-2024-2025学年五年级下册数学北师大版
文档属性
| 名称 | 【同步分层培优】2.2展开与折叠基础卷(含解析)-2024-2025学年五年级下册数学北师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 404.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-07 00:00:00 | ||
图片预览


文档简介
2.2展开与折叠
一.选择题(共3小题)
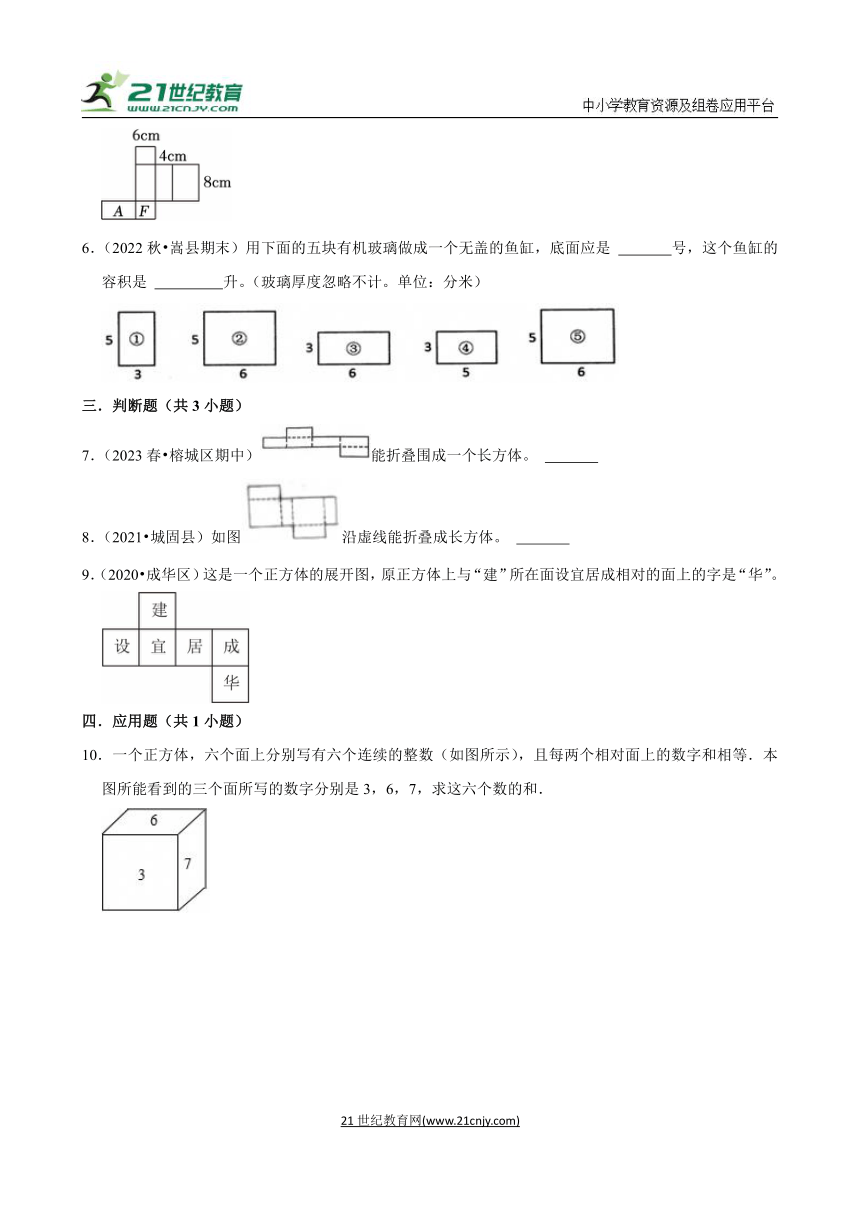
1.(2024 霞浦县)下面的图形中,能按虚线折成正方体的是( )
A. B. C. D.
2.(2024春 顺德区期末)下面图形中,( )是长方体的展开图。
A. B.
C. D.
3.(2024春 阿荣旗期末)下面( )沿虚线折叠后不能围成长方体。
A. B.
C. D.
二.填空题(共3小题)
4.(2024春 大冶市期末)如图是一个正方体的展开图.在这个正方体中,与a面相对的是 面,与b面相对的是 面.
5.(2024春 上蔡县期中)如图所示是一个长方体的展开图,如果F在前面,A在左面,那么,底面的面积是 cm2。
6.(2022秋 嵩县期末)用下面的五块有机玻璃做成一个无盖的鱼缸,底面应是 号,这个鱼缸的容积是 升。(玻璃厚度忽略不计。单位:分米)
三.判断题(共3小题)
7.(2023春 榕城区期中)能折叠围成一个长方体。
8.(2021 城固县)如图沿虚线能折叠成长方体。
9.(2020 成华区)这是一个正方体的展开图,原正方体上与“建”所在面设宜居成相对的面上的字是“华”。
四.应用题(共1小题)
10.一个正方体,六个面上分别写有六个连续的整数(如图所示),且每两个相对面上的数字和相等.本图所能看到的三个面所写的数字分别是3,6,7,求这六个数的和.
2.2展开与折叠
参考答案与试题解析
一.选择题(共3小题)
1.(2024 霞浦县)下面的图形中,能按虚线折成正方体的是( )
A. B. C. D.
【考点】正方体的展开图.
【答案】A
【分析】正方体的展开图种类1﹣4﹣1型,2﹣3﹣1型,2﹣2﹣2型,3﹣3型,只有A是2﹣3﹣1型,据此选择.
【解答】解:各选项的图形中,能按虚线折成正方体的是A,
故选:A。
【点评】此题考查正方体的展开图,记住正方体的展开图的4种类型.
2.(2024春 顺德区期末)下面图形中,( )是长方体的展开图。
A. B.
C. D.
【考点】长方体的展开图.
【专题】几何直观.
【答案】C
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的形状和大小完全相同。再根据长方体展开图的特征可知,图B、图C都属于长方体展开图的“1﹣4﹣1”结构,都能折叠成长方体;选项A不属于长方体展开图,不能折叠成长方体。据此解答。
【解答】解:根据长方体展开图的特征可知,图C都属于长方体展开图的“1﹣4﹣1”结构,其余选项不是长方体展开图。
故选:C。
【点评】此题考查的目的是理解掌握长方体的特征,特别是长方体的展开图的特征及应用。
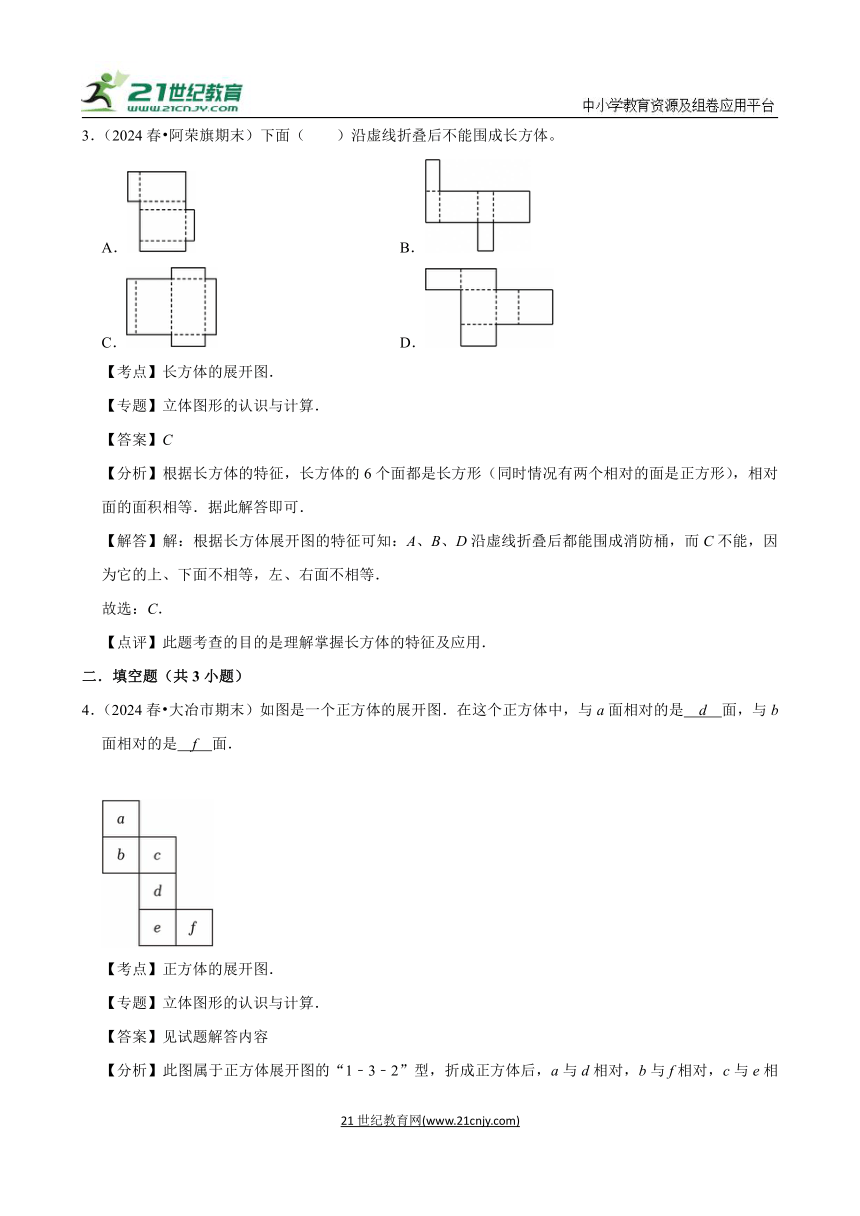
3.(2024春 阿荣旗期末)下面( )沿虚线折叠后不能围成长方体。
A. B.
C. D.
【考点】长方体的展开图.
【专题】立体图形的认识与计算.
【答案】C
【分析】根据长方体的特征,长方体的6个面都是长方形(同时情况有两个相对的面是正方形),相对面的面积相等.据此解答即可.
【解答】解:根据长方体展开图的特征可知:A、B、D沿虚线折叠后都能围成消防桶,而C不能,因为它的上、下面不相等,左、右面不相等.
故选:C.
【点评】此题考查的目的是理解掌握长方体的特征及应用.
二.填空题(共3小题)
4.(2024春 大冶市期末)如图是一个正方体的展开图.在这个正方体中,与a面相对的是 d 面,与b面相对的是 f 面.
【考点】正方体的展开图.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】此图属于正方体展开图的“1﹣3﹣2”型,折成正方体后,a与d相对,b与f相对,c与e相对.
【解答】解:如图
在这个正方体中,与a面相对的是d面,与b面相对的是f面.
故答案为:D,F.
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住,能快速解答此类题.
5.(2024春 上蔡县期中)如图所示是一个长方体的展开图,如果F在前面,A在左面,那么,底面的面积是 48 cm2。
【考点】长方体的展开图.
【专题】应用题;几何直观.
【答案】48。
【分析】如果字母A在前面,字母F在左面,那么长方体下面长8厘米、宽6厘米,利用长方形面积公式:S=ab,计算其面积即可。
【解答】解:8×6=48(平方厘米)
答:底面的面积是48cm2。
故答案为:48。
【点评】本题主要考查长方体展开图的应用,关键是根据所给信息判断哪个面是下面。
6.(2022秋 嵩县期末)用下面的五块有机玻璃做成一个无盖的鱼缸,底面应是 ③ 号,这个鱼缸的容积是 90 升。(玻璃厚度忽略不计。单位:分米)
【考点】长方体的展开图.
【专题】应用意识.
【答案】③,90。
【分析】用下面的五块有机玻璃做成一个无盖的鱼缸,底面应是③号,这个长方体的长是6分米,宽是3分米,高是5分米,由此求出它的容积即可。
【解答】解:这个长方体的底面应是③号,长是6分米,宽是3分米,高是5分米
6×3×5
=18×5
=90(平方分米)
90平方分米=90升
答:底面应是③号,这个鱼缸的容积是90升。
故答案为:③,90。
【点评】本题关键是找出底面,再根据底面的情况,找出其它面进而进行解答即可。
三.判断题(共3小题)
7.(2023春 榕城区期中)能折叠围成一个长方体。 ×
【考点】长方体的展开图.
【专题】几何直观.
【答案】×
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等,相对的四条棱长度相等;据此解答。
【解答】解:根据长方体的特征可知,上下两个长方形的宽较短,不符合长方体的特征,所以不能围成一个长方体。
不能折叠成一个长方体。所以原题干说法错误。
故答案为:×。
【点评】熟练掌握长方体的特征是解答本题的关键。
8.(2021 城固县)如图沿虚线能折叠成长方体。 √
【考点】长方体的展开图.
【专题】应用意识.
【答案】√
【分析】此图属于长方体展开图的“1﹣4﹣1”结构,沿虚线折叠能围成正方体。
【解答】解:如图:
沿虚线折叠能围成长方体,原题说法正确。
故答案为:√。
【点评】长方体展开图有11种特征,分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
9.(2020 成华区)这是一个正方体的展开图,原正方体上与“建”所在面设宜居成相对的面上的字是“华”。 √
【考点】正方体的展开图.
【专题】立体图形的认识与计算;空间观念.
【答案】√
【分析】正方体的展开图中,相对的两个面中间必须隔着一个小正方形,根据这一特点,结合题意解答即可。
【解答】解:正方体的展开图中,相对的面之间一定相隔一个正方形,
“设”与“居”是相对面;
“宜”与“成”是相对面;
“建”与“华”是相对面。
所以,原正方体上与“建”所在面设宜居成相对的面上的字是“华”;原题说法正确。
故答案为:√。
【点评】本题主要考查辨识正方体展开图的相对面。通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键。
四.应用题(共1小题)
10.一个正方体,六个面上分别写有六个连续的整数(如图所示),且每两个相对面上的数字和相等.本图所能看到的三个面所写的数字分别是3,6,7,求这六个数的和.
【考点】正方体的展开图.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】从3,6,7三个数字看出可能是2,3,4,5,6,7或3,4,5,6,7,8,因为相对面上的数字和相等,所以第一种情况必须3和6处于邻面,所以这六个数字只能是3,4,5,6,7,8,所以3与8,6与5,7与4处于对面位置.
【解答】解:由题意可知,这6个连续整数是3,4,5,6,7,8
3+4+5+6+7+8=33
答:这六个数的和是33.
【点评】解答此题的关键是根据题意求出这6个连续整数分别是多少.
21世纪教育网(www.21cnjy.com)
一.选择题(共3小题)
1.(2024 霞浦县)下面的图形中,能按虚线折成正方体的是( )
A. B. C. D.
2.(2024春 顺德区期末)下面图形中,( )是长方体的展开图。
A. B.
C. D.
3.(2024春 阿荣旗期末)下面( )沿虚线折叠后不能围成长方体。
A. B.
C. D.
二.填空题(共3小题)
4.(2024春 大冶市期末)如图是一个正方体的展开图.在这个正方体中,与a面相对的是 面,与b面相对的是 面.
5.(2024春 上蔡县期中)如图所示是一个长方体的展开图,如果F在前面,A在左面,那么,底面的面积是 cm2。
6.(2022秋 嵩县期末)用下面的五块有机玻璃做成一个无盖的鱼缸,底面应是 号,这个鱼缸的容积是 升。(玻璃厚度忽略不计。单位:分米)
三.判断题(共3小题)
7.(2023春 榕城区期中)能折叠围成一个长方体。
8.(2021 城固县)如图沿虚线能折叠成长方体。
9.(2020 成华区)这是一个正方体的展开图,原正方体上与“建”所在面设宜居成相对的面上的字是“华”。
四.应用题(共1小题)
10.一个正方体,六个面上分别写有六个连续的整数(如图所示),且每两个相对面上的数字和相等.本图所能看到的三个面所写的数字分别是3,6,7,求这六个数的和.
2.2展开与折叠
参考答案与试题解析
一.选择题(共3小题)
1.(2024 霞浦县)下面的图形中,能按虚线折成正方体的是( )
A. B. C. D.
【考点】正方体的展开图.
【答案】A
【分析】正方体的展开图种类1﹣4﹣1型,2﹣3﹣1型,2﹣2﹣2型,3﹣3型,只有A是2﹣3﹣1型,据此选择.
【解答】解:各选项的图形中,能按虚线折成正方体的是A,
故选:A。
【点评】此题考查正方体的展开图,记住正方体的展开图的4种类型.
2.(2024春 顺德区期末)下面图形中,( )是长方体的展开图。
A. B.
C. D.
【考点】长方体的展开图.
【专题】几何直观.
【答案】C
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的形状和大小完全相同。再根据长方体展开图的特征可知,图B、图C都属于长方体展开图的“1﹣4﹣1”结构,都能折叠成长方体;选项A不属于长方体展开图,不能折叠成长方体。据此解答。
【解答】解:根据长方体展开图的特征可知,图C都属于长方体展开图的“1﹣4﹣1”结构,其余选项不是长方体展开图。
故选:C。
【点评】此题考查的目的是理解掌握长方体的特征,特别是长方体的展开图的特征及应用。
3.(2024春 阿荣旗期末)下面( )沿虚线折叠后不能围成长方体。
A. B.
C. D.
【考点】长方体的展开图.
【专题】立体图形的认识与计算.
【答案】C
【分析】根据长方体的特征,长方体的6个面都是长方形(同时情况有两个相对的面是正方形),相对面的面积相等.据此解答即可.
【解答】解:根据长方体展开图的特征可知:A、B、D沿虚线折叠后都能围成消防桶,而C不能,因为它的上、下面不相等,左、右面不相等.
故选:C.
【点评】此题考查的目的是理解掌握长方体的特征及应用.
二.填空题(共3小题)
4.(2024春 大冶市期末)如图是一个正方体的展开图.在这个正方体中,与a面相对的是 d 面,与b面相对的是 f 面.
【考点】正方体的展开图.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】此图属于正方体展开图的“1﹣3﹣2”型,折成正方体后,a与d相对,b与f相对,c与e相对.
【解答】解:如图
在这个正方体中,与a面相对的是d面,与b面相对的是f面.
故答案为:D,F.
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住,能快速解答此类题.
5.(2024春 上蔡县期中)如图所示是一个长方体的展开图,如果F在前面,A在左面,那么,底面的面积是 48 cm2。
【考点】长方体的展开图.
【专题】应用题;几何直观.
【答案】48。
【分析】如果字母A在前面,字母F在左面,那么长方体下面长8厘米、宽6厘米,利用长方形面积公式:S=ab,计算其面积即可。
【解答】解:8×6=48(平方厘米)
答:底面的面积是48cm2。
故答案为:48。
【点评】本题主要考查长方体展开图的应用,关键是根据所给信息判断哪个面是下面。
6.(2022秋 嵩县期末)用下面的五块有机玻璃做成一个无盖的鱼缸,底面应是 ③ 号,这个鱼缸的容积是 90 升。(玻璃厚度忽略不计。单位:分米)
【考点】长方体的展开图.
【专题】应用意识.
【答案】③,90。
【分析】用下面的五块有机玻璃做成一个无盖的鱼缸,底面应是③号,这个长方体的长是6分米,宽是3分米,高是5分米,由此求出它的容积即可。
【解答】解:这个长方体的底面应是③号,长是6分米,宽是3分米,高是5分米
6×3×5
=18×5
=90(平方分米)
90平方分米=90升
答:底面应是③号,这个鱼缸的容积是90升。
故答案为:③,90。
【点评】本题关键是找出底面,再根据底面的情况,找出其它面进而进行解答即可。
三.判断题(共3小题)
7.(2023春 榕城区期中)能折叠围成一个长方体。 ×
【考点】长方体的展开图.
【专题】几何直观.
【答案】×
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等,相对的四条棱长度相等;据此解答。
【解答】解:根据长方体的特征可知,上下两个长方形的宽较短,不符合长方体的特征,所以不能围成一个长方体。
不能折叠成一个长方体。所以原题干说法错误。
故答案为:×。
【点评】熟练掌握长方体的特征是解答本题的关键。
8.(2021 城固县)如图沿虚线能折叠成长方体。 √
【考点】长方体的展开图.
【专题】应用意识.
【答案】√
【分析】此图属于长方体展开图的“1﹣4﹣1”结构,沿虚线折叠能围成正方体。
【解答】解:如图:
沿虚线折叠能围成长方体,原题说法正确。
故答案为:√。
【点评】长方体展开图有11种特征,分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
9.(2020 成华区)这是一个正方体的展开图,原正方体上与“建”所在面设宜居成相对的面上的字是“华”。 √
【考点】正方体的展开图.
【专题】立体图形的认识与计算;空间观念.
【答案】√
【分析】正方体的展开图中,相对的两个面中间必须隔着一个小正方形,根据这一特点,结合题意解答即可。
【解答】解:正方体的展开图中,相对的面之间一定相隔一个正方形,
“设”与“居”是相对面;
“宜”与“成”是相对面;
“建”与“华”是相对面。
所以,原正方体上与“建”所在面设宜居成相对的面上的字是“华”;原题说法正确。
故答案为:√。
【点评】本题主要考查辨识正方体展开图的相对面。通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键。
四.应用题(共1小题)
10.一个正方体,六个面上分别写有六个连续的整数(如图所示),且每两个相对面上的数字和相等.本图所能看到的三个面所写的数字分别是3,6,7,求这六个数的和.
【考点】正方体的展开图.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】从3,6,7三个数字看出可能是2,3,4,5,6,7或3,4,5,6,7,8,因为相对面上的数字和相等,所以第一种情况必须3和6处于邻面,所以这六个数字只能是3,4,5,6,7,8,所以3与8,6与5,7与4处于对面位置.
【解答】解:由题意可知,这6个连续整数是3,4,5,6,7,8
3+4+5+6+7+8=33
答:这六个数的和是33.
【点评】解答此题的关键是根据题意求出这6个连续整数分别是多少.
21世纪教育网(www.21cnjy.com)
